قضیه کوشی یا به طور دقیقتر، «قضیه مقدار میانگین کوشی» (Cauchy’s Mean Value Theorem) تعمیم قضیه مقدار میانگین لاگرانژ است. این قضیه، قضیه مقدار میانگین گسترش یافته یا دوم نیز نامیده میشود و رابطه بین مشتق دو تابع و تغییرات این توابع را در یک بازه متناهی بیان میکند.
شکل ۱: آگوستین لویی کوشی (۱۷۸۹-۱۸۵۷) قضیه کوشی
دو تابع f ( x ) f ( x ) f ( x ) g ( x ) g ( x ) g ( x ) [ a , b ] [a , b ] [ a , b ] ( a , b ) ( a , b ) ( a , b ) x ∈ ( a , b ) x \in \left( {a,b} \right) x ∈ ( a , b ) g ’ ( x ) ≠ 0 g’\left( x \right) \ne 0 g ’ ( x ) = 0 x = c x = c x = c
f ( b ) – f ( a ) g ( b ) – g ( a ) = f ’ ( c ) g ’ ( c ) . \large { \frac { { f \left ( b \right ) – f \left ( a \right ) } }{ { g \left ( b \right ) – g \left ( a \right ) } } } = { \frac { { f’ \left ( c \right ) } } { { g’ \left ( c \right ) } } . } g ( b ) – g ( a ) f ( b ) – f ( a ) = g ’ ( c ) f ’ ( c ) .
اثبات: ابتدا باید گفت که مخرج کسر سمت چپ تساوی صفر نیست: g ( b ) – g ( a ) ≠ 0 {g\left( b \right) – g\left( a \right)} \ne 0 g ( b ) – g ( a ) = 0 g ( b ) = g ( a ) {g\left( b \right) = g\left( a \right)} g ( b ) = g ( a ) قضیه رول ، نقطه d ∈ ( a , b ) d \in \left( {a,b} \right) d ∈ ( a , b ) g ’ ( d ) = 0 g’\left( {d} \right) = 0 g ’ ( d ) = 0 g ’ ( x ) ≠ 0 g’\left( x \right) \ne 0 g ’ ( x ) = 0 x ∈ ( a , b ) x \in \left( {a,b} \right) x ∈ ( a , b )
تابع کمکی زیر را معرفی میکنیم:
F ( x ) = f ( x ) + λ g ( x ) \large F \left ( x \right ) = f \left ( x \right ) + \lambda g \left ( x \right ) F ( x ) = f ( x ) + λ g ( x )
و λ \lambda λ F ( a ) = F ( b ) { F \left ( a \right ) = F \left ( b \right ) } F ( a ) = F ( b )
f ( a ) + λ g ( a ) = f ( b ) + λ g ( b ) , ⇒ f ( b ) – f ( a ) = λ [ g ( a ) – g ( b ) ] , ⇒ λ = – f ( b ) – f ( a ) g ( b ) – g ( a ) . \large \begin {align*} & f \left ( a \right ) + \lambda g \left ( a \right ) = f \left ( b \right ) + \lambda g \left ( b \right ) , \; \; \\ & \Rightarrow { f \left ( b \right ) – f \left ( a \right ) = \lambda \left [ { g \left ( a \right ) – g \left ( b \right ) } \right ] , \; \; } \\ & \Rightarrow { \lambda = – \frac { { f \left ( b \right ) – f \left ( a \right ) } }{ { g \left ( b \right ) – g \left ( a \right ) } } . } \end {align*} f ( a ) + λ g ( a ) = f ( b ) + λ g ( b ) , ⇒ f ( b ) – f ( a ) = λ [ g ( a ) – g ( b ) ] , ⇒ λ = – g ( b ) – g ( a ) f ( b ) – f ( a ) .
و تابع F ( x ) F ( x ) F ( x )
F ( x ) = f ( x ) – f ( b ) – f ( a ) g ( b ) – g ( a ) g ( x ) . \large { F \left ( x \right ) } = { f \left ( x \right ) – \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { g \left ( b \right ) – g \left ( a \right ) } } g \left ( x \right ) . } F ( x ) = f ( x ) – g ( b ) – g ( a ) f ( b ) – f ( a ) g ( x ) .
این تابع در بازه بسته [ a , b ] [ a , b ] [ a , b ] پیوسته و در بازه باز ( a , b ) ( a , b ) ( a , b ) λ \lambda λ c c c ( a , b ) ( a , b ) ( a , b )
F ’ ( c ) = 0. \large F’\left( c \right) = 0. F ’ ( c ) = 0.
بنابراین، داریم:
f ’ ( c ) − f ( b ) – f ( a ) g ( b ) – g ( a ) g ’ ( c ) = 0 \large { f’ \left ( c \right ) } - { \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { g \left ( b \right ) – g \left ( a \right ) } } g’ \left ( c \right ) = 0 } f ’ ( c ) − g ( b ) – g ( a ) f ( b ) – f ( a ) g ’ ( c ) = 0
یا
f ( b ) – f ( a ) g ( b ) – g ( a ) = f ’ ( c ) g ’ ( c ) . \large { \frac { { f \left ( b \right ) – f \left ( a \right ) } }{ { g \left ( b \right ) – g \left ( a \right ) } } } = { \frac { { f’ \left ( c \right ) } } { { g’ \left ( c \right ) } } . } g ( b ) – g ( a ) f ( b ) – f ( a ) = g ’ ( c ) f ’ ( c ) .
با قرار دادن g ( x ) = x g ( x ) = x g ( x ) = x
f ( b ) – f ( a ) b – a = f ’ ( c ) . \large \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { b – a } } = f’ \left ( c \right ) . b – a f ( b ) – f ( a ) = f ’ ( c ) .
تعبیر هندسی قضیه مقدار میانگین کوشی را نیز میتوان بیان کرد. فرض کنید منحنی γ \gamma γ x = f ( t ) x = f\left( t \right) x = f ( t ) y = g ( t ) y = g \left ( t \right ) y = g ( t ) t t t [ a , b ] [a , b ] [ a , b ] t t t A ( f ( a ) , g ( a ) ) A\left( {f\left( a \right), g\left( a \right)} \right) A ( f ( a ) , g ( a ) ) B ( f ( b ) , g ( b ) ) B\left( {f\left( b \right),g\left( b \right)} \right) B ( f ( b ) , g ( b ) )
γ \gamma γ شکل ۲: منحنی γ \gamma γ مثالهای قضیه کوشی
در این بخش، چند مثال را از قضیه کوشی حل میکنیم.
مثال ۱
تابع f ( x ) f ( x ) f ( x ) [ a , b ] [ a , b ] [ a , b ] a b > 0 a b > 0 ab > 0 c ∈ ( a , b ) c \in \left( {a,b} \right) c ∈ ( a , b )
$$ \large { \frac { 1 } { { a – b } } \left | { \begin {array} { * { 2 0 } { c } }<br />
a & b \\<br />
{ f \left ( a \right ) } & { f \left ( b \right ) }<br />
\end {array} } \right | } = { f \left ( c \right ) – c f’ \left ( c \right ) } $$
حل: از آنجا که a b > 0 a b > 0 ab > 0 [ a , b ] [ a , b ] [ a , b ] x = 0 x = 0 x = 0 F ( x ) F( x ) F ( x ) G ( x ) G ( x ) G ( x )
F ( x ) = f ( x ) x , G ( x ) = 1 x . \large { F \left ( x \right ) = \frac { { f \left ( x \right ) } }{ x } , } \; \; \; \kern-0.3pt { G \left ( x \right ) = \frac { 1 } { x } . } F ( x ) = x f ( x ) , G ( x ) = x 1 .
فرمول کوشی برای این توابع به شکل زیر نوشته میشود:
F ( b ) – F ( a ) G ( b ) – G ( a ) = F ’ ( c ) G ’ ( c ) , \large { \frac { { F \left ( b \right ) – F \left ( a \right ) } } { { G \left ( b \right ) – G \left ( a \right ) } } } = { \frac { { F’ \left ( c \right ) } } { { G’ \left ( c \right ) } } , } G ( b ) – G ( a ) F ( b ) – F ( a ) = G ’ ( c ) F ’ ( c ) ,
که در آن، x = c x = c x = c ( a , b ) ( a , b ) ( a , b )
مشتق دو تابع را محاسبه میکنیم:
F ’ ( x ) = ( f ( x ) x ) ′ = f ’ ( x ) x – f ( x ) x 2 , G ’ ( x ) = ( 1 x ) ′ = – 1 x 2 . \large { F’ \left ( x \right ) = { \left ( { \frac { { f \left ( x \right ) } } { x} } \right ) ^ \prime } = \frac { { f’ \left ( x \right ) x – f \left ( x \right ) } } { { { x ^ 2 } } } , } \; \; \; \kern-0.3pt { G’ \left ( x \right ) = { \left ( { \frac { 1 } { x } } \right ) ^ \prime } = – \frac { 1 } { { { x ^ 2 } } } . } F ’ ( x ) = ( x f ( x ) ) ′ = x 2 f ’ ( x ) x – f ( x ) , G ’ ( x ) = ( x 1 ) ′ = – x 2 1 .
با جایگذاری در فرمول کوشی، خواهیم داشت:
f ( b ) b – f ( a ) a 1 b – 1 a = c f ’ ( c ) – f ( c ) c 2 – 1 c 2 , ⇒ a f ( b ) – b f ( a ) a b a – b a b = – c f ’ ( c ) – f ( c ) c 2 1 c 2 , ⇒ a f ( b ) – b f ( a ) a – b = f ( c ) – c f ’ ( c ) \large \begin {align*} & \frac { { \frac { { f \left ( b \right ) } } { b } – \frac { { f \left ( a \right ) } } { a } } } { { \frac { 1 } { b } – \frac { 1 } { a } } } = { \frac { { \frac { { c f’ \left ( c \right ) – f \left ( c \right ) } } { { { c ^ 2 } } } } } { { – \frac { 1 } { { {c ^ 2 } } } } } , \; \; } \\ & \Rightarrow { \frac { { \frac { { a f \left ( b \right ) – b f \left ( a \right ) } } { { a b } } } } { { \frac { { a – b } } { { a b } } } } } = { – \frac { { \frac { { c f’ \left ( c \right ) – f \left ( c \right ) } }{ { { c ^ 2 } } } } } { { \frac { 1 } { { { c ^ 2 } } } } } , \; \; } \\ & \Rightarrow { \frac { { a f \left ( b \right ) – b f \left ( a \right ) } } { { a – b } } = f \left ( c \right ) – c f’ \left ( c \right ) } \end {align*} b 1 – a 1 b f ( b ) – a f ( a ) = – c 2 1 c 2 c f ’ ( c ) – f ( c ) , ⇒ ab a – b ab a f ( b ) – b f ( a ) = – c 2 1 c 2 c f ’ ( c ) – f ( c ) , ⇒ a – b a f ( b ) – b f ( a ) = f ( c ) – c f ’ ( c )
دترمینان سمت چپ تساوی به صورت زیر نوشته شده و تساوی اثبات میشود:
$$ \large { \frac { 1 } { { a – b } } \left | { \begin {array} { *{ 2 0 } { c } } a & b \\ { f \left ( a \right ) } & { f \left ( b \right ) } \end {array} } \right | } = { f \left ( c \right ) – c f’ \left ( c \right ) . } $$
مثال ۲
قضیه مقدار میانگین کوشی را برای دو تابع f ( x ) = x 4 f\left( x \right) = {x^4} f ( x ) = x 4 g ( x ) = x 2 g\left( x \right) = {x^2} g ( x ) = x 2 [ 1 , 2 ] [ 1 , 2 ] [ 1 , 2 ]
حل: مشتق این دو تابع به صورت زیر است:
f ’ ( x ) = ( x 4 ) = 4 x 3 , g ’ ( x ) = ( x 2 ) = 2 x . \large { f’ \left ( x \right ) = \left ( { { x ^ 4 } } \right ) = 4 { x ^ 3 } , } \; \; \; \kern-0.3pt { g’ \left ( x \right ) = \left ( { { x ^ 2 } } \right ) = 2 x . } f ’ ( x ) = ( x 4 ) = 4 x 3 , g ’ ( x ) = ( x 2 ) = 2 x .
توابع و مشتقهای آنها را در فرمول کوشی قرار داده و خواهیم داشت:
$$ \large \begin {align*}<br />
\require {cancel} & { \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { g \left ( b \right ) – g \left ( a \right ) } } = \frac { { f’ \left ( c \right ) } } { { g’ \left ( c \right ) } } , \; \; } \Rightarrow { \frac { { { b ^ 4 } – { a ^ 4 } } } { { { b ^ 2 } – { a ^ 2 } } } = \frac { { 4 { c ^ 3 } } } { { 2 c } } , \; \; } \\ & \Rightarrow { \frac { { \cancel { \left ( { { b ^ 2 } – { a ^ 2 } } \right ) } \left ( { { b ^ 2 } + { a ^ 2 } } \right ) } } { \cancel { { b ^ 2 } – { a ^ 2 } } } = 2 { c ^ 2 } , \; \; } \Rightarrow { { c ^ 2 } = \frac { { { a ^ 2 } + { b ^ 2 } } }{ 2 } , \; \; } \\ & \Rightarrow { c = \pm \sqrt { \frac { { { a ^ 2 } + { b ^ 2 } } } { 2 } } . }<br />
\end {align*} $$
با در نظر گرفتن مرزهای a = 1 a = 1 a = 1 b = 2 b = 2 b = 2
c = ± 1 2 + 2 2 2 = ± 5 2 ≈ ± 1.58. \large { c = \pm \sqrt { \frac { { { 1 ^ 2 } + { 2 ^ 2 } } } { 2 } } } = { \pm \sqrt { \frac { 5 } { 2 } } \approx \pm 1.58.} c = ± 2 1 2 + 2 2 = ± 2 5 ≈ ± 1.58.
در اینجا، مقدار مثبت c = 5 2 ≈ 1.58 c = \sqrt {\large\frac{5}{2}\normalsize} \approx 1.58 c = 2 5 ≈ 1.58
بدیهی است که این عدد در بازه ( 1 , 2 ) ( 1 , 2 ) ( 1 , 2 )
مثال ۳
قضیه کوشی را برای دو تابع f ( x ) = x 3 f\left( x \right) = {x^3} f ( x ) = x 3 g ( x ) = arctan x g\left( x \right) = \arctan x g ( x ) = arctan x [ 0 , 1 ] [ 0 , 1 ] [ 0 , 1 ]
حل: ابتدا مشتق دو تابع را مینویسیم:
f ’ ( x ) = ( x 3 ) ′ = 3 x 2 , g ’ ( x ) = ( arctan x ) ′ = 1 1 + x 2 . \large { f’ \left ( x \right ) = { \left ( { { x ^ 3 } } \right ) ^ \prime } = 3 { x ^ 2 } , } \; \; \; \kern-0.3pt { g’ \left ( x \right ) = { \left ( { \arctan x } \right ) ^ \prime } = \frac { 1 } { { 1 + { x ^ 2 } } } . } f ’ ( x ) = ( x 3 ) ′ = 3 x 2 , g ’ ( x ) = ( arctan x ) ′ = 1 + x 2 1 .
توابع f ( x ) f ( x ) f ( x ) g ( x ) g ( x ) g ( x )
f ( b ) – f ( a ) g ( b ) – g ( a ) = f ’ ( c ) g ’ ( c ) , ⇒ b 3 – a 3 arctan b – arctan a = 3 c 2 1 1 + c 2 , ⇒ b 3 – a 3 arctan b – arctan a = 1 + c 2 3 c 2 . \large \begin {align*} & \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { g \left ( b \right ) – g \left ( a \right ) } } = \frac { { f’ \left ( c \right ) } } { { g’ \left ( c \right ) } } , \; \; \Rightarrow { \frac { { { b ^ 3 } – { a ^ 3 } } } { { \arctan b – \arctan a } } = \frac { { 3 { c ^ 2 } } } { { \frac { 1 } { { 1 + { c ^ 2 } } } } } , \; \; } \\ & \Rightarrow { \frac { { { b ^ 3 } – { a ^ 3 } } } { { \arctan b – \arctan a } } = \frac { { 1 + { c ^ 2 } } } { { 3 { c ^ 2 } } } . } \end {align*} g ( b ) – g ( a ) f ( b ) – f ( a ) = g ’ ( c ) f ’ ( c ) , ⇒ arctan b – arctan a b 3 – a 3 = 1 + c 2 1 3 c 2 , ⇒ arctan b – arctan a b 3 – a 3 = 3 c 2 1 + c 2 .
برای a = 0 a = 0 a = 0 b = 1 b = 1 b = 1
1 3 – 0 3 arctan 1 – arctan 0 = 1 + c 2 3 c 2 , ⇒ 1 – 0 π 4 – 0 = 1 + c 2 3 c 2 , ⇒ 4 π = 1 + c 2 3 c 2 , ⇒ 12 c 2 = π + π c 2 , ⇒ ( 12 – π ) c 2 = π , ⇒ c 2 = π 12 – π , ⇒ c = ± π 12 – π . \large \begin {align*} & \frac { { { 1 ^ 3 } – { 0 ^ 3 } } } { { \arctan 1 – \arctan 0 } } = \frac { { 1 + { c ^ 2 } } } { { 3 { c ^ 2 } } } , \; \; \Rightarrow { \frac { { 1 – 0 } } { { \frac { \pi } { 4 } – 0 } } = \frac { { 1 + { c ^ 2 } } } { { 3 { c ^ 2 } } } , \; \; } \\\ & \Rightarrow { \frac { 4 } { \pi } = \frac { { 1 + { c ^ 2 } } } { { 3 { c ^ 2 } } } , \; \; } \Rightarrow { 1 2 { c ^ 2 } = \pi + \pi { c ^ 2 } , \; \; } \Rightarrow { \left ( { 1 2 – \pi } \right ){ c ^ 2 } = \pi , \; \; } \\ & \Rightarrow { { c ^ 2 } = \frac { \pi }{ { 1 2 – \pi } } , \; \; } \Rightarrow { c = \pm \sqrt { \frac { \pi } { { 1 2 – \pi } } } . } \end {align*} arctan 1– arctan 0 1 3 – 0 3 = 3 c 2 1 + c 2 , ⇒ 4 π –0 1–0 = 3 c 2 1 + c 2 , ⇒ π 4 = 3 c 2 1 + c 2 , ⇒ 12 c 2 = π + π c 2 , ⇒ ( 12– π ) c 2 = π , ⇒ c 2 = 12– π π , ⇒ c = ± 12– π π .
از آنجا که بازه [ 0 , 1 ] [ 0 , 1 ] [ 0 , 1 ] c c c c c c ( 0 , 1 ) ( 0 , 1 ) ( 0 , 1 )
c = π 12 – π ≈ 3.14 8.86 ≈ 0.60. \large { c = \sqrt { \frac { \pi } { { 1 2 – \pi } } } } { \approx \sqrt { \frac { { 3 . 1 4 } } { { 8 . 8 6 } } } \approx 0 . 6 0 . } c = 12– π π ≈ 8.86 3.14 ≈ 0.60.
در نتیجه، قضیه مقدار میانگین کوشی بری توابع و بازه داده شده برقرار است.
مثال ۴
قضیه کوشی را برای دو تابع f ( x ) = cos x f\left( x \right) = \cos x f ( x ) = cos x g ( x ) = sin x g\left( x \right) = \sin x g ( x ) = sin x [ a , b ] [ a , b ] [ a , b ]
حل: فرمول کوشی برای این توابع به صورت زیر نوشته میشود:
f ( b ) – f ( a ) g ( b ) – g ( a ) = f ’ ( c ) g ’ ( c ) , ⇒ cos b – cos a sin b – sin a = ( cos c ) ′ ( sin c ) ′ , ⇒ cos b – cos a sin b – sin a = – sin c cos c = − tan c , \large \begin {align*} & \frac { { f \left ( b \right ) – f \left ( a \right ) } } { { g \left ( b \right ) – g \left ( a \right ) } } = \frac { { f’ \left ( c \right ) } } { { g’ \left ( c \right ) } } , \; \; \Rightarrow { \frac { { \cos b – \cos a } } { { \sin b – \sin a } } = \frac { { { { \left ( { \cos c } \right ) } ^ \prime } } } { { { { \left ( { \sin c } \right ) } ^ \prime } } } , \; \; } \\ & \Rightarrow { \frac { { \cos b – \cos a } } { { \sin b – \sin a } } = – \frac { { \sin c } } { { \cos c } } } = { - \tan c , } \end {align*} g ( b ) – g ( a ) f ( b ) – f ( a ) = g ’ ( c ) f ’ ( c ) , ⇒ sin b – sin a cos b – cos a = ( sin c ) ′ ( cos c ) ′ , ⇒ sin b – sin a cos b – cos a = – cos c sin c = − tan c ,
که در آن، نقطه c c c ( a , b ) ( a , b ) ( a , b )
با استفاده از اتحادهای جمع به ضرب مثلثاتی، داریم:
$$ \large \begin {align*}<br />
\require {cancel} & { \frac { { – \cancel { 2 } \sin \frac { { b + a } } { 2 } \cancel { \sin \frac { { b – a } } { 2 } } } } { { \cancel { 2 } \cos \frac { { b + a } } { 2 } \cancel { \sin \frac { { b – a } } { 2 } } } } = – \tan c , \; \; } \Rightarrow { - \tan \frac { { a + b } } { 2 } = – \tan c , \; \; } \\ & \Rightarrow { c = \frac { { a + b } } { 2 } + \pi n , \; n \in Z . }<br />
\end {align*} $$
با توجه به مسئله، میخواهیم جواب را در n = 0 n = 0 n = 0
c = a + b 2 . \large c = \frac { { a + b } } { 2 } . c = 2 a + b .
همانطور که میبینیم، c c c ( a , b ) ( a , b ) ( a , b )
جواب بالا تنها در صورتی صحیح است که a a a b b b
{ cos b + a 2 ≠ 0 sin b – a 2 ≠ 0 , ⇒ { b + a 2 ≠ π 2 + π n b – a 2 ≠ π k , ⇒ { a + b ≠ π + 2 π n b – a ≠ 2 π k , ⇒ { a ≠ π 2 + π n b ≠ π 2 + π k , \large \begin {align*} & { \left \{ \begin {array} { l } \cos \frac { { b + a } } { 2 } \ne 0 \\ \sin \frac { { b – a } } { 2 } \ne 0 \end {array} \right. , \; \; } \Rightarrow { \left \{ \begin {array} { l } \frac { { b + a } } { 2 } \ne \frac { \pi } { 2 } + \pi n \\ \frac { { b – a } } { 2 } \ne \pi k \end {array} \right. , \; \; } \\ & \Rightarrow { \left \{ \begin {array} { l } a + b \ne \pi + 2 \pi n \\ b – a \ne 2 \pi k \end {array} \right. , \; \; } \Rightarrow { \left \{ \begin {array} { l } a \ne \frac { \pi } { 2 } + \pi n \\ b \ne \frac { \pi } { 2 } + \pi k \end {array} \right . , } \end {align*} { cos 2 b + a = 0 sin 2 b – a = 0 , ⇒ { 2 b + a = 2 π + πn 2 b – a = πk , ⇒ { a + b = π + 2 πn b – a = 2 πk , ⇒ { a = 2 π + πn b = 2 π + πk ,
که در آن، n , k ∈ Z n, k \in \mathbb{Z} n , k ∈ Z
مثال ۵
نشان دهید به ازای x ≠ 0 x \neq 0 x = 0
1 – x 2 2 < cos x \large 1 – \frac { { { x ^ 2 } } } { 2 } \lt \cos x 1– 2 x 2 < cos x
حل: توابع زیر را در نظر میگیریم:
f ( x ) = 1 – cos x , g ( x ) = x 2 2 \large { f \left ( x \right ) = 1 – \cos x , } \; \; \; \kern-0.3pt { g \left ( x \right ) = \frac { { { x ^ 2 } } } { 2 } } f ( x ) = 1– cos x , g ( x ) = 2 x 2
و فرمول کوشی را در بازه [ 0 , x ] [ 0 , x ] [ 0 , x ]
f ( x ) – f ( 0 ) g ( x ) – g ( 0 ) = f ’ ( ξ ) g ’ ( ξ ) , ⇒ 1 – cos x – ( 1 – cos 0 ) x 2 2 – 0 = sin ξ ξ , ⇒ 1 – cos x x 2 2 = sin ξ ξ , \large \begin {align*} & \frac { { f \left ( x \right ) – f \left ( 0 \right ) } } { { g \left ( x \right ) – g \left ( 0 \right ) } } = \frac { { f’ \left ( \xi \right ) } } { { g’ \left ( \xi \right ) } } , \; \; \\ & \Rightarrow { \frac { { 1 – \cos x – \left ( { 1 – \cos 0 } \right ) } }{ { \frac { { { x ^ 2 } } } { 2 } – 0 } } = \frac { { \sin \xi } } { \xi } , \; \; } \\ & \Rightarrow { \frac { { 1 – \cos x } } { { \frac { { { x ^ 2 } } } { 2 } } } = \frac { { \sin \xi } } { \xi } , } \end {align*} g ( x ) – g ( 0 ) f ( x ) – f ( 0 ) = g ’ ( ξ ) f ’ ( ξ ) , ⇒ 2 x 2 –0 1– cos x – ( 1– cos 0 ) = ξ sin ξ , ⇒ 2 x 2 1– cos x = ξ sin ξ ,
که ξ \xi ξ ( 0 , 1 ) ( 0 , 1 ) ( 0 , 1 )
عبارت sin ξ ξ {\large\frac{{\sin \xi }}{\xi }\normalsize} ξ sin ξ ξ ≠ 0 ) {\xi \ne 0} ) ξ = 0 ) ξ \xi ξ طول کمان حاصل از زاویه ξ \xi ξ دایره واحد است و sin ξ \sin \xi sin ξ O M OM OM y y y
1 – cos x x 2 2 = sin ξ ξ < 1 , ⇒ 1 – cos x < x 2 2 ⇒ 1 – x 2 2 < cos x . \large { \frac { { 1 – \cos x } } { { \frac { { { x ^ 2 } }} { 2 } } } = \frac { { \sin \xi } } { \xi } \lt 1 , \; \; } \Rightarrow { 1 – \cos x \lt \frac { { { x ^ 2 } } } { 2 } \; \; } \Rightarrow { 1 – \frac { { { x ^ 2 } } } { 2 } \lt \cos x . } 2 x 2 1– cos x = ξ sin ξ < 1 , ⇒ 1– cos x < 2 x 2 ⇒ 1– 2 x 2 < cos x .
شکل ۳: دایره واحد اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^
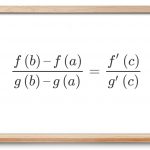
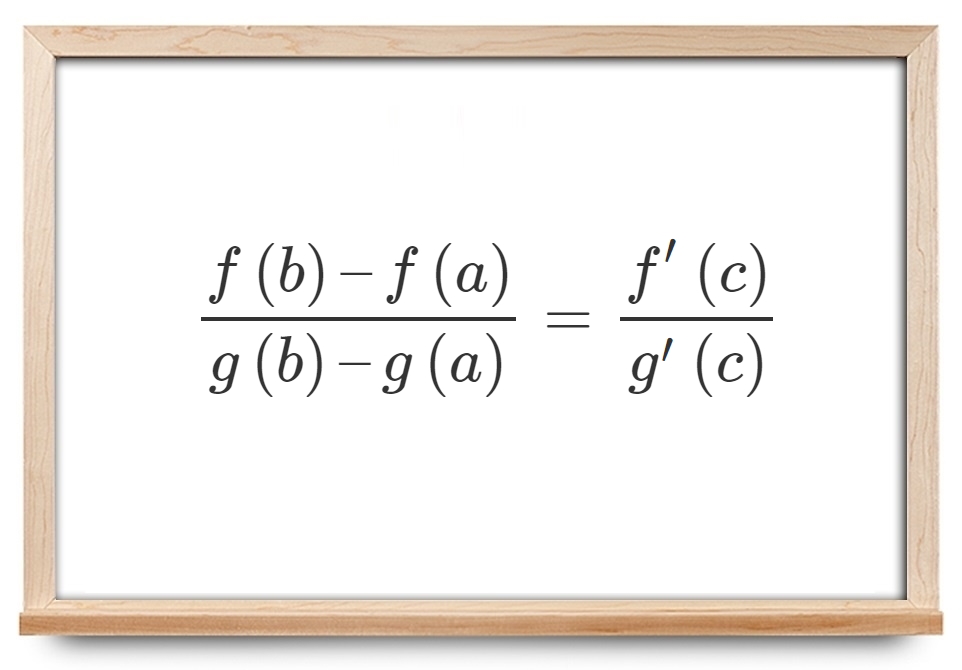

 " width="394" height="374">
" width="394" height="374">













لطفاً اثبات قضیه ریس انجام شود
با سلام و تشکر از شما . خیلی عالی است که اینطور تخصصی وارد موضوع مهجور آموزش شده اید واقعا باید دست مریزاد گفت . فقط به نویسنده ی عزیز مقاله یاداوری می کنم نام توابع و خروجی توابع دو چیز متفاوتند . باید بگوییم تابع f نه تابع f(x) . در واقع اشتباه بکار بردن این دو بجای هم همانقدر اشتباه است که چرخ گوشت و گوشت چرخکرده را به جای هم استفاده کنیم.
سلام.
از توجه و دلگرمیتان بسیار خوشحال و سپاسگزاریم.
این نوع نگارش در ریاضیات معمول و تأکیدی بر متغیر مستقل بودن x است.
در مثالتان، چرخگوشت نیز در اصل چرخی است که اغلب گوشت را چرخ میکند. اما چنین رایج شده که به آن چرخگوشت میگوییم. رابطه x و گوشت نیز چنین است.
سالم و سربلند باشید.