قضیه کارنو – به زبان ساده

همان‌طور که می‌دانید، بیان‌ کلوین -- پلانک و کلازیوس از قانون دوم ترمودینامیک، نشان می‌دهد عملکرد دستگاه‌هایی که به صورت چرخه‌ای کار می‌کنند، با محدودیت مواجه است. یک موتور گرمایی نمی‌تواند فقط با یک منبع گرما تبادل حرارت داشته باشد و یک یخچال قادر نخواهد بود بدون دریافت انرژی به صورت کار، انرژی گرمایی را از منبع سرد به منبع گرم انتقال دهد. قانون دوم ترمودینامیک، نتایج ارزشمندی به همراه دارد. دو مورد از نتایج این قانون، تحت عنوان قضیه کارنو شناخته می‌شود. قضیه کارنو در ارتباط با راندمان حرارتی موتورهای گرمایی در حالت برگشت‌پذیر و برگشت‌ناپذیر تعریف می‌شود.

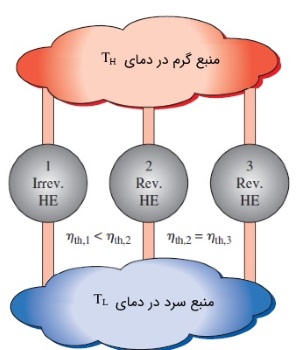
1. اگر یک موتور گرمایی برگشت‌پذیر و یک موتور گرمایی برگشت‌ناپذیر، هر دو بین دو منبع گرمایی یکسان کار کنند، راندمان موتور برگشت‌ناپذیر همیشه کمتر خواهد بود.
2. راندمان تمام موتورهای برگشت‌پذیری که بین دو منبع گرمایی یکسان کار می‌کنند، با یکدیگر برابر است.

اثبات اولین قضیه کارنو

برای اثبات دو مورد بالا، کافیست تا نشان دهیم نقض هریک از آنها، قانون دوم ترمودینامیک را نیز نقض خواهد کرد. برای اثبات جمله اول، شکل زیر را در نظر بگیرید. دو موتور گرمایی بین منابع گرمایی یکسان قرار گرفته‌اند. به هر دو موتور، مقدار $$\large Q_H$$ برابری منتقل شده است.

فیلم آموزش ترمودینامیک 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

میزان کار تولید شده توسط موتور گرمایی برگشت‌پذیر را با $$\large W_{\text {rev}}$$ و مقدار کار خروجی موتور گرمایی برگشت‌ناپذیر را با $$\large W_{\text {irrev}}$$ نشان می‌دهیم.

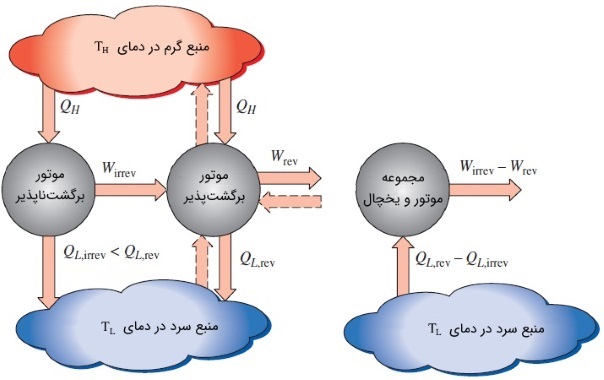
ابتدا فرض می‌کنیم نقیض اولین قضیه کارنو برقرار باشد. به این ترتیب، موتور گرمایی برگشت‌ناپذیر، نسبت به موتور گرمایی برگشت‌پذیر، راندمان بیشتری دارد و رابطه زیر برقرار است.

$$\large \eta_ {\text {th, irrev}} \:>\: \eta_ {\text {th, rev}}$$

از این رو، کار تولید شده توسط موتور برگشت‌ناپذیر هم بیشتر از کار تولید شده توسط رقیبش خواهد بود. اکنون، چرخه موتور گرمایی برگشت‌پذیر را معکوس می‌کنیم تا به یک یخچال تبدیل شود. این یخچال، کار ورودی $$\large W_{\text {rev}}$$ را دریافت کرده و انرژی گرمایی را به منبع گرم منتقل می‌کند. از آنجایی که در این حالت، یخچال مقدار گرمایی برابر با $$\large Q_H$$ را به منبع گرم تحویل می‌دهد و موتور گرمایی برگشت‌ناپذیر نیز همان مقدار گرما را از منبع دریافت می‌کند، انتقال حرارت خالص با این منبع صفر است. بنابراین، انرژی گرمایی $$\large Q_H$$ مستقیماً از یخچال به موتور گرمایی برگشت‌ناپذیر منتقل می‌شود و می‌توانیم منبع گرم را حذف کنیم.

حالا یخچال و موتور گرمایی برگشت‌ناپذیر را به عنوان یک مجموعه در هم ادغام می‌کنیم. در نتیجه، موتوری داریم که کار خالصی برابر با $$\large W_{\text {irrev}} - W_{\text {rev}}$$ تولید می‌کند و فقط با یک منبع گرما به تبادل حرارت می‌پردازد. این موضوع دقیقاً با قانون دوم ترمودینامیک به بیان کلوین -- پلانک متناقض است. بنابراین فرض اولیه ($$\large \eta_ {\text {th, irrev}} > \eta_ {\text {th, rev}}$$) باطل خواهد بود. می‌توانیم این‌گونه نتیجه‌گیری کنیم که هیچ‌یک از انواع موتورهای گرمایی قادر نخواهند بود به راندمانی بالاتر از راندمان موتور گرمایی برگشت‌پذیر که بین همان دو منبع کار می‌کند، دست یابد.

اثبات دومین قضیه کارنو

دومین قضیه کارنو نیز به طریقی مشابه با آنچه گفته شد، قابل اثبات است. این بار موتور برگشت‌ناپذیر را با یک موتور برگشت‌پذیر دیگر جایگزین می‌کنیم که راندمان بالاتری دارد و قادر است نسبت به موتور برگشت‌پذیر اول، کار بیشتری تولید کند. با دنبال کردن همان روندی که پیش‌تر ارائه شد، در نهایت به یک موتور گرمایی می‌رسیم که با وجود تبادل حرارت با تنها یک منبع گرمایی، کار خروجی تولید می‌کند.

فیلم آموزش مخلوط های گازی در ترمودینامیک 2 (رایگان) در فرادرس

کلیک کنید

به این ترتیب این مورد هم قانون دوم ترمودینامیک را نقض می‌کند و چنین فرضی باطل است. در نتیجه، موتور گرمایی برگشت‌پذیری وجود ندارد که راندمان حرارتی آن نسبت به یک موتور برگشت‌پذیر دیگر که بین همان دو منبع گرمایی کار می‌کند، بیشتر باشد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• آموزش ترمودینامیک 2
• ترمودینامیک — از صفر تا صد
• فرآیند آدیاباتیک — به زبان ساده
• فرآیند احتراق یا سوختن — از صفر تا صد
• تعریف گرما و دما در ترمودینامیک — به زبان ساده

^^