سیم پیچ (Solenoid) — به زبان ساده

در مقاله «ظرفیت خازن -- یادگیری با مثال» با تعریف و فیزیک خازن آشنا شدیم. دیدیم که خازن در ساده‌ترین حالت ساختاری صفحه‌ای داشته که به واسطه جمع شدن بارهای الکتریکی روی دو صفحه مذکور، می‌تواند میدان الکتریکی یکنواختی را بین صفحات خود ایجاد کند. در خصوص میدان مغناطیسی چطور؟ آیا ساختاری وجود دارد که بتوان با آن میدان مغناطیسی یکنواخت به وجود آورد؟ پاسخ مثبت است، به وسیله یک سیم پیچ (Solenoid) می‌توان میدان مغناطیسی یکنواخت را ایجاد کرد.

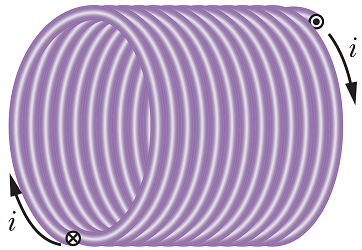
در ادامه این مقاله با ما همراه باشید تا با زبانی ساده بیشتر به معرفی و بررسی ساختار سیم پیچ بپردازیم.

سیم پیچ (Solenoid)

شکل زیر ساختاری از یک سیم پیچ کوتاه را نشان می‌دهد که جریان الکتریکی یکنواخت $$I$$ از آن عبور می‌کند. همان‌طور که از واژه سیم پیچ برمی‌آید، سیم پیچ ساختاری است که از پیچانده شدن یک سیم حاصل می‌شود.

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

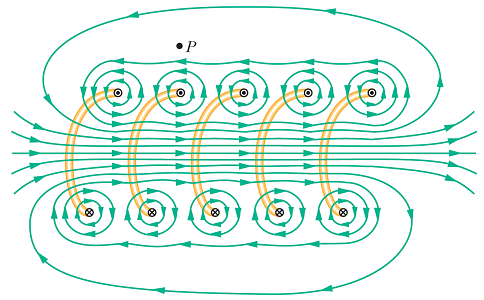
در مقاله «میدان مغناطیسی جریان -- به زبان ساده» با میدان مغناطیسی حاصل از جریان الکتریکی آشنا شدیم. همان‌طور که مشاهده می‌کنید، به واسطه عبور جریان الکتریکی از سیم پیچ، میدان مغناطیسی در نزدیکی هر قسمت از سیم به وجود آمده و به صورت دایره‌وار اطراف سیم را احاطه کرده است. همان‌طور که می‌دانید، برآیند میدان مغناطیسی کل در یک نقطه، حاصل جمع برداری همه میدان‌های مغناطیسی ناشی از تمامی قسمت‌های سیم پیچ است.

مطابق با شکل، می‌توان دید که در داخل سیم پیچ، میدان مغناطیسی ناشی از جریان بالا و پایین سیم پیچ (جریان گذرنده از هر جزء طولی سیم پیچ)، مولفه‌هایی به سمت راست دارند. در نتیجه میدان مغناطیسی برآیند (کل) در داخل سیم پیچ زیاد است. در خارج از سیم پیچ، جهت میدان مغناطیسی ناشی از جریان‌ بالا و پایین سیم پیچ در خلاف یکدیگر بوده که در نتیجه بردار میدان مغناطیسی حاصل از آن‌ها نیز در خلاف جهت یکدیگر است. در نتیجه میدان مغناطیسی برآیند (کل) در خارج از سیم پیچ ضعیف‌تر از میدان داخل آن می‌شود. مطابق با شکل (۲)، میدان مغناطیسی در خارج از سیم پیچ به سمت چپ است.

حال ساختاری مشابه با شکل (۲) را تصور کنید که طولی بلند‌تر داشته و سیم‌های آن به یکدیگر نزدیک‌تر (فشرده‌تر) باشند. چنین ساختاری را سیم پیچ بلند یا سیم لوله می‌نامند (شکل ۱). با بلند‌تر شدن طول سیم پیچ می‌توان دید که برآیند میدان مغناطیسی در خارج از آن کاهش پیدا می‌کند. در اینجا فرض می‌کنیم که طول سیم پیچ یا سیم لوله بیشتر از قطر آن باشد. بنابراین برای یک سیم پیچ بلند یا سیم لوله آرمانی که طول آن زیاد است، می‌توان برآیند میدان مغناطیسی را در خارج از آن صفر تقریب زد. در این حالت میدان مغناطیسی در داخل سیم پیچ در راستای محور سیم پیچ است.

حال شکل زیر را در نظر بگیرید. شکل زیر برشی از وجه طولی یک سیم پیچ طولانی است که میدان مغناطیسی تنها در داخل آن وجود دارد. در ادامه می‌خواهیم توسط قانون آمپر به بررسی ساختار مذکور بپردازیم. جهت آشنایی با قانون آمپر و تعمیم آن توسط ماکسول، به مقاله «قانون آمپر -- به زبان ساده» مراجعه کنید.

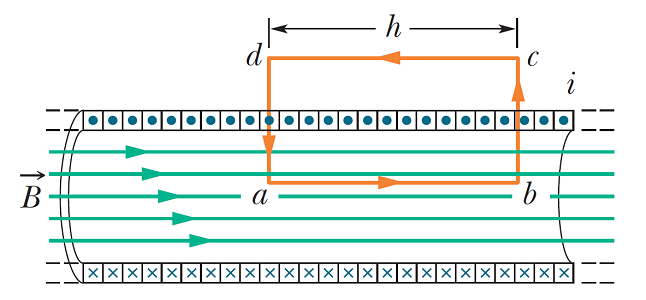
همان‌طور که در شکل فوق مشخص است، حلقه آمپر فرض شده، به شکل یک مستطیل است. به عبارت دیگر، انتگرال خطی $$\oint \overrightarrow{B} . d\overrightarrow{l}$$ مطابق با شکل فوق باید مسیر بسته $$abcda$$ را طی کند. پس طبق قانون آمپر داریم:

$$\large \oint \overrightarrow{B} . d\overrightarrow{l} = \mu_{0} i_{enc}$$

$$\large \oint \overrightarrow{B} . d\overrightarrow{l} = \int_{a}^{b} \overrightarrow{B} . d\overrightarrow{l} + \int_{b}^{c} \overrightarrow{B} . d\overrightarrow{l} +\int_{c}^{d} \overrightarrow{B} . d\overrightarrow{l} +\int_{d}^{a} \overrightarrow{B} . d\overrightarrow{l} = \int_{a}^{b} \overrightarrow{B} . d\overrightarrow{l} = B h$$

انتگرال اول از سمت چپ طرف راست تساوی برابر با $$Bh$$ می‌شود که در آن $$h$$ طول حلقه آمپر مستطیلی است. انتگرال‌های دوم و چهارم نیز به دلیل اینکه جزء دیفرانسیلی طول $$dl$$ بر میدان مغناطیسی $$B$$ عمود است، صفر است. انتگرال خطی سوم که مسیر $$cd$$ را می‌پیماید نیز به دلیل اینکه سیم پیچ را بسیار بلند (آرمانی) فرض کردیم، صفر می‌شود. چرا که میدان مغناطیسی در خارج از سیم پیچ آرمانی صفر است. در نتیجه حاصل انتگرال فوق، برابر با مقدار زیر می‌شود:

$$\large \oint \overrightarrow{B} . d\overrightarrow{l} = B h = \mu_{0} i_{enc}$$

در رابطه فوق، $$i_{enc}$$ جریان خالصی است که حلقه بسته‌ آمپر آن را در بر می‌گیرد. با توجه به شکل، بدیهی است که جریان $$i_{enc}$$ برابر با جریان $$i$$ که از هر دور سیم پیچ گذر می‌کند، نیست. مطابق با شکل (۳)، حلقه مستطیلی آمپر، بیش از ۱ دور سیم را احاطه کرده است. حال اگر فرض کنیم که سیم پیچ از $$n$$ دور سیم پیچانده شده تشکیل شده باشد ($$n$$ تعداد دورهای سیم پیچ در واحد طول)، در این صورت حلقه آمپر تعداد $$nh$$ دور از سیم پیچ را در بر می‌گیرد. پس جریان $$i_{enc}$$ برابر با مقدار زیر می‌شود:

$$\large i_{enc} = inh$$

با توجه به رابطه فوق، میدان مغناطیسی درون سیم پیچ یا سیم لوله آرمانی به شکل زیر نتیجه می‌شود:

$$\large B h = i n h$$

$$\large \Rightarrow B = \mu_{0} i n$$

رابطه فوق که برای یک سیم پیچ آرمانی با طول بی‌نهایت نتیجه شد، برای سیم پیچ یا سیم لوله واقعی نیز با تقریب خیلی خوبی جوابگو است. دقت داشته باشید که رابطه فوق تنها برای مشخص کردن میدان مغناطیسی در داخل سیم پیچ به کار می‌رود. طبق رابطه فوق، میدان مغناطیسی درون سیم پیچ به طول یا قطر سیم پیچ بستگی نداشته که این امر با تجربه نیز همخوانی دارد. همچنین از آنجایی که جریان $$i$$ را ثابت فرض کردیم، میدان مغناطیسی درون سیم پیچ ثابت است. با توجه به این امر، با استفاده از جریانی ثابت و یک سیم پیچ بلند در محیط آزمایشگاهی می‌توانیم میدان مغناطیسی یکنواخت را تولید کنیم.

چنبره (Toroid)

به بیانی ساده، اگر یک سیم پیچ یا سیم لوله را به شکل یک دایره، مطابق با شکل زیر خم کنیم، توانسته‌ایم یک چنبره (Toroid) بسازیم. چنبره شکلی همانند یک دونات داشته که شعاع داخلی آن را $$a$$ و شعاع خارجی آن را $$b$$ می‌نامیم.

شکل (۵) نمایی از بالا را از یک چنبره نشان می‌دهد. به جهت‌های جریان الکتریکی (به سمت داخل کاغذ با علامت $$\circledcirc$$) و (به سمت خارج از کاغذ با علامت $$\otimes$$) توجه کنید. تقارن در شکل (۵) ایجاب می‌کند که خطوط میدان مغناطیسی درون یک چنبره دایروی باشند. از آنجایی که میدان مغناطیسی در چنبره نیز یکنواخت است (روی هر خط رنگی در شکل)، می‌توانیم انتگرال خطی را مطابق با یک حلقه آمپری دایروی محاسبه کنیم.

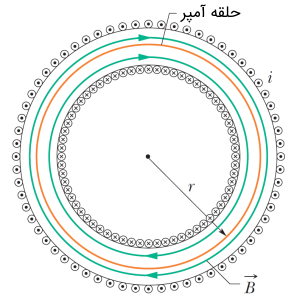
با فرض کردن حلقه آمپری دایروی به شعاع $$r$$ با شرط ($$a < r <b$$) در قانون آمپر داریم:

$$\large \oint \overrightarrow{B} . d \overrightarrow{l} = \mu_{0} i N \Rightarrow B 2 \pi r = \mu_{0} i N$$

فیلم آموزش فیزیک ۲ دانشگاه در فرادرس

کلیک کنید

در رابطه فوق، $$i$$ جریان الکتریکی گذرنده از سیم پیچ چنبره و $$N$$ تعداد کل دورهای سیم پیچ چنبره است. با تنها کردن میدان مغناطیسی از رابطه فوق داریم:

$$\large B = \frac{ \mu_{0} i N }{ 2 \pi } \frac{ 1 }{ r }$$

از رابطه فوق مشخص است که میدان مغناطیسی $$B$$ تنها در شعاع ثابتی از $$r$$ یکنواخت است. همچنین بدیهی است که میدان مغناطیسی تنها برای مقادیر $$r$$ بین دو شعاع داخلی $$a$$ و خارجی $$b$$ وجود دارد. به عبارت دیگر برای حلقه‌های آمپری $$r < a$$ به دلیل اینکه هیچ جریانی توسط حلقه محصور نمی‌شود، میدان مغناطیسی صفر است. در شعاع‌های $$r > b$$ نیز همان مقدار جریان که از حلقه آمپری خارج می‌شود، توسط‌ سیم‌های خارجی به آن وارد می‌شود. در نتیجه برآیند جریان صفر شده و از همین رو میدان مغناطیسی نیز صفر می‌شود. در اینجا فرض شده است که یک سیم پیچ آرمانی به شکل چنبره در آمده است. با این اوصاف رابطه به دست آمده را برای سیم پیج چنبره‌ای واقعی نیز می‌توان به کار برد.

با استفاده از قانون دست راست می‌توانیم جهت میدان مغناطیسی را به دست آوریم. اگر چنبره را در دست راست خود بگیریم به گونه‌ای که انگشتان دست در جهت جریان گذرنده از چنبره باشند، انگشت شست کشیده شده جهت میدان مغناطیسی را نشان می‌دهد.

مثال

سیم‌پیچ یا سیم‌لوله‌ای را به طول $$L = 1.4\ m$$ و قطر درونی $$d = 3\ cm$$ در نظر بگیرید. از سیم‌لوله مذکور جریان الکتریکی ثابت $$6\ A$$ گذر می‌کند. سیم‌لوله مذکور از $$6$$ لایه سیم‌پیچ که هر یک از $$900$$ دور سیم پیچانده شده در امتداد طول $$L$$ ساخته شده‌اند، تشکیل شده است. با توجه به ساختار سیم‌لوله مذکور، اندازه میدان مغناطیسی $$B$$ در مرکز سیم‌لوله را به شکل زیر به دست می‌آوریم.

از آنجایی که مقدار $$B$$ در رابطه $$B = \mu_{0} i n$$ وابستگی به قطر سیم‌پیچ ندارد، بدیهی است که مقدار $$n$$ برای $$6$$ لایه که به صورت متوالی پشت یکدیگر قرار گرفته‌اند، $$6$$ برابر مقدار یک لایه است. به عبارت دیگر مقدار دور سیم به صورت زیر در می‌آید:

$$\large n = \frac{ 6 \times 900 }{ 1.4 } \cong 3857 $$

$$\large B = \mu_{0} i n = ( 4 \pi \times 10^{-7}\ T.m/A ) ( 6\ A ) ( 3857\ 1/m )$$

اگر مطالب ارائه شده در این مقاله برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۲
• مجموعه آموزش‌های مهندسی برق
• آموزش الکترومغناطیس ۱
• مادون قرمز (Infrared) -- به زبان ساده
• امواج رادیویی -- به زبان ساده
• طیف مرئی -- به زبان ساده

^^