روش مقطع خرپا – به زبان ساده

خرپا سازهایست که از اتصال تعداد زیادی عضو تحت نیروهای کششی و فشاری تشکیل شده است و کاربرد زیادی در مسئلههای مربوط به درس استاتیک دارد. برای تحلیل نیروهای وارد بر عضوهای میانی خرپا با استفاده از روش مفصل، نیروی وارد بر تمام عضوها باید تحلیل شود. این روش در تحلیل خرپاهای کوچک با تعداد عضوهای کم، به سرعت انجام میشود. اما برای تحلیل خرپاهایی که در سازههایی عظیمالجثه مانند پلها مورد استفاده قرار میگیرند، چه باید کرد؟ این سازهها دارای عضوهای بسیار زیادی هستند. آیا راه دیگری برای تحلیل نیرو در چنین سازههایی وجود دارد؟ در این مقاله به روش مقطع (Section Method) به عنوان راه حلی برای این مشکل پرداخته میشود.
معرفی روش مقطع
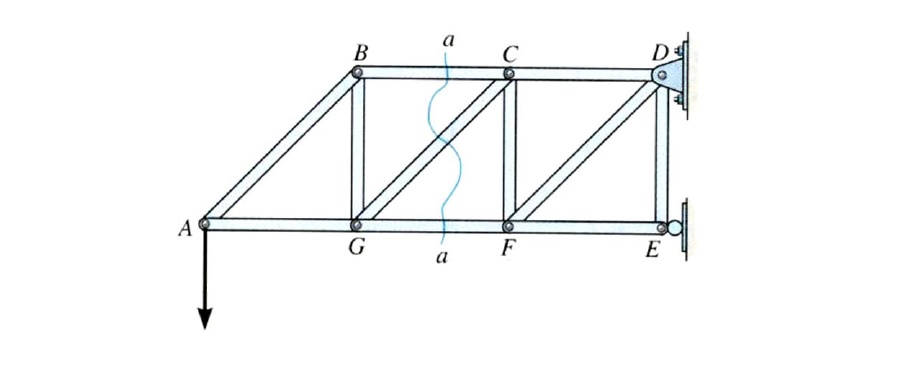
در روش مقطع مطابق شکل زیر، با اعمال برش فرضی a-a، خرپا به دو نیمه تقسیم میشود. مطابق قانون سوم نیوتن و براساس مفهوم تعادل، به هریک از عضوهای خرپا، فقط نیروهای کششی یا فشاری در راستای طولی وارد میشوند.
در اینجا نیز نیروهای داخلی در عضوهای بریده شده، از نوع کششی یا فشاری و به همان مقدار خواهند بود. پس از برش مقطع، سازه مانند یک جسم صلب فرض میشود و قانون برآیند نیروها را میتوان برای آن نوشت.
برای استفاده از روش مقطع باید مطابق گامهای زیر پیش رفت:
- در ابتدا باید مناسبترین محل برای برش مشخص شود. این موضوع مستلزم دانستن این است که نیروهای مجهول در کدام قسمت از خرپا قرار گرفتهاند. همچنین باید توجه کرد که تعداد نیروهای مجهول در حالت کلی از عدد سه فراتر نرود (برای مسائل دوبعدی، دو معادله برای تعادل نیروها در جهت X و Y و یک معادله برای تعادل گشتاور میتوان نوشت).
- در مرحله دوم باید این نکته را مد نظر قرار داد که حل کردن کدام یک از دو نیمه سازه، سادهتر انجام میشود (به عنوان مثال باید دقت کرد که در کدام نیمه، تعداد نیروهای عکسالعمل مجهول کمتر است).
- در صورت نیاز با ترسیم نمودار جسم آزاد و نوشتن تعادل برای آن، نیروی عکسالعمل تکیهگاهها محاسبه میشود.
- در این مرحله، نمودار جسم آزاد برای نیمه مورد نظر رسم میشود تا نیروهای مجهول در عضوهای بریده شده مشخص شوند. در ابتدا ممکن است فرض شود تمام عضوها تحت نیروی کششی هستند. پس از حل مسئله، اگر پاسخ به دست آمده مثبت باشد، آن عضو مطابق فرض اولیه، تحت نیروی کششی است. اما اگر پاسخ منفی باشد، نیروی وارد بر عضو مذکور از نوع فشاری است.
- در مرحله پایانی با نوشتن معادلات تعادل برای نیمه مورد نظر (مطابق شکل زیر)، نیروهای مجهول به دست میآیند. باید به این نکته توجه شود که در بسیاری از موارد، ممکن است نوشتن تنها یک معادله برای به دست آوردن هر یک از مجهولها کافی باشد.
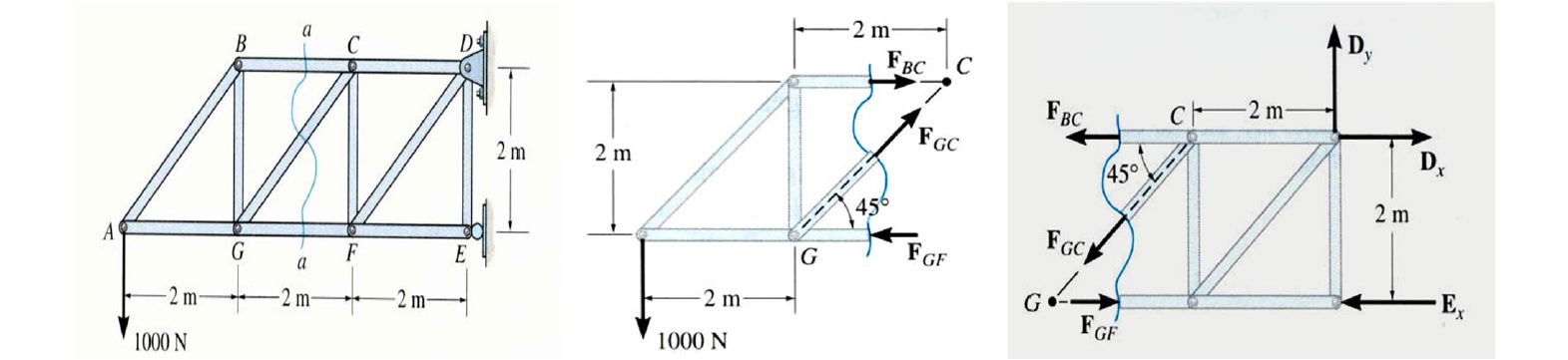
در ادامه با ارائه دو مثال تکمیلی، شیوه حل مسئله و چگونگی استفاده از گامهای پنجگانه برای به دست آوردن نیروهای داخلی مجهول با روش مقطع روشنتر میشود.
مثال ۱
در این مثال، نیروهایی مطابق شکل زیر به خرپا وارد میشود. تکیه گاه A از نوع لولایی و تکیهگاه از نوع غلتکی است. نیروی داخلی در عضوهای DE ،DL و ML مجهول است.
گامهای مورد نیاز برای به دست آوردن این نیروها با استفاده از روش مقطع به تفصیل ارائه میشود.
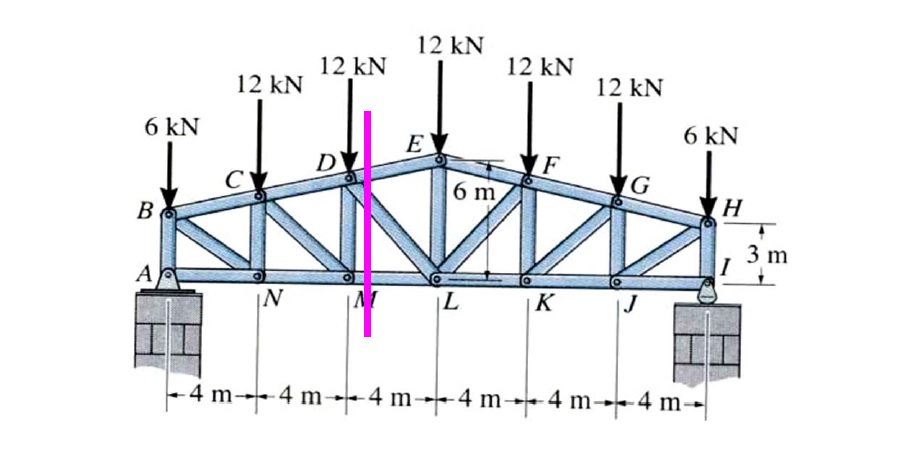
مطابق شکل بالا، خرپا از محل عضوهای DE ،DL و ML برش زده شده است. برای سادگی بیشتر و به دلیل تعداد کم نیروها در نیمه سمت چپ، این نیمه برای ادامه حل مثال انتخاب میشود. ابتدا نیروی عکسالعمل تکیهگاه در نقطه A محاسبه میشود. سپس با ترسیم نمودار جسم آزاد برای نیمه سمت چپ (مانند شکل زیر) و نوشتن معادلات تعادل برای آن، نیروهای داخلی در عضوهای DE ،DL و ML به دست میآیند.
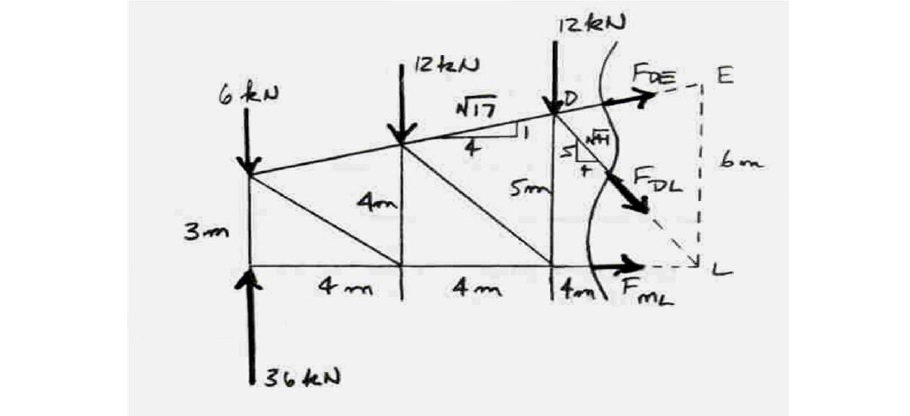
مثال ۲
در این مثال، نیروهایی مطابق شکل زیر به خرپا وارد میشود. تکیهگاه F از نوع غلتکی و تکیهگاه C از نوع لولایی است. نیروی داخلی در عضوهای BE و DE مجهول است. گامهای مورد نیاز برای به دست آوردن این نیروها با استفاده از روش مقطع به تفصیل ارائه میشود.
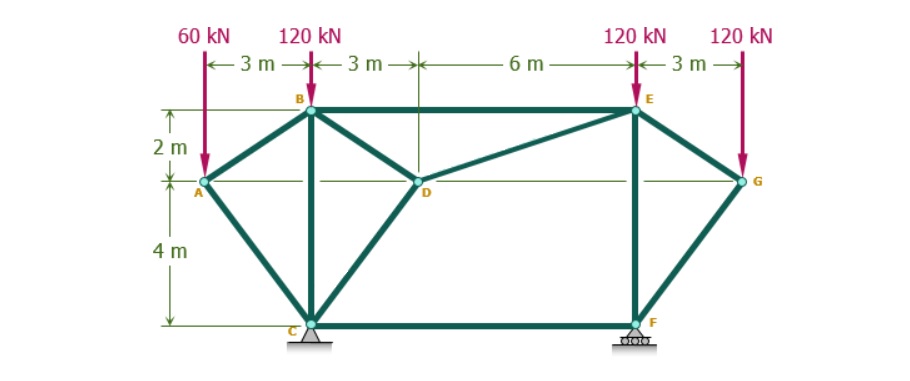
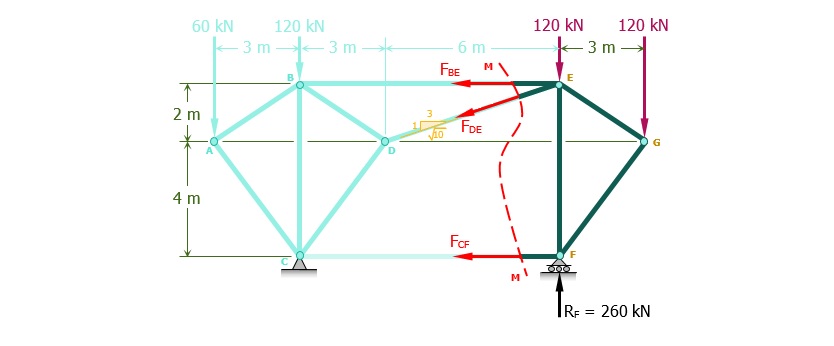
خرپا از محل مشخص شده در شکل زیر برش زده شده است. برای سادگی بیشتر و به دلیل تعداد کم نیروها در نیمه سمت راست، این نیمه برای ادامه حل مثال انتخاب میشود. ابتدا برای به دست آوردن نیروی تکیهگاهی RF، مجموع گشتاورهای کل سازه خرپا حول نقطه C نوشته میشود. در ادامه با ترسیم نمودار جسم آزاد برای نیمه سمت راست (مطابق شکل زیر) و نوشتن معادلات تعادل برای آن، نیروهای داخلی در عضوهای BE و DE به دست میآیند.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:












دیگه درس نده
اعداد رو میخوندی فقط
تعداد از کجا اومدن رو نمیگی چرا
بلد بودن یه چیزه آموزش دادن کار دیگه که تو بلد نیستی
فرادرس عزیز لطفا خودتونو با این اساتید پایین نیارید