در این آموزش، روش و الگوریتم نظاممند رسم توابع مختلف را ارائه میکنیم. چند مثال مختلف نیز برای درک بهتر رسم تابع ارائه شده است.
رسم تابع
گامهای کلی رسم نمودار تابع y = f ( x ) y = f (x ) y = f ( x )
دامنه تابع، نقاط ناپیوستگی و مجانبهای قائم (در صورت وجود) را تعیین کنید.
زوج و فرد یا متناوب بودن تابع را مشخص کنید.مجانبهای مایل و افقی تابع را به دست آورید.نقاط تقاطع منحنی با محورهای مختصات و بازههایی را تعیین کنید که در آن، تابع یک علامت ثابت (f ( x ) > 0 f (x)>0 f ( x ) > 0 f ( x ) < 0 f (x ) < 0 f ( x ) < 0
مشتق اول (f ’ ( x ) f’\left( x \right) f ’ ( x ) اکسترمم و بازههای صعودی یا نزولی بودن تابع را محاسبه کنید.مشتق دوم (f ′ ′ ( x ) f ^ {\prime \prime} (x) f ′′ ( x ) نقاط عطف و بازههای مقعر یا محدب بودن تابع را تعیین کنید.
نمودار تابع را رسم کنید.
مثالها
در ادامه، مثالهای متنوعی را برای رسم نمودار توابع بررسی میکنیم.
مثال ۱
نمودار تابع زیر را رسم کنید.
y = x 3 – 3 x 2 + 2 x \large y = { x ^ 3 } – 3 { x ^ 2 } + 2 x y = x 3 –3 x 2 + 2 x
حل: تابع در همه x ∈ R x \in \mathbb{R} x ∈ R
k = lim x → ± ∞ y ( x ) x = lim x → ± ∞ x 3 – 3 x 2 + 2 x x = lim x → ± ∞ ( x 2 – 3 x + 2 ) = + ∞ . \large \begin {align*} k & = \lim \limits _ { x \to \pm \infty } \frac { { y \left ( x \right ) } } { x } = { \lim \limits _ { x \to \pm \infty } \frac { { { x ^ 3 } – 3 { x ^ 2 } + 2 x } } { x } }\\ & = { \lim \limits _ { x \to \pm \infty } \left ( { { x ^ 2 } – 3 x + 2 } \right ) = + \infty . } \end {align*} k = x → ± ∞ lim x y ( x ) = x → ± ∞ lim x x 3 –3 x 2 + 2 x = x → ± ∞ lim ( x 2 –3 x + 2 ) = + ∞.
در نتیجه، تابع مجانب مایل نیز ندارد. اکنون نقاط برخورد نمودار را با محورهای مختصات تعیین میکنیم:
y ( 0 ) = 0 \large y\left( 0 \right) = 0 y ( 0 ) = 0
در ادامه، معادله زیر را حل میکنیم:
x 3 – 3 x 2 + 2 x = 0 \large {x^3} – 3{x^2} + 2x = 0 x 3 –3 x 2 + 2 x = 0
جوابهای این معادله به صورت زیر هستند:
x ( x 2 – 3 x + 2 ) = 0 , ⇒ x 1 = 0 , x 2 = 1 , x 3 = 2 \large { x \left ( { { x ^ 2 } – 3 x + 2 } \right ) = 0 , \; \; } \Rightarrow { { x _ 1 } = 0 , \; { x _ 2 } = 1 , \; { x _ 3 } = 2 } x ( x 2 –3 x + 2 ) = 0 , ⇒ x 1 = 0 , x 2 = 1 , x 3 = 2
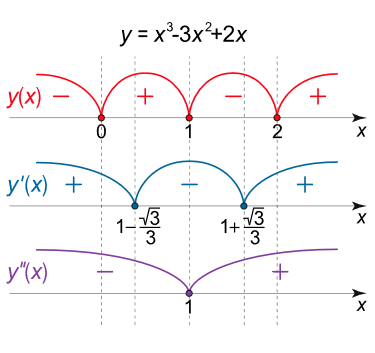
بازههایی را که در آنها تابع مثبت یا منفی است، میتوان با حل نامساویهای زیر تعیین کرد (شکل 1 (الف)):
x 3 – 3 x 2 + 2 x > 0 , ⇒ x ( x – 1 ) ( x – 2 ) > 0. \large { { x ^ 3 } – 3 { x ^ 2 } + 2 x > 0 , \; \; } \Rightarrow { x \left ( { x – 1 } \right ) \left ( { x – 2 } \right ) > 0 . } x 3 –3 x 2 + 2 x > 0 , ⇒ x ( x –1 ) ( x –2 ) > 0.
شکل ۱ (الف) مشتق اول تابع برابر است با:
y ’ ( x ) = ( x 3 – 3 x 2 + 2 x ) ′ = 3 x 2 – 6 x + 2. \large { y ’ \left ( x \right ) = { \left ( { { x ^ 3 } – 3 { x ^ 2 } + 2 x } \right ) ^ \prime } } = { 3 { x ^ 2 } – 6 x + 2 . } y ’ ( x ) = ( x 3 –3 x 2 + 2 x ) ′ = 3 x 2 –6 x + 2.
نقاط اکسترمم یا مانای تابع، با صفر قرار دادن مشق اول آن به دست میآیند:
y ’ ( x ) = 0 , ⇒ 3 x 2 – 6 x + 2 = 0 , ⇒ D = 36 – 4 ⋅ 3 ⋅ 2 = 12 , ⇒ x 1 , 2 = 6 ± 12 6 = 1 ± 3 ≈ 0.42 ; 1.58. \large \begin {align*} y ’ \left ( x \right ) & = 0 , \; \; \Rightarrow { 3 { x ^ 2 } – 6 x + 2 = 0 , \; \; } \Rightarrow { D = 3 6 – 4 \cdot 3 \cdot 2 = 12 , \; \; } \\ & \Rightarrow { { x _ { 1 , 2 } } = \frac { { 6 \pm \sqrt { 1 2 } } } { 6 } } = { 1 \pm \sqrt 3 \approx 0.42 ; \; 1.58.} \end {align*} y ’ ( x ) = 0 , ⇒ 3 x 2 –6 x + 2 = 0 , ⇒ D = 36–4 ⋅ 3 ⋅ 2 = 12 , ⇒ x 1 , 2 = 6 6 ± 12 = 1 ± 3 ≈ 0.42 ; 1.58.
وقتی از نقطه x = 1 – 3 3 x = 1 – {\large\frac{{\sqrt 3 }}{3}\normalsize} x = 1– 3 3 x = 1 + 3 3 x = 1 + {\large\frac{{\sqrt 3 }}{3}\normalsize} x = 1 + 3 3
$$ \large \begin {align*}<br />
\require {cancel}<br />
y \left ( { 1 – \frac { { \sqrt 3 } } { 3 } } \right ) &<br />
= { { \left ( { 1 – \frac { { \sqrt 3 } } { 3 } } \right ) ^ 3 } }<br />
– { 3 { \left ( { 1 – \frac { { \sqrt 3 } } { 3 } } \right ) ^ 2 } }<br />
+ { 2 \left ( { 1 – \frac { { \sqrt 3 } } { 3 } } \right ) }<br />
\\ & = { 1 – 3 \cdot \frac { { \sqrt 3 } } { 3 } }<br />
+ { 3 \cdot { \left ( { \frac { { \sqrt 3 } } { 3 } } \right ) ^ 2 } }<br />
– { { \left ( { \frac { { \sqrt 3 } } { 3 } } \right ) ^ 3 } } \\ &<br />
\, \, \, \, \, \, \, \, \, \, – { 3 \left [ { 1 – \frac { { 2 \sqrt 3 } } { 3 } }<br />
+ { { { \left ( { \frac { { \sqrt 3 } } { 3 } } \right ) } ^ 2 } } \right ] }<br />
+ { 2 – \frac { { 2 \sqrt 3 } } { 3 } }<br />
\\ & = { \cancel { 1 } – \sqrt 3 + \cancel { 1 } }<br />
– { \frac { { \sqrt 3 } } { 9 } – \cancel { 3 } }<br />
+ { 2 \sqrt 3 – \cancel { 1 } + \cancel { 2 } }<br />
– { \frac { { 2 \sqrt 3 } } { 3 } }<br />
\\ & = { \frac { { 9 \sqrt 3 – \sqrt 3 – 6 \sqrt 3 } } { 9 } }<br />
= { \frac { { 2 \sqrt 3 } } { 9 } \approx 0.38 ; }<br />
\end {align*} $$
به طریق مشابه، داریم:
y ( 1 + 3 3 ) = − 2 3 9 ≈ − 0.38. \large { y \left ( { 1 + \frac { { \sqrt 3 } } { 3 } } \right ) } = -{ \frac { { 2 \sqrt 3 } } { 9 } \approx -0.38 . } y ( 1 + 3 3 ) = − 9 2 3 ≈ − 0.38.
بنابراین، تابع یک ماکزیمم محلی در نقطه زیر دارد:
( 1 – 3 3 , 2 3 9 ) ≈ ( 0.42 ; 0.38 ) . \large \left ( { 1 – \frac { { \sqrt 3 } } { 3 } , \frac { { 2 \sqrt 3 } } { 9 } } \right ) \approx \left ( { 0 .42 ; \; 0.38 } \right ) . ( 1– 3 3 , 9 2 3 ) ≈ ( 0.42 ; 0.38 ) .
به همین ترتیب، نقطه زیر یک مینیمم محلی برای تابع است:
( 1 + 3 3 , − 2 3 9 ) ≈ ( 1.58 ; − 0.38 ) \large \left ( { 1 + \frac { { \sqrt 3 } } { 3 } , - \frac { { 2 \sqrt 3 } } { 9 } } \right ) \approx \left ( { 1 .5 8 ; \; - 0. 3 8 } \right) ( 1 + 3 3 , − 9 2 3 ) ≈ ( 1.58 ; − 0.38 )
بازههای صعودی و نزولی بودن تابع، در شکل ۱ (الف) نشان داده شدهاند.
اکنون مشتق دوم تابع را محاسبه میکنیم:
y ′ ′ ( x ) = ( 3 x 2 – 6 x + 2 ) ′ = 6 x – 6 ; y ′ ′ ( x ) = 0 , ⇒ 6 x – 6 = 0 , ⇒ x = 1. \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { \left ( { 3 { x ^ 2 } – 6 x + 2 } \right ) ^ \prime } = { 6 x – 6 ; } \\ y ^ { \prime \prime } \left ( x \right ) & = 0 , \; \; \Rightarrow { 6 x – 6 = 0 , \; \; } \Rightarrow { x = 1 . } \end {align*} y ′′ ( x ) y ′′ ( x ) = ( 3 x 2 –6 x + 2 ) ′ = 6 x –6 ; = 0 , ⇒ 6 x –6 = 0 , ⇒ x = 1.
اگر x ≤ 1 x \le 1 x ≤ 1 x ≥ 1 x \ge 1 x ≥ 1 x = 1 x = 1 x = 1
y ( 1 ) = 1 3 – 3 ⋅ 1 2 + 2 ⋅ 1 = 0. \large y \left ( 1 \right ) = { 1 ^ 3 } – 3 \cdot { 1 ^ 2 } + 2 \cdot 1 = 0 . y ( 1 ) = 1 3 –3 ⋅ 1 2 + 2 ⋅ 1 = 0.
مهارت رسم درست نمودار توابع هم از لحاظ کاربردی بسیار مفید است و هم از جهت تحصیلی برای شرکت در امتحانات و آزمونهای مختلف لازم است. برای کسب این مهارت پیشنهاد میکنیم فیلم آموزشی رایگان زیر را مشاهده کنید. در این فیلم مفاهیم و مثالهای مختلفی را بررسی کردهایم.
توصیف مختصات تقاطع با محور x x x ( 0 , 0 ) (0,0) ( 0 , 0 ) تقاطع با محور x x x ( 1 , 0 ) (1,0) ( 1 , 0 ) تقاطع با محور x x x ( 2 , 0 ) (2,0) ( 2 , 0 ) مینیمم محلی ( 1 + 3 3 , − 2 3 9 ) (1+\frac{\sqrt{3}}{3} , -\frac{2\sqrt{3}}{9}) ( 1 + 3 3 , − 9 2 3 ) ماکزیمم محلی ( 1 − 3 3 , 2 3 9 ) (1-\frac{\sqrt{3}}{3} , \frac{2\sqrt{3}}{9}) ( 1 − 3 3 , 9 2 3 )
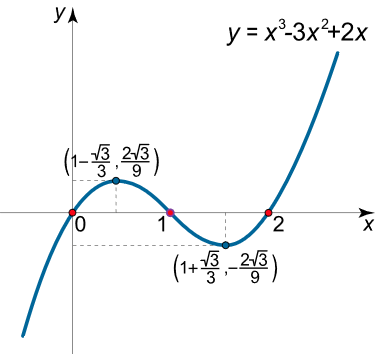
با اطلاعاتی که به دست آوردیم، میتوانیم نمودار تابع را رسم کنیم (شکل ۱ (ب)).
شکل ۱ (ب) مثال ۲
نمودار تابع زیر را رسم کنید:
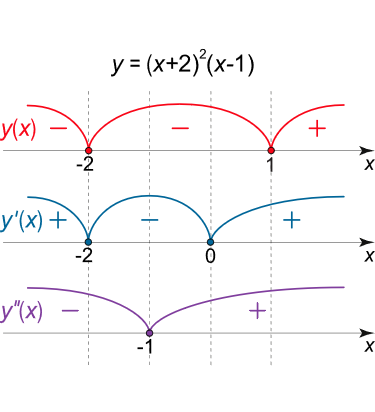
y = ( x + 2 ) 2 ( x – 1 ) . \large y = {\left( {x + 2} \right)^2}\left( {x – 1} \right). y = ( x + 2 ) 2 ( x –1 ) .
حل: تابع فوق برای همه x x x حقیقی تعریف شده است. بنابراین، مجانب قائم وجود نخواهد داشت. در نتیجه، وجود مجانب مایل یا افقی را تحقیق میکنیم:
k = lim x → ± ∞ y ( x ) x = lim x → ± ∞ ( x + 2 ) 2 ( x – 1 ) x = lim x → ± ∞ ( x 2 + 4 x + 4 ) ( x – 1 ) x = lim x → ± ∞ x 3 + 3 x 2 – 4 x = lim x → ± ∞ ( x 2 + 3 x – 4 x ) = + ∞ . \large \begin {align*} k & = \lim \limits _ { x \to \pm \infty } \frac { { y \left ( x \right ) } } { x } = { \lim \limits _ { x \to \pm \infty } \frac { { { { \left ( { x + 2 } \right ) } ^ 2 } \left ( { x – 1 } \right ) } } { x } } \\ & = { \lim \limits _ { x \to \pm \infty } \frac { { \left ( { { x ^ 2 } + 4 x + 4 } \right ) \left ( { x – 1 } \right ) } } { x } } \\ & = { \lim \limits _ { x \to \pm \infty } \frac { { { x ^ 3 } + { 3 { x ^ 2 } } – { 4 } } } { x } } \\ & = { \lim \limits _ { x \to \pm \infty } \left ( { { x ^ 2 } + 3 x – \frac { 4 } { x } } \right ) = + \infty . } \end {align*} k = x → ± ∞ lim x y ( x ) = x → ± ∞ lim x ( x + 2 ) 2 ( x –1 ) = x → ± ∞ lim x ( x 2 + 4 x + 4 ) ( x –1 ) = x → ± ∞ lim x x 3 + 3 x 2 – 4 = x → ± ∞ lim ( x 2 + 3 x – x 4 ) = + ∞.
از آنجایی که شیب k k k
نقاط تقاطع منحنی با محورهای مختصات به صورت زیر هستند:
y ( 0 ) = 2 2 ⋅ ( – 1 ) = – 4 ; y ( x ) = 0 , ⇒ ( x + 2 ) 2 ( x – 1 ) = 0 , ⇒ x 1 = – 2 , x 2 = 1. \large \begin {align*} y \left ( 0 \right ) & = { 2 ^ 2 } \cdot \left ( { – 1 } \right ) = – 4 ;\\ y \left ( x \right ) & = 0 , \; \; \Rightarrow { { \left ( { x + 2 } \right ) ^ 2 } \left ( { x – 1 } \right ) = 0 , \; \; } \\ &\Rightarrow { { x _ 1 } = – 2 , \; { x _ 2 } = 1 . } \end {align*} y ( 0 ) y ( x ) = 2 2 ⋅ ( –1 ) = –4 ; = 0 , ⇒ ( x + 2 ) 2 ( x –1 ) = 0 , ⇒ x 1 = –2 , x 2 = 1.
تابع در x > 1 x > 1 x > 1 x ∈ ( – ∞ , – 2 ) ∪ ( – 2 , 1 ) x \in \left( { – \infty , – 2} \right) \cup \left( { – 2,1} \right) x ∈ ( –∞ , –2 ) ∪ ( –2 , 1 )
شکل 2 (الف) مشتق اول تابع به صورت زیر است:
$$ \large \begin {align*}<br />
\require {cancel} y ’ \left ( x \right ) & = { \left [ { { { \left ( { x + 2 } \right ) } ^ 2 } \left ( { x – 1 } \right ) } \right ] ^ \prime } = { 2 \left ( { x + 2 } \right ) \left ( { x – 1 } \right ) + { \left ( { x + 2 } \right ) ^ 2 } } \\ &= { \left ( { x + 2 } \right ) \left ( { 2 x – \cancel { 2 } + x + \cancel { 2 } } \right ) } = { 3 x \left ( { x + 2 } \right ) . }<br />
\end {align*} $$
نقاط مانا نیز به صورت زیر محاسبه میشوند:
y ’ ( x ) = 0 , ⇒ 3 x ( x + 2 ) = 0 , ⇒ x 1 = 0 , x 2 = – 2. \large { y ’ \left ( x \right ) = 0 , \; \; } \Rightarrow { 3 x \left ( { x + 2 } \right ) = 0 , \; \; } \Rightarrow { { x _ 1 } = 0 , \;{ x _ 2 } = – 2 . } y ’ ( x ) = 0 , ⇒ 3 x ( x + 2 ) = 0 , ⇒ x 1 = 0 , x 2 = –2.
تغییر علامت مشتق در شکل 2 (الف) نشان داده شده است. بنابراین، x = − 2 x = - 2 x = − 2 x = 0 x = 0 x = 0
y ( – 2 ) = – 4 , y ( 0 ) = 0. \large { y \left ( { – 2 } \right ) = – 4 , } \; \; \; \kern-0.3pt { y \left ( 0 \right ) = 0 . } y ( –2 ) = –4 , y ( 0 ) = 0.
اکنون مشتق دوم را محاسبه میکنیم:
y ′ ′ ( x ) = [ 3 x ( x + 2 ) ] ′ = 3 ( x + 2 ) + 3 x = 6 x + 6. \large { y ^ { \prime \prime } \left ( x \right ) = { \left [ {3x\left( {x + 2} \right)} \right]^\prime } } = {3\left( {x + 2} \right) + 3x } = {6x + 6.} y ′′ ( x ) = [ 3 x ( x + 2 ) ] ′ = 3 ( x + 2 ) + 3 x = 6 x + 6.
بنابراین، تابع در x < − 1 x <-1 x < − 1 x > − 1 x \gt -1 x > − 1 x = − 1 x = -1 x = − 1
y ( – 1 ) = ( – 1 + 2 ) 2 ( – 1 – 1 ) = – 2. \large y \left ( { – 1 } \right ) = { \left ( { – 1 + 2 } \right ) ^ 2 } \left ( { – 1 – 1 } \right ) = – 2 . y ( –1 ) = ( –1 + 2 ) 2 ( –1–1 ) = –2.
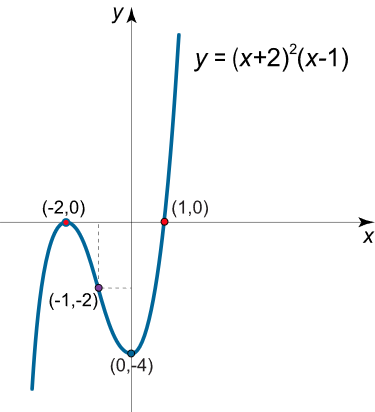
شکل 2 (ب) نمودار تابع مورد نظر را نشان میدهد.
شکل 2 (ب) مثال ۳
نمودار تابع زیر را رسم کنید:
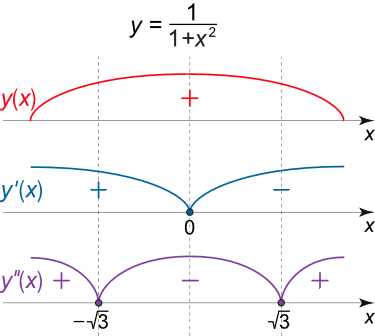
y = 1 1 + x 2 . \large y = \frac { 1 } { { 1 + { x ^ 2 } } } . y = 1 + x 2 1 .
حل: تابع برای تمام مقادیر حقیقی x x x y = 0 y = 0 y = 0
lim x → ± ∞ y ( x ) = lim x → ± ∞ 1 1 + x 2 = 0 \large { \lim \limits _ { x \to \pm \infty } y \left ( x \right ) } = { \lim \limits _ { x \to \pm \infty } \frac { 1 } { { 1 + { x ^ 2 } } } = 0 } x → ± ∞ lim y ( x ) = x → ± ∞ lim 1 + x 2 1 = 0
تابع این مثال زوج است. در واقع، داریم:
y ( – x ) = 1 1 + ( – 1 ) 2 = 1 1 + x 2 = y ( x ) . \large { y \left ( { – x } \right ) = \frac { 1 } { { 1 + { { \left ( { – 1 } \right ) } ^ 2 } } } } = { \frac { 1 } { { 1 + { x ^ 2 } } } = y \left ( x \right ) . } y ( – x ) = 1 + ( –1 ) 2 1 = 1 + x 2 1 = y ( x ) .
واضح است که تابع ریشه مثبت ندارد و مقدار آن در x = 0 x = 0 x = 0
y ( 0 ) = 1 1 + 0 2 = 1. \large y \left ( 0 \right ) = \frac { 1 } { { 1 + { 0 ^ 2 } } } = 1 . y ( 0 ) = 1 + 0 2 1 = 1.
مشتق اول تابع به صورت زیر است:
y ’ ( x ) = ( 1 1 + x 2 ) ′ = – 1 ( 1 + x 2 ) 2 ⋅ ( 1 + x 2 ) ′ = – 2 x ( 1 + x 2 ) 2 . \large \begin {align*} y ’ \left ( x \right ) & = { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) ^ \prime } = { – \frac { 1 } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } \cdot { \left ( { 1 + { x ^ 2 } } \right ) ^ \prime } } \\ & = { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } . } \end {align*} y ’ ( x ) = ( 1 + x 2 1 ) ′ = – ( 1 + x 2 ) 2 1 ⋅ ( 1 + x 2 ) ′ = – ( 1 + x 2 ) 2 2 x .
با توجه به رابطه اخیر، x = 0 x = 0 x = 0 x = 0 x = 0 x = 0 y ( 0 ) = 1 y (0) = 1 y ( 0 ) = 1
شکل ۳ (الف) اکنون مشتق دوم تابع را محاسبه میکنیم:
y ′ ′ ( x ) = ( – 2 x ( 1 + x 2 ) 2 ) ′ = – 2 ( 1 + x 2 ) 2 – 2 x ⋅ 2 ( 1 + x 2 ) ( 1 + x 2 ) 4 = 8 x 2 – 2 – 2 x 2 ( 1 + x 2 ) 3 = 6 x 2 – 2 ( 1 + x 2 ) 3 . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { \left( { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } \right ) ^ \prime } = { – \frac { { 2 { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } – 2 x \cdot 2 \left ( { 1 + { x ^ 2 } } \right ) } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 4 } } } } \\ & = { \frac { { 8 { x ^ 2 } – 2 – 2 { x ^ 2 } } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 3 } } } } = { \frac { { 6 { x ^ 2 } – 2 } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 3 } } } . } \end {align*} y ′′ ( x ) = ( – ( 1 + x 2 ) 2 2 x ) ′ = – ( 1 + x 2 ) 4 2 ( 1 + x 2 ) 2 –2 x ⋅ 2 ( 1 + x 2 ) = ( 1 + x 2 ) 3 8 x 2 –2–2 x 2 = ( 1 + x 2 ) 3 6 x 2 –2 .
مشتق دوم، در نقاط زیر برابر با صفر میشود:
y ′ ′ ( x ) = 0 , ⇒ 6 x 2 – 2 ( 1 + x 2 ) 3 = 0 , ⇒ 2 ( x – 3 ) ( x + 3 ) ( 1 + x 2 ) 3 = 0 , ⇒ x 1 = – 3 , x 2 = 3 . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = 0 , \; \; \Rightarrow { \frac { { 6 { x ^ 2 } – 2 } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 3 } } } = 0 , \; \; } \\ & \Rightarrow { \frac { { 2 \left ( { x – \sqrt 3 } \right ) \left ( { x + \sqrt 3 } \right ) } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 3 } } } = 0 , \; \; } \\ & \Rightarrow { { x _ 1 } = – \sqrt 3 , \; { x _ 2 } = \sqrt 3 . } \end {align*} y ′′ ( x ) = 0 , ⇒ ( 1 + x 2 ) 3 6 x 2 –2 = 0 , ⇒ ( 1 + x 2 ) 3 2 ( x – 3 ) ( x + 3 ) = 0 , ⇒ x 1 = – 3 , x 2 = 3 .
هنگام گذر از این نقاط، علامت مشتق دوم تغییر میکند. بنابراین، هر دو نقطه، نقاط عطف تابع هستند. تابع در بازههای ( – ∞ , – 3 ) \left( { – \infty , – \sqrt 3 } \right) ( –∞ , – 3 ) ( 3 , + ∞ ) \left( {\sqrt 3 , + \infty } \right) ( 3 , + ∞ ) ( – 3 , 3 ) \left( { – \sqrt 3 ,\sqrt 3 } \right) ( – 3 , 3 )
y ( ± 3 ) = 1 1 + ( ± 3 ) 2 = 1 1 + 3 = 1 4 . \large { y \left ( { \pm \sqrt 3 } \right ) = \frac { 1 } { { 1 + { { \left ( { \pm \sqrt 3 } \right ) } ^ 2 } } } } = { \frac { 1 } { { 1 + 3 } } = \frac { 1 } { 4 } . } y ( ± 3 ) = 1 + ( ± 3 ) 2 1 = 1 + 3 1 = 4 1 .
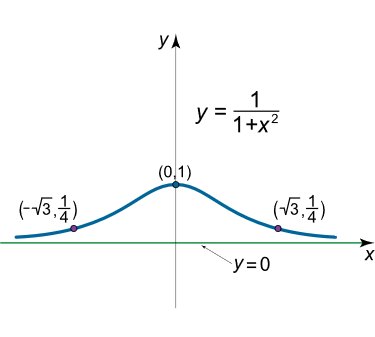
شکل ۳ (ب) نمودار منحنی تابع را نشان میدهد.
شکل ۳ (ب) مثال ۴
نمودار تابع زیر را رسم کنید:
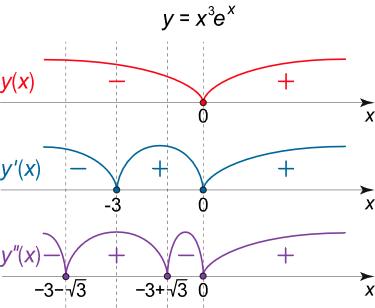
y = x 3 e x . \large y = { x ^ 3 } { e ^ x } . y = x 3 e x .
حل: تابع، در کل محدوده اعداد حقیقی تعریف شده و مشتقپذیر است. در این حالت، مجانب قائم وجود ندارد. بنابراین، وجود مجانبهای مایل را تحقیق میکنیم. بدین منظور حدهای زیر را مینویسیم:
$$ \large \begin {align*}<br />
\lim \limits _ { x \to + \infty } \left ( { { x ^ 3 } { e ^ x } } \right ) & = + \infty ; \\<br />
{ \lim \limits _ { x \to – \infty } \left ( { { x ^ 3 } { e ^ x } } \right ) }<br />
& = { \lim \limits _ { x \to – \infty } \frac { { \left ( { – { { \left ( { – x } \right ) } ^ 3 } } \right ) } } { { { e ^ { – x } } } } }<br />
= { \left [ { \begin {array} { * { 2 0 } {l} }<br />
{ – x = z , } \\<br />
{ x \to – \infty , } \\<br />
{ z \to + \infty } \\<br />
\end {array} } \right ] } \\ &<br />
= { – \lim \limits _ { z \to + \infty } \frac { { { z ^ 3 } } } { { { e ^ z } } } }<br />
= { – \lim \limits _ { z \to + \infty } \frac { { 3 { z ^ 2 } } } { { { e ^ z } } } }<br />
\\ & = { – \lim \limits _ { z \to + \infty } \frac { { 6 z } } { { { e ^ z } } } }<br />
= { – \lim \limits _ { z \to + \infty } \frac { 6 } { { { e ^ z } } } = 0 . }<br />
\end {align*} $$
برای محاسبه حد دوم، از تغییر متغیر ( – x ) → z \left( { – x} \right) \to z ( – x ) → z قاعده هوپیتال استفاده شده است. مشاهده میکنیم که وقتی x → − ∞ x \to -\infty x → − ∞ y = 0 y = 0 y = 0
ریشههای تابع به صورت زیر به دست میآیند:
y ( x ) = 0 , ⇒ x 3 e x = 0 , ⇒ x 3 = 0 , ⇒ x = 0. \large { y \left ( x \right ) = 0 , \; \; } \Rightarrow { { x ^ 3 } { e ^ x } = 0 , \; \; } \Rightarrow { { x ^ 3 } = 0 , \; \; } \Rightarrow { x = 0 . } y ( x ) = 0 , ⇒ x 3 e x = 0 , ⇒ x 3 = 0 , ⇒ x = 0.
تابع برای x > 0 x \gt 0 x > 0 x < 0 x \lt 0 x < 0
شکل ۴ (الف) اکنون مشتق اول را محاسبه و نقاط اکسترمم و بازههای یکنوا بودن تابع را بررسی میکنیم:
y ′ ( x ) = ( x 3 e x ) ′ = ( x 3 ) ′ e x + x 3 ( e x ) ′ = 3 x 2 e x + x 3 e x = x 2 e x ( 3 + x ) . \large \begin {align*} y ^ \prime \left ( x \right ) & = { \left ( { { x ^ 3 } { e ^ x } } \right ) ^ \prime } = { { \left ( { { x ^ 3 } } \right ) ^ \prime } { e ^ x } + { x ^ 3 } { \left ( { { e ^ x } } \right ) ^ \prime } } \\ & = { 3 { x ^ 2 } { e ^ x } + { x ^ 3 } { e ^ x } } = { { x ^ 2 } { e ^ x } \left ( { 3 + x } \right ) . } \end {align*} y ′ ( x ) = ( x 3 e x ) ′ = ( x 3 ) ′ e x + x 3 ( e x ) ′ = 3 x 2 e x + x 3 e x = x 2 e x ( 3 + x ) .
بازههای ثابت بودن علامت مشتق اول در شکل ۴ (الف) نشان داده شده است. تابع در بازه ( – ∞ , – 3 ) \left( { – \infty , – 3} \right) ( –∞ , –3 ) ( − 3 , 0 ) \left( { -3,0} \right) ( − 3 , 0 ) ( 0 , + ∞ ) \left( {0, + \infty} \right) ( 0 , + ∞ ) x = − 3 x = - 3 x = − 3 x = 0 x = 0 x = 0
y ( – 3 ) = ( – 3 ) 3 e – 3 ≈ – 27 ⋅ 0.0498 ≈ – 1.34 \large { y \left ( { – 3 } \right ) = { \left ( { – 3 } \right ) ^ 3 } { e ^ { – 3 } } } \kern0pt { \approx – 27 \cdot 0.0 4 9 8 \approx – 1 . 3 4 } y ( –3 ) = ( –3 ) 3 e –3 ≈ –27 ⋅ 0.0498 ≈ –1.34
حال مشتق دوم را محاسبه میکنیم:
y ′ ′ ( x ) = [ x 2 e x ( 3 + x ) ] ′ = [ e x ( 3 x 2 + x 3 ) ] ′ = ( e x ) ′ ( 3 x 2 + x 3 ) + e x ( 3 x 2 + x 3 ) ′ = e x ( 3 x 2 + x 3 ) + e x ( 6 x + 3 x 2 ) = e x ( x 3 + 6 x 2 + 6 x ) = x e x ( x 2 + 6 x + 6 ) . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { \left [ { { x ^ 2 } { e ^ x } \left ( { 3 + x } \right ) } \right ] ^ \prime } = { { \left [ { { e ^ x } \left ( { 3 { x ^ 2 } + { x ^ 3 } } \right ) } \right ] ^ \prime } } \\ & = { { \left ( { { e ^ x } } \right ) ^ \prime } \left ( { 3 { x ^ 2 } + { x ^ 3 } } \right ) + { e ^ x } { \left ( { 3 { x ^ 2 } + { x ^ 3 } } \right ) ^ \prime } } \\ &= { { e ^ x } \left ( { 3 { x ^ 2 } + { x ^ 3 } } \right ) + { e ^ x } \left ( { 6 x + 3 { x ^ 2 } } \right ) } \\ & = { { e ^ x } \left ( { { x ^ 3 } + 6 { x ^ 2 } + 6 x } \right ) } = { x { e ^ x } \left ( { { x ^ 2 } + 6 x + 6 } \right ) . } \end {align*} y ′′ ( x ) = [ x 2 e x ( 3 + x ) ] ′ = [ e x ( 3 x 2 + x 3 ) ] ′ = ( e x ) ′ ( 3 x 2 + x 3 ) + e x ( 3 x 2 + x 3 ) ′ = e x ( 3 x 2 + x 3 ) + e x ( 6 x + 3 x 2 ) = e x ( x 3 + 6 x 2 + 6 x ) = x e x ( x 2 + 6 x + 6 ) .
ریشههای مشتق دوم را به دست میآوریم:
y ′ ′ ( x ) = 0 , ⇒ x e x ( x 2 + 6 x + 6 ) = 0 , ⇒ x 2 + 6 x + 6 = 0 , ⇒ D = 36 – 4 ⋅ 6 = 12 , ⇒ x 1 , 2 = – 6 ± 12 2 = – 3 ± 3 ≈ – 4.73 ; – 1.27. \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = 0 , \; \; \Rightarrow { x { e ^ x } \left ( { { x ^ 2 } + 6 x + 6 } \right ) = 0 , \; \; } \\ & \Rightarrow { { x ^ 2 } + 6 x + 6 = 0 , \; \; } \Rightarrow { D = 3 6 – 4 \cdot 6 = 1 2 , \; \; } \\ & \Rightarrow { { x _ { 1 , 2 } } = \frac { { – 6 \pm \sqrt { 1 2 } } } { 2 } = – 3 \pm \sqrt 3 \; } \kern0pt { \approx – 4.73 ; \; – 1.27 . } \end {align*} y ′′ ( x ) = 0 , ⇒ x e x ( x 2 + 6 x + 6 ) = 0 , ⇒ x 2 + 6 x + 6 = 0 , ⇒ D = 36–4 ⋅ 6 = 12 , ⇒ x 1 , 2 = 2 –6 ± 12 = –3 ± 3 ≈ –4.73 ; –1.27.
این ریشهها برابرند با:
x 1 = – 3 – 3 , x 2 = – 3 + 3 , x 3 = 0. \large { { x _ 1 } = – 3 – \sqrt 3 , } \; \; \; \kern-0.3pt { { x _ 2 } = – 3 + \sqrt 3 , } \; \; \; \kern-0.3pt { { x _ 3 } = 0 . } x 1 = –3– 3 , x 2 = –3 + 3 , x 3 = 0.
وقتی نمودار تابع از هر یک از این نقاط میگذرد، علامت مشتق تغییر میکند (شکل ۴ (الف)). بنابراین، این نقاط، نقاط عطف هستند. مقادیر تقریبی مربوط به مختصه y y y
y ( – 3 – 3 ) = ( – 3 – 3 ) 3 e – 3 – 3 ≈ – 0.93 ; y ( – 3 + 3 ) = ( – 3 + 3 ) 3 e – 3 + 3 ≈ – 0.57 ; y ( 0 ) = 0. \large \begin {align*} y \left ( { – 3 – \sqrt 3 } \right) & = { { \left ( { – 3 – \sqrt 3 } \right ) ^ 3 } { e ^ { – 3 – \sqrt 3 } } } { \approx – 0.9 3 ; } \\ { y \left ( { – 3 + \sqrt 3 } \right ) } & = { { \left ( { – 3 + \sqrt 3 } \right ) ^ 3 } { e ^ { – 3 + \sqrt 3 } } } { \approx – 0. 5 7 ; } \\ y \left ( 0 \right ) & = 0 . \end {align*} y ( –3– 3 ) y ( –3 + 3 ) y ( 0 ) = ( –3– 3 ) 3 e –3– 3 ≈ –0.93 ; = ( –3 + 3 ) 3 e –3 + 3 ≈ –0.57 ; = 0.
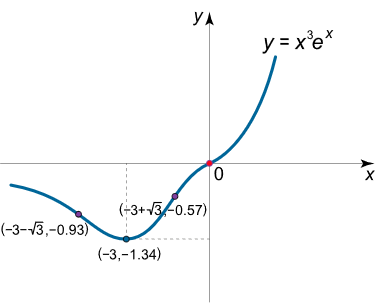
با مشخصاتی که از تابع به دست آوردیم، میتوانیم نمودار آن را به صورت شکل ۴ (ب) رسم کنیم.
شکل ۴ (ب) مثال ۵
نمودار تابع زیر را رسم کنید:
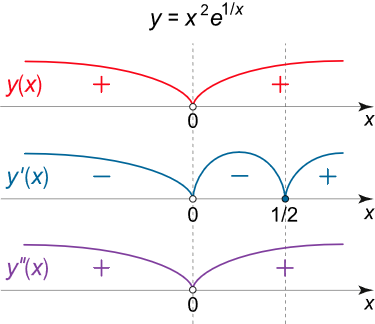
y = x 2 e 1 x . \large y = {x^2}{e^{\large\frac{1}{x}\normalsize}}. y = x 2 e x 1 .
حل: تابع در نقطه x = 0 x =0 x = 0 حدهای یکطرفه این نقطه به صورت زیر هستند:
$$ \large \begin {align*}<br />
{ \lim \limits _ { x \to 0 – 0 } y \left ( x \right ) } & = { \lim \limits _ { x \to 0 – 0 } \left ( { { x ^ 2 } { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) = 0 ; } \\<br />
{ \lim \limits _ { x \to 0 + 0 } y \left ( x \right ) }<br />
& = { \lim \limits _ { x \to 0 + 0 } \left ( { { x ^ 2 } { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) }<br />
= { \lim \limits _ { x \to 0 + 0 } \frac { { { e ^ { \large \frac { 1 } { x } \normalsize } } } } { { { { \left ( { \frac { 1 } { x} } \right ) } ^ 2 } } } }<br />
\\ & = { \left [ { \begin {array} { * { 2 0 } { l } }<br />
{ \frac { 1 } { x } = z , } \\<br />
{ x \to 0 + , } \\<br />
{ z \to + \infty }<br />
\end {array} } \right ] }<br />
= { \lim \limits _ { z \to + \infty } \frac { { { e ^ z } } } { { { z ^ 2 } } } }<br />
= { \lim \limits _ { z \to + \infty } \frac { { { e ^ z } } } { { 2 z } } } \\ &<br />
= { \lim \limits _ { z \to + \infty } \frac { { { e ^ z } } } { 2 } = + \infty . }<br />
\end {align*} $$
در محاسبه حد دوم، از تغییر متغیر 1 x → z {{\large\frac{1}{x}\normalsize} \to z} x 1 → z
بنابراین، خط x = 0 x = 0 x = 0 y y y x = 0 x=0 x = 0 y ( – 0 ) = 0 y\left( { – 0} \right) = 0 y ( –0 ) = 0 x → ± ∞ x \to \pm \infty x → ± ∞
$$ \large \begin {align*}<br />
k & = \lim \limits _ { x \to \pm \infty } \frac { { y \left ( x \right ) } } { x }<br />
= { \lim \limits _ { x \to \pm \infty } \frac { { { x ^ 2 } { e ^ { \large \frac { 1 } { x } \normalsize } } } } { x } }<br />
\\ & = { \lim \limits _ { x \to \pm \infty } \left ( { x { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) }<br />
= { \lim \limits _ { x \to \pm \infty } \frac { {{ e ^ { \large \frac { 1 } { x } \normalsize } } } } { { \frac { 1 } { x } } } }<br />
\\ & = { \left [ { \begin {array} { * { 2 0 } { l } }<br />
{ \frac { 1 } { x } = z , } \\<br />
{ x \to \pm \infty , } \\<br />
{ z \to 0 }<br />
\end{array} } \right ] }<br />
= { \lim \limits _ { z \to 0 } \frac { { { e ^ z } } } { z } = \infty .}<br />
\end {align*} $$
در نتیجه، مجانب مایل وجود ندارد.
اکنون مشتق اول و نقاط مانا را تعیین میکنیم:
y ’ ( x ) = ( x 2 e 1 x ) ′ = ( x 2 ) ′ e 1 x + x 2 ( e 1 x ) ′ = 2 x e 1 x + x 2 e 1 x ⋅ ( – 1 x 2 ) = 2 x e 1 x – e 1 x = e 1 x ( 2 x – 1 ) ; y ’ ( x ) = 0 , ⇒ e 1 x ( 2 x – 1 ) = 0 , ⇒ 2 x – 1 = 0 , ⇒ x = 1 2 . \large \begin {align*} y ’ \left ( x \right ) & = { \left ( { { x ^ 2 } { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) ^ \prime } = { { \left ( { { x ^ 2 } } \right ) ^ \prime } { e ^ { \large \frac { 1 } { x } \normalsize } } + { x ^ 2 } { \left ( { { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) ^ \prime } } \\ & = { 2 x { e ^ { \large \frac { 1 } { x } \normalsize } } + { x ^ 2 } { e ^ { \large \frac { 1 } { x } \normalsize } } \cdot \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) } \\ & = { 2 x { e ^ { \large \frac { 1 } { x } \normalsize } } – { e ^ { \large \frac { 1 } { x } \normalsize } } } = { { e ^ { \large \frac { 1 } { x } \normalsize } } \left ( { 2 x – 1 } \right ) ; } \\ y’\left( x \right) & = 0 , \; \; \Rightarrow { { e ^ { \large \frac { 1 } { x } \normalsize } } \left ( { 2 x – 1 } \right ) = 0 , \; \; } \\ & \Rightarrow { 2 x – 1 = 0 , \; \; } \Rightarrow { x = \frac { 1 } { 2 } . } \end {align*} y ’ ( x ) y ’ ( x ) = ( x 2 e x 1 ) ′ = ( x 2 ) ′ e x 1 + x 2 ( e x 1 ) ′ = 2 x e x 1 + x 2 e x 1 ⋅ ( – x 2 1 ) = 2 x e x 1 – e x 1 = e x 1 ( 2 x –1 ) ; = 0 , ⇒ e x 1 ( 2 x –1 ) = 0 , ⇒ 2 x –1 = 0 , ⇒ x = 2 1 .
مشتق در سمت چپ x = 1 2 x = {\large\frac{1}{2}\normalsize} x = 2 1 x = 1 2 x = {\large\frac{1}{2}\normalsize} x = 2 1
y ( 1 2 ) = ( 1 2 ) 2 e 1 1 2 = 1 4 e 2 ≈ 1.85. \large { y \left ( { \frac { 1 } { 2 } } \right ) } = { { \left ( { \frac { 1 } { 2 } } \right ) ^ 2 } { e ^ { \large \frac { 1 }{ { \frac { 1 } { 2 } } } \normalsize } } } = { \frac { 1 } { 4 } { e ^ 2 } \approx 1 . 8 5 . } y ( 2 1 ) = ( 2 1 ) 2 e 2 1 1 = 4 1 e 2 ≈ 1.85.
شکل ۵ (الف) مشتق دوم تابع به صورت زیر است:
y ′ ′ ( x ) = [ e 1 x ( 2 x – 1 ) ] ′ = ( e 1 x ) ′ ( 2 x – 1 ) + e 1 x ( 2 x – 1 ) ′ = e 1 x ⋅ ( – 1 x 2 ) ( 2 x – 1 ) + 2 e 1 x = e 1 x ( 2 – 2 x – 1 x 2 ) = e 1 x 2 x 2 – 2 x + 1 x 2 . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { \left [ { { e ^ { \large \frac { 1 } { x } \normalsize } } \left ( { 2 x – 1 } \right ) } \right ] ^ \prime } = { { \left ( { { e ^ { \large \frac { 1 } { x } \normalsize } } } \right ) ^ \prime } \left ( { 2 x – 1 } \right ) + { e ^ { \large \frac { 1 } { x } \normalsize } } { \left ( { 2 x – 1 } \right ) ^ \prime } } \\ & = { { e ^ { \large \frac { 1 } { x } \normalsize } } \cdot \left ( { – \frac { 1 } { { { x ^ 2 } } } } \right ) \left ( { 2 x – 1 } \right ) + 2 { e ^ { \large \frac { 1 } { x } \normalsize } } } \\ &= { { e ^ { \large \frac { 1 } { x } \normalsize } } \left ( { 2 – \frac { { 2 x – 1 } } { { { x ^ 2 } } } } \right ) } = { { e ^ { \large \frac { 1 } { x } \normalsize } } \frac { { 2 { x ^ 2 } – 2 x + 1 } } { { { x ^ 2 } } } . } \end {align*} y ′′ ( x ) = [ e x 1 ( 2 x –1 ) ] ′ = ( e x 1 ) ′ ( 2 x –1 ) + e x 1 ( 2 x –1 ) ′ = e x 1 ⋅ ( – x 2 1 ) ( 2 x –1 ) + 2 e x 1 = e x 1 ( 2– x 2 2 x –1 ) = e x 1 x 2 2 x 2 –2 x + 1 .
صورت کسر عبارت اخیر ریشه حقیقی ندارد و همیشه مثبت است. با توجه به وجود جمله x 2 x ^ 2 x 2 x ≠ 0 x \ne 0 x = 0 ( – ∞ , 0 ) \left( { – \infty ,0} \right) ( –∞ , 0 ) ( 0 , + ∞ ) \left( {0, +\infty} \right) ( 0 , + ∞ )
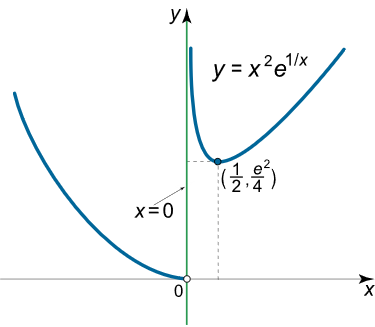
نمودار تابع در شکل ۵ (ب) رسم شده است.
شکل ۵ (ب) مثال ۶
نمودار تابع زیر را رسم کنید.
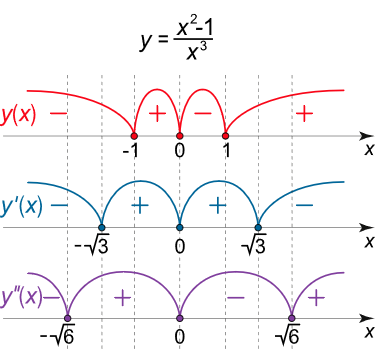
y = x 2 – 1 x 3 . \large y = \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 } } } . y = x 3 x 2 –1 .
حل: تابع جز در x = 0 x = 0 x = 0 x x x
lim x → 0 – 0 x 2 – 1 x 3 = + ∞ , lim x → 0 + 0 x 2 – 1 x 3 = – ∞ . \large { \lim \limits _ { x \to 0 – 0 } \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 } } } = + \infty , } \; \; \; \kern-0.3pt { \lim \limits _ { x \to 0 + 0 } \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 } } } = – \infty . } x → 0–0 lim x 3 x 2 –1 = + ∞ , x → 0 + 0 lim x 3 x 2 –1 = –∞.
بنابراین، خط x = 0 x =0 x = 0 y y y
k = lim x → ± ∞ y ( x ) x = lim x → ± ∞ x 2 – 1 x 3 x = lim x → ± ∞ x 2 – 1 x 4 = lim x → ± ∞ 1 x 2 – 1 x 4 1 = 0 ; b = lim x → ± ∞ [ y ( x ) – k x ] = lim x → ± ∞ [ x 2 – 1 x 3 – 0 ] = lim x → ± ∞ 1 x – 1 x 3 1 = 0. \large \begin {align*} k & = \lim \limits _ { x \to \pm \infty } \frac { { y \left ( x \right ) } } { x } = { \lim \limits _ { x \to \pm \infty } \frac { { \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 } } } } } { x } } \\ & = { \lim \limits _ { x \to \pm \infty } \frac { { { x ^ 2 } – 1 } } { { { x ^ 4 } } } } = { \lim \limits _ { x \to \pm \infty } \frac { { \frac { 1 } { { { x ^ 2 } } } – \frac { 1 } { { { x ^ 4 } } } } } { 1 } = 0 ; } \\ b & = \lim \limits _ { x \to \pm \infty } \left [ { y \left ( x \right ) – k x } \right ] = { \lim \limits _ { x \to \pm \infty } \left [ { \frac { { { x ^ 2 } – 1 } } { { {x ^ 3 } } } – 0 } \right ] } \\ & = { \lim \limits _ { x \to \pm \infty } \frac { { \frac { 1 } { x } – \frac { 1 } { { { x ^ 3 } } }} } { 1 } = 0 . } \end {align*} k b = x → ± ∞ lim x y ( x ) = x → ± ∞ lim x x 3 x 2 –1 = x → ± ∞ lim x 4 x 2 –1 = x → ± ∞ lim 1 x 2 1 – x 4 1 = 0 ; = x → ± ∞ lim [ y ( x ) – k x ] = x → ± ∞ lim [ x 3 x 2 –1 –0 ] = x → ± ∞ lim 1 x 1 – x 3 1 = 0.
بنابراین، y = 0 y = 0 y = 0
تابع فرد است، زیرا:
y ( – x ) = ( – x ) 2 – 1 ( – x ) 3 = – x 2 – 1 x 3 = – y ( x ) . \large { y \left ( { – x } \right ) } = { \frac { { { { \left ( { – x } \right ) } ^ 2 } – 1 } } { { { { \left ( { – x } \right ) } ^ 3 } } } } = { – \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 }} } = – y \left ( x \right ) . } y ( – x ) = ( – x ) 3 ( – x ) 2 –1 = – x 3 x 2 –1 = – y ( x ) .
اکنون نقاط تقاطع نمودار تابع را با محور x x x
$$ \large \begin {align*}<br />
y \left ( x \right ) & = 0 , \; \; \Rightarrow<br />
{ \frac { { { x ^ 2 } – 1 } } { { {x ^ 3 } } } = 0 , \; \; } \\ & \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } { l } }<br />
{ { x ^ 2 } – 1 = 0 } \\<br />
{ { x ^ 4 } \ne 0 }<br />
\end {array} } \right . , \; \; } \Rightarrow<br />
{ { x _ { 1 , 2 } } = \pm 1 . }<br />
\end {align*} $$
مقدار تابع در بازههای ( – 1 , 0 ) \left( { – 1,0} \right) ( –1 , 0 ) ( 1 , + ∞ ) \left( {1, +\infty} \right) ( 1 , + ∞ ) ( − ∞ , − 1 ) \left( {-\infty, -1} \right) ( − ∞ , − 1 ) ( 0 , 1 ) \left( {0,1} \right) ( 0 , 1 )
شکل ۶ (الف) مشتق اول تابع، به صورت زیر است:
y ’ ( x ) = ( x 2 – 1 x 3 ) ′ = ( 1 x – 1 x 3 ) ′ = ( x – 1 – x – 3 ) ′ = – x – 2 + 3 x – 4 = – 1 x 2 + 3 x 4 = 3 – x 2 x 4 . \large \begin {align*} y ’ \left ( x \right ) & = { \left ( { \frac { { { x ^ 2 } – 1 } } { { { x ^ 3 } } } } \right ) ^ \prime } = { { \left( { \frac { 1 } { x } – \frac { 1 } { { { x ^ 3 } } } } \right ) ^ \prime } } \\ & = { { \left ( { { x ^ { – 1 } } – { x ^ { – 3 } } } \right ) ^ \prime } } = { – { x ^ { – 2 } } + 3 { x ^ { – 4 } } } \\ & = { – \frac { 1 } { { { x ^ 2 } } } + \frac { 3 } { { { x ^ 4 } } } } = { \frac { { 3 – { x ^ 2 } } } { { { x ^ 4 } } } . } \end {align*} y ’ ( x ) = ( x 3 x 2 –1 ) ′ = ( x 1 – x 3 1 ) ′ = ( x –1 – x –3 ) ′ = – x –2 + 3 x –4 = – x 2 1 + x 4 3 = x 4 3– x 2 .
نقاط مانا برابرند با:
$$ \large \begin {align*}<br />
y ’ \left ( x \right ) = 0 , \; \; & \Rightarrow<br />
{ \frac { { 3 – { x ^ 2 } } } { { { x ^ 4 } } } = 0 , \; \; } \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } { l } }<br />
{ 3 – { x ^ 2 } = 0 } \\<br />
{ { x ^ 4 } \ne 0 }<br />
\end {array} } \right . , \; \; }\\ & \Rightarrow<br />
{ { x _ { 1 , 2 } } = \pm \sqrt 3 \approx 1.73 . }<br />
\end {align*} $$
نقطه x = – 3 x = – \sqrt 3 x = – 3 x = 3 x = \sqrt 3 x = 3
y ( – 3 ) = ( – 3 ) 2 – 1 ( – 3 ) 3 = – 2 3 3 ≈ – 0.38 y ( 3 ) = 2 3 3 ≈ 0.38. \large \begin {align*} { y \left ( { – \sqrt 3 } \right) } & = { \frac { { { { \left ( { – \sqrt 3 } \right ) } ^ 2 } – 1 } } { { { { \left ( { – \sqrt 3 } \right ) } ^ 3 } } } } = { – \frac { 2 } { { 3 \sqrt 3 } } \approx – 0 . 3 8 } \\ y \left ( { \sqrt 3 } \right) & = \frac { 2 } { { 3 \sqrt 3 } } \approx 0 . 3 8 . \end {align*} y ( – 3 ) y ( 3 ) = ( – 3 ) 3 ( – 3 ) 2 –1 = – 3 3 2 ≈ –0.38 = 3 3 2 ≈ 0.38.
مشتق دوم تابع نیز برابر است با:
y ′ ′ ( x ) = ( – x – 2 + 3 x – 4 ) ′ = 2 x – 3 – 12 x – 5 = 2 x 3 – 12 x 5 = 2 x 2 – 12 x 5 = 2 ( x 2 – 6 ) x 5 . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { { \left ( { – { x ^ { – 2 } } + 3 { x ^ { – 4 } } } \right ) ^ \prime } } = { 2 { x ^ { – 3 } } – 1 2 { x ^ { – 5 } } } \\ & = { \frac { 2 } { { { x ^ 3 } } } – \frac { { 1 2 } } { { { x ^ 5 } } } } = { \frac { { 2 { x ^ 2 } – 1 2 } } { { { x ^ 5 } } } } = { \frac { { 2 \left ( { { x ^ 2 } – 6 } \right ) } } { { { x ^ 5 } } } .} \end {align*} y ′′ ( x ) = ( – x –2 + 3 x –4 ) ′ = 2 x –3 –12 x –5 = x 3 2 – x 5 12 = x 5 2 x 2 –12 = x 5 2 ( x 2 –6 ) .
عبارت بالا در نقاط زیر برابر با صفر است:
$$ \large \begin {align*}<br />
y ^ { \prime \prime } \left ( x \right ) & = 0 , \; \; \Rightarrow<br />
{ \frac { { 2 \left ( { { x ^ 2 } – 6 } \right ) } } { { { x ^ 5 } } } = 0 , \; \; } \\ & \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } { l } }<br />
{ { x ^ 2 } – 6 = 0 } \\<br />
{ { x ^ 5 } \ne 0 }<br />
\end{array}} \right . , \; \; } \Rightarrow<br />
{ { x _ { 1 , 2 } } = \pm \sqrt 6 \approx \pm 2 . 4 5 . }<br />
\end {align*} $$
همانطور که در شکل ۶ (الف) میبینیم، تابع در بازههای ( – ∞ , – 6 ) \left( { – \infty , – \sqrt 6 } \right) ( –∞ , – 6 ) ( 0 , 6 ) \left( {0, \sqrt 6 } \right) ( 0 , 6 ) ( − 3 , 0 ) \left( {-\sqrt 3, 0 } \right) ( − 3 , 0 ) ( 6 , + ∞ ) \left( {\sqrt 6, +\infty } \right) ( 6 , + ∞ ) x = – ۶ x = – \sqrt ۶ x = – ۶ x = ۶ x = \sqrt ۶ x = ۶
y ( – 6 ) = ( – 6 ) 2 – 1 ( – 6 ) 3 = – 5 6 6 ≈ – 0.34 y ( 6 ) = 5 6 6 ≈ 0.34. \large \begin {align*} { y \left ( { – \sqrt 6 } \right ) } & = { \frac { { { { \left ( { – \sqrt 6 } \right ) } ^ 2 } – 1 } } { { { { \left ( { – \sqrt 6 } \right ) } ^ 3 } } } } = { – \frac { 5 } { { 6 \sqrt 6 } } \approx – 0 . 3 4 } \\ y \left ( { \sqrt 6 } \right) & = \frac { 5 } { { 6 \sqrt 6 } } \approx 0 . 3 4 . \end {align*} y ( – 6 ) y ( 6 ) = ( – 6 ) 3 ( – 6 ) 2 –1 = – 6 6 5 ≈ –0.34 = 6 6 5 ≈ 0.34.
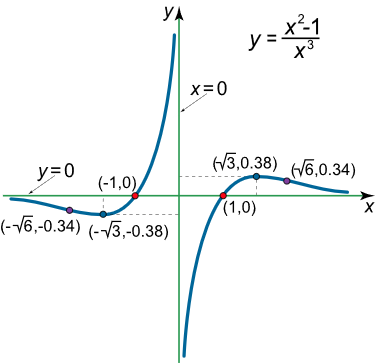
اکنون با اطلاعاتی که از تابع به دست آوردیم میتوانیم نمودار تابع را مطابق شکل ۶ (ب) رسم کنیم.
شکل ۶ (ب) مثال ۷
نمودار تابع زیر را رسم کنید:
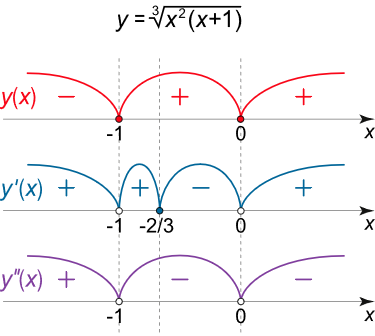
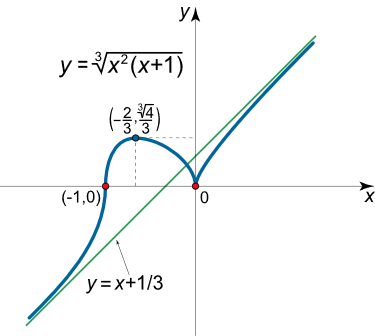
حل: تابع در کل بازه اعداد حقیقی تعریف شده است و همانطور که میبینیم از نقاط x = 0 x = 0 x = 0 x = − 1 x = -1 x = − 1 ( – 1 , 0 ) \left( { – 1,0} \right) ( –1 , 0 ) ( 0 , + ∞ ) \left( {0, +\infty} \right) ( 0 , + ∞ ) ( − ∞ , − 1 ) \left( {-\infty, -1} \right) ( − ∞ , − 1 )
شکل ۷ (الف) از آنجایی که تابع در کل بازه اعداد حقیقی پیوسته است، مجانب قائم ندارد. بنابراین باید وجود مجانب مایل یا افقی را تحقیق کنیم:
در نتیجه، مجانب مایل زیر را داریم:
y = x + 1 3 . \large y = x + { \large \frac { 1 } { 3 }\normalsize } . y = x + 3 1 .
مشتق تابع، برابر است با:
بنابراین، نقاط بحرانی تابع به صورت زیر هستند:
x 1 = 0 , x 2 = – 1 , x 3 = – 2 3 . \large { { x _ 1 } = 0 , } \; \; \; \kern-0.3pt { { x _ 2 } = – 1 , } \; \; \; \kern-0.3pt { { x _ 3 } = – \frac { 2 } { 3 } . } x 1 = 0 , x 2 = –1 , x 3 = – 3 2 .
در دو نقطه نخست، مشتق وجود ندارد. البته وقتی تابع از نقطه x = 0 x = 0 x = 0 x = 0 x = 0 x = 0 y ( 0 ) = 0 y (0) = 0 y ( 0 ) = 0 x = − 1 x = - 1 x = − 1 x = – 2 3 x = – {\large\frac{2}{3}\normalsize} x = – 3 2 x = – 2 3 x = – {\large\frac{2}{3}\normalsize} x = – 3 2
اکنون نقاط عطف ممکن و تحدب تابع را بررسی میکنیم. ابتدا مشتق دوم تابع را به صورت زیر محاسبه میکنیم:
بنابراین، مشتق دوم در هیچ نقطهای صفر نمیشود. البته نقطه تکین x = − 1 x = - 1 x = − 1 x = 0 x = 0 x = 0 ( – ∞ , – 1 ) \left( { – \infty , – 1} \right) ( –∞ , –1 ) ( – 1 , 0 ) \left( { – 1,0} \right) ( –1 , 0 ) ( 0 , + ∞ ) \left( {0, +\infty} \right) ( 0 , + ∞ )
با توجه به اطلاعاتی که از تابع استخراج کردیم، نمودار آن در شکل ۷ (ب) رسم شده است.
شکل ۷ (ب) مثال ۸
نمودار تابع زیر را رسم کنید:
y = x 2 x + 1 . \large y = { x ^ 2 } \sqrt { x + 1 } . y = x 2 x + 1 .
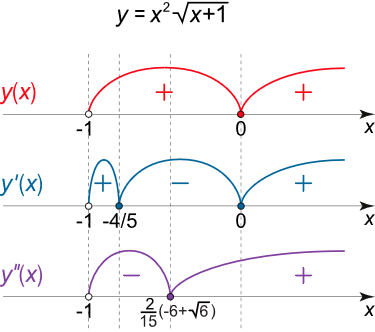
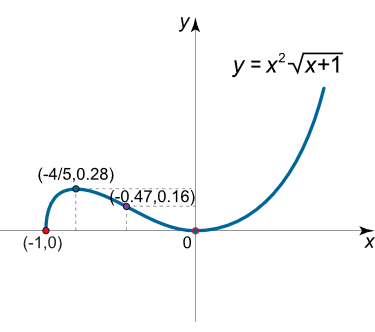
حل: واضح است که تابع در x ≥ − 1 x \ge -1 x ≥ − 1
نقاط تقاطع منحنی و محورهای مختصات، به صورت زیر هستند:
y ( 0 ) = 0 2 0 + 1 = 0 ; y ( x ) = 0 , ⇒ x 2 x + 1 = 0 , ⇒ x 1 = 0 , x 2 = – 1. \large \begin {align*} y \left ( 0 \right ) & = { 0 ^ 2 } \sqrt { 0 + 1 } = 0 ; \\ y \left ( x \right ) & = 0 , \; \; \Rightarrow { { x ^ 2 } \sqrt { x + 1 } = 0 , \; \; } \Rightarrow { { x _ 1 } = 0 , \; { x _ 2 } = – 1 . } \end {align*} y ( 0 ) y ( x ) = 0 2 0 + 1 = 0 ; = 0 , ⇒ x 2 x + 1 = 0 , ⇒ x 1 = 0 , x 2 = –1.
در نتیجه، نقاط تقاطع، ( 0 , 0 ) (0,0) ( 0 , 0 ) ( − 1 , 0 ) (-1,0) ( − 1 , 0 )
مشتق تابع، برابر است با:
y ’ ( x ) = ( x 2 x + 1 ) ′ = 2 x ⋅ x + 1 + x 2 ⋅ 1 2 x + 1 = 2 x x + 1 + x 2 2 x + 1 = 4 x ( x + 1 ) + x 2 2 x + 1 = 5 x 2 + 4 x 2 x + 1 . \large \begin {align*} y’ \left ( x \right ) & = { { \left ( { { x ^ 2 } \sqrt { x + 1 } } \right ) ^ \prime } } = { 2 x \cdot \sqrt { x + 1 } + { x ^ 2 } \cdot \frac { 1 } { { 2 \sqrt { x + 1 } } } } \\ & = { 2 x \sqrt { x + 1 } + \frac { { { x ^ 2 } } } { { 2 \sqrt { x + 1 } }} } = { \frac { { 4 x \left ( { x + 1 } \right ) + { x ^ 2 } } }{ { 2 \sqrt { x + 1 } } } } \\ & = { \frac { { 5 { x ^ 2 } + 4 x } } { { 2 \sqrt { x + 1 } } } . } \end {align*} y ’ ( x ) = ( x 2 x + 1 ) ′ = 2 x ⋅ x + 1 + x 2 ⋅ 2 x + 1 1 = 2 x x + 1 + 2 x + 1 x 2 = 2 x + 1 4 x ( x + 1 ) + x 2 = 2 x + 1 5 x 2 + 4 x .
نقاط بحرانی تابع، به صورت زیر هستند:
x 1 = – 1 , x 2 = 0 , x 3 = – 4 5 . \large { { x _ 1 } = – 1 , } \; \; \; \kern-0.3pt { { x _ 2 } = 0 , } \; \; \; \kern-0.3pt { { x _ 3 } = – \frac { 4 } { 5 } . } x 1 = –1 , x 2 = 0 , x 3 = – 5 4 .
تابع در بازههای ( – 1 , – 4 5 ) \left( { – 1, – {\large\frac{4}{5}\normalsize}} \right) ( –1 , – 5 4 ) ( 0 , + ∞ ) \left( {0, + \infty } \right) ( 0 , + ∞ ) ( − 4 5 , 0 ) \left( {- {\large\frac{4}{5}\normalsize}, 0} \right) ( − 5 4 , 0 )
در نقطه x = – 4 5 x = – {\large\frac{4}{5}\normalsize} x = – 5 4
y ( – 4 5 ) = ( – 4 5 ) 2 – 4 5 + 1 = 16 25 5 ≈ 0.28. \large { y \left ( { – \frac { 4 } { 5 } } \right ) } = { { \left ( { – \frac { 4 } { 5 } } \right ) ^ 2 } \sqrt { – \frac { 4 } { 5 } + 1 } } = { \frac { { 1 6 } } { { 2 5 \sqrt 5 } } \approx 0.28.} y ( – 5 4 ) = ( – 5 4 ) 2 – 5 4 + 1 = 25 5 16 ≈ 0.28.
در نقطه x = 0 x=0 x = 0 y ( 0 ) = 0 y\left( 0 \right) = 0 y ( 0 ) = 0
اکنون مشتق دوم را به دست میآوریم:
$$ \large \begin {align*}<br />
y ^ { \prime \prime } \left ( x \right ) & = { { \left ( { \frac { {5 { x ^ 2 } + 4 x } } { { 2 \sqrt {x + 1 } } } } \right ) ^ \prime } } = { \frac { { \left ( { 2 0 x + 8 } \right ) \left ( { x + 1 } \right ) – \left ( { 5 { x ^ 2 } + 4 x } \right ) } } { { 4 \sqrt { { { \left ( { x + 1 } \right ) } ^ 3 } } } } } \\ & = { \frac { { \color{ blue } { 2 0 { x ^ 2 } } + \color { red } { 8 x } + \color {red} { 2 0 x } + \color {green} { 8 } – \color {blue} { 5 { x ^ 2 } } – \color {red} { 4 x } } } { { 4 \sqrt { { { \left ( { x + 1 } \right ) } ^ 3 } } } } } = { \frac { { \color {blue} { 1 5 { x ^ 2 } } + \color {red} { 2 4 x } + \color {green} { 8 } } } { { 4 \sqrt { { { \left ( { x + 1 } \right ) } ^ 3 } } } } .}<br />
\end {align*} $$
عبارت بالا، در نقاط زیر برابر با صفر است:
$$ \large \begin {align*}<br />
y ^ { \prime \prime } \left ( x \right ) & = 0 , \; \; \Rightarrow<br />
{ \frac { { 1 5 { x ^2 } + 2 4 x + 8 } } { { 4 \sqrt { { { \left ( { x + 1 } \right ) } ^ 3 } } } } = 0 , \; \; } \\ & \Rightarrow<br />
{ \left\{ { \begin {array} { * { 2 0 } { l } }<br />
{ 1 5 { x ^ 2 } + 2 4 x + 8 = 0 } \\<br />
{ x \ne – 1 }<br />
\end {array} } \right. , \; \; } \Rightarrow<br />
{ D = 5 7 6 – 4 \cdot 1 5 \cdot 8 = 9 6 , \; \; } \\ & \Rightarrow<br />
{ { x _ { 1 , 2 } } = \frac { { – 2 4 \pm \sqrt { 9 6 } } } { { 3 0 } } }<br />
= { \frac { { – 2 4 \pm 4 \sqrt 6 } } { { 3 0 } } }<br />
\\ & = { \frac { 2 } { { 1 5 } } \left ( { – 6 \pm \sqrt 6 } \right ) } \approx { - 1 . 1 3 ; \; – 0.47. }<br />
\end {align*} $$
یکی از ریشهها برابر است با:
x = 2 15 ( – 6 – 6 ) ≈ – 1.13 \large x = { \frac { 2 } { { 1 5 } } } \left ( { – 6 – \sqrt 6 } \right ) \approx – 1 . 1 3 x = 15 2 ( –6– 6 ) ≈ –1.13
همانطور که میبینیم، این ریشه در دامنه تابع وجود ندارد. ریشه دیگر، به صورت زیر است:
x = 2 15 ( – 6 + 6 ) ≈ – 0.47 \large x = { \frac { 2 } { { 1 5 } } } \left ( { – 6 + \sqrt 6 } \right ) \approx – 0 . 4 7 x = 15 2 ( –6 + 6 ) ≈ –0.47
وقتی از نقطه بالا عبور میکنیم، علامت مشتق دوم تغییر میکند (شکل ۸ (الف)). بنابراین، این نقطه یک نقطه عطف است. مقدار تابع در این نقطه، تقریباً برابر است با:
y ( 2 15 ( – 6 + 6 ) ) ≈ y ( – 0.47 ) ≈ 0.16. \large { y \left ( { \frac { 2 } { { 1 5 } } \left ( { – 6 + \sqrt 6 } \right ) } \right ) } \approx { y \left ( { – 0 . 4 7 } \right ) \approx 0 . 1 6 . } y ( 15 2 ( –6 + 6 ) ) ≈ y ( –0.47 ) ≈ 0.16.
منحنی تابع، در سمت چپ این نقطه محدب رو به بالا و در سمت راست آن محدب رو به پایین است.
شکل ۸ (ب) نمودار تابع، در شکل ۸ (ب) نشان داده شده است.
شکل ۸ (ب) مثال ۹
نمودار تابع زیر را رسم کنید:
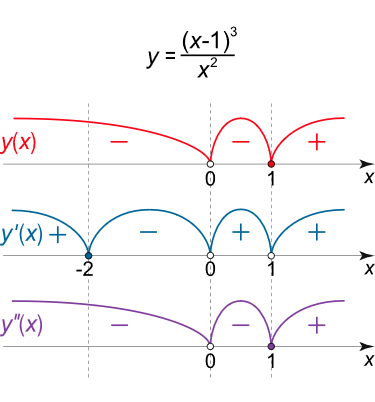
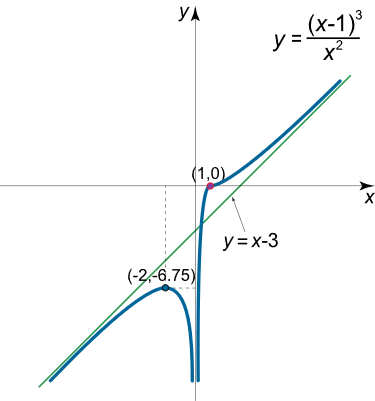
y = ( x – 1 ) 3 x 2 . \large y = \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } } { { { x ^ 2 } } } . y = x 2 ( x –1 ) 3 .
حل: دامنه تابع، x ≠ 0 x \ne 0 x = 0 x = 0 x = 0 x = 0
lim x → 0 – 0 y ( x ) = lim x → 0 – 0 ( x – 1 ) 3 x 2 = − ∞ , lim x → 0 + 0 y ( x ) = lim x → 0 + 0 ( x – 1 ) 3 x 2 = − ∞ . \large \begin {align*} \lim \limits _ { x \to 0 – 0 } y \left ( x \right ) & = { \lim \limits _ { x \to 0 – 0 } \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } }{ { { x ^ 2 } } } } = { - \infty , } \\ { \lim \limits _ { x \to 0 + 0 } y \left ( x \right ) } & = { \lim \limits _ { x \to 0 + 0 } \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } } { { { x ^ 2 } } } } = { - \infty . } \end {align*} x → 0–0 lim y ( x ) x → 0 + 0 lim y ( x ) = x → 0–0 lim x 2 ( x –1 ) 3 = − ∞ , = x → 0 + 0 lim x 2 ( x –1 ) 3 = − ∞.
بنابراین، x = 0 x = 0 x = 0
اکنون وجود مجانبهای مایل را بررسی میکنیم:
$$ \large \begin {align*}<br />
\require {cancel} k & = \lim \limits _ { x \to \pm \infty } \frac { { y \left ( x \right ) } } { x } = { \lim \limits _ { x \to \pm \infty } \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } } { { { x ^ 3 } } } } = { \lim \limits _ { x \to \pm \infty } { \left ( { 1 – \frac { 1 } { x } } \right ) ^ 3 } = 1 ; } \\<br />
b & = \lim \limits _ { x \to \pm \infty } \left [ { y \left ( x \right ) – k x } \right ] = { \lim \limits _ { x \to \pm \infty } \left [ { \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } } {{ { x ^ 2 }} } – x } \right ] } \\ & = { \lim \limits _ { x \to \pm \infty } \frac { { \cancel { x ^ 3 } – 3 { x ^ 2 } + 3 x – 1 – \cancel { x ^ 3 } } } { { { x ^ 2 } } } } = { \lim \limits _ { x \to \pm \infty } \left ( { – 3 + \frac { 3 } { x } – \frac { 1 } { { { x ^ 2 } } } } \right ) = – 3 . }<br />
\end {align*} $$
در نتیجه، مجانب مایل با رابطه زیر بیان میشود:
y = x – 3. \large y = x – 3 . y = x –3.
تقاطع تابع با محور x x x x = 1 x = 1 x = 1 x > 1 x > 1 x > 1 x < 1 x < 1 x < 1 x = 0 x = 0 x = 0
مشتق اول با فرمول زیر بیان میشود:
y ’ ( x ) = ( ( x – 1 ) 3 x 2 ) ′ = ( ( x – 1 ) 3 ) ′ x 2 – ( x – 1 ) 3 ( x 2 ) ′ x 4 = 3 ( x – 1 ) 2 x 2 – 2 x ( x – 1 ) 3 x 4 = ( x – 1 ) 2 ( x + 2 ) x 3 . \large \begin {align*} y’ \left ( x \right ) & = { \left ( { \frac { { { { \left ( { x – 1 } \right ) } ^ 3 } } } { { { x ^ 2 } } } } \right ) ^ \prime } = { \frac { { { { \left ( { { { \left ( { x – 1 } \right ) } ^ 3 } } \right ) } ^ \prime } { x ^ 2 } – { { \left ( { x – 1 } \right ) } ^ 3 } { { \left ( { { x ^ 2 } } \right ) } ^ \prime } } } { { { x ^ 4 } } } } \\ & = { \frac { { 3 { { \left ( { x – 1 } \right ) } ^ 2 } { x ^ 2 } – 2 x { { \left ( { x – 1 } \right ) } ^ 3 } } } { { { x ^ 4 } } } } = { \frac { { { { \left ( { x – 1 } \right ) } ^ 2 } \left ( { x + 2 } \right ) } } { { { x ^ 3 } } } . } \end {align*} y ’ ( x ) = ( x 2 ( x –1 ) 3 ) ′ = x 4 ( ( x –1 ) 3 ) ′ x 2 – ( x –1 ) 3 ( x 2 ) ′ = x 4 3 ( x –1 ) 2 x 2 –2 x ( x –1 ) 3 = x 3 ( x –1 ) 2 ( x + 2 ) .
بنابراین، نقاط بحرانی به صورت زیر هستند:
x 1 = 1 , x 2 = – 2 , x 3 = 0. \large \begin {align*} { { x _ 1 } = 1 , } \; \; \; \kern-0.3pt { { x _ 2 } = – 2 , } \; \; \; \kern-0.3pt { { x _ 3 } = 0 . } \end {align*} x 1 = 1 , x 2 = –2 , x 3 = 0.
تابع، در بازه ( − 2 , 0 ) \left({- 2,0}\right) ( − 2 , 0 ) ( − ∞ , − 2 ) \left({-\infty, -2}\right) ( − ∞ , − 2 ) ( 0 , 1 ) \left({0, 1}\right) ( 0 , 1 ) ( 1 , + ∞ ) \left({1, +\infty}\right) ( 1 , + ∞ )
در نقطه x = − 2 x = - 2 x = − 2
y ( – 2 ) = ( – 2 – 1 ) 3 2 2 = – 27 4 = – 6.75. \large { y \left ( { – 2 } \right ) = \frac { { { { \left ( { – 2 – 1 } \right ) } ^ 3 } } } { { { 2 ^ 2 } } } } = { – \frac { { 2 7 } }{ 4 } } = { – 6 . 7 5 .} y ( –2 ) = 2 2 ( –2–1 ) 3 = – 4 27 = –6.75.
در نقطه x = 1 x = 1 x = 1
اکنون مشتق دوم را محاسبه میکنیم:
y ′ ′ ( x ) = [ ( x – 1 ) 2 ( x + 2 ) x 3 ] ′ = [ ( 1 – 1 x ) 2 ( 1 + 1 x ) ] ′ = [ ( 1 – 2 x + 1 x 2 ) ( 1 + 1 x ) ] ′ = ( 2 x 3 – 3 x 2 + 1 ) ′ = ( 2 x – 3 – 3 x – 2 + 1 ) ′ = – 6 x – 4 + 6 x – 3 = 6 x 3 – 6 x 4 = 6 ( x – 1 ) x 4 . \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { { \left [ { \frac { { { { \left ( { x – 1 } \right ) } ^ 2 } \left ( { x + 2 } \right ) } } {{ { x ^ 3 } } } } \right ] ^ \prime } } = { { \left [ { { { \left ( { 1 – \frac { 1 } { x } } \right ) } ^ 2 } \left ( { 1 + \frac { 1 }{ x } } \right ) } \right ] ^ \prime } } \\ & = { { \left [ { \left ( { 1 – \frac { 2 } { x } + \frac { 1 } { { { x ^ 2 } } } } \right ) \left ( { 1 + \frac { 1 } { x } } \right ) } \right ] ^ \prime } } = { { \left ( { \frac { 2 } { { { x ^ 3 } } } – \frac { 3 } { { { x ^ 2 } } } + 1 } \right ) ^ \prime } } \\ & = { { \left ( { 2 { x ^ { – 3 } } – 3 { x ^ { – 2 } } + 1 } \right ) ^ \prime } } = { – 6 { x ^ { – 4 } } + 6 { x ^ { – 3 } } = \frac { 6 } { { { x ^ 3 } } } – \frac { 6 } { { { x ^ 4 } } } } = { \frac { { 6 \left ( { x – 1 } \right ) } } { { { x ^ 4 } } } . } \end {align*} y ′′ ( x ) = [ x 3 ( x –1 ) 2 ( x + 2 ) ] ′ = [ ( 1– x 1 ) 2 ( 1 + x 1 ) ] ′ = [ ( 1– x 2 + x 2 1 ) ( 1 + x 1 ) ] ′ = ( x 3 2 – x 2 3 + 1 ) ′ = ( 2 x –3 –3 x –2 + 1 ) ′ = –6 x –4 + 6 x –3 = x 3 6 – x 4 6 = x 4 6 ( x –1 ) .
با توجه به فرمول بالا، در x = 0 x = 0 x = 0 y ′ ′ = 0 y^{\prime\prime} = 0 y ′′ = 0 y ′ ′ > 0 y^{\prime\prime} \gt 0 y ′′ > 0 y ′ ′ < 0 y^{\prime\prime} \lt 0 y ′′ < 0 ( – ∞ , 0 ) \left( { – \infty ,0} \right) ( –∞ , 0 ) ( 0 , 1 ) \left( { 0, 1} \right) ( 0 , 1 ) ( 1 , + ∞ ) \left( {1, +\infty} \right) ( 1 , + ∞ ) x = 1 x = 1 x = 1 y ( 1 ) = 0 y\left( 1 \right) = 0 y ( 1 ) = 0
شکل ۹ (الف) نمودار تابع در شکل ۹ (ب) رسم شده است.
شکل ۹ (ب) مثال ۱۰
منحنی تابع زیر را رسم کنید:
حل: تابع برای همه x x x
با محاسبه حدهای زیر، وجود مجانب مایل یا افقی را بررسی میکنیم:
بنابراین، نمودار تابع، مجانبی دارد که معادله آن y = x y = x y = x x → + ∞ x \to +\infty x → + ∞ x → − ∞ x \to -\infty x → − ∞
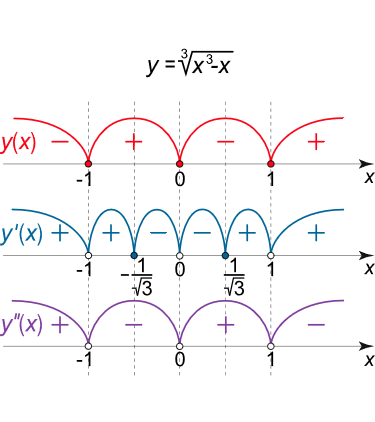
نقاط تقاطع منحنی با محورهای مختصات و بازههایی را که در آن، علامت تابع تغییر نمیکند نیز به صورت زیر محاسبه میکنیم:
نامساوی y ( x ) > 0 y\left( x \right) \gt 0 y ( x ) > 0
نامعادله بالا را میتوان با استفاده از روش بازهها حل کرد (شکل ۱۰ (الف)). میبینیم که تابع در بازههای ( – 1 , 0 ) \left( { – 1,0} \right) ( –1 , 0 ) ( 1 , + ∞ ) \left( { 1, +\infty} \right) ( 1 , + ∞ ) ( − ∞ , − 1 ) \left( { -\infty, -1} \right) ( − ∞ , − 1 ) ( 0 , 1 ) \left( {0,1} \right) ( 0 , 1 )
مشتق تابع، برابر است با:
y ’ ( x ) = ( x 3 – x 3 ) ′ = ( ( x 3 – x ) 1 3 ) ′ = 1 3 ( x 3 – x ) – 2 3 ⋅ ( 3 x 2 – 1 ) = 3 x 2 – 1 3 ( x 3 – x ) 2 3 . \large \begin {align*} y’ \left ( x \right ) & = { \left ( { \sqrt [ \large 3 \normalsize ]{ { { x ^ 3 } – x } } } \right ) ^ \prime } = { { \left ( { { { \left ( { { x ^ 3 } – x } \right ) } ^ { \large \frac { 1 }{ 3 } \normalsize } } } \right ) ^ \prime } } \\ & = { \frac { 1 } { 3 }{ \left ( { { x ^ 3 } – x } \right ) ^ { – \large \frac { 2 }{ 3 } \normalsize } } \cdot \left ( { 3 { x ^ 2 } – 1 } \right ) } = { \frac { { 3 { x ^ 2 } – 1 } } { { 3 \sqrt [ \large 3 \normalsize ]{ { { { \left ( { { x ^ 3 } – x } \right ) } ^ 2 } } } } } . } \end {align*} y ’ ( x ) = ( 3 x 3 – x ) ′ = ( ( x 3 – x ) 3 1 ) ′ = 3 1 ( x 3 – x ) – 3 2 ⋅ ( 3 x 2 –1 ) = 3 3 ( x 3 – x ) 2 3 x 2 –1 .
مشتق در x = 0 x = 0 x = 0 x = ± 1 x = \pm 1 x = ± 1
بنابراین، تابع پنج نقطه بحرانی دارد. تغییر علامت مشتق، هنگام عبور از این نقاط در شکل ۱۰ (الف) نشان داده شده است. نقطه x = – 1 3 x = – {\large\frac{1}{{\sqrt 3 }}\normalsize} x = – 3 1 x = 1 3 x = {\large\frac{1}{{\sqrt 3 }}\normalsize} x = 3 1
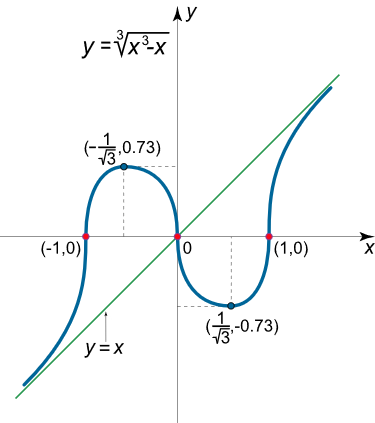
y ( – 1 3 ) = ( – 1 3 ) 3 – ( – 1 3 ) 3 = – 1 3 3 – 1 3 3 = – 1 – 3 3 3 3 = – 2 3 3 3 ≈ − 0.73 ; ⇒ y ( 1 3 ) = 0.73. \large \begin {align*} y \left ( { – \frac { 1 } { { \sqrt 3 } } } \right ) & = { \sqrt [ \large 3 \normalsize ] { { { { \left ( { – \frac { 1 } { { \sqrt 3 } } } \right ) } ^ 3 } – \left ( { – \frac { 1 } { { \sqrt 3 } } } \right ) } } } = { – \sqrt [ \large 3 \normalsize ]{ { \frac { 1 }{ { 3 \sqrt 3 } } – \frac { 1 } { { \sqrt 3 } } } } } \\ & = { – \sqrt [ \large 3 \normalsize ] { { \frac { { 1 – 3 } } { { 3 \sqrt 3 } } } } } = { – \sqrt [ \large 3 \normalsize ] { { \frac { 2 } { { 3 \sqrt 3 } } } } \approx - 0 . 7 3 ; \; \; } \\ & \Rightarrow { y \left ( { \frac { 1 } { { \sqrt 3 } } } \right ) = 0 . 7 3 .} \end {align*} y ( – 3 1 ) = 3 ( – 3 1 ) 3 – ( – 3 1 ) = – 3 3 3 1 – 3 1 = – 3 3 3 1–3 = – 3 3 3 2 ≈ − 0.73 ; ⇒ y ( 3 1 ) = 0.73.
مشتق دوم به صورت زیر محاسبه میشود:
شکل ۱۰ (الف) مشتق دوم در هیچ نقطهای صفر نمیشود و (مشابه مشتق اول) در نقاط x = 0 x = 0 x = 0 x = ± 1 x = \pm 1 x = ± 1 ( 0 , 0 ) \left( {0,0} \right) ( 0 , 0 ) ( − 1 , 0 ) \left( {-1,0} \right) ( − 1 , 0 ) ( 1 , 0 ) \left( {1,0} \right) ( 1 , 0 )
شکل ۱۰ (ب) مثال ۱۱
منحنی معادلات پارامتری زیر را رسم کنید.
x = t 3 + t 2 – t , y = t 3 + 2 t 2 – 4 t . \large { x = { t ^ 3 } + { t ^ 2 } – t , } \; \; \; \kern-0.3pt { y = { t ^ 3 } + 2 { t ^ 2 } – 4 t . } x = t 3 + t 2 – t , y = t 3 + 2 t 2 –4 t .
حل: نمودارهای دو تابع x ( t ) x (t) x ( t ) y ( t ) y (t) y ( t ) x ∈ R x \in \mathbb{R} x ∈ R x ( t ) x (t) x ( t )
x ’ ( t ) = ( t 3 + t 2 – t ) ′ = 3 t 2 + 2 t – 1. \large { x ’ \left ( t \right ) = { \left ( { { t ^ 3 } + { t ^ 2 } – t } \right ) ^ \prime } } = { 3 { t ^ 2 } + 2 t – 1 . } x ’ ( t ) = ( t 3 + t 2 – t ) ′ = 3 t 2 + 2 t –1.
با حل معادله x ’ ( t ) = 0 x’\left( t \right) = 0 x ’ ( t ) = 0 x ( t ) x (t) x ( t )
x ’ ( t ) = 0 , ⇒ 3 t 2 + 2 t – 1 = 0 , ⇒ t 1 , 2 = – 2 ± 16 6 = – 1 ; 1 3 . \large \begin{align*} x ’ \left ( t \right ) & = 0 , \; \; \Rightarrow { 3 { t ^ 2 } + 2 t – 1 = 0 , \; \; } \\ &\Rightarrow { { t _ { 1 , 2 } } = \frac { { – 2 \pm \sqrt { 1 6 } } } { 6 } = – 1 ; \; \frac { 1 } { 3 } . } \end {align*} x ’ ( t ) = 0 , ⇒ 3 t 2 + 2 t –1 = 0 , ⇒ t 1 , 2 = 6 –2 ± 16 = –1 ; 3 1 .
در t = 1 t = 1 t = 1 x ( t ) x (t) x ( t )
x ( – 1 ) = ( – 1 ) 3 + ( – 1 ) 2 – ( – 1 ) = 1 \large { x \left ( { – 1 } \right ) } = { { \left ( { – 1 } \right ) ^ 3 } + { \left ( { – 1 } \right ) ^ 2 } – \left ( { – 1 } \right ) } = { 1 } x ( –1 ) = ( –1 ) 3 + ( –1 ) 2 – ( –1 ) = 1
و در نقطه t = 1 3 t = {\large\frac{1}{3}\normalsize} t = 3 1
x ( 1 3 ) = ( 1 3 ) 3 + ( 1 3 ) 2 – ( 1 3 ) = 1 27 + 1 9 – 1 3 = – 5 27 . \large \begin{align*} x \left ( { \frac { 1 } { 3 } } \right ) & = { { \left ( { \frac { 1 } { 3 } } \right ) ^ 3 } + { \left ( { \frac { 1 } { 3 } } \right ) ^ 2 } – \left ( { \frac { 1 } { 3 } } \right ) } \\ &= { \frac { 1 } { { 2 7 } } + \frac { 1 } { 9 } – \frac { 1 } { 3 } = – \frac { 5 } { { 2 7 } } . } \end {align*} x ( 3 1 ) = ( 3 1 ) 3 + ( 3 1 ) 2 – ( 3 1 ) = 27 1 + 9 1 – 3 1 = – 27 5 .
اکنون مشتق تابع y ( t ) y (t) y ( t )
y ’ ( t ) = ( t 3 + 2 t 2 – 4 t ) ′ = 3 t 2 + 4 t – 4. \large { y ’ \left ( t \right ) = { \left ( { { t ^ 3 } + 2 { t ^ 2 } – 4 t } \right ) ^ \prime } } = { 3 { t ^ 2 } + 4 t – 4 .} y ’ ( t ) = ( t 3 + 2 t 2 –4 t ) ′ = 3 t 2 + 4 t –4.
به طریق مشابه، نقاط مانای y ( t ) y(t) y ( t )
y ’ ( t ) = 0 , ⇒ 3 t 2 + 4 t – 4 = 0 , ⇒ t 1 , 2 = – 4 ± 64 6 = – 2 ; 2 3 . \large \begin {align*} { y’ \left ( t \right ) = 0 , \; \; } & \Rightarrow { 3 { t ^ 2 } + 4 t – 4 = 0 , \; \; } \\ & \Rightarrow { { t _ { 1 , 2 } } = \frac { { – 4 \pm \sqrt { 6 4 } } } { 6 } = – 2 ; \; \frac {2 } { 3 } .} \end {align*} y ’ ( t ) = 0 , ⇒ 3 t 2 + 4 t –4 = 0 , ⇒ t 1 , 2 = 6 –4 ± 64 = –2 ; 3 2 .
تابع y ( t ) y(t) y ( t ) t = − 2 t = -2 t = − 2
y ( – 2 ) = ( – 2 ) 3 + 2 ( – 2 ) 2 – 4 ( – 2 ) = 8 \large y \left ( { – 2 } \right ) = { \left ( { – 2 } \right ) ^ 3 } + 2 { \left ( { – 2 } \right ) ^ 2 } – 4 \left ( { – 2 } \right ) = 8 y ( –2 ) = ( –2 ) 3 + 2 ( –2 ) 2 –4 ( –2 ) = 8
همچنین، در نقطه t = 2 3 t = {\large\frac{2}{3}\normalsize} t = 3 2
y ( 2 3 ) = ( 2 3 ) 3 + 2 ( 2 3 ) 2 – 4 ⋅ 2 3 = 8 27 + 8 9 – 8 3 = – 40 27 . \large \begin {align*} y \left ( { \frac { 2 } { 3 } } \right ) & = { { \left ( { \frac { 2 } { 3 } } \right ) ^ 3 } + 2 { \left ( { \frac { 2 } { 3 } } \right ) ^ 2 } – 4 \cdot \frac { 2 } { 3 } } \\ & = { \frac { 8 } { { 2 7 } } + \frac { 8 } { 9 } – \frac { 8 } { 3 } } = { – \frac { { 4 0 } }{ { 2 7 } } . } \end {align*} y ( 3 2 ) = ( 3 2 ) 3 + 2 ( 3 2 ) 2 –4 ⋅ 3 2 = 27 8 + 9 8 – 3 8 = – 27 40 .
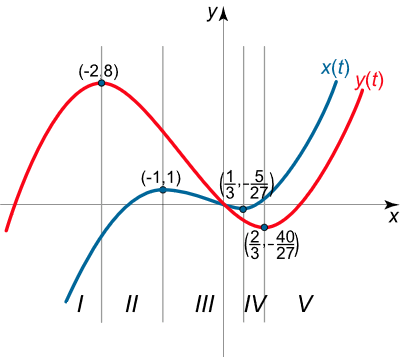
نمودار توابع x ( t ) x (t) x ( t ) y ( t ) y(t) y ( t )
شکل ۱۱ (الف) حدود این دو تابع در بینهایت، برابر است با:
lim t → ± ∞ x ( t ) = ± ∞ , lim t → ± ∞ y ( t ) = ± ∞ \large { \lim \limits _ { t \to \pm \infty } x \left ( t \right ) = \pm \infty , \; \; \; } \kern-0.3pt { \lim \limits _ { t \to \pm \infty } y \left ( t \right ) = \pm \infty } t → ± ∞ lim x ( t ) = ± ∞ , t → ± ∞ lim y ( t ) = ± ∞
بنابراین، نمودار y ( x ) y (x) y ( x )
k = lim t → ± ∞ y ( t ) x ( t ) = lim t → ± ∞ t 3 + 2 t 2 – 4 t t 3 + t 2 – t = lim t → ± ∞ 1 + 2 t – 4 t 2 1 + 1 t – 1 t 2 = 1 , b = lim t → ± ∞ [ y ( t ) – k x ( t ) ] = lim t → ± ∞ ( t 2 – 3 t ) = + ∞ , \large \begin {align*} k & = \lim \limits _ { t \to \pm \infty } \frac { { y \left ( t \right ) } } { { x \left ( t \right ) } } = { \lim \limits _ { t \to \pm \infty } \frac { { { t ^ 3 } + 2 { t ^ 2 } – 4 t } } { { { t ^ 3 } + { t ^ 2 } – t } } } = { \lim \limits _ { t \to \pm \infty } \frac { { 1 + \frac { 2 } { t } – \frac { 4 } { { { t ^ 2 } } } } } { { 1 + \frac { 1 } { t } – \frac { 1 } { { { t ^ 2 } } } } } = 1,} \\ b & = \lim \limits _ { t \to \pm \infty } \left [ { y \left ( t \right ) – k x \left ( t \right ) } \right ] = { \lim \limits _ { t \to \pm \infty } \left ( { { t ^ 2 } – { 3 t } } \right ) } = { + \infty , } \end {align*} k b = t → ± ∞ lim x ( t ) y ( t ) = t → ± ∞ lim t 3 + t 2 – t t 3 + 2 t 2 –4 t = t → ± ∞ lim 1 + t 1 – t 2 1 1 + t 2 – t 2 4 = 1 , = t → ± ∞ lim [ y ( t ) – k x ( t ) ] = t → ± ∞ lim ( t 2 – 3 t ) = + ∞ ,
اکنون، نقاط تقاطع منحنی y ( x ) y (x) y ( x ) x x x
y ( t ) = t 3 + 2 t 2 – 4 t = 0 , ⇒ t ( t 2 + 2 t – 4 ) = 0 ; \large { y \left ( t \right ) = { t ^ 3 } + 2 { t ^ 2 } – 4 t = 0 , \; \; } \Rightarrow { t \left ( { { t ^ 2 } + 2 t – 4 } \right ) = 0 ; } y ( t ) = t 3 + 2 t 2 –4 t = 0 , ⇒ t ( t 2 + 2 t –4 ) = 0 ;
نقطه تقاطع نخست به صورت زیر است:
t 1 = 0 ; \large {t_1} = 0; t 1 = 0 ;
نقاط تقاطع دیگر نیز برابرند با:
t 2 + 2 t – 4 = 0 , ⇒ D = 4 – 4 ⋅ ( – 4 ) = 20 , ⇒ t 2 , 3 = – 2 ± 20 2 = – 1 ± 5 . \large \begin {align*} { t ^ 2 } + 2 t – 4 = 0, & \Rightarrow { D = 4 – 4 \cdot \left ( { – 4 } \right ) = 2 0 , } \\ & \Rightarrow { { t _ { 2 , 3 } } = { \large \frac { { – 2 \pm \sqrt { 2 0 } } } { 2 } \normalsize } } = { – 1 \pm \sqrt 5 .} \end {align*} t 2 + 2 t –4 = 0 , ⇒ D = 4–4 ⋅ ( –4 ) = 20 , ⇒ t 2 , 3 = 2 –2 ± 20 = –1 ± 5 .
مقدار x x x
x ( t 1 ) = x ( 0 ) = 0 ; \large x \left ( { { t _ 1 } } \right ) = x \left ( 0 \right ) = 0 ; x ( t 1 ) = x ( 0 ) = 0 ;
x ( t 2 ) = x ( – 1 – 5 ) = ( – 1 – 5 ) 3 + ( – 1 – 5 ) 2 − ( – 1 – 5 ) = – ( 1 + 3 5 + 15 + 5 5 ) + ( 1 + 2 5 + 5 ) + 1 + 5 = – 16 – 8 5 + 6 + 2 5 + 1 + 5 = – 9 – 5 5 ≈ 20.18 ; \large \begin {align*} x \left ( { { t _ 2 } } \right ) & = x \left ( { – 1 – \sqrt 5 } \right ) = { { \left ( { – 1 – \sqrt 5 } \right ) ^ 3 } + { \left ( { – 1 – \sqrt 5 } \right ) ^ 2 } } - { \left ( { – 1 – \sqrt 5 } \right ) } \\ &= { – \left ( { 1 + 3 \sqrt 5 + 1 5 + 5 \sqrt 5 } \right ) } + { \left ( { 1 + 2 \sqrt 5 + 5 } \right ) + 1 + \sqrt 5 } \\&= { – 1 6 – 8 \sqrt 5 + 6 + 2 \sqrt 5 + 1 + \sqrt 5 } = { – 9 – 5 \sqrt 5 \approx 2 0 . 1 8 ; } \end {align*} x ( t 2 ) = x ( –1– 5 ) = ( –1– 5 ) 3 + ( –1– 5 ) 2 − ( –1– 5 ) = – ( 1 + 3 5 + 15 + 5 5 ) + ( 1 + 2 5 + 5 ) + 1 + 5 = –16–8 5 + 6 + 2 5 + 1 + 5 = –9–5 5 ≈ 20.18 ;
x ( t 3 ) = x ( – 1 + 5 ) = ( – 1 + 5 ) 3 + ( – 1 + 5 ) 2 − ( – 1 + 5 ) = – ( 1 – 3 5 + 15 – 5 5 ) + ( 1 – 2 5 + 5 ) + 1 – 5 = – 16 + 8 5 + 6 – 2 5 + 1 – 5 = – 9 + 5 5 ≈ 2.18. \large \begin {align*} x \left ( { { t _ 3 } } \right ) & = x \left ( { – 1 + \sqrt 5 } \right ) = { { \left ( { – 1 + \sqrt 5 } \right ) ^ 3 } + { \left ( { – 1 + \sqrt 5 } \right ) ^ 2 } } - { \left ( { – 1 + \sqrt 5 } \right ) } \\ & = { – \left ( { 1 – 3 \sqrt 5 + 1 5 – 5 \sqrt 5 } \right ) } + { \left ( { 1 – 2 \sqrt 5 + 5 } \right ) + 1 – \sqrt 5 } \\ & = { – 1 6 + 8 \sqrt 5 + 6 – 2 \sqrt 5 + 1 – \sqrt 5 } = { – 9 + 5 \sqrt 5 \approx 2. 1 8 .} \end {align*} x ( t 3 ) = x ( –1 + 5 ) = ( –1 + 5 ) 3 + ( –1 + 5 ) 2 − ( –1 + 5 ) = – ( 1–3 5 + 15–5 5 ) + ( 1–2 5 + 5 ) + 1– 5 = –16 + 8 5 + 6–2 5 + 1– 5 = –9 + 5 5 ≈ 2.18.
به طریق مشابه، نقاط تقاطع با محور y y y
x ( t ) = t 3 + t 2 – t = 0 , ⇒ t ( t 2 + t – 1 ) = 0 ; \large { x \left ( t \right ) = { t ^ 3 } + { t ^ 2 } – t = 0 , \; \; } \Rightarrow { t \left ( { { t ^ 2 } + t – 1 } \right ) = 0 ; } x ( t ) = t 3 + t 2 – t = 0 , ⇒ t ( t 2 + t –1 ) = 0 ;
این نقاط به صورت زیر به دست میآیند:
t 1 = 0 ; \large { t _ 1 } = 0 ; t 1 = 0 ;
t 2 + t – 1 = 0 , ⇒ D = 1 – 4 ⋅ ( – 1 ) = 5 , ⇒ t 2 , 3 = – 1 ± 5 2 . \large \begin {align*} { t ^ 2 } + t – 1 = 0 , & \Rightarrow { D = 1 – 4 \cdot \left ( { – 1 } \right ) = 5 , } \\ &\Rightarrow { { t _ { 2 , 3 } } = { \large \frac { { – 1 \pm \sqrt { 5 } } } { 2 } \normalsize } . } \end {align*} t 2 + t –1 = 0 , ⇒ D = 1–4 ⋅ ( –1 ) = 5 , ⇒ t 2 , 3 = 2 –1 ± 5 .
مقدار y y y
y ( t 1 ) = y ( 0 ) = 0 ; y ( t 2 ) = y ( – 1 – 5 2 ) = 3 + 2 5 ≈ 7.47 ; y ( t 3 ) = y ( – 1 + 5 2 ) = 3 – 2 5 ≈ – 1.47. \large \begin {align*} y \left ( { { t _ 1 } } \right ) & = y \left ( 0 \right ) = 0 ; \\ y \left ( { { t _ 2 } } \right ) & = y \left ( { \frac { { – 1 – \sqrt 5 } } { 2 } } \right) = { 3 + 2 \sqrt 5 \approx 7 . 4 7 ; } \\ y \left ( { { t _ 3 } } \right ) & = y \left ( { \frac { { – 1 + \sqrt 5 } } { 2 } } \right ) = { 3 – 2 \sqrt 5 \approx – 1.47.} \end {align*} y ( t 1 ) y ( t 2 ) y ( t 3 ) = y ( 0 ) = 0 ; = y ( 2 –1– 5 ) = 3 + 2 5 ≈ 7.47 ; = y ( 2 –1 + 5 ) = 3–2 5 ≈ –1.47.
پارامتر t t t
( – ∞ , – 2 ) , ( – 2 , – 1 ) , ( – 1 , 1 3 ) , ( 1 3 , 2 3 ) , ( 2 3 , + ∞ ) . \large { \left ( { – \infty , – 2 } \right ) , \; \; } \kern-0.3pt { \left ( { – 2 , – 1 } \right ) , \; \; } \kern-0.3pt { \left ( { – 1 , \frac { 1 } { 3 } } \right ) , \; \; } \kern-0.3pt { \left ( { \frac { 1 } { 3 } , \frac { 2 } { 3 } } \right ) , \; \; } \kern-0.3pt { \left ( { \frac { 2 } { 3 } , + \infty } \right ) . } ( –∞ , –2 ) , ( –2 , –1 ) , ( –1 , 3 1 ) , ( 3 1 , 3 2 ) , ( 3 2 , + ∞ ) .
در بازه ( – ∞ , – 2 ) \left( { – \infty , – 2} \right) ( –∞ , –2 ) x x x y y y − ∞ -\infty − ∞ x ( – 2 ) = – 2 x\left( { – 2} \right) = – 2 x ( –2 ) = –2 y ( – 2 ) = 8 y\left( { – 2} \right) = 8 y ( –2 ) = 8
شکل ۱۱ (ب) در بازه دوم ( – 2 , – 1 ) \left( { – 2, – 1} \right) ( –2 , –1 ) x x x x ( – 2 ) = – 2 x\left( { – 2} \right) = – 2 x ( –2 ) = –2 x ( – 1 ) = 1 x\left( { – 1} \right) = 1 x ( –1 ) = 1 y y y y ( – 2 ) = 8 y\left( { – 2} \right) = 8 y ( –2 ) = 8 y ( – 1 ) = 5. y\left( { – 1} \right) = 5. y ( –1 ) = 5.
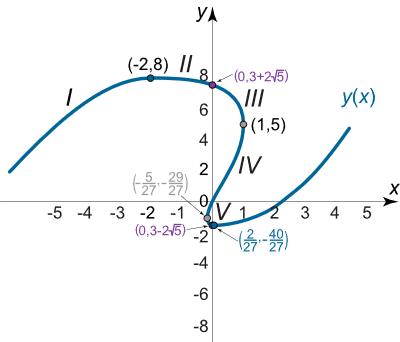
منحنی y ( x ) y (x) y ( x ) ( 0.3 + 2 5 ) \left( {0.3 + 2\sqrt 5 } \right) ( 0.3 + 2 5 )
در بازه سوم ( – 1 , 1 3 ) \left( { – 1,{\large\frac{1}{3}\normalsize}} \right) ( –1 , 3 1 ) x x x x ( – 1 ) = 1 x\left( { – 1} \right) = 1 x ( –1 ) = 1 x ( 1 3 ) = – 5 27 x\left( {\large\frac{1}{3}\normalsize} \right) = – {\large\frac{5}{{27}}\normalsize} x ( 3 1 ) = – 27 5 y ( x ) y(x) y ( x )
در بازه چهارم ( 1 3 , 2 3 ) \left( {\large\frac{1}{3}\normalsize,\large\frac{2}{3}\normalsize} \right) ( 3 1 , 3 2 ) x x x x ( 1 3 ) = – 5 27 x\left( {\large\frac{1}{3}\normalsize} \right) = – {\large\frac{5}{{27}}\normalsize} x ( 3 1 ) = – 27 5 x ( 2 3 ) = 2 27 x\left( {\large\frac{2}{3}\normalsize} \right) = {\large\frac{2}{{27}}\normalsize} x ( 3 2 ) = 27 2 y y y y ( 1 3 ) = – 29 27 y\left( {\large\frac{1}{3}\normalsize} \right) = – {\large\frac{29}{{27}}\normalsize} y ( 3 1 ) = – 27 29 y ( 2 3 ) = – 40 27 y\left( {\large\frac{2}{3}\normalsize} \right) = – {\large\frac{40}{{27}}\normalsize} y ( 3 2 ) = – 27 40 y ( x ) y (x) y ( x ) y y y ( 0.3 – 2 5 ) \left( {0.3 – 2\sqrt 5 } \right) ( 0.3–2 5 )
در بازه آخر ( 2 3 , + ∞ ) \left( {{\large\frac{2}{3}\normalsize}, + \infty } \right) ( 3 2 , + ∞ ) x ( t ) x (t) x ( t ) y ( t ) y (t) y ( t ) y ( x ) y (x) y ( x ) x x x x = – 9 + 5 5 ≈ 2.18 x = – 9 + 5\sqrt 5 \approx 2.18 x = –9 + 5 5 ≈ 2.18
برای واضحتر شدن منحنی y ( x ) y (x) y ( x ) y ’ ( x ) y’\left( x \right) y ’ ( x )
y ’ ( x ) = y ’ x = y ’ t x ’ t = ( t 3 + 2 t 2 – 4 t ) ′ ( t 3 + t 2 – t ) ′ = 3 t 2 + 4 t – 4 3 t 2 + 2 t – 1 = 3 ( t + 2 ) ( t – 2 3 ) 3 ( t + 1 ) ( t – 1 3 ) = ( t + 2 ) ( t – 2 3 ) ( t + 1 ) ( t – 1 3 ) . \large \begin {align*} y’ \left ( x \right ) & = { y’ _ x } = { \frac { { { y’ _ t } } }{ { { x ’ _ t } } } } = { \frac { { { { \left ( { { t ^ 3 } + 2 { t ^ 2 } – 4 t } \right ) } ^ \prime } } } { { { { \left ( { { t ^ 3 } + { t ^ 2 } – t } \right ) } ^ \prime } } } } = { \frac { { 3 { t ^ 2 } + 4 t – 4 } } { { 3 { t ^ 2 } + 2 t – 1 } } } \\ &= { \frac { { \cancel { 3 } \left ( { t + 2 } \right ) \left ( { t – \frac { 2 } { 3 } } \right ) } } { { \cancel { 3 } \left ( { t + 1 } \right ) \left ( { t – \frac { 1 } { 3 } } \right ) } } } = { \frac { { \left ( { t + 2 } \right ) \left ( { t – \frac { 2 } { 3 } } \right ) } } { { \left ( { t + 1 } \right ) \left ( { t – \frac { 1 } { 3 } } \right ) } } . } \end {align*} y ’ ( x ) = y ’ x = x ’ t y ’ t = ( t 3 + t 2 – t ) ′ ( t 3 + 2 t 2 –4 t ) ′ = 3 t 2 + 2 t –1 3 t 2 + 4 t –4 = 3 ( t + 1 ) ( t – 3 1 ) 3 ( t + 2 ) ( t – 3 2 ) = ( t + 1 ) ( t – 3 1 ) ( t + 2 ) ( t – 3 2 ) .
با توجه به رابطه اخیر، میتوان نشان داد که منحنی در t = − 2 t = - 2 t = − 2 t = 2 3 t = \large\frac{2}{3}\normalsize t = 3 2 t = 1 3 t = {\large\frac{1}{3}\normalsize} t = 3 1 y ( x ) y (x) y ( x )
اکنون درباره تقعر/تحدب منحنی بحث میکنیم. مشتق دوم y ′ ′ ( x ) y^{\prime\prime}\left( x \right) y ′′ ( x )
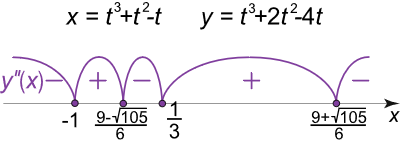
y ′ ′ ( x ) = y x x ′ ′ = ( y ’ x ) ’ t x ’ t = ( 3 t 2 + 4 t – 4 3 t 2 + 2 t – 1 ) ′ ( t 3 + t 2 – t ) ′ = – 6 t 2 + 18 t + 4 ( 3 t 2 + 2 t – 1 ) 3 = – 6 ( t – 9 – 105 6 ) ( t – 9 + 105 6 ) ( t + 1 ) 3 ( 3 t – 1 ) 3 \large \begin {align*} y ^ { \prime \prime } \left ( x \right ) & = { y ^ { \prime \prime } _ { x x } } = \frac { { { { \left ( { { y’ _ x } } \right ) }’ _ t } } } { { { x’ _ t } } } = \frac { { { { \left ( { \frac { { 3 { t ^ 2 } + 4 t – 4 } } { { 3 { t ^ 2 } + 2 t – 1 } } } \right ) } ^ \prime } } } { { { { \left ( { { t ^ 3 } + { t ^ 2 } – t } \right ) } ^ \prime } } } \\ & = \frac { { – { 6 { t ^ 2 } } + { 1 8 t } + { 4 } } } { { { { \left ( { 3 { t ^ 2 } + 2 t – 1 } \right ) } ^ 3 } } } = \frac { { – 6 \left ( { t – \frac { { 9 – \sqrt { 1 0 5 } } } { 6 } } \right ) \left ( { t – \frac { { 9 + \sqrt { 1 0 5 } } } { 6 } } \right ) } } { { { { \left ( { t + 1 } \right ) } ^ 3 }{ { \left ( { 3 t – 1 } \right ) } ^ 3 } } } \end {align*} y ′′ ( x ) = y xx ′′ = x ’ t ( y ’ x ) ’ t = ( t 3 + t 2 – t ) ′ ( 3 t 2 + 2 t –1 3 t 2 + 4 t –4 ) ′ = ( 3 t 2 + 2 t –1 ) 3 – 6 t 2 + 18 t + 4 = ( t + 1 ) 3 ( 3 t –1 ) 3 –6 ( t – 6 9– 105 ) ( t – 6 9 + 105 )
شکل ۱۱ (ج) علامت مشتق دوم با عبور از نقاط زیر تغییر میکند:
t 1 = – 1 : x ( – 1 ) = 1 , y ( – 1 ) = 5 ; t 2 = 9 – 105 6 : x ( 9 – 105 6 ) ≈ 0.24 ; y ( 9 – 105 6 ) ≈ 0.91 ; t 3 = 1 3 : x ( 1 3 ) = – 5 27 , y ( 1 3 ) = – 29 27 ; t 4 = 9 + 105 6 : x ( 9 + 105 6 ) ≈ 40.1 ; y ( 9 + 105 6 ) ≈ 40.8. \large \begin {align*} { t _ 1 } & = – 1 : \; \; x \left ( { – 1 } \right ) = 1 , \; \; { y \left ( { – 1 } \right ) = 5 ; } \\ { t _ 2 } & = \frac { { 9 – \sqrt { 1 0 5 } } } { 6 } : \; \; \kern-0.3pt { x \left ( { \frac { { 9 – \sqrt { 1 0 5 } } } { 6 } } \right ) \approx 0 . 2 4 ; \; \; } \kern-0.3pt { y \left ( { \frac { { 9 – \sqrt { 1 0 5 } } } { 6 } } \right ) \approx 0 . 9 1 ; } \\ { t _ 3 } & = \frac { 1 } { 3 } : \; \; \kern-0.3pt { x \left ( { \frac { 1 } { 3 } } \right ) = – \frac { 5 } { { 2 7 } } , \; \; } \kern-0.3pt { y \left ( { \frac { 1 } { 3 } } \right ) = – \frac { { 2 9 } } { { 2 7 } } ; } \\ { t _ 4 } & = \frac { { 9 + \sqrt { 10 5 } } } { 6 } : \; \; \kern-0.3pt { x \left ( { \frac { { 9 + \sqrt { 1 0 5 } } } { 6 } } \right ) \approx 4 0 . 1 ; \; \; } \kern-0.3pt { y \left ( { \frac { { 9 + \sqrt { 1 0 5 } } } { 6 } } \right ) \approx 4 0 . 8 .} \end {align*} t 1 t 2 t 3 t 4 = –1 : x ( –1 ) = 1 , y ( –1 ) = 5 ; = 6 9– 105 : x ( 6 9– 105 ) ≈ 0.24 ; y ( 6 9– 105 ) ≈ 0.91 ; = 3 1 : x ( 3 1 ) = – 27 5 , y ( 3 1 ) = – 27 29 ; = 6 9 + 105 : x ( 6 9 + 105 ) ≈ 40.1 ; y ( 6 9 + 105 ) ≈ 40.8.
بنابراین، این نقاط، نقاط عطف منحنی y ( x ) y (x) y ( x )
شکل ۱۱ (ب)، منحنی تابع را نشان میدهد.

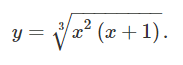
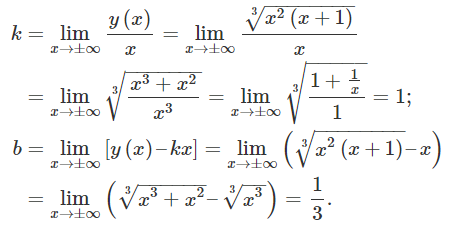
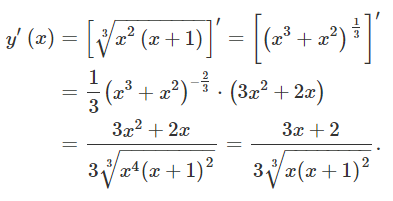
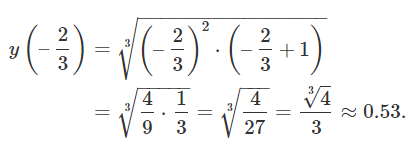
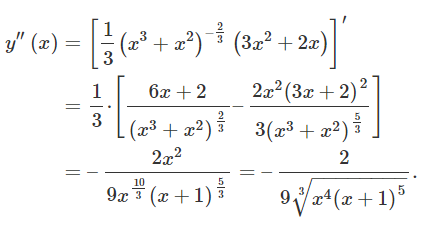
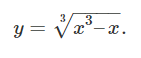
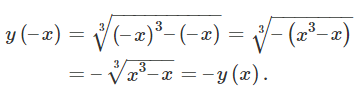
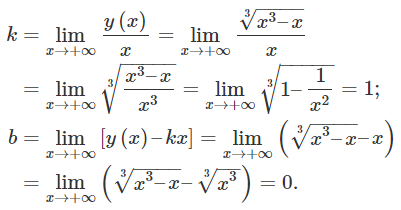
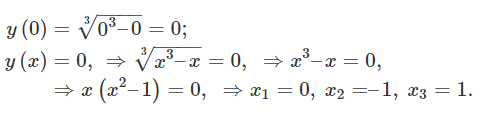
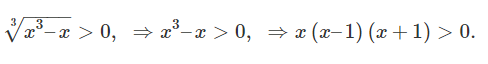
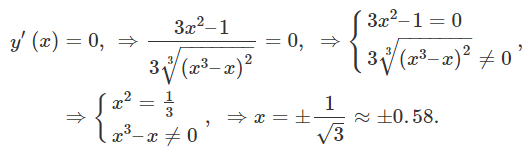
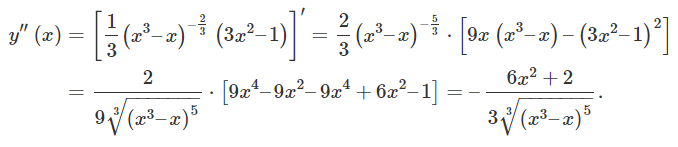













مثلا من بخوام تابع
X3+1-
X3 منظورم تابع درجه ۳ هستش
اول باید قرینه محور x رو انجام بدم بعد یک واحد برم بالا یا برعکس؟
ابتدا نسبت به محور افقی قرینه سپس یکی ب بالا، در تابع
kf(ax+b)+c
اول اولویت با b سپس با a و بعد k ث در آخر با c