تابع همساز چیست؟ — به زبان ساده + مثال و تمرین

تابع همساز یا هارمونیک در ریاضیات پیشرفته به تابعی حقیقی گفته می‌شود که مشتقات جزئی مرتبه دوم داشته باشد و این مشتق‌ها در معادله لاپلاس صدق کنند. در این آموزش از مجله فرادرس، با «تابع همساز» (Harmonic Function) آشنا می‌شویم.

عملگر لاپلاسین و مفهوم آن

عملگرهای مهمی در ریاضیات وجود دارد که هر مهندس و فیزیکدانی باید با آن‌ها آشنایی داشته باشد. یکی از این عملگرها لاپلاسین است که در اینجا سعی می‌کنیم به‌خوبی با آن آشنا شویم. لاپلاسین عملگری است که در بسیاری از مسائل و فرمول‌های فیزیک ظاهر می‌شود. اما لاپلاسین دقیقاً چیست و چه ارتباطی با توابع هارمونیک دارد؟

به عبارت ساده، عملگر در ریاضیات چیزی است که یک تابع را به‌عنوان ورودی می‌گیرد و تابع دیگری را به‌عنوان خروجی به ما می‌دهد. فرض کنید تابع اسکالر دومتغیره $$f = f(x,y)$$ را داریم. لاپلاسین $$f = f(x,y)$$ به‌عنوان دیورژانس یا واگرایی گرادیان آن تعریف می‌شود که برابر با مجموع مشتقات فضایی مرتبه دوم تابع در مختصات دکارتی است.

$$ \nabla \cdot \nabla f = \nabla ^ { 2 } f = \frac { \partial ^ { 2 } f } { \partial x ^ { 2 } } + \frac { \partial ^ { 2 } f } { \partial y ^ { 2 } } $$

نمادی که معمولاً برای نشان دادن لاپلاسین به کار می‌بریم، یا مربع عملگر دل ($$\nabla$$) یا مثلث رو به بالا ($$\Delta$$) است.

توجه داشته باشید که این شکل لاپلاسین فقط برای مختصات دکارتی است. وقتی از دستگاه مختصات دیگری مانند قطبی، استوانه‌ای یا کروی استفاده می‌کنیم، فرمول لاپلاسین تغییر می‌کند.

دیدیم که لاپلاسین در مختصات دکارتی این‌گونه است:

$$ \nabla ^ { 2 } = \frac { \partial ^ { 2 } } { \partial x ^ { 2 } } + \frac { \partial ^ { 2 } } { \partial y ^ { 2 } } + \frac { \partial ^ { 2 } } { \partial z ^ { 2 } } $$

لاپلاسین در مختصات استوانه‌ای به‌شکل زیر خواهد بود:

$$ \nabla ^ { 2 } = \frac { \partial ^ { 2 } } { \partial r ^ { 2 } } + \frac { 1 } { r } \frac { \partial } { \partial r } + \frac { 1 } { r ^ { 2 } } \frac { \partial ^ { 2 } } { \partial \phi ^ { 2 } } + \frac { \partial ^ { 2 } } { \partial { z } ^ { 2 } } $$

در مختصات کروی نیز، تعریف زیر را برای لاپلاسین داریم:

$$ \nabla ^ { 2 } = \frac { 1 } { { r } ^ { 2 } } \frac { \partial } { \partial r } \left ( { r } ^ { 2 } \frac { \partial } { \partial r } \right ) + \frac { 1 } { { r } ^ { 2 } \sin \theta } \frac { \partial } { \partial \theta } \left ( \sin \theta \frac { \partial } { \partial \theta } \right ) + \frac { 1 } { { r } ^ { 2 } \sin ^ { 2 } \theta } \frac { \partial ^ { 2 } } { \partial \phi ^ { 2 } } $$

به‌جای به خاطر سپردن همه این فرمول‌ها — که ضروری هم نیست — بر مفهم لاپلاسین و آنچه این عملگر واقعاً نشان می‌دهد، تمرکز خواهیم کرد. مطمئناً شکل لاپلاسین ممکن است برای دستگاه‌های مختصات مختلف تغییر کند، اما مفهوم آن ثابت است. 

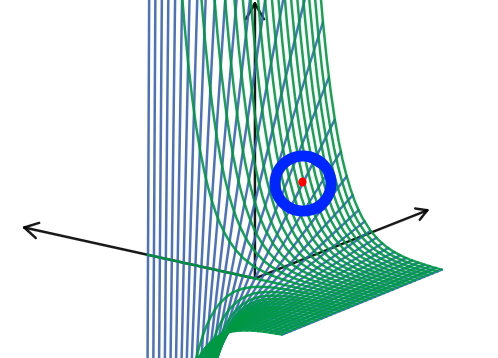
می‌دانیم که گرادیان یک تابع اسکالر، یک میدان برداری است که در جهت بزرگ‌ترین شیب صعودی نمودار آن تابع است.

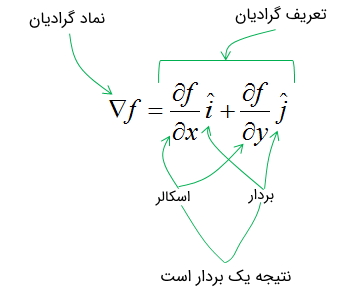
اگر در یک کمینه (مینیمم) محلی یک تابع باشیم، پیکان‌های میدان گرادیان آن در همه جهات از آن نقطه دور خواهند شد. اگر ما در بیشینه (ماکزیمم) محلی باشیم، همه آن‌ها در آن نقطه همگرا می‌شوند، زیرا هیچ نقطه بالاتر دیگری در آن نزدیکی وجود ندارد. شکل زیر، یک تابع اسکالر (نمودار آبی) و میدان گرادیان آن (پیکان‌ها در صفحه x-y) را نشان می‌دهد. 

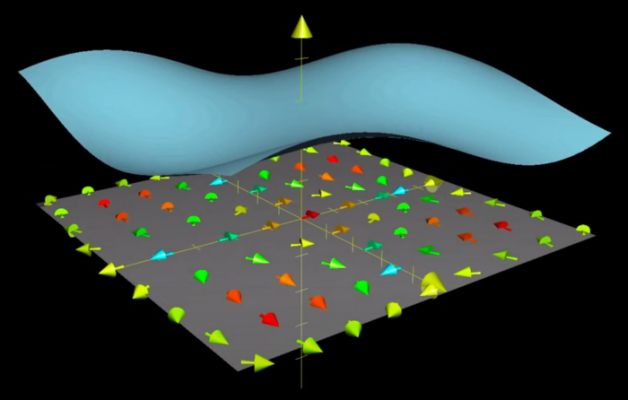
بنابراین، دیورژانس یک میدان برداری در یک نقطه خاص، میزان تمایل میدان برداری به «گسترش» یا «واگرایی» در آن نقطه است.

$$ \nabla \cdot \vec { A } = \frac { \partial A _ { x } } { \partial x } + \frac { \partial A _ { y } } { \partial y } + \frac { \partial A _ { z } } { \partial z } $$

به بیان ساده، اگر پیکان‌های میدان برداری تمایل به همگرا شدن در یک نقطه داشته باشند، واگرایی در آن نقطه منفی خواهد بود. در مقابل، اگر پیکان‌ها از هم جدا شوند، واگرایی مثبت خواهد بود.

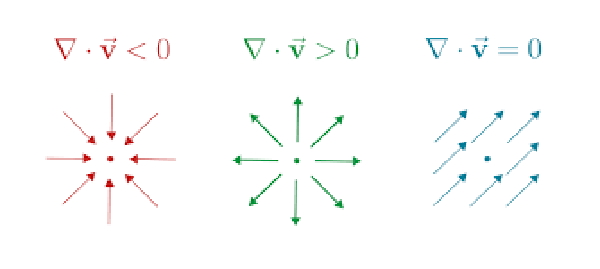
به موضوع اصلی برمی‌گردیم. قبل‌تر لاپلاسین را به‌عنوان واگرایی گرادیان یک تابع اسکالر تعریف کردیم. با نگاهی همه مواردی که در بالا گفتیم، به‌راحتی می‌توان دریافت که واگرایی گرادیان در نقاطی که شبیه کمینه‌های محلی هستند مثبت و بسیار زیاد است، در حالی که در نقاطی که شبیه بیشینه‌های محلی هستند، منفی و کم است.

اگر کمی در این مفهوم تأمل کنیم به این نتیجه می‌رسیم که لاپلاسین یک تابع اسکالر در یک نقطه اندازه‌گیری و سنجه‌ای است که مقدار تابع در آن نقطه با میانگین مقادیر همسایه‌اش تفاوت دارد.

اگر لاپلاسین در یک نقطه مثبت (منفی) باشد، به این معنی است که میانگین مقادیر همسایه آن نقطه بزرگ‌تر (کوچک‌تر) از مقدار در آن نقطه است. برای مثال، فرض کنید تابع $$f = f (x , y) = y ^ x $$ را داریم و نقطه‌ دلخواهی را از نمودار آن انتخاب می‌کنیم. طبق مفهوم لاپلاسین، دایره‌‌ای از نقاط در اطراف آن نقطه (همه همسایه‌های آن) را در نظر می‌گیریم و این پرسش را مطرح می‌کنیم: «میانگین مقادیر آن نقطه‌ها از مقدار تابع در نقطه انتخابی ما کوچک‌تر است یا مساوی یا بزرگ‌تر؟

البته همه این مفاهیم به ابعاد بالاتر نیز قابل تعمیم است.

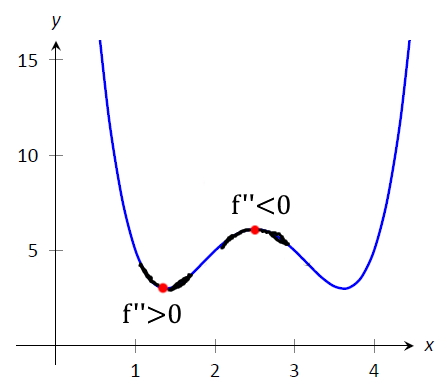
از ریاضیات دوره دبیرستان می‌دانیم که علامت مشتق دوم تابع یک‌متغیره مربوط به تقعر آن است. اگر مشتق دوم مثبت باشد، تابع به سمت بالا تقعر دارد و اگر مشتق دوم آن منفی باشد، به پایین تقعر خواهد داشت. شهودِ پسِ این رابطه همان شهودی است که برای درک لاپلاسین داشتیم. دقیقاً مانند لاپلاسین، علامت مشتق دوم یک تابع در یک بُعد، رابطه مقدار در آن نقطه و میانگین همسایه‌هایش را نشان می‌دهد،.

بنابراین، می‌توانیم بگوییم که لاپلاسین در یک بُعد مشابه مشتق دوم است.

معادله لاپلاس و مفهوم تابع همساز

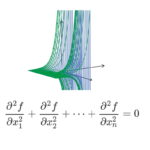
معادله لاپلاس به همراه معادله گرما و معادله موج، سه معادله اساسی در ریاضی فیزیک را تشکیل می‌دهند. معادله لاپلاس یک معادله دیفرانسیل جزئی مرتبه دوم است که بیان می‌کند لاپلاسین تابع $$f$$ برابر با صفر است.

$$ \Delta f = 0 $$ یا $$ \nabla ^ { 2 } f = 0 $$

جواب‌های این معادله به توابع همساز یا هارمونیک (Harmonic Functions) معروف هستند. توابع همساز توابعی هستند که لاپلاسین آن‌ها در تمام نقاط برابر با صفر است. طبق آنچه تاکنون بحث کردیم، در نمودار یک تابع همساز، جدای از این مسئله که کدام نقطه را انتخاب کنیم، همسایه‌های آن به طور متوسط مقدار یکسانی خواهند داشت. تابع $$ f = f (x , y ) = e ^ x \sin (y) $$ مثالی از یک تابع همساز دومتغیره است که در شکل زیر نشان داده شده است. 

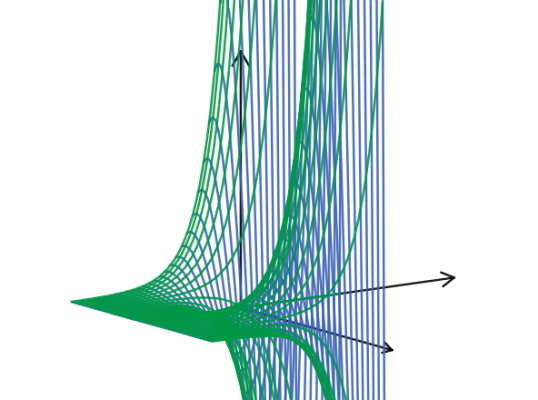
اگر بخواهیم مشابه توابع همساز را در یک بعد پیدا کنیم باید به دنبال توابعی بگردیم که مشتق دوم آن‌ها در همه نقاط برابر با صفر باشد. بدیهی است که تنها توابعی که این شرط را برآورده می‌کنند، توابع ثابت و خطی هستند. توابع ثابت و خطی در یک بعد توابع همساز هستند، زیرا مشتق دوم آن‌ها در همه نقاط برابر با صفر است.

«رویه مینیمال» (Minimal Surface) رویه‌ای است که به‌طور موضعی مساحت خود را کمینه می‌کند. این تعریف معادل است با داشتن انحنای میانگین صفر. یک مثال ساده برای درک و پیش‌بینی شکل یک تابع همساز، مقایسه آن با حباب‌های صابون یا دقیق‌تر از آن، فیلم‌های صابون است که در شکل زیر نشان داده شده است. 

فیلم صابون این ویژگی را دارد که رویه مینیمال باشد. بسته به ساختاری که فیلم صابون روی آن پخش می‌شود، شکل فیلم سعی می‌کند کوچک‌ترین سطح ممکن را داشته باشد تا کشش کلی را به حداقل برساند. همان‌طور که گفتیم، سطوح مینیمال در همه جا انحنای متوسط خود را صفر می‌کنند، یعنی در معادله لاپلاس صدق می‌کنند. هنگامی که یک تابع همساز دومتغره را به‌صورت سه‌بعدی تجسم کنیم خواهیم دید که در واقع توابع همساز رویه مینیمال هستند و دقیقاً شبیه حباب‌های صابون‌اند. 

تعریف تابع همساز

تابع $$f: \mathbb R^n \rightarrow \mathbb R$$ را یک تابع همساز یا هارمونیک می‌گوییم، اگر مجموع مشتقات دوم آن برابر با صفر باشد. بنابراین، تابع همساز باید معادله را برآورده کند:

$$ \begin {equation} \frac { \partial ^ 2 f } { \partial x _ 1 ^ 2 } + \frac { \partial ^ 2 f }{ \partial x _ 2 ^ 2 } + \cdots + \frac { \partial ^ 2 f } { \partial x _ n ^ 2 } = 0 \end {equation} $$

یا

$$\Delta f = 0$$

که برای تابع دومتغیره بعدی $$f(x,y)$$، بسته به نحوه نوشتن مشتقات، $$\frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0 $$ یا $$f_{xx} + f_{yy} = 0$$ خواهد بود. این معادله یک معادله دیفرانسیل است. با این حال، این یک نوع خاص از معادلات دیفرانسیل است. زیرا $$f $$ دارای چند متغیره است و به آن معادله دیفرانسیل جزئی (PDE) می‌گویند. در میان معادلات دیفرنسیل جزئی، معادله اخیر معادله لاپلاس نیز نامیده می‌شود که به آن اشاره کردیم.

تابع همساز یک‌متغیره

در این بخش، جواب معادله لاپلاس را در یک بعد بررسی می‌کنیم تا نحوه رفتار آن را بهتر درک کنیم. در یک بعد، ما به‌دنبال $$f : \mathbb R \rightarrow \mathbb R$$ هستیم که $$f''(x) = 0$$ را برآورده کند. پیدا کردن آن چندان سخت نیست:

$$ \begin{eqnarray*} \iint f''(x) & = & \iint 0 \\ \int f'(x) & = & \int a \\ f(x) & = & ax + b \\ \end{eqnarray*} $$

این جواب تحلیلی نکته جالبی را نشان می‌دهد که توابع همساز تک‌متغیره همیشه خطی هستند.

تابع همساز دومتغیره

نسخه دومتغیره تابع همساز که قبل‌تر به آن اشاره نیز کردیم، کمی مشکل‌تر است. برای برقراری $$f_{xx} + f_{yy} = 0$$ جواب بدیهی این است که $$f$$ در جهت‌های اصلی $$x$$ و $$y$$ خطی باشد. در واقع، اگر $$f$$ در جهت‌های $$x $$ و $$y$$ خطی باشد، $$f_{xx}=0$$ و $$f_{yy}=0$$ را داریم. از آنچه گفتیم، می‌توان چنین استنباط کرد که که توابعی به فرم زیر توابعی همساز هستند:

$$f(x,y)=ax+by$$

در واقع هر صفحه دارای یک انحنای متوسط صفر است. اما این بدین معنا نیست که این فرم تنها نوع توابع همساز دومتغیره است، زیرا معادله ما $$f_{xx}+f_{yy}$$ است نه $$f_{xx}=0$$ و $$f_{yy}=0$$.

یک جواب محتمل دیگر این است که مشتقات دوم $$f_{xx}$$ و $$f_{yy}$$ یکدیگر را خنثی کنند، بدون اینکه به‌صورت جداگانه برابر با صفر باشند. یک مثال تحلیلی مانند $$f(x,y) = x^2 - y^2$$ را در نظر بگیرید. مشتقات دوم $$f_{xx}=2$$ و $$f_{yy}=2$$ هستند و یکدیگر را حذف می‌کنند. این یک تابع یک زینی به فرم زیر است:

$$f(x,y) = ax^2 - by^2$$

یک مثال دیگر از توابع دومتغیره، تابع $$ f(x,y) = \ln{ \sqrt{x^2 + y^2} }$$ است. مشتقات دوم این تابع به‌صورت زیر محاسبه می‌شوند:

$$ f _ { x x } ( x , y) = \frac { - 2 x ^ 2 }{ ( x ^ 2 + y ^ 2 ) ^ 2 } + \frac { 1 } { x ^ 2 + y ^ 2 } , \;\;\;\;\;\; f _ { y y } ( x , y ) = \frac { - 2 y ^ 2 } { ( x ^ 2 + y ^ 2 ) ^ 2 } + \frac { 1 } { x ^ 2 + y ^ 2 } $$

که می‌بینیم در معادله لاپلاس صدق می‌کنند:

$$ \begin {eqnarray*} f _ { x x } + f _ { y y } & = & \frac { - 2 x ^ 2 } { ( x ^ 2 + y ^ 2 ) ^ 2 } + \frac { 1 } { x ^ 2 + y ^ 2 } + \frac { - 2 y ^ 2 } { ( x ^ 2 + y ^ 2 ) ^ 2 } + \frac { 1 } { x ^ 2 + y ^ 2 } \\ & = & \frac { - 2 ( x ^ 2 + y ^ 2 ) } { ( x ^ 2 + y ^ 2 ) ^ 2 } + \frac { 2 } { x ^ 2 + y ^ 2 } \\ & = & \frac { - 2 } { x ^ 2 + y ^ 2 } + \frac { 2 } { x ^ 2 + y ^ 2 } \\ & = & 0 \end {eqnarray*} $$

توابع همساز در فیزیک

توابع همساز در ریاضیات کاربردی و ریاضی فیزیک اهمیت زیادی دارند، به‌گونه‌ای که یک شاخه کامل از معادلات دیفرانسیل — و به‌طور کلی سیستم‌های دینامیکی — به مطالعه توابع همساز می‌پردازد. در اینجا، به چند نکته جالب در رابطه با این توابع اشاره می‌کنیم.

توابع همساز ارتباط نزدیکی با مفهوم تعادل دارند. در واقع، جواب لاپلاس یک جواب تعادلی برای یک معادله گرما، یک معادله موج یا یک معادله انتشار (بدون منبع یا فشار خارجی) است. به‌عبارت ساده، وقتی ما به‌دنبال یک جواب تعادلی هستیم، می‌خواهیم تمام مشتقات زمانی در معادله دیفرانسیل برابر با صفر باشد. به‌عنوان مثال، در مورد معادله گرما، می‌دانیم که پروفایل دما با گذشت زمان هموارتر می‌شود. مقدار گرادیان دما و شار حرارتی با افزایش زمان $$t$$ کاهش می‌یابد. وقتی $$t$$ به بی‌نهایت میل می‌کند، فرایند انتقال حرارت به بازده نزولی می‌رسد و دیگر خبری از جابه‌جایی انرژی گرمایی نیست.

از دیدگاه ریاضی، این موضوع نشان می‌دهد که مشتق زمانی تابعی که دما را به ما می‌دهد برابر با صفر است و معادله گرما به معادله لاپلاس تبدیل می‌شود. نکته مهم دیگری که باید به آن توجه داشت این است که، در فیزیک و مهندسی، توابع همساز به‌عنوان توابع پتانسیل نیز شناخته می‌شوند. توابع پتانسیل بسیار مفید هستند، به‌عنوان مثال، در الکترومغناطیس، که مطالعه یک میدان برداری سه‌مؤلفه‌ای را به یک تابع اسکالر یک‌مؤلفه‌ای کاهش می‌دهد.

مزدوج همساز

در ریاضیات، می‌گوییم تابع حقیقی $$u(x,y)$$ که روی یک مجموعه باز همبند $${\Omega \subset \mathbb {R} ^{2}} $$ تعریف شده است، دارای مزدوج $$v(x,y)$$ است اگر و تنها اگر این دو تابع، به‌ترتیب بخش‌های حقیقی و موهومی یک تابع هولومورفیک (Holomorphic Function) $$ f(z) $$ از متغیر مختلط $$ z:=x+iy\in \Omega $$ باشد. این یعنی $$v $$ مزدوج $$u$$ است اگر $$ f(z):=u( x,y)+iv(x,y) $$ در $$ \Omega $$ هولومورفیک باشد. اولین نتیجه این تعریف این است که هر دو تابع همساز حقیقی در $$\Omega$$ هستند. علاوه بر این، مزدوج $$u$$، اگر وجود داشته باشد، یکتا است (با تفاوت یک ثابت که با آن جمع می‌شود). همچنین، $$u$$ مزدوج $$v$$ است اگر و تنها اگر $$v$$ مزدوج $$-u$$ باشد.

به طور معادل، $$v$$ مزدوج $$u$$ در $$\Omega$$ است اگر و تنها اگر $$u$$ و $$v$$ معادلات کوشی-ریمان را در $$\Omega$$ برآورده کنند. به‌عنوان یک نتیجه از تعریف معادل اخیر، می‌توان گفت که اگر $$u$$ هر تابع همسازی در $$ \Omega \subset \mathbb {R} ^{2} $$ باشد، آنگاه تابع $$u_x $$ مزدوج $$-u_y$$ است. سپس معادلات کوشی-ریمان $$\Delta u=0$$ است و تقارن مشتقات مرتبه‌دوم $$ u_{{xy}}=u_{{yx}}$$ را داریم. بنابراین، یک تابع همساز $$u$$ تابع همساز مزدوج دارد اگر و تنها اگر تابع هولومورفیک $$ g(z):=u_{x}(x,y)-iu_{y}(x,y) $$ دارای اولیه $$f (z)$$ در $$\Omega$$ باشد، که در این صورت، مزدوج $$u$$ تابع $$ { \operatorname {Im} f( x+iy)} $$ است. بنابراین، هر تابع همساز، اگر دامنه‌اش همبند ساده باشد، همواره یک تابع مزدوج خواهد داشت، و در هر صورت یک مزدوج برای آن به‌صورت محلی در هر نقطه از دامنه‌اش وجود دارد.

از نظر هندسی، $$u$$ و $$v$$ دارای مسیرهای متعامد و دور از صفرهای تابع هولومورفیک هستند؛ کانتورهایی که در آن‌ها $$u$$ و $$v$$ در زوایای قائم متقاطع ثابت هستند. از این نظر، $$u + iv$$ پتانسیل مختلط خواهد بود، که در آن $$u$$ تابع پتانسیل و $$v$$ تابع جریان است.

برای مثال، تابع $$ u(x,y) = e^x \sin y $$ را در نظر بگیرید. از آنجا که

$$ {\partial u \over \partial x } = e^x \sin y, \quad {\partial^2 u \over \partial x^2} = e^x \sin y $$

و

$${\partial u \over \partial y} = e^x \cos y, \quad {\partial^2 u \over \partial y^2} = - e^x \sin y,$$

رابطه زیر برقرار خواهد بود:

$$\Delta u = \nabla^2 u = 0 $$

اکنون فرض کنید که یک $$ v(x,y) $$ داریم که در معادلات کوشی-ریمان صدق می‌کند:

$$ \begin {align} {\partial u \over \partial x} & = {\partial v \over \partial y} = e^x \sin y, \\
{\partial u \over \partial y} & = -{\partial v \over \partial x} = e^x \cos y.
\end {align}$$

با ساده‌سازی، خواهیم داشت:

$$ \begin {align} {\partial v \over \partial y} & = e^x \sin y, \\
{\partial v \over \partial x} & = -e^x \cos y.
\end {align}$$

حل این دو رابطه، تابع زیر را نتیجه خواهد داد:

$$ v = -e^x \cos y + C . $$

توجه کنید که اگر جای توابع $$u$$ و $$v$$ را با هم عوض کنیم، مزدوج همساز نخواهند بود، زیرا علامت منفی در معادلات کوشی-ریمان رابطه را نامتقارن می‌کند.

ویژگی نگاشت همدیس توابع تحلیلی (در نقاطی که مشتق صفر نیست) ویژگی هندسی مزدوج همساز را نتیجه می‌دهد. واضح است که مزدوج همساز $$ x $$، برابر با $$y$$ است و خطوط ثابت $$x$$ و ثابت $$y$$ متعامد هستند. خاصیت همدیسی می‌گوید که خطوط ثابت $$u(x,y)$$ و $$v(x,y)$$ نیز در جایی که از صفرهای $$f '(z)$$ عبور می‌کنند، متعامد خواهند بود. این یعنی $$v$$ یک جواب خصوصی برای مسئله مسیرهای متعامد برای خانواده کانتورهای ارائه‌شده توسط $$u$$ است (طبیعاً تنها جواب نیست، زیرا می‌توانیم توابع $$v$$ را نیز در نظر بگیریم). این مسئله یافتن منحنی‌هایی از یک خانواده معین که از منحنی‌های غیرمتقاطع با زوایای قائمه عبور می‌کنند به ریاضیات قرن هفدهم برمی‌گردد.

آنچه را که گفتیم، مرور می‌کنیم. اگر بخش حقیقی یک تابع مختلط همساز باشد، یک بخش موهومی همساز وجود دارد، به طوری که تابع تحلیلی است. قسمت موهومی به‌عنوان مزدوج همساز بخش حقیقی شناخته می‌شود. به عبارت دیگر، مزدوج همساز یک تابع حقیقی تابعی موهومی است، به‌طوری که تابع مختلط متشکل از آن‌ها تحلیلی باشد. مزدوج همساز هم در معادلات کوشی-ریمان و هم در معادله لاپلاس صدق می‌کند.

قضیه: فرض کنید تابع مختلط $$f(z)$$ , بخش حقیقی $$u ( x , y ) $$ و بخش موهومی $$v (x , y)$$ آن را داریم. آنگاه می‌توانیم تابع را به‌صورت زیر بنویسیم:

$$f(z) = u(x,y) + vi(x,y)$$

اگر $$u(x,y)$$ تابع همساز باشد، یک بخش همساز $$v(x,y)$$ وجود دارد، بنابراین $$f(z)$$ تحلیلی است. برای اثبات همساز بودن یک تابع، باید ثابت کنیم که تابع مختلط تحلیلی است.

برای ادامه، باید بدانیم که چگونه یک تابع مختلط می‌تواند تحلیلی باشد.

یک تابع مختلط تنها زمانی تحلیلی است که دو شرط زیر را برآورده کند:

1. تابع مختلط باید پیوسته باشد.
2. باید معادلات کوشی-ریمان را برآورده کند:

$$ \begin {align}
\frac { ∂u } { ∂x} & = \frac { ∂v} { ∂y} \\
\frac { ∂u } { ∂y} & = - \frac { ∂v} { ∂x}
\end {align} $$

ممکن است در بحث توابع مختلط با اصطلاحاتی برخورد کنید که بهتر است مفهوم آن‌ها را بدانید:

• اگر $$u$$ مزدوج همساز $$v$$ باشد، لزومی ندارد $$v$$ مزدوج همساز $$u$$ باشد.
• ناحیه $$D$$ را باز می‌گویند اگر نقاط مرزي موجود نباشد. ناحیه بسته ناحیه‌ای است که نقاط مرزي را شامل می‌شود.
• مجموعه $$S$$ را همبند می‌گویند اگر بتوان هر دو نقطه آن را توسط خطوطی شکسته به هم متصل کرد به شرط اینکه کلیه خطوط متعلق به $$S$$ باشند.
• همسایگی حول $$z_0$$ یک ناحیه باز است که دایره‌اي با مرکز $$ z _0$$ و شعاع $$\epsilon$$ را نشان می‌دهد.

$$ | z - z _ 0 | < \epsilon$$

• مجموعه بسته همبند را مجموعه فشرده می‌گویند.
• تابع $$ f ( z ) $$ را در ناحیه $$ \mathcal { R} $$ از صفحه مختلط تحلیلی می‌گوییم، اگر $$ f ( z ) $$ در هر نقطه از $$ \mathcal { R} $$ دارای مشتق بوده و همچنین، تک‌مقداره باشد.
• تابع $$ f ( z ) $$ را در نقطه $$ z $$ تحلیلی می‌گوییم، اگر $$ z $$ یک نقطه درون ناحیه‌ای باشد که $$ f ( z ) $$ در آن تحلیلی است. بنابراین، مفهوم تابع تحلیلی در یک نقطه بیان می‌کند که آن تابع در دایره‌ای به مرکز آن نقطه تحلیلی است.

مثال‌های تابع همساز

در این بخش، مثال‌هایی را از تابع همساز بررسی می‌کنیم.

مثال اول

اگر $$ u ( x , y ) = y ^ 3 - 3 x ^ 2 y $$، آنگاه نشان دهید $$ u $$ همساز است. مزدوج همساز $$ u $$ را محاسبه کنید.

جواب: ابتدا مشتقات دوم تابع را محاسبه می‌کنیم:

$$ \frac { \partial { u} } { \partial { x } } = 0 - 6 x y \rightarrow \frac { \partial ^{ 2 } u } { \partial { x } ^ { 2 } } = - 6 { y } \quad, \quad \frac { \partial { u } } { \partial { y } } = 3 { y } ^ { 2} - 3 x^ { 2 } \rightarrow \frac { \partial ^ {2 } { u } } { \partial { y } ^ { 2 } } = 6 { y } $$

می‌بینیم که شرط همساز بودن تابع برقرار است:

$$ \frac { \partial ^{ 2 } u } { \partial { x } ^ { 2 } } + \frac { \partial ^ {2 } { u } } { \partial { y } ^ { 2 } } = 6 { y } - 6 { y } = 0 $$

از آنجا که $$u $$ همساز است، پس یک $$ v $$ به‌عنوان همساز آن یافت می‌شود که $$ f ( z ) = u + i v $$ تحلیلی باشد. بنابراین، قضیه کوشی-ریمان صادق است.

$$ \left \{ \begin {array}{l}
\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \longrightarrow-6 x y=\frac{\partial v}{\partial y} \longrightarrow v = - 3 x y ^ 2 + \varphi ( x ) \\
\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} \longrightarrow 3 y^{2}- 3 x^{2} = - (- 3 y ^ 2 + \varphi ^\prime (x)) \rightarrow \varphi ^\prime (x) = 3 x ^ 2 \Rightarrow \varphi (x) = x ^ 3 + C
\end{array}\right. $$

در نتیجه، خواهیم داشت:

$$ v = - 3 x y ^ 2 + x ^ 3 + C $$

مثال دوم

تابع $$u(x,y)$$ یک تابع همساز است و $$f(z) = u(x,y) + vi(x,y)$$. مزدوج همساز $$$$ u(x,y) = x^2 – y^2 – x + y $$$$ را بیابید.

جواب: بخش حقیقی تابع را داریم. بنابراین، باید بخش موهومی $$ v (x , y ) $$ را پیدا کنیم، به نحوی که تابع مختلط $$f (z ) $$ تحلیلی باشد.

برای مشتق‌پذیر بودن $$f(z)$$، طبق معادلات کوشی-ریمان، بخش حقیقی باید معادلات زیر را برآورده کند.

$$ \begin {align}
\frac { ∂u } { ∂x} & = \frac { ∂v} { ∂y} \\
\frac { ∂u } { ∂y} & = - \frac { ∂v} { ∂x}
\end {align} $$

مشتقات جزئی $$u(x,y)$$ را نسبت به $$x $$ و $$y$$ محاسبه می‌کنیم:

$$ \begin {align}
\frac { ∂u } { ∂x} & = 2 x - 1 \\
\frac { ∂u } { ∂y} & =-2 y + 1
\end {align} $$

بنابراین، داریم:

$$ \begin {align}
\frac { ∂v } { ∂y} & =\frac { ∂u } { ∂x} = 2 x - 1 \\
\frac { ∂v } { ∂x} & =-\frac { ∂u } { ∂y} =2 y - 1
\end {align} $$

دو روش برای ادامه حل مسئله وجود دارد.

روش اول: انتگرال جزئی $$ \frac { ∂v } { ∂x } $$ نسبت به $$x $$ نتیجه زیر را خواهد داشت:

$$v = 2xy – x + h(x)$$

همچنین، انتگرال جزئی $$ \frac { ∂v } { ∂y } $$ نسبت به $$y$$ برابر خواهد بود با

$$v = 2xy - y + g(x) $$

بنابراین، $$h(x) = – y$$ و $$g(x) = – x$$.

در نتیجه، مزدوج همساز $$v$$ برابر خواهد بود با

$$v(x,y) = 2xy – x – y$$

روش دوم:‌ انتگرال جزئی $$ \frac { ∂v } { ∂x } $$ نسبت به $$y $$ نتیجه زیر را خواهد داشت:

$$v = 2xy - y + g(x)$$

با محاسبه مشتق جزئی $$v$$ نسبت به $$x$$، خواهیم داشت:

$$ \frac { ∂v} { ∂x} = 2y + g'(x) $$

از آنجا که $$\frac {∂v} { ∂x} = 2y – 1 $$، داریم:

$$ 2y – 1 = 2y + g'(x) \;\;\; \Rightarrow \;\;\; g'(x) = -1 $$

مشتق جزئی $$g'(x)$$ نسبت به $$x$$ برابر است با

$$g(x) = – x$$

بنابراین، مزدوج همساز $$v $$ به‌صورت زیر است:‌

$$v(x,y) = 2xy – x – y$$

مثال سوم

نشان دهید که $$ u(x,y) = e ^ x \sin(y) $$ یک تابع همساز است و مزدوج همساز $$v(x,y)$$ را به‌گونه‌ای بیابید که $$f(z) = u(x,y) + vi(x,y)$$ تحلیلی باشد.

جواب: برای اثبات همساز بودن یک تابع باید ثابت کنیم که تابع دارای مشتقات جزئی مرتبه‌دوم پیوسته است.

ابتدا مشتقات جزئی $$u(x,y)$$ را نسبت به $$x$$ و $$y$$ به‌دست می‌آوریم:

$$ \begin {align}
\frac { ∂u } { ∂x } &= e^x \sin(y) \\
\frac { ∂u } { ∂y} & = e^x \cos(y)
\end {align} $$

از آنجا که باید ثابت کنیم $$ u(x,y) = e ^ x \sin(y) $$ یک تابع همساز است، باید مشتقات جزئی مرتبه‌دوم را محاسبه کنیم:

$$ \begin {align}
\frac { ∂^2u } { ∂x^ 2 } &= e^x \cos(y) \\
\frac { ∂^2u } { ∂y ^ 2} & = - e^x \sin(y)
\end {align} $$

از آنجایی که تابع دارای مشتقات جزئی مرتبه‌دوم است، $$ u(x,y) = e ^ x \sin(y) $$ یک تابع همساز است.

حال، مزدوج همساز را پیدا می‌کنیم. با توجه به معادلات کوشی-ریمان، داریم:

$$ \begin {align}
\frac { ∂v } { ∂y } &=\frac { ∂u } { ∂x }= e^x \sin(y) \\
\frac { ∂v } { ∂x } &= -\frac { ∂u } { ∂y }= - e^x \cos(y)
\end {align} $$

انتگرال جزئی $$ \frac { ∂v} { ∂y } $$ روی $$y$$ برابر است با

$$ v = – e ^ x \cos(y) + g(x) $$

با یافتن مشتق جزئی $$v$$ نسبت به $$x$$، خواهیم داشت،

$$ \frac {∂v} { ∂x} = – e ^ x \cos(y) + g'(x) $$

از آنجا که $$ \frac { ∂v } { ∂x} =- e ^ x \cos(y) $$،

$$ – e^ x \cos(y) = – e ^ x \cos(y) + g'(x) \;\;\; \Rightarrow
\;\; \; g'(x) = 0 $$

انتگرال جزئی $$g'(x)$$ روی $$x$$، نتیجه زیر را دارد:

$$g(x) = C$$

بنابراین، مزدوج همساز $$v(x,y)$$ به‌صورت زیر خواهد بود:

$$ v(x,y) = – e ^ x \cos(y) + C $$

مثال چهارم

ثابت کنید که اگر $$z\neq 0 $$، آنگاه تابع $$ u(x,y) = \ln \sqrt{|z|}$$ همساز است. سپس، $$ v ( x , y) $$ را طوری پیدا کنید که تابع $$ f (z ) = u + i v $$ یک تابع تحلیلی باشد.

جواب: برای بررسی همساز بودن تابع، مشتقات دوم را محاسبه می‌کنیم و معادله لاپلاس را تشکیل می‌دهیم:

$$ \begin{aligned}
&u=\ln \sqrt{|z|}=\ln \sqrt{\sqrt{x^{2}+y^{2}}}=\ln \left(x^{2}+y^{2}\right)^{\frac{1}{2}}=\frac{1}{2} \ln \left(x^{2}+y^{2}\right) \\
&u_{x}=\frac{1}{2} \times \frac{2 x}{x^{2}+y^{2}} \rightarrow u_{xx}=\frac{1}{2} \times \frac{\left(x^{2}+y^{2}\right)-2 x^{2}}{\left(x^{2}+y^{2}\right)^{2}}=\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}} \\
&u_{y}=\frac{1}{2} \times \frac{2 y}{x^{2}+y^{2}} \rightarrow u_{y y}=\frac{1}{2} \times \frac{\left(x^{2}+y^{2}\right)-2 y^{2}}{\left(x^{2}+y^{2}\right)^{2}}=\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}} \\
&\rightarrow u_{x x}+u_{y y}=\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}+\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}=0
\end{aligned} $$

بنابراین، تابع $$u$$ همساز است.

برای اینکه $$v$$ مزدوج همساز $$u$$ باشد، باید داشته باشیم:

$$\begin{aligned}
& u_x = v _y , \;\;\;\;u_y = -v _x \\
&u_{x}=\frac{1}{2} \times \frac{x}{x^{2}+y^{2}}=\frac{d v}{d y} \rightarrow v=\frac{1}{2} \int \frac{x d y}{x^{2}+y^{2}}=\frac{1}{2} \operatorname{Arctan}\left(\frac{y}{x}\right)+h(x) \\
&v_{x}=-u_{y} \rightarrow \frac{-y}{\left.{2}(x^{2}+y^{2}\right)}+h^{\prime}(x) =\frac{-y}{2\left(x^{2}+y^{2}\right)} \rightarrow h^{\prime}(x) =0\rightarrow h(x)=\operatorname{Arctan}\left(\frac{y}{x}\right)+c \\
&v=\frac{1}{2}\operatorname{Arctan}\left(\frac{y}{x}\right)+c
\end{aligned} $$

جمع‌بندی

در این آموزش، به مفهوم لاپلاسین و چگونگی ارتباط آن با توابع همساز پرداختیم. علاوه بر این، معادله لاپلاس را بررسی کردیم و با تابع همساز و مزدوج همساز آشنا شدیم و مثال‌هایی از آن‌ها را حل کردیم.