مسیرهای متعامد — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله دیفرانسیل چبیشف پرداختیم. در این آموزش، یکی از مباحث مربوط به معادلات دیفرانسیل،‌ یعنی مسیرهای متعامد را معرفی می‌کنیم. مسیرهای متعامد یا قائم، منحنی‌هایی هستند که یک دسته منحنی دیگر را با زوایای قائم قطع می‌کنند. در ادامه، روش به دست آوردن این منحنی‌ها را بیان می‌کنیم.

تعریف

دسته منحنی $$ g \left ( { x , y } \right ) = C $$ را در نظر بگیرید، که در آن، $$ C $$ یک ثابت است. برای این دسته منحنی‌های معین، می‌توانیم مسیرهای متعامد را رسم کنیم. این مسیرهای متعامد دسته دیگری از منحنی‌ها به‌ صورت $$ f \left ( { x , y } \right ) = C $$ هستند که منحنی‌های معین را با زوایای قائم قطع می‌کنند.

فیلم آموزش معادلات دیفرانسیل به همراه حل سوالات آزمون کارشناسی ارشد

اینجا کلیک کنید

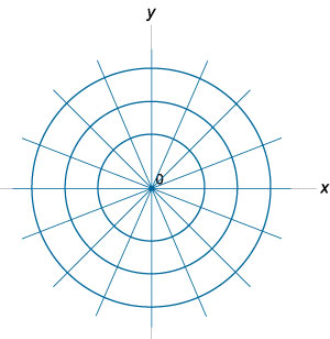
برای مثال، مسیر متعامد دسته خطوط راست که به‌ صورت $$ y = k x $$ تعریف می‌شوند ($$k$$ یک پارامتر و برابر با شیب خط راست است)، دایره‌ای است که مرکز آن در مبدأ قرار دارد (شکل 1):

$$ \large { x ^ 2 } + { y ^ 2 } = { R ^ 2 } $$

که در آن، $$R$$ شعاع دایره است.

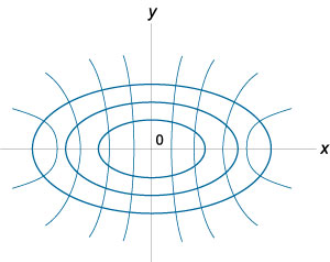
به‌طور مشابه، مسیرهای متعامد دسته بیضی‌هایِ

$$ \large { \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { c ^ 2 } – { a ^ 2 } } } = 1 , \;\;}\kern0pt{\text{ }\;\;}\kern-0.3pt { 0 \lt a \lt c} $$

هذلولی‌های هم‌کانون هستند که در معادله زیر صدق می‌کنند:

$$ \large { \frac { { { x ^ 2 } } } { { { b ^ 2 } } } – \frac { { { y ^ 2 } } } { { { b ^ 2 } – { c ^ 2 } } } = 1,\;\;}\kern0pt{\text{}\;\;} \kern-0.3pt{ 0 \lt c \lt b.} $$

این دو دسته منحنی در شکل 2 رسم شده‌اند. در این‌جا $$ a $$ و $$ b $$ پارامترهایی هستند که به‌ترتیب، دسته بیضی‌ها و هذلولی‌ها را توصیف می‌کنند.

روش کلی یافتن مسیرهای متعامد

روش رایج برای تعیین مسیرهای متعامد بر اساس حل معادله دیفرانسیل جزئی زیر است:

$$ \large \nabla f \left ( { x , y } \right ) \cdot \nabla g \left( { x , y } \right ) = 0 $$

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد

اینجا کلیک کنید

در این‌جا نماد $$ \nabla $$ گرادیان تابع $$f(x,y)$$ یا $$g(x,y)$$ و نقطه بین آن‌ها ضرب داخلی دو بردار گرادیان است.

با استفاده از تعریف گرادیان، می‌توان نوشت:

$$ \large \begin{align*}
{ \nabla f \left ( { x , y } \right ) = \mathbf{grad}\, f \left ( { x , y } \right ) } = { \left ( { \frac { { \partial f } } { { \partial x } } ,\frac { { \partial f } } { { \partial y } } } \right ) , } \\
{ \nabla g \left ( { x , y } \right ) = \mathbf{grad} \, g \left ( { x , y } \right ) } = { \left ( { \frac { { \partial g } } { { \partial x } } , \frac { { \partial g } } { { \partial y } } } \right ) . }
\end{align*} $$

بنابراین، معادله دیفرانسیل جزئی به‌ صورت زیر نوشته می‌شود:

$$ \large { \nabla f \left ( { x , y } \right ) \cdot \nabla g \left( { x , y } \right ) = 0 ,\;\; } \\ \large \Rightarrow
{ \left ( { \frac { { \partial f } } { { \partial x } } ,\frac { { \partial f } } { { \partial y } } } \right) \cdot \left ( { \frac { { \partial g } } { { \partial x } } ,\frac { { \partial g } } { { \partial y } } } \right ) = 0,\;\;}\\ \large \Rightarrow
{ \frac { { \partial f } } { { \partial x } } \frac { { \partial g }}{ { \partial x } } + \frac { { \partial f } } { { \partial y } } \frac { { \partial g } } { { \partial y } } = 0 . } $$

با حل معادله دیفرانسیل به دست‌آمده می‌توانیم معادله مسیرهای متعامد $$f(x,y)=C$$ را تعیین کنیم.

یک روش کاربردی برای به‌ دست آوردن مسیرهای متعامد

در این بخش، یک روش آسان برای یافتن مسیرهای متعامد $$f(x,y)=C$$ دسته منحنی‌های معین $$g(x,y)=C$$ را با استفاده از معادلات دیفرانسیل معمولی شرح می‌دهیم. این روش شامل مراحل زیر است:

1. معادله دیفرانسیل $$ G\left( {x,y,y’} \right) = 0 $$ را برای دسته منحنی های معین $$g(x,y)=C$$ تشکیل دهید.
2. در این معادله دیفرانسیل، $$ \left( { – \large\frac{1}{{y’}}\normalsize} \right) $$ را جایگزین $$y’$$ قرار دهید تا معادله دیفرانسیل مسیرهای متعامد را به دست آورید.
3. معادله دیفرانسیل جدید را حل کنید تا معادله جبری دسته مسیرهای متعامد $$f(x,y)=C$$ به دست آید.

مثال‌ها

در ادامه، چند مثال را بررسی می‌کنیم.

فیلم آموزش معادلات دیفرانسیل با میپل Maple

اینجا کلیک کنید

مثال ۱

مسیرهای متعامد دسته خطوط راست $$y=Cx$$ را بیابید که $$C$$ یک پارامتر است.

حل: در این‌جا روشی را به‌کار می‌بریم که در بالا گفته شد.

1. ابتدا معادله دیفرانسیل را برای دسته خطوط راست $$y=Cx$$ به دست می‌آوریم. با مشتق‌گیری از این معادله نسبت به $$x$$ داریم:

$$ \large y ’ = C = \text {const}. $$

ثابت $$C$$ را از مجموعه معادلات زیر حذف می‌کنیم:

$$ \large { \left\{ \begin{array}{l}
y = C x \\
y ’ = C
\end{array} \right.,\;\; }\Rightarrow { y ’ = \frac { y } { x } . } $$

در نتیجه، معادله دیفرانسیل اولیه مجموعه خطوط راست به دست می‌آید.

2. $$y’$$ را با $$\left( { – \large\frac{1}{{y’}}\normalsize} \right)$$ جایگزین می‌کنیم. این کار معادله دیفرانسیل مسیرهای متعامد را نتیجه می‌دهد:

$$ \large { – \frac { 1 } { { y ’ } } = \frac { y } { x } , \;\; }\Rightarrow { y ’ = – \frac { x } { y } .} $$

3. اکنون معادله دیفرانسیل حاصل را حل می‌کنیم تا معادله جبری دسته مسیرهای متعامد را بیابیم:

$$ \large \begin {align*} y ’ & = – \frac { x } { y } ,\;\;\Rightarrow
{ \frac { { d y } } { { d x } } = – \frac { x }{ y } ,\;\;}\Rightarrow
{ y d y = – x d x ,\;\;} \\ &\Rightarrow
{ \int { y d y } = – \int { x d x } ,\;\; } \Rightarrow
{ \frac { { { y ^ 2 } } } { 2 } = – \frac { { { x ^ 2 } } } { 2 } + C , \;\;} \\ & \Rightarrow
{ \frac { { { x ^ 2 } } } { 2 } + \frac { { { y ^ 2 } } } { 2 } = C , \;\; } \Rightarrow
{ { x ^ 2 } + { y ^ 2 } = 2 C } . \end{align*}$$

اگر $$R^2$$ را به‌جای $$2C$$ قرار دهیم، می‌بینیم که مسیرهای متعامد برای دسته خطوط راست، دایره‌های هم‌مرکز هستند (شکل 1):

$$ \large { x ^ 2 } + { y ^ 2 } = { R ^ 2 } . $$

مثال ۲

دسته منحنی‌های هذلولی با رابطه $$ y = {\large\frac{C}{x}\normalsize} $$ نشان داده می‌شوند. مسیرهای متعامد را برای این منحنی‌ها بیابید.

حل: 

۱. معادله دیفرانسیل را برای دسته منحنی‌های هذلولی تعیین می‌کنیم. با مشتق گرفتن از این معادله نسبت به $$x$$ داریم:

$$ \large y ’ = – \frac { C } { { { x ^ 2 } } } . $$

اکنون پارامتر $$C$$ را از دو معادله زیر حذف می‌کنیم:

$$ \large \left\{ \begin {array} {l}
y = \frac { C } { x } \\
y ’ = – \frac { C } { { { x ^ 2 } } }
\end{array} \right.. $$

از معادله نخست می‌توان تساوی $$C=xy$$ را نوشت. بنابراین، با جایگذاری این عبارت در معادله دوم خواهیم داشت:

$$ \large y ’ = – \frac { { x y } } { { { x ^ 2 } } } = – \frac { y } { x } . $$

۲. با قرار داردن $$ \left( { – \large\frac{1}{{y’}}\normalsize} \right) $$ به‌جای $$y’ $$ داریم:

$$ \large { – \frac { 1 } { { y ’ } } = – \frac { y } { x } , \;\; } \Rightarrow { y ’ = \frac { x } { y } . } $$

۳. اکنون از معادله دیفرانسیل مسیرهای متعامد انتگرال می‌گیریم:

$$ \large { y ’ = \frac { x } { y } ,\;\; } \Rightarrow
{ \frac { { d y } } { { d x } } = \frac { x } { y } ,\;\; } \Rightarrow
{ y d y = x d x , \;\; } \\ \large \Rightarrow
{ \int { y d y } = \int { x d x } , \;\; } \Rightarrow
{ \frac { { { y ^ 2 } } } { 2 } = \frac { { { x ^ 2 } } } { 2 } + C , \;\; } \Rightarrow
{ { x ^ 2 } – { y ^ 2 } = C . } $$

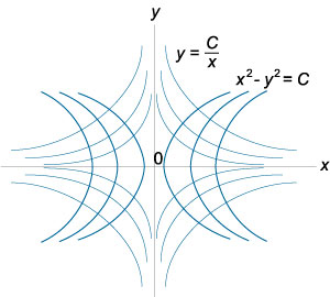
در معادله آخر، به‌جای $$2C$$ مقدار $$C$$ را قرار داده‌ایم و معادله دسته مسیرهای متعامد به دست آمده است. همان‌گونه که می‌بینیم، این مسیرهای متعامد نیز هذلولی هستند. در شکل 3 هر دو دسته هذلولی به‌طور خلاصه نشان داده شده‌اند.

مثال ۳

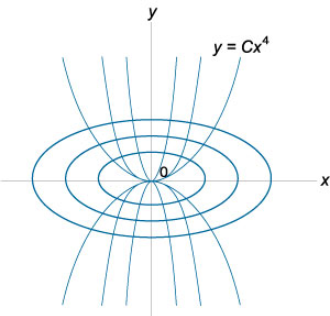
مسیرهای متعامد دسته منحنی‌هایی را بیابید که با تابع توانی $$ y = C{x^4} $$ نمایش داده می‌شوند.

حل:

۱. معادله دیفرانسیل را برای دسته منحنی‌های توانی به دست می‌آوریم:

$$ \large { y = C { x ^ 4 } , \;\; } \Rightarrow { y ’ = 4 C { x ^ 3 } . } $$

با حل مجموعه دو معادله و حذف $$C$$ داریم:

$$ \large { C = \frac { y } { { { x ^ 4 } } } , \;\; } \Rightarrow
{ y ’ = 4 \cdot \frac { y } { { { x ^ 4 } } } \cdot { x ^ 3 } = \frac { { 4 y } } { x } . } $$

۲. اگر $$ \left( { – \large\frac{1}{{y’}}\normalsize} \right) $$ را به‌جای $$ y’ $$ قرار دهیم، داریم:

$$ \large { – \frac { 1 } { { y ’ } } = \frac { { 4 y } } { x } , \;\; } \Rightarrow { y ’ = – \frac { x } { { 4 y } } . } $$

عبارت حاصل، معادله دیفرانسیل مسیرهای متعامد است.

۳. با انتگرال‌گیری می‌توانیم معادله جبری مسیرهای متعامد را محاسبه کنیم:

$$ \large { y ’ = – \frac { x } { { 4 y } } , \;\; } \Rightarrow
{ \frac { { d y } } { { d x } } = – \frac { x } { { 4 y } } ,\;\; } \\ \large \Rightarrow
{ 4 y d y = – x d x ,\;\; } \Rightarrow
{ 4 \int { y d y } = – \int { x d x } , \;\; }\\ \large \Rightarrow
{ 4 \cdot \frac { { { y ^ 2 } } } { 2 } = – \frac { { { x ^ 2 } } } { 2 } + C , \;\; } \Rightarrow
{ 4 { y ^ 2 } + { x ^ 2 } = 2 C . } $$

طرفین را به $$2C$$ تقسیم می‌کنیم:

$$ \large { \frac { { 4 { y ^ 2 } } } { {2 C } } + \frac { { { x ^2 } } } { { 2 C } } = \frac { { 2 C } } { {2 C } } , \;\; } \Rightarrow
{ \frac { { { y ^ 2 } } } { { \frac { C } { 2 } } } + \frac { { { x^ 2 } } } { { 2 C } } = 1 , \;\; } \\ \large \Rightarrow
{ \frac { { { y ^ 2 } } } { { { { \left ( { \sqrt { \frac { C } { 2 } } } \right ) } ^ 2 } } } + \frac { { { x ^ 2 } } } { { { { \left ( { \sqrt { 2 C } } \right ) } ^ 2 } } } } = { 1 . } $$

معادله دسته بیضی‌ها را به دست می‌آوریم که مسیرهای متعامد دسته منحنی‌های توانی $$y=Cx^4$$ هستند. نسبت طول نیم‌محورهای این بیضی‌ها برابر است با:

$$ \large { \frac { { \sqrt { 2 C } } } { { \sqrt { \frac { C } { 2 } } } } = \frac { { \sqrt 2 } } { { \sqrt { \frac { 1 } { 2 } } } } } = { { \left ( { \sqrt 2 } \right ) ^ 2 } } = { 2 . } $$

نمودارهای این دسته منحنی‌ها به‌طور خلاصه در شکل 4 نشان داده شده‌اند.

مثال ۴

مسیرهای متعامد دسته منحنی‌های سینوسی $$y= C \sin x $$ را تعیین کنید.

حل: 

۱. با مشتق‌گیری از این معادله نسبت به $$x$$ داریم:

$$ \large y ’ = C \cos x . $$

با جایگذاری $$ C = {\large\frac{y}{{\sin x}}\normalsize} $$ معادله دیفرانسیل منحنی‌های سینوسی را به دست می‌آوریم:

$$ \large { y ’ = \frac { y } { { \sin x } } \cos x } = { y \cot x . } $$

۲. اگر $$ \left( { – \large\frac{1}{{y’}}\normalsize} \right) $$ را به‌جای $$ y’ $$ قرار دهیم، داریم:

$$ \large { - \frac { 1 } { { y ’ } } = y \cot x , \;\; } \Rightarrow
{ y ’ = – \frac { 1 } { { y \cot x } } } = { – \frac { { \tan x } } { y } . } $$

۳. با انتگرال‌گیری می‌توانیم معادله جبری مسیرهای متعامد را محاسبه کنیم:

$$ \large { y ’ = – \frac { { \tan x } } { y } , \;\; } \Rightarrow
{ \frac { { d y } } { { d x } } = – \frac { { \tan x } }{ y } , \;\; } \\ \large\Rightarrow
{ y d y = – \tan x d x , \;\; } \Rightarrow
{ \int { y d y } = – \int { \tan x d x } , \;\; } \\ \large \Rightarrow
{ \frac { { { y ^ 2 } } } { 2 } = \ln \left| { \cos x } \right| + \ln C , \;\; } \Rightarrow
{ \frac { { { y ^ 2 } } } { 2 } = \ln \left ( { C \left| { \cos x } \right| } \right ) . } $$

در نتیجه:

$$ \large { C \left| { \cos x } \right| = \exp \left ( { \frac { { { y ^ 2 } } } { 2 } } \right ) , \;\; } \Rightarrow
{ \cos x = \pm \frac { 1 } { C } \exp \left ( { \frac { { { y ^ 2 } } } { 2 } } \right ) . } $$

با قرار دادن $$ {C_1} = \pm {\large\frac{1}{C}\normalsize}$$، معادله ضمنی نهایی مسیرهای متعامد به دست می‌آید:

$$ \large \cos x = { C _ 1 } \exp \left ( { \frac { { { y ^ 2 } } } {2 } } \right ) . $$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌‌شوند:

• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• معادله دیفرانسیل بسل — به زبان ساده
• معادلات دیفرانسیل ضمنی — به زبان ساده

^^

فیلم‌ های آموزش مسیرهای متعامد — به زبان ساده (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی روش کلی یافتن مسیرهای متعامد

فیلم آموزشی یک روش کاربردی برای یافتن مسیرهای متعامد

فیلم آموزشی حل مثال یافتن مسیرهای متعامد