گشتاور چیست؟ – به زبان ساده (+ دانلود فیلم آموزش رایگان)

به تمایل یک نیرو برای دوران جسمی حول یک محور، گشتاور گفته می‌شود. همان‌طور که نیرو موجب می‌شود تا جسمی در حرکت خطی، شتاب بگیرد، شتاب زاویه‌ای هم ناشی از وارد شدن گشتاور است. گشتاور، یک کمیت برداری بوده و جهت آن به جهت نیرو نسبت به محور بستگی دارد.

برای باز کردن درِ یک اتاق، باید به قسمتی از در که با لولاها فاصله دارد، نیرو وارد کنیم. هرچه این فاصله کوتاه‌تر باشد، به نیروی بزرگتری احتیاج داریم. با این حال، کارِ انجام شده در هر دو حالت، برابر است. هرچه مقدار نیروی مورد نیاز، کوچکتر باشد، انجام این کار، راحت‌تر خواهد بود. بنابراین بهترین نقطه برای وارد کردن این نیرو، دستگیره در است. به شکل زیر توجه کنید.

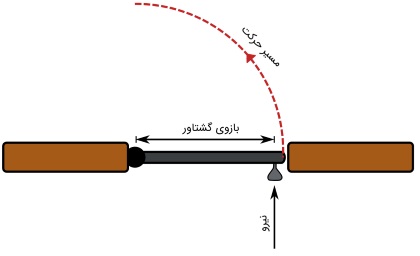
می‌توانیم گشتاور را به دو دسته استاتیک و دینامیک تقسیم کنیم. در گشتاور استاتیک، هیچ‌گونه شتاب زاویه‌ای ایجاد نمی‌شود. به عنوان مثال، شخصی را در نظر بگیرید که به یک درِ بسته نیرو وارد می‌کند. در این حالت، با وجود اینکه نیرو وارد می‌شود، ولی حرکتی وجود ندارد. در نتیجه، گشتاور از نوع استاتیک است. دوچرخه‌سواری که با سرعت ثابت رکاب می‌زند هم نمونه دیگری از گشتاور استاتیک محسوب می‌شود. زیرا شتاب حرکت برابر صفر است.

محور محرک اتومبیلی که در حال شتاب گرفتن است، گشتاور دینامیکی منتقل می‌کند. زیرا وظیفه تأمین شتاب زاویه‌ای چرخ‌ها که موجب شتاب گرفتن اتومبیل در طول مسیرش می‌شود، به عهده این محور است. در ادبیات مهندسی گاهی به جای گشتاور (Torque)، از عبارت‌هایی مانند ممان (Moment) یا گشتاور نیرو استفاده می‌شود و شعاع اعمال نیرو، به بازوی گشتاور (Torque Arm) معروف است.

محاسبه گشتاور

مقدار بردار گشتاور، $$\large \tau$$، که توسط نیروی $$\large F$$ و در طول بازوی $$\large r$$ ایجاد شده باشد، با رابطه زیر تعریف می‌شود.

$$\large \tau \: = \: F \: . \: r \: \sin ( \theta )$$

در رابطه بالا، زاویه بین نیرو و بازوی گشتاور را با $$\large \theta$$ نشان داده‌ایم. در حالت نشان داده شده در شکل قبل، زاویه بین نیرو و بازوی گشتاور، $$\large 90$$ درجه است. بنا به قرارداد، برای تعیین جهت بردار گشتاور از قانون دست راست استفاده می‌کنیم. همان‌گونه که در شکل زیر مشاهده می‌کنید، مطابق این قانون، هر گاه انگشتان دست راست در جهت وارد شدن نیرو قرار بگیرند، انگشت شست در جهت گشتاور وارد شده خواهد بود. اکنون می‌توانیم رابطه قبل را به طور دقیق‌تر و به صورت زیر بازنویسی کنیم که ضرب برداری بین دو کمیت $$\large F$$ و $$\large r$$ را نشان می‌دهد.

$$\large \overrightarrow{\tau} \: = \: \overrightarrow{r} \: \times \: \overrightarrow{F}$$

فاصله $$\large r$$، بردار موقعیت نقطه وارد شدن نیروی $$\large F$$ را نسبت به محور دوران نشان می‌دهد. در ادامه، برخی از حالت‌های مختلف گشتاور را بررسی می‌کنیم.

• در حالت اول، $$\large \theta \: = \: 0 ^ \circ$$ است. به عبارت دیگر، زاویه بین نیرو و بردار $$\large r$$ صفر درجه بوده و این دو بردار هم جهت هستند. در این وضعیت، هیچ دورانی رخ نمی‌دهد و مقدار گشتاور هم برابر صفر است.
• در حالت دوم، $$\large \theta \: = \: 180 ^ \circ$$ است. در واقع، نیرو و بردار $$\large r$$ هم راستا و در خلاف جهت یکدیگر هستند. با توجه به رابطه تعریف شده، سینوس این زاویه برابر صفر بوده و در این وضعیت هم دورانی اتفاق نمی‌افتد. از این رو، مقدار $$\large \tau$$، صفر است.
• بالاخره در حالت سوم، $$\large \theta \: = \: 90 ^ \circ$$ است. در این حالت، بردار نیرو و بردار موقعیت، به هم عمود هستند. با توجه به رابطه بالا، سینوس این زاویه برابر یک است. به عبارت دیگر، در این زاویه، تابع گشتاور به ماکسیمم مقدار خود می‌رسد و مساوی با $$\large \tau \: = \: r F$$ می‌شود.

تعادل گشتاور

برای اینکه جسمی از لحاظ استاتیکی در تعادل باشد، برآیند نیروها و گشتاورهای وارد به آن جسم باید مساوی صفر باشد. برای صفر شدن مقدار برآیند گشتاورها، مجموع گشتاورها در جهت عقربه‌های ساعت باید با مجموع گشتاورها در خلاف جهت حرکت عقربه‌های ساعت برابر باشد.

می‌توان این مفهوم را با قانون اول نیوتن برای یک سیستم دوّار هم‌ارز دانست. هر جسمی که در حال دوران نباشد، تا وقتی که گشتاور خارجی به آن وارد نشود، همچنان غیر دوّار باقی خواهد ماند. به طور مشابه، جسمی که با سرعت زاویه‌ای ثابت در حال دوران است، تا وقتی که هیچ گشتاور خارجی به آن وارد نشود، به دوران خود ادامه می‌دهد. از این مفهوم می‌توان در مسائلی استفاده کرد که چند گشتاور به یک جسم دوار وارد می‌شوند. در چنین حالتی، گشتاور خالص از اهمیت برخوردار است. اگر گشتاور خالص وارد به یک جسم صفر باشد، در تعادل دورانی قرار دارد و شتاب زاویه‌ای نخواهد داشت.

مثال ۱

سؤال: قرقره نشان داده شده در شکل زیر را در نظر بگیرید. برای اینکه قرقره در حالت تعادل قرار داشته باشد، مقدار نیروی $$\large F_2$$ را به دست آورید.

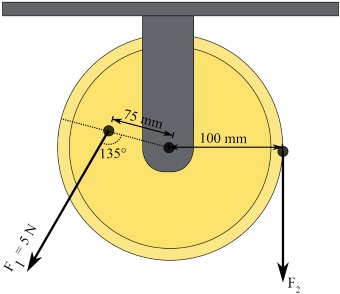
پاسخ: ابتدا گشتاور ناشی از نیروی $$\large F_1$$ را حول مرکز قرقره محاسبه می‌کنیم.

$$\large \tau_1 \: =\: Fr \sin \theta \:= \:(5\: N) (0.075 \:m) \sin (135 ^\circ) \\~\\ \large \tau _1 \:= \:+0.265 \:Nm$$

اکنون با نوشتن برآیند گشتاورها حول مرکز قرقره و قرار دادن آن برابر صفر، گشتاور حاصل از نیروی $$\large F_2$$ و در نهایت نیز خودِ نیروی $$\large F_2$$ به صورت زیر خواهد بود.

$$\large \tau _1 \: +\: \tau _2 \:= \:0 \\~\\ \large \tau _2 \:= \:- \: 0.265 \: Nm \:= \:-\: F_2 (0.1 \:m) \sin 90 ^\circ\\~\\ \large F_2 \:= \:2.65 \:N$$

کوپل چیست؟

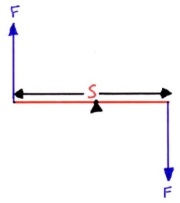
هنگامی که دو نیروی مساوی در یک راستا ولی در دو جهت متفاوت به دو نقطه از یک جسم وارد شوند، کوپل (Couple) تشکیل می‌شود. کوپل مانند گشتاور عمل کرده و جسم را وادار به چرخش می‌کند. ممان حاصل از کوپل را می‌توان با ضرب اندازه یکی از نیروها ($$\large F$$) در فاصله عمودی بین دو نیرو ($$\large S$$) محاسبه کرد. به عبارت دیگر، گشتاور ناشی از کوپل در شکل زیر، برابر با $$\large \tau \: = \: SF$$ است.

گشتاور و ممنتوم زاویه‌ای

گشتاور و ممنتوم زاویه‌ای به صورت حاصل‌ضرب برداری موقعیت در نیرو و ممنتوم به دست می‌آیند. فرض کنید نیروی $$\large \overrightarrow{F}$$ به ذره‌ای وارد می‌شود که فاصله آن نسبت به مبدأ $$\large O$$ با بردار $$\large \overrightarrow{r}$$ مشخص می‌شود. حال، اگر این ذره نسبت به مبدأ دارای ممنتوم زاویه‌ای $$\large \overrightarrow{p}$$‌ باشد، ممان و ممنتوم زاویه‌ای این ذره به ترتیب به صورت $$\large \overrightarrow{\tau} \: = \: \overrightarrow{r} \: \times \: \overrightarrow{F}$$ و $$\large \overrightarrow{L} \: = \: \overrightarrow{r} \: \times \: \overrightarrow{p}$$ تعریف می‌شود. جهت بردارهای ممان و ممنتوم زاویه‌ای را در شکل زیر مشاهده می‌کنید.

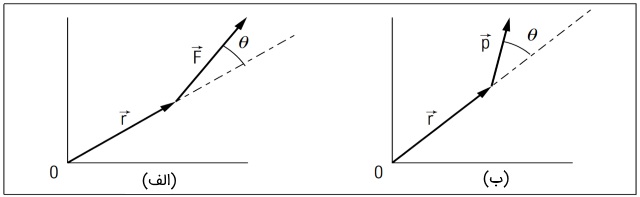
اکنون با کمک تعاریف ممان و ممنتوم زاویه‌ای، می‌توانیم رابطه‌ای بین این دو کمیت بیابیم. از قانون دوم نیوتن آغاز می‌کنیم که به صورت $$\large \overrightarrow{F} \: = \: \frac{ \text{d} \overrightarrow{p} }{ \text{d} t }$$ نوشته می‌شود. تعریف گشتاور به صورت زیر است.

$$\large \overrightarrow{\tau} \: = \: \overrightarrow{r} \: \times \: \overrightarrow{F} \: = \: \overrightarrow{r} \: \times \: \frac{ \text{d} \overrightarrow{p} }{ \text{d} t }$$

از تعریف ضرب برداری کمک می‌گیریم.

$$\large \frac{\text{d}}{\text{d} t } (\overrightarrow{r} \: \times \: \overrightarrow{p}) \: = \: \overrightarrow{r} \: \times \: \frac{ \text{d} \overrightarrow{p}}{\text{d} t} \: + \: \frac{ \text{d} \overrightarrow{r}}{\text{d} t} \: \times \: \overrightarrow{p} \\~\\ \large \overrightarrow{\tau} \: = \: \frac{\text{d}}{\text{d}t} (\overrightarrow{r} \: \times \: \overrightarrow{p}) \: - \: \frac{ \text{d} \overrightarrow{r}}{\text{d} t} \: \times \: \overrightarrow{p} \\ ~ \\ \large \Rightarrow~~~ \overrightarrow{\tau} \: = \: \frac{\text{d}\overrightarrow{L}}{\text{d}t} \: - \: \overrightarrow{v} \: \times \: \overrightarrow{p}$$

می‌دانیم $$\large \overrightarrow{p} \: = \: m \overrightarrow{v}$$ است. به همین دلیل حاصل $$\large \overrightarrow{v} \: \times \: \overrightarrow{p} \: = 0$$ برابر صفر می‌شود. بنابراین، رابطه قبلی به شکل زیر ساده می‌شود.

$$\large \overrightarrow{\tau} \: = \: \frac{\text{d}\overrightarrow{L}}{\text{d}t}$$

می‌توان این‌گونه نتیجه گرفت که گشتاور وارد به یک جسم، با نرخ تغییرات ممنتوم زاویه‌ای آن جسم برابر است. ذره‌ای را مطابق شکل زیر در نظر بگیرید که در صفحه $$\large x-y$$ حرکت می‌کند. گشتاور وارد به این جسم و در نتیجه، ممنتوم زاویه‌ای آن، همیشه عمود به صفحه $$\large x-y$$ است. به عبارت دیگر می‌توان گفت $$\large \overrightarrow{\tau}$$ و $$\large \overrightarrow{L}$$ فقط دارای مؤلفه‌ای در جهت محور $$\large z$$ هستند. بنابراین، جهت آنها ثابت باقی می‌ماند و تنها مقدارشان متغیر است. از این رو، رابطه بین ممان و ممنتوم زاویه‌ای را در حرکت صفحه‌ای می‌توان به شکل زیر و بدون نماد بردار نوشت.

$$\large \tau \: = \: \frac{\text{d}L}{\text{d}t}$$

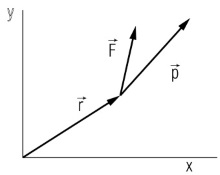
حرکت ذره روی محیط دایره

در حالتی که ذره‌ای روی محیط یک دایره حرکت می‌کند، گشتاور و ممنتوم زاویه‌ای را می‌توان به راحتی برحسب متغیرهای زاویه‌ای ذره بیان کرد. ذره‌ای به جرم $$\large m$$ و مطابق شکل زیر، با سرعت خطی $$\large v$$، روی محیط دایره‌ای به شعاع $$\large r$$ در حال حرکت است.

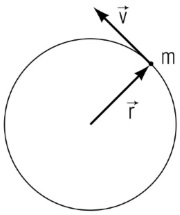
ممنتوم زاویه‌ای این ذره برابر $$\large \overrightarrow{L} \: = \: \overrightarrow{r} \: \times \: m \overrightarrow{v}$$ خواهد بود. از آنجایی که بردارهای $$\large \overrightarrow{r}$$ و $$\large \overrightarrow{v}$$ به یکدیگر عمود هستند، اندازه بردار ممنتوم زاویه‌ای برابر با رابطه زیر به دست می‌آید.

$$\large L \: = \: mvr$$

(رابطه ۱)

جهت بردار ممنتوم زاویه‌ای نیز با توجه به قانون دست راست، به سمت بیرون صفحه و عمود به آن است. می‌توانیم در رابطه ۱، سرعت خطی را برحسب سرعت زاویه‌ای بنویسیم.

$$\large v \: = \: \omega r \\~\\ \large \Rightarrow ~~~ L \: = \: m r^2 \omega$$

با مشتق‌گیری از این رابطه نسبت به زمان، گشتاور نیز قابل محاسبه خواهد بود.

$$\large \tau \: = \: \frac{\text{d}L}{\text{d}t} \: = \: mr^2\frac { \text{d} \omega} {\text{d} t} \: = \: m r^2 \alpha$$

در رابطه بالا، شتاب زاویه‌ای ذره با نماد $$\large \alpha$$ نشان داده شده است.

گشتاور و ممنتوم زاویه‌ای در سیستم ذرات

برای محاسبه گشتاور و ممنتوم زاویه‌ای در سیستم ذرات، فقط کافی است مجموع گشتاور و ممنتوم‌های زاویه‌ای تک‌تک ذرات محاسبه شود. گشتاور ناشی از نیروهای داخلی صفر است. زیرا مطابق قانون سوم نیوتن، نیروی متقابل بین هر دو ذره با یکدیگر برابر، در راستای خط اتصال آنها و در خلاف جهت یکدیگر است. به همین دلیل، گشتاور کل ناشی از هر جفت نیروی عمل و عکس‌العمل صفر بوده و در نتیجه، گشتاور درونی کل نیز صفر خواهد بود. گشتاور و ممنتوم زاویه‌ای کل را در سیستم ذرات می‌توان به شکل زیر نوشت.

$$\large \overrightarrow{\tau} \: = \: \sum _ { i \: = \: 1} ^ N \overrightarrow{\tau} _ i \: = \: \sum _ { i \: = \: 1} ^ N \overrightarrow{\tau} _ {i , ext } \\~\\ \large \overrightarrow {L} \: = \: \overrightarrow {L} _ 1 \: + \: \overrightarrow {L} _ 2 \: + \: ... \: = \: \sum _ {i \: = \: 1} ^ N \overrightarrow {L} _ i$$

حرکت جسم صلب حول محور ثابت

جسم صلب، سیستمی از ذرات است که موقعیت ذرات آن نسبت به یکدیگر تغییر نمی‌کند. از آنجایی که برای هریک از ذرات، رابطه $$\large L \: = \: m v r \: = \: m r^2 \omega$$ برقرار است، ممنتوم زاویه‌ای کل را می‌توان به صورت زیر نوشت.

$$\large L \: = \: (\sum_ i ^ {} m_i r ^ 2 _ i ) \omega$$

حال، با کمک تعریف ممان اینرسی (Moment of Inertia) جسم صلب ($$\large I \: = \: \sum_ i ^ {} m_i r ^ 2 _ i$$)، رابطه قبل را به صورت $$\large L \: = \: I \omega$$ بازنویسی می‌کنیم. از آنجایی که محور دوران ثابت است، گشتاور هم به شکل زیر بیان می‌شود.

$$\large \tau \: = \: \frac{\text{d}L}{\text{d}t} \: = \: \: I \frac{\text{d} \omega}{\text{d} t} \: = \: I \alpha$$

مثال ۲

سؤال: تمام جرم فلایویل نشان داده شده در شکل زیر، به طور یکنواخت در قسمت طوقه آن توزیع شده است. گشتاور و ممنتوم زاویه‌ای را به دست آورید.

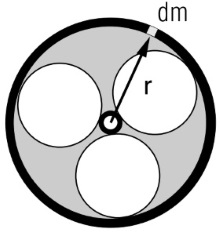
پاسخ: ناحیه دیفرانسیلی با جرم $$\large dm$$ را در نظر بگیرید. ممنتوم زاویه‌ای برای این قسمت به صورت رابطه زیر محاسبه می‌شود.

$$\large dL \: = \: d m \: r ^ 2 \omega$$

از آنجایی که شعاع $$\large r$$ و سرعت زاویه‌ای $$\large \omega$$ برای تمام نقاط روی طوقه یکسان است، ممنتوم زاویه‌ای کل برای فلایویل به راحتی به دست می‌آید.

$$\large L \: = \: \int_{ }^{ } dL \: = \: r ^ 2 \omega \int_{ }^{ } dm \: = \: M r ^ 2 \omega \: = \: I \omega$$

در رابطه بالا، $$\large M$$ جرم کل فلایویل است. با مشتق‌گیری از این رابطه نسبت به زمان، ممان برابر با $$\large \tau \: = \: M r ^ 2 \alpha \: = \: I \alpha$$ نتیجه می‌شود.

انرژی جنبشی دورانی

انرژی جنبشی کل مربوط به یک سیستم را می‌توان برحسب ممان اینرسی و سرعت زاویه‌ای آن سیستم نوشت. فرض کنید هریک از ذرات دارای جرم $$\large m _ i$$ باشد و روی محیط دایره‌ای به شعاع $$\large r _ i$$ حرکت کند. اگر موقعیت تمام این ذرات، نسبت به یکدیگر ثابت باشد (مانند جسم صلب)، سرعت زاویه‌ای تمام آنها یکسان و برابر $$\large \omega$$ خواهد بود. در این حالت، انرژی جنبشی هریک از این ذرات را می‌توان به صورت زیر بیان کرد.

$$\large E _ {i k} \: = \: \frac {1} { 2} m_i v^2 _i \: = \: \frac {1} { 2} m_i r ^2 _i \omega ^2$$

به این ترتیب، انرژی جنبشی کل به قرار زیر خواهد بود.

$$\large E _ k \: = \: \frac {1} { 2} m_1 r ^2 _1 \omega ^2 \: + \: \frac {1} { 2} m_2 r ^2 _2 \omega ^2 \: + \: ... \: = \frac {1} {2} [\sum_ {i \: = \: 1} ^N m_i r ^2 _ i] \omega ^ 2$$

حال با استفاده از تعریف ممان اینرسی جسم صلب، رابطه بالا به صورت $$\large E_k \: = \: \frac {1} {2} I \omega ^2$$ خلاصه می‌شود.

حرکت خطی و دایره‌ای

در این بخش، مقایسه‌ای کوتاه بین معادلات دینامیکی در حرکت خطی و دایره‌ای انجام خواهیم داد. به جدول زیر توجه کنید. برخی از این رابطه‌ها را می‌توان به صورت برداری یا تانسور هم نوشت. در نتیجه فراتر از محدوده حرکت خطی یا دایره‌ای، معتبر هستند.

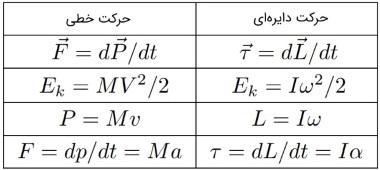
پایستگی ممنتوم زاویه‌ای

اگر هیچ گشتاور خارجی به یک سیستم ذرات وارد نشود، ممنتوم زاویه‌ای خالص مربوط به آن سیستم، پایسته است. این موضوع را می‌توان به صورت رابطه زیر نشان داد.

$$\large \overrightarrow{\tau}\: =\: 0\: =\: \frac{\text {d} \overrightarrow {L}}{\text{d} t}$$

در نتیجه، $$\large \overrightarrow{L}$$ ثابت می‌ماند. برای جسم صلبی که حول یک محور می‌چرخد، رابطه $$\large L \:= \:I\omega$$ برقرار است. بنابراین، اگر $$\large I$$ تغییر کند، برای ثابت ماندن $$\large L$$، مقدار $$\large \omega$$ نیز باید تغییر کند. اما اگر مجموع گشتاورهای خارجی وارد به سیستم، صفر نباشد، ممنتوم زاویه‌ای پایستار نخواهد بود.

مثال ۳

دو فلایویل نشان داده شده در شکل زیر را در نظر بگیرید. یکی از این دو فلایویل در حال دوران و دیگری ساکن است. اکنون و به طور ناگهانی هر دو فلایویل در تماس با یکدیگر قرار گرفته‌اند. در ابتدا ممنتوم زاویه‌ای کل برای فلایویل چرخان، برابر $$\large L_0 \:= \:M r^ 2\omega _0$$ است. هنگامی که فلایویل‌ها در تماس با هم قرار می‌گیرند، به دلیل اصطکاک به وجود آمده بین آنها، گشتاوری به فلایویل چرخان وارد می‌شود. از آنجایی که منشأ این گشتاور، خارجی است، ممنتوم زاویه‌ای آن پایستار نمی‌ماند و تغییر می‌کند. حال اگر هر دو فلایویل را یک سیستم در نظر بگیریم، گشتاور وارد شده به هر فلایویل، از نوع داخلی به حساب آمده و باز هم گشتاور خارجی صفر می‌شود. بنابراین برای این سیستم جدید که شامل هر دو فلایویل می‌شود، ممنتوم زاویه‌ای پایسته می‌ماند و رابطه زیر برقرار است.

$$\large M r^ 2\omega _0 \:= \:M r^ 2\omega _f \:+ \:M r^ 2\omega _f \:= \:2M r^ 2\omega _f$$

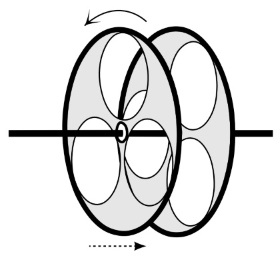
در رابطه بالا، $$\large \omega _f$$ سرعت زاویه‌ای نهایی را نشان می‌دهد که در نهایت هر دو فلایویل با این سرعت در حال دوران خواهند بود. تغییر سرعت زاویه‌ای در یکی از فلایویل‌ها به صورت $$\large \omega _0 \:\rightarrow \:\omega _f$$ و در دیگری به صورت $$\large 0 \:\rightarrow \:\omega _f$$ رخ داده است. جرم هریک برابر $$\large M$$ و سرعت زاویه‌ای نهایی نیز برابر $$\large \omega _f \:= \:\omega _0 /2$$ خواهد بود.

هنگامی که دو فلایویل با سرعت‌های متفاوت را در تماس با یکدیگر قرار می‌دهیم، می‌توانیم انتظار داشته باشیم که انرژی جنبشی پایستار نباشد. زیرا نیروهای غیرپایستار اصطکاکی به هر دو فلایویل وارد می‌شوند. انرژی جنبشی اولیه به صورت زیر تعریف می‌شود.

$$\large E _{k0} \:= \:\frac {1} {2} M r^2\omega _0 ^2$$

اما پس از برقراری تماس، انرژی جنبشی ثانویه به شیوه زیر محاسبه می‌شود.

$$\large E _{kf} \:= \:M r^2\omega _f ^2 \:= \:\frac {1} {4} M r^2\omega _0 ^2$$

به این ترتیب، نسبت انرژی جنبشی نهایی به انرژی جنبشی اولیه برابر $$\large \frac {E _{kf}} {E _{k0}} \:= \:\frac {1} {2}$$ است. به عبارت دیگر، نیمی از انرژی جنبشی اولیه به دلیل نیروهای اصطکاکی بین سطوح دو فلایویل، از بین رفته است. بنابراین، با وجود اینکه انرژی جنبشی کل پایستار نبوده، ولی ممنتوم زاویه‌ای کل سیستم پایستگی خود را حفظ کرده است.

گشتاور و توان

گشتاور، توان و انرژی مفاهیمی هستند که باید به درستی آنها را از یکدیگر متمایز ساخت. گشتاور و انرژی، کمیت‌هایی هستند که دیمانسیون آنها یکسان ولی مفهومشان کاملاً متفاوت است. اگر سرعت دوران معلوم باشد، می‌توانیم توان را با کمک گشتاور محاسبه کنیم. در واقع، توان اسب بخار هیچ‌گاه به تنهایی قابل محاسبه نیست و باید از روی گشتاور و سرعت دورانی به دست بیاید. رابطه‌های زیر را در نظر بگیرید.

$$\large P \: =\: \frac {F.D} {t} \:= \:\frac {F. 2\pi r} {t} \\~\\ \large P \:= \: 2\pi \tau \omega ~~~ (\omega ~~ \rightarrow ~~ \: revolutions /sec) \\~\\ \large P \:= \: \tau \omega ~~~ (\omega ~~ \rightarrow ~~ \: radian /sec)$$

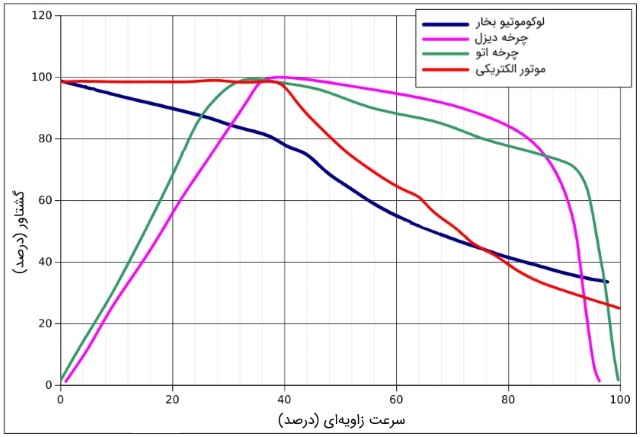
در بحث مقایسه موتور خودروها، گشتاور ماکسیمم نیز در کنار مفهوم اسب بخار، از اهمیت زیادی برخوردار است. در ادبیات عامیانه، گشتاور ماکسیمم معیاری از شتاب گرفتن اتومبیل و توانایی آن در کشیدن بار به حساب می‌آید. در سوی مقابل، اسب بخار به ماکسیمم سرعت اتومبیل دلالت دارد. با این حال، باید به این نکته نیز توجه داشت که هنگام انجام محاسبات مربوط به حرکت کلی اتومبیل، گشتاور ماکسیمم و اسب بخار، هر دو تابعی از دورِ موتور و در نتیجه متغیر هستند. این رابطه غیر خطی بوده و برای انواع گوناگون موتور، متفاوت است. نمودار گشتاور برحسب دورِ موتور برای چند نمونه موتور مختلف در شکل زیر رسم شده است.

افزایش و کاهش گشتاور

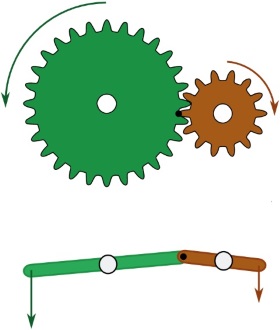
در کاربردهای مختلف، همواره نیاز است تا گشتاور خروجی موتور تغییر کرده، افزایش یا کاهش یابد. همان‌طور که می‌دانید، در یک اهرم، با تنظیم طول بازوی محرک و مقاوم، می‌توانیم مزیت مکانیکی اهرم و به دنبال آن، نیروی محرک را کمتر یا بیشتر کنیم. به طریق مشابه، گشتاور تولید شده در یک موتور را نیز می‌توان با استفاده از چرخ‌دنده، افزایش یا کاهش داد. با کمتر شدن سرعت زاویه‌ای، گشتاور افزایش می‌یابد. به شکل زیر توجه کنید. شبکه تشکیل شده توسط دندانه‌های درگیر دو چرخ‌دنده با یک جفت اهرم نشان داده شده در این شکل، هم‌ارز است.

برای عملکرد بهتر اتومبیل‌ها که توانشان از طریق یک موتور احتراق داخلی تأمین می‌شود، استفاده از چرخ‌دنده‌های قابل تنظیم، یک ضرورت است. در این موتورها، گشتاور ماکسیمم فقط در دامنه کوچکی از دورِ بالای موتور رخ می‌دهد. استفاده از دنده‌های قابل تنظیم این امکان را فراهم می‌کند که در تمام سرعت‌ها، گشتاور کافی به چرخ‌ها منتقل شود. به عنوان مثالی دیگر، دوچرخه را در نظر بگیرید. به دلیل اینکه ریتم رکاب‌زنی دوچرخه‌سوار نمی‌تواند دوچرخه را به سرعت مورد نظر برساند، از دنده‌های قابل تنظیم استفاده می‌شود. در غیر این صورت باید از دوچرخه‌های قدیمی استفاده کرد که می‌توانند به سرعت $$\large 15 \:-\: 25 \:km /h$$ برسند.

فراموش نکنید که در موتورهای بخار و موتورهای الکتریکی، گشتاور ماکسیمم در سرعت‌های پایین و در دامنه‌های نسبتاً بزرگی فراهم است. از این رو نیازی به استفاده از دنده‌های قابل تنظیم نیست.

مثال ۴

سؤال: یک موتور گازوئیلی قادر است در سرعت $$\large 300 \:rad /s$$، گشتاوری برابر با $$\large 150 \:Nm$$ تولید کند. از این موتور برای راه‌اندازی یک جرثقیل و بلند کردن وزنه نشان داده شده در شکل زیر استفاده شده است. اگر شعاع قرقره $$\large 0.25 \:m$$ و نسبت کاهش سرعت دنده $$\large 50 :1$$ باشد، الف) جرم وزنه $$\large m$$ ب) سرعت بالا رفتن وزنه را محاسبه کنید (فرض کنید حرکت وزنه با سرعت ثابت در حال انجام باشد).

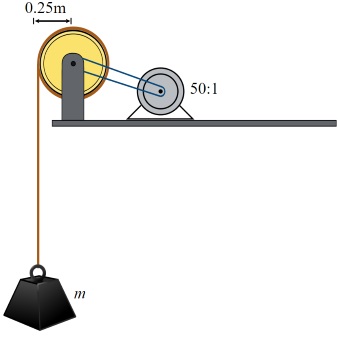
پاسخ: می‌دانیم که اگر قرقره در حالت تعادل باشد (چون سرعت وزنه ثابت است)، گشتاور ایجاد شده توسط موتور با گشتاور ناشی از وزنه آویزان برابر است. اگر کاهش سرعت دنده را $$\large R$$ بنامیم و گشتاور تولید شده توسط موتور را با $$\large \tau _m$$ نشان دهیم، گشتاور خروجی قرقره به صورت زیر به دست می‌آید.

$$\large \tau _w \:= \:\frac {\tau _m} {R}$$

حال، می‌توانیم جرم وزنه را پیدا کنیم.

$$\large \tau _w \:= \:Fr \\ ~\\ \large \Rightarrow ~~~ F \:= \:\frac {\tau _m} {Rr} \\ ~\\ \large F \:= \:mg \\ ~\\ \large \Rightarrow ~~~ m \:= \:\frac {\tau _m} {Rr g} \:= \:\frac {150 \:Nm} {\frac {1} {50} (0.25 \:m) (9.81 \: m/ s^2)} \\ ~\\ \large m \:= \:3060 \:kg$$

ب) می‌دانیم افزایش گشتاور، با کاهش سرعت زاویه‌ای همراه است. سرعت زاویه‌ای قرقره از رابطه $$\large \omega _w \:= \:\omega _mR$$ تبعیت می‌کند. در این رابطه، $$\large \omega _m$$ سرعت زاویه‌ای موتور را نشان می‌دهد. سرعت خطی در طوقه قرقره با سرعت بالا کشیدن وزنه $$\large m$$ برابر است. به همین منظور، رابطه‌های زیر را می‌توان نوشت.

$$\large v\: =\: r\omega _w \:= \:r\omega _mR \\ ~\\ \large v\: =\: (0.25 \:m) (300 \:rad /s) (\frac {1} {50}) \\ ~\\ \large v\: =\: 1.5 \:m /s$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• لختی دورانی چیست — به زبان ساده
• تکانه از صفر تا صد — بخش اول: اصول و مفاهیم
• تکانه از صفر تا صد — بخش دوم: تکانه زاویه‌ای
• آموزش مروری دینامیک مهندسی و حل سؤالات

^^