فلایویل (Flywheel) – از صفر تا صد

فلایویل (Flywheel) که در فارسی به چرخ طیار یا چرخ لنگر هم معروف است، به جرم دوّاری گفته میشود که برای ذخیره انرژی در ماشین به کار میرود. همانطور که میدانید، انرژی جنبشی یک جسم دوار را میتوان با کمک رابطه $$\large \frac {1}{2} I \omega ^ 2$$ به دست آورد. در این رابطه، $$\large I$$ گشتاور اینرسی حول محور دوران و $$\large \omega$$ سرعت زاویهای است. اگر سرعت ماشین بالا برود، انرژی در فلایویل ذخیره میشود. از طرف دیگر هم با کاهش سرعت، فلایویل کمبود انرژی را جبران میکند. تاریخچه فلایویل به هزاران سال پیش از میلاد مسیح و تمدن بینالنهرین بازمیگردد. در ابتدا از این وسیله در ماشین ریسندگی و چرخهای سفالگری استفاده میشد. شکل زیر، فلایویل نصب شده در یک موتور بخار قدیمی را نشان میدهد.

دو دسته ماشین از وجود فلایویل بهره میبرند. به عنوان مثالی از دسته اول، میتوان به یک ژنراتور الکتریکی اشاره کرد که محرک آن، یک موتور احتراق داخلی است. موتور احتراق داخلی چهار زمانه و تکسیلندری را در نظر بگیرید. گشتاور انتقالی به ژنراتور متغیر است. زیرا در هر دو دور کامل، فقط یک مرحله توان اتفاق میافتد. ولتاژ خروجی ژنراتور هم تابعی از سرعت است. در نتیجه، تغییر ولتاژ موجب سوسو زدن چراغها میشود. در اینجا برای اینکه سرعت و گشتاور انتقالی به ژنراتور یکنواخت باشد، از فلایویل استفاده میشود.
دسته دوم، دستگاههای پرس پانچ (Press Punch) هستند. فرآیند پانچ به توان زیادی نیاز دارد و در غیاب فلایویل، این توان باید با استفاده از موتورهای بزرگ تأمین شود. با استفاده از فلایویل، میتوان اندازه موتور را بسیار کوچکتر کرد. در این حالت، انرژی موتور در حد فاصل بازههای زمانی عملکرد پانچ، در فلایویل ذخیره میشود. به این ترتیب، میتوان از این انرژی ذخیره شده، در فرآیند پانچ استفاده کرد. در شکل زیر، نمونهای از دستگاه پرس پانچ را مشاهده میکنید.

ضریب نوسان
انحراف مجاز از سرعت زاویهای فلایویل را به عنوان ضریب نوسان (Fluctuation Coefficient) و به صورت رابطه زیر تعریف میکنیم.
$$\large C = \frac {\omega_1 - \omega_2} {\omega}$$
در رابطه بالا، $$\large \omega_1$$ ماکسیمم سرعت زاویهای فلایویل و $$\large \omega_2$$ مینیمم سرعت زاویهای آن است. سرعت زاویهای متوسط هم با $$\large \omega$$ نشان داده شده است. این رابطه را میتوان به شکل $$\large C = \frac {V_1 - V_2} {V}$$ و براساس سرعت خطی هم تعریف کرد. در کاربردهای عملی، بازه تغییرات این ضریب از $$\large 0.2$$ برای دستگاه خردکن سنگ تا $$\large 0.002$$ برای ژنراتور الکتریکی است.
محاسبه جرم فلایویل
فلایویل شکل زیر را در نظر بگیرید. سرعت زاویهای طوری تغییر میکند که سرعت خطی روی طوقه (rim) فلایویل از مقدار مینیمم $$\large V_2$$ تا مقدار ماکسیمم $$\large V_1$$ متغیر باشد. سرعت خطی متوسط را به صورت $$\large V = \frac {V_1 + V_2}{2}$$ تعریف میکنیم. اکنون با ضرب طرفین این رابطه در رابطه ضریب نوسان، نتیجه زیر حاصل میشود.
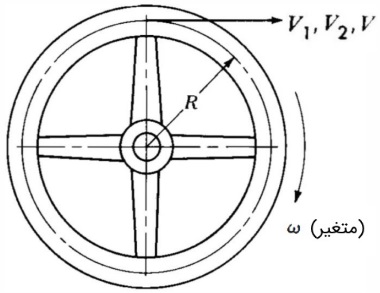
$$\large 2CV^2 = V^2_1 - V^2_2$$
(رابطه ۱)
فرض کنید کل جرم فلایویل $$\large M$$ بوده و در شعاع طوقه متوسط $$\large R$$ متمرکز شده باشد. انرژی جنبشی را به اختصار با $$\large KE$$ نشان داده و به ترتیب برای سرعتهای $$\large V_1$$ و $$\large V_2$$ مینویسیم.
$$\large KE_1 = \frac {1}{2} MV^2_1, ~~~~~ KE_2 = \frac {1}{2} MV^2_2$$
اگر تغییرات انرژی جنبشی را $$\large E$$ بنامیم، رابطه $$\large E = \frac {1}{2} M (V^2_1 - V^2_2)$$ برقرار است. با مقایسه این رابطه و رابطه شماره ۱، تغییر انرژی جنبشی به صورت زیر به دست میآید.
$$\large E = M C V^2$$
در رابطه بالا، $$\large M$$ جرم مؤثر فلایویل در طوقه است و به صورت جرم طوقه به اضافه اثر پرهها و توپی محاسبه میشود. در یک فلایویل واقعی و دارای پره، جرم طوقه در حدود %$$\large 90$$ از کل جرم مؤثر $$\large M$$ است. تنش در طوقه و پرهها ناشی از نیروهای گریز از مرکز است که آن هم با سرعت تغییر میکند. سرعت پره $$\large V$$ معمولاً برای چدن ریختهگری $$\large 30\: \frac {m}{s}$$ و برای فولاد $$\large 40\: \frac {m}{s}$$ است. میتوانید مقادیر چگالی را برای چدن ریختهگری و فولاد، به ترتیب برابر $$\large 7090 \: \frac {kg}{m^3}$$ و $$\large 7830 \: \frac {kg}{m^3}$$ در نظر بگیرید.
مثال
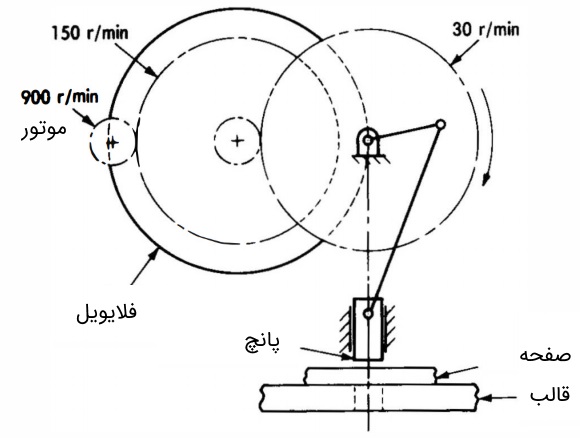
سؤال: در این مثال میخواهیم اندازه فلایویل مورد نیاز در یک دستگاه پرس پانچ را محاسبه کنیم. شماتیک دستگاه پرس در شکل زیر، نشان داده شده است. در مکانیزم لنگ و لغزندهای که مشاهده میکنید، لغزنده نقش پرس را بازی میکند. این دستگاه پرس قرار است تعداد $$\large 30$$ سوراخ را در هر دقیقه پانچ کند. در نتیجه مدت زمان بین هر دو پانچ، $$\large 2$$ ثانیه است. فرض میکنیم مدت زمان هر پانچ هم به اندازه $$\large \frac {1}{3}$$ ثانیه باشد. سوراخی با قطر $$\large 20$$ میلیمتر و ضخامت $$\large 13$$ میلیمتر باید در صفحهای از جنس فولاد $$\large 1025$$ پانچ شود. سرعت موتور محرک برابر $$\large 900$$ دور در دقیقه است. با کمک چرخدندهها، سرعت پانچ به $$\large 30$$ بار در هر دقیقه میرسد.
پاسخ: ابتدا انرژی مورد نیاز برای پانچ را محاسبه میکنیم. بیشترین نیروی مورد نیاز برای برش یک صفحه را میتوان با کمک رابطه زیر به دست آورد.
$$\large P = \pi d t \tau$$
در رابطه بالا، $$\large d$$ قطر سوراخ و برحسب متر است. ضخامت صفحه را با $$\large t$$ نشان دادهایم و برحسب متر وارد میکنیم. پارامتر $$\large \tau$$ مقاومت برشی است و با واحد پاسکال تعریف میشود. بنابراین، نیروی ماکسیمم، به صورت زیر محاسبه میشود.
$$\large P = \pi (0.020)(0.013)(310 \times 10^6) = 253000 \:N$$
شکل زیر، نمودار نیرو برحسب جابجایی را برای پانچ کردن یک سوراخ نشان میدهد. سطح زیر نمودار الف را میتوان به عنوان یک مثلث فرض کرد. در این حالت، کار انجام شده در پانچ کردن سوراخ با کمک رابطه $$\large W_k = \frac {1}{2} P t$$ به دست میآید. با این رابطه، کار برحسب ژول به دست میآید. با جایگذاری مقادیر قبلی در این رابطه، مقدار کار برابر با $$\large W_k = \frac {1}{2} (253000)(0.013) = 1640 \:J$$ قابل محاسبه است.
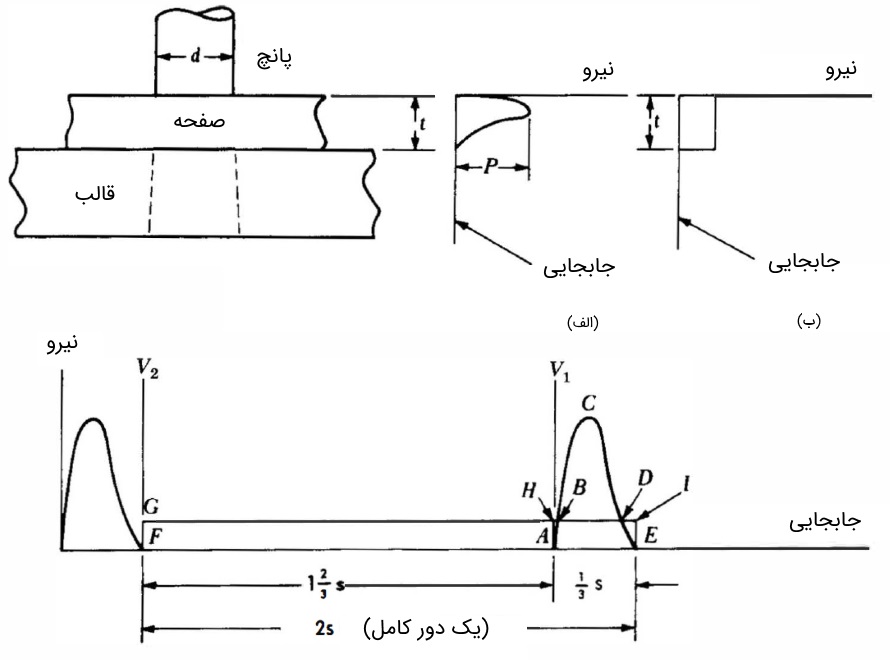
تحلیل حالت بدون فلایویل: فرض میکنیم نمودار نیرو-جابجایی، مطابق شکل ب، مستطیلی باشد. در این حالت، توان میانگین مورد نیاز برای پانچ کردن، با تقسیم مقدار $$\large W_k$$ به مدت زمان هر پانچ ($$\large \frac {1} {3}$$ ثانیه) و برابر $$\large 4920$$ وات به دست میآید. از آنجایی که نیروی $$\large p$$ در تصویر الف، دو برابر نیروی متوسط در تصویر ب است، توان لحظهای ماکسیمم را میتوان تقریباً برابر با $$\large 9840$$ وات محاسبه کرد.
تحلیل حالت همراه با فلایویل: اگر از یک فلایویل استفاده شود، میتوان تا حد زیادی توان موتور را کاهش داد. تصویر پ را در نظر بگیرید. کار انجام شده در هر سیکل را برابر $$\large 1640$$ ژول به دست آوردیم. این مقدار برابر با مساحت ناحیه $$\large ABCDE$$ در تصویر است و باید در فاصله زمانی $$\large \frac {1} {3}$$ ثانیه تأمین شود. اگر از فلایویل استفاده شود، مساحت ناحیه $$\large FGIE$$ برابر این مقدار میشود و این انرژی باید برای هر سیکل فراهم شود. در نتیجه، با فلایویل، انرژی $$\large 1640$$ ژول باید در طول مدت $$\large 2$$ ثانیه تأمین شود. با یک بررسی ساده مشخص است که در این حالت به موتوری با توان $$\large \frac {1640} {2} = 840 \:W$$ نیاز داریم.
برای محاسبه جرم و اندازه فلایویل، قطر طوقه میانگین را برابر با $$\large 900 \:mm$$ فرض میکنیم. در این حالت، سرعت طوقه میانگین به صورت زیر خواهد بود.
$$\large V = \frac {\pi n D} {60} = \frac {\pi (150) (0.900)} {60} = 7.07 \: \frac {m}{s}$$
فرض کنیم ضریب نوسان مجاز برای سرعت، $$\large C = 0.10$$ باشد. بنابراین، سرعت مینیمم و ماکسیمم به طریق زیر قابل محاسبهاند.
$$\large V_1 + V_2 = 14.14 , ~~~~~ V_1 - V_2 = 0.707\\~\\
\large \begin{cases} V_1 = 7.42 \:\frac {m} {s} \\ V_2 = 6.72 \:\frac {m} {s} \end{cases}$$
اکنون، جرم فلایویل به راحتی به دست میآید.
$$\large M = \frac {E} {CV^2} = \frac {1376 \:N.m} {(0.10) (7.07 \:m/s)} = 273\: kg$$
اگر فلایویل را دارای پره فرض کنیم، جرم واقعی طوقه در حدود $$\large 90$$ درصد از جرم کل و برابر $$\large 246$$ کیلوگرم خواهد بود.
کاربرد فلایویل در موتور احتراق داخلی
همانطور که در ابتدای این مقاله از فرادرس گفتیم، کاربرد دیگر فلایویل، در موتورهای احتراق داخلی است. به عنوان مثال، یک موتور احتراق داخلی چهار زمانه و تکسیلندر را در نظر بگیرید. شکل زیر، گشتاور خروجی را برحسب موقعیت میللنگ نشان میدهد. چهار مرحله حرکت پیستون در یک چرخه انجام میشود و در هر دو کورس کامل پیستون، فقط یک مرحله تولید توان اتفاق میافتد.
گشتاور خروجی کل با مجموع گشتاور حاصل از فشار گاز و گشتاور اینرسی برابر است. فشار گاز روی پیستون را میتوان با کمک یک نمودار شاخص به دست آورد. در این نمودار، فشار گاز تابعی از موقعیت پیستون است. برای یافتن گشتاور خروجی ناشی از فشار گاز، میتوانیم نیروی استاتیک را تحلیل کنیم. این تحلیل به صورت نموداری برحسب موقعیت زاویهای میللنگ رسم شده است. برای به دست آوردن، گشتاور اینرسی خروجی، از تحلیل نیروی اینرسی استفاده شده است.

ناحیههایی از نمودار که بالای خط گشتاور صفر قرار دارند، کار انجام شده مثبت توسط موتور را نشان میدهند. مشخص است که نواحی زیر این خط نیز، بیانگر کار منفی هستند. برای به دست آوردن گشتاور میانگین، کافی است جمع جبری این نواحی را محاسبه و به جابجایی $$\large 720$$ درجهای میللنگ تقسیم کنیم. حال اگر ماشینی که قرار است با این موتور به حرکت دربیاید، گشتاوری برابر گشتاور میانگین ولی در جهت خلاف آن ایجاد کند، باید از وسیلهای استفاده کرد تا منحنی گشتاور مجموع، هموار شود. وظیفه فلایویل، تأمین گشتاور خروجی یکنواخت است. نواحی هاشور خورده بالای خط گشتاور میانگین، نشان دهنده این است که انرژی مازاد وجود دارد. در این حالت، سرعت و انرژی ذخیره شده در فلایویل افزایش مییابد. نواحی هاشور خورده در زیر خط گشتاور میانگین، کمبود انرژی را نشان میدهد. در این وضعیت، از سرعت و انرژی ذخیره شده در فلایویل کاسته میشود.
به منظور تعیین انرژی لازم برای ذخیره در فلایویل، باید به دنبال موقعیتهایی باشیم که سرعت میللنگ ماکسیمم و مینیمم میشود. فرض میکنیم سرعت در ابتدای مرحله احتراق، مینیمم و در پایان این مرحله، ماکسیمم باشد. ولی با دقت در نمودار قبل درمییابیم که ماکسیمم و مینیمم در این نقاط رخ نمیدهد. از نقطه $$\large A$$ شروع میکنیم و به سمت نقطه $$\large B$$ میرویم.
در این مسیر، انتگرال نمودار گشتاور ترکیبی، منفی است. در نتیجه، کمبود انرژی رخ داده و سرعت کاهش مییابد. با شروع از نقطه $$\large B$$ و حرکت به سمت نقطه $$\large C$$ درمییابیم که سطح زیر نمودار مثبت بوده و انرژی مازاد است. در این مرحله سرعت افزایش مییابد. میتوان اینطور نتیجهگیری کرد که سرعتهای ماکسیمم و مینیمم در محل تقاطع نمودار گشتاور ترکیبی و نمودار گشتاور میانگین اتفاق میافتد. فرض کنید سرعت و انرژی جنبشی در نقطه $$\large D$$ به ترتیب برابر $$\large \omega_1$$ و $$\large E_1$$ باشد. حال اگر روی نمودار به سمت نقطه $$\large A$$ حرکت کنیم، انرژی در نقطه جدید برابر $$\large E_1+100$$ میشود. به طریق مشابه، انرژی جنبشی در نقطه $$\large B$$ به میزان $$\large E_1+ 25$$ میرسد. در بالای نمودار، انرژی نسبی برای تمام نقاط نوشته شده است. میبینیم که ماکسیمم انرژی در نقطه $$\large A$$ و مینیمم آن در نقطه $$\large E$$ رخ میدهد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:
- مجموعه آموزشهای دروس مهندسی مکانیک
- مجموعه آموزشهای نرمافزارهای مهندسی مکانیک
- چرخ دنده – به زبان ساده
- لختی دورانی چیست؟ — به زبان ساده
- حرکت دایره ای – به زبان ساده
- بادامک – از صفر تا صد
- آشنایی با تبدیلات تنش — مبانی مقاومت مصالح
^^










درود بر شما. خدا قوت. با تشکر از ارائه مطلب بالا، لطفا میفرمائید که آیا قطر فلایویل در کل عملکرد آن موثر است یا صرفا وزن فلایویل برای انجام وظیفهاش کفایت میکند.
عالی بود
با سلام و خسته نباشید به عزیزان و مدیران و مهندسین شرکت
مطالبی که عنوان کردید عالی هستند.
عزیز سوالی دارم.
قطر و وزن فلایویل برای موتور ۳ فاز ۱.۵ کیلو وات با دور ۱۶۰۰ کاری و دور ۳۰۰۰ نامی با شفت مستقیم به اسیاب کوپلینگ شده است که وزنی حدود۲۰ تا ۲۵ کیلو را بچرخاند ..چقدر باید باشد. دور موتور با درایو کنترل می شود..ممنونم