نیروی لورنتس (Lorentz Force) — از صفر تا صد

پیش‌تر در بلاگ فرادرس نیروی وارد شده به ذره باردار را در نتیجه حرکت در میدان الکتریکی و میدان مغناطیسی توضیح دادیم. در این مطلب قصد داریم تا نیروی وارد شده را با جزئیات بیشتری در قالب «نیروی لورنتس» (Lorentz Force) توضیح دهیم.

مقدمه

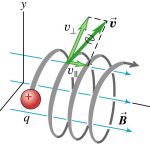
در فیزیک، به نیروی وارد شده به ذره باردار الکتریکی در حال حرکت در میدان الکترومغناطیسی، نیروی لورنتس گفته می‌شود. فرض کنید ذره‌ای با بار q و با سرعت v در میدان الکتریکی E و میدان مغناطیسی B در حال حرکت باشد. در این شرایط نیروی الکترومغناطیسی وارد شده به ذره مذکور برابر است با:

$${\mathbf { F }} = q {\mathbf { E }} + q {\mathbf { v }}\times {\mathbf { B }}$$

فیلم آموزش فیزیک 2 دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

رابطه فوق در حقیقت نقطه‌ شروعی برای تحلیل نیروی وارد به سیم حامل جریان است. برای اولین بار، این «الیور هویساید» (Oliver Heaviside) بود که در سال ۱۸۸۹ رابطه مربوط به نیروی لورنتس را بدست آورد. البته برخی از تاریخدانان معتقدند در ابتدا «جیمز کلارک ماکسول» (James Clerk Maxwell) مفهوم این نیرو را ارائه داد. البته در سال ۱۸۹۵، «هندریک لورنتز» (Hendrik Lorentz) نسخه کامل‌تری از این رابطه را ارائه داد.

رابطه نیروی لورنتس

همان‌طور که در فوق نیز عنوان شد، نیروی وارد به ذره باردار در میدانی الکترومغناطیسی برابر است با:

$${\mathbf { F }} = q {\mathbf { E }} + q {\mathbf { v }}\times {\mathbf { B }}$$
رابطه ۱

فیلم آموزش الکترومغناطیس 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

توجه داشته باشید که در رابطه فوق،‌ علامت × نشان دهنده ضرب خارجی است. رابطه‌ی برداری فوق را می‌توان به‌صورت مولفه‌ای نیز بیان کرد.

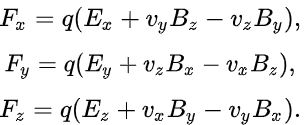
اگر میدان‌های الکتریکی و مغناطیسی به‌صورت توابعی از مکان و زمان تصور شوند، نیروی لورنتس را نیز می‌توان به‌صورت زیر بیان کرد:

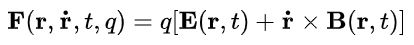
در رابطه فوق r بردار ذره‌ی q در زمان t است. $$\dot r$$ نیز برابر با مشتق زمانی بردار r در نظر گرفته می‌شود. ذره باردار مثبت در راستای میدان الکتریکی شتاب گرفته و در راستای عمود به جهت حرکتش و عمود به میدان مغناطیسی منحرف می‌شود. جهت انحراف ذره با استفاده از قانون دست راست قابل تعیین است. در حقیقت به‌منظور تعیین جهت انحراف ذره‌ی باردار -در نتیجه‌ی میدان مغناطیسی- دستان خود را در جهت حرکت ذره قرار داده و انگشتانتان را در راستای جهت میدان مغناطیسی منحرف کنید. در این حالت شستتان،‌ جهت انحراف ذره را نشان می‌دهد. برای نمونه، شکل زیر مسیر انحراف یک ذره در میدانی الکترومغناطیسی را نشان می‌دهد.

در رابطه ۱، qE نشان دهنده نیروی الکتریکی است. این در حالی است که $$q v × B$$، نیروی مغناطیسی وارد به ذره‌ی باردار تلقی می‌شود. در برخی از منابع، تنها نیروی مغناطیسی به عنوان نیروی لورنتس در نظر گرفته می‌شود. اما در این مطلب مجموع دو نیروی مغناطیسی و الکتریکی برابر با نیروی لورنتس در نظر گرفته شده است. مولفه مغناطیسی نیروی لورنتس، عاملی است که منجر به وارد شدن نیرو به سیم حامل جریانِ قرار گرفته در میدان مغناطیسی می‌شود. در مواردی این نیرو را نیروی لاپلاس نیز می‌نامند.

نیروی لورنتس، نیرویی است که به ذره‌ی باردار وارد شده و در نتیجه به آن مومنتوم نیز منتقل می‌کند. در حقیقت با گذشت زمان انرژی به ذره منتقل می‌شود. با استفاده از روابط مربوط به تکانه، توان منتقل شده به ذره را می‌توان با استفاده از رابطه $${ \displaystyle \mathbf {v} \cdot \mathbf { F } = q \,\mathbf { v } \cdot \mathbf { E } }$$ بدست آورد.

توزیع بار

بدیهی است که به توزیع پیوسته‌ای از بار‌های الکتریکی نیز نیرو وارد خواهد شد. در ابتدا توزیعی از بار‌های الکتریکی را مطابق با شکل زیر در نظر بگیرید.

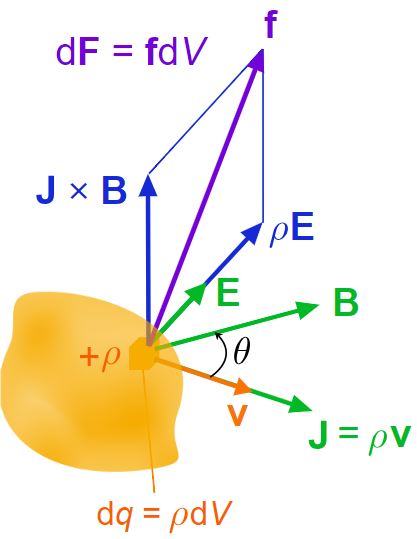
نیروی وارد به توده باردار را نیز می‌توان به‌ صورت $$\mathrm { d } \mathbf { F } = \mathrm { d } q \left(\mathbf { E } + \mathbf { v } \times \mathbf { B } \right)\,\!$$ بیان کرد. در رابطه مذکور، dF برابر با نیروی وارد به دیفرانسیل حجمی بار است. اگر هر دو سمت این رابطه به حجم توده تقسیم شوند، رابطه زیر بدست خواهد آمد.

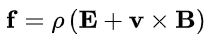
در رابطه فوق $$\rho$$ و $$f$$ به ترتیب نشان دهنده چگالی بار و چگالی نیرو هستند. در مواردی که توده‌ای از بار‌های الکتریکی مورد بررسی قرار می‌گیرد، کمیتی تحت عنوان چگالی حجمی جریان الکتریکی نیز مطابق با رابطه زیر تعریف می‌شود.

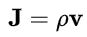
توجه داشته باشید که در رابطه فوق v، نشان دهنده سرعت توده‌ی بار بوده و نبایستی با حجمِ بار اشتباه گرفته شود. با توجه به تعریف فوق، نیروی لورنتس را می‌توان بر حسب چگالی حجمی جریان، به صورت زیر بیان کرد:

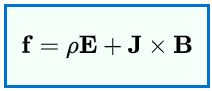
با انتگرال‌گیریِ حجمی از رابطه فوق، کل نیروی وارد به توده‌‌‌ی بار در حال حرکت برابر خواهد بود با:

به منظور محاسبه رابطه فوق در ابتدا $$\rho$$ و J به ترتیب با استفاده از قوانین گاوس و آمپر بر حسب E و B بیان می‌شوند. قانون گاوس (که در حقیقت یکی از معادلات ماکسول نیز محسوب می‌شود) رابطه زیر را عنوان می‌کند.

$$\large \rho = \epsilon_0 \triangledown.E$$

هم‌چنین J را می‌توان بر حسب میدان مغناطیسی، به شکل زیر نوشت.

$$\large J = \frac { \nabla × B } { \mu _ 0 } - \epsilon _ 0 \frac{\partial E } { \partial t }$$

با جایگذاری دو رابطه بالا در رابطه ۲، عبارت زیر بدست می‌آید.

پیش‌تر در مبحث امواج الکترومغناطیسی، برداری تحت عنوان بردار پوئینتینگ تعریف شد که برابر با حاصل‌ضرب خارجی دو میدان مغناطیسی و الکتریکی در نظر گرفته شد. در حقیقت این بردار معادل با E×B بوده و معیاری از میزان انرژی موجود در موج است. در نتیجه تغییرات زمانی بردار پوئینتینگ را می‌توان به‌ صورت زیر بیان کرد:

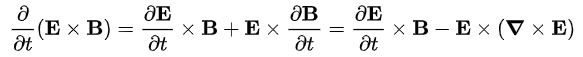
با استفاده از عبارت فوق، رابطه ۳ به‌ شکل زیر قابل بازنویسی می‌شود.

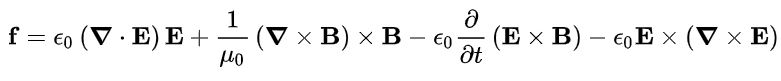
عبارت‌های حاوی E و B را مطابق با رابطه زیر به صورت جداگانه کنار یکدیگر می‌نویسیم. در نتیجه رابطه فوق، به‌ شکل زیر قابل بازنویسی خواهد بود.

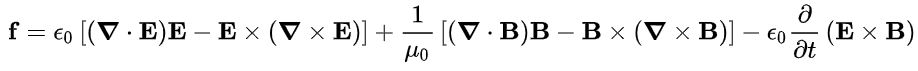
با توجه به وجود نداشتن تک قطبی مغناطیسی در طبیعت و هم‌چنین قانون گاوس برای مغناطیس، می‌توان گفت دیورژانسِ میدان مغناطیسی روی یک سطح بسته برابر با صفر است ($$\overrightarrow { \triangledown } . \overrightarrow{ B } = 0$$). بنابراین به‌منظور متقارن کردن رابطه فوق، عبارت  $$( ∇ . B ) B$$ به آن اضافه می‌شود. در نتیجه داریم:

از طرفی همواره رابطه زیر برای ضرب داخلی یک بردار در خودش برقرار است.

با استفاده از رابطه فوق، رابطه ۴ به‌ صورت زیر قابل بازنویسی می‌شود.

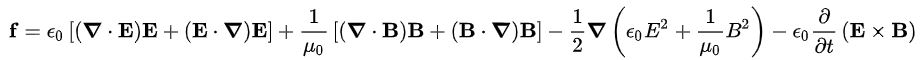
رابطه فوق را می‌توان به صورت تانسوری نیز بیان کرد. در حقیقت مفهومی تحت عنوان «تانسور تنش ماکسول» (Maxwell's Stress Tensor) به شکل زیر تعریف می‌شود:

$$\large {\displaystyle \sigma _{ i j }\equiv \epsilon _{0}\left(E _ { i } E_{j}-{\frac { 1 } {2}}\delta _{ i j }E^{2}\right)+{\frac { 1 }{\mu _{0}}}\left(B _ { i }B _{ j }-{ \frac { 1 }{2}}\delta _{ i j }B ^ { 2 } \right)}$$

با استفاده از تعریف فوق،‌ رابطه ۵ را می‌توان به صورت تانسوری که در ادامه آمده بیان کرد:

$$\large \mathbf {f}= { \displaystyle \nabla \cdot \mathbf { \sigma } - \epsilon _{0} \mu _ { 0 } { \frac { \partial \mathbf { S } } { \partial t}}\,}$$

توجه داشته باشید که در رابطه فوق، S بردار پوئینتینگ بوده و برابر با $${ \mathbf { S } } = { \frac { 1 } { \mu _ { 0 } } }{\mathbf { E } }\times {\mathbf { B } }$$ تعریف می‌شود. باتوجه به این‌ که حاصل‌ضرب $$\mu _ 0 \epsilon _ 0$$ برابر با سرعت نور است؛ در نتیجه رابطه فوق نیز به شکل زیر قابل بازنویسی خواهد بود.

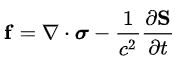
در رابطه فوق، c برابر با سرعت نور و $$\triangledown$$ گرادیان میدانِ تانسور تنش ماکسول است. بردار پوئینتینگ معیاری از میزان انرژی ذخیره شده در میدان الکتریکی و مغناطیسی است. از این رو رابطه فوق نیز نشان دهنده رابطه بین انرژی ذخیره شده در میدان‌ها و نیروی وارد شده به توزیع بار است.

اگر بار‌های ساکن و جریان الکتریکی را به صورت مجزا تصور کنیم. در این صورت رابطه توصیف کننده چگالی نیروی لورنتس را نیز می‌توان به صورت زیر بیان کرد:

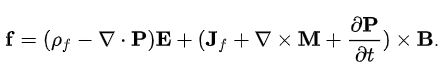
در رابطه فوق، $$\rho _ f$$ برابر با چگالی بار آزاد و P برابر با چگالی قطبش است. هم‌چنین $$J _ f$$ نماد جریان آزاد و M نشان دهنده چگالی مغناطیسی است. رابطه فوق به نحوی بیان شده که توصیف کننده گشتاور وارد شده به دو قطبی مغناطیسی در حضور میدان مغناطیسی است.

مسیر حرکت ذرات

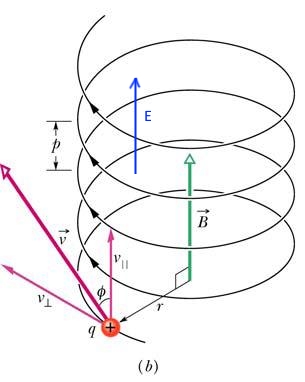
در بسیاری از موارد عملی که ذره‌ای باردار در میدانی مغناطیسی قرار می‌گیرد (به عنوان نمونه زمانی که الکترون در پلاسما قرار می‌گیرد)، حرکت ذره به صورت برآیند حرکت چرخشی حول نقطه‌ای ثابت و حرکتی خطی در نظر گرفته می‌شود.

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

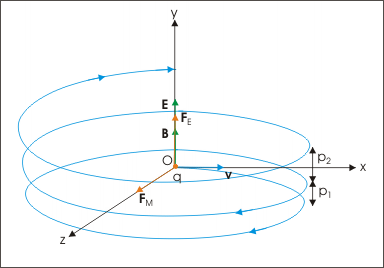
حرکت خطی در نتیجه میدان الکتریکی و حرکت چرخشی در نتیجه میدان مغناطیسی است. در شکل زیر نحوه حرکت ذره در حضور میدان الکتریکی و مغناطیسی نشان داده شده است.

نقاط قوت و ضعف

معادلات ماکسول نحوه ایجاد میدان‌های مغناطیسی و الکتریکی در نتیجه حرکت ذرات باردار را توضیح می‌دهد. نیروی لورنتس، توصیف معادلات ماکسول را با بررسی نیروی وارد شده به ذره‌ی باردار قرار گرفته در میدان الکترومغناطیسی کامل می‌کند.

حرکت ذرات باردار وابسته به دیگر عواملی همچون میدان مغناطیسی و الکتریکی نیز هست. بنابراین معادلات ماکسول نیز وابسته به این پدیده‌ها هستند. در حقیقت معادلات ماکسول از طریق چگالی‌های بار و جریان با این عوامل کوپل می‌شوند.

بنابراین پاسخ یک ذره در نتیجه حضور میدان‌های الکتریکی الکتریکی و مغناطیسی پدیده‌ای است که وابسته به عاملی خارجی نیست. این در حالی است که تولید میدان‌های مذکور در نتیجه حرکت ذرات باردار را نمی‌توان تنها با استفاده از معادلات ماکسول توصیف کرد.

توجه داشته باشید که به تنهایی و با استفاده از مفهوم نیروی لورنتس نمی‌توان رفتار توده‌ای از بار‌های الکتریکی را توصیف کرد. فرض کنید مجموعه‌ای از ذرات باردار در محیطی از یک ماده در حال حرکت باشند. میدان‌های الکتریکی و مغناطیسی به این ذرات نیرو وارد می‌کنند اما نکته این جا است که حرکت خود ذرات نیز منجر به تولید میدان الکتریکی و مغناطیسی می‌شود. در این حالت معادلات انتقالی هم‌چون معادلات ناویر-استوکس بایستی حل شوند.

مبنای تعریف میدان الکتریکی و مغناطیسی

در بسیاری از منابع علمی الکترومغناطیس کلاسیک، از نیروی لورنتس به منظور مفهومی برای تعریف میدان الکتریکی و مغناطیسی استفاده می‌شود. برای نمونه یکی از تعریف‌های جالب صورت گرفته برای نیروی لورنتس به صورت زیر است:

نیروی الکترومغناطیسی F به ذره‌ باردار q که با سرعت V در حال حرکت است، را می‌توان با استفاده از دو بردار، به‌صورت زیر تعریف کرد:

$$\large \mathbf { F } = q (\mathbf { E } + \mathbf { v } \times \mathbf { B } )$$

جالب است بدانید که تعریف فوق بسیار قوی است چرا که حتی در مواردی که سرعت ذره به سرعت نور نیز نزدیک شود ($$v = | v | ≈ c$$)، این توصیف از میدان الکتریکی و مغناطیسی درست است. با توجه به این تعریف، میدان‌های الکتریکی و مغناطیسی در زمان و مکان تعریف می‌شوند چرا که نیروی وارد شده به ذره‌ی آزمون، به صورت وابسته به زمان و مکان، تغییر جهت و اندازه می‌دهد.

نیروی وارد به سیم حامل جریان

زمانی که سیمی حاوی جریانی الکتریکی باشد و در میدانی مغناطیسی قرار گیرد، هریک از ذرات باردار در حال حرکت نیرویی را تجربه می‌کنند. بنابراین به کل سیم، نیرویی از جانب میدان مغناطیسی وارد می‌شود. با ترکیب نیروی لورنتس و تعریف جریان الکتریکی، نیروی وارد به سیم حامل جریان برابر با رابطه زیر بدست می‌آید.

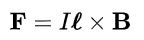
البته رابطه فوق در حالتی عمومی به صورت زیر نوشته می‌شود.

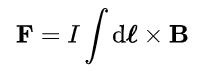
ایجاد نیروی محرکه

مولفه مغناطیسی نیروی لورنتس (qv×B) منجر به ایجاد نیروی محرکه الکتریکی می‌شود. نیروی محرکه الکتریکی پدیده‌ای است که مبنای کاری بسیاری از ژنراتور‌های تولید برق است. در حقیقت هنگامی که رسانایی در میدانی مغناطیسی در حال حرکت باشد، به الکترون‌های موجود در رسانا نیرو وارد شده و منجر به ایجاد جریانی الکتریکی در سیستم می‌شود.

در دیگر ژنراتور‌های الکتریکی، آهنربا به حرکت در آمده و رسانا ثابت است. در چنین مواردی نیروی محرکه در نتیجه تغییر بخش الکتریکی نیروی لورنتس ایجاد می‌شود. در حقیقت تغییرات زمانی میدان الکتریکی منجر به تولید میدان مغناطیسی متغیر شده و در نتیجه نیروی محرکه القایی نیز تولید می‌شود.

دو روش تولید نیروی محرکه ارائه شده در بالا ذاتا متفاوت هستند اما با استفاده از یک معادله هر دوی آن‌ها قابل توصیف‌اند. جهت توصیف نحوه ایجاد نیروی محرکه، مطابق با شکل زیر حلقه‌ای رسانا را در نظر بگیرید که میدانی مغناطیسی از آن عبور کرده است.

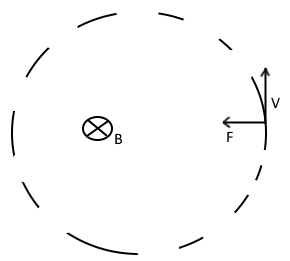
قانون القای فارادی عنوان می‌کند:

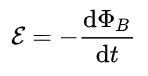
در رابطه فوق:

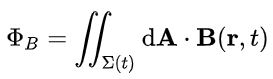
$$\Phi_B$$ برابر با شار عبوری از حلقه مفروض است که در نتیجه‌ی میدان مغناطیسی B ایجاد شده. هم‌چنین (Σ(t سطحی است که شار از آن عبور کرده و (Σ(t∂ برابر با منحنی بسته‌ای است که این سطح را احاطه کرده است. dA در انتگرال فوق نیز برداری است که به صفحه حلقه عمود است.

علامت نیروی محرکه القایی با استفاده از قانون لنز تعیین می‌شود. قانون لنز در مطلب القای فارادی به تفصیل توضیح داده شده است. توجه داشته باشید که این قانون برای رسانای متحرک و رسانای ثابت نیز صادق است. قانون القای فارادی را می‌توان از معادلات ماکسول و نیروی لورنتس نیز، نتیجه گرفت. جالب است بدانید که عکس این داستان نیز صادق است. در حقیقت با استفاده از قانون القای فارادی و معادلات ماکسول نیز می‌توان نیروی لورنتس را بدست آورد.

فرض کنید (Σ(t،‌ حقله‌ای متحرک بوده که با سرعت ثابت v در حال حرکت است. با فرض این‌که (Σ(t برابر با مساحت سطح درون حلقه باشد، نیروی محرکه القایی درون حلقه برابر است با:

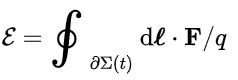
در رابطه فوق، $$E= \frac{F}{q}$$ بوده و dl بردار جزئی روی خم $$\partial \Sigma (t)$$ است. رابطه فوق را می‌توان با توصیف ماکسول از القای فارادی برابر قرار داده که در نتیجه آن، رابطه ماکسول-فارادی حاصل می‌شود.

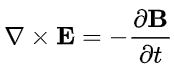
البته رابطه ماکسول-فارادی را می‌توان به شکل انتگرالی نیز بیان کرد. در حقیقت در ابتدا طرفین رابطه فوق را در بردار dA ضرب داخلی کرده و سپس از آن انتگرال دوگانه می‌گیریم. در این صورت سمت چپ با استفاده از قضیه استوکس ساده شده و نهایتا رابطه فوق به صورت زیر در می‌آید.

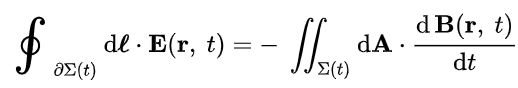
حال با استفاده از قانون القای فارادی، رابطه فوق به صورت زیر در می‌آید.

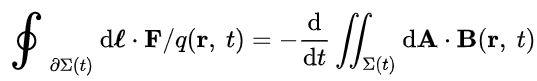
با استفاده از قانون انتگرال لایب‌نیتز و این واقعیت که div B=0 است، رابطه فوق به صورت زیر قابل بازنویسی خواهد بود.

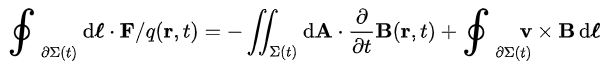
هم‌چنین با استفاده از معادله ماکسول-فارادی، رابطه فوق به‌ صورت زیر در می‌آید.

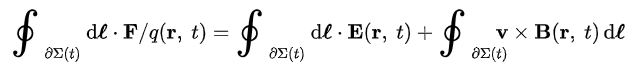
با توجه به این که رابطه فوق به ازای هر حالتی از موقعیت سیم برقرار است؛‌ بنابراین آن را می‌توان به شکل زیر نیز بیان کرد:

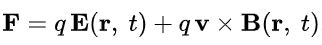
قانون القای فارادی فارغ از این که حلقه صلب یا غیر صلب، ساکن یا متحرک باشد، برقرار است. هم‌چنین در حالاتِ میدان مغناطیسی ثابت و یا متغیر، این قانون برقرار است.

تعریف با استفاده از پتانسیل

میدان‌های الکتریکی و مغناطیسی E و B را می‌توان با استفاده از بردار پتانسیل مغناطیسی A و پتانسیل الکترواستاتیکی $$\phi$$ به‌ صورت زیر تعریف کرد:

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

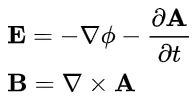
در رابطه فوق، ∇ عملگر گرادیان، .∇ عملگر دیورژانس و ×∇، کرل هستند. با این تفاسیر نیروی لورنتس را می‌توان در قالب دو پتانسیل A و $$\phi$$، به شکل زیر تعریف کرد:

در ریاضیات برداری رابطه زیر را می‌توان برای ضرب خارجی سه بردار نوشت.

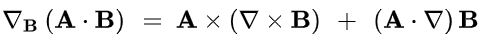
با استفاده از عبارت فوق، رابطه ۶ را می‌توان به صورت زیر بازنویسی کرد.

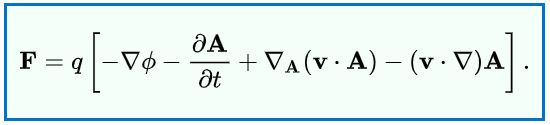
در ترم $$\triangledown_A$$، نماد A، زیر نویس فاینمن است که نشان دهنده عمل کردن اوپراتورِ $$\triangledown$$ بر روی فقط A است. البته در رابطه فوق می‌توان از مشتق زنجیره‌ای استفاده کرده و $$\frac { \partial A } { \partial t }$$ را به شکل زیر بازنویسی کرد.

در نتیجه نیروی لورنتس نیز بر حسب مشتق کامل A، به شکل زیر قابل بیان خواهد بود.

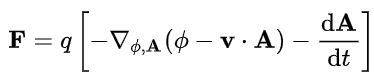
با فهم این که اوپراتور $$\triangledown$$ روی $$v = \dot { x }$$ عمل نمی‌کند، صورت اویلر لاگرانژی نیروی لورنتس نیز به صورت زیر بدست می‌آید.

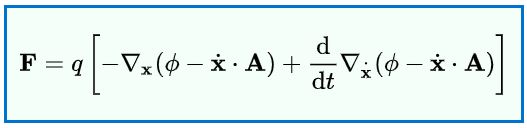
در رابطه فوق $$\triangledown _ x$$ و $$\triangledown _ { \dot { x } }$$، به صورت زیر تعریف می‌شوند.

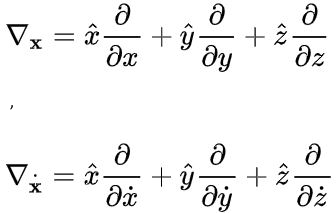
بنابراین همان‌طور که در بالا نشان داده شد، نیروی لورنتس را می‌توان به شکل‌های متفاوتی تعریف کرد. حتی می‌توان تفسیری نسبیتی از این نیرو داشت که نیازمند ریاضیات پیچیده و قدرتمند تانسوری است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه الکترومغناطیس و فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• موج الکترومغناطیسی چگونه ایجاد می شود؟ - آموزش جامع
• میدان مغناطیسی سیم حامل جریان — از صفر تا صد

^^