در این آموزش از مجله فرادرس، با مهمترین اتحاد های مثلثاتی آشنا میشویم و علاوه بر بیان اثبات آنها، مثالهایی را نیز ارائه خواهیم کرد. برای دسترسی سریع به فرمولهای اتحادهای مثلثاتی، پیشنهاد میکنیم به بخش «خلاصه اتحاد های مثلثاتی» در انتهای این متن مراجعه کنید.
نسبتهای مثلثاتی
در این بخش، به معرفی نسبتهای مثلثاتی با استفاده از مثلث قائمالزاویه می پردازیم. شش نسبت مثلثاتی اصلی وجود دارد: سینوس ، کسینوس ، تانژانت ، کتانژانت ، سکانت و کسکانت. برای زوایای حاده، این نسبتها را میتوان بهعنوان نسبت بین اضلاع یک مثلث قائمالزاویه تعریف کرد.
مثلث قائمالزاویه ABC با زاویه حاده A = α A =\alpha A = α b b b α \alpha α C C C α \alpha α α \alpha α
فرمول سینوس
سینوس زاویه α \alpha α sin α \sin \alpha sin α
sin α = a c \large \boxed {\sin \alpha = \frac { a } { c } } sin α = c a
فرمول کسینوس
کسینوس زاویه α \alpha α cos α \cos \alpha cos α
cos α = b c \large \boxed {\cos \alpha = \frac { b } { c } } cos α = c b
فرمول تانژانت
تانژانت زاویه α \alpha α tan α \tan \alpha tan α
tan α = a b \large \boxed {\tan \alpha = \frac { a } { b } } tan α = b a
تانژانت را می توان بر حسب سینوس و کسینوس بیان کرد:
tan α = a b = a c ⋅ c b = a c b c = sin α cos α \tan \alpha = \frac { a } { b } = \frac { a } { c } \cdot \frac { c } { b } = \frac { { \frac { a } { c} } } { { \frac { b } { c } } } = \frac { { \sin \alpha } } { { \cos \alpha } } tan α = b a = c a ⋅ b c = c b c a = cos α sin α
tan α = sin α cos α \large \boxed { \tan \alpha = \frac { { \sin \alpha } } { { \cos \alpha } } } tan α = cos α sin α
فرمول کتانژانت
نسبت متقابل تانژانت را کتانژانت میگویند و با cot α \cot \alpha cot α
cot α = b a \large \boxed {\cot \alpha = \frac { b } { a } } cot α = a b
cot α = 1 tan α \large \boxed { \cot \alpha = \frac { { 1 } } { { \tan \alpha } } } cot α = tan α 1
کتانژانت را، مشابه تانژانت، میتوان برحسب سینوس و کسینوس نوشت:
cot α = cos α sin α \large \boxed { \cot \alpha = \frac { { \cos \alpha } } { { \sin \alpha } } } cot α = sin α cos α
فرمول سکانت
نسبت اندازه وتر به اندازه ضلع مجاور را سکانت میگویند و با sec α \sec \alpha sec α
sec α = c b \large \boxed { \sec \alpha = \frac { { c } } { {b } } } sec α = b c
رابطه سکانت با کسینوس بهصورت زیر است:
sec α = 1 cos α \large \boxed { \sec \alpha = \frac { { 1 } } { { \cos \alpha } } } sec α = cos α 1
فرمول کسکانت
نسبت اندازه وتر به اندازه ضلع مقابل را کسکانت میگویند و با csc α \csc \alpha csc α
csc α = c a \large \boxed { \csc \alpha = \frac { { c } } { {a } } } csc α = a c
رابطه کسکانت با سینوس بهصورت زیر است:
csc α = 1 sin α \large \boxed { \csc \alpha = \frac { { 1 } } { { \sin \alpha } } } csc α = sin α 1
برای آشنایی بیشتر با نسبتهاب مثلثاتی، میتوانید به آموزشهای زیر مراجعه کنید:
جدول نسبتهای مثلثاتی زاویههای مهم
جدول زیر، جدول نسبتهای مثلثاتی زاویههای مهم را نشان میدهد که بهتر است آنها را به خاطر بسپارید، زیرا در حل مسائل مختلف به آنها نیاز خواهید داشت:
اتحاد های مثلثاتی فیثاغورسی
اتحاد مثلثاتی یک تساوی شامل نسبتهای مثلثاتی است و برای همه مقادیر متغیری که هر دو طرف برابری برای آنها تعریف شده است صادق است. قضیه فیثاغورس را به یاد بیاورید که طول اضلاع یک مثلث قائمالزاویه را به هم مربوط میکند:
a 2 + b 2 = c 2 {a^2} + {b^2} = {c^2} a 2 + b 2 = c 2
همچنین، مثلث شکل زیر را در نظر بگیرید:
در بخش قبل دیدیم که رابطههای زیر را برای سینوس و کسینوس داریم:
sin α = a c cos α = b c \sin \alpha = \frac{a}{c}\,\;\;\cos \alpha = \frac{b}{c} sin α = c a cos α = c b
با به توان دو رساندن و جمع این معادلات به رابطه معروف زیر میرسیم:
sin 2 α + cos 2 α = a 2 c 2 + b 2 c 2 = a 2 + b 2 c 2 = c 2 c 2 = 1 { \sin ^ 2 } \alpha + { \cos ^ 2 } \alpha = \frac { { { a ^ 2 } } }{ { { c ^ 2 } } } + \frac { { { b ^ 2 } } } { { { c ^ 2 } } } = \frac { { { a ^ 2 } + { b ^ 2 } } } { { { c ^ 2 } } } = \frac { { { c ^ 2 } } } { {{c^2}}} = 1 sin 2 α + cos 2 α = c 2 a 2 + c 2 b 2 = c 2 a 2 + b 2 = c 2 c 2 = 1
که به آن اتحاد مثلثاتی فیثاغورسی میگویند. بنابراین، برای هر زاویه α \alpha α 0 ≤ α ≤ π 2 0 \le \alpha \le \frac{\pi}{2} 0 ≤ α ≤ 2 π
sin 2 α + cos 2 α = 1 \large \boxed { {\sin ^2}\alpha + {\cos ^2}\alpha = 1} sin 2 α + cos 2 α = 1
با فرض cos α ≠ 0 \cos \alpha \ne 0 cos α = 0 α ≠ π 2 \alpha \ne \frac{\pi }{2} α = 2 π cos 2 α {\cos^2}\alpha cos 2 α
r e q u i r e sin 2 α cos 2 α + cos 2 α cos 2 α = 1 cos 2 α require{}\frac{{{{\sin }^2}\alpha }}{{{{\cos } ^ 2 } \alpha }} + \frac { { { { \cos }^ 2 } \alpha }} { { { { \cos } ^ 2 } \alpha }} = \frac { 1} {{ { { \cos } ^ 2 } \alpha }} re q u i re cos 2 α sin 2 α + cos 2 α cos 2 α = cos 2 α 1
یا
tan 2 α + 1 = sec 2 α \large \boxed {\tan ^ 2 \alpha + 1 = \sec ^ 2 \alpha } tan 2 α + 1 = sec 2 α
این اتحاد، تانژانت را به سکانت ربط میدهد.
بهطور مشابه، اگر sin α ≠ 0 \sin \alpha \ne 0 sin α = 0 α ≠ 0 \alpha \ne 0 α = 0 sin 2 α + cos 2 α = 1 {\sin^2}\alpha + {\cos^2}\alpha = 1 sin 2 α + cos 2 α = 1 sin 2 α {\sin^2}\alpha sin 2 α
sin 2 α sin 2 α + cos 2 α sin 2 α = 1 sin 2 α \frac { { { { \sin } ^ 2 } \alpha } } { { { { \sin } ^ 2 } \alpha } } + \frac { { { { \cos } ^ 2 } \alpha } }{ { { { \sin } ^ 2 }\alpha } } = \frac { 1 } { { { { \sin } ^ 2 } \alpha } } sin 2 α sin 2 α + sin 2 α cos 2 α = sin 2 α 1
یا
cot 2 α + 1 = csc 2 α \large \boxed { \cot ^ 2 \alpha + 1 = \csc ^ 2 \alpha } cot 2 α + 1 = csc 2 α
به دو اتحاد اخیر نیز اتحادهای مثلثاتی فیثاغورسی نیز گفته میشود.
این اتحادها به ما کمک میکنند تا بین توابع مثلثاتی یک زاویه، بدون دانستن خود زاویه، تبدیلات را انجام دهیم و عبارات مثلثاتی را ساده کنیم.
مثال های اتحاد های مثلثاتی فیثاغورسی
در این بخش، چند مثال از کاربرد اتحاد های مثلثاتی فیثاغورسی را بررسی میکنیم.
مثال اول اتحاد های مثلثاتی فیثاغورسی
عبارت زیر را ساده کنید.
tan α + cos α 1 + sin α \tan \alpha + \frac { { \cos \alpha } } { { 1 + \sin \alpha } } tan α + 1 + sin α cos α
حل: با استفاده از اتحاهای مثلثاتی فیثاغورسی، داریم:
tan α + cos α 1 + sin α = sin α cos α + cos α 1 + sin α = sin α ( 1 + sin α ) + cos α cos α cos α ( 1 + sin α ) = sin α + sin 2 α + cos 2 α ⏞ = 1 cos α ( 1 + sin α ) = sin α + 1 cos α ( sin α + 1 ) = 1 cos α = sec α \begin {align} \tan \alpha + \frac{{\cos \alpha } } { { 1 + \sin \alpha } } & = \frac { { \sin \alpha } } { { \cos \alpha } } + \frac { { \cos \alpha } } { { 1 + \sin \alpha }} = \frac { { \sin \alpha \left ( { 1 + \sin \alpha } \right ) + \cos \alpha \cos \alpha } } { { \cos \alpha \left ( { 1 + \sin \alpha } \right ) } } \ &= \frac{{\sin \alpha + \overbrace {{{\sin }^2}\alpha + {{\cos }^2}\alpha } ^ { = 1 } } } { { \cos \alpha \left( {1 + \sin \alpha } \right)}} = \frac{{\sin \alpha + 1 } } { { \cos \alpha \left ( { \sin \alpha + 1 } \right )} } = \frac { 1} { { \cos \alpha } } = \sec \alpha \end {align} tan α + 1 + sin α cos α = cos α sin α + 1 + sin α cos α = cos α ( 1 + sin α ) sin α ( 1 + sin α ) + cos α cos α = cos α ( 1 + sin α ) sin α + sin 2 α + cos 2 α = 1 = cos α ( sin α + 1 ) sin α + 1 = cos α 1 = sec α
مثال دوم اتحاد های مثلثاتی فیثاغورسی
اتحاد زیر را اثبات کنید.
tan 2 α 1 + tan 2 α ⋅ 1 + cot 2 α cot 2 α = tan 2 α \frac { { { { \tan } ^ 2 } \alpha } } { { 1 + { { \tan } ^ 2 } \alpha } } \cdot \frac { { 1 + { { \cot } ^ 2 } \alpha } } { { { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha 1 + tan 2 α tan 2 α ⋅ cot 2 α 1 + cot 2 α = tan 2 α
حل: از اتحادهای فیثاغورسی استفاده میکنیم:
1 + tan 2 α = sec 2 α = 1 cos 2 α 1 + cot 2 α = csc 2 α = 1 sin 2 α \begin {align} 1 + { \tan ^ 2 } \alpha & = { \sec ^ 2 } \alpha = \frac { 1 } { { { { \cos } ^ 2 } \alpha } } \ 1 + { \cot ^ 2 } \alpha & = { \csc ^ 2 } \alpha = \frac { 1 } { { { { \sin } ^ 2 } \alpha } } \end {align} 1 + tan 2 α = sec 2 α = cos 2 α 1 1 + cot 2 α = csc 2 α = sin 2 α 1
سمت چپ تساوی اصلی بهصورت زیر است:
tan 2 α 1 cos 2 α ⋅ 1 sin 2 α cot 2 α = tan 2 α \frac { { { { \tan } ^ 2 } \alpha } } { { \frac { 1 } { { { { \cos } ^ 2 } \alpha } } } } \cdot \frac { { \frac { 1 } { { { { \sin } ^ 2 } \alpha } } } } { { { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha c o s 2 α 1 tan 2 α ⋅ cot 2 α s i n 2 α 1 = tan 2 α
یا
tan 2 α cos 2 α sin 2 α cot 2 α = tan 2 α \frac { { { { \tan } ^ 2 } \alpha \, { { \cos } ^ 2 } \alpha } } { { { { \sin } ^ 2 } \alpha \, { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha sin 2 α cot 2 α tan 2 α cos 2 α = tan 2 α
از آنجا که cot 2 α = cos 2 α sin 2 α { \cot ^ 2 } \alpha = \frac { { { { \cos } ^ 2 } \alpha } }{ { { { \sin } ^ 2 } \alpha } } cot 2 α = sin 2 α cos 2 α
r e q u i r e tan 2 α cot 2 α cot 2 α = tan 2 α ⇒ tan 2 α = tan 2 α require {} \frac { { { { \tan } ^ 2 } \alpha { { { \cot } ^ 2 } \alpha } } } { { { { { \cot } ^ 2 } \alpha } } } = { \tan ^ 2 } \alpha \,\; \; \Rightarrow { \tan ^ 2 } \alpha = { \tan ^ 2 } \alpha re q u i re cot 2 α tan 2 α cot 2 α = tan 2 α ⇒ tan 2 α = tan 2 α
مثال سوم اتحاد های مثلثاتی فیثاغورسی
فرض کنید tan α = 2 15 . \tan \alpha = \frac{2}{{15}}. tan α = 15 2 .
5 sin α + 6 cos α 4 cos α − 3 sin α \frac { { 5 \sin \alpha + 6 \cos \alpha } } { { 4 \cos \alpha - 3 \sin \alpha } } 4 cos α − 3 sin α 5 sin α + 6 cos α
حل : از آنجا که tan α \tan \alpha tan α cos α ≠ 0 \cos \alpha \ne 0 cos α = 0
5 sin α + 6 cos α 4 cos α − 3 sin α = 5 sin α + 6 cos α cos α 4 cos α − 3 sin α cos α = 5 sin α cos α + 6 cos α cos α 4 cos α cos α − 3 sin α cos α = 5 tan α + 6 4 − 3 tan α = 5 × 2 15 + 6 4 − 3 × 2 15 = 2 3 + 6 4 − 2 5 = 2 + 18 3 20 − 2 5 = 20 3 18 5 = 100 54 = 50 27 \begin {align} \frac{{5\sin \alpha + 6\cos \alpha }}{{4\cos \alpha - 3\sin \alpha }} & = \frac { { \frac { { 5 \sin \alpha + 6 \cos \alpha } }{ { \cos \alpha } } } } { { \frac { { 4 \cos \alpha - 3 \sin \alpha } } { { \cos \alpha } } } } = \frac { { \frac { { 5 \sin \alpha }} { { \cos \alpha } } + \frac { { 6 { \cos \alpha } } }{ { { \cos \alpha } } } } } { { \frac { { 4 { \cos \alpha } } } { { { \cos \alpha } } } - \frac { { 3 \sin \alpha } } { { \cos \alpha } } } } = \frac { { 5 \tan \alpha + 6 } } { { 4 - 3 \tan \alpha } } \ & = \frac { { 5 \times \frac { 2 } { { 1 5 } } + 6 } } { { 4 - 3 \times \frac { 2 } { { 1 5 } } } } = \frac { { \frac { 2 } { 3 } + 6 } } { { 4 - \frac { 2 } { 5 } } } = \frac { { \frac { { 2 + 1 8 } } {3 } } } { { \frac { { 2 0 - 2 } } { 5 } } } = \frac { { \frac { { 2 0 } } { 3 } } } { { \frac { { 1 8 } } { 5 } } } = \frac { { 1 0 0 } } { { 5 4 } } = \frac { { 5 0 } } { { 2 7 } } \end {align} 4 cos α − 3 sin α 5 sin α + 6 cos α = c o s α 4 c o s α − 3 s i n α c o s α 5 s i n α + 6 c o s α = c o s α 4 c o s α − c o s α 3 s i n α c o s α 5 s i n α + c o s α 6 c o s α = 4 − 3 tan α 5 tan α + 6 = 4 − 3 × 15 2 5 × 15 2 + 6 = 4 − 5 2 3 2 + 6 = 5 20 − 2 3 2 + 18 = 5 18 3 20 = 54 100 = 27 50
مثال چهارم اتحاد های مثلثاتی فیثاغورسی
اگر sin α + cos α = m \sin \alpha + \cos \alpha = m sin α + cos α = m sin 4 α + cos 4 α {\sin ^4}\alpha + {\cos ^4}\alpha sin 4 α + cos 4 α
حل: هر دو طرف اتحاد مثلثاتی فیثاغورسی را به توان دو میرسانیم:
sin 2 α + cos 2 α = 1 ⇒ ( sin 2 α + cos 2 α ) 2 = 1 ⇒ sin 4 α + 2 sin 2 α cos 2 α + cos 4 α = 1 { \sin ^ 2 } \alpha + { \cos ^ 2 } \alpha = 1 \, \ \Rightarrow { \left ( { { { \sin } ^ 2 } \alpha + { { \cos } ^ 2 } \alpha } \right ) ^ 2 } = 1 \, \ \Rightarrow { \sin ^ 4 } \alpha + 2 \, { \sin ^ 2 } \alpha \, { \cos ^ 2 } \alpha + { \cos ^ 4 } \alpha = 1 sin 2 α + cos 2 α = 1 ⇒ ( sin 2 α + cos 2 α ) 2 = 1 ⇒ sin 4 α + 2 sin 2 α cos 2 α + cos 4 α = 1
بنابراین:
sin 4 α + cos 4 α = 1 − 2 ( sin α cos α ) 2 { \sin ^ 4 } \alpha + { \cos ^ 4 } \alpha = 1 - 2 { \left ( { \sin \alpha \cos \alpha } \right ) ^ 2 } sin 4 α + cos 4 α = 1 − 2 ( sin α cos α ) 2
اکنون sin α cos α \sin \alpha \cos \alpha sin α cos α sin α + cos α = m \sin \alpha + \cos \alpha = m ~ sin α + cos α = m
( sin α + cos α ) 2 = m 2 ⇒ sin 2 α + 2 sin α cos α + cos 2 α = m 2 ⇒ 1 + 2 sin α cos α = m 2 ⇒ sin α cos α = m 2 − 1 2 \left ( { \sin \alpha + \cos \alpha } \right ) ^ 2 = { m ^ 2 } \, \; \; \Rightarrow { \sin ^ 2 } \alpha + 2 \sin \alpha \cos \alpha + { \cos ^ 2 } \alpha = { m ^ 2 } \, \;\; \ \Rightarrow 1 + 2 \sin \alpha \cos \alpha = { m ^ 2 } \, \;\; \Rightarrow \sin \alpha \cos \alpha = \frac { { { m ^ 2 } - 1 } } { 2 } ( sin α + cos α ) 2 = m 2 ⇒ sin 2 α + 2 sin α cos α + cos 2 α = m 2 ⇒ 1 + 2 sin α cos α = m 2 ⇒ sin α cos α = 2 m 2 − 1
اتحاد های تناوب توابع مثلثاتی
همانطور که میدانیم توابع مثلثاتی متناوب هستند. با توجه به این دوره تناوب، میتوان اتحادهایی را برار توابع مثلثاتی بیان کرد.
دوره تناوب توابع سینوس و کسینوس 2 π 2 \pi 2 π
cos θ = cos ( θ + 2 π ) \large \boxed {\cos \theta = \cos ( \theta + 2 \pi ) } cos θ = cos ( θ + 2 π )
sin θ = sin ( θ + 2 π ) \large \boxed {\sin \theta = \sin ( \theta + 2 \pi ) } sin θ = sin ( θ + 2 π )
دوره تناوب توابع تانژانت و کتانژانت π \pi π
tan θ = tan ( θ + π ) \large \boxed {\tan \theta = \tan ( \theta + \pi ) } tan θ = tan ( θ + π )
cot θ = cot ( θ + π ) \large \boxed {\cot \theta = \cot ( \theta + \pi ) } cot θ = cot ( θ + π )
همانطور که میدانیم، سکانت و کسکانت، بهترتیب، توابع معکوس کسینوس و سینوس هستند. بنابراین، دوره تناوب این توابع نیز 2 π 2 \pi 2 π
sec θ = sec ( θ + 2 π ) \large \boxed {\sec \theta = \sec ( \theta + 2 \pi ) } sec θ = sec ( θ + 2 π )
csc θ = csc ( θ + 2 π ) \large \boxed {\csc \theta = \csc ( \theta + 2 \pi ) } csc θ = csc ( θ + 2 π )
مثال های اتحاد های تناوب توابع مثلثاتی
در این بخش، چند مثال را از اتحادهای تناوب توابع مثلثاتی بررسی میکنیم.
مثال اول اتحاد های تناوب توابع مثلثاتی
حاصل عبارت زیر را محاسبه کنید:
sin ( − 13 π 2 ) + tan ( − 7 π ) cos ( − 7 π ) + cot ( − 65 π 4 ) \frac { { \sin \left ( { - \frac { { 1 3 \pi } } { 2 } } \right ) + \tan \left ( { - 7 \pi } \right ) } } { { \cos \left ( { - 7 \pi } \right ) + \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) } } cos ( − 7 π ) + cot ( − 4 65 π ) sin ( − 2 13 π ) + tan ( − 7 π )
حل: هر جمله را جدا حساب میکنیم:
sin ( − 13 π 2 ) = sin ( 3 π 2 − 16 π 2 ) = sin ( 3 π 2 − 8 π ) = sin ( 3 π 2 − 2 π × 4 ) = sin 3 π 2 = − 1 \begin {align} \sin \left ( { - \frac { {1 3 \pi } } { 2 } } \right ) & = \sin \left ( { \frac { { 3 \pi } } { 2 } - \frac { { 1 6 \pi } } { 2 } } \right ) = \sin \left ( { \frac { { 3 \pi } } { 2 } - 8 \pi } \right ) \ & = \sin \left ( { \frac { { 3 \pi } } { 2 } - 2 \pi \times 4 } \right ) = \sin \frac { { 3 \pi } } { 2 } = - 1\, \end {align} sin ( − 2 13 π ) = sin ( 2 3 π − 2 16 π ) = sin ( 2 3 π − 8 π ) = sin ( 2 3 π − 2 π × 4 ) = sin 2 3 π = − 1
tan ( − 7 π ) = tan ( 0 − π × 7 ) = tan 0 = 0 \tan \left( { - 7 \pi } \right ) = \tan \left ( { 0 - \pi \times 7 } \right ) = \tan 0 = 0\, tan ( − 7 π ) = tan ( 0 − π × 7 ) = tan 0 = 0
cos ( − 7 π ) = cos ( π − 8 π ) = cos ( π − 2 π × 4 ) = cos π = − 1 \cos \left ( { - 7 \pi } \right ) = \cos \left ( {\pi - 8 \pi } \right ) = \cos \left ( { \pi - 2 \pi \times 4 } \right ) = \cos \pi = - 1 \, cos ( − 7 π ) = cos ( π − 8 π ) = cos ( π − 2 π × 4 ) = cos π = − 1
cot ( − 65 π 4 ) = cot ( 3 π 4 − 68 π 4 ) = cot ( 3 π 4 − 17 π ) = cot 3 π 4 . \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) = \cot \left ( { \frac { { 3 \pi } } { 4 } - \frac { { 6 8 \pi } } { 4 } } \right ) = \cot \left ( { \frac { { 3 \pi } } { 4} - 1 7 \pi } \right ) = \cot \frac { { 3 \pi } } { 4 } . cot ( − 4 65 π ) = cot ( 4 3 π − 4 68 π ) = cot ( 4 3 π − 17 π ) = cot 4 3 π .
زاویه 3 p i 4 \frac{{3pi }}{4} 4 3 p i 3 p i 4 \frac{{3pi }}{4} 4 3 p i π 4 \frac{{\pi }}{4} 4 π
cot ( − 65 π 4 ) = cot 3 π 4 = − cot π 4 = − 1 \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) = \cot \frac { { 3 \pi } } { 4 } = - \cot \frac { \pi } { 4 } = - 1 cot ( − 4 65 π ) = cot 4 3 π = − cot 4 π = − 1
در نتیجه:
sin ( − 13 π 2 ) + tan ( − 7 π ) cos ( − 7 π ) + cot ( − 65 π 4 ) = − 1 + 0 − 1 − 1 = 1 2 \frac { { \sin \left ( { - \frac { { 1 3 \pi } } { 2 } } \right ) + \tan \left ( { - 7 \pi } \right ) } } { { \cos \left ( { - 7 \pi } \right ) + \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) } } = \frac { { - 1 + 0 } } { { - 1 - 1 } } = \frac { 1 } { 2 } cos ( − 7 π ) + cot ( − 4 65 π ) sin ( − 2 13 π ) + tan ( − 7 π ) = − 1 − 1 − 1 + 0 = 2 1
مثال دوم اتحاد های تناوب توابع مثلثاتی
عبارت زیر را ساده کنید:
cos ( − 3 π ) + sin 8 π 3 tan 9 π 4 + cot 13 π 6 \frac { { \cos \left ( { - 3 \pi } \right ) + \sin { \frac { { 8 \pi }} {3 } } }} { {\tan { \frac { { 9 \pi } } { 4 } } + \cot { \frac { { 1 3 \pi } }{ 6 } } } } tan 4 9 π + cot 6 13 π cos ( − 3 π ) + sin 3 8 π
حل: مقدار هر جمله را محاسبه میکنیم:
cos ( − 3 π ) = cos ( π − 4 π ) = cos ( π − 2 π × 2 ) = cos π = − 1 sin 8 π 3 = sin ( 2 π 3 + 6 π 3 ) = sin ( 2 π 3 + 2 π ) = sin 2 π 3 . \cos \left ( { - 3 \pi } \right ) = \cos \left ( { \pi - 4 \pi } \right ) = \cos \left ( { \pi - 2 \pi \times 2 } \right ) = \cos \pi = - 1 \, \ \sin \frac { { 8 \pi } } { 3 } = \sin \left ( { \frac { { 2 \pi } } { 3 } + \frac { { 6 \pi } } { 3 } } \right ) = \sin \left ( { \frac { { 2 \pi } } { 3 } + 2 \pi } \right ) = \sin \frac { { 2 \pi } } { 3 } . cos ( − 3 π ) = cos ( π − 4 π ) = cos ( π − 2 π × 2 ) = cos π = − 1 sin 3 8 π = sin ( 3 2 π + 3 6 π ) = sin ( 3 2 π + 2 π ) = sin 3 2 π .
زاویه مرجع 2 p i 3 \frac{{2pi }}{3} 3 2 p i π 3 \frac{{\pi }}{3} 3 π
sin 8 π 3 = sin 2 π 3 = sin π 3 = 3 2 \sin \frac { { 8 \pi } } { 3 } = \sin \frac { { 2 \pi } } { 3 } = \sin \frac { \pi } { 3 } = \frac { { \sqrt 3 } } { 2 } sin 3 8 π = sin 3 2 π = sin 3 π = 2 3
جملات دیگر نیز بهصورت زیر هستند:
tan 9 π 4 = tan ( π 4 + 8 π 4 ) = tan ( π 4 + 2 π ) = tan π 4 = 1 cot 13 π 6 = cot ( π 6 + 12 π 6 ) = cot ( π 6 + 2 π ) = cot π 6 = 3 . \tan \frac { { 9 \pi } } { 4 } = \tan \left ( { \frac { \pi } { 4 } + \frac { { 8 \pi } } { 4 } } \right ) = \tan \left ( { \frac { \pi }{ 4 } + 2 \pi } \right ) = \tan \frac { \pi } { 4 } = 1 \, \ \cot \frac { { 1 3 \pi } } { 6 } = \cot \left ( { \frac { \pi } { 6 } + \frac { { 1 2 \pi } } { 6 } } \right ) = \cot \left ( { \frac { \pi }{ 6 } + 2 \pi } \right ) = \cot \frac { \pi } { 6 } = \sqrt 3 . tan 4 9 π = tan ( 4 π + 4 8 π ) = tan ( 4 π + 2 π ) = tan 4 π = 1 cot 6 13 π = cot ( 6 π + 6 12 π ) = cot ( 6 π + 2 π ) = cot 6 π = 3 .
با جایگذاری مقادیر، خواهیم داشت:
cos ( − 3 π ) + sin ( 8 π 3 ) tan ( 9 π 4 ) + cot ( 13 π 6 ) = − 1 + 3 2 1 + 3 = − 2 + 3 2 ( 1 + 3 ) = ( − 2 + 3 ) ( 1 − 3 ) 2 ( 1 + 3 ) ( 1 − 3 ) = − 2 + 3 + 2 3 − 3 2 ( 1 2 − ( 3 ) 2 ) = 3 3 − 5 2 ( 1 − 3 ) = 5 − 3 3 4 . \begin {align} \frac { { \cos \left ( { - 3 \pi } \right ) + \sin \left ( { \frac { { 8 \pi } } {3 } } \right ) } } { { \tan \left ( { \frac { { 9 \pi } }{ 4 } } \right ) + \cot \left ( { \frac { { 1 3 \pi } } { 6 } } \right ) } } & = \frac { { - 1 + \frac { { \sqrt 3 } } { 2 } } } { { 1 + \sqrt 3 } } = \frac { { - 2 + \sqrt 3 } } { { 2 \left ( { 1 + \sqrt 3 } \right ) } } = \frac { { \left ( { - 2 + \sqrt 3 } \right ) \left ( { 1 - \sqrt 3 } \right ) } } { { 2 \left ( { 1 + \sqrt 3 } \right ) \left ( { 1 - \sqrt 3 } \right ) } } \ & = \frac { { - 2 + \sqrt 3 + 2 \sqrt 3 - 3 } } { { 2 \left ( { { 1 ^ 2 } - { { \left ( { \sqrt 3 } \right ) } ^ 2 } } \right ) } } = \frac { { 3 \sqrt 3 - 5 } } { { 2 \left ( { 1 - 3 } \right ) } } = \frac { { 5 - 3 \sqrt 3 } } { 4 } . \end {align} tan ( 4 9 π ) + cot ( 6 13 π ) cos ( − 3 π ) + sin ( 3 8 π ) = 1 + 3 − 1 + 2 3 = 2 ( 1 + 3 ) − 2 + 3 = 2 ( 1 + 3 ) ( 1 − 3 ) ( − 2 + 3 ) ( 1 − 3 ) = 2 ( 1 2 − ( 3 ) 2 ) − 2 + 3 + 2 3 − 3 = 2 ( 1 − 3 ) 3 3 − 5 = 4 5 − 3 3 .
اتحاد های مثلثاتی جمع و تفریق دو زاویه
فرمولهایی وجود دارد که با کمک آنها میتوانیم جمع یا تفریق دو زاویه را ساده کنیم. در ادامه، با این فرمولها آشنا میشویم.
فرمول کسینوس تفریق دو زاویه
دو زاویه α \alpha α β \beta β α > β \alpha >\; \beta α > β A ( o ) A(o) A ( o ) M ( α ) M(\alpha) M ( α ) N ( β ) N(\beta) N ( β ) P ( α − β ) P(\alpha - \beta ) P ( α − β )
مختصات این نقاط بهصورت زیر هستند:
A = A ( 1 0 ) M = M ( cos α sin α ) N = N ( cos β sin β ) P = P ( cos ( α − β ) sin ( α − β ) ) \begin {align} & A = A \left( { 1 \, 0 } \right)\,\;\;M = M \left ( { \cos \alpha \, \sin \alpha } \right)\, \ & N = N \left ( { \cos \beta \,\sin \beta } \right ) \, \; \; P = P \left ( { \cos \left ( { \alpha - \beta } \right ) \, \sin \left ( { \alpha - \beta } \right ) } \right) \end {align} A = A ( 1 0 ) M = M ( cos α sin α ) N = N ( cos β sin β ) P = P ( cos ( α − β ) sin ( α − β ) )
از آنجا که ∠ M O N = ∠ P O A = α − β \angle MON = \angle POA = \alpha - \beta ∠ MON = ∠ PO A = α − β M N \color{#cc00ff}{MN} MN A P \color{#0099ff}{AP} A P
∣ M N ∣ = ∣ A P ∣ . \left| \color{#cc00ff}{MN} \right| = \left| \color{#0099ff}{AP} \right|. ∣ MN ∣ = ∣ A P ∣ .
فاصله بین دو نقطه روی یک صفحه با فرمول زیر بهدست میآید:
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d = \sqrt { { { \left( { { x _ 1 } - { x _ 2 } } \right ) } ^ 2 } + { { \left ( { { y _ 1 } - { y _ 2 } } \right ) } ^2 } } d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2
بنابراین، خواهیم داشت:
∣ M N ∣ 2 = ( x M − x N ) 2 + ( y M − y N ) 2 = ( cos α − cos β ) 2 + ( sin α − sin β ) 2 = cos 2 α − 2 cos α cos β + cos 2 β + sin 2 α − 2 sin α sin β + sin 2 β = cos 2 α + sin 2 α ⏟ 1 + cos 2 β + sin 2 β ⏟ 1 − 2 ( cos α cos β + sin α sin β ) = 2 − 2 ( cos α cos β + sin α sin β ) \begin{align} { \left | \color{#cc00ff} { M N } \right | ^ 2 } & = { \left ( { { x _ M } - { x _ N } } \right ) ^ 2} + { \left ( { { y _ M } - { y _ N } } \right ) ^ 2 } = { \left ( { \cos \alpha - \cos \beta } \right ) ^ 2 } + { \left ( { \sin \alpha - \sin \beta } \right ) ^ 2 } \ & = { \cos ^ 2 } \alpha - 2 \cos \alpha \cos \beta + { \cos ^ 2 } \beta + { \sin ^ 2 } \alpha - 2 \sin \alpha \sin \beta + { \sin ^ 2 } \beta \ & = \underbrace { { { \cos } ^ 2 } \alpha + { { \sin } ^ 2 } \alpha } _ 1 + \underbrace { { { \cos } ^ 2 } \beta + { { \sin } ^ 2 } \beta } _ 1 - 2 \left ( { \cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) \ & = 2 - 2 \left ( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) \end {align} ∣ MN ∣ 2 = ( x M − x N ) 2 + ( y M − y N ) 2 = ( cos α − cos β ) 2 + ( sin α − sin β ) 2 = cos 2 α − 2 cos α cos β + cos 2 β + sin 2 α − 2 sin α sin β + sin 2 β = 1 cos 2 α + sin 2 α + 1 cos 2 β + sin 2 β − 2 ( cos α cos β + sin α sin β ) = 2 − 2 ( cos α cos β + sin α sin β )
بهطور مشابه، مجذور فاصله ∣ A P ∣ \left| \color{#0099ff}{AP} \right| ∣ A P ∣
∣ A P ∣ 2 = ( x A − x P ) 2 + ( y A − y P ) 2 = ( 1 − cos ( α − β ) ) 2 + ( 0 − sin ( α − β ) ) 2 = 1 − 2 cos ( α − β ) + cos 2 ( α − β ) + sin 2 ( α − β ) ⏟ 1 = 2 − 2 cos ( α − β ) \begin{align} { \left | \color {#0099ff} { A P } \right | ^ 2 } & = { \left ( { { x _ A } - { x _ P } } \right ) ^ 2 } + { \left ( { { y _ A } - { y _ P } } \right ) ^ 2 } = { \left ( { 1 - \cos \left ( { \alpha - \beta } \right ) } \right ) ^ 2 } + { \left ( { 0 - \sin \left ( { \alpha - \beta } \right ) } \right ) ^ 2 } \ & = 1 - 2 \cos \left ( { \alpha - \beta } \right ) + \underbrace { { { \cos } ^ 2 } \left ( { \alpha - \beta } \right) + { { \sin } ^ 2 } \left ( { \alpha - \beta } \right ) } _ 1 = 2 - 2 \cos \left ( { \alpha - \beta } \right ) \end {align} ∣ A P ∣ 2 = ( x A − x P ) 2 + ( y A − y P ) 2 = ( 1 − cos ( α − β ) ) 2 + ( 0 − sin ( α − β ) ) 2 = 1 − 2 cos ( α − β ) + 1 cos 2 ( α − β ) + sin 2 ( α − β ) = 2 − 2 cos ( α − β )
فرمول کسینوس تفریق دو زاویه از تساوی ∣ M N ∣ 2 = ∣ A P ∣ 2 {\left| \color{#cc00ff}{MN} \right|^2} = {\left| \color{#0099ff}{AP} \right|^2} ∣ MN ∣ 2 = ∣ A P ∣ 2
cos ( α – β ) = cos α cos β + sin α sin β \large \boxed { \cos ( \alpha – \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta } cos ( α – β ) = cos α cos β + sin α sin β
فرمول کسینوس جمع دو زاویه
دو نقطه ( β ) \left( \beta \right) ( β ) ( − β ) \left( { - \beta } \right) ( − β ) β \beta β − β -\beta − β
این نقاط نسبت به محور x x x قدر مطلق مختصات y y y زوج و تابع سینوس فرد است:
cos ( − β ) = cos β sin ( − β ) = − sin β \cos (-\beta)=\cos \beta\, \quad \sin (-\beta)=-\sin \beta cos ( − β ) = cos β sin ( − β ) = − sin β
اکنون از فرمول کسینوس تفریق دو زاویه استفاده میکنیم و بهجای β \beta β − β -\beta − β
cos ( α + β ) = cos α cos ( − β ) + sin α sin ( − β ) \cos \left ( { \alpha + \beta } \right ) = \cos \alpha \cos \left ( { - \beta } \right ) + \sin \alpha \sin \left ( { - \beta } \right ) cos ( α + β ) = cos α cos ( − β ) + sin α sin ( − β )
از آنجا که کسینوس زوج است و سینوس فرد، آتحاد کسینوس جمع دو زاویه بهشکل زیر بهدست میآید:
cos ( α + β ) = cos α cos β − sin α sin β \large \boxed { \cos ( \alpha + \beta ) = \cos \alpha \cos \beta-\sin \alpha \sin \beta } cos ( α + β ) = cos α cos β − sin α sin β
حالتهای خاص
اگر از فرمولهای بالا استفاده کنیم، به روابطی بسیار کاربردی میرسیم. برای مثال، اگر α = π 2 \alpha = \frac{\pi }{2} α = 2 π
cos ( π 2 − β ) = cos π 2 cos β + sin π 2 sin β = 0 ⋅ cos β + 1 ⋅ sin β = sin β \cos \left ( { \frac { \pi } { 2 } - \beta } \right ) = \cos \frac { \pi } { 2 } \cos \beta + \sin \frac { \pi } { 2 } \sin \beta = 0 \cdot \cos \beta + 1 \cdot \sin \beta = \sin \beta cos ( 2 π − β ) = cos 2 π cos β + sin 2 π sin β = 0 ⋅ cos β + 1 ⋅ sin β = sin β
یا بهطور خلاصه، داریم:
cos ( π 2 − β ) = sin β \large \boxed {\cos \left ( { \frac{ \pi }{2} - \beta } \right) = \sin \beta } cos ( 2 π − β ) = sin β
بهطور مشابه، فرمولهای زیر بهدست میآیند:
sin ( π 2 − β ) = cos β \large \boxed {\sin \left ( { \frac{ \pi }{2} - \beta } \right) = \cos \beta } sin ( 2 π − β ) = cos β
cos ( π 2 + β ) = − sin β \large \boxed {\cos \left ( { \frac{ \pi }{2} + \beta } \right) = -\sin \beta } cos ( 2 π + β ) = − sin β
sin ( π 2 + β ) = cos β \large \boxed {\sin \left ( { \frac{ \pi }{2} + \beta } \right) = \cos \beta } sin ( 2 π + β ) = cos β
فرمول سینوس تفریق دو زاویه
با استفاده از اتحادهای بخش قبل بخش قبل، فرمول تفریق سینوسی را به دست می آوریم:
sin ( α – β ) = sin α cos β – cos α sin β \large \boxed {\sin ( \alpha – \beta ) = \sin \alpha \cos \beta – \cos \alpha \sin \beta } sin ( α – β ) = sin α cos β – cos α sin β
فرمول سینوس جمع دو زاویه
برای بهدست آوردن فرمول سینوس جمع دو زاویه، کافی است در فرمول بالا، بهجای β \beta β − β -\beta − β
sin ( α + β ) = sin α cos ( − β ) − cos α sin ( − β ) = sin α cos β + cos α sin β \begin {align} \sin \left( {\alpha + \beta } \right) & = \sin \alpha \cos \left( { - \beta } \right) - \cos \alpha \sin \left( { - \beta } \right) \ &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \end {align} sin ( α + β ) = sin α cos ( − β ) − cos α sin ( − β ) = sin α cos β + cos α sin β
بنابراین، میتوان نوشت:
sin ( α + β ) = sin α cos β + cos α sin β \large \boxed { \sin ( \alpha + \beta ) = \sin \alpha \cos \beta+\cos \alpha \sin \beta } sin ( α + β ) = sin α cos β + cos α sin β
برای آشنایی بیشتر با این دسته از اتحاد های مثلثاتی، به آموزش «سینوس و کسینوس جمع دو زاویه — به زبان ساده (+ دانلود فیلم آموزش گام به گام) » مراجعه کنید.
فرمول تانژانت جمع دو زاویه
در بخشهای قبل با دو اتحاد زیر آشنا شدیم:
sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β \begin {align} \sin \left( {\alpha + \beta } \right) & = \sin \alpha \cos \beta + \cos \alpha \sin \beta \ \cos \left( {\alpha + \beta } \right) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \end {align} sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β
فرض کنید cos ( α + β ) ≠ 0 \cos \left( {\alpha + \beta } \right) \ne 0 cos ( α + β ) = 0 α + β ≠ π 2 + π n n ∈ Z \alpha + \beta \ne \frac{\pi }{2} + \pi n\, n \in \mathbb{Z} α + β = 2 π + πn n ∈ Z cos β ≠ 0 \cos \beta \ne 0 cos β = 0 cos β ≠ 0 \cos \beta \ne 0 cos β = 0 α β ≠ π 2 + π n n ∈ Z \alpha\, \beta \ne \frac{\pi }{2} + \pi n\,n \in \mathbb{Z} α β = 2 π + πn n ∈ Z cos α cos β \cos \alpha\cos \beta cos α cos β
فرمول تانژانت جمع دو زاویه بهصورت زیر محاسبه میشود:
r e q u i r e tan ( α + β ) = sin ( α + β ) cos ( α + β ) = sin α cos β + cos α sin β cos α cos β − sin α sin β & = sin α cos β + cos α sin β cos α cos β cos α cos β − sin α sin β cos α cos β = sin α cos β cos α cos β + cos α sin β cos α cos β cos α cos β cos α cos β − sin α sin β cos α cos β & = tan α + tan β 1 − tan α tan β require{} \begin {align} \tan \left( {\alpha + \beta } \right) & = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \left( {\alpha + \beta } \right)}} = \frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }} \& = \frac{{\frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}}{{\frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}} = \frac{{\frac{{\sin \alpha {\cos \beta} }}{{\cos \alpha {\cos \beta} }} + \frac{{{\cos \alpha} \sin \beta }}{{{\cos \alpha} \cos \beta }}}}{{\frac{{\cos \alpha \cos \beta }}{{\cos \alpha \cos \beta }} - \frac{{\sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}} \& = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \end {align} re q u i re tan ( α + β ) = cos ( α + β ) sin ( α + β ) = cos α cos β − sin α sin β sin α cos β + cos α sin β & = c o s α c o s β c o s α c o s β − s i n α s i n β c o s α c o s β s i n α c o s β + c o s α s i n β = c o s α c o s β c o s α c o s β − c o s α c o s β s i n α s i n β c o s α c o s β s i n α c o s β + c o s α c o s β c o s α s i n β & = 1 − tan α tan β tan α + tan β
در نتیجه:
tan ( α + β ) = tan α + tan β 1 − tan α tan β \large \boxed { \begin {align} \tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \end {align} } tan ( α + β ) = 1 − tan α tan β tan α + tan β
فرمول تانژانت تفریق دو زاویه
میدانیم که تانژانت یک تابع فرد است:
tan ( − β ) = sin ( − β ) cos ( − β ) = − sin β cos β = − tan β \tan \left( { - \beta } \right) = \frac{{\sin \left( { - \beta } \right)}}{{\cos \left( { - \beta } \right)}} = \frac{{ - \sin \beta }}{{\cos \beta }} = - \tan \beta tan ( − β ) = cos ( − β ) sin ( − β ) = cos β − sin β = − tan β
با قرار دادن − β -\beta − β β \beta β
tan ( α − β ) = tan α + tan ( − β ) 1 − tan α tan ( − β ) = tan α − tan β 1 + tan α tan β \tan \left ( { \alpha - \beta } \right ) = \frac { { \tan \alpha + \tan \left ( { - \beta } \right ) } } { { 1 - \tan \alpha \tan \left ( { - \beta } \right ) } } = \frac { { \tan \alpha - \tan \beta } } { { 1 + \tan \alpha \tan \beta } } tan ( α − β ) = 1 − tan α tan ( − β ) tan α + tan ( − β ) = 1 + tan α tan β tan α − tan β
بنابراین، داریم:
tan ( α − β ) = = tan α − tan β 1 + tan α tan β \large \boxed { \tan \left ( { \alpha - \beta } \right ) = = \frac { { \tan \alpha - \tan \beta } } { { 1 + \tan \alpha \tan \beta } }} tan ( α − β ) == 1 + tan α tan β tan α − tan β
فرمول کتانژانت جمع دو زاویه
فرض کنید sin ( α + β ) ≠ 0 \sin \left( {\alpha + \beta } \right) \ne 0 sin ( α + β ) = 0 α + β ≠ π n n ∈ Z \alpha + \beta \ne \pi n\,n \in \mathbb{Z} α + β = πn n ∈ Z sin α ≠ 0 \sin \alpha \ne 0 sin α = 0 sin β ≠ 0 \sin \beta \ne 0 sin β = 0 α β ≠ π n n ∈ Z \alpha \,\beta \ne \pi n\,n \in \mathbb{Z} α β = πn n ∈ Z sin α sin β \sin \alpha\sin \beta sin α sin β
در نتیجه، خواهیم داشت:
r e q u i r e cot ( α + β ) = cos ( α + β ) sin ( α + β ) = cos α cos β − sin α sin β sin α cos β + cos α sin β = cos α cos β − sin α sin β sin α sin β sin α cos β + cos α sin β sin α sin β = cos α cos β sin α sin β − sin α sin β sin α sin β sin α cos β sin α sin β + cos α sin β sin α sin β = cot α cot β − 1 cot β + cot α require {}\begin {align} \cot \left( {\alpha + \beta } \right) & = \frac{{\cos \left( {\alpha + \beta } \right)}}{{\sin \left( {\alpha + \beta } \right)}} = \frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }} \ & = \frac{{\frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\sin \alpha \sin \beta }}}}{{\frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\sin \alpha \sin \beta }}}} = \frac{{\frac{{\cos \alpha \cos \beta }}{{\sin \alpha \sin \beta }} - \frac{{\sin \alpha \sin \beta }}{{\sin \alpha \sin \beta }}}}{{\frac{{{\sin \alpha} \cos \beta }}{{{\sin \alpha} \sin \beta }} + \frac{{\cos \alpha {\sin \beta} }}{{\sin \alpha {\sin \beta} }}}} \ & = \frac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }} \end {align} re q u i re cot ( α + β ) = sin ( α + β ) cos ( α + β ) = sin α cos β + cos α sin β cos α cos β − sin α sin β = s i n α s i n β s i n α c o s β + c o s α s i n β s i n α s i n β c o s α c o s β − s i n α s i n β = s i n α s i n β s i n α c o s β + s i n α s i n β c o s α s i n β s i n α s i n β c o s α c o s β − s i n α s i n β s i n α s i n β = cot β + cot α cot α cot β − 1
و میتوان نوشت:
cot ( α + β ) = cot α cot β − 1 cot β + cot α \large \boxed {\begin {align} \cot \left( {\alpha + \beta } \right) = \frac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }} \end {align}} cot ( α + β ) = cot β + cot α cot α cot β − 1
کتانژانت مجموع دو زاویه را میتوان برحسب تانژانتها نیز نوشت:
cot ( α + β ) = 1 − tan α tan β tan α + tan β \large \boxed { \cot ( \alpha + \beta ) = \frac { 1 - \tan \alpha \tan \beta } { \tan \alpha + \tan \beta }} cot ( α + β ) = tan α + tan β 1 − tan α tan β
فرمول کتانژانت تفریق دو زاویه
میدانیم که کتانژانت یک تابع فرد است:
cot ( − α ) = cos ( − α ) sin ( − α ) = cos α − sin α = − cot α \cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} = - \cot \alpha cot ( − α ) = sin ( − α ) cos ( − α ) = − sin α cos α = − cot α
اکنون با قرار دادن − β -\beta − β β \beta β
cot ( α − β ) = cot α cot ( − β ) − 1 cot α + cot ( − β ) = − cot α cot β − 1 cot α − cot β = cot α cot β + 1 cot β − cot α \cot \left ( { \alpha - \beta } \right ) = \frac { { \cot \alpha \cot \left ( { - \beta } \right ) - 1 } } { { \cot \alpha + \cot \left ( { - \beta } \right ) } } = \frac { { - \cot \alpha \cot \beta - 1 } } { { \cot \alpha - \cot \beta } } = \frac { { \cot \alpha \cot \beta + 1 } } { { \cot \beta - \cot \alpha } } cot ( α − β ) = cot α + cot ( − β ) cot α cot ( − β ) − 1 = cot α − cot β − cot α cot β − 1 = cot β − cot α cot α cot β + 1
و خواهیم داشت:
cot ( α − β ) = cot α cot β + 1 cot β − cot α \large \boxed { \cot \left ( { \alpha - \beta } \right ) = \frac { { \cot \alpha \cot \beta + 1 } } { { \cot \beta - \cot \alpha } } } cot ( α − β ) = cot β − cot α cot α cot β + 1
این فرمول را برحسب تانژانت نیز میتوان نوشت:
cot ( α − β ) = 1 + tan α tan β tan α − tan β \large \boxed { \cot ( \alpha - \beta ) = \frac { 1 + \tan \alpha \tan \beta } { \tan \alpha - \tan \beta } } cot ( α − β ) = tan α − tan β 1 + tan α tan β
کاربرد اتحاد های مثلثاتی جمع و تفریق دو زاویه
یکی از کاربردهای ساده اتحاد های مثلثاتی جمع و تفریق دو زاویه، سادهسازی عبارتهای مثلثاتی است که در حل مسائل مختلف با آنها سر و کار داریم. جدول زیر، مهمترین این فرمولها را نشان میدهد. اثبات این فرمولها را میتوانید با استفاده از آنچه در بخشهای قبل گفتیم، انجام دهید.
مثال های اتحاد های مثلثاتی جمع و تفریق دو زاویه
در این بخش، مثالهایی را از اتحاد های مثلثاتی جمع و تفریق دو زاویه بررسی میکنیم.
مثال اول اتحاد های مثلثاتی جمع و تفریق دو زاویه
مقدار عبارت cos 5 p i 12 \cos \frac{{5pi }}{{12}} cos 12 5 p i
حل: عبارت 5 p i 12 \frac{{5pi }}{{12}} 12 5 p i
5 p i 12 = 3 p i + 2 p i 12 = 3 p i 12 + 2 p i 12 = π 4 + π 6 . \frac{{5pi }}{{12}} = \frac{{3pi + 2pi }}{{12}} = \frac{{3pi }}{{12}} + \frac{{2pi }}{{12}} = \frac{\pi }{4} + \frac{\pi }{6}. 12 5 p i = 12 3 p i + 2 p i = 12 3 p i + 12 2 p i = 4 π + 6 π .
با استفاده از فرمول کسینوس جمع، داریم:
cos 5 π 12 = cos ( π 4 + π 6 ) = cos π 4 cos π 6 − sin π 4 sin π 6 = 2 2 ⋅ 3 2 − 2 2 ⋅ 1 2 = 6 4 − 2 4 = 6 − 2 4 . \begin {align} \cos \frac { { 5 \pi } } { { 12 } } & = \cos \left ( { \frac { \pi }{4} + \frac { \pi } { 6 } } \right ) = \cos \frac{\pi }{4}\cos \frac{\pi }{6} - \sin \frac { \pi } { 4 } \sin \frac { \pi } { 6 } \ & = \frac { { \sqrt 2 } } { 2 } \cdot \frac { { \sqrt 3 } } { 2 } - \frac { { \sqrt 2 } } { 2 } \cdot \frac { 1 } { 2 } = \frac { { \sqrt 6 } } { 4 } - \frac { { \sqrt 2 } } { 4 } = \frac { { \sqrt 6 - \sqrt 2 } } { 4 } . \end {align} cos 12 5 π = cos ( 4 π + 6 π ) = cos 4 π cos 6 π − sin 4 π sin 6 π = 2 2 ⋅ 2 3 − 2 2 ⋅ 2 1 = 4 6 − 4 2 = 4 6 − 2 .
مثال دوم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر مقدار sin α = 1 3 \sin \alpha = \frac{1}{{\sqrt 3 }} sin α = 3 1 cos ( π 3 + α ) \cos \left( {\frac{\pi }{3} + \alpha } \right) cos ( 3 π + α )
حل: تابع کسینوس در ربع اول مثبت است. بنابراین، خواهیم داشت:
cos α = 1 − sin 2 α = 1 − ( 1 3 ) 2 = 1 − 1 3 = 2 3 = 2 3 \cos \alpha = \sqrt { 1 - { { \sin } ^ 2 } \alpha } = \sqrt { 1 - { { \left ( { \frac { 1 } { { \sqrt 3 } } } \right ) } ^ 2 } } = \sqrt { 1 - \frac { 1 } { 3 } } = \sqrt { \frac { 2 } { 3 } } = \frac { { \sqrt 2 } } { { \sqrt 3 } } cos α = 1 − sin 2 α = 1 − ( 3 1 ) 2 = 1 − 3 1 = 3 2 = 3 2
اکنون از فرمول کسینوس جمع استفاده میکنیم:
cos ( π 3 + α ) = cos π 3 cos α − sin π 3 sin α = 1 2 ⋅ 2 3 − 3 2 ⋅ 1 3 = 2 − 3 2 3 = 6 − 3 6 \begin {align} \cos \left ( { \frac { \pi } { 3 } + \alpha } \right ) & = \cos \frac { \pi } { 3 } \cos \alpha - \sin \frac { \pi } { 3 } \sin \alpha \ & = \frac { 1 } { 2 } \cdot \frac { { \sqrt 2 } } { { \sqrt 3 } } - \frac { { \sqrt 3 } } { 2 } \cdot \frac { 1 } { { \sqrt 3 }} \ & = \frac{{\sqrt 2 - \sqrt 3 } } { { 2 \sqrt 3 } } = \frac { { \sqrt 6 - 3 } } { 6 } \end {align} cos ( 3 π + α ) = cos 3 π cos α − sin 3 π sin α = 2 1 ⋅ 3 2 − 2 3 ⋅ 3 1 = 2 3 2 − 3 = 6 6 − 3
میتوان گفت که کسینوس این زاویه منفی است.
مثال سوم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر cos β = − f r a c 12 \cos \beta = -frac{1}{2} cos β = − f r a c 1 2 β \beta β sin ( π 4 − β ) \sin \left( {\frac{\pi }{4} - \beta } \right) sin ( 4 π − β )
حل: سینوس در ربع دوم مثبت است. بنابراین، داریم:
sin β = 1 − cos 2 β = 1 − ( − 1 2 ) 2 = 1 − 1 4 = 3 4 = 3 2 \sin \beta = \sqrt {1 - {{\cos } ^ 2 } \beta } = \sqrt { 1 - { { \left ( { - \frac { 1 } { 2 } } \right ) } ^ 2 } } = \sqrt { 1 - \frac { 1 } { 4 } } = \sqrt { \frac { 3 } { 4 } } = \frac { { \sqrt 3 } } { 2 } sin β = 1 − cos 2 β = 1 − ( − 2 1 ) 2 = 1 − 4 1 = 4 3 = 2 3
با استفاده از سینوس جمع دو زاویه، میتوان نوشت:
sin ( π 4 − β ) = sin π 4 cos β − cos π 4 sin β = 2 2 ⋅ ( − 1 2 ) − 2 2 ⋅ 3 2 = − 2 − 6 4 \begin {align} \sin \left ( { \frac { \pi } { 4 } - \beta } \right ) & = \sin \frac { \pi } { 4 } \cos \beta - \cos \frac { \pi } { 4 } \sin \beta \ & = \frac { { \sqrt 2 } } { 2 } \cdot \left ( { - \frac { 1 }{ 2 } } \right ) - \frac { { \sqrt 2 } } { 2 } \cdot \frac { { \sqrt 3 } } { 2 } \ & = \frac { {- \sqrt 2 - \sqrt 6 } } { 4 } \end {align} sin ( 4 π − β ) = sin 4 π cos β − cos 4 π sin β = 2 2 ⋅ ( − 2 1 ) − 2 2 ⋅ 2 3 = 4 − 2 − 6
مثال چهارم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اتحاد cos ( α + β ) cos ( α − β ) = cos 2 α − sin 2 β \cos \left( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right)= {\cos ^2}\alpha - {\sin ^2}\beta cos ( α + β ) cos ( α − β ) = cos 2 α − sin 2 β
حل: با استفاده از اتحادهای کسینوس جمع و تفریق، سمت چپ تساوی را بازنویسی میکنیم:
cos ( α + β ) cos ( α − β ) = ( cos α cos β − sin α sin β ) ( cos α cos β + sin α sin β ) & = cos 2 α cos 2 β − sin 2 α sin 2 β \begin{align} \cos \left( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right) & = \left( {\cos \alpha \cos \beta - \sin \alpha \sin \beta } \right) \left( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) \& = {\cos ^2}\alpha \,{\cos ^2}\beta - {\sin ^2}\alpha\,{\sin ^2}\beta \end {align} cos ( α + β ) cos ( α − β ) = ( cos α cos β − sin α sin β ) ( cos α cos β + sin α sin β ) & = cos 2 α cos 2 β − sin 2 α sin 2 β
از تساویهای زیر استفاده میکنیم:
cos 2 β = 1 − sin 2 β t e x t sin 2 α = 1 − cos 2 α {\cos ^2}\beta = 1 - {\sin ^2}\beta \;\;text{\,}\;\;{\sin ^2}\alpha = 1 - {\cos ^2}\alpha cos 2 β = 1 − sin 2 β t e x t sin 2 α = 1 − cos 2 α
و خواهیم داشت:
r e q u i r e cos 2 α ( 1 − sin 2 β ) − ( 1 − cos 2 α ) sin 2 β & = cos 2 α − cos 2 α sin 2 β − sin 2 β + cos 2 α sin 2 β = cos 2 α − sin 2 β \begin{align} require{} &{\cos ^2}\alpha \left( {1 - {{\sin }^2}\beta } \right) - \left( {1 - {{\cos }^2}\alpha } \right){\sin ^2}\beta \& = {\cos ^2}\alpha - {{\cos ^2}\alpha \,{\sin ^2}\beta } - {\sin ^2}\beta + {{\cos ^2}\alpha \,{\sin ^2}\beta} \ & = {\cos ^2}\alpha - {\sin ^2}\beta \end {align} re q u i re cos 2 α ( 1 − sin 2 β ) − ( 1 − cos 2 α ) sin 2 β & = cos 2 α − cos 2 α sin 2 β − sin 2 β + cos 2 α sin 2 β = cos 2 α − sin 2 β
مثال پنجم اتحاد های مثلثاتی جمع و تفریق دو زاویه
بیشترین و کمترین مقدار عبارت sin β − 3 cos β \sin \beta - \sqrt{3}\cos \beta sin β − 3 cos β
حل: مقدار این عبارت را با B B B
B 2 = 1 2 sin β − 3 2 cos β = sin π 6 sin β − cos π 6 cos β = − ( cos π 6 cos β − sin π 6 sin β ) = − cos ( π 6 + β ) \begin{align} \frac { B } { 2 } & = \frac { 1 } { 2 } \sin \beta - \frac { { \sqrt 3 } } { 2 } \cos \beta = \sin \frac { \pi } { 6 } \sin \beta - \cos \frac { \pi } { 6 } \cos \beta \ & = - \left ( { \cos \frac { \pi }{ 6 } \cos \beta - \sin \frac { \pi } { 6 } \sin \beta } \right ) = - \cos \left ( { \frac { \pi } { 6 } + \beta } \right) \end {align} 2 B = 2 1 sin β − 2 3 cos β = sin 6 π sin β − cos 6 π cos β = − ( cos 6 π cos β − sin 6 π sin β ) = − cos ( 6 π + β )
بنابراین:
B = − 2 cos ( π 6 + β ) B = - 2\cos \left( {\frac{\pi }{6} + \beta } \right) B = − 2 cos ( 6 π + β )
مثال ششم اتحاد های مثلثاتی جمع و تفریق دو زاویه
مقدار tan 5 p i 12 \tan \frac{{5pi }}{{12}} tan 12 5 p i
حل: زاویه 5 p i 12 \frac{{5pi }}{{12}} 12 5 p i
5 p i 12 = 3 π + 2 π 12 = 3 π 12 + 2 π 12 = π 4 + π 6 \frac{{5pi } } { { 1 2 } } = \frac { { 3 \pi + 2 \pi } } { { 1 2 } } = \frac { { 3 \pi } } { { 1 2 } } + \frac { { 2 \pi } } { { 1 2 } } = \frac { \pi } { 4 } + \frac { \pi } { 6 } 12 5 p i = 12 3 π + 2 π = 12 3 π + 12 2 π = 4 π + 6 π
اکنون، از اتحاد تانژانت جمع دو زاویه استفاده میکنیم:
tan 5 π 12 = tan ( π 4 + π 6 ) = tan π 4 + tan π 6 1 − tan π 4 tan π 6 = 1 + 1 3 1 − 1 ⋅ 1 3 = 3 + 1 3 − 1 = ( 3 + 1 ) 2 ( 3 − 1 ) ( 3 + 1 ) = 3 + 2 3 + 1 3 − 1 = 4 + 2 3 2 = 2 + 3 \begin {align} \tan \frac { { 5 \pi } } { { 1 2 } } & = \tan \left ( { \frac { \pi } { 4 } + \frac { \pi } { 6 } } \right ) = \frac { { \tan \frac { \pi } { 4 } + \tan \frac { \pi } { 6 } }} { { 1 - \tan \frac { \pi } { 4 } \tan \frac { \pi } { 6 } } } \ & = \frac { { 1 + \frac { 1 } { { \sqrt 3 } } } } { { 1 - 1 \cdot \frac { 1 }{ { \sqrt 3 } } } } = \frac { { \sqrt 3 + 1 } } { { \sqrt 3 - 1 } } = \frac { { { { \left ( { \sqrt 3 + 1 } \right ) } ^ 2 } } } { { \left ( { \sqrt 3 - 1 } \right ) \left ( { \sqrt 3 + 1 } \right ) } } \ &= \frac { { 3 + 2 \sqrt 3 + 1 } } { { 3 - 1 } } = \frac { { 4 + 2 \sqrt 3 } } { 2 } = 2 + \sqrt 3 \end {align} tan 12 5 π = tan ( 4 π + 6 π ) = 1 − tan 4 π tan 6 π tan 4 π + tan 6 π = 1 − 1 ⋅ 3 1 1 + 3 1 = 3 − 1 3 + 1 = ( 3 − 1 ) ( 3 + 1 ) ( 3 + 1 ) 2 = 3 − 1 3 + 2 3 + 1 = 2 4 + 2 3 = 2 + 3
مثال هفتم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر cos α = 0.6 \cos \alpha = 0.6 cos α = 0.6 α \alpha α tan ( π 3 + α ) \tan \left( {\frac{\pi }{3} + \alpha } \right) tan ( 3 π + α )
حل: ابتدا مقدار sin α \sin \alpha sin α
sin α = − 1 − cos 2 α = − 1 − 0.6 2 = − 1 − 0.36 = − 0.64 = − 0.8 \sin \alpha = - \sqrt {1 - {{\cos }^2}\alpha } = - \sqrt {1 - {{0.6}^2}} = - \sqrt {1 - 0.36} = - \sqrt {0.64} = - 0.8 sin α = − 1 − cos 2 α = − 1 − 0.6 2 = − 1 − 0.36 = − 0.64 = − 0.8
در نتیجه، تانژانت برابر است با
tan α = sin α cos α = − 0.8 0.6 = − 4 3 \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - 0.8}}{{0.6}} = - \frac{4}{3} tan α = cos α sin α = 0.6 − 0.8 = − 3 4
اکنون میتوانیم عبارت tan ( π 3 + α ) \tan \left( {\frac{\pi }{3} + \alpha } \right) tan ( 3 π + α )
tan ( π 3 + α ) = tan π 3 + tan α 1 − tan π 3 tan α = 3 − 4 3 1 − 3 ⋅ ( − 4 3 ) = 3 3 − 4 4 3 + 3 = ( 3 3 − 4 ) ( 4 3 − 3 ) ( 4 3 + 3 ) ( 4 3 − 3 ) = 36 − 16 3 − 9 3 + 12 48 − 9 = 48 − 25 3 39 \begin {align} \tan \left ( { \frac { \pi } { 3 } + \alpha } \right ) & = \frac { { \tan \frac { \pi } { 3 } + \tan \alpha } } { { 1 - \tan \frac { \pi } { 3 } \tan \alpha } } = \frac { { \sqrt 3 - \frac { 4 } { 3 } } } { { 1 - \sqrt 3 \cdot \left ( { - \frac { 4 }{ 3 } } \right ) } } \ & = \frac { { 3 \sqrt 3 - 4 } } { { 4 \sqrt 3 + 3 } } = \frac { { \left ( { 3 \sqrt 3 - 4 } \right ) \left ( { 4 \sqrt 3 - 3 } \right ) } } { { \left ( { 4 \sqrt 3 + 3 } \right ) \left ( { 4 \sqrt 3 - 3 } \right ) } } \ & = \frac { { 3 6 - 1 6 \sqrt 3 - 9 \sqrt 3 + 1 2 } } { { 4 8 - 9 } } = \frac { { 4 8 - 2 5 \sqrt 3 } } { { 3 9 } } \end {align} tan ( 3 π + α ) = 1 − tan 3 π tan α tan 3 π + tan α = 1 − 3 ⋅ ( − 3 4 ) 3 − 3 4 = 4 3 + 3 3 3 − 4 = ( 4 3 + 3 ) ( 4 3 − 3 ) ( 3 3 − 4 ) ( 4 3 − 3 ) = 48 − 9 36 − 16 3 − 9 3 + 12 = 39 48 − 25 3
مثال هشتم اتحاد های مثلثاتی جمع و تفریق دو زاویه
عبارت زیر را ساده کنید:
2 t a n α 1 − tan 2 α cos 2 α − sin 2 α \frac{{2tan \alpha }}{{1 - {{\tan }^2}\alpha }}\cos 2\alpha - \sin 2\alpha 1 − tan 2 α 2 t an α cos 2 α − sin 2 α
حل: میدانیم
2 t a n α 1 − tan 2 α = tan α + tan α 1 − tan α tan α = tan ( α + α ) = tan 2 α \frac{{2tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha \tan \alpha }} = \tan \left( {\alpha + \alpha } \right) = \tan 2\alpha 1 − tan 2 α 2 t an α = 1 − tan α tan α tan α + tan α = tan ( α + α ) = tan 2 α
در نتیجه، خواهیم داشت:
r e q u i r e 2 tan α 1 − tan 2 α cos 2 α − sin 2 α = tan 2 α cos 2 α − sin 2 α = sin 2 α cos 2 α cos 2 α − sin 2 α = sin 2 α − sin 2 α = 0 \begin {align} require {} \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } \cos 2 \alpha - \sin 2 \alpha & = \tan 2 \alpha \cos 2 \alpha - \sin 2 \alpha \ & = \frac{{\sin 2\alpha {\cos 2\alpha} }}{{\cos 2\alpha }} - \sin 2\alpha \ &= \sin 2\alpha - \sin 2\alpha = 0 \end {align} re q u i re 1 − tan 2 α 2 tan α cos 2 α − sin 2 α = tan 2 α cos 2 α − sin 2 α = cos 2 α sin 2 α cos 2 α − sin 2 α = sin 2 α − sin 2 α = 0
مثال نهم اتحاد های مثلثاتی جمع و تفریق دو زاویه
حاصل عبارت زیر را بهدست آورید:
tan 2 7 p i 24 − tan 2 π 24 1 − tan 2 7 p i 24 tan 2 π 24 \frac{{{{\tan }^2}\frac{{7pi }}{{24}} - {{\tan }^2}\frac{\pi }{{24}}}}{{1 - {{\tan }^2}\frac{{7pi }}{{24}}\,{{\tan }^2}\frac{\pi }{{24}}}} 1 − tan 2 24 7 p i tan 2 24 π tan 2 24 7 p i − tan 2 24 π
حل: از اتحاد مزدوج کمک میگیریم.
a 2 − b 2 = ( a − b ) ( a + b ) {a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right) a 2 − b 2 = ( a − b ) ( a + b )
با به کار بردن این اتحاد در صورت و مخرج عبارت و استفاده از فرمولهای تانژانت جمع و تانژانت تفریق دو زاویه، خواهیم داشت:
tan 2 7 π 24 − tan 2 π 24 1 − tan 2 7 π 24 tan 2 π 24 = ( tan 7 π 24 − tan π 24 ) ( tan 7 π 24 + tan π 24 ) ( 1 − tan 7 π 24 tan π 24 ) ( 1 + tan 7 π 24 tan π 24 ) = tan 7 π 24 − tan π 24 1 + tan 7 π 24 tan π 24 ⋅ tan 7 π 24 + tan π 24 1 − tan 7 π 24 tan π 24 & = tan ( 7 π 24 − π 24 ) tan ( 7 π 24 + π 24 ) & = tan 6 π 24 tan 8 π 24 = tan π 4 tan π 3 = 1 ⋅ 3 = 3 \begin {align} \frac { { { { \tan } ^ 2 } \frac { { 7 \pi } }{ { 2 4 } } - { { \tan } ^ 2 } \frac { \pi } { { 2 4 } } } } { { 1 - { { \tan } ^ 2 } \frac { { 7 \pi } } { { 2 4 } } { { \tan } ^ 2 } \frac { \pi } { { 2 4 } } } } & = \frac { { \left ( { \tan \frac { { 7 \pi } } { { 2 4 } } - \tan \frac { \pi } { { 2 4 } } } \right ) \left ( { \tan \frac { { 7 \pi } } { { 2 4 } } + \tan \frac { \pi }{ { 2 4 } } } \right ) } } { { \left ( { 1 - \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } \right ) \left ( { 1 + \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } \right ) } } \ &= \frac { { \tan \frac { { 7 \pi } } { { 2 4 } } - \tan \frac { \pi } { { 2 4 } } } } { { 1 + \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } } \cdot \frac { { \tan \frac { { 7 \pi } } { { 2 4 } } + \tan \frac { \pi }{ { 2 4 } } } } { { 1 - \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } } \& = \tan \left ( { \frac { { 7 \pi } } { { 2 4 } } - \frac { \pi } { { 2 4 } } } \right ) \tan \left ( { \frac { { 7 \pi } } { { 2 4 } } + \frac { \pi } { { 2 4 } } } \right ) \& = \tan \frac { { 6 \pi } } { { 2 4 } } \tan \frac { { 8 \pi } } { { 2 4} } = \tan \frac { \pi } { 4 } \tan \frac { \pi } { 3 } = 1 \cdot \sqrt 3 = \sqrt 3 \end {align} 1 − tan 2 24 7 π tan 2 24 π tan 2 24 7 π − tan 2 24 π = ( 1 − tan 24 7 π tan 24 π ) ( 1 + tan 24 7 π tan 24 π ) ( tan 24 7 π − tan 24 π ) ( tan 24 7 π + tan 24 π ) = 1 + tan 24 7 π tan 24 π tan 24 7 π − tan 24 π ⋅ 1 − tan 24 7 π tan 24 π tan 24 7 π + tan 24 π & = tan ( 24 7 π − 24 π ) tan ( 24 7 π + 24 π ) & = tan 24 6 π tan 24 8 π = tan 4 π tan 3 π = 1 ⋅ 3 = 3
اتحاد های مثلثاتی دو برابر کمان
اتحادهای مثلثاتی دو برابر کمان را میتوان بهسادگی با توجه به آنچه برای نسبتهای مثلثاتی جمع دو زاویه گفتیم، بهدست آورد.
فرمول سینوس دو برابر کمان
برای بهدست آوردن فرمول سینوس دو برابر کمان، از فرمول سینوس جمع دو زاویه استفاده میکنیم:
sin ( α + β ) = sin α cos β + cos α sin β \sin \left ( { \alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta sin ( α + β ) = sin α cos β + cos α sin β
با قرار دادن β = α \beta = \alpha β = α
sin ( α + α ) = sin 2 α = sin α cos α + cos α sin α = 2 sin α cos α \sin \left ( { \alpha + \alpha } \right ) = \sin 2 \alpha = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha = 2\sin \alpha \cos \alpha sin ( α + α ) = sin 2 α = sin α cos α + cos α sin α = 2 sin α cos α
بنابراین، میتوان نوشت:
sin 2 α = 2 sin α cos α \large \boxed {\sin {2 \alpha } = 2\sin \alpha \cos \alpha } sin 2 α = 2 sin α cos α
فرمول کسینوس دو برابر کمان
مشابه آنچه برای سینوس گفتیم، از تساوی زیر استفاده میکنیم:
cos ( α + β ) = cos α cos β − sin α sin β \cos \left ( { \alpha + \beta } \right ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta cos ( α + β ) = cos α cos β − sin α sin β
با قرار دادن β = α \beta = \alpha β = α
cos ( α + α ) = cos 2 α = cos α cos α − sin α sin α = cos 2 α − sin 2 α \cos \left ( { \alpha + \alpha } \right ) = \cos 2 \alpha = \cos \alpha \cos \alpha - \sin \alpha \sin \alpha = { \cos ^ 2 } \alpha - { \sin ^ 2 } \alpha cos ( α + α ) = cos 2 α = cos α cos α − sin α sin α = cos 2 α − sin 2 α
یا
cos ( 2 α ) = cos 2 α − sin 2 α \large \boxed { \cos \left ( { 2\alpha } \right ) = { \cos ^ 2 } \alpha - { \sin ^ 2 } \alpha } cos ( 2 α ) = cos 2 α − sin 2 α
اگر از تساوی cos 2 α = 1 − sin 2 α {\cos ^2}\alpha = 1 - {\sin ^2}\alpha cos 2 α = 1 − sin 2 α
cos 2 α = 1 − 2 sin 2 α \large \boxed { \cos 2\alpha = 1 - 2 \, { \sin ^ 2 } \alpha } cos 2 α = 1 − 2 sin 2 α
یا با استفاده از تساوی sin 2 α = 1 − cos 2 α {\sin ^2}\alpha = 1 - {\cos ^2}\alpha sin 2 α = 1 − cos 2 α
cos 2 α = 2 cos 2 α − 1 \large \boxed { \cos 2\alpha= 2\,{\cos ^ 2 } \alpha - 1 } cos 2 α = 2 cos 2 α − 1
فرمول تانژانت دو برابر کمان
برای بهدست آوردن فرمول تانژانت دو برابر کمان، از اتحاد تانژانت جمع دو زاویه استفاده میکنیم:
tan ( α + β ) = tan α + tan β 1 − tan α tan β \tan \left ( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta } } { { 1 - \tan \alpha \tan \beta } } tan ( α + β ) = 1 − tan α tan β tan α + tan β
با قرار دادن β = α \beta = \alpha β = α
tan ( α + α ) = tan 2 α = tan α + tan α 1 − tan α tan α = 2 tan α 1 − tan 2 α \tan \left ( { \alpha + \alpha } \right ) = \tan 2 \alpha = \frac { { \tan \alpha + \tan \alpha } } { { 1 - \tan \alpha \tan \alpha } } = \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } tan ( α + α ) = tan 2 α = 1 − tan α tan α tan α + tan α = 1 − tan 2 α 2 tan α
یا
tan 2 α = 2 tan α 1 − tan 2 α \large \boxed {\tan { 2\alpha } = \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } } tan 2 α = 1 − tan 2 α 2 tan α
فرمول کتانژانت دو برابر کمان
مشابه تانژانت، برای کتانژانت میتوان نوشت:
cot ( α + β ) = cot α cot β − 1 cot α + cot β ⇒ cot 2 α = cot α cot α − 1 cot α + cot α = cot 2 α − 1 2 cot α \cot \left ( { \alpha + \beta } \right ) = \frac { { \cot \alpha \cot \beta - 1 } } { { \cot \alpha + \cot \beta } } \, \; \; \Rightarrow \cot 2 \alpha = \frac{{\cot \alpha \cot \alpha - 1}}{{\cot \alpha + \cot \alpha } } = \frac { { { { \cot } ^ 2 } \alpha - 1 } } { { 2 \cot \alpha } } cot ( α + β ) = cot α + cot β cot α cot β − 1 ⇒ cot 2 α = cot α + cot α cot α cot α − 1 = 2 cot α cot 2 α − 1
یا
cot 2 α = cot 2 α − 1 2 cot α \large \boxed {\cot 2 \alpha = \frac { { { { \cot } ^ 2 } \alpha - 1 } } { { 2 \cot \alpha } }} cot 2 α = 2 cot α cot 2 α − 1
اتحاد های مثلثاتی سه برابر کمان
اتحاد های مثلثاتی سه برابر کمان، مشابه اتحاد های مثلثاتی دو برابر کمان محاسبه میشوند.
فرمول سینوس سه برابر کمان
مشابه فرمول سینوس دو برابر کمان، مینویسیم:
بنابراین، میتوان نوشت:
sin 3 α = sin ( 2 α + α ) = sin 2 α cos α + cos 2 α sin α = 2 sin α cos α cos α + ( cos 2 α − sin 2 α ) sin α = 2 sin α cos 2 α + ( 1 − 2 sin 2 α ) sin α = 2 sin α ( 1 − sin 2 α ) + ( 1 − 2 sin 2 α ) sin α = 2 sin α − 2 sin 3 α + sin α − 2 sin 3 α = 3 sin α − 4 sin 3 α \begin {align} \sin 3 \alpha & = \sin \left( {2\alpha + \alpha } \right) = \sin 2\alpha \cos \alpha + \cos 2\alpha \sin \alpha \ &= 2\sin \alpha \cos \alpha \cos \alpha + \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right ) \sin \alpha \ & = 2 \sin \alpha \,{ \cos ^ 2 } \alpha + \left ( { 1 - 2 { { \sin } ^ 2 } \alpha } \right ) \sin \alpha \ & = 2 \sin \alpha \left ( { 1 - { { \sin } ^ 2 } \alpha } \right ) + \left ( { 1 - 2 \,{ { \sin } ^ 2 } \alpha } \right ) \sin \alpha \ & = 2\sin \alpha - 2 \, { \sin ^ 3 } \alpha + \sin \alpha - 2 \, { \sin ^ 3 } \alpha = 3 \sin \alpha - 4 \, { \sin ^ 3 } \alpha \end {align} sin 3 α = sin ( 2 α + α ) = sin 2 α cos α + cos 2 α sin α = 2 sin α cos α cos α + ( cos 2 α − sin 2 α ) sin α = 2 sin α cos 2 α + ( 1 − 2 sin 2 α ) sin α = 2 sin α ( 1 − sin 2 α ) + ( 1 − 2 sin 2 α ) sin α = 2 sin α − 2 sin 3 α + sin α − 2 sin 3 α = 3 sin α − 4 sin 3 α
در نتیجه، داریم:
sin 3 α = 3 sin α − 4 sin 3 α \large \boxed { \begin {align} \sin 3 \alpha = 3 \sin \alpha - 4 \, { \sin ^ 3 } \alpha \end {align} } sin 3 α = 3 sin α − 4 sin 3 α
فرمول کسینوس سه برابر کمان
مشابه سینوس، فرمول کسینوس سه برابر کمان بهصورت زیر است:
cos 3 α = 4 cos 3 α − 3 cos α \large \boxed { \cos 3 \alpha = 4 \, { \cos ^ 3 } \alpha - 3 \cos \alpha } cos 3 α = 4 cos 3 α − 3 cos α
فرمول تانژنت سه برابر کمان
با طی گامهایی مشابه بخشهای قبل، فرمول تانژنت سه برابر کمان بهصورت زیر است:
tan 3 α = 3 tan α − tan 3 α 1 − 3 tan 2 α \large \boxed { \tan 3 \alpha = \frac { { 3 \tan \alpha - { { \tan } ^ 3 } \alpha } } { { 1 - 3 \, { { \tan } ^ 2 } \alpha } } } tan 3 α = 1 − 3 tan 2 α 3 tan α − tan 3 α
فرمول کتانژانت سه برابر کمان
فرمول کتانژانت سه برابر کمان بهصورت زیر است:
cot 3 α = cot 3 α − 3 cot α 3 cot 2 α − 1 \large \boxed { \cot 3 \alpha = \frac { { { { \cot } ^ 3 } \alpha - 3 \cot \alpha } } { { 3 \, { { \cot } ^ 2 } \alpha - 1 } } } cot 3 α = 3 cot 2 α − 1 cot 3 α − 3 cot α
مثال های اتحاد های مثلثاتی چند برابر کمان
در این بخش، مثالهایی را از اتحاد های مثلثاتی دو برابر کمان و سه برابر کمان بررسی میکنیم.
مثال اول اتحاد های مثلثاتی چند برابر کمان
اگر tan α 2 = 3 \tan \frac{\alpha}{2} = 3 tan 2 α = 3 cos α 2 − 3 sin α \frac{{\cos \alpha }}{{2 - 3\sin \alpha }} 2 − 3 sin α cos α
حل: از اتحادهای دو برابر کمان استفاده میکنیم:
cos α = 1 − tan 2 α 2 1 + tan 2 α 2 sin α = 2 tan α 2 1 + tan 2 α 2 \cos \alpha = \frac { { 1 - { { \tan } ^ 2 } \frac { \alpha }{ 2 } } } { { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } } \, \; \; \sin \alpha = \frac { { 2 \tan \frac { \alpha } { 2 } } } { { 1 + { { \tan } ^ 2 } \frac{ \alpha } { 2 } } } cos α = 1 + tan 2 2 α 1 − tan 2 2 α sin α = 1 + tan 2 2 α 2 tan 2 α
با قرار دادن این فرمولها در عبارت اصلی، خواهیم داشت:
cos α 2 − 3 sin α = 1 − tan 2 α 2 1 + tan 2 α 2 2 − 3 ⋅ 2 tan α 2 1 + tan 2 α 2 = 1 − tan 2 α 2 1 + tan 2 α 2 2 ( 1 + tan 2 α 2 ) − 6 t a n α 2 1 + tan 2 α 2 = 1 − tan 2 α 2 2 + 2 tan 2 α 2 − 6 t a n α 2 = 1 − 3 2 2 + 2 ⋅ 3 2 − 6 ⋅ 3 = 1 − 9 2 + 18 − 18 = − 8 2 = − 4 \begin {align} \frac { { \cos \alpha } } { { 2 - 3 \sin \alpha } } & = \frac{{\frac{{1 - {{\tan }^2}\frac{\alpha }{2}}}{{1 + {{\tan }^2}\frac{\alpha } { 2 } } } } } { { 2 - 3 \cdot \frac { { 2 \tan \frac { \alpha } { 2 } } } { { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } } } } = \frac { { \frac { { 1 - { { \tan } ^ 2 } \frac { \alpha } { 2 } } } { { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } }} } } { { \frac { { 2 \left ( { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } \right) - 6tan \frac { \alpha } { 2 } } } { {1 + {{\tan }^2}\frac { \alpha } { 2 } } } } } \ &= \frac{{1 - {{\tan }^2}\frac{\alpha }{2}}}{{2 + 2\,{{\tan }^2}\frac{\alpha }{2} - 6tan \frac{\alpha }{2}}} = \frac{{1 - {3^2}}}{{2 + 2 \cdot {3^2} - 6 \cdot 3}} \ & = \frac{{1 - 9}}{{2 + {18} - {18}}} = \frac{{ - 8}}{2} = - 4 \end {align} 2 − 3 sin α cos α = 2 − 3 ⋅ 1 + t a n 2 2 α 2 t a n 2 α 1 + t a n 2 2 α 1 − t a n 2 2 α = 1 + t a n 2 2 α 2 ( 1 + t a n 2 2 α ) − 6 t an 2 α 1 + t a n 2 2 α 1 − t a n 2 2 α = 2 + 2 tan 2 2 α − 6 t an 2 α 1 − tan 2 2 α = 2 + 2 ⋅ 3 2 − 6 ⋅ 3 1 − 3 2 = 2 + 18 − 18 1 − 9 = 2 − 8 = − 4
مثال دوم اتحاد های مثلثاتی چند برابر کمان
عبارت زیر را ساده کنید:
1 + sin 2 α ( sin α + cos α ) 2 \frac { { 1 + \sin 2 \alpha } } { { { { \left ( { \sin \alpha + \cos \alpha } \right ) } ^ 2 } } } ( sin α + cos α ) 2 1 + sin 2 α
حل: با استفاده از فرمول سینوس دو برابر زاویه، خواهیم داشت:
1 + sin 2 α ( sin α + cos α ) 2 = 1 + sin 2 α sin 2 α + 2 sin α cos α + cos 2 α & = 1 + sin 2 α 1 + 2 sin α cos α = 1 + sin 2 α 1 + sin 2 α = 1 \begin {align} \frac { { 1 + \sin 2 \alpha } } { { { { \left ( {\sin \alpha + \cos \alpha } \right ) } ^ 2 }} } & = \frac { { 1 + \sin 2 \alpha } } { { { { \sin } ^ 2 } \alpha + 2 \sin \alpha \cos \alpha + {{\cos } ^ 2 } \alpha } } \&= \frac { { 1 + \sin 2\alpha }}{{1 + 2\sin \alpha \cos \alpha }} = \frac{{1 + \sin 2\alpha }}{{1 + \sin 2\alpha }} = 1 \end {align} ( sin α + cos α ) 2 1 + sin 2 α = sin 2 α + 2 sin α cos α + cos 2 α 1 + sin 2 α & = 1 + 2 sin α cos α 1 + sin 2 α = 1 + sin 2 α 1 + sin 2 α = 1
مثال سوم اتحاد های مثلثاتی چند برابر کمان
عبارت زیر را ساده کنید:
2 sin β − sin 2 β 2 sin β + sin 2 β \frac { { 2 \sin \beta - \sin 2\beta } } { { 2\sin \beta + \sin 2\beta } } 2 sin β + sin 2 β 2 sin β − sin 2 β
با استفاده از فرمول سینوس و کسینوس دو برابر زاویه، خواهیم داشت:
2 sin β − sin 2 β 2 sin β + sin 2 β = 2 sin β − 2 sin β cos β 2 sin β + 2 sin β cos β = 2 sin β ( 1 − cos β ) 2 sin β ( 1 + cos β ) = 1 − cos β 1 + cos β = 1 − cos 2 β 2 + sin 2 β 2 1 + cos 2 β 2 − sin 2 β 2 = sin 2 β 2 + sin 2 β 2 cos 2 β 2 + cos 2 β 2 = 2 sin 2 β 2 2 cos 2 β 2 = tan 2 β 2 \begin {align} \frac { { 2 \sin \beta - \sin 2 \beta } } { { 2 \sin \beta + \sin 2\beta } } & = \frac{{2\sin \beta - 2\sin \beta \cos \beta }}{{2\sin \beta + 2\sin \beta \cos \beta }} = \frac{{{2\sin \beta} \left ( { 1 - \cos \beta } \right ) }} { { { 2 \sin \beta } \left ( { 1 + \cos \beta } \right ) } } \ & = \frac { { 1 - \cos \beta } } { { 1 + \cos \beta } } = \frac { { 1 - { { \cos } ^ 2 } \frac { \beta }{ 2 } + { { \sin } ^ 2}\frac{\beta } { 2 } } } { { 1 + { { \cos } ^ 2 } \frac { \beta } { 2 } - { { \sin } ^ 2 } \frac { \beta } { 2 } } } = \frac { { { { \sin } ^ 2 } \frac { \beta } { 2 } + { { \sin } ^ 2 } \frac { \beta } { 2 } } } { { { { \cos } ^ 2 } \frac { \beta } { 2 } + { { \cos }^2}\frac{\beta }{2}}} \ &= \frac{{{2}{{\sin }^2}\frac{\beta }{2}}}{{{2}{{\cos }^2}\frac{\beta }{2}}} = {\tan ^2}\frac{\beta }{2} \end {align} 2 sin β + sin 2 β 2 sin β − sin 2 β = 2 sin β + 2 sin β cos β 2 sin β − 2 sin β cos β = 2 sin β ( 1 + cos β ) 2 sin β ( 1 − cos β ) = 1 + cos β 1 − cos β = 1 + cos 2 2 β − sin 2 2 β 1 − cos 2 2 β + sin 2 2 β = cos 2 2 β + cos 2 2 β sin 2 2 β + sin 2 2 β = 2 cos 2 2 β 2 sin 2 2 β = tan 2 2 β
مثال چهارم اتحاد های مثلثاتی چند برابر کمان
درستی تساوی زیر را بررسی کنید:
sin 3 α sin α − cos 3 α cos α = 2 \frac { { \sin 3 \alpha } } { { \sin \alpha } } - \frac { { \cos 3 \alpha } } { { \cos \alpha } } = 2 sin α sin 3 α − cos α cos 3 α = 2
حل: از فرمولهای سه برابر کمان استفاده میکنیم:
sin 3 α = 3 sin α − 4 sin 3 α cos 3 α = 4 cos 3 α − 3 cos α \begin {align} \sin 3\alpha & = 3\sin \alpha - 4{\sin ^3}\alpha \ \cos 3\alpha & = 4{\cos ^3}\alpha - 3\cos \alpha \end {align} sin 3 α = 3 sin α − 4 sin 3 α cos 3 α = 4 cos 3 α − 3 cos α
سمت چپ عبارت دادهشده بهصورت زیر است و تساوی اثبات میشود:
sin 3 α sin α − cos 3 α cos α = 3 sin α − 4 sin 3 α sin α − 4 cos 3 α − 3 cos α cos α \frac { { \sin 3 \alpha } } { { \sin \alpha } } - \frac { { \cos 3 \alpha } } { { \cos \alpha } } = \frac{{3\sin \alpha - 4\,{{\sin } ^ 3 } \alpha } } { { \sin \alpha } } - \frac { { 4 \, { { \cos } ^ 3 } \alpha - 3 \cos \alpha } } { { \cos \alpha }} sin α sin 3 α − cos α cos 3 α = sin α 3 sin α − 4 sin 3 α − cos α 4 cos 3 α − 3 cos α
3 sin α − 4 sin 3 α sin α − 4 cos 3 α − 3 cos α cos α = sin α ( 3 − 4 sin 2 α ) sin α − cos α ( 4 cos 2 α − 3 ) cos α \frac{{3\sin \alpha - 4\,{{\sin } ^ 3 } \alpha } } { { \sin \alpha } } - \frac { { 4 \, { { \cos } ^ 3 } \alpha - 3 \cos \alpha } } { { \cos \alpha }} = \frac{{{\sin \alpha} \left( {3 - 4\,{{\sin }^2}\alpha } \right)}}{{ { \sin \alpha} } } - \frac { { { \cos \alpha} \left( {4\,{{\cos }^2}\alpha - 3} \right)}}{{{\cos \alpha} }} sin α 3 sin α − 4 sin 3 α − cos α 4 cos 3 α − 3 cos α = sin α sin α ( 3 − 4 sin 2 α ) − cos α cos α ( 4 cos 2 α − 3 )
sin α ( 3 − 4 sin 2 α ) sin α − cos α ( 4 cos 2 α − 3 ) cos α = 3 − 4 sin 2 α − 4 cos 2 α + 3 = 6 − 4 ( sin 2 α + cos 2 α ⏟ 1 ) \frac{{{\sin \alpha} \left( {3 - 4\,{{\sin }^2}\alpha } \right)}}{{ { \sin \alpha} } } - \frac { { { \cos \alpha} \left( {4\,{{\cos }^2}\alpha - 3} \right)}}{{{\cos \alpha} }} = 3 - 4\,{\sin ^2}\alpha - 4\,{\cos ^2}\alpha + 3 = 6 - 4\left( {\underbrace {{{\sin }^2}\alpha + {{\cos }^2}\alpha }_1} \right) sin α sin α ( 3 − 4 sin 2 α ) − cos α cos α ( 4 cos 2 α − 3 ) = 3 − 4 sin 2 α − 4 cos 2 α + 3 = 6 − 4 ( 1 sin 2 α + cos 2 α )
3 − 4 sin 2 α − 4 cos 2 α + 3 = 6 − 4 ( sin 2 α + cos 2 α ⏟ 1 ) = 6 − 4 3 - 4\,{\sin ^2}\alpha - 4\,{\cos ^2}\alpha + 3 = 6 - 4\left( {\underbrace {{{\sin }^2}\alpha + {{\cos }^2}\alpha }_1} \right) = 6 - 4 3 − 4 sin 2 α − 4 cos 2 α + 3 = 6 − 4 ( 1 sin 2 α + cos 2 α ) = 6 − 4
6 − 4 = 2 6- 4 = 2 6 − 4 = 2
مثال پنجم اتحاد های مثلثاتی چند برابر کمان
اگر cot β = − 3 \cot\beta = -3 cot β = − 3 sin 4 β \sin 4\beta sin 4 β
حل: پیش از هر چیز، میدانیم:
tan β = 1 cot β = − 1 3 \tan \beta = \frac{1}{{\cot \beta }} = - \frac { 1 } { 3 } tan β = cot β 1 = − 3 1
با استفاده از فرمول سینوس دو برابر زاویه، میتوانیم بنویسیم:
sin 4 β = 2 sin 2 β cos 2 β \sin 4\beta = 2\sin 2\beta \cos 2\beta sin 4 β = 2 sin 2 β cos 2 β
در ادامه، مقدار مورد نظر بهصورت زیر حاصل میشود:
sin 4 β = 2 sin 2 β cos 2 β = 2 ⋅ 2 tan β 1 + tan 2 β ⋅ 1 − tan 2 β 1 + tan 2 β = 2 ⋅ 2 ⋅ ( − 1 3 ) 1 + ( − 1 3 ) 2 ⋅ 1 − ( − 1 3 ) 2 1 + ( − 1 3 ) 2 = 2 ⋅ − 2 3 1 + 1 9 ⋅ 1 − 1 9 1 + 1 9 = 2 ⋅ − 2 3 10 9 ⋅ 8 9 10 9 = 2 ⋅ ( − 6 10 ) ⋅ 8 10 = − 96 100 = − 24 25 \begin {align} \sin 4 \beta & = 2 \sin 2 \beta \cos 2 \beta = 2 \cdot \frac { { 2 \tan \beta } } { { 1 + { { \tan } ^ 2 } \beta } } \cdot \frac { { 1 - { { \tan } ^ 2 } \beta } } { { 1 + { { \tan } ^ 2 } \beta } } \ &= 2 \cdot \frac { { 2 \cdot \left ( { - \frac { 1 } { 3 } } \right ) } } { { 1 + { { \left ( { - \frac { 1 } { 3 } } \right ) } ^ 2 } } } \cdot \frac { { 1 - { { \left ( { - \frac{1}{3}} \right)}^2}}}{{1 + {{\left( { - \frac{1}{3}} \right)}^2}}} = 2 \cdot \frac{{ - \frac{2}{3}}}{{1 + \frac{1}{9}}} \cdot \frac{{1 - \frac{1}{9}}}{{1 + \frac{1}{9}}} \ & = 2 \cdot \frac{{ - \frac{2}{3}}}{{\frac{{10}}{9}}} \cdot \frac{{\frac{8}{9}}}{{\frac{{10}}{9}}} = 2 \cdot \left( { - \frac { 6 } { { 1 0 } } } \right ) \cdot \frac { 8 } { { 1 0 } } = - \frac { { 9 6 } } { { 1 0 0 } } = - \frac { { 2 4 } } { { 2 5 } } \end {align} sin 4 β = 2 sin 2 β cos 2 β = 2 ⋅ 1 + tan 2 β 2 tan β ⋅ 1 + tan 2 β 1 − tan 2 β = 2 ⋅ 1 + ( − 3 1 ) 2 2 ⋅ ( − 3 1 ) ⋅ 1 + ( − 3 1 ) 2 1 − ( − 3 1 ) 2 = 2 ⋅ 1 + 9 1 − 3 2 ⋅ 1 + 9 1 1 − 9 1 = 2 ⋅ 9 10 − 3 2 ⋅ 9 10 9 8 = 2 ⋅ ( − 10 6 ) ⋅ 10 8 = − 100 96 = − 25 24
اتحاد های مثلثاتی نصف کمان
در این بخش، اتحاد های مثلثاتی نصف کمان را معرفی میکنیم.
فرمول سینوس نصف کمان
همانطور که میدانیم، کسینوس دو برابر کمان بهصورت زیر است:
cos 2 β = 1 − 2 sin 2 β \cos 2 \beta = 1 - 2\,{\sin ^2}\beta cos 2 β = 1 − 2 sin 2 β
این فرمول را بهصورت زیر مینویسیم:
sin 2 β = 1 − cos 2 β 2 { \sin ^ 2 } \beta = \frac { { 1 - \cos 2\beta } } { 2 } sin 2 β = 2 1 − cos 2 β
با قرار دادن β = α 2 \beta = \frac{\alpha }{2} β = 2 α
sin 2 α 2 = 1 − cos α 2 ⇒ ∣ sin α 2 ∣ = 1 − cos α 2 ⇒ sin α 2 = ± 1 − cos α 2 { \sin ^ 2 } \frac { \alpha } { 2 } = \frac { { 1 - \cos \alpha }} { 2 } \, \; \; \Rightarrow \left| {\sin \frac{\alpha }{2}} \right| = \sqrt {\frac { { 1 - \cos \alpha } } { 2 } } \,\; \; \Rightarrow \sin \frac { \alpha } { 2 } = \pm \sqrt { \frac { { 1 - \cos \alpha } }{ 2 } } sin 2 2 α = 2 1 − cos α ⇒ sin 2 α = 2 1 − cos α ⇒ sin 2 α = ± 2 1 − cos α
بنابراین، میتوان نوشت:
sin α 2 = ± 1 − cos α 2 \large \boxed { { \sin } \frac { \alpha } { 2 } = \pm \sqrt { \frac { { 1 - \cos \alpha } } { 2 } } } sin 2 α = ± 2 1 − cos α
علامت ± \pm ± α 2 \frac \alpha 2 2 α
فرمول کسینوس نصف کمان
مشابه سینوس، برای کسینوس میتوان نوشت:
cos α 2 = ± 1 + cos α 2 \large \boxed { {\cos } \frac{\alpha } { 2 } = \pm \sqrt { \frac { { 1 + \cos \alpha } } { 2 } } } cos 2 α = ± 2 1 + cos α
فرمول تانژانت نصف کمان
برای محاسبه تانژانت نصف کمان، بهراحتی میتوان نوشت:
tan 2 α 2 = sin 2 α 2 cos 2 α 2 = 1 − cos α 1 + cos α { \tan ^ 2 } \frac { \alpha } { 2 } = \frac { { { { \sin } ^ 2 } \frac { \alpha } { 2 } } } { { { { \cos } ^ 2 } \frac { \alpha } { 2 } } } = \frac { { 1 - \cos \alpha } } { { 1 + \cos \alpha } } tan 2 2 α = cos 2 2 α sin 2 2 α = 1 + cos α 1 − cos α
در نتیجه، داریم:
tan α 2 = ± 1 − cos α 1 + cos α \large \boxed { \tan \frac { \alpha } { 2 } = \pm \sqrt { \frac { 1 - \cos \alpha } { 1 + \cos \alpha } } } tan 2 α = ± 1 + cos α 1 − cos α
این فرمول را میتوانیم بهگونهای دیگر نیز بیان کنیم. فرمول زیر را میدانیم:
tan α 2 = sin α 2 cos α 2 \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha }{2 } } } { { \cos \frac { \alpha } { 2 } } } tan 2 α = cos 2 α sin 2 α
با ضرب صورت و مخرج کسر بالا در cos α 2 {\cos \frac{\alpha }{2}} cos 2 α
tan α 2 = sin α 2 cos α 2 = 2 sin α 2 cos α 2 2 cos α 2 cos α 2 = sin α 2 cos 2 α 2 = sin α 1 + cos α \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha } { 2 } } } { { \cos \frac { \alpha } { 2 } } } = \frac { { 2 \sin \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } { { 2 \cos \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } = \frac { { \sin \alpha } } { { 2 { { \cos }^ 2 } \frac { \alpha } { 2 } } } = \frac { { \sin \alpha } } { { 1 + \cos \alpha } } tan 2 α = cos 2 α sin 2 α = 2 cos 2 α cos 2 α 2 sin 2 α cos 2 α = 2 cos 2 2 α sin α = 1 + cos α sin α
بنابراین، میتوان نوشت:
tan α 2 = sin α 1 + cos α \large \boxed { \tan \frac { \alpha } { 2 } = \frac { { \sin \alpha } } { { 1 + \cos \alpha } } } tan 2 α = 1 + cos α sin α
با طی گامهای مشابه، داریم:
tan α 2 = sin α 2 cos α 2 = 2 sin α 2 sin α 2 2 sin α 2 cos α 2 = 2 sin 2 α 2 sin α = 1 − cos α sin α \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha }{ 2 } } } { { \cos \frac { \alpha } { 2 } } } = \frac { { 2 \sin \frac { \alpha } { 2 } \sin \frac { \alpha } { 2 } } } { { 2 \sin \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } = \frac { { 2 { { \sin } ^ 2 } \frac { \alpha } { 2 } } } { { \sin \alpha } } = \frac { { 1 - \cos \alpha } } { { \sin \alpha } } tan 2 α = cos 2 α sin 2 α = 2 sin 2 α cos 2 α 2 sin 2 α sin 2 α = sin α 2 sin 2 2 α = sin α 1 − cos α
یا
tan α 2 = 1 − cos α sin α \large \boxed { \tan \frac { \alpha} { 2 } = \frac { 1 - \cos \alpha } { \sin \alpha } } tan 2 α = sin α 1 − cos α
فرمول کتانژانت نصف کمان
فرمول ساده زیر را میدانیم:
cot α 2 = 1 tan α 2 \cot \frac { \alpha } { 2 } = \frac { 1 } { { \tan \frac { \alpha } { 2 } } } cot 2 α = tan 2 α 1
بنابراین، به توجه به فرمول تانژانت نصف کمان، فرمولهای زیر را برای کتانژانت داریم:
cot α 2 = sin α 1 − cos α \large \boxed { \cot \frac { \alpha } { 2 } = \frac { \sin \alpha } { 1 - \cos \alpha } } cot 2 α = 1 − cos α sin α
cot α 2 = 1 + cos α sin α \large \boxed {\cot \frac{\alpha}{2}=\frac{1+\cos \alpha}{\sin \alpha} } cot 2 α = sin α 1 + cos α
مثال های اتحاد های مثلثاتی نصف کمان
در این بخش، چند مثال را بررسی میکنیم.
مثال اول اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
2 sin 2 α 2 + cos α 2\,{\sin ^2}\frac{\alpha }{2} + \cos \alpha 2 sin 2 2 α + cos α
حل: با استفاده از سینوس نصف کمان، داریم:
r e q u i r e 2 sin 2 α 2 + cos α = 2 ⋅ 1 − cos α 2 + cos α = 1 − cos α + cos α = 1 require {} 2\, { \sin ^ 2 } \frac { \alpha } { 2 } + \cos \alpha = 2 \cdot \frac { { 1 - \cos \alpha } } { 2 } + \cos \alpha = 1 - { \cos \alpha } + { \cos \alpha } = 1 re q u i re 2 sin 2 2 α + cos α = 2 ⋅ 2 1 − cos α + cos α = 1 − cos α + cos α = 1
مثال دوم اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
1 − cos 2 α sin 2 α \frac{{1 - \cos 2\alpha }}{{\sin 2\alpha }} sin 2 α 1 − cos 2 α
حل: با استفاده از اتحادهایی که یاد گرفتیم، میتون نوشت:
r e q u i r e 1 − cos 2 α sin 2 α = 2 sin 2 α 2 sin α cos α = sin α cos α = tan α require {} \frac{{1 - \cos 2\alpha }}{{\sin 2\alpha }} = \frac{{{2}\,{{\sin }^{2}}\alpha }}{{{2}{\sin \alpha} \cos \alpha }} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha re q u i re sin 2 α 1 − cos 2 α = 2 sin α cos α 2 sin 2 α = cos α sin α = tan α
مثال سوم اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
1 − tan 2 β 2 1 + tan 2 β 2 \frac{{1 - {{\tan }^2}\frac{\beta }{2}}}{{1 + {{\tan }^2}\frac{\beta }{2}}} 1 + tan 2 2 β 1 − tan 2 2 β
حل: از اتحاد تانژانت نصف کمان بهصورت زیر استفاده میکنیم:
tan β 2 = ± 1 − cos β 1 + cos β \tan \frac{\beta }{2} = \pm \sqrt {\frac{{1 - \cos \beta }}{{1 + \cos \beta }}} tan 2 β = ± 1 + cos β 1 − cos β
در نتیجه، خواهیم داشت:
1 − tan 2 β 2 1 + tan 2 β 2 = 1 − 1 − cos β 1 + cos β 1 + 1 − cos β 1 + cos β = 1 + cos β − ( 1 − cos β ) 1 + cos β 1 + cos β + 1 − cos β 1 + cos β = 1 + cos β − 1 + cos β 1 + cos β + 1 − cos β = 2 cos β 2 = cos β \begin {align} \frac { { 1 - { { \tan } ^ 2 } \frac{\beta } { 2 } }} { { 1 + { { \tan } ^ 2 } \frac{\beta } { 2 } } } & = \frac{{1 - \frac{{1 - \cos \beta }}{{1 + \cos \beta }}}}{{1 + \frac{{1 - \cos \beta }}{{1 + \cos \beta }}}} = \frac{{\frac{{1 + \cos \beta - \left( {1 - \cos \beta } \right)}}{{1 + \cos \beta }}}}{{\frac{{1 + \cos \beta + 1 - \cos \beta }}{{1 + \cos \beta }}}} \ & = \frac{{{1} + \cos \beta - {1} + \cos \beta }}{{1 + {\cos \beta} + 1 - {\cos \beta} }} = \frac{{{2}\cos \beta }}{{2}} = \cos \beta \end {align} 1 + tan 2 2 β 1 − tan 2 2 β = 1 + 1 + c o s β 1 − c o s β 1 − 1 + c o s β 1 − c o s β = 1 + c o s β 1 + c o s β + 1 − c o s β 1 + c o s β 1 + c o s β − ( 1 − c o s β ) = 1 + cos β + 1 − cos β 1 + cos β − 1 + cos β = 2 2 cos β = cos β
مثال چهارم اتحاد های مثلثاتی نصف کمان
اتحاد زیر را اثبات کنید:
1 + sin β = 2 cos 2 ( π 4 − β 2 ) 1 + \sin \beta = 2\,{\cos ^2}\left( {\frac{\pi }{4} - \frac{\beta }{2}} \right) 1 + sin β = 2 cos 2 ( 4 π − 2 β )
حل: از اتحاد کسینوس نصف کمان استفاده میکنیم:
2 cos 2 θ 2 = 1 + cos θ 2\,{\cos ^2}\frac{\theta }{2} = 1 + \cos \theta 2 cos 2 2 θ = 1 + cos θ
تساوی زیر را نیز میدانیم:
cos ( π 2 − θ ) = sin θ \cos \left( {\frac{\pi }{2} - \theta } \right) = \sin \theta cos ( 2 π − θ ) = sin θ
عبارت سمت راست تساوی صورت سؤال را بهشکل زیر مینویسیم:
2 cos 2 ( π 4 − β 2 ) = 1 + cos ( π 2 − β ) = 1 + sin β 2\,{\cos ^2}\left( {\frac{\pi }{4} - \frac{\beta }{2}} \right) = 1 + \cos \left( {\frac{\pi }{2} - \beta } \right) = 1 + \sin \beta 2 cos 2 ( 4 π − 2 β ) = 1 + cos ( 2 π − β ) = 1 + sin β
و میبینیم که با عبارت سمت چپ برابر است.
اتحاد های مثلثاتی تبدیل جمع به ضرب
در این بخش، با اتحاد های مثلثاتی تبدیل جمع و تفریق به ضرب آشنا میشویم.
اتحاد های مثلثاتی تبدیل جمع و تفریق سینوس به ضرب
در بخشهای قبل، با فرمول سینوس جمع و تفریق دو زاویه آشنا شدیم:
sin ( x + y ) = sin x cos y + cos x sin y sin ( x − y ) = sin x cos y − cos x sin y \begin {align} \sin \left( {x + y} \right) & = \sin x \cos y + \cos x \sin y \ \sin \left( {x - y} \right) & = \sin x \cos y - \cos x \sin y \end {align} sin ( x + y ) = sin x cos y + cos x sin y sin ( x − y ) = sin x cos y − cos x sin y
این دو معادله را با هم جمع و از هم کم میکنیم:
sin ( x + y ) + sin ( x − y ) = 2 sin x cos y sin ( x + y ) − sin ( x − y ) = 2 cos x sin y \begin {align} \sin \left( {x + y} \right) + \sin \left( {x - y} \right) & = 2\sin x \cos y\ \sin \left( {x + y} \right) - \sin \left( {x - y} \right) & = 2\cos x \sin y \end {align} sin ( x + y ) + sin ( x − y ) = 2 sin x cos y sin ( x + y ) − sin ( x − y ) = 2 cos x sin y
تغیر متغیرهای x + y = α x + y = \alpha x + y = α x − y = β x-y = \beta x − y = β
x = α + β 2 y = α − β 2 x = \frac{{\alpha + \beta }}{2}\,\;\;y = \frac{{\alpha - \beta }}{2} x = 2 α + β y = 2 α − β
اکنون عبارتهای اخیر را در فرمول جایگذاری میکنیم و به اتحادهای مهم زیر میرسیم:
sin α + sin β = 2 sin α + β 2 cos α − β 2 \large \boxed { \sin \alpha+\sin \beta=2 \sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} } sin α + sin β = 2 sin 2 α + β cos 2 α − β
sin α − sin β = 2 cos α + β 2 sin α − β 2 \large \boxed {\sin \alpha-\sin \beta=2 \cos \frac{\alpha+\beta}{2} \sin \frac{\alpha - \beta } { 2 } } sin α − sin β = 2 cos 2 α + β sin 2 α − β
اتحاد های مثلثاتی تبدیل جمع و تفریق کسینوس به ضرب
مشابه روندی که برای تبدیل جمع و تفریق سینوس به ضرب طی کردیم، برای کسینوس به فرمولهای زیر میرسیم:
cos α + cos β = 2 cos α + β 2 cos α − β 2 \large \boxed { \cos \alpha+\cos \beta=2 \cos \frac{\alpha+\beta} { 2 } \cos \frac { \alpha - \beta } { 2 } } cos α + cos β = 2 cos 2 α + β cos 2 α − β
cos α − cos β = − 2 sin α + β 2 sin α − β 2 \large \boxed { \cos \alpha-\cos \beta=-2 \sin \frac{\alpha+\beta}{2} \sin \frac{\alpha-\beta}{2} } cos α − cos β = − 2 sin 2 α + β sin 2 α − β
اتحاد های مثلثاتی تبدیل جمع و تفریق تانژانت به ضرب
جمع تانژانتهای دو زاویه را میتوان بهصورت زیر نوشت:
tan α + tan β = sin α cos α + sin β cos β = sin α cos β + cos α sin β cos α cos β \tan \alpha + \tan \beta = \frac{{\sin \alpha }}{{\cos \alpha }} + \frac { { \sin \beta } } { { \cos \beta } } = \frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta } } { { \cos \alpha \cos \beta } } tan α + tan β = cos α sin α + cos β sin β = cos α cos β sin α cos β + cos α sin β
که با توجه به فرمول سینوس جمع زاویهها، بهصورت زیر درمیآید:
tan α + t a n β = sin ( α + β ) cos α cos β \large \boxed { \tan \alpha+tan \beta=\frac{\sin (\alpha+\beta)}{\cos \alpha \cos \beta} } tan α + t an β = cos α cos β sin ( α + β )
فرمول بالا در حالتی معتبر است که cos α ≠ 0 \cos \alpha \ne 0 cos α = 0 cos β ≠ 0 \cos \beta \ne 0 cos β = 0
بهطور مشابه و با شرایطی که بیان شده، برای تفاضل تانژانتها، داریم:
tan α − t a n β = sin ( α − β ) cos α cos β \large \boxed { \tan \alpha-tan \beta=\frac{\sin (\alpha-\beta)}{\cos \alpha \cos \beta} } tan α − t an β = cos α cos β sin ( α − β )
اتحاد های مثلثاتی تبدیل جمع و تفریق کتانژانت به ضرب
مشابه آنچه برای تانژانتها گفتیم، فرمولهای زیر را با شروط sin α ≠ 0 \sin \alpha \ne 0 sin α = 0 sin β ≠ 0 \sin \beta \ne 0 sin β = 0
cot α + c o t β = sin ( α + β ) sin α sin β \large \boxed { \cot \alpha+cot \beta=\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta} } cot α + co tβ = sin α sin β sin ( α + β )
cot α − c o t β = − f r a c sin ( α − β ) sin α sin β \large \boxed { \cot \alpha-cot \beta=-frac{\sin (\alpha-\beta)}{\sin \alpha \sin \beta} } cot α − co tβ = − f r a c sin ( α − β ) sin α sin β
مثال های اتحاد های مثلثاتی تبدیل جمع به ضرب
در این بخش، چند مثال از مثال های اتحاد های مثلثاتی تبدیل جمع و تفریق به ضرب را حل میکنیم.
مثال اول اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
cos 4 7 ∘ + cos 7 3 ∘ = cos 1 3 ∘ \cos { 4 7 ^ \circ } + \cos { 7 3 ^ \circ } = \cos { 1 3 ^ \circ} cos 4 7 ∘ + cos 7 3 ∘ = cos 1 3 ∘
حل: با استفاده از فرمول جمع کسینوس، داریم:
cos 4 7 ∘ + cos 7 3 ∘ = 2 cos 47 ∘ + 73 ∘ 2 cos 47 ∘ − 73 ∘ 2 = 2 cos 120 ∘ 2 cos − 26 ∘ 2 = 2 cos 6 0 ∘ cos ( − 13 ∘ ) = 2 ⋅ 1 2 ⋅ cos ( − 13 ∘ ) = cos ( − 13 ∘ ) \begin {align} \cos { 4 7 ^ \circ } + \cos { 7 3 ^ \circ } & = 2 \cos \frac { { { { 4 7 } ^ \circ } + { { 7 3 } ^ \circ } } } { 2 } \cos \frac { { { { 4 7 } ^ \circ } - { { 7 3 } ^ \circ } } } { 2 } = 2 \cos \frac { { { { 12 0 } ^ \circ } } } { 2 } \cos \frac { { - { { 2 6 } ^ \circ } } } { 2 } \ & = 2 \cos { 6 0 ^ \circ } \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = 2 \cdot \frac { 1 } { 2 } \cdot \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = \cos \left ( { - { { 1 3 } ^ \circ } } \right ) \end {align} cos 4 7 ∘ + cos 7 3 ∘ = 2 cos 2 47 ∘ + 73 ∘ cos 2 47 ∘ − 73 ∘ = 2 cos 2 120 ∘ cos 2 − 26 ∘ = 2 cos 6 0 ∘ cos ( − 13 ∘ ) = 2 ⋅ 2 1 ⋅ cos ( − 13 ∘ ) = cos ( − 13 ∘ )
میدانیم که تابع کسینوس زوج است. بنابراین، میتوانیم بنویسیم:
cos ( − 13 ∘ ) = cos 1 3 ∘ \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = \cos { 1 3 ^ \circ } cos ( − 13 ∘ ) = cos 1 3 ∘
و اثبات کامل میشود.
مثال دوم اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
sin 8 7 ∘ − sin 2 7 ∘ = cos 5 7 ∘ \begin {align} \sin { 8 7 ^ \circ } - \sin { 2 7 ^ \circ } = \cos { 5 7 ^ \circ } \end {align} sin 8 7 ∘ − sin 2 7 ∘ = cos 5 7 ∘
حل: با کمک اتحاد مثلثاتی تفاضل سینوسها، میتوانیم بنویسیم:
sin 8 7 ∘ − sin 2 7 ∘ = 2 cos 87 ∘ + 27 ∘ 2 sin 87 ∘ − 27 ∘ 2 = 2 cos 114 ∘ 2 sin 60 ∘ 2 = 2 cos 5 7 ∘ sin 3 0 ∘ = 2 ⋅ cos 5 7 ∘ ⋅ 1 2 = cos 5 7 ∘ \begin {align} \sin { 8 7 ^ \circ } - \sin { 2 7 ^ \circ } & = 2 \cos \frac { { { { 8 7 } ^ \circ } + { { 2 7 } ^ \circ } } } { 2 } \sin \frac { { { { 8 7 } ^ \circ } - { { 2 7 } ^ \circ } } } { 2 } \ &= 2 \cos \frac { { { { 1 1 4 } ^ \circ} } } { 2 } \sin \frac { { { { 6 0 } ^ \circ } } } { 2} = 2 \cos { 57 ^ \circ } \sin { 3 0 ^ \circ } \ & = 2 \cdot \cos { 5 7 ^ \circ } \cdot \frac { 1 } { 2 } = \cos { 57 ^ \circ } \end {align} sin 8 7 ∘ − sin 2 7 ∘ = 2 cos 2 87 ∘ + 27 ∘ sin 2 87 ∘ − 27 ∘ = 2 cos 2 114 ∘ sin 2 60 ∘ = 2 cos 5 7 ∘ sin 3 0 ∘ = 2 ⋅ cos 5 7 ∘ ⋅ 2 1 = cos 5 7 ∘
مثال سوم اتحاد های مثلثاتی تبدیل جمع به ضرب
جمع زیر را به ضرب تبدیل کنید.
sin β + cos 2 β − sin 3 β \sin \beta + \cos 2 \beta - \sin 3 \beta sin β + cos 2 β − sin 3 β
حل: با استفاده از فرمول تفاضل سینوسها، داریم:
sin β + cos 2 β − sin 3 β = ( sin β − sin 3 β ) + cos 2 β = 2 cos β + 3 β 2 sin β − 3 β 2 + cos 2 β = 2 cos 2 β sin ( − β ) + cos 2 β = cos 2 β ( 1 − 2 sin β ) \begin {align} \sin \beta + \cos 2 \beta - \sin 3 \beta & = \left ( { \sin \beta - \sin 3 \beta } \right ) + \cos 2 \beta \ & = 2 \cos \frac { { \beta + 3 \beta } } { 2 } \sin \frac { { \beta - 3 \beta } } { 2 } + \cos 2 \beta \ & = 2 \cos 2 \beta \sin \left ( { - \beta } \right ) + \cos 2 \beta \ & = \cos 2 \beta \left ( { 1 - 2 \sin \beta } \right ) \end {align} sin β + cos 2 β − sin 3 β = ( sin β − sin 3 β ) + cos 2 β = 2 cos 2 β + 3 β sin 2 β − 3 β + cos 2 β = 2 cos 2 β sin ( − β ) + cos 2 β = cos 2 β ( 1 − 2 sin β )
مثال چهارم اتحاد های مثلثاتی تبدیل جمع به ضرب
عبارت زیر را ساده کنید:
cos α − cos β sin α + sin β \frac { { \cos \alpha - \cos \beta } } { { \sin \alpha + \sin \beta } } sin α + sin β cos α − cos β
حل: با استفاده از اتحادهای جمع به ضرب، خواهیم داشت:
r e q u i r e cos α − cos β sin α + sin β = − 2 sin α + β 2 sin α − β 2 2 sin α + β 2 cos α − β 2 = − sin α − β 2 cos α − β 2 = − tan α − β 2 require {} \frac { { \cos \alpha - \cos \beta } } { { \sin \alpha + \sin \beta } } = \frac { { - { 2 } { \sin \frac { { \alpha + \beta } } { 2 } } \sin \frac { { \alpha - \beta } } { 2 } }} { { { 2 } { \sin \frac { { \alpha + \beta } } { 2 } } \cos \frac { { \alpha - \beta } } { 2 } } } = - \frac { { \sin \frac { { \alpha - \beta } } { 2 } } } { { \cos \frac { { \alpha - \beta } } { 2 } } } = - \tan \frac { { \alpha - \beta } } { 2 } re q u i re sin α + sin β cos α − cos β = 2 sin 2 α + β cos 2 α − β − 2 sin 2 α + β sin 2 α − β = − cos 2 α − β sin 2 α − β = − tan 2 α − β
مثال پنجم اتحاد های مثلثاتی تبدیل جمع به ضرب
عبارت زیر را ساده کنید.
sin 3 α − sin 7 α cos 4 α + cos 6 α \frac { { \sin 3 \alpha - \sin 7 \alpha } } { { \cos 4 \alpha + \cos 6 \alpha } } cos 4 α + cos 6 α sin 3 α − sin 7 α
حل: این عبارت را با E E E
r e q u i r e E = sin 3 α − sin 7 α cos 4 α + cos 6 α = 2 cos 3 α + 7 α 2 sin 3 α − 7 α 2 2 cos 4 α + 6 α 2 cos 4 α − 6 α 2 = cos 5 α sin ( − 2 α ) cos 5 α cos ( − α ) = sin ( − 2 α ) cos ( − α ) require {} \begin {align} E & = \frac { { \sin 3 \alpha - \sin 7 \alpha } } { { \cos 4 \alpha + \cos 6 \alpha } } = \frac { { { 2 } \cos \frac { { 3 \alpha + 7 \alpha } } { 2 } \sin \frac { { 3 \alpha - 7 \alpha } } { 2 } } } { { { 2 } \cos \frac { { 4 \alpha + 6 \alpha } } { 2 } \cos \frac { { 4 \alpha - 6 \alpha } } { 2 } } } \ & = \frac { { { \cos 5 \alpha } \sin \left ( { - 2 \alpha } \right ) } } { { { \cos 5 \alpha } \cos \left ( { - \alpha } \right ) } } = \frac { { \sin \left ( { - 2 \alpha } \right ) } } { { \cos \left ( { - \alpha } \right ) } } \end {align} re q u i re E = cos 4 α + cos 6 α sin 3 α − sin 7 α = 2 cos 2 4 α + 6 α cos 2 4 α − 6 α 2 cos 2 3 α + 7 α sin 2 3 α − 7 α = cos 5 α cos ( − α ) cos 5 α sin ( − 2 α ) = cos ( − α ) sin ( − 2 α )
تابع سینوس فرد و تابع کسینوس زوج است. از این رو، میتوان نوشت:
E = sin ( − 2 α ) cos ( − α ) = − sin 2 α cos α E = \frac { { \sin \left ( { - 2 \alpha } \right ) } } { { \cos \left ( { - \alpha } \right ) } } = - \frac { { \sin 2 \alpha } } { { \cos \alpha } } E = cos ( − α ) sin ( − 2 α ) = − cos α sin 2 α
با استفاده از اتحاد سینوس دو برابر زاویه، داریم:
E = − sin 2 α cos α = − 2 sin α cos α cos α = − 2 sin α E = - \frac { { \sin 2 \alpha } } { { \cos \alpha } } = - \frac { { 2 \sin \alpha { \cos \alpha } } } { { { \cos \alpha } } } = - 2 \sin \alpha E = − cos α sin 2 α = − cos α 2 sin α cos α = − 2 sin α
مثال ششم اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
cos π 5 + cos 3 π 5 = 1 2 \cos \frac { \pi } { 5 } + \cos \frac { { 3 \pi } } { 5 } = \frac { 1 }{ 2 } cos 5 π + cos 5 3 π = 2 1
حل: ابتدا مجموع کسینوسها را به یک حاصلضرب تبدیل میکنیم:
cos π 5 + cos 3 π 5 = 2 cos π 5 + 3 π 5 2 cos π 5 − 3 π 5 2 = 2 cos 4 π 10 cos ( − 2 π 10 ) = 2 cos 2 π 5 cos π 5 \begin {align} \cos \frac { \pi } { 5 } + \cos \frac { { 3 \pi } } { 5 } & = 2 \cos \frac { { \frac { \pi } { 5 } + \frac { { 3 \pi } }{ 5 } } } { 2 } \cos \frac { { \frac { \pi } { 5 } - \frac { { 3 \pi } } { 5 } } } { 2 } \ & = 2 \cos \frac { { 4 \pi } } { { 1 0 } } \cos \left ( { - \frac { { 2 \pi } } { { 1 0 } } } \right ) = 2 \cos \frac { { 2 \pi } } { 5 } \cos \frac { \pi } { 5 } \end {align} cos 5 π + cos 5 3 π = 2 cos 2 5 π + 5 3 π cos 2 5 π − 5 3 π = 2 cos 10 4 π cos ( − 10 2 π ) = 2 cos 5 2 π cos 5 π
اکنون سمت چپ را در sin π 5 \sin \frac{\pi }{5} sin 5 π
2 cos 2 π 5 cos π 5 sin π 5 sin π 5 = sin 2 π 5 cos 2 π 5 sin π 5 = 2 sin 2 π 5 cos 2 π 5 2 sin π 5 = sin 4 π 5 2 sin π 5 \begin {align} \frac { { 2 \cos \frac { { 2 \pi } } { 5 } \cos \frac { \pi } { 5 } \sin \frac { \pi } { 5 } } } { { \sin \frac { \pi } { 5 } } } & = \frac { { \sin \frac { { 2 \pi } } { 5 } \cos \frac { { 2 \pi } }{ 5 } } } { { \sin \frac { \pi } { 5 } } } \ & = \frac { { 2 \sin \frac { { 2 \pi } } { 5 } \cos \frac { { 2 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { { \sin \frac { { 4 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } } \end {align} sin 5 π 2 cos 5 2 π cos 5 π sin 5 π = sin 5 π sin 5 2 π cos 5 2 π = 2 sin 5 π 2 sin 5 2 π cos 5 2 π = 2 sin 5 π sin 5 4 π
از فرمول زیر استفاده میکنیم:
sin ( π − α ) = sin α \sin \left ( { \pi - \alpha } \right ) = \sin \alpha sin ( π − α ) = sin α
بنابراین، خواهیم داشت:
r e q u i r e sin 4 π 5 2 sin π 5 = sin ( π − π 5 ) 2 sin π 5 = sin π 5 2 sin π 5 = 1 2 require {}\frac { { \sin \frac { { 4 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { { \sin \left ( { \pi - \frac { \pi } { 5 } } \right ) } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { { \sin \frac { \pi } { 5 } } } { { 2 { \sin \frac { \pi } {5 } } } } = \frac { 1 } { 2 } re q u i re 2 sin 5 π sin 5 4 π = 2 sin 5 π sin ( π − 5 π ) = 2 sin 5 π sin 5 π = 2 1
اتحاد های مثلثاتی تبدیل ضرب به جمع
در این بخش، با اتحاد های مثلثاتی تبدیل ضرب به جمع و تفریق آشنا میشویم.
اتحاد مثلثاتی تبدیل ضرب سینوس به جمع
فرمولهای زیر را از قبل میدانیم:
cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β \begin {align} \cos \left( {\alpha + \beta } \right) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \ \cos \left( {\alpha - \beta } \right) & = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end {align} cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β
با کم کردن تساوی دوم از تساوی اول، خواهیم داشت:
cos ( α + β ) − cos ( α − β ) = − 2 sin α sin β \cos \left( {\alpha + \beta } \right) - \cos \left( {\alpha - \beta } \right ) = - 2\sin \alpha \sin \beta cos ( α + β ) − cos ( α − β ) = − 2 sin α sin β
بنابراین، فرمول تبدیل ضرب به جمع برای سینوس بهصورت زیر است:
sin α sin β = 1 2 [ cos ( α − β ) − cos ( α + β ) ] \large \boxed { \sin \alpha \sin \beta=\frac{1}{2}[\cos (\alpha-\beta)-\cos (\alpha+\beta)]} sin α sin β = 2 1 [ cos ( α − β ) − cos ( α + β )]
اتحاد مثلثاتی تبدیل ضرب کسینوس به جمع
اگر اتحادهای مجموع و تفاضل بخش قبل را با هم جمع کنیم، خواهیم داشت:
cos ( α − β ) + cos ( α + β ) = 2 cos α cos β \cos \left( {\alpha - \beta } \right) + \cos \left( {\alpha + \beta } \right) = 2\cos \alpha \cos \beta cos ( α − β ) + cos ( α + β ) = 2 cos α cos β
در نتیجه، به فرمول زیر میرسیم:
cos α cos β = 1 2 [ cos ( α − β ) + cos ( α + β ) ] \large \boxed { \cos \alpha \cos \beta=\frac{1}{2}[\cos (\alpha-\beta)+\cos (\alpha+\beta)]} cos α cos β = 2 1 [ cos ( α − β ) + cos ( α + β )]
اتحاد مثلثاتی تبدیل ضرب سینوس و کسینوس به جمع
به طور مشابه، میتوانیم حاصلضرب سینوس و کسینوس را بهصورت مجموع توابع مثلثاتی بیان کنیم. دو تساوی زیر را با هم جمع میکنیم:
sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β \begin {align} \sin \left( {\alpha + \beta } \right) & = \sin \alpha \cos \beta + \cos \alpha \sin \beta \ \sin \left( {\alpha - \beta } \right) & = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end {align} sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β
و خواهیم داشت:
sin ( α + β ) + sin ( α − β ) = 2 sin α cos β \sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right) = 2\sin \alpha \cos \beta sin ( α + β ) + sin ( α − β ) = 2 sin α cos β
بنابراین، میتوان نوشت:
sin α cos β = 1 2 [ sin ( α − β ) + sin ( α + β ) ] \large \boxed { \sin \alpha \cos \beta=\frac{1}{2}[\sin (\alpha-\beta)+\sin (\alpha+\beta)] } sin α cos β = 2 1 [ sin ( α − β ) + sin ( α + β )]
اتحاد مثلثاتی تبدیل ضرب تانژانت به جمع
فرمولهای زیر را برای تانژانت و کتانژانت داریم:
tan α + tan β = sin ( α + β ) cos α cos β cot α + cot β = sin ( α + β ) sin α sin β \begin {align} \tan \alpha + \tan \beta & = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \alpha \cos \beta }} \ \cot \alpha + \cot \beta & = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha \sin \beta }} \end {align} tan α + tan β = cos α cos β sin ( α + β ) cot α + cot β = sin α sin β sin ( α + β )
دو اتحاد را بر هم تقسیم میکنیم:
r e q u i r e tan α + tan β cot α + cot β = sin ( α + β ) cos α cos β sin ( α + β ) sin α sin β = sin ( α + β ) ⋅ sin α sin β cos α cos β ⋅ sin ( α + β ) = sin α sin β cos α cos β = tan α tan β \begin {align} require{} \frac{{\tan \alpha + \tan \beta }}{{\cot \alpha + \cot \beta }} & = \frac{{\frac{{\sin \left( {\alpha + \beta } \right ) } } { { \cos \alpha \cos \beta }}}}{{\frac{{\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha \sin \beta }}}} = \frac{{ { \sin \left( {\alpha + \beta } \right)} \cdot \sin \alpha \sin \beta }}{{\cos \alpha \cos \beta \cdot {\sin \left( {\alpha + \beta } \right)}}} \ &= \frac{{\sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }} = \tan \alpha \tan \beta \end {align} re q u i re cot α + cot β tan α + tan β = s i n α s i n β s i n ( α + β ) c o s α c o s β s i n ( α + β ) = cos α cos β ⋅ sin ( α + β ) sin ( α + β ) ⋅ sin α sin β = cos α cos β sin α sin β = tan α tan β
بنابراین، خواهیم داشت:
tan α tan β = tan α + t a n β cot α + cot β \large \boxed { \tan \alpha \tan \beta=\frac{\tan \alpha+tan \beta}{\cot \alpha + \cot \beta } } tan α tan β = cot α + cot β tan α + t an β
اتحاد مثلثاتی تبدیل ضرب کتانژانت به جمع
از آنجا که cot θ = 1 tan θ \cot \theta = \frac{1}{{\tan \theta }} cot θ = tan θ 1
cot α cot β = 1 tan α tan β = cot α + cot β tan α + tan β \cot \alpha \cot \beta = \frac{1}{{\tan \alpha \tan \beta }} = \frac{{\cot \alpha + \cot \beta } } { { \tan \alpha + \tan \beta } } cot α cot β = tan α tan β 1 = tan α + tan β cot α + cot β
در نتیجه، داریم:
cot α cot β = cot α + cot β tan α + tan β \large \boxed { \cot \alpha \cot \beta = \frac{{\cot \alpha + \cot \beta } } { { \tan \alpha + \tan \beta } } } cot α cot β = tan α + tan β cot α + cot β
اتحاد مثلثاتی تبدیل ضرب تانژانت در کتانژانت به جمع
از فرمول بخش قبل استفاده میکنیم و تغییر متغیر β → π 2 − β \beta \to \frac{\pi }{2} - \beta β → 2 π − β
tan ( π 2 − β ) = cot β t e x t c o t ( π 2 − β ) = tan β \tan \left( {\frac{\pi }{2} - \beta } \right) = \cot \beta\;\;text{\,}\;\;cot \left( {\frac{\pi }{2} - \beta } \right) = \tan \beta tan ( 2 π − β ) = cot β t e x t co t ( 2 π − β ) = tan β
بنابراین، میتوانیم بنویسیم:
tan α cot β = tan α tan ( π 2 − β ) = tan α + tan ( π 2 − β ) cot α + cot ( π 2 − β ) = tan α + cot β cot α + tan β \tan \alpha \cot \beta = \tan \alpha \tan \left( {\frac{\pi }{2} - \beta } \right) = \frac{{\tan \alpha + \tan \left( {\frac{\pi }{2} - \beta } \right)}}{{\cot \alpha + \cot \left( {\frac{\pi }{2} - \beta } \right ) } } = \frac { { \tan \alpha + \cot \beta } } { { \cot \alpha + \tan \beta } } tan α cot β = tan α tan ( 2 π − β ) = cot α + cot ( 2 π − β ) tan α + tan ( 2 π − β ) = cot α + tan β tan α + cot β
در نتیجه:
tan α cot β = tan α + c o t β cot α + tan β \large \boxed { \tan \alpha \cot \beta=\frac{\tan \alpha+cot \beta}{\cot \alpha + \tan \beta } } tan α cot β = cot α + tan β tan α + co tβ
مثال های اتحاد های مثلثاتی تبدیل ضرب به جمع
در این بخش، چند مثال را از اتحاد های مثلثاتی تبدیل ضرب به جمع بررسی میکنیم.
مثال اول اتحاد های مثلثاتی تبدیل ضرب به جمع
عبارت cos 4 α cos 6 α \cos 4\alpha \cos 6\alpha cos 4 α cos 6 α
حل: با استفاده از فرمولهای ضرب کسینوسها میتوان نوشت:
cos 4 α cos 6 α = 1 2 [ cos ( 4 α − 6 α ) + cos ( 4 α + 6 α ) ] = 1 2 [ cos ( − 2 α ) + cos 10 α ] = 1 2 cos 2 α + 1 2 cos 10 α \begin {align} \cos 4\alpha \cos 6\alpha & = \frac{1}{2}\left[ {\cos \left( {4\alpha - 6\alpha } \right) + \cos \left( {4\alpha + 6\alpha } \right)} \right] \ & = \frac{1}{2}\left[ {\cos \left( { - 2\alpha } \right) + \cos 10\alpha } \right] \ &= \frac{1}{2}\cos 2\alpha + \frac{1}{2}\cos 10\alpha \end {align} cos 4 α cos 6 α = 2 1 [ cos ( 4 α − 6 α ) + cos ( 4 α + 6 α ) ] = 2 1 [ cos ( − 2 α ) + cos 10 α ] = 2 1 cos 2 α + 2 1 cos 10 α
مثال دوم اتحاد های مثلثاتی تبدیل ضرب به جمع
ضرب زیر را با جمع توابع مثلثاتی نشان دهید:
sin α sin 2 α sin 3 α \sin \alpha \sin 2\alpha \sin 3\alpha sin α sin 2 α sin 3 α
حل: این عبارت را با E E E sin α sin 3 α \sin \alpha\sin 3\alpha sin α sin 3 α
sin α sin 3 α = 1 2 [ cos ( α − 3 α ) − cos ( α + 3 α ) ] = 1 2 [ cos ( − 2 α ) − cos 4 α ] = 1 2 ( cos 2 α − cos 4 α ) \begin {align} \sin \alpha \sin 3\alpha & = \frac{1}{2}\left[ {\cos \left( {\alpha - 3\alpha } \right) - \cos \left( {\alpha + 3\alpha } \right)} \right] \ &= \frac{1}{2}\left[ {\cos \left( { - 2\alpha } \right) - \cos 4\alpha } \right] = \frac { 1 } { 2 } \left ( { \cos 2\alpha - \cos 4\alpha } \right) \end {align} sin α sin 3 α = 2 1 [ cos ( α − 3 α ) − cos ( α + 3 α ) ] = 2 1 [ cos ( − 2 α ) − cos 4 α ] = 2 1 ( cos 2 α − cos 4 α )
سپس، عبارت اصلی را اینگونه مینویسیم:
E = sin α sin 2 α sin 3 α = sin 2 α ⋅ 1 2 ( cos 2 α − cos 4 α ) = 1 2 sin 2 α cos 2 α − 1 2 sin 2 α cos 4 α \begin {align} E & = \sin \alpha \sin 2\alpha \sin 3\alpha = \sin 2\alpha \cdot \frac { 1 } { 2 } \left ( { \cos 2\alpha - \cos 4\alpha } \right ) \ & = \frac { 1 } { 2} \sin 2\alpha \cos 2\alpha - \frac{1}{2}\sin 2\alpha \cos 4 \alpha \end {align} E = sin α sin 2 α sin 3 α = sin 2 α ⋅ 2 1 ( cos 2 α − cos 4 α ) = 2 1 sin 2 α cos 2 α − 2 1 sin 2 α cos 4 α
داریم:
sin 2 α cos 2 α = 1 2 sin 4 α \sin 2\alpha \cos 2\alpha = \frac{1}{2}\sin 4\alpha sin 2 α cos 2 α = 2 1 sin 4 α
و
sin 2 α cos 4 α = 1 2 [ sin ( 2 α − 4 α ) + sin ( 2 α + 4 α ) ] = 1 2 [ sin ( − 2 α ) + sin 6 α ] = 1 2 sin 6 α − 1 2 sin 2 α \begin {align} \sin 2\alpha \cos 4\alpha & = \frac{1}{2}\left[ {\sin \left( {2\alpha - 4\alpha } \right) + \sin \left( {2\alpha + 4\alpha } \right)} \right] \ &= \frac{1}{2}\left[ {\sin \left( { - 2\alpha } \right) + \sin 6\alpha } \right] = \frac{1}{2}\sin 6\alpha - \frac{1}{2}\sin 2\alpha \end {align} sin 2 α cos 4 α = 2 1 [ sin ( 2 α − 4 α ) + sin ( 2 α + 4 α ) ] = 2 1 [ sin ( − 2 α ) + sin 6 α ] = 2 1 sin 6 α − 2 1 sin 2 α
در نتیجه، حاصل عبارت بهصورت زیر خواهد بود:
E = 1 2 ⋅ 1 2 sin 4 α − 1 2 ( 1 2 sin 6 α − 1 2 sin 2 α ) = 1 4 sin 2 α + 1 4 sin 4 α − 1 4 sin 6 α \begin {align} E & = \frac{1}{2} \cdot \frac{1}{2}\sin 4\alpha - \frac{1}{2} \left( {\frac { 1 } { 2 } \sin 6\alpha - \frac{1}{2}\sin 2\alpha } \right) \ & = \frac { 1 } { 4 } \sin 2\alpha + \frac { 1 } { 4 } \sin 4 \alpha - \frac { 1 } { 4 } \sin 6 \alpha \end {align} E = 2 1 ⋅ 2 1 sin 4 α − 2 1 ( 2 1 sin 6 α − 2 1 sin 2 α ) = 4 1 sin 2 α + 4 1 sin 4 α − 4 1 sin 6 α
مثال سوم اتحاد های مثلثاتی تبدیل ضرب به جمع
عبارت 2 sin 1 0 ∘ cos 10 0 ∘ 2\sin 10^\circ \cos 100^\circ 2 sin 1 0 ∘ cos 10 0 ∘
حل: با استفاده از فرمولهایی که گفتیم، میتوانیم بنویسیم:
2 sin 1 0 ∘ cos 10 0 ∘ = 2 ⋅ 1 2 [ sin ( 10 ∘ − 100 ∘ ) + sin ( 10 ∘ + 100 ∘ ) ] = sin ( − 90 ∘ ) + sin 11 0 ∘ . \begin {align} 2 \sin {10 ^ \circ } \cos {100 ^ \circ} & = 2 \cdot \frac{1}{2}\left[ {\sin \left( {{{10}^\circ} - {{100}^\circ}} \right) + \sin \left( {{{10}^\circ} + {{100}^\circ}} \right)} \right] \ &= \sin \left( { - {{90}^\circ}} \right) + \sin {110^\circ}. \end {align} 2 sin 1 0 ∘ cos 10 0 ∘ = 2 ⋅ 2 1 [ sin ( 10 ∘ − 100 ∘ ) + sin ( 10 ∘ + 100 ∘ ) ] = sin ( − 90 ∘ ) + sin 11 0 ∘ .
میدانیم:
sin ( − 90 ∘ ) = − sin 9 0 ∘ = − 1 sin 11 0 ∘ = sin ( 180 ∘ − 110 ∘ ) = sin 7 0 ∘ \sin \left( { - {{90}^\circ}} \right) = - \sin {90^\circ} = - 1\ \sin {110^\circ} = \sin \left( {{{180}^\circ} - {{110}^\circ}} \right) = \sin {70^\circ} sin ( − 90 ∘ ) = − sin 9 0 ∘ = − 1 sin 11 0 ∘ = sin ( 180 ∘ − 110 ∘ ) = sin 7 0 ∘
در نهایت، خواهیم داشت:
2 sin 1 0 ∘ cos 10 0 ∘ = sin 7 0 ∘ − 1 2\sin {10^\circ}\cos {100^\circ} = \sin {70^\circ} - 1 2 sin 1 0 ∘ cos 10 0 ∘ = sin 7 0 ∘ − 1
مثال چهارم اتحاد های مثلثاتی تبدیل ضرب به جمع
ضرب زیر را به جمع تبدیل کنید:
cos ( α + β ) cos ( α − β ) \cos \left ( {\alpha + \beta } \right ) \cos \left( {\alpha - \beta } \right ) cos ( α + β ) cos ( α − β )
حل: از اتحاد ضرب کسینوسها استفاده میکنیم و خواهیم داشت:
cos ( α + β ) cos ( α − β ) = 1 2 cos [ ( α − β ) − ( α + β ) ] + 1 2 cos [ ( α − β ) + ( α + β ) ] = 1 2 cos ( α − β − α − β ) + 1 2 cos ( α − β + α + β ) = 1 2 cos ( − 2 β ) + 1 2 cos 2 α = 1 2 cos 2 α + 1 2 cos 2 β \begin {align} \cos \left ( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right) & = \frac{1}{2}\cos \left[ {\left( {\alpha - \beta } \right) - \left( {\alpha + \beta } \right)} \right] + \frac{1}{2}\cos \left[ {\left( {\alpha - \beta } \right) + \left( {\alpha + \beta } \right)} \right] \ &= \frac{1}{2}\cos \left( {{\alpha} - \beta - {\alpha} - \beta } \right) + \frac{1}{2}\cos \left( {\alpha - {\beta} + \alpha + {\beta} } \right) \ &= \frac{1}{2}\cos \left( { - 2\beta } \right) + \frac{1}{2}\cos 2\alpha = \frac{1}{2}\cos 2\alpha + \frac{1}{2}\cos 2\beta \end {align} cos ( α + β ) cos ( α − β ) = 2 1 cos [ ( α − β ) − ( α + β ) ] + 2 1 cos [ ( α − β ) + ( α + β ) ] = 2 1 cos ( α − β − α − β ) + 2 1 cos ( α − β + α + β ) = 2 1 cos ( − 2 β ) + 2 1 cos 2 α = 2 1 cos 2 α + 2 1 cos 2 β
خلاصه اتحاد های مثلثاتی
در این آموزش، اتحادهای مثلثاتی را معرفی کردیم و علاوه بر روش بهدست آوردن آنها، مثالهای متنوعی را نیز بررسی کردیم. در این بخش، فهرستی خلاصه از مهمترین اتحادها را آوردهایم که میتوانید در صورت نیاز از آنها استفاده کنید.
نسبتهای مثلثاتی:
$$ \large \boxed { \begin {array} {\ll}
\tan \theta = \frac { \sin \theta } { \cos \theta } &\; \cot \theta = \frac { 1 } { \tan \theta } = \frac { \cos \theta } { \sin \theta } \
\sec \theta = \frac { 1 } { \cos \theta } &\; \csc \theta = \frac { 1 } { \sin \theta }
\end {array} } $$
اتحاد فیثاغورسی:
sin 2 θ + cos 2 θ = 1 \large \boxed { \sin ^ { 2 } \theta + \cos ^ { 2 } \theta = 1 } sin 2 θ + cos 2 θ = 1
نسبتهای مثلثاتی متمم زاویه:
cos θ = sin ( π 2 − θ ) sin θ = cos ( π 2 − θ ) cot θ = tan ( π 2 − θ ) tan θ = cot ( π 2 − θ ) csc θ = sec ( π 2 − θ ) sec θ = csc ( π 2 − θ ) \large \begin{array} {|ll|} \hline \cos \theta = \sin \left ( \frac { \pi } { 2 } - \theta \right ) &\; \sin \theta = \cos \left ( \frac { \pi } { 2 } - \theta \right ) \ \cot \theta = \tan \left ( \frac { \pi } { 2 } - \theta \right ) &\; \tan \theta = \cot \left ( \frac { \pi } { 2 } - \theta \right ) \ \csc \theta = \sec \left ( \frac { \pi } { 2 } - \theta \right ) &\; \sec \theta = \csc \left ( \frac { \pi } { 2 } - \theta \right ) \\ \hline \end {array} cos θ = sin ( 2 π − θ ) sin θ = cos ( 2 π − θ ) cot θ = tan ( 2 π − θ ) tan θ = cot ( 2 π − θ ) csc θ = sec ( 2 π − θ ) sec θ = csc ( 2 π − θ )
تناوب نسبتهای مثلثاتی:
sin ( θ + 2 π ) = sin θ cos ( θ + 2 π ) = cos θ tan ( θ + π ) = tan θ cot ( θ + π ) = cot θ \large \boxed { \begin {aligned} \sin ( \theta + 2 \pi ) & = \sin \theta \ \cos ( \theta + 2 \pi ) & = \cos \theta \ \tan ( \theta + \pi ) & = \tan \theta \ \cot ( \theta + \pi ) & = \cot \theta \end {aligned} } sin ( θ + 2 π ) = sin θ cos ( θ + 2 π ) = cos θ tan ( θ + π ) = tan θ cot ( θ + π ) = cot θ
نسبتهای مثلثاتی زاویه منفی:
sin ( − θ ) = − sin θ cos ( − θ ) = cos θ tan ( − θ ) = − tan θ cot ( − θ ) = − cot θ \large \boxed { \begin {aligned} \sin ( - \theta ) & = - \sin \theta \ \cos ( - \theta ) & = \cos \theta \ \tan ( - \theta ) & = - \tan \theta \ \cot ( - \theta ) & = - \cot \theta \ \end {aligned} } sin ( − θ ) = − sin θ cos ( − θ ) = cos θ tan ( − θ ) = − tan θ cot ( − θ ) = − cot θ
سینوس و کسینوس جمع و تفریق دو زاویه:
sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α − β ) = cos α cos β + sin α sin β \large \boxed { \begin {aligned} & \sin ( \alpha + \beta ) = \sin \alpha \cos \beta+\cos \alpha \sin \beta \ & \cos ( \alpha + \beta ) = \cos \alpha \cos \beta-\sin \alpha \sin \beta \ & \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \ & \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end {aligned} } sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α − β ) = cos α cos β + sin α sin β
سینوس دو برابر زاویه:
sin 2 θ = 2 sin θ cos θ \large \boxed { \sin 2 \theta = 2 \sin \theta \cos \theta } sin 2 θ = 2 sin θ cos θ
کسینوس دو برابر زاویه:
cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ \large \boxed { \begin {aligned} \cos 2 \theta & = \cos ^ { 2 } \theta - \sin ^ { 2 } \theta \ & = 2 \cos ^ { 2 } \theta - 1 \ & = 1 - 2 \sin ^ { 2 } \theta \end {aligned} } cos 2 θ = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ
رابطه سکانت و تانژانت:
sec 2 θ = 1 + tan 2 θ \large \boxed { \sec ^ { 2 } \theta = 1 + \tan ^ { 2 } \theta } sec 2 θ = 1 + tan 2 θ
نسبتهای مثلثاتی مکمل زاویه:
sin ( π − θ ) = sin θ cos ( π − θ ) = − cos θ tan ( π − θ ) = − tan θ cot ( π − θ ) = − cot θ \large \boxed { \begin {gathered} \sin ( \pi - \theta ) = \sin \theta \ \cos ( \pi - \theta ) = - \cos \theta \ \tan ( \pi - \theta ) = - \tan \theta \ \cot ( \pi - \theta ) = - \cot \theta \end {gathered} } sin ( π − θ ) = sin θ cos ( π − θ ) = − cos θ tan ( π − θ ) = − tan θ cot ( π − θ ) = − cot θ
تانژانت جمع و تفریق و دو برابر زاویه:
tan 2 θ = 2 tan θ 1 − tan 2 θ tan ( α + β ) = tan α + tan β 1 − t a n α tan β tan ( α − β ) = tan α − tan β 1 + tan α tan β \large \boxed { \begin {aligned} \tan 2 \theta & = \frac { 2 \tan \theta } { 1 - \tan ^ { 2 } \theta } \ \tan ( \alpha + \beta ) & = \frac { \tan \alpha + \tan \beta } { 1 -tan \alpha \tan \beta } \ \tan ( \alpha - \beta ) & = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta } \end {aligned} } tan 2 θ = 1 − tan 2 θ 2 tan θ tan ( α + β ) = 1 − t an α tan β tan α + tan β tan ( α − β ) = 1 + tan α tan β tan α − tan β
نسبتهای مثلثاتی نصف کمان:
sin θ 2 = ± 1 − cos θ 2 cos θ 2 = ± 1 + cos θ 2 tan θ 2 = sin θ 1 + cos θ = 1 − cos θ sin θ cot θ 2 = 1 + cos θ sin θ = sin θ 1 − cos θ \large \boxed { \begin {aligned} \sin \frac { \theta } { 2 } & = \pm \sqrt { \frac { 1 - \cos \theta } { 2 } } \ \cos \frac { \theta } { 2 } & = \pm \sqrt { \frac { 1 + \cos \theta } { 2 } } \ \tan \frac { \theta } { 2 } & = \frac { \sin \theta } { 1 + \cos \theta } = \frac { 1 - \cos \theta } { \sin \theta } \ \cot \frac { \theta } { 2 } & = \frac { 1 + \cos \theta } {\sin \theta} = \frac { \sin \theta } {1 - \cos \theta } \end {aligned} } sin 2 θ = ± 2 1 − cos θ cos 2 θ = ± 2 1 + cos θ tan 2 θ = 1 + cos θ sin θ = sin θ 1 − cos θ cot 2 θ = sin θ 1 + cos θ = 1 − cos θ sin θ
تبدیل جمع و تفریق به ضرب:
sin α + sin β = 2 sin α + β 2 cos α − β 2 cos α + cos β = 2 cos α + β 2 cos α − β 2 sin α − sin β = 2 cos α + β 2 sin α − β 2 cos α − cos β = − 2 sin α + β 2 sin α − β 2 \large \boxed { \begin {aligned} & \sin \alpha + \sin \beta = 2 \sin \frac { \alpha + \beta } { 2 } \cos \frac { \alpha - \beta } { 2 } \ & \cos \alpha + \cos \beta = 2 \cos \frac { \alpha + \beta } { 2 } \cos \frac { \alpha - \beta } { 2 } \ & \sin \alpha - \sin \beta = 2 \cos \frac { \alpha + \beta } { 2 } \sin \frac { \alpha - \beta } { 2 } \ & \cos \alpha - \cos \beta = - 2 \sin \frac { \alpha + \beta } { 2 } \sin \frac { \alpha - \beta } { 2 } \end {aligned} } sin α + sin β = 2 sin 2 α + β cos 2 α − β cos α + cos β = 2 cos 2 α + β cos 2 α − β sin α − sin β = 2 cos 2 α + β sin 2 α − β cos α − cos β = − 2 sin 2 α + β sin 2 α − β
تبدیل ضرب به جمع و تفریق:
sin α cos β = sin ( α + β ) + sin ( α − β ) 2 cos α cos β = cos ( α + β ) + cos ( α − β ) 2 sin α sin β = cos ( α − β ) − cos ( α + β ) 2 \large \boxed { \begin {aligned} \sin \alpha \cos \beta & = \frac { \sin ( \alpha + \beta ) + \sin ( \alpha - \beta ) } { 2 } \ \cos \alpha \cos \beta & = \frac { \cos ( \alpha + \beta ) + \cos ( \alpha - \beta ) } { 2 } \ \sin \alpha \sin \beta & = \frac { \cos ( \alpha - \beta ) - \cos ( \alpha + \beta ) } { 2 } \end {aligned} } sin α cos β = 2 sin ( α + β ) + sin ( α − β ) cos α cos β = 2 cos ( α + β ) + cos ( α − β ) sin α sin β = 2 cos ( α − β ) − cos ( α + β )
نسبتهای مثلثاتی سه برابر زاویه:
sin 3 θ = 3 sin θ − 4 sin 3 θ cos 3 θ = 4 cos 3 θ − 3 cos θ tan 3 θ = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ cot 3 θ = cot 3 θ – 3 cot θ 3 cot 2 θ – 1 \large \boxed { \begin {aligned} \sin 3 \theta & = 3 \sin \theta - 4 \sin ^ { 3 } \theta \ \cos 3 \theta & = 4 \cos ^ { 3 } \theta - 3 \cos \theta \ \tan 3 \theta & = \frac { 3 \tan \theta - \tan ^ { 3 } \theta } { 1 - 3 \tan ^ { 2 } \theta } \ \cot 3 \theta &= \frac { { { { \cot } ^ 3 } \theta – 3 \cot \theta } } { { 3 \, { { \cot } ^ 2 } \theta – 1 } } \end {aligned} } sin 3 θ = 3 sin θ − 4 sin 3 θ cos 3 θ = 4 cos 3 θ − 3 cos θ tan 3 θ = 1 − 3 tan 2 θ 3 tan θ − tan 3 θ cot 3 θ = 3 cot 2 θ –1 cot 3 θ –3 cot θ
۱. در مثلث قائمالزاویه، نسبتهای تانژانت و کوتانژانت با چه تعریفی از اضلاع معرفی میشوند؟
تانژانت برابر است با تقسیم ضلع مجاور بر وتر، کوتانژانت برابر است با تقسیم وتر بر ضلع مقابل.
تانژانت برابر است با تقسیم ضلع مقابل بر ضلع مجاور، کوتانژانت برابر است با تقسیم ضلع مجاور بر ضلع مقابل.
تانژانت برابر است با تقسیم وتر بر ضلع مجاور، کوتانژانت برابر است با تقسیم ضلع مجاور بر وتر.
تانژانت برابر است با تقسیم وتر بر ضلع مقابل، کوتانژانت برابر است با تقسیم ضلع مقابل بر ضلع مجاور.
مشاهده گزینه صحیح
در مثلث قائمالزاویه، برای یک زاویه تند، نسبت تانژانت با تقسیم طول ضلع مقابل آن زاویه بر ضلع مجاور تعریف میشود و کوتانژانت با نسبت ضلع مجاور به ضلع مقابل معرفی میشود.
۲. فرمول پایه فیثاغورسی sin²α + cos²α = 1 چگونه و بر اساس چه مفهومی اثبات میشود؟
با فرمول جمع و تفریق زاویهها میتوان آن را ثابت کرد.
استدلال جبری بر مبنای جدول زوایای مهم این اتحاد را میدهد.
به کمک خاصیت تناوب توابع سینوس و کسینوس بهدست میآید.
بر اساس رابطه اضلاع در مثلث قائمالزاویه و قضیه فیثاغورس اثبات میشود.
مشاهده گزینه صحیح
در اثبات فرمول sin²α + cos²α = 1، از رابطه اضلاع مثلث قائمالزاویه و قضیه فیثاغورس استفاده میشود. چون نسبت سینوس و کسینوس به اضلاع روبهرو و مجاور تقسیم بر وتر مربوط میشوند و طبق قضیه فیثاغورس مجموع مربع این دو ضلع برابر مربع وتر است، جمع مربع سینوس و کسینوس برابر یک خواهد بود.
۳. برای اثبات اتحاد tan²α + 1 = sec²α معمولا چه نسبتی بین دو طرف اتحاد فیثاغورسی sin²α + cos²α = 1 برقرار میشود؟
هر دو طرف را بر cos²α تقسیم میکنند.
هر دو طرف را بر sec²α تقسیم میکنند.
هر دو طرف را بر sin²α تقسیم میکنند.
هر دو طرف را بر tan²α تقسیم میکنند.
مشاهده گزینه صحیح
برای رسیدن به رابطه tan²α + 1 = sec²α، باید هر دو طرف اتحاد فیثاغورسی "sin²α + cos²α = 1" را بر "cos²α" تقسیم کنیم. این کار باعث میشود سمت چپ عبارت به "tan²α + 1" و سمت راست به "sec²α" تبدیل شود و اتحاد جدید به دست آید.
۴. اگر مقدار cos(α) برای یک زاویه α در ربع اول داده باشد، برای یافتن مقدار sin(α) با استفاده از اتحاد فیثاغورسی کدام روش صحیح است؟
مقدار sin(α) را مستقیما برابر ۱ منهای cos(α) قرار میدهیم.
فرمول tan(α) = cos(α) را استفاده و مقدار را جایگذاری میکنیم.
مقدار sin(α) را با همان مقدار cos(α) برابر قرار میدهیم.
از فرمول sin²α = 1 - cos²α استفاده و ریشه مثبت را انتخاب میکنیم.
مشاهده گزینه صحیح
اگر زاویه α در ربع اول باشد، مقدار sin(α) مثبت است. باید از اتحاد فیثاغورسی یعنی «sin²α + cos²α = ۱» استفاده کنیم و با جایگذاری cos(α)، داریم sin²α = ۱ - cos²α. سپس چون در ربع اول هستیم، فقط ریشه مثبت را برای sin(α) انتخاب میکنیم.
۵. ویژگی تناوبی توابع سینوس و کسینوس چیست و این ویژگی چگونه موجب سادهتر شدن محاسبات عبارات مثلثاتی میشود؟
افزایش زاویه ورودی همیشه مقدار تابع را افزایش میدهد و فرمولهای سادهتری بهدست میآید.
تابع Sin فقط تناوب ۴π دارد ولی کسینوس هیچ تناوب مشخصی ندارد.
تناوب این توابع فقط در زوایای زوج رخ میدهد و برای زوایای فرد باید فرمول جدا نوشت.
این توابع با افزودن هر ۲π به زاویه مقدارشان ثابت میماند و میتوان زاویه را به بازه ۰ تا ۲π محدود کرد.
مشاهده گزینه صحیح
در توابع مثلثاتی سینوس و کسینوس، با اضافه شدن هر ۲π به زاویه، مقدار تابع تغییر نمیکند. یعنی sin(θ) = sin(θ+2π) و cos(θ) = cos(θ+2π). این ویژگی تناوبی باعث میشود بتوان هر زاویه را به زاویهای بین ۰ تا ۲π یا یک زاویه مرجع کاهش داد و محاسبات راحتتر و کوتاهتر انجام شود.
۶. اگر sin(θ) را بدانیم، بهترین راه برای یافتن sin(θ+2π) چیست؟
استفاده از فرمول جمع زاویه و جایگذاری مقدار اولیه
تقسیم مقدار sin(θ) بر مقدار cos(2π) برای یافتن مقدار جدید
استفاده از جدول نسبتهای مثلثاتی برای محاسبه مقدار جدید
در نظر گرفتن خاصیت تناوب توابع مثلثاتی و برابر گرفتن مقدار دو زاویه
مشاهده گزینه صحیح
تابع سینوس (Sin) دارای خاصیت تناوبی با پریود ۲π است، بنابراین مقدار sin(θ+2π) همواره با مقدار sin(θ) برابر است. استفاده از این خاصیت سریعترین و دقیقترین راه برای محاسبه مقدار sin(θ+2π) است. استفاده از جدول فقط برای زوایای خاص کاربرد دارد و فرمول جمع زاویه هم در این حالت ساده میشود اما نیازمند محاسبه مقدار cos(2π) و sin(2π) خواهد بود. تقسیم sin(θ) بر cos(2π) معنای مرتبط با مقدار sin(θ+2π) ندارد.
۷. فرمول جمع دو زاویه برای سینوس چیست و این اتحاد معمولا در چه نوع مسائلی سادهسازی ایجاد میکند؟
سینوس جمع دو زاویه برابر است با sin(A+B)=sin A cos B + cos A sin B و در تبدیل و اثبات روابط مثلثاتی کاربرد مهمی دارد.
سینوس جمع دو زاویه برابر است با حاصل جمع سینوس هر دو زاویه
سینوس جمع دو زاویه فقط برای محاسبه زاویههای خاص مورد استفاده است.
سینوس جمع دو زاویه از ضرب سینوسهای دو زاویه به دست میآید.
مشاهده گزینه صحیح
فرمول جمع دو زاویه برای سینوس به صورت «sin(A+B)=sin A cos B + cos A sin B» بیان میشود. این اتحاد در تبدیل و سادهسازی عبارات پیچیده مثلثاتی بسیار کاربرد دارد، مخصوصا هنگام اثبات روابط جبری، محاسبه با زاویههای دلخواه یا کاهش پیچیدگی عبارات در مسائل پیشرفته.
۸. در چه شرایطی استفاده از اتحاد جمع زاویه برای cos(α+β) میتواند کمک به سادهتر شدن محاسبات کند؟
وقتی که مقادیر سینوس و کسینوس جداگانه زاویههای α و β در دسترس باشد.
وقتی هیچکدام از نسبتهای مثلثاتی زاویههای α یا β مشخص نباشد.
زمانی که زاویههای α و β برابر با هم باشند.
هنگامی که فقط مقدار کسینوس مجموع زاویهها معلوم باشد.
مشاهده گزینه صحیح
کاربرد اتحاد جمع زاویه برای کسینوس زمانی مفید است که مقادیر سینوس (Sin) و کسینوس (Cos) زاویههای α و β به طور جداگانه موجود باشند، زیرا فرمول جمع زاویه کسینوس cos(α+β) را به صورت ترکیبی از سینوس و کسینوس این دو زاویه ارائه میکند و این باعث سادگی و سرعت حل عبارت میشود.
۹. تبدیل عبارات حاوی دو برابر کمان مانند sin(2α) و cos(2α) چه هدفی دارد و از چه فرمولهایی برای این کار استفاده میشود؟
سادهسازی محاسبات توسط فرمولهای دو برابر کمان
تحلیل تناوب تابع با تبدیل به جمع زاویهها
بدست آوردن مقدار دقیق تابع معکوس با استفاده از جدول
یافتن مشتق توابع با روش فیثاغورسی
مشاهده گزینه صحیح
هدف اصلی تبدیل عبارات مانند sin(2α) و cos(2α) سادهسازی محاسبات است و این کار با استفاده از فرمولهای دو برابر کمان انجام میشود. این فرمولها مستقیما از اتحادهای جمع زاویه استخراج میشوند و در سادهتر کردن عبارات یا محاسبه مقادیر مختلف توابع مثلثاتی کاربرد دارند.
۱۰. برای محاسبه عددی sin(2α) وقتی مقدار sin(α) و cos(α) داده شده است، مناسبترین روش با توجه به اتحادهای مثلثاتی چیست؟
استفاده از جدول مقدار توابع برای زوایای خاص
تبدیل sin(2α) به tan(α) و استفاده از tan(2α)
استفاده از فرمول sin(2α) = 2sin(α)cos(α) و جایگذاری مستقیم مقادیر
محاسبه sin²(α) و اضافه کردن آن به cos²(α)
مشاهده گزینه صحیح
وقتی sin(α) و cos(α) داده شده باشد، بهترین راه استفاده از اتحاد اصلی دو برابر کمان است که میگوید sin(2α) برابر ۲ برابر sin(α) ضربدر cos(α) است. بنابراین، باید مقدار sin(α) و cos(α) را در هم ضرب کرد و نتیجه را دو برابر کرد.
۱۱. کدام گزینه بهترین روش استخراج فرمولهای نصف کمان برای سینوس و کسینوس را بیان میکند و به نکته کلیدی انتخاب علامت اشاره دارد؟
فرمولهای نصف کمان با استفاده از اثبات تصویری دایره واحد و فرمول جمع به دست میآیند، و انتخاب علامت باید بر اساس ربع زاویه صورت گیرد.
این فرمولها با جایگذاری زاویههای خاص به جدول مقادیر مثلثاتی به دست میآیند و انتخاب علامت تفاوتی ندارد.
فرمولهای نصف کمان تنها با روش عددی و بدون توجه به علامت ریشه تشکیل میشوند.
فرمولهای نصف کمان از تقسیم اتحادهای جمع دو زاویه و انتخاب همواره علامت مثبت استخراج میشوند.
مشاهده گزینه صحیح
فرمولهای نصف کمان برای توابع مثلثاتی مانند سینوس و کسینوس از طریق استخراج جبری و استفاده از اتحادهای جمع زاویه به دست میآیند. برای تعیین علامت ریشه، باید به ربع زاویه توجه کرد، زیرا بسته به اینکه زاویه اصلی در کدام ربع قرار دارد، علامت سینوس یا کسینوس تغییر میکند.
۱۲. برای محاسبه sin(α+β) وقتی که مقدار sin(α) و cos(β) را داریم، بهترین روش کدام است؟
جمع کردن مستقیم دو مقدار دادهشده و تقسیم بر دو
جایگذاری مقدارهای دادهشده بدون نیاز به cos(α) و sin(β)
استفاده مستقیم از فرمول جمع زاویه و پیداکردن مقدارهای ناشناخته با استفاده از اتحادهای مثلثاتی
تنها با ضرب کردن sin(α) در cos(β) مقدار sin(α+β) را بدست میآوریم
مشاهده گزینه صحیح
هنگامی که مقدار sin(α) و cos(β) موجود است، باید از فرمول جمع زاویه یعنی sin(α+β) = sin(α)cos(β) + cos(α)sin(β) استفاده کرد. با جایگذاری مقدارهای دادهشده و پیداکردن بخشهای ناشناخته مثلا cos(α) یا sin(β) با کمک اتحادهای فیثاغورسی، میتوان مقدار نهایی را به دست آورد.
نتیجه آزمون در مجله فرادرس
شما هیچ پاسخ صحیحی ندادید
امتیاز: ۰ از ۰
این آموزش را به خوبی یاد گرفتهاید.

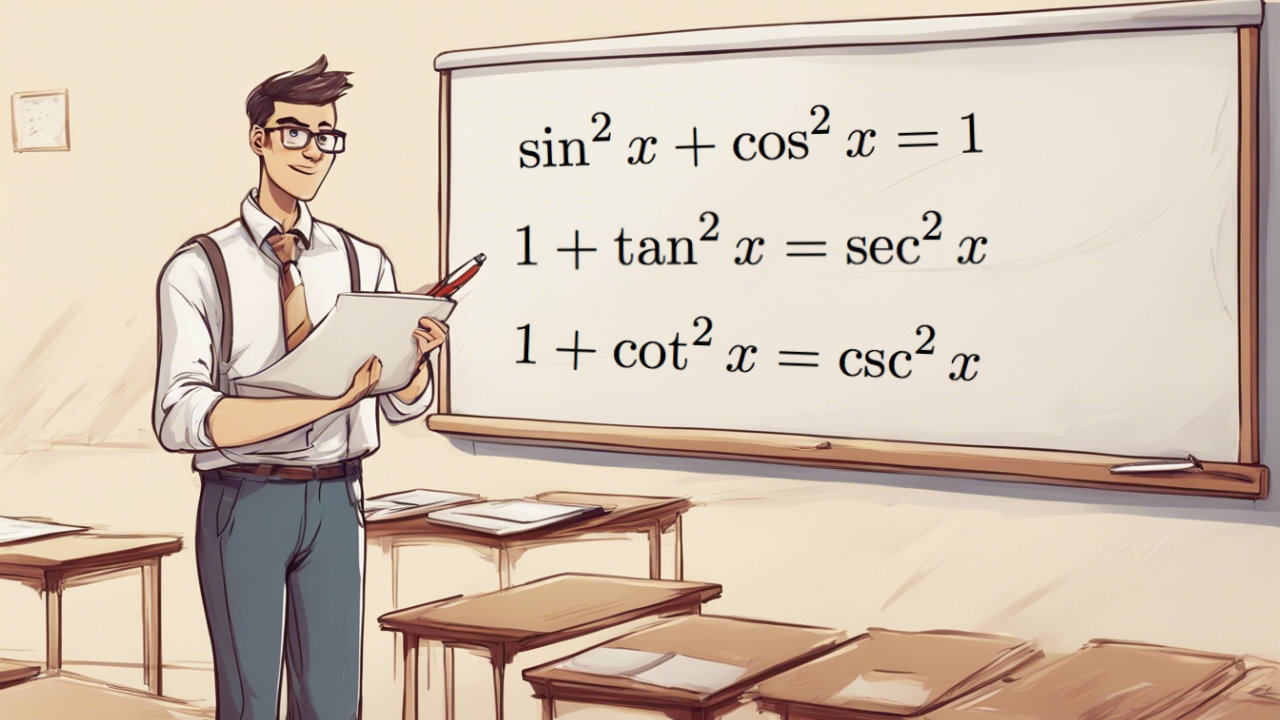
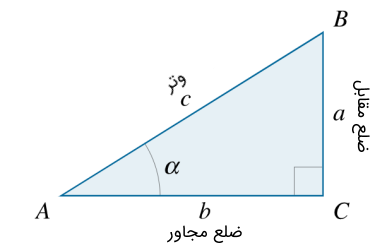

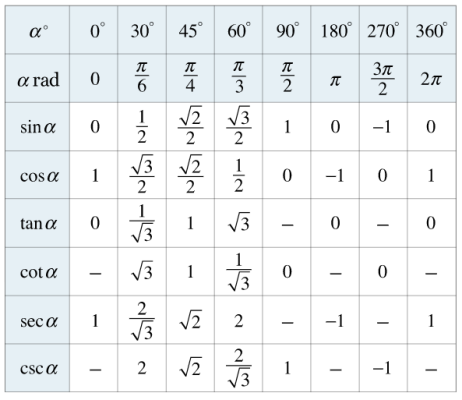
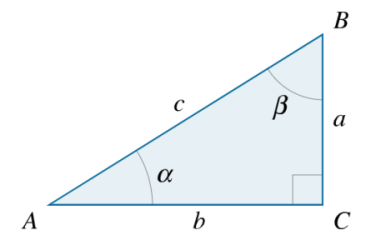



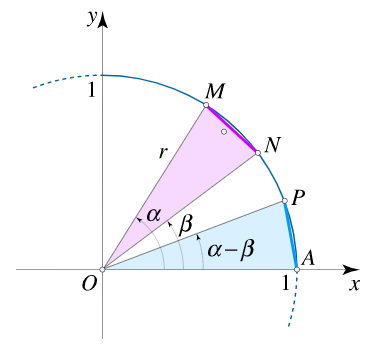
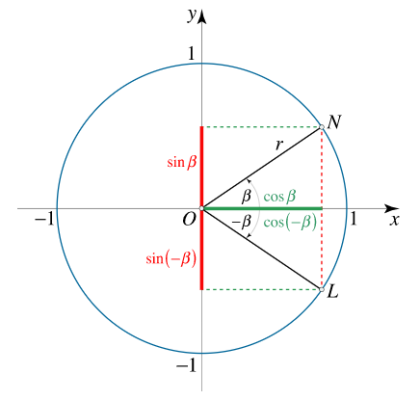


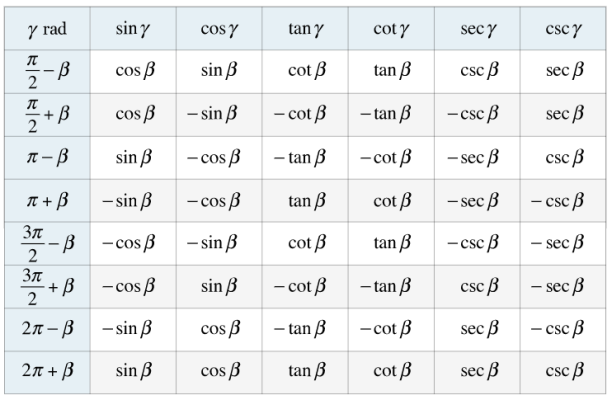























سلام و خسته نباشید خدمت گروه فرا درس.
بسیار مفید
با سلام خدمت گروه مجله فرادرس
مطالب بسیار عالی و کاربردی. اجرتون با حضرت
سلام ممنون از مقاله فوق العاده خوبتون
فقط تو مثال سوم اتحاد های مثلثاتی جمع و تفریق دو زاویه بخش آخر فکر کنم منفی به جای پشت کل کسر باید پشت رادیکال دو باشه که جواب کسر بشه منهای رادیکال دو منهای رادیکال شش تقسیم بر دو
با سلام؛
متن ویرایش شد،
با تشکر از همراهی شما با مجله فرادرس