استاتیک چیست؟ – مفاهیم پایه ایستایی به زبان ساده + حل مثال

در «استاتیک» (Statics) یاد می‌گیریم زمانی که یک جسم صلب در معرض بار‌های مختلف (نیروها و گشتاورها) قرار می‌گیرد، چگونه می‌تواند حالت تعادل خود را حفظ کرده و دچار تغییر شکل نشود. حالت تعادل در استاتیک به معنای سکون یا حرکت جسم با سرعت ثابت است، به گونه‌ای که برآیند نیروها یا گشتاورهای خارجی وارد بر آن صفر شود. در این مطلب از مجله فرادرس توضیح می‌دهیم مفاهیم و اصول پایه در استاتیک چیست و به شما کمک می‌کنیم تا مهارت‌هایی در زمینه حل مسائل این حوزه نیز به دست آورید.

استاتیک چیست و چه مباحثی در آن مطرح می‌ شود؟

در استاتیک نیروها و گشتاورهای وارد بر سیستم‌هایی را بررسی می‌کنیم که شتاب ندارند. استاتیک را ایستایی هم می‌نامند، چون با ذرات و اجسام صلبی سروکار دارد که همگی در حالت تعادل هستند. منظور از حالت تعادل، سکون یا ایستا بودن است که در نتیجه وارد نشدن هیچ‌‌گونه نیرو یا گشتاوری به جسم یا سیستم مورد بررسی ایجاد می‌شود. هدف از مطالعه استاتیک استفاده از قوانین مکانیک کلاسیک به منظور طراحی سیستم‌ها و سازه‌ها است.

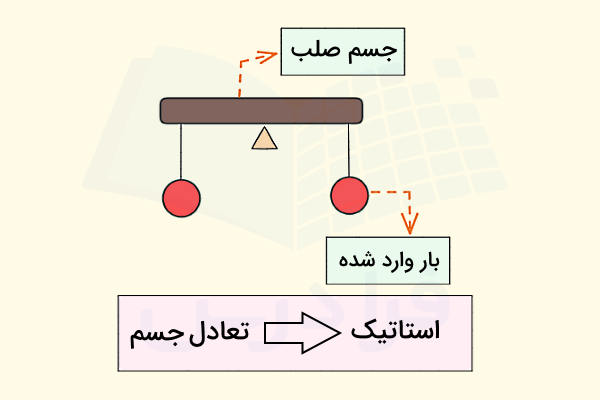
سه فرض زیر نشان می‌دهند وضعیت سیستم فیزیکی مورد مطالعه ما در استاتیک چیست:

• جسم موردنظر یک جسم صلب است: یعنی جسمی است که در اثر قرارگیری بار روی آن تغییرشکل نداریم و دچار خمش، پیچش یا کشیدگی نمی‌شود.
• بارها یا Loads روی جسم قرار می‌گیرند: منظور از بار مجموعه‌ای است از نیروها و/یا گشتاورهای وارد بر جسم.
• حالت تعادل برقرار می‌ماند: یعنی مجموع نیروها و گشتاورهای خارجی وارد بر جسم صفر می‌شود. در نتیجه اگر جسم ساکن است، ساکن می‌ماند و اگر در حال حرکت با سرعت ثابت است، با همین سرعت به حرکت خود ادامه می‌دهد.

از اصول استاتیک در طراحی پل‌ها، خانه‌ها، تونل‌ها و دیگر ساختارهای ایستا به نحوی استفاده می‌شود که از عد‌م‌فروپاشی آن‌ها اطمینان لازم حاصل شود. دقت کنید در برخی از محاسبات استاتیکی می‌توان از شکل، بعد و خواص ذاتی اجسام صرف‌نظر کرد. به این ترتیب در اولین تقریب، حتی اجسامی به بزرگی زمین و خورشید نیز شبیه یک ذره نقطه‌ای رفتار می‌کنند. برای مثال، در بخشی از فیزیک مکانیک به نام «مکانیک تحلیلی» محاسبه مدار حرکت دایره‌ای سیارات با نقطه‌ای در نظر گرفتن آن‌‌ها انجام می‌شود. این در حالی است که در بخش دیگری از فیزیک مکانیک به نام «دینامیک اجسام صلب»، گستردگی اجسام و نحوه توزیع جرم آن‌ها در محاسبات در نظر گرفته می‌شود. اما در اینجا هم فرضیاتی وجود دارد، برای نمونه این فرض که اجسام صلب توانایی تغییر شکل ندارند.

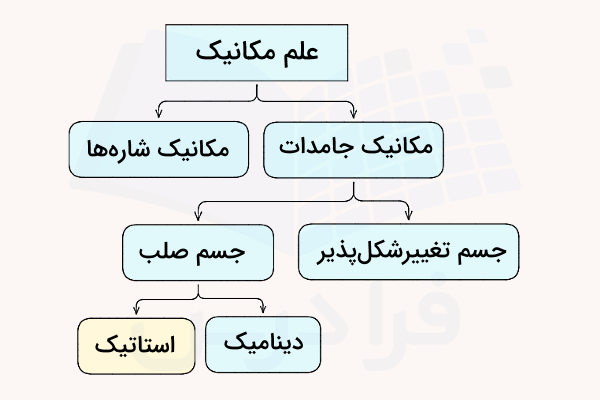
برای شروع استاتیک لازم است ابتدا با سه قانون مهم نیوتن برای حرکت آشنا شویم. درک قوانین حرکت نیوتن و نحوه استفاده از آن‌ها نیازمند شناخت انواع کمیت‌های فیزیکی از نظر نرده‌ای یا برداری بودن است. اغلب کمیت‌هایی که در استاتیک با آن‌ها سروکار داریم، در گروه کمیت‌های برداری قرار می‌گیرند، یعنی علاوه بر اندازه، جهت آن‌ها نیز بسیار مهم است و باید در محاسبات و بررسی وضعیت حرکتی جسم حتما در نظر گرفته شود.

برای مثال، کمیت‌هایی مانند نیرو و گشتاور برداری هستند. پایه اصلی استاتیک قوانین نیوتن است که در بخش انتهایی مطلب توضیح داده شده است. با مطالعه این قوانین بهتر متوجه می‌شوید ارتباط برآیند نیروها و گشتاورهای وارد بر جسم و وضعیت تعادلی در استاتیک چیست.

چطور استاتیک را با فرادرس یاد بگیریم؟

در بخش قبل تا حدودی یاد گرفتیم کلیات استاتیک چیست. در واقع فیزیک مکانیک شامل دو بخش مهم به نام سینماتیک و دینامیک است. در سینماتیک حرکت اجسام بررسی و توصیف می‌شود، در حالی که دینامیک به بررسی علت حرکت اجسام یا نیروها می‌پردازد. همچنین در دینامیک یاد می‌گیریم که تعادل در حرکت یک جسم چه معنایی دارد، موضوعی که مورد توجه استاتیک نیز هست.

نکته مهمی که در فیزیک مکانیک و در نتیجه در استاتیک باید به آن دقت کنیم این است که در این دو مبحث گسترده اجسام یا ذرات با سرعت‌های خیلی پایین‌تر از سرعت نور مطالعه می‌شوند و اگر بخواهیم سرعت‌هایی نزدیک به سرعت نور را مطالعه کنیم، وارد حوزه مکانیک کوانتومی شده‌ایم که شاخه دیگری از فیزیک است. شاخه‌های دیگری مانند «الاستیسیته» (مطالعه مکانیک جامدات تغییرشکل‌پذیر)، «هیدرواستاتیک» (مطالعه مکانیک سیالات در حالت سکون) و «هیدرودینامیک» (مطالعه مکانیک سیالات در حال حرکت) نیز زیرمجموعه‌های دیگری از فیزیک مکانیک هستند که گاهی با استاتیک ترکیب می‌شوند. در این بخش می‌توانید با برخی از فیلم‌های آموزشی فرادرس در این زمینه آشنا شوید:

• فیلم آموزش استاتیک – جامع و کاربردی فرادرس
• فیلم آموزش استاتیک – مرور و حل تست کنکور ارشد فرادرس
• فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد فرادرس
• فیلم آموزش استاتیک – مرور و حل مساله فرادرس

تعادل در استاتیک

در نمودار بخش اول ملاحظه کردید که در استاتیک مطالعه وضعیت تعادلی و میزان تحمل در مقابل شکست و قرار گرفتن بارها برای یک جسم صلب مطالعه می‌شود. شرایط تعادل در استاتیک به این معنا است که جسم شتاب ندارد. بنابراین طبق قانون دوم نیوتن یا جسم ساکن است و یا در حال حرکت با سرعت ثابت است. دقت کنید این سرعت ثابت می‌تواند به شکل خطی یا دورانی باشد. به این ترتیب اگر بخواهیم ببینیم معادلات شرایط تعادل در استاتیک چیست، کافی است به دو فرمول زیر مراجعه کنیم:

$$\sum \vec{ F} = 0$$

$$\sum \vec{ \tau} = 0$$

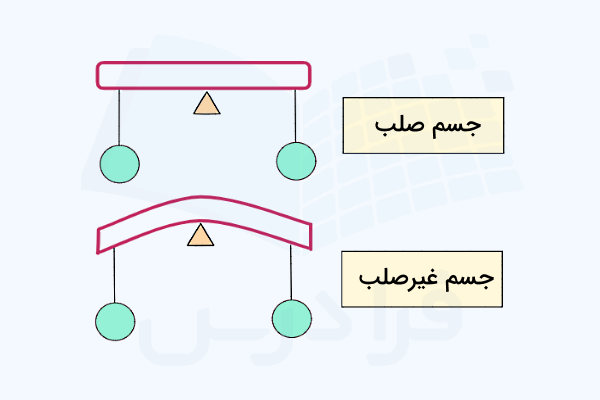
جسم صلب چیست؟

جسم صلب یا Rigid Body جسمی است که در اثر قرار گرفتن بار روی آن دفرمه نمی‌شود یا تغییر شکل نمی‌دهد. به این ترتیب زمانی که بارهای مختلفی روی چنین جسمی قرار می‌گیرد، دچار هیچ‌گونه خمیدگی، کشیدگی یا پیچش نخواهد شد. دقت کنید چنین جسمی در دنیای واقعی وجود ندارد و این فرضیات به نوعی در نظر گرفتن یک تقریب است با هدف ساده‌سازی محاسبات در استاتیک. بنابراین با این ایده‌آل‌سازی سعی می‌کنیم بررسی وضعیت تعادلی سیستم‌های فیزیکی در استاتیک را ساده‌تر کنیم.

اگر فرض جسم صلب را در نظر نگیریم، لازم است فرآیند تغییرشکل جسم در اثر قرارگیری بار را مطالعه کنیم. به این ترتیب مباحثی مانند تنش یا Stress و کرنش یا Strain را خواهیم داشت که موضوع دروس دیگری هستند. در این زمینه مطالعه مطلب «مفهوم تنش و کرنش – آشنایی با مفاهیم مقاومت مصالح» از مجله فرادرس نیز برای شما مفید خواهد بود.

می‌دانیم هر جسم متشکل است از تعداد زیادی ذره. در استاتیک هر جسم صلب را به شکل یک کل و بدون در نظر گرفتن ذرات سازنده آن و نیروهای بین این اجزا در نظر می‌گیریم. بر این اساس در استاتیک تمام نیروهای وارد بر یک جسم تنها به یک نقطه از آن وارد می‌شوند. نکته مهم دیگر در استاتیک و به‌ویژه در حل مسائل آن این است که بسته به هدف خود، جسم موردنظر را درست انتخاب کنیم. برای مثال، اگر بخواهیم فونداسیون یک برج بلند را از نظر استاتیکی و میزان تحمل آن بررسی کنیم، در اولین قدم لازم است کل برج را به عنوان یک جسم در نظر گرفته و نیروهای وارد بر آن را تحلیل کنیم. در مرحله بعد با در نظر گرفتن هر کدام از ستون‌ها به عنوان اجسام بعدی، می‌توانیم تحلیل و بررسی خود را با اجرای محاسبات جزئی‌تر دقیق‌تر کنیم.

گشتاور چیست و چه فرمولی دارد؟

در این بخش می‌‌خواهیم ببینیم حرکت زاویه‌ای یا چرخش در استاتیک چیست و چه متغیرهایی در آن باید مطالعه شود. هر نیرویی چرخش ایجاد نمی‌کند، بلکه فقط نیروهایی منجر به چرخش می‌شوند که دارای مولفه‌ای عمود بر خط متصل کننده نقطه اثر نیرو و محور یا بازوی چرخش‌اند. به این ترتیب در چرخش علاوه‌بر نیرو و محور چرخش (بازوی گشتاور)، با مفاهیم جدیدی به نام گشتاور نیرو یا $$\vec{\tau}$$، تکانه زاویه‌ای یا $$L$$ و شتاب زاویه‌ای یا $$\alpha$$ سروکار داریم. گشتاور نیرو یکی از مهم‌ترین کمیت‌های برداری در استاتیک است که به‌صورت زیر محاسبه می‌شود:

$$\vec{\tau} = \vec{r} \times \vec{F}$$

در این رابطه علامت به معنای ضرب خارجی دو بردار است. بنابراین گشتاور برداری است که بر نیروی ایجاد کننده آن و بر بازوی گشتاور عمود است (تعیین جهت توسط قانون دست راست انجام می‌شود). همچنین طبق فرمول ضرب برداری می‌توانیم فرمول بالا را با در نظر گرفتن زاویه بین نیرو و بازوی گشتاور به شکل $$\theta$$ به‌صورت زیر نیز بنویسیم:

$$\tau = r F \sin \theta$$

مفهوم کوپل چیست؟

در بخش‌های قبل به گشتاور حاصل از نیروهای مختلف اشاره کردیم و گفتیم اهمیت در نظر گرفتن گشتاورها به منظور بررسی تعادل در استاتیک چیست. در حالت عادی گشتاورهای ایجاد شده توسط نیروهای مختلف موجب چرخش حول یک نقطه مشخص خواهند شد. کوپل یا Couple-moment به شرایطی در استاتیک گفته می‌شود که دو نیروی هم‌اندازه و کاملا موازی هم داریم که فقط از نظر جهت مخالف هم هستند.

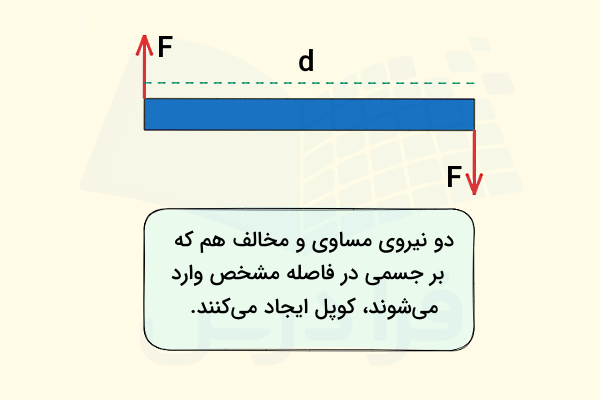
کوپل‌ها حالت‌ خاصی در استاتیک ایجاد می‌کنند، از این جهت که دو جفت نیرو با این شرایط همیشه یکدیگر را خنثی می‌کنند. در واقع طبق قواعد اولیه فیزیک، انتظار داریم برآیند این دو نیرو صفر شود. این توصیف به این معنا است که یک کوپل با اینکه هیچ‌گونه انتقالی ایجاد نمی‌کند، اما موجب چرخش خواهد شد. اگر بخواهیم گشتاور حاصل از یک کوپل را پیدا کنیم، کافی است نقطه‌ای مانند وسط فاصله d را انتخاب کنیم. طبق فرمول گشتاور، هر کدام از این دو نیرو یک گشتاور حول چنین نقطه‌ای ایجاد خواهند کرد:

$$\tau_1 = F \frac{d}{2} \sin90$$

$$\tau_2 = F \frac{d}{2} \sin90$$

اما نکته مهم این است که به علت جهت‌گیری نیروها، گشتاورهای $$\tau_1$$ و $$\tau_2$$ هم‌جهت‌اند. پس اگر بخواهیم گشتاور کل این کوپل را پیدا کنیم، کافی است $$\tau_1$$ و $$\tau_2$$ را با هم جمع کنیم:

$$\tau_{couple} = \tau_1 + \tau_2 = F \frac{d}{2} \sin90 + F \frac{d}{2} \sin90 = F d \sin90$$

به بیانی دیگر اگر بخواهیم بدانیم گشتاور کوپل متشکل از دو نیروی F در فاصله d در استاتیک چیست، کافی است از فرمول زیر استفاده کنیم:

$$\tau_{couple} = F d \sin90$$

روش حل مسائل استاتیک چیست؟

اولین قدم برای حل مسائل استاتیک رسم نمودار جسم آزاد یا Free Body Diagram است، نموداری که در آن یک جسم یا سیستم موردنظر خود را از باقی سیستم جدا می‌کنیم و تمامی نیروها و گشتاورهای وارد بر آن را مشخص می‌کنیم. هر نیرو توسط یک پیکان با جهت مناسب نشان داده می‌شود، ضمن اینکه سایر نیروهای وارد شده بر اجسام دیگر توسط این جسم را نادیده می‌گیریم. در ادامه نشان می‌دهیم اصول حل مسئله در استاتیک چیست.

برای نمونه شکل‌هایی که در ادامه توضیح می‌دهیم هر کدام یک نوع نمودار جسم آزاد را نشان می‌دهند. فرض کنید کتابی روی یک میز قرار دارد. اگر وزن کتاب و میز در مرکز جرم آن‌ها متمرکز باشد، در نمودارهای جسم آزاد مرکز جرم هر کدام از این دو جسم را به عنوان نقطه اثر نیرو در نظر می‌گیریم. رسم نمودار جسم آزاد به این بستگی دارد که هدف ما بررسی نیروهای وارد بر کدام جسم است. در این مثال ساده، سه جسم مختلف به هم نیرو وارد می‌کنند، کتاب، میز و زمین.

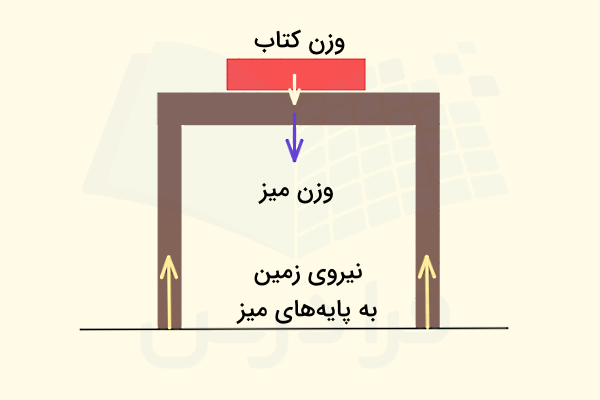
پس اگر بخواهیم نیروهای وارد بر پایه‌های میز را نشان دهیم، نمودار جسم آزادی به شکل بالا خواهیم داشت که در آن کتاب و میز به عنوان یک سیستم واحد در نظر گرفته شده‌اند و زمین با نیروهایی که بر میز وارد می‌کند، مشخص می‌شود. در نمودار دیگر می‌توانیم کتاب و میز را به‌ عنوان دو جسم مستقل از هم در نظر بگیریم و با جدا کردن آن‌ها، نیروهایی برابر و مخالف هم در نتیجه برهم‌کنش کتاب با میز و میز با کتاب را مشخص کنیم.

پس از رسم نمودار جسم آزاد، نوبت می‌رسد به حل مسئله. در حالت کلی در استاتیک نمی‌توانید فقط یک فرمول را حفظ کنید و با جایگذاری مستقیم به جواب برسید، بلکه اغلب راه‌‌های متعددی برای حل یک مسئله وجود دارد و همه آن‌ها به یک اندازه ساده نیستند. بنابراین پیش از شروع، بهتر است با استفاده از تقارن‌ها و داده‌های مسئله برآوردی داشته باشید از بهترین راه‌حل ممکن. اگر می‌خواهید در این زمینه مهارت لازم را کسب کنید باید حل مسائل متنوع را تمرین کنید. همچنین راهکارهای زیر به شما کمک می‌کند تا در استاتیک پیشرفت بهتری داشته باشید:

• تقویت دانش ریاضی به‌ ویژه در زمینه مثلثات، جبر و حساب
• آشنایی با اصول و قواعد در استاتیک
• آشنایی با انواع نیروها و تمرین نحوه تشخیص هر کدام
• آشنایی و تمرین رسم نمودار جسم آزاد برای هر مسئله
• به خاطر سپردن فرمول‌های استاتیک و پیش‌فرض‌ها یا شرایط استفاده از هر کدام
• تمرین و حل مسائل متنوع

به عنوان مثال، در فهرست زیر یاد می‌گیرید که مراحل حل مسئله تعادل در استاتیک چیست:

1. خواندن دقیق صورت مسئله
2. مشخص کردن داده‌ها و مجهولات
3. مشخص کردن استراتژی حل مسئله
4. رسم نمودار جسم آزاد شامل تمام اجسام، بارها، عکس‌العمل‌ها، محورها و بردارهای موردنیاز
5. نوشتن معادلات یا فرمول‌های لازم
6. چک هم‌خوانی تعداد معادلات و مجهول‌ها
7. عددگذاری و انجام محاسبات

حل مثال و تمرین از استاتیک

پس از اینکه آموختید استاتیک چیست و اصول پایه آن چه هستند، در این بخش با حل و بررسی چند سوال تشریحی و چهار گزینه‌ای قدم به قدم به شما کمک می‌کنیم تا شیوه استفاده از این قوانین را در پاسخ به سوالات استاتیک بهتر بیاموزید.

مثال ۱

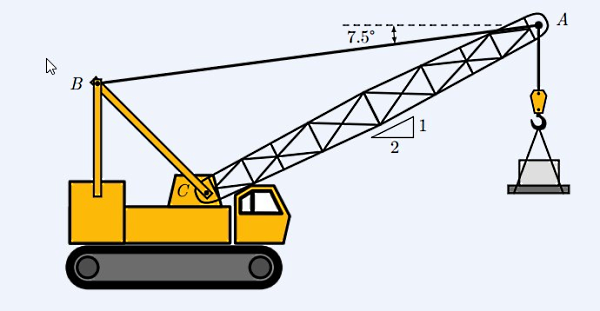
از یک جرثقیل برای بلند کردن بار $$500 \ Ib$$ شامل مواد ساختمانی استفاده می‌شود. اگر میله AC طولی برابر با $$40 \ ft$$ داشته باشد و کشش متناظر در میله‌ AB برابر با $$1500 \ Ib$$ باشد، با بکارگیری تعریف گشتاور اندازه و جهت موارد خواسته شده در سوالات زیر را پیدا کنید:

1. $$M_1$$ یا گشتاوری در نقطه C که توسط بار W ایجاد می‌شود:
2. $$M_2$$ یا گشتاوری در نقطه C که توسط کشش T ایجاد می‌شود:

پاسخ

در این سوال از ما خواسته شده است که از تعریف گشتاور استفاده کنیم. می‌دانیم گشتاور $$\tau$$ برای نیروی $$F$$ توسط رابطه زیر محاسبه می‌شود:

$$\vec{\tau} = \vec{r} \times \vec{F}$$

$$r$$ بازوی گشتاور نامیده می‌شود و معادل است با فاصله‌ نقطه اثر نیرو تا نقطه‌ای که می‌خواهیم گشتاور را در آن پیدا کنیم. فرمول بالا به نوعی یک ضرب خارجی یا ضرب برداری است که اگر آن را باز کنیم، به شکل زیر نوشته می‌شود:

$$\tau = rF\sin \theta$$

$$\theta$$ زاویه بین بازوی گشتاور و نیرو است. این رابطه همان شکل عددی فرمول گشتاور است. دقت کنید در استاتیک مرسوم است گشتاور را به‌جای $$\tau$$ با $$M$$ نشان دهیم. در این مسئله داده‌های مسئله به شکل زیر هستند:

$$W = 500 \ Ib$$

$$T = 1500 \ Ib$$

$$AC = 40 \ ft$$

اگر این دو نیرو را به همراه بازوی گشتاور هر کدام نسبت به نقطه C رسم کنیم، شکل زیر را خواهیم داشت که همان نمودار جسم آزاد در این سوال است:

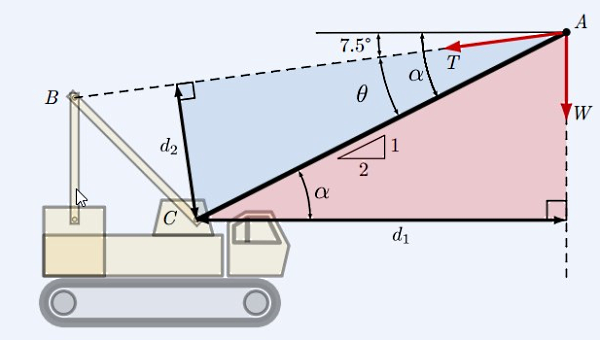
حال برای محاسبه گشتاور هر کدام از این دو نیرو در نقطه C کافی است فرمول بالا را برای هر کدام جداگانه بنویسیم. برای مثال در مورد اولین سوال، $$M_1$$ همان گشتاوری در نقطه C است که توسط بار W ایجاد می‌شود. نقطه اثر نیروی W نقطه A است و نقطه‌ای که می‌خواهیم گشتاور را در آن محاسبه کنیم، نقطه C است. بنابراین در اینجا بازوی گشتاور یا $$r$$ همان AC است. پس کافی است زاویه بین W و AC را پیدا کنیم که طبق شکل بالا معادل است با $$90 - \alpha$$.

به این ترتیب لازم است اول زاویه $$\alpha$$ را مشخص کنیم. طبق مثلث کوچکی که به عنوان راهنما در تصویر صورت سوال قرار داده شده است، می‌توانیم زاویه $$\alpha$$ را با کمک گرفتن از فرمول تانژانت (تقسیم ضلع روبرو بر ضلع مجاور در یک مثلث قائم‌الزاویه) به شکل زیر پیدا کنیم:

$$\alpha = \tan^{-1} (\frac{1}{2}) = 26.6$$

پس برای گشتاور حاصل از وزن بار در این نقطه خواهیم داشت:

$$M_1 = r W \sin (90 - \alpha)$$

در این مرحله می‌توانیم بخش سینوسی فرمول بالا را طبق روابط مثلثاتی به شکل زیر بنویسیم تا محاسبات ساده‌تری داشته باشیم:

$$\sin (90 - \alpha) = \cos \alpha$$

$$M_1 = 40 \times 500 \times \cos 26.6 = 17885 \ ft.Ib$$

در سوال بعدی نیز نقطه اثر نیرو و نقطه‌ای که می‌خواهیم گشتاور را در آن پیدا کنیم مشابه سوال یک است. پس بازوی گشتاور ما در این سوال فرقی نخواهد کرد. اما اندازه نیرو، جهت آن و در نتیجه زاویه بین نیرو و بازو متفاوت است. این زاویه در این سوال طبق نمودار جسم آزاد برابر است با $$\theta$$ که به شکل زیر محاسبه می‌شود:

$$\theta = \alpha - 7.5 = 19.1$$

پس خواهیم داشت:

$$M_2 = r T \sin \theta$$

$$M_2 = 40 \times 1500 \times \sin 19.1 = 19590 \ ft.Ib$$

تا اینجا اندازه دو گشتاور را پیدا کردیم. برای به‌ دست آوردن جهت هر کدام، کافی است به جهت هر کدام از دو نیرو و جهت بازوی گشتاور (از نقطه اثر نیرو تا نقطه اثر گشتاور) توجه کنیم. سپس با استفاده از قاعده ضرب برداری یا همان قاعده دست راست، خواهیم توانست جهت گشتاور را تعیین کنیم. در مورد $$M_1$$ گشتاور به سمت داخل صفحه است که معمولا جهت منفی در نظر گرفته می‌شود. این در حالی است که در مورد $$M_2$$ گشتاور به سمت خارج از صفحه یا در جهت مثبت است. در واقع با اینکه اثر هر دو گشتاور روی یک نقطه بررسی می‌شود و نیروی ایجاد کننده هر دو دقیقا به یک نقطه وارد شده است، اما به علت متفاوت بودن جهت نیروها، جهت گشتاورها متفاوت شد.

مثال ۲

صفحه نازکی به نام OABC در صفحه xy مطابق شکل زیر قرار گرفته است. اگر کابل BD با کششی برابر $$2 \ kN$$ و از طریق نقطه بدون اصطکاک D به این صفحه متصل شود، بردار گشتاور حاصل از این نیرو را حول نقطه O محاسبه کنید:

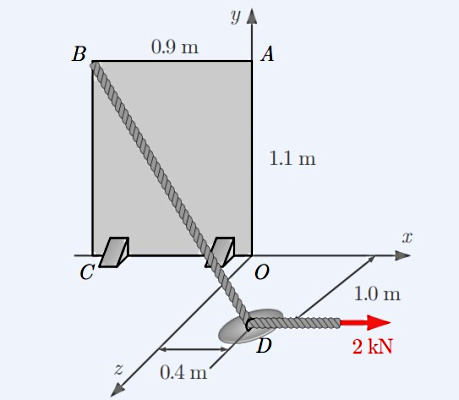
پاسخ

در اولین مرحله لازم است ابتدا فاصله نقطه B را تا D پیدا کنیم. با توجه به اینکه در این سوال صفحه موردنظر در یک دستگاه مختصات سه بعدی داده شده است، می‌توانیم با نوشتن مختصات نقاط B و D به شکل زیر این فاصله را پیدا کنیم:

$$\vec{BD} = D - B$$

$$\Rightarrow \vec{BD} = (-0.9, 1.1,0) - (0.4, 0,1) = (1.3,-1.1,1)$$

دقت کنید در این سوال که مختصات سیستم فیزیکی داده شده سه بعدی است، برای محاسبه گشتاور از فرمول برداری آن که به شکل یک ضرب خارجی است، استفاده می‌کنیم. پس راه‌حل درست این است که بردار یکه در راستای هر کدام را پیدا کنیم. برای مثال، بردار یکه BD به شکل زیر حساب می‌شود:

$$\hat{BD} = \frac { \vec{BD}}{BD}$$

پس ابتدا اندازه BD را پیدا می‌کنیم و سپس آن را همراه با شکل برداری BD در فرمول بالا قرار می‌دهیم:

$$|\vec{BD}| = BD = \sqrt {(1.3)^2 + (1.1)^2 +1^2} = 1.975 \ m$$

$$\Rightarrow \hat{BD} = \frac { \ (1.3,-1.1,1)}{1.975} = (0.65,-0.55,0.50)$$

حالا با ضرب کردن این بردار یکه در اندازه نیرو، بردار نیرو در راستای این بردار یکه پیدا خواهد شد:

$$\vec{F_{BD}} = F_{BD} \hat{BD}$$

$$\Rightarrow \vec{F_{BD}} = 2 (0.65,-0.55,0.50) = (1.317,-1.114,1.013)$$

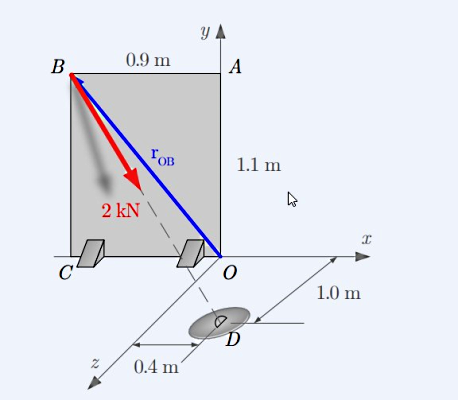
در نهایت برای یافتن گشتاور این نیرو حول نقطه O می‌توانیم با در نظر گرفتن بازوی گشتاوری به شکل $$\vec{r_{OB}}$$ مسئله را حل کنیم. بازوی گشتاور $$\vec{r_{OB}}$$ از مبدا یا نقطه‌ای شروع می‌شود که قرار است گشتاور را در آن پیدا کنیم. این بردار با داشتن مختصات دو نقطه O و B به شکل زیر خواهد بود:

$$\vec{OB} = B - O$$

$$\Rightarrow \vec{OB} = (-0.9, 1.1,0) - (0, 0,0) = (-0.9,1.1,0)$$

آخرین مرحله انجام ضرب برداری است که کمی پیچیده‌تر است و باید به شکل ماتریسی انجام شود:

$$\vec{M_O} = \vec{r_{OB}} \times \vec{F_{BD}}$$

$$\Rightarrow \vec{M_O} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\-0.9 & 1.1 & 0 \\ 1.317 & -1.114 & 1.013 \end{vmatrix}$$

$$\Rightarrow \vec{M_O} = (1.114,0.911,-0.446) \ kN.m$$

پاسخ نهایی نشان دهنده بردار گشتاور موردنظر ما است و کاملا جهت آن را در فضای سه بعدی مشخص می‌کند. پیشنهاد می‌کنیم در مورد محاسبه دترمینان و ضرب ماتریس‌های سه در سه مطلب «دترمینان یک ماتریس و محاسبه آن – به زبان ساده» از مجله فرادرس را مطالعه نمایید. دقت کنید راه‌حل این سوالات یکتا نیست و می‌توانید با انتخاب مولفه‌‌های دیگر نیرو یا بردارهای دیگری به عنوان بازوی گشتاور محاسبات خود را متفاوت انجام دهید. نکته مهم در نظر گرفتن نقطه اثر نیرو و نقطه‌ای است که گشتاور را در آن‌جا باید حساب کنیم. در مثال بعدی خواهید آموخت روش حل یک نمونه سوال سه بعدی در استاتیک چیست.

مثال ۳

اگر مکعبی با طول ضلع $$2 \ ft$$ مطابق شکل زیر به لوله‌ BG توسط دو نقطه اتصال بدون اصطکاک B و G متصل شده باشد، با در نظر گرفتن دو نیروی $$P_1 = 30 \ lb$$ و $$P_2 = 25 \ lb$$ به عنوان نیروهای وارد بر جعبه، به سوالات زیر پاسخ دهید:

• گشتاور چرخشی نیروی $$P_1$$ را حول خط BG محاسبه کنید:
• گشتاور نیروی $$P_2$$ را حول خط BG محاسبه کنید:

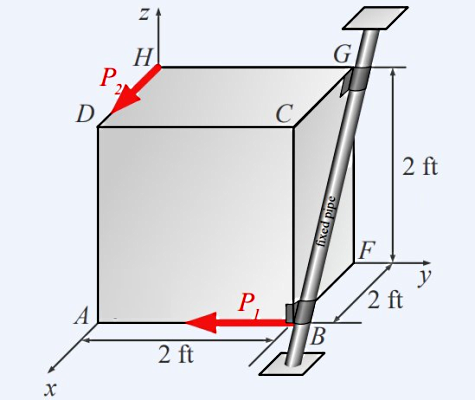
پاسخ

در پاسخ به اولین سوال، نکته کلیدی این است که گشتاور نیروی $$P_1$$ حول خط BG چرخشی را حول این خط ایجاد نمی‌کند. به بیان دقیق‌تر، هیچ بازوی گشتاوری بین این نیرو و خط BG وجود ندارد. در نتیجه پاسخ سوال اول صفر است. اما در سوال بعدی این فاصله وجود دارد، پس گشتاور در این حالت مخالف صفر است. در ادامه روش محاسبه این گشتاور را که کمی پیچیده نیز هست، توضیح می‌دهیم. ابتدا بردار یکه یا بردار واحدی که نشان‌دهنده جهت BG است را پیدا می‌کنیم:

$$\hat{BG} = \frac { \vec{BG}}{BG}$$

پس ابتدا اندازه BG را پیدا می‌کنیم و سپس آن را همراه با شکل برداری BG در فرمول بالا قرار می‌دهیم:

$$|\vec{BG}| = BG = \sqrt {(-2)^2 + (0)^2 +2^2}$$

$$\Rightarrow \hat{BG} = \frac { \ (-2,-0,2)}{ \sqrt {(-2)^2 + (0)^2 +2^2}} = (-0.707,0,0.707)$$

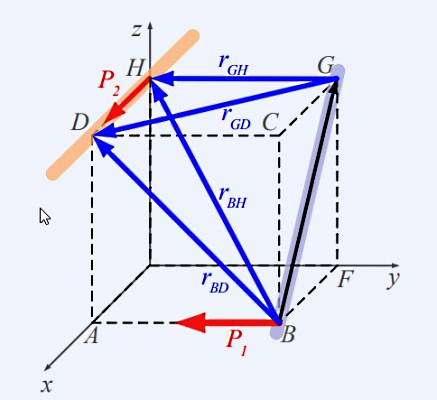
طبق تصویر بالا از نقطه B دو بردار به ابتدا و انتهای بردار نیرو رسم می‌کنیم و همین کار را برای نقطه G نیز انجام می‌دهیم. به این ترتیب چهار بردار جدید داریم که مولفه‌های هر کدام به شکل زیر است:

$$\vec{r_{GH}} = (0,-2,0)$$

$$\vec{r_{GD}} = (2,-2,0)$$

$$\vec{r_{BH}} = (-2,-2,2)$$

$$\vec{r_{BD}} = (0,-2,2)$$

روش به‌دست آوردن این بردارها در مثال قبل توضیح داده شد. کافی است مختصات نقاط ابتدا و انتهای هر بردار را پیدا کنیم و سپس مقادیر متناظر با هر محور را از هم کم کنیم. حالا می‌توانیم از بین این چهار بردار یک مورد را انتخاب کنیم و محاسبات خود را با آن به پیش ببریم. انتخاب هوشمندانه $$\vec{r_{GH}} = (0,-2,0)$$ است، چون دو مولفه آن صفر است و این روند محاسبات دترمینان را ساده‌تر می‌کند. همچنین نیروی $$P_2$$ را نیز به شکل برداری می‌نویسیم:

$$\vec{P_2} = (25,0,0)$$

در نهایت گشتاور را با در نظر گرفتن این سه بردار به شکل زیر می‌توان به دست آورد:

$$\Rightarrow \vec{M_{P_2}} = \begin{vmatrix} -0.707 & 0 & 0.707 \\ 0 & -2 & 0 \\ 25 & 0 & 0 \end{vmatrix}$$

$$\Rightarrow \vec{M_{P_2}} = 35.355 \ ft.Ib$$

دقت کنید ردیف اول این دترمینان همان بردار یکه در راستای BG است. در مثال قبل از بردار‌های یکه i و j و k استفاده کردیم. از آن‌جا که پاسخ به‌ دست آمده مثبت است، پس می‌توانیم نتیجه‌گیری کنیم که چرخش ایجاد شده توسط این نیرو در همان راستای بردار BG است.

مثال ۴

فرض کنید شخصی با وزن $$60 \ N$$ روی طنابی که بین دو درخت کشیده شده است، راه می‌رود. اگر زاویه‌های $$\alpha$$ و $$\theta$$ مطابق شکل زیر تعریف شوند، رابطه بین نیروی کشش طناب در هر دو سمت با زاویه‌ها چگونه است؟

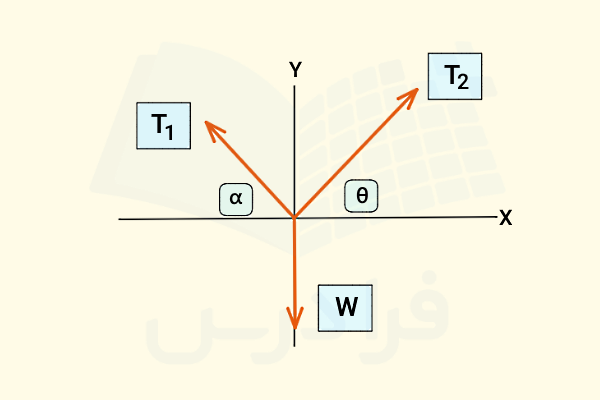
پاسخ

برای حل این سوال کافی است نقطه تعادل تماس فرد با طناب را پیدا کنیم. سپس تمام نیروهای وارد بر این نقطه را همراه با جهت و زاویه‌ها مشخص کنیم. تصویری که در صورت سوال داده شده است، این نقطه و نیروهای وارد بر آن را به خوبی نشان می‌دهد. دو نیروی کشش طناب مختلف با نام‌های $$T_1$$ و $$T_2$$ را برای هر طرف داریم که هر کدام طبق قانون سوم نیوتن برابر هستند با نیروی متقابلی که شخص در آن طرف به طناب وارد می‌کند یا آن را می‌کشد.

این دو نیرو به علت متفاوت بودن زاویه‌ها، یکی نیستند. همچنین نیروی سومی به نام نیروی وزن شخص نیز باید در محاسبات در نظر گرفته شود. انتظار داریم در حالی که این سه نیرو به شخص وارد می‌شوند، او بتواند تعادل خود را روی طناب حفظ کند و نیفتد. حفظ تعادل به معنای برقراری شرایط استاتیکی است که در آن برآیند نیروهای وارد بر شخص صفر است. پس با نوشتن قانون دوم نیوتن در هر کدام از دو راستای x و y خواهیم داشت:

$$\sum F_x = 0$$

$$\sum F_y = 0$$

سپس با مثبت در نظر گرفتن سمت راست محور افقی به عنوان جهت مثبت محور xها و سمت بالای محور عمودی به عنوان جهت مثبت محور yها، نیروها را تجزیه می‌کنیم:

$$\sum F_x = 0 \Rightarrow -T_1 \cos \alpha + T_2 \cos \theta = 0$$

$$\sum F_y = 0 \Rightarrow T_1 \sin \alpha + T_2 \sin \theta - W = 0$$

دقت کنید در نوشتن مولفه‌های نیرو در راستای محور y، نیروی وزن را نباید فراموش کرد. حالا با جایگذاری وزن در رابطه بالا و ساده‌سازی بیشتر خواهیم داشت:

$$T_1 \cos \alpha = T_2 \cos \theta$$

$$T_1 \sin \alpha + T_2 \sin \theta =60$$

این روابط را می‌توان ساده‌تر هم کرد، اما تا همین قسمت نیز به سوال پاسخ داده‌ایم.

دسته بندی نیروها در استاتیک

در این بخش قصد داریم به این سوال پاسخ دهیم که مرسوم‌ترین انواع نیروها در استاتیک چیست و چرا اغلب، نیروهای گسترده در استاتیک را با نیروهای نقطه‌ای معادل‌سازی می‌کنیم. نیرو در ساده‌ترین تعریف خود به هر نوع کشش یا فشار خطی گفته می‌شود که از منابع مختلفی ناشی شده و یکی از آثار آن چرخش است. شکل‌های زیر چند نمونه از انواع نیروها در استاتیک را نشان می‌دهد که در آن جعبه‌ای سنگین توسط طنابی روی یک سطح زبر کشیده می‌شود.

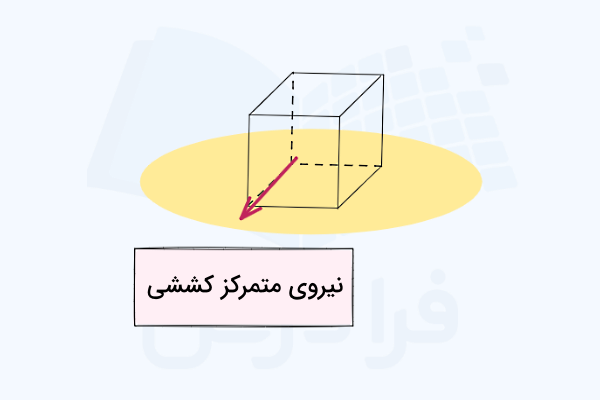
طبق تصویر، نیروی کشش ایجاد شده توسط طناب به همراه وزن جعبه هر دو بار محسوب می‌شوند. طناب نیروی خود را در یک نقطه اعمال می‌کند، بنابراین این نیرو یک نیروی متمرکز است. همچنین نیرویی که زمین برای نگه‌ داشتن جعبه در حالت تعادل وارد می‌کند، یک نیروی عکس‌العملی است که می‌توانیم آن را به دو مولفه تجزیه کنیم:

• یک مولفه اصطکاکی مماسی که موازی با زمین عمل می‌کند و در برابر کشش طناب مقاومت می‌کند.
• یک مولفه نرمال که عمود بر سطح زیرین جعبه عمل کرده و وزن آن را تحمل می‌کند.

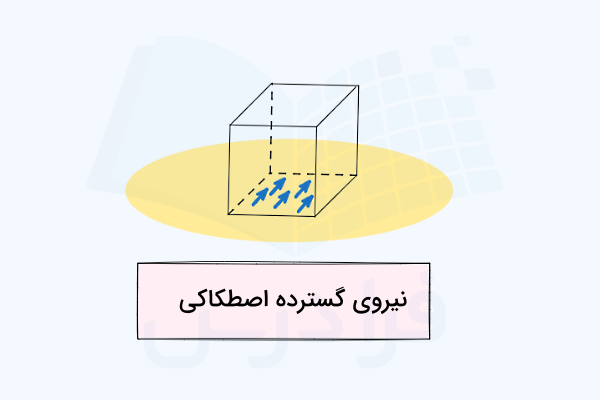
این مولفه‌های نرمال و مماسی نیروهای گسترده‌اند، زیرا روی کل سطح زیرین جعبه عمل می‌کنند. وزن نیز یک نیروی گسترده است، اما چون روی کل حجم جعبه اثر می‌گذارد، به‌عنوان یک نیروی حجمی در نظر گرفته می‌شود. برای اینکه حل مسئله ساده‌تر شود، معمولا تمام این نیروهای گسترده را به نیروهای متمرکز معادل تبدیل می‌کنیم. این فرآیند در بخش‌های بعد توضیح داده خواهد شد اما پیش از آن مروری داریم بر ویژگی‌های هر کدام از این نیرو‌ها تا ببینیم روش استفاده از آن‌ها در استاتیک چیست.

نیروهای متمرکز

نیروهای نقطه‌ای (Point Forces) یا نیروهای متمرکز (‌Concentrated Forces) نیروهایی هستند که بر یک نقطه از جسم اعمال می‌شوند. فشاری که برای باز کردن در وارد می‌کنید یا رانش موتور یک راکت از جمله مثال‌های این نوع نیرو هستند. نیروی نقطه‌ای در واقع مفهومی برای ساده‌سازی مسائل استاتیک است، چون نیروهای واقعی همیشه روی یک سطح عمل می‌کنند، نه روی یک نقطه ریاضیاتی.

نیروهای گسترده

نیروهای گسترده یا Distributed Forces روی یک خط، سطح یا حجم پخش می‌شوند. فشار آب روی دیواره استخر و وزن برف روی سقف، نمونه‌هایی از نیروهای گسترده روی سطح هستند. نمایش این نوع نیروها توسط آرایه‌ یا مجموعه‌ای از بردارهای نیرو است که در ابتدای این بخش نمونه‌ای از آن را مشاهده کردید.

نیروهای حجمی

نیروهای حجمی (Body Forces) همان نیروی گسترده‌اند ولی به جای سطح، روی حجم جسم اثر می‌گذارند. رایج‌ترین نیروی حجمی وزن جسم است، اما نیروهای دیگری نیز در این گروه قرار می‌گیرند از جمله نیروی شناوری و نیروهای ناشی از میدان‌های الکتریکی و مغناطیسی.

بارها

بارها (Loads) نیروهایی هستند که یک جسم به منظور اجرای عملکرد خود تحمل می‌کند. بارها می‌توانند استاتیکی (ایستا) یا دینامیکی باشند. در این مطلب تنها بارهای ایستا موردبررسی قرار می‌گیرد. دقت کنید، آن دسته از نیروهایی که جسم بارگذاری‌ شده را در تعادل نگه می‌دارند یا اجزای جسم را به هم متصل می‌کنند، بار محسوب نمی‌شوند.

نیروهای عکس‌ العملی

پس از اینکه آموختید مفهوم بار در استاتیک چیست، به توضیح نیروهای عکس‌العملی می‌پردازیم. نیروهای عکس‌العملی (Reaction Forces) که به اختصار عکس‌العمل نیز نامیده می‌‌شوند، در حقیقت نیروها و گشتاورهایی هستند که یک جسم یا سیستم مکانیکی را در تعادل نگه می‌دارد یا آن را محدود می‌کند. علت چنین نامگذاری این است که با تغییر سایر نیروهای وارد بر سیستم، آن‌ها نیز واکنش نشان می‌دهند. در واقع اگر بار روی یک سیستم افزایش یابد، نیروهای عکس‌العمل به شکل خودکار افزایش می‌یابند تا تعادل حفظ شود.

نیروهای برهم‌ کنشی

نیروهای برهم‌کنشی یا Interaction Forces نیروهایی هستند که بین اجسام صلب دیده می‌شوند. طبق قانون سوم نیوتن این نیروها برابر و مخالف‌ هم هستند. نیروهای برهم‌کنشی هنگام کار با سازه‌های چندجسمی اهمیت پیدا می‌کنند.

نیروهای داخلی

در نهایت می‌آموزیم آخرین نوع نیروها در استاتیک چیست. نیروهای داخلی (Internal Forces) نیروها و گشتاورهایی‌اند که درون ماده یک جسم صلب وجود دارند و در برابر بارهای خارجی مقاومت می‌کنند تا جسم صلب نشکند. این نیروهای داخلی به صورت نیروی محوری، نیروی برشی و گشتاور خمشی مدل می‌شوند.

یادگیری دروس رشته مهندسی مکانیک با فرادرس

در این مطلب از مجله فرادرس آموختیم که استاتیک چیست و چه جایگاهی بین دروس مختلف رشته مهندسی مکانیک دارد. در حقیقت فیزیک ۱ دانشگاهی، دینامیک و استاتیک از جمله دروس مهم و پایه‌ در اغلب رشته‌های مهندسی از جمله مهندسی عمران نیز هستند. بنابراین اگر علاقه‌مند هستید با جزئیات بیشتر و در قالب مشاهده فیلم، یادگیری خود را تکمیل کنید و یا در این زمینه مسائل متنوع و گسترده‌تری حل کنید، پیشنهاد ما این است که از دوره‌‌های آموزشی تهیه شده در مجموعه فرادرس به شرح زیر استفاده کنید:

• فیلم آموزش رایگان سینتیک اجسام صلب در صفحه
• فیلم آموزش رایگان سینتیک سیستم ذرات در دینامیک مهندسی
• فیلم آموزش دینامیک مهندسی – مرور و حل سوالات
• فیلم آموزش حل مساله در دینامیک مهندسی
• فیلم آموزش دینامیک پیشرفته - مرور و حل تمرین

قوانین نیوتن

دانشمند انگلیسی «آیزاک نیوتن» (Isaac Newton) برای اولین بار در سال ۱۶۸۷ با ارائه سه قانون حرکت خود استاتیک را پایه‌گذاری کرد. این قوانین رابطه بین نیروها، اجسام و حرکت را توصیف می‌کنند. نیوتن قوانین خود را برای نوع خاصی از حرکت به نام «حرکت خطی یا انتقالی» بیان کرد، اما در استاتیک این قوانین را به نوع دیگر حرکت یعنی «حرکت چرخشی» نیز تعمیم می‌دهیم. به همین دلیل بهتر است ابتدا با انواع حرکت در استاتیک و کمیت‌های توصیف کننده هر کدام آشنا شویم.

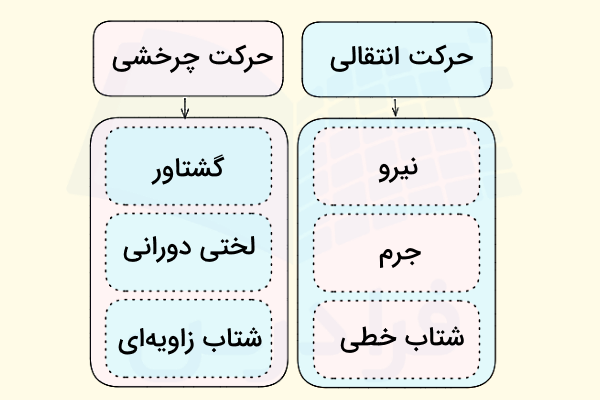
دو تعریف زیر نشان می‌دهد انواع حرکت در استاتیک چیست:

• حرکت انتقالی: در این نوع حرکت جسم مکان خود را تغییر می‌دهد، بدون اینکه جهت‌گیری‌ آن در فضا تغییر کند.
• حرکت چرخشی: در این نوع حرکت جسم حول محوری ثابت در فضا می‌چرخد، بدون اینکه میانگین موقعیت مکانی آن تغییر کند.

برخی از اجسام فقط حرکت انتقالی دارند، برخی دیگر فقط حرکت چرخشی و بسیاری هر دو نوع حرکت را با هم انجام می‌دهند. در استاتیک این امکان وجود دارد که حرکت انتقالی و چرخشی را از هم جدا کرده و هر کدام را به طور مستقل با استفاده از قوانین نیوتن تحلیل کنیم.

قانون اول نیوتن

در اولین بخش توضیح می‌دهیم ارتباط قانون اول نیوتن و استاتیک چیست. در قانون اول به بررسی وضعیت حرکت جسم در شرایطی می‌پردازیم که هیچ نیرویی به آن وارد نمی‌شود. وارد نشدن نیرو به جسم معادل است با این وضعیت که چندین نیرو به جسم وارد شوند، اما برآیند یا جمع برداری آن‌ها صفر شود. چنین وضعیتی همان وضعیت تعادلی است که در استاتیک به دنبال آن هستیم.

اگر بخواهیم این توضیحات را توسط فرمول‌ نشان دهیم، از رابطه زیر می‌توانیم استفاده کنیم:

$$\sum \vec{F} = 0$$

علامت زیگما به معنای مجموع و نماد $$F$$ نشان دهنده کمیت نیرو است که با واحد استاندارد نیوتن ($$N$$) اندازه‌گیری می‌شود. همچنین روی حرف $$F$$ از علامت پیکان استفاده شده است که بیانگر برداری بودن نیرو و در نتیجه، جمع برداری است. بنابراین اگر چند نیرو به یک جسم وارد شوند، اما جهت‌گیری این نیروها و اندازه آن‌ها به گونه‌ای باشد که در مجموع یکدیگر را خنثی کنند، می‌گوییم برآیند نیروهای وارد بر جسم صفر است یا هیچ‌ نیرویی به جسم وارد نشده است یا جسم در شرایط تعادل استاتیکی قرار دارد.

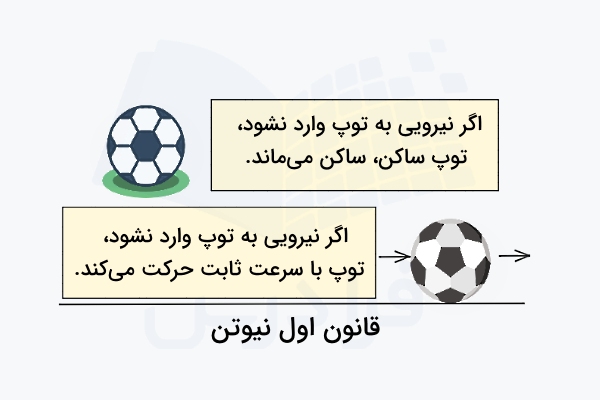
در این شرایط اگر جسم ساکن بوده است، ساکن می‌ماند و اگر در حال حرکت در مسیر مستقیم و با سرعت ثابتی بوده است، به حرکت خود با سرعت ثابت (حرکت یکنواخت) ادامه خواهد داد. قانون اول نیوتن «قانون اینرسی، لختی یا ماند» نیز نامیده می‌شود. علت این نام‌گذاری تمایل اجسام برای حفظ وضعیت حرکتی خود است، چون طبق این قانون یک جسم در حالت سکون باقی می‌ماند یا با سرعت ثابت در یک خط راست حرکت می‌کند، مگر اینکه نیروی خارجی بر آن وارد شود.

این قانون به ما می‌گوید اگر نیروی خالصی به جسم وارد نشود، سرعت فعلی خود را حفظ می‌کند. به عبارت دیگر، جسمی که در حال سکون است در همان حالت می‌ماند و جسم متحرک سرعت و جهت فعلی حرکت خود را حفظ می‌کند، مگر اینکه نیروی نامتعادلی باعث تغییر سرعت آن شود. می‌دانیم سرعت یک کمیت برداری و شامل اندازه و جهت است، بنابراین یک نیروی نامتعادل می‌تواند باعث افزایش یا کاهش سرعت و یا موجب تغییر جهت حرکت جسم شود.

این توضیحات در مورد حرکت چرخشی نیز صادق است، با این تفاوت که در این حرکت به جای نیرو گشتاور داریم. گشتاور تمایل اجسام برای چرخش در اثر اعمال نیرو است. همان‌طور که نیرو باعث تغییر در سرعت خطی می‌شود، گشتاور نیز باعث تغییر در سرعت زاویه‌ای می‌شود. این پدیده را می‌توان در وسایلی مانند فرفره‌ها، دوچرخه‌های ثابت و دیگر اجسامی که با اعمال گشتاور حول یک محور می‌چرخند، مشاهده کرد. قانون اول نیوتن برای حرکت چرخشی به شکل زیر است:

$$\sum \vec{ \tau} = 0$$

پس اگر مجموع گشتاورهای وارد شده به جسمی برابر با صفر شود، جسم اگر ساکن بوده، ساکن می‌ماند و اگر در حال چرخش با سرعت زاویه‌ای ثابتی بوده است، با همین سرعت به چرخش خود ادامه می‌دهد. برای مثال، در شکل بالا فرفره‌ای را مشاهده می‌کنید که در غیاب اصطکاک تا ابد خواهد چرخید. در بخش بعد خواهید دانست ارتباط قانون دوم و استاتیک چیست.

قانون دوم نیوتن

همان‌طور که گفتیم، مادامی که به جسمی نیرویی وارد نشود، تمایلی برای تغییر وضعیت حرکت خود ندارد. یعنی اگر ساکن است، ساکن می‌ماند و اگر در حال حرکت با سرعت ثابت است، به حرکت خود با سرعت ثابت ادامه می‌دهد. اما در صورتی که مجموع نیروهای وارد بر یک جسم مخالف صفر شود، حرکت جسم از حالت یکنواخت خارج می‌شود. در این شرایط طبق قانون دوم چون سرعت جسم تغییر می‌کند، پس شتاب داریم:

$$\sum \vec{F} = m \vec{a}$$

• نیروی $$F$$ بر حسب نیوتن ($$N$$)
• جرم $$m$$ بر حسب کیلوگرم ($$kg$$)
• شتاب $$a$$ بر حسب متر بر مجذور ثانیه ($$\frac{m}{s^2}$$)

توجه کنید در فرمول قانون دوم نیوتن نیرو و شتاب هر دو کمیت‌های برداری و دارای اندازه و جهت هستند، اما جرم یک کمیت نرده‌ای (اسکالر) است که فقط اندازه دارد. رابطه بالا نشان می‌دهد که نیرو باعث می‌شود جسم در جهت نیروی برآیند شتاب بگیرد و اندازه این شتاب نیز متناسب با اندازه نیروی برآیند و معکوس جرم جسم خواهد بود. اما همان‌طور که پیش‌تر اشاره شد، در استاتیک ما با اجسامی سروکار داریم که شتاب ندارند، یعنی:

$$a = 0$$

این رابطه بیانگر این است که تعادل در استاتیک چیست، یعتی یا جسم در حالت سکون است و یا با سرعت ثابتی حرکت می‌کند (همان قانون اول نیوتن). پس موضوع قانون دوم نیوتن نیروی برآیند مخالف صفر است و طبق آن، وارد شدن نیرو به جسم موجب تغییر سرعت و در نتیجه شتابدار شدن حرکت جسم خواهد شد. همچنین نتیجه می‌گیریم که وضعیت جسم در قانون دوم نیوتن آن شرایط تعادلی مطلوب ما در استاتیک محسوب نمی‌شود. همچنین لازم است بررسی کنیم مفهوم قانون دوم در حرکت چرخشی و ارتباط آن با استاتیک چیست.

قانون دوم برای حرکت چرخشی نیز دقیقا مانند قانون دوم برای حرکت انتقالی است، با این تفاوت که به‌ جای مجموع نیروها مجموع گشتاورها را داریم. همچنین شتاب زاویه‌ای جایگزین شتاب خطی و لختی دورانی جایگزین جرم می‌شود. به این ترتیب فرمول زیر را برای قانون دوم نیوتن در حرکت چرخشی خواهیم داشت:

$$\sum \vec{ \tau} = I \vec{\alpha}$$

• گشتاور $$\tau$$ بر حسب نیوتن در متر ($$N.m$$)
• لختی دورانی $$I$$ بر حسب کیلوگرم متر مربع ($$kg.m^2$$)
• شتاب زاویه‌ای $$\alpha$$ بر حسب رادیان بر مجذور ثانیه ($$\frac{rad}{s^2}$$)

این رابطه بیان می‌کند زمانی که گشتاور برآیند $$\tau$$ بر یک جسم اعمال شود، شتاب زاویه‌ای $$/alpha$$ ایجاد خواهد شد. این شتاب با گشتاور برآیند تناسب مستقیم و با لختی دورانی یا ممان اینرسی $$I$$ نسبت معکوس دارد. ممان اینرسی در مورد شتاب زاویه‌ای همان نقشی را دارد که جرم برای شتاب خطی دارد. در اینجا نیز گشتاور برآیند و شتاب زاویه‌ای کمیت‌های برداری هستند، در حالی که لختی دورانی یک کمیت عددی است.

همچنین با توجه به اینکه در استاتیک اجسام بدون شتاب را مطالعه می‌کنیم (یعنی اجسامی که یا همواره در حالت سکون‌اند و یا در حال چرخش با سرعت زاویه‌ای ثابت هستند)، بنابراین گشتاور برآیند وارد بر تمام اجسام ایستا حتما صفر است. پس در این بخش متوجه شدیم ارتباط فرمول قانون دوم با استاتیک چیست.

قانون سوم نیوتن

در نهایت سومین قانون نیوتن را داریم که «قانون عمل و عکس‌العمل» یا «کنش و واکنش» هم نامیده می‌شود و قانونی است که به بررسی نیروهای متقابل دو جسم بر هم می‌پردازد. در قانون اول و دوم فقط نیروهای وارد بر یک جسم بررسی می‌شود، اما در این قانون دو جسم یا دو ذره را مدنظر داریم و می‌خواهیم ببینیم این دو چه نیروهایی به هم وارد می‌کنند.

طبق قانون سوم اگر جسم اول به جسم دوم نیرویی به‌صورت $$\vec{ F_{12} }$$ وارد کند، جسم دوم هم به جسم اول نیرویی برابر با $$\vec{ F_{21} }$$ وارد می‌کند، طوری که داریم:

$$\vec{ F_{12} } = -\vec{ F_{21} }$$

$$|\vec{ F_{12} }| = |\vec{ F_{21} }|$$

بنابراین نتیجه قانون سوم نیوتن این است که نیروهای عمل و عکس‌العمل همواره مساوی و در خلاف جهت هم هستند. به خاطر داریم که نیروها زمانی به وجود می‌آیند که یک جسم با جسم دیگر برهم‌کنش مستقیم یا تماسی (مانند هل دادن یا کشیدن) و غیرمستقیم یا غیرتماسی (مانند نیروی جاذبه مغناطیسی یا گرانشی) داشته باشد. طبق قانون سوم، هر نیرویی که بر یک جسم وارد می‌شود همواره با نیرویی برابر و مخالف که بر جسم دیگری وارد می‌شود، همراه است.

البته این جفت نیروهای برابر و مخالف هم ممکن است گیج‌کننده بنظر برسند، به‌ ویژه زمانی که چندین جسم با هم برهم‌کنش دارند. به همین دلیل است که معمولا حل مسائل استاتیک را با رسم دیاگرام جسم آزاد شروع می‌کنیم. به عنوان جمع‌بندی، با اینکه در حل مسائل استاتیک از این قانون و قانون دوم نیوتن مستقیما استفاده نمی‌شود، اما درک مفاهیم این دو قانون مکمل درک بهتر قانون اول است و به شما کمک می‌کند متوجه شوید کاربرد آن در استاتیک چیست.