الگوریتم جستجوی محدوده در جاوا — از صفر تا صد

در این مقاله به بررسی مفهوم جستجو برای همسایگی در فضای دوبعدی می‌پردازیم. بدین ترتیب با الگوریتم جستجوی محدوده در جاوا و پیاده‌سازی آن آشنا خواهیم شد.

جستجوی تک‌بعدی چه فرقی با جستجوی دوبعدی دارد؟

به طوری که می‌دانیم «جستجوی دودویی» (binary search) الگوریتم کارآمدی برای یافتن تطبیق دقیق در یک لیست از آیتم‌ها با استفاده از رویکرد «تقسیم و حل» (divide-and-conquer) محسوب می‌شود.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

اینک یک مساحت دوبعدی را تصور ‌کنید که هر آیتم به وسیله مختصات XY در یک صفحه نمایش می‌یابد. با این حال به جای تطبیق دقیق، فرض کنید که می‌خواهیم همسایگی‌های یک نقطه مفروض را در یک صفحه بیابیم. روشن است که اگر بخواهیم نزدیک‌ترین n مطابقت را پیدا کنیم، جستجوی دودویی عمل نخواهد کرد. دلیل این امر آن است که جستجوی دودویی می‌تواند دو آیتم را صرفاً در یک محور مقایسه کند، در حالی که باید بتوانیم آن‌ها را در دو محور مقایسه کنیم. در بخش بعدی نگاهی به جایگزین‌های ساختمان داده درخت دودویی خواهیم داشت.

Quadtree

«درخت چهارتایی» (Quadtree) یک ساختمان داده به صورت درخت فضایی است که در آن هر گره دقیقاً چهار فرزند دارد. هر فرزند می‌تواند یک نقطه یا یک لیست شامل چهار درخت چهارتایی فرعی باشد.

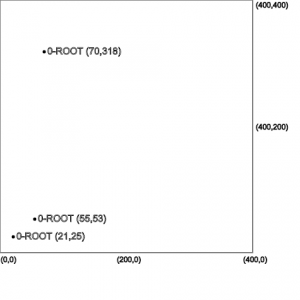
یک نقطه (Point) داده‌هایی را ذخیره می‌کند که برای نمونه شامل مختصات XY هستند. یک منطقه (Region) نماینده یک کران بسته است که درون آن می‌توان یک نقطه را ذخیره کرد. از آن برای تعریف مساحت هر درخت چهارتایی استفاده می‌کنیم. برای درک بهتر به مثال زیر با 10 مختصات در ترتیب دلخواه توجه کنید:

(21,25), (55,53), (70,318), (98,302), (49,229), (135,229), (224,292), (206,321), (197,258), (245,238)

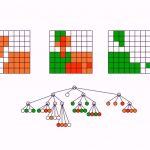
سه مقدار نخست به صوت نقاطی زیر گره ریشه مانند آنچه در تصویر اول دیده می‌شود، ذخیره خواهند شد.

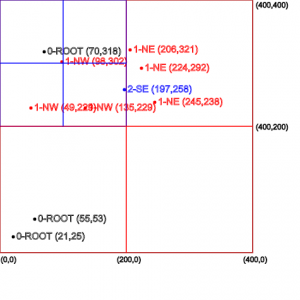
گره ریشه در حال حاضر نمی‌تواند نقاط جدید بپذیرد، زیرا به ظرفیت بیشینه سه نقطه خود رسیده است. از این رو این منطقه گره ریشه را به چهار ربع مساوی تقسیم می‌کنیم.

هر کدام از این ربع ها می‌توانند سه نقطه ذخیره کنند و علاوه بر آن شامل چهار ربع درون کران خود هستند. این کار می‌تواند به صورت بازگشتی انجام یابد که منجر به ایجاد یک درخت چهارتایی از ربع‌ها می‌شود. در واقع نام ساختمان داده درخت چهارتایی نیز از همین واقعیت ناشی می‌شود.

در تصویر وسط در بخش قبلی، می‌بینیم که ربع‌ها از گره ریشه ایجاد می‌شوند و چهار نقطه بعدی در این ربع ها ذخیره می‌شود. در نهایت تصویر پایین در بخش فوق، شیوه تقسیم مجدد ربع برای پذیرش نقاط بیشتری که در آن منطقه هستند را نشان می‌دهد و همزمان ربع‌های دیگر همچنان نقاط جدید را قبول می‌کنند. اینک به بررسی شیوه پیاده‌سازی این الگوریتم در جاوا می‌پردازیم.

ساختمان داده

ابتدا یک ساختمان داده درخت چهارتایی ایجاد می‌کنیم.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

به این منظور به سه کلاس دامنه نیاز داریم. ابتدا یک کلاس Point برای ذخیره مختصات XY می‌سازیم:

1public class Point {
2    private float x;
3    private float y;
4 
5    public Point(float x, float y) {
6        this.x = x;
7        this.y = y;
8    }
9 
10    // getters & toString()
11}

سپس یک کلاس Region می‌سازیم که کران‌های یک ربع را تعریف می‌کند:

1public class Region {
2    private float x1;
3    private float y1;
4    private float x2;
5    private float y2;
6 
7    public Region(float x1, float y1, float x2, float y2) {
8        this.x1 = x1;
9        this.y1 = y1;
10        this.x2 = x2;
11        this.y2 = y2;
12    }
13 
14    // getters & toString()
15}

در نهایت یک کلاس به نام QuadTree ایجاد می‌کنیم که داده‌ها را به صورت وهله‌هایی از Point و فرزندان را به صورت کلاس‌های QuadTree ذخیره می‌کند:

1public class QuadTree {
2    private static final int MAX_POINTS = 3;
3    private Region area;
4    private List<Point> points = new ArrayList<>();
5    private List<QuadTree> quadTrees = new ArrayList<>();
6 
7    public QuadTree(Region area) {
8        this.area = area;
9    }
10}

برای وهله‌سازی از شیء QuadTree مساحت آن را با استفاده از کلاس Region از طریق سازنده تعیین می‌کنیم.

الگوریتم

پیش از نوشتن منطق اصلی کد برای ذخیره‌سازی داده‌ها، ابتدا چند متد کمکی می‌سازیم. این متدها در ادامه مفید واقع خواهند شد.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

متدهای کمکی

ابتدا کلاس Region را ویرایش می‌کنیم. قبل از هر چیز یک متد به نام containsPoint داریم که در صورت افتادن یک نقطه درون یا بیرون مساحت یک منطقه آن را معلوم می‌سازد:

1public boolean containsPoint(Point point) {
2    return point.getX() >= this.x1 
3        && point.getX() < this.x2 
4        && point.getY() >= this.y1 
5        && point.getY() < this.y2;
6}

سپس یک متد به نام doesOverlap داریم که معلوم می‌سازد آیا یک منطقه مفروض با منطقه دیگر همپوشانی دارد یا نه:

1public boolean doesOverlap(Region testRegion) {
2    if (testRegion.getX2() < this.getX1()) {
3        return false;
4    }
5    if (testRegion.getX1() > this.getX2()) {
6        return false;
7    }
8    if (testRegion.getY1() > this.getY2()) {
9        return false;
10    }
11    if (testRegion.getY2() < this.getY1()) {
12        return false;
13    }
14    return true;
15}

در نهایت یک متد به نام getQuadrant ایجاد می‌کنیم که یک محدوده را به چهار ربع برابر تقسیم می‌کند و یکی از آن‌ها را که تعیین شده بازگشت می‌دهد:

1public Region getQuadrant(int quadrantIndex) {
2    float quadrantWidth = (this.x2 - this.x1) / 2;
3    float quadrantHeight = (this.y2 - this.y1) / 2;
4 
5    // 0=SW, 1=NW, 2=NE, 3=SE
6    switch (quadrantIndex) {
7    case 0:
8        return new Region(x1, y1, x1 + quadrantWidth, y1 + quadrantHeight);
9    case 1:
10        return new Region(x1, y1 + quadrantHeight, x1 + quadrantWidth, y2);
11    case 2:
12        return new Region(x1 + quadrantWidth, y1 + quadrantHeight, x2, y2);
13    case 3:
14        return new Region(x1 + quadrantWidth, y1, x2, y1 + quadrantHeight);
15    }
16    return null;
17}

ذخیره‌سازی داده‌ها

اکنون می‌توانیم منطق خود را برای ذخیره‌سازی داده‌ها بنویسیم. کار خود را با تعریف کردن متد جدیدی به نام addPoint روی کلاس QuadTree جهت افزودن یک نقطه جدید آغاز می‌کنیم. این متد در صورتی که یک نقطه با موفقیت اضافه شود، مقدار true بازگشت می‌دهد:

1public boolean addPoint(Point point) {
2    // ...
3}

سپس منطق مدیریت نقطه را می‌نویسیم. ابتدا باید بررسی کنیم که آیا نقطه درون کران‌های یک وهله از QuadTree قرار دارد یا نه. همچنین باید مطمئن شویم که وهله QuadTree به ظرفیت بیشینه (MAX_POINTS) نقاط نرسیده باشد.

اگر هر دو شرط تأمین باشند، می‌توانیم نقطه جدیدی اضافه کنیم:

1if (this.area.containsPoint(point)) {
2    if (this.points.size() < MAX_POINTS) {
3        this.points.add(point);
4        return true;
5    }
6}

از سوی دیگر، اگر به مقدار MAX_POINTS برسیم، باید نقطه جدیدی به یکی از ربع‌های فرعی اضافه کنیم. به این منظور حلقه‌ای روی فرزند لیست quadTrees تعریف می‌کنیم و همان متد addPoint را که روی افزودن موفقیت‌آمیز، مقدار true بازگشت داده فرامی‌خوانیم. سپس بی‌درنگ از حلقه خارج می‌شویم چون یک نقطه باید دقیقاً به یک ربع اضافه شود. همه این منطق را می‌توانیم درون یک متد کمکی کپسوله‌سازی کنیم:

1private boolean addPointToOneQuadrant(Point point) {
2    boolean isPointAdded;
3    for (int i = 0; i < 4; i++) {
4        isPointAdded = this.quadTrees.get(i)
5            .addPoint(point);
6        if (isPointAdded)
7            return true;
8    }
9    return false;
10}

علاوه بر آن یک متد کارآمد دیگر به نام createQuadrants برای تقسیم quadtree جاری به چهار quadtree فرعی می‌سازیم:

1private void createQuadrants() {
2    Region region;
3    for (int i = 0; i < 4; i++) {
4        region = this.area.getQuadrant(i);
5        quadTrees.add(new QuadTree(region));
6    }
7}

این متد را برای ایجاد درخت‌های چهارتایی تنها زمانی فراخوانی می‌کنیم که دیگر نتوانیم نقاط جدیدی اضافه کنیم. بدین ترتیب اطمینان می‌یابیم که این ساختمان داده استفاده بهینه‌ای از فضای حافظه دارد. در نهایت متد addPoint به صورت زیر به‌روزرسانی می‌شود:

1public boolean addPoint(Point point) {
2    if (this.area.containsPoint(point)) {
3        if (this.points.size() < MAX_POINTS) {
4            this.points.add(point);
5            return true;
6        } else {
7            if (this.quadTrees.size() == 0) {
8                createQuadrants();
9            }
10            return addPointToOneQuadrant(point);
11        }
12    }
13    return false;
14}

جستجوی داده‌ها

اینک که ساختمان داده quadtree را برای ذخیره‌سازی داده‌ها تعریف کردیم، می‌توانیم به منطق اجرای جستجو فکر کنیم. از آنجا که ما به دنبال یافتن آیتم‌های مجاور هستیم، می‌توانیم searchRegion را به عنوان یک نقطه آغازین تعیین کنیم. سپس بررسی می‌کنیم که آیا با منطقه ریشه همپوشانی دارد یا نه. اگر چنین باشد، همه نقاط فرزند آن را به درون searchRegion قرار می‌گیرند اضافه می‌کنیم.

پس از منطقه ریشه وارد هر ربع می‌شویم و همین فرایند را تکرار می‌کنیم. این وضعیت تا زمانی که به انتهای درخت برسیم تکرار می‌شود. منطق فوق را به صورت یک متد بازگشتی در کلاس QuadTree می‌نویسیم:

1public List<Point> search(Region searchRegion, List<Point> matches) {
2    if (matches == null) {
3        matches = new ArrayList<Point>();
4    }
5    if (!this.area.doesOverlap(searchRegion)) {
6        return matches;
7    } else {
8        for (Point point : points) {
9            if (searchRegion.containsPoint(point)) {
10                matches.add(point);
11            }
12        }
13        if (this.quadTrees.size() > 0) {
14            for (int i = 0; i < 4; i++) {
15                quadTrees.get(i)
16                    .search(searchRegion, matches);
17            }
18        }
19    }
20    return matches;
21}

تست کردن

اکنون الگوریتم را به دست آورده‌ایم و تلاش می‌کنیم آن را تست کنیم.

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

پر کردن داده‌ها

ابتدا درخت چهارتایی را با همان 10 مختصاتی که قبلاً استفاده کردیم، پر می‌کنیم:

1Region area = new Region(0, 0, 400, 400);
2QuadTree quadTree = new QuadTree(area);
3 
4float[][] points = new float[][] { { 21, 25 }, { 55, 53 }, { 70, 318 }, { 98, 302 }, 
5    { 49, 229 }, { 135, 229 }, { 224, 292 }, { 206, 321 }, { 197, 258 }, { 245, 238 } };
6 
7for (int i = 0; i < points.length; i++) {
8    Point point = new Point(points[i][0], points[i][1]);
9        quadTree.addPoint(point);
10}

جستجوی محدوده

سپس یک جستجوی محدوده در ناحیه‌ای که از سوی مختصات کران پایین (200,200) و کران بالا (250,250) مشخص شده اجرا می‌کنیم:

1Region searchArea = new Region(200, 200, 250, 250);
2List<Point> result = quadTree.search(searchArea, null);

با اجرای کد فوق، یک مختصات همسایگی درون ناحیه جستجو در اختیار ما قرار می‌گیرد:

[[245.0, 238.0]]

اگر ناحیه جستجوی متفاوتی بین مختصات (0,0) و (100,100) امتحان کنیم:

1Region searchArea = new Region(0, 0, 100, 100);
2List<Point> result = quadTree.search(searchArea, null);

با اجرای کد فوق، دو مختصات مجاور برای ناحیه جستجوی تعیین شده بازگشت می‌یابد:

[[21.0, 25.0], [55.0, 53.0]]

مشاهده کردیم که بسته به اندازه ناحیه جستجو، می‌توانیم صفر، یک یا چند نقطه به دست آوریم. بنابراین اگر نقطه‌ای به ما داده شود و از ما خواسته شود که n نزدیک‌ترین همسایگی را بیابیم، می‌توانیم یک ناحیه جستجوی مناسب تعریف کنیم که نقطه مفروض در مرکز آن باشد. بدین ترتیب از روی همه نقطه‌های حاصل از عملیات جستجو، می‌توانیم مسافت اقلیدسی بین نقاط مفروض را محاسبه کرده و آن‌ها را برای یافتن نزدیک‌ترین همسایگی مرتب‌سازی کنیم.

پیچیدگی زمانی

پیچیدگی زمانی یک کوئری محدوده برابر با O(n) است. دلیل آن این است که در سناریوی بدترین حالت، در صورتی که ناحیه جستجو برابر یا بزرگ‌تر از ناحیه مقداردهی شده باشد، باید همه آیتم‌ها پیمایش شوند.

سخن پایانی

در این مقاله ابتدا به بررسی مفهوم یک درخت چهارتایی به وسیله مقایسه آن با درخت دودویی پرداختیم. سپس شیوه استفاده مؤثر از آن برای ذخیره‌سازی داده‌ها روی یک فضای دوبعدی را مشاهده کردیم. سپس شیوه ذخیره‌سازی داده‌ها و اجرای یک جستجوی محدوده را بررسی کردیم. سورس کد این مقاله به همراه تست‌ها در این ریپوی گیت‌هاب (+) در دسترس شما قرار دارد.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌نویسی جاوا (Java)
• مجموعه آموزش‌های برنامه‌‌نویسی
• گنجینه آموزش های جاوا (Java)
• ۱۰ مفهوم اصلی زبان جاوا که هر فرد مبتدی باید بداند
• پیاده سازی درخت دودویی در جاوا — راهنمای جامع

==