پیاده سازی درخت دودویی در جاوا — راهنمای جامع

در این مقاله به بررسی روش پیاده‌سازی درخت دودویی در جاوا می‌پردازیم. ما در این راهنما از یک درخت دودویی مرتب استفاده می‌کنیم که شامل مقادیر عدد صحیح (int) است.

درخت دودویی در جاوا

درخت دودویی یک ساختمان داده بازگشتی است که در آن هر گره حداکثر می‌تواند دو فرزند داشته باشد. نوع رایجی از درخت دودویی به نام درخت جستجوی دودویی شناخته می‌شود که در آن هر گره مقداری دارد که بزرگ‌تر یا مساوی مقادیر گره زیردرخت چپ خود است و کمتر یا مساوی مقادیر گره در زیردرخت راستش است.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

در زیر بازنمایی مختصری از این نوع درخت دودویی را می‌بینید:

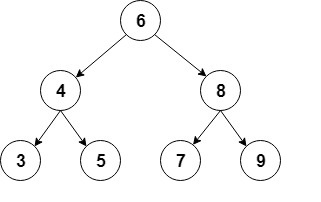
ما برای پیاده‌سازی این درخت از یک کلاس کمکی Node استفاده می‌کنیم که مقادیر int را ذخیره می‌کند و ارجاعی به هر فرزند نگه می‌دارد:

1class Node {
2    int value;
3    Node left;
4    Node right;
5 
6    Node(int value) {
7        this.value = value;
8        right = null;
9        left = null;
10    }
11}

در ادامه گره آغازین درخت را که «ریشه» (Root) نامیده می‌شود اضافه می‌کنیم:

1public class BinaryTree {
2 
3    Node root;
4 
5    // ...
6}

عملیات رایج

در این بخش برخی از رایج‌ترین عملیات که می‌توان روی یک درخت دودویی اجرا کرد را بررسی می‌کنیم.

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

درج عنصر

نخستین عملیاتی که بررسی می‌کنیم درج گره‌های جدید در درخت دودویی است. ابتدا باید مکانی را بیابیم که می‌خواهیم گره جدید را به صورت ترتیبی اضافه کنیم تا کل درخت مرتب باقی بماند. برای درج گره جدید قواعد زیر را با آغاز از گره ریشه پیگیری می‌کنیم:

• اگر مقدار گره جدید کمتر از گره کنونی باشد، به فرزند سمت چپ می‌رویم.
• اگر مقدار گره جدید بزرگ‌تر از گره جاری باشد، به فرزند سمت راست می‌رویم.
• زمانی که گره کنونی null باشد، به گره رسیده‌ایم و می‌توانیم گره جدید را در این موقعیت درج کنیم.

ابتدا یک متد بازگشتی برای انجام این عملیات درج ایجاد می‌کنیم:

1private Node addRecursive(Node current, int value) {
2    if (current == null) {
3        return new Node(value);
4    }
5 
6    if (value < current.value) {
7        current.left = addRecursive(current.left, value);
8    } else if (value > current.value) {
9        current.right = addRecursive(current.right, value);
10    } else {
11        // value already exists
12        return current;
13    }
14 
15    return current;
16}

سپس متد عمومی را ایجاد می‌کنیم که فرایند بازگشتی را از گره ریشه آغاز می‌کند:

1public void add(int value) {
2    root = addRecursive(root, value);
3}

اکنون بررسی می‌کنیم که چگونه می‌توانیم از این متد برای ایجاد درخت در مثال خود استفاده کنیم:

1private BinaryTree createBinaryTree() {
2    BinaryTree bt = new BinaryTree();
3 
4    bt.add(6);
5    bt.add(4);
6    bt.add(8);
7    bt.add(3);
8    bt.add(5);
9    bt.add(7);
10    bt.add(9);
11 
12    return bt;
13}

یافتن یک عنصر

در این بخش یک متد اضافه می‌کنیم تا بررسی کنیم آیا درخت شامل مقدار خاصی است یا نه. همانند عملیات قبل ابتدا یک متد بازگشتی می‌نویسیم تا درخت را پیمایش کنیم:

1private boolean containsNodeRecursive(Node current, int value) {
2    if (current == null) {
3        return false;
4    } 
5    if (value == current.value) {
6        return true;
7    } 
8    return value < current.value
9      ? containsNodeRecursive(current.left, value)
10      : containsNodeRecursive(current.right, value);
11}

در این متد با مقایسه مقدار مورد نظر با مقادیر گره جاری به جستجوی آن می‌پردازیم و سپس بسته به نتیجه مقایسه، ادامه کار را در فرزندان سمت چپ یا راست ادامه می‌دهیم.

سپس متد عمومی را ایجاد می‌کنیم که از گره ریشه آغاز می‌شود.

1public boolean containsNode(int value) {
2    return containsNodeRecursive(root, value);
3}

اکنون می‌توانیم یک تست ساده بنویسیم که تأیید کند آیا درخت واقعاً شامل عنصر درج شده است یا نه.

1@Test
2public void givenABinaryTree_WhenAddingElements_ThenTreeContainsThoseElements() {
3    BinaryTree bt = createBinaryTree();
4 
5    assertTrue(bt.containsNode(6));
6    assertTrue(bt.containsNode(4));
7  
8    assertFalse(bt.containsNode(1));
9}

همه گره‌های اضافه شده باید در درخت موجود باشند.

حذف یک عنصر

عملیات رایج دیگری که روی درخت‌های دودویی استفاده می‌شود، حذف یک گره از درخت است. ابتدا باید گرهی را که می‌خواهیم حذف کنیم به روشی که قبلاً معرفی کردیم بیابیم:

1private Node deleteRecursive(Node current, int value) {
2    if (current == null) {
3        return null;
4    }
5 
6    if (value == current.value) {
7        // Node to delete found
8        // ... code to delete the node will go here
9    } 
10    if (value < current.value) {
11        current.left = deleteRecursive(current.left, value);
12        return current;
13    }
14    current.right = deleteRecursive(current.right, value);
15    return current;
16}

زمانی که گره مورد نظر را یافتیم، 3 حالت متفاوت وجود دارد:

• این گره هیچ فرزندی ندارد: این ساده‌ترین حالت است و کافی است که گره را در والدینش با مقدار null عوض کنیم.
• گره مورد نظر دقیقاً یک فرزند دارد: در این حالت در گره والد، این گره را با آن فرزند عوض می‌کنیم.
• گره مورد نظر دو فرزند دارد: این پیچیده‌ترین حالت است، چون نیازمند سازماندهی مجدد درخت است.

در ادامه شیوه پیاده‌سازی حالت نخست را می‌بینید که در آن گره مورد نظر یک برگ است:

1if (current.left == null && current.right == null) {
2    return null;
3}

اکنون به بررسی حالتی می‌پردازیم که گره یک فرزند دارد:

1if (current.right == null) {
2    return current.left;
3}
4 
5if (current.left == null) {
6    return current.right;
7}

در کد فوق یک فرزند غیر تهی بازگشت می‌دهیم تا بتواند به گره والد انتساب یابد.

در نهایت باید حالتی را مدیریت کنیم که گره دو فرزند دارد. در این حالت ابتدا باید گرهی را که جایگزین گره حذف شده خواهد شد بیابیم. به این منظور از کوچک‌ترین گرهی که در زیردرخت سمت راست گره مورد نظر قرار دارد استفاده می‌کنیم:

1private int findSmallestValue(Node root) {
2    return root.left == null ? root.value : findSmallestValue(root.left);
3}

سپس کمترین مقدار را به گرهی که باید حذف شود انتساب می‌دهیم و سپس آن را از زیردرخت راست حذف می‌کنیم.

1int smallestValue = findSmallestValue(current.right);
2current.value = smallestValue;
3current.right = deleteRecursive(current.right, smallestValue);
4return current;

در نهایت متد عمومی را ایجاد می‌کنیم که فرایند حذف را از ریشه آغاز می‌کند:

1public void delete(int value) {
2    root = deleteRecursive(root, value);
3}

اکنون بررسی می‌کنیم که آیا عملیات حذف مطابق انتظار پیش می‌رود یا نه.

1@Test
2public void givenABinaryTree_WhenDeletingElements_ThenTreeDoesNotContainThoseElements() {
3    BinaryTree bt = createBinaryTree();
4 
5    assertTrue(bt.containsNode(9));
6    bt.delete(9);
7    assertFalse(bt.containsNode(9));
8}

پیمایش یک درخت

در این بخش روش‌های مختلف پیمایش یک درخت را بررسی می‌کنیم و جستجوهای «عمق-اول» و «سطح-اول» را بررسی می‌کنیم. ما از همان درختی که قبلاً استفاده کردیم بهره می‌گیریم و ترتیب پیمایش را در هر حالت نمایش می‌دهیم.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

جستجوی عمق-اول

جستجوی عمق-اول نوعی از پیمایش است که ابتدا تا حد امکان به عمق درخت می‌رود همه فرزندان را بررسی می‌کند و سپس به کاوش هم‌نیاها می‌پردازد. چند روش برای اجرای جستجوی عمق-اول وجود دارد که به صورت پیش‌ترتیبی، میان‌ترتیبی و پس‌ترتیبی نامیده می‌شوند. پیمایش میان‌ترتیبی شامل بازدید زیردرخت چپ در وهله اول است و سپس گره ریشه بازدید می‌شود و در نهایت زیردرخت راست مورد بازدید قرار می‌گیرد.

1public void traverseInOrder(Node node) {
2    if (node != null) {
3        traverseInOrder(node.left);
4        System.out.print(" " + node.value);
5        traverseInOrder(node.right);
6    }
7}

اگر این متد را فراخوانی کنیم، پیمایش میان‌ترتیبی در کنسول به صورت زیر نمایش پیدا می‌کند:

3 4 5 6 7 8 9

در پیمایش پیش‌ترتیبی ابتدا گره ریشه مورد بازدید قرار می‌گیرد، سپس زیردرخت چپ و در نهایت زیردرخت راست بازدید می‌شود:

1public void traversePreOrder(Node node) {
2    if (node != null) {
3        System.out.print(" " + node.value);
4        traversePreOrder(node.left);
5        traversePreOrder(node.right);
6    }
7}

خروجی پیمایش پیش‌ترتیبی در کنسول به صورت زیر خواهد بود:

6 4 3 5 8 7 9

در روش پیمایش پس‌ترتیبی، ابتدا زیردرخت چپ مورد بازدید قرار می‌گیرد و سپس زیردرخت راست و در نهایت گره ریشه بازدید می‌شود:

1public void traversePostOrder(Node node) {
2    if (node != null) {
3        traversePostOrder(node.left);
4        traversePostOrder(node.right);
5        System.out.print(" " + node.value);
6    }
7}

خروجی پیمایش پس‌ترتیبی گره‌ها به صورت زیر است:

3 5 4 7 9 8 6

جستجوی سطح-اول

این نوع جستجو نیز یکی دیگر از روش‌های رایج پیمایش درخت است و در آن ابتدا همه گره‌های یک سطح مورد بازدید قرار می‌گیرند و سپس به سطح بعدی مراجعه می‌شود. این نوع از پیمایش به نام پیمایش ترتیب سطح نیز نامید می‌شود و در آن همه سطوح درخت با آغاز از ریشه و از چپ به راست مورد بازدید قرار می‌گیرد.

برای پیاده‌سازی این نوع جستجو از «صف» (Queue) استفاده می‌کنیم تا گره‌ها را در هر سطح به ترتیب حفظ کنیم. به این منظور هر گره را از لیست استخراج و مقدار آن را پرینت می‌کنیم، سپس فرزندانش را به صف اضافه می‌کنیم:

1public void traverseLevelOrder() {
2    if (root == null) {
3        return;
4    }
5 
6    Queue<Node> nodes = new LinkedList<>();
7    nodes.add(root);
8 
9    while (!nodes.isEmpty()) {
10 
11        Node node = nodes.remove();
12 
13        System.out.print(" " + node.value);
14 
15        if (node.left != null) {
16            nodes.add(node.left);
17        }
18 
19        if (node.right!= null) {
20            nodes.add(node.right);
21        }
22    }
23}

در این حالت، ترتیب گره‌ها به صورت زیر خواهد بود:

6 4 8 3 5 7 9

سخن پایانی

در این مقاله با شیوه پیاده‌سازی درخت دودویی در جاوا و رایج‌ترین عملیات مربوط به آن آشنا شدیم. مانند همیشه همه کدهای معرفی شده در این مقاله را می‌توانید در این آدرس گیت‌هاب (+) مشاهده کنید.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های جاوا (Java)
• آموزش درخت در نظریه گراف و کاربردها
• مجموعه آموزش‌های برنامه‌‌نویسی
• ساختمان داده (Data Structure) — راهنمای جامع و کاربردی
• درخت جستجوی دودویی (BST) — ساختار داده و الگوریتم‌ها

==