دینامیک سیالات محاسباتی (CFD) — از صفر تا صد

طراحی و بهینه‌سازی سیستم‌های مختلف مکانیکی، نیازمند انجام آزمایش‌ها و تست‌های مختلف است. این آزمایش‌ها و طراحی‌های مجددی که در پی دارند، معمولا بسیار پرهزینه و زمان‌بر هستند و فرایند طراحی و ساخت را با چالش‌های زیادی رو به رو می‌کنند. به همین دلیل، به مرور و با بهبود توان محاسباتی کامپیوترها، تمایل مهندسان برای شبیه‌سازی فرایند‌های مختلف مکانیکی افزایش پیدا کرد. برای مثال شبیه‌سازی میدان جریان سیال را با استفاده از علم «دینامیک سیالات محاسباتی» (Computational Fluid Dynamic) انجام می‌دهند.

این مطلب ابتدا به صورت دقیق مفاهیم پایه و ضروری موجود در دینامیک سیالات محاسباتی را مورد بررسی قرار می‌دهد. در ادامه، تاریخچه این علم به صورت مختصر بیان می‌شود و پیشرفت‌هایی که به مرور در دینامیک سیالات محاسباتی شکل گرفته، مورد مطالعه قرار می‌گیرند. سپس معادلات حاکم بر جریان سیال مانند معادله پیوستگی، ناویر استوکس و انرژی بیان می‌شوند. در ادامه روند کلی یک حل عددی درست، مورد بررسی قرار می‌گیرد و کاربرد معادلات دیفرانسیل با مشتقات جزئی در دینامیک سیالات محاسباتی بیان می‌شود. سپس شیوه گسسته سازی معادلات، پارامترهای مهم برای انتخاب یک شبکه مطلوب و نحوه تولید شبکه مورد مطالعه قرار می‌گیرد. در ادامه مطلب نحوه رسیدن به یک حل مستقل از شبکه و همگرایی درست بیان می‌شود و در انتهای مطلب نیز به صورت مختصر، انواع نرم‌افزارهای دینامیک سیالات محاسباتی، ویژگی‌های آن‌ها و روش‌های مختلف انجام حل عددی در آن‌ها مانند روش تفاضل محدود و روش حجم محدود مورد مطالعه قرار می‌گیرد. البته روش‌هایی همچون تابع جریان نیز در سیالات وجود دارد که با استفاده از آن می‌توان به صورت تحلیلی یک جریان را تحلیل کرد.

دینامیک سیالات محاسباتی چیست؟

همانطور که می‌دانید یکی از اهداف مهمی که مهندسان به دنبال آن هستند، بهبود طراحی و افزایش بازده سیستم‌های مختلف است. برای مثال علم آیرودینامیک مهم‌ترین نقش را در طراحی و ساخت یک ماشین مسابقه جدید ایفا می‌کند. اما یافتن مقادیر بهینه مختلف در طول یک فرایند آزمایشگاهی در علم آیرودینامیک کار بسیار پیچیده‌ای است و چالش‌های مختلفی را همراه خود دارد و معمولا تنها راه مهندسان برای بهینه‌سازی طراحی‌های خود این است که آزمایش‌های مختلف آیرودینامیکی را در تونل باد روی نمونه‌های اولیه خود انجام دهند.

بهبود سیستم‌های کامپیوتری و افزایش توان محاسباتی آن‌ها، دینامیک سیالات محاسباتی را به یکی از پر کاربردترین ابزارها برای انجام محاسبات و شبیه‌سازی‌های مهندسی در زمینه مکانیک سیالات تبدیل کرده است. دینامیک سیالات محاسباتی را به صورت اختصاری با نام «سی اف دی» (CFD) نیز نمایش می‌دهند. به طور کلی می‌توان اشاره کرد که برای انجام یک شبیه‌سازی درست CFD، داشتن اطلاعات کافی در سه زمینه مختلف، الزامی است. این سه مورد عبارتند از:

1. سخت افزارها و منابع محاسباتی
2. الگوریتم عددی
3. معادلات دیفرانسیل با مشتقات جزئی

«معادلات با مشتق‌های جزئی» (Partial Differential Equations) را به صورت اختصاری با نماد PDE نیز نمایش می‌دهند. سه موردی که در بالا اشاره شد، سه ضلع مثلث CFD هستند. این موضوع در شکل زیر نمایش داده شده است.

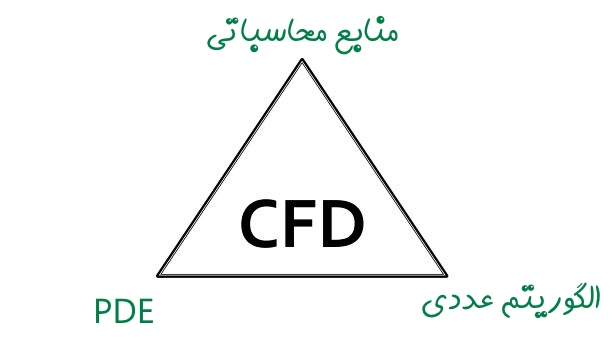
یک شبیه‌سازی سی اف دی به بررسی پارامترهای مختلف سیال مانند سرعت، فشار، دما، چگالی و ویسکوزیته می‌پردازد و برای آن که یک پاسخ با دقت بالا برای یک جریان سیال به دست بیاید، باید پارامترهای مختلف سیال که در بالا معرفی شدند، به ترتیب محاسبه شوند.

مراحل مختلف شبیه‌سازی جریان سیال این است که ابتدا یک مدل ریاضی برای پدیده فیزیکی ارائه می‌شود و در ادامه با استفاده از یک روش عددی و نرم‌افزاری خاص به انجام محاسبات و به دست آوردن پارامترهای مختلف جریان سیال پرداخته می‌شود. برای مثال، معادلات ناویر استوکس (Navier-Stokes Equations) به عنوان مدل ریاضی برای پدیده فیزیکی ما به حساب می‌آیند. در واقع با انجام این محاسبات، تغییرات خواص فیزیکی مختلف یک سیال هنگام انتقال حرارت و جریان سیال، قابل توصیف خواهد بود.

مدل ریاضی که در بالا به آن اشاره شد، با توجه به حالات مختلف مسئله مورد نظر تغییر می‌کند. حالات مختلف یک مسئله می‌تواند شامل انتقال حرارت، انتقال جرم، تغییر فاز، واکنش شیمیایی و سایر موارد موجود در علم مکانیک سیالات باشد.

یکی از چالش‌های اساسی که در شبیه‌سازی جریان سیال به کمک دینامیک سیالات محاسباتی وجود دارد، قابل اعتبار بودن نتایج است که این موضوع به ساختار کلی فرایند شبیه‌سازی بستگی دارد. در واقع «صحه‌گذاری» (Verification) یا صحت سنجی مدل ریاضی استفاده شده اهمیت بسیار زیادی در مسیر شبیه‌سازی مسئله مورد نظر دارد. در کنار مدل ریاضی، انتخاب درست روش عددی در مسیر حل مسئله، اهمیت بسیار زیادی دارد.

موضوع دیگری که در دینامیک سیالات محاسباتی اهمیت بسیار زیادی دارد، انتخاب درست نرم افزاری است که محاسبات به کمک آن انجام می‌شود. انتخاب نادرست نرم‌افزار می‌تواند دقت نتایج حاصل را تحت تاثیر خود قرار بدهد. شکل زیر خطوط جریان اطراف یک اتومبیل فرمول وان را به تصویر کشیده است. در واقع دینامیک سیالات محاسباتی می‌تواند این اطلاعات را بدون انجام تست‌های تونل باد در اختیار مهندسان قرار بدهد.

تاریخچه دینامیک سیالات محاسباتی

از دوران کهن تا به امروز، بشر به دنبال فهم دقیق پدیده‌هایی بوده که به جریان سیال مرتبط هستند. بنابراین دانش دینامیک سیالات محاسباتی یا سی اف دی یک دانش با قدمت بالا است. انجام آزمایش‌های تجربی در محدوده مسائل مکانیک سیالات یک عیب بزرگ دارد. این عیب این است که اگر نیاز به دقت بالایی داشته باشیم، زمان و هزینه زیادی برای انجام آزمایش صرف خواهد شد. بنابراین در آن زمان، حضور مدل ریاضی برای معرفی به کامپیوتر و انجام محاسبات به کمک آن یک امر مهم به حساب می‌آید.

همانطور که اشاره شد کلید اصلی انجام شبیه‌سازی در علم دینامیک سیالات محاسباتی، بهبود مدل‌های ریاضی و روش‌های عددی است. انجام این موارد در سال‌های قبل از 1910 میلادی توسط محققان مختلف شروع شده بود. در طول سال‌های بین 1910 تا 1940، مدل‌ها و روش‌های مختلف با یکدیگر ادغام شدند و اولین حل‌های عددی به وجود آمدند. این حل‌ها با استفاده از دست انجام می‌شدند.

در طول سال‌های 1940 تا 1950، انتقال این علم به سمت محاسبات به کمک کامپیوترها و در واقع با استفاده از اولین کامپیوترها انجام شد. برای مثال، برای حل جریان در اطراف استوانه در همین محدوده سال‌ها به کمک اولین کامپیوترها، تلاش بسیار زیادی انجام شد.

در محدوده سال‌های 1950 تا 1960، اولین مطالعات به کمک کامپیوتر برای شبیه‌سازی جریان سیال با استفاده از معادلات ناویر استوکس توسط آزمایشگاه ملی Los Alamos آمریکا انجام شد. در این شبیه‌سازی از روش «تابع جریان - گردابه» (Vorticity - Stream Function) برای به دست آوردن پارامترهای مختلف جریان استفاده شد. در واقع این شبیه‌سازی، اولین شبیه‌سازی سیال غیر قابل تراکم، دو بعدی و گذرا در جهان است.

در بین سال‌های 1960 تا 1970 اولین مقاله با عنوان «محاسبه جریان پتانسیل اطراف اجسام دلخواه» (Calculation of potential flow about arbitrary bodies)، درباره شبیه‌سازی اجسام سه بعدی چاپ شد. این مقاله توسط «هس و اسمیت» (Hess and Smith) در سال 1967 مورد مطالعه قرار گرفت. در این محدوده سال‌ها، کدهای تجاری مختلف و روش‌هایی مانند k-ε توسعه یافتند. این روش‌ها هم اکنون نیز به صورت گسترده در شبیه‌سازی‌های عددی مورد استفاده قرار می‌گیرند.

یکی دیگر از پیشرفت‌هایی که در محدوده سال‌های 1960 تا 1970 انجام شد، توسعه «الگوریتم سیمپل» (SIMPLE Algorithm) بود که کاربرد بسیار زیادی در شبیه‌سازی‌های سی اف دی دارد.

در محدوده سال‌های 1970 تا 1980، کدهایی توسط شرکت بوئینگ و ناسا توسعه پیدا کردند و جریان سیال اطراف برخی از اجسام مانند زیردریایی، سطح کشتی، خودروها، هلی‌کوپتر و هواپیما انجام شد. این شبیه‌سازی‌ها کمک بسیار زیادی به پیشرفت علم هوافضا، توربوماشین و آیرودینامیک کرد و طراحی تجهیزات موجود در این علوم را بهبود بخشید.

در سال‌های 1980 تا 1990، روش‌های مختلف برای شبیه‌سازی سه بعدی جریان مافوق صوت مورد مطالعه قرار گرفت. کدهای تجاری مختلفی در این محدوده سال‌ها به منظور استفاده در مطالعات صنعتی و آکادمیک توسعه یافتند.

در سال‌های 1990 تا کنون پیشرفت‌های بسیار زیادی در سیستم‌های محاسباتی و توسعه الگوریتم‌های مختلف انجام شده و روش‌های گوناگون دینامیک سیالات محاسباتی به صورت رایج و دقیق در نرم‌افزارهای تجاری مختلف برنامه نویسی شدند؛ به گونه‌ای که این علم در تمام مسئله‌هایی که سیال با خواص مختلف، درون و یا اطراف یک جسم در حال جریان است، کاربرد دارد. در واقع به کمک دینامیک سیالات محاسباتی تمام شبیه‌سازی‌ها در مکانیک سیالات را می‌توان انجام داد و این روش کمک بسیار زیادی به طراحی ابزار و تجهیزات مختلف و بهینه‌سازی آن‌ها کرده است.

توصیف دقیق تمام مدل‌های تئوری موجود در دینامیک سیالات با استفاده از معادلات ناویر استوکس انجام می‌شود. این معادلات شیوه حرکت جریان سیال ویسکوز را نشان می‌دهند. در واقع معادلات معروف ناویر استوکس توسط دو دانشمند به نام‌های «ناویر» (Claude-Louis Navier) و «استوکس» (George Gabriel Stokes) بیان شد، در حالی که این دو دانشمند هیچوقت یکدیگر را ملاقات نکرده بودند.

معادلات ناویر استوکس ابتدا در سال‌های 1822 توس ناویر به دست آمد و سپس در سال 1845، استوکس آن‌ها را تکمیل کرد و اصلاحاتی روی آن‌ها انجام داد. تصویر این دو دانشمند در شکل زیر نشان داده شده است. شکل سمت چپ ناویر را نشان می‌دهد و شکل سمت راست نشان دهنده استوکس است.

معادلات حاکم

ساختار اصلی مسائل وابسته به انتقال حرارت و سیالات، معادلات حاکمی هستند که به صورت مستقیم از قوانین بقای خواص فیزیکی سیال ناشی می‌شوند.

قوانین بقا شامل سه قانون در تمام مسائل مکانیک سیالات هستند. قانون اول قانون بقای جرم است که با معادله پیوستگی نشان داده می‌شود. قانون دوم قانون بقای مومنتوم را نشان می‌دهد که با استفاده از معادله مومنتوم و قانون دوم نیوتن قابل محاسبه هستند و قانون سوم، بقای انرژی را نشان می‌دهد. توجه شود که رابطه بقای انرژی به کمک قانون اول ترمودینامیک یا معادله انرژی قابل محاسبه است.

قوانین بالا نشان می‌دهند که جرم، مومنتوم و انرژی در یک سیستم بسته، ثابت هستند. در واقع به صورت پایه می‌توان بیان کرد که هر آن‌چه (جرم، مومنتوم و انرژی) به درون سیستم می‌آید، باید به بیرون از سیستم یا جای دیگری برود.

تعیین خواص سیالی که پارامترهای حرارتی آن در حال تغییر است با استفاه از این سه قانون بقا قابل انجام است. در واقع با استفاده از این سه معادله حاکم، سه پارامتر اصلی یعنی فشار p، سرعت v و دما T قابل اندازه‌گیری خواهند بود.

برای مثال زمانی که در معادلات حاکم، فشار و دما به عنوان دو متغیر مستقل ترمودینامیکی مورد نیاز شناخته می‌شوند، خواص دیگر سیال مانند چگالی، آنتالپی، ویسکوزیته و ضریب هدایت حرارتی را می‌توان بر حسب این دو پارامتر (فشار و دما) بیان کرد.

دیدگاه لاگرانژی و اویلری

یکی دیگر از نکاتی که در شروع استفاده از معادلات حاکم و معادلات ناویر استوکس باید به آن دقت کرد، حضور دو دیدگاه «اویلری» (Eulerian) و «لاگرانژی» (Lagrangian) در مکانیک سیالات است. دیدگاه لاگرانژی، خواص یک ذره سیال به اندازه کافی بزرگ را دنبال می‌کند. در این حالت، موقعیت اولیه در زمان t0 و موقعیت نهایی در زمان t₁ باید محاسبه شوند ولی دنبال کردن میلیون‌ها ذره جدا از هم در یک جریان سیال، امری غیر ممکن است. در روش دوم یعنی روش اویلری، ذرات به صورت مجزا دنبال نمی‌شوند و به جای آن، میدان سرعت به صورت تابعی از مکان و زمان مورد مطالعه قرار می‌گیرد.

در واقع مشابه شکل بالا، دیدگاه لاگرانژی همراه یک ذره سیال حرکت و مسیر آن را از ابتدا تا انتها دنبال می‌کند. ولی دیدگاه اویلری یک پنجره (حجم کنترل) را در نظر می‌گیرد و به عنوان یک بیننده خارجی، ذرات عبوری از این پنجره را مورد مطالعه قرار می‌دهد.

یکی از نکات بسیار مهمی که باید به آن اشاره کرد این است که دیدگاه لاگرانژی، همواره یک حل وابسته به زمان دارد. در واقع با توجه به اینکه این دیدگاه، حرکت ذره سیال را در طول زمان دنبال می‌کند، می‌توان نتیجه گرفت که این دیدگاه همواره تابعی از زمان خواهد بود. بنابراین اگر مکان اولیه یک ذره با استفاده از b ،a و c نشان داده شود. موقعیت این ذره در زمان t به صورت زیر قابل نمایش است.

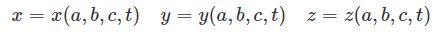
در دیدگاه اویلری، v ،u و w سه مولفه سرعت یک نقطه با مختصات (x, y, z) و در زمان t را نشان می‌دهند. در واقع در این حالت، v ،u و w مجهول‌های ما هستند که تابعی از متغیر‌های مستقل z ،y ،x و t در نظر گرفته می‌شوند. بنابراین توصیف حرکت در دیدگاه لاگرانژی برای هر ذره در زمان t با استفاده از توابع زیر انجام می‌شود.

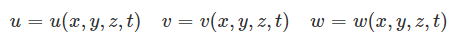
بقای جرم

معادله بقای جرم با استفاده از رابطه زیر قابل نمایش است.

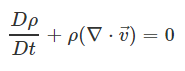
ρ در رابطه بالا، چگالی را نشان می‌دهد و بردار v بیان کننده سرعت است. همچنین نماد ∇ گرادیان را نشان می‌دهد. در مطالب قبل وبلاگ فرادرس نشان دادیم که بردار گرادیان با استفاده از رابطه زیر تعریف می‌شود.

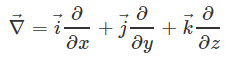
در صورتی که چگالی در یک مسئله مقداری ثابت داشته باشد، سیال به صورت غیر قابل تراکم در نظر گرفته می‌شود و رابطه زیر برای چگالی قابل بیان است.

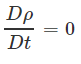
با اعمال شرط بالا در معادله پیوستگی، در نهایت معادله پیوستگی به فرم ساده شده زیر در می‌آید.

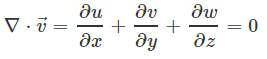
بقای مومنتوم

معادله بقای مومنتوم به صورت کلی با استفاده از معادله ناویر استوکس به شکل زیر قابل نمایش است.

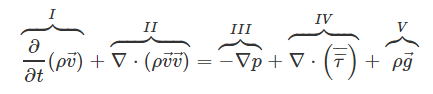
در این رابطه، p فشار استاتیکی را نشان می‌دهد و $$ \overline {\overline { \tau}}$$ تانسور تنش ویسکوز را بیان می‌کند. همچنین عبارت $$ \rho \overrightarrow {g}$$ نشان دهنده نیروی گرانش است.

ترم اول سمت چپ این معادله، تغییر محلی با زمان را بیان می‌کند. ترم دوم سمت چپ این معادله ترم «کانوکشن» (Convection) است. همچنین ترم اول سمت راست که با نماد (|||) نشان داده شده، نیروهای سطحی را بیان می‌کند. ترم دوم سمت راست نشان دهنده ترم «دیفیوژن» (Diffusion) است و ترم آخر نیز نیروی وزن و گرانش را بیان می‌کند.

تانسور تنش ویسکوز که در رابطه بالا با نماد $$ \overline {\overline { \tau}}$$ معرفی شد را می‌توان به شکل زیر بیان کرد. این رابطه با فرض استوکس نوشته شده است.

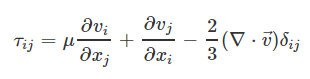
اگر سیال مورد نظر مسئله، به صورت تراکم ناپذیر در نظر گرفته شود و بتوان چگالی آن را ثابت فرض کرد، معادلات به صورت ساده‌تری در می‌آیند. در این حالت می‌توان ویسکوزیته یا لزجت را نیز ثابت در نظر گرفت. بنابراین با استفاده از این فرضیات، تعداد زیادی از ترم‌ها حذف می‌شوند و فرم ساده شده معادله ناویر استوکس به شکل زیر در می‌آید.

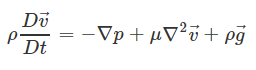
بقای انرژی

معادله بقای انرژی، در واقع همان قانون اول ترمودینامیک است. این قانون بیان می‌کند که مجموع کار و حرارتی که به سیستم داده می‌شود انرژی سیستم را افزایش می‌دهد. این موضوع با استفاده از رابطه زیر بیان می‌شود.

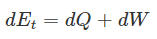
در رابطه بالا، ‌dQ میزان حرارتی است که به سیستم داده می‌شود. dW کار انجام شده توسط سیستم را بیان می‌کند و dE_t نیز برابر با میزان افزایش انرژی کلی سیستم است. یکی از انواع رایج معادله انرژی به شکل زیر نمایش داده می‌شود.

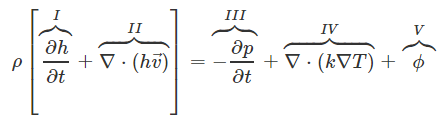
ترم | تغییر محلی با زمان را نشان می‌دهد. عبارتی که با نماد || نشان داده شده، «ترم کانوکشن» (Convection Term) را بیان می‌کند. ||| کار فشار را نشان می‌دهد. V| و V نیز به ترتیب «فلاکس حرارتی» (Heat Flux) و «ترم منبع» (Source Term) را بیان می‌کنند.

معادله با مشتقات جزئی

مدل ریاضی که در ابتدای این مطلب مورد مطالعه قرار گرفت، تنها رابطه میان پارامترهای موجود در فرایند را به صورت مستقیم و غیر مستقیم در اختیار ما قرار می‌دهد. این در حالی است که هر ترم موجود در این روابط، تاثیر مستقیمی روی پدیده فیزیکی دارد. بنابراین تغییر این پارامترها باید به صورت همزمان در حل عددی و به صورت مجموعه‌ای از معادلات با مشتق‌های جزئی در نظر گرفته شود.

به صورت کلی می‌توان بیان کرد که اگر یک تابع شامل چند متغیر مستقل باشد، مشتق آن به صورت مشتق جزئی بیان می‌شود. در واقع مشتق جزئی و شیوه حل معادلات آن، یکی از مباحث بسیار مهمی است که به عنوان پیش نیاز برای انجام محاسبات دینامیک سیالات محاسباتی در نظر گرفته می‌شود.

در مسیر حل «سی اف دی» (CFD) و زمانی که معادله را به صورت یک مشتق جزئی بیان کردیم، می‌توانیم آن را با استفاده از روش‌های مختلف حل کنیم. توجه کنید که در معادله ناویر استوکس با توجه به حضور ترم غیر خطی، امکان حل صریح وجود ندارد و رابطه آن با استفاده از یک حل عددی قابل حل است.

در مکانیک سیالات، مسائلی مانند جریان کوئت و پوازی حضور دارند که معادله ناویر استوکس در آن‌ها حل دقیق دارد. به این حل دقیق، حل تحلیلی نیز گفته می‌شود. اما باید توجه کرد که در حالت کلی و مسائل پیچیده مانند اکثر مسائل توربوماشین و آیرودینامیک، معادله ناویر استوکس حل دقیق و تحلیلی ندارد و برای یافتن پارامترهای مختلف میدان جریان باید معادله را به صورت عددی مورد مطالعه قرار داد.

همانطور که در بالا اشاره شد، برای حل مسائل پیچیده نیاز به اجرای روش‌های مختلف عددی و گسسته‌سازی معادلات داریم. برخی از این روش‌ها شامل روش «تفاضل محدود» (Finite Difference)، «حجم محدود» (Finite Volume)، «المان محدود» (Finite Element)، «روش اسپکترال» (Spectral Method) و «روش المان مرزی» (Boundary Element Method) هستند.

بنابراین به صورت کلی روند حل یک مسئله در دینامیک سیالات محاسباتی این است که ابتدا با استفاده از قوانین فیزیکی، یک مدل ریاضی از مسئله فیزیکی خود تولید می‌کنیم. در ادامه با انجام گسسته سازی، معادلات ریاضی را به دست می‌آوریم و سپس این معادلات را حل می‌کنیم. این روند در شکل زیر به خوبی نشان داده شده است.

شبکه حل

در دینامیک سیالات محاسباتی، برای انجام محاسبات، «ناحیه» (Domain) حل، به چند «زیر ناحیه» (Sub-Domain) تقسیم می‌شود. این زیر ناحیه‌ها، «سلول» (Cell) نامیده می‌شوند. به صورت کلی نیز می‌توان بیان کرد که مجموع این سلول‌ها یک شبکه را تشکیل می‌دهند. شبکه را در ادبیات علمی مهندسی مکانیک، «مش» (Mesh) نیز می‌نامند.

شکل زیر، شبکه حل و مش اطراف یک اتومبیل فرمول یک را به تصویر کشیده است. همانطور که مشاهده می‌شود، شبکه حل در نزدیکی این اتومبیل که تغییرات اندازه و جهت بردار سرعت مقادیر زیادی دارد، ریز است و زمانی که از اتومبیل فاصله می‌گیریم اندازه شبکه درشت می‌شود. در واقع در نقاطی که تغییرات در میدان جریان کم است، اندازه شبکه بزرگ در نظر گرفته می‌شود. بنابراین توجه کنید که میزان تغییرات و حساسیت حل، سایز شبکه و مش را در نقاط مختلف ناحیه تعیین می‌کند.

در واقع همانطور که بیان شد، شبکه حل، روند شبیه‌سازی جریان را ساده می‌کند و امکان به دست آوردن پاسخ معادلات ناویر استوکس، پیوستگی و انرژی را با استفاده از روش عددی فراهم می‌سازد ولی از آن‌جایی که در این معادلات، مشتق‌های جزئی حضور دارند، اگر در قسمتی از حل، شبکه بزرگ و تغییرات پارامترهای سیال زیاد باشد، گسسته‌سازی معادلات به درستی صورت نخواهد گرفت و معادله گسسته شده نماینده درستی از جریان واقعی سیال نخواهد بود.

بنابراین همانطور که توضیح داده شد، در نواحی که تغییرات جریان شدید است، مانند دیواره‌ها، اندازه شبکه و مش به صورت ریز انتخاب می‌شود. روندی که در دینامیک سیالات محاسباتی برای محاسبه اندازه شبکه انتخاب می‌شود، تحت عنوان «استقلال از شبکه» (Mesh Independency) و «آنالیز همگرایی شبکه» (Mesh Convergence Analysis) شناخته می‌شود.

استقلال حل از شبکه

مسائلی که در بخش قبل در مورد شبکه حل بیان شد، مسائل بسیار مهمی هستند. بنابراین توجه کنید که وقتی خطای زیادی در شبکه وجود داشته باشد، شبیه‌سازی درستی انجام نخواهد شد و روند حل عددی معادلات با شکست مواجه می‌شود.

به منظور توضیح دقیق اثر گذاری سایز شبکه در نتایج نهایی، در ادامه یک مثال آورده می‌شود. این مثال می‌تواند فهم دقیق و عمیقی از تاثیر اندازه شبکه در اختیار ما قرار دهد. بر این اساس حالتی را در نظر بگیرید که طول هر المان شبکه برابر با 2h و تغییرات تابع مورد نظر ما (مانند سرعت) در طول مکان به شکل زیر رسم شده است.

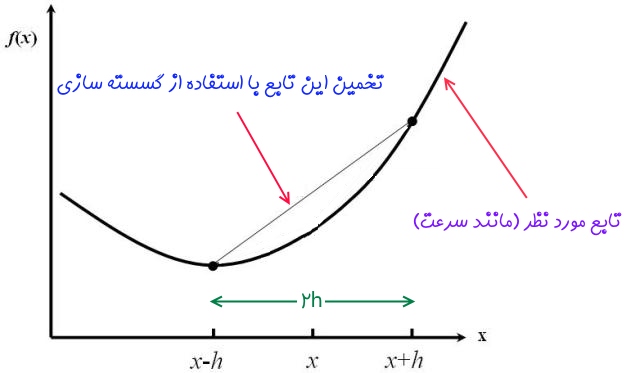
همانطور که مشاهده می‌شود، گسسته سازی معادلات در یک شبکه که طول المان شبکه آن برابر با 2h است، نمی‌تواند تخمین درستی از این تابع در اختیار ما قرار دهد. دلیل این موضوع این است که با گسسته شدن محیط پیوسته، اطلاعات جریان سیال در نقاط میان دو نقطه حل، از بین می‌رود. توجه شود که نقاط نمایش داده شده در شکل بالا، نقاط مرکز یک المان از شبکه مورد نظر ما را نشان می‌دهند. نکته دیگری که باید به آن اشاره کرد این است که گسسته سازی، تغییرات یک تابع را میان دو المان به صورت خطی در نظر می‌گیرد و شیوه این تغییرات را بین دو نقطه یا «نود» (Node) متوالی نمی‌تواند محاسبه کند.

حال شرایطی را در نظر بگیرید که یک نود در مکان x نیز قرار بگیرد و طول هر المان از 2h به h برسد. در این حالت گسسته سازی روی شبکه به شکل زیر در می‌آید.

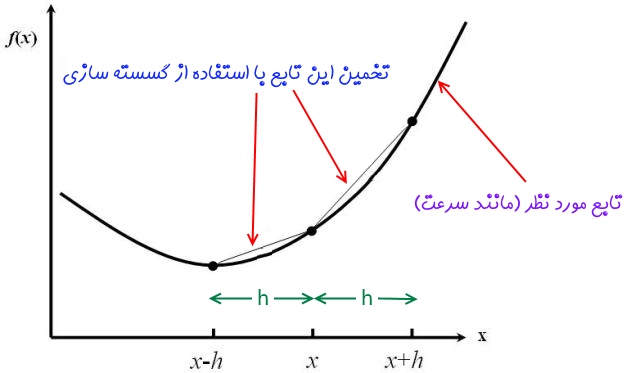
همانطور که در شکل بالا نشان داده شده است، ریز کردن شبکه می‌تواند به تخمین درست یک تابع با استفاده از گسسته سازی کمک بسیار زیادی بکند. در واقع با ریز کردن شبکه، خطوط حاصل از شبیه‌سازی تابعی مانند سرعت، توانایی شبیه‌سازی درست تمام انحناهای تابع اصلی را دارد. بر این اساس بررسی استقلال حل از شبکه، امری حیاتی در دینامیک سیالات محاسباتی است.

در فرایند بررسی استقلال حل از شبکه، هدف ما یافتن درشت‌ترین شبکه‌ای است که با استفاده از آن می‌توانیم تابع مورد نظر خود را (مثلا ضریب لیفت یک ایرفویل در علم آیرودینامیک) با دقت مطلوبی شبیه‌سازی کنیم. بنابراین دقت حل کاملا به ساختار و سایز شبکه و مش وابسته است و با افزایش تعداد سلول‌های شبکه، حجم محاسبات و زمان لازم برای شبیه‌سازی افزایش می‌یابد.

گام اول در بررسی استقلال حل از شبکه این است که یک شبکه با سایز درشت تولید کنیم و شبیه‌سازی را با استفاده از آن انجام دهیم. در این شرایط و پس از همگرایی حل، نتیجه مطلوب (مانند ضریب لیفت) خود را یادداشت می‌کنیم. در اینجا منظور از نتیجه مطلوب، پارامتر است که قرار است در بررسی روند استقال حل از شبکه، بین شبکه‌های مختلف مورد مقایسه قرار بگیرد. برای مثال در یک لوله، افت فشار یا فشار استاتیکی می‌تواند یک پارامتر مهم باشد و یا برای شبیه‌سازی جریان اطراف ایرفویل، نیروی لیفت یا درگ می‌تواند یک پارامتر مهم در نظر گرفته شود.

گام دوم این است که ابتدا شبکه مورد نظر را ریز کنیم و تعداد المان‌ها و سلول‌ها را افزایش دهیم. سپس شبیه‌سازی را با استفاده از شبکه جدید تکرار کنیم. پارامتر مطلوبی که در گام اول مشخص کردیم را در شبیه‌سازی جدید نیز یادداشت می‌کنیم و در نهایت نیاز به رسم یک نمودار داریم که محور عمودی آن مقادیر پارامتر مطلوب ما (مثلا ضریب لفت یا افت فشار) را نشان بدهد و محور افقی آن، بیان کننده اندازه شبکه باشد.

گام سوم بررسی استقال حل از شبکه این است که شبکه را اندکی ریزتر می‌کنیم و سپس مراحل ذکر شده در گام دوم را مجددا با استفاده از شبکه جدید انجام می‌دهیم. در نهایت مقدار پارامتر مطلوب حاصل از این گام را در نموداری که در گام دوم رسم کردیم، قرار می‌دهیم. این روند ریز کردن و شبیه‌سازی تا زمانی ادامه پیدا می‌کند که اختلاف پارامتر مطلوب در دو شبیه‌سازی انتهایی بسیار ناچیز باشد و اختلاف آن‌ها از خطای مورد نظر ما کمتر باشد. در این حالت فرایند بررسی استقلال حل از شبکه متوقف می‌شود و شبکه یکی مانده به آخر که جوابی مشابه شبکه آخر داشته به عنوان شبکه حل مطلوب در نظر گرفته می‌شود.

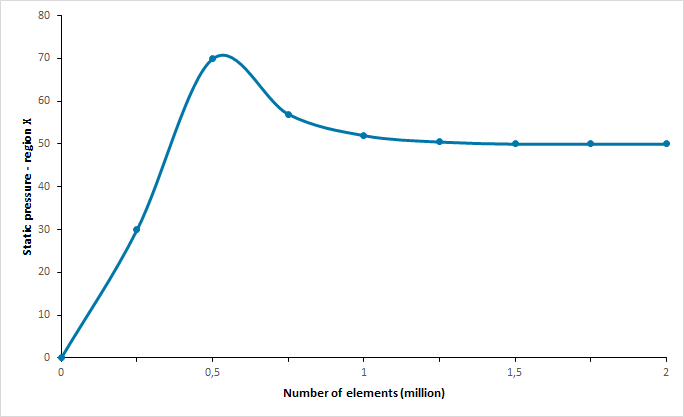
دقت کنید که ما با توجه به محدود سخت افزار و زمان، نیاز به درشت‌ترین شبکه‌ای داریم که جواب درستی را در اختیار ما قرار می‌دهد. بنابراین شبکه یکی مانده به آخر که جوابی مشابه با شبکه آخر دارد را به عنوان شبکه مطلوب انتخاب می‌کنیم. در شکل زیر نمونه‌ای از فرایند بررسی استقال حل از شبکه به تصویر کشیده شده است.

همگرایی حل در دینامیک سیالات محاسباتی

همانطور که در بخش قبل اشاره شد، برای رسیدن به جواب درست در یک حل عددی، باید شبکه یا مش ما در نقاط حساس با گرادیان بالا، ریز باشد. در دینامیک سیالات محاسباتی و برای مثال در نرم افزارهایی مانند گمبیت و انسیس به این کار «اصلاح مش» (Mesh Refinement) گفته می‌شود. شکل زیر نمونه‌ای از اصلاح مش و شبکه را اطراف نقاط حساس یک اتومبیل فرمول یک نشان می‌دهد.

در کنار مفاهیمی که تاکنون اشاره شد، مفهوم همگرایی اهمیت زیادی در علم دینامیک سیالات محاسباتی دارد. حرکت سیال درون یا اطراف اجسام مختلف، از مدل‌های ریاضی و غیر خطی مختلفی پیروی می‌کند و با استفاده از مدل‌های گوناگونی مانند مدل‌های توربولانس، تغییر فاز و انتقال جرم می‌توان به توصیف و شبیه‌سازی آن پرداخت.

روند حل محاسبات در یک حل تحلیلی اینگونه است که یک معادله حل می‌شود و در نهایت جواب آن به صورت صریح به دست می‌آید ولی حل عددی در دینامیک سیالات محاسباتی، شامل یک «الگوی تکرارپذیر» (Iterative Scheme) است. در این روند تکرار پذیر، ابتدا معادلات با یک حدس اولیه حل می‌شوند. در ادامه، حل انجام شده در مرحله اول به عنوان حدس اولیه در مرحله دوم در نظر گرفته می‌شود و معادلات مجددا تکرار می‌شوند. این روند بارها تکرار می‌شود.

روند بیان شده در بالا، تا زمانی ادامه پیدا می‌کند که تفاوت پاسخ مسئله در یک مرحله و مرحله قبل آن، کمتر از مقدار خطای مورد نظر باشد. در واقع در محاسبات دینامیک سیالات محاسباتی، یک مقدار خطا یا باقی‌مانده تعیین می‌شود و زمانی که تفاوت پاسخ در یک مرحله و مرحله قبل، از این مقدار کمتر باشد، حل مورد نظر همگرا شده است و محاسبات متوقف می‌شوند.

توجه کنید که انتظار ما از یک حل عددی درست این است که اختلاف پاسخ یک مرحله و مرحله قبلی‌اش به مرور کمتر شود تا در نهایت این اختلاف از مقدار خطای تعیین شده کوچکتر شود. در صورتی که نمودار این اختلاف را بر حسب شماره مرحله رسم کنیم، یک نمودار با شیب مشخصی به دست می‌آید. شیب این نمودار، روند همگرایی را نشان می‌دهد که مقدار آن به نوع مسئله، مدل ریاضی استفاده شده برای حل معادلات ناویر استوکس و ویژگی‌های سیال مورد استفاده (چگالی، ویسکوزیته و فشار بخار) بستگی دارد. شکل زیر نمونه‌ای از روند همگرایی یک حل عددی در نرم افزار تجاری انسیس فلوئنت را به تصویر کشیده است.

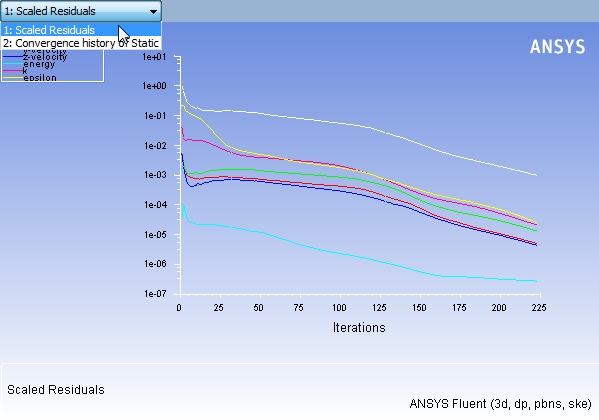
حالتی را در نظر بگیرید که زمان از معادلات حذف شده و یک حل در «حالت پایا» (Steady State) مد نظر ما است. در این حالت و به محض ارضای شرط همگرایی، حالت پایا به دست می‌آید.

حالت دیگر و در مسائلی که حالت «گذرا» (Transient) وجود دارد، مسئله به تعداد زیادی گام زمانی تقسیم می‌شود و این همگرایی باید در تمام گام‌های زمانی انجام شود. در واقع ابتدا در یک گام زمانی مسئله تکرار می‌شود تا شرط همگرایی ارضا شود و سپس وارد گام زمانی بعدی می‌شویم.

به صورت کلی می‌توان بیان کرد که همگرایی و سرعت آن به عوامل متنوعی بستگی دارد و برای انجام یک حل عددی در دینامیک سیالات محاسباتی باید به نکات زیر توجه داشت:

1. سرعت همگرایی یک حل عددی را می‌توان با انتخاب مناسب پارامتر‌هایی مانند «شرایط اولیه» (Initial Condition)، «ضریب زیر تخفیف» (َUnder Relaxation Factor) و «عدد کورانت» (Courant Number)، افزایش داد.
2. در صورتی که حل همگرا شود، نمی‌توان با قطعیت اعلام کرد که حل ما درست است و پاسخ یکسانی با نتایج تجربی دارد؛ زیرا ممکن است مدل ریاضی و یا شبکه حل ابهاماتی داشته باشند.
3. همگرایی یک حل عددی در علم دینامیک سیالات محاسباتی را می‌توان با استفاده از روش‌های مختلفی مانند افزایش کیفیت مش، تصحیح مش و به کار بستن روش‌هایی با دقت بالا برای گسسته‌سازی معادلات، بهبود بخشید.

کاربرد دینامیک سیالات محاسباتی

هرجا که سیال وجود دارد، دینامیک سیالات محاسباتی یا CFD نیز حضور دارد. در قسمت‌های قبل اشاره شد که اولین قدم برای آغاز یک شبیه‌سازی CFD، ارائه یک مدل ریاضی مناسب است که بتواند حالت واقعی پدیده مورد نظر ما را توصیف کند.

برای مثال جریان اطراف استوانه، یکی از پر کاربردترین جریان‌ها در مکانیک سیالات است که در این مطلب نیز به بیان آن پرداخته می‌شود. فرایندی مشابه با این پدیده هنگام حرکت ابرها در اتمسفر نیز مشاهده می‌شود. حقیقت این است که اندازه پدیده حرکت ابرها در هواشناسی و جریان اطراف استوانه بسیار متفاوت است ولی هر دو از الگوی یکسانی پیروی می‌کنند. بنابراین می‌توان از جریان اطراف استوانه به عنوان یک مدل ریاضی مناسب برای توصیف حرکت ابرها استفاده کرد.

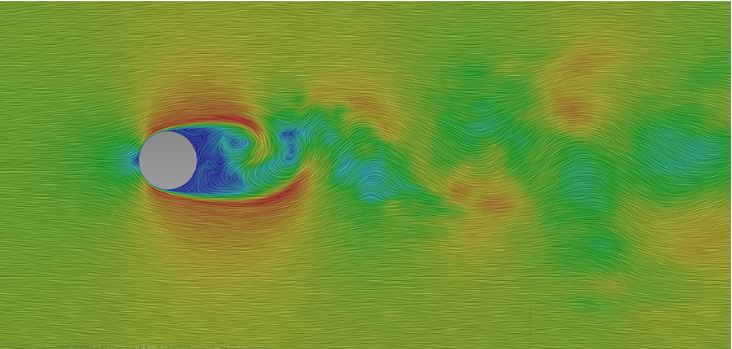
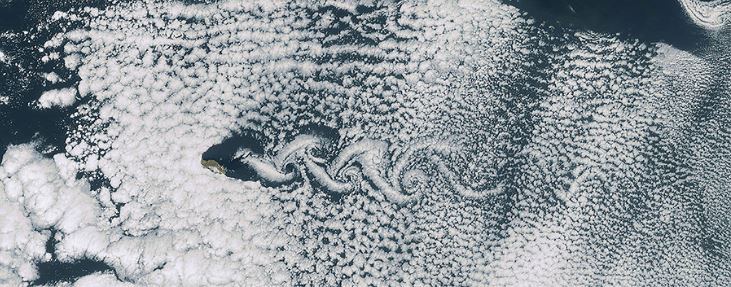
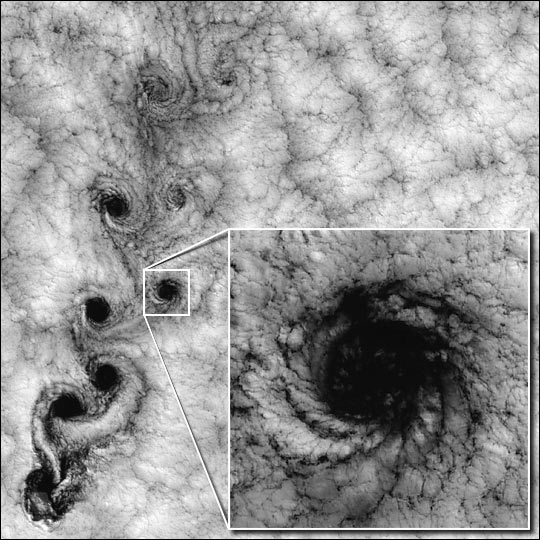
بنابراین می‌توان اشاره کرد که یکی از کاربردهای مهم دینامیک سیالات محاسباتی، پیش‌بینی آب و هوا و حرکت ابرها است. شکل بالا «گردابه‌های کارمن» (Karman Vortex) در پشت استوانه و درون اتمسفر را نشان می‌دهند. یکی دیگر از عکس‌های هوایی که هنگام عبور ابرها از اطراف کوه‌ها گرفته شده، عکس زیر است. در این شکل گردابه‌های کارمن به خوبی نشان داده شده است.

مقایسه ابزارهای مختلف انجام یک شبیه‌سازی CFD

ابزارهای مختلفی برای انجام یک حل عددی وجود دارد. این ابزارها با توجه به مدل ریاضی، روش عددی و شیوه تحلیل داده‌ها انواع مختلفی دارند. توجه شود که در تمامی فرایندهای دینامیک سیالات محاسباتی یک پیش پردازش، یک پردازش و یک «پس پردازش» (Post-Processing) وجود دارد.

در واقع دو راه برای اجرای یک شبیه‌سازی CFD وجود دارد، راه اول این است که با زبان‌های برنامه نویسی مختلف مانند فرترن، C و ++C یک کد بنویسیم که بتواند حل عددی را انجام دهد. راه دیگر برای اجرای یک شبیه‌سازی عددی در دینامیک سیالات محاسباتی، استفاده از نرم افزارهای آماده تجاری مانند فلوئنت و CFX است.

به عنوان مثال می‌توان اشاره کرد که نرم افزار فلوئنت با استفاده از روش حجم محدود به بررسی مسائل دینامیک سیالات محاسباتی می‌پردازد، سرعت پردازش بالاتری دارد و برای محدوده گسترده‌ای از مسائل کاربرد دارد ولی تنظیمات بسیار زیادی را از کاربر برای حل جریان دریافت می‌کند. در سمت مقابل نرم افزار CFX قرار دارد که برای مسائل توربوماشین و ماشین‌های دوار پاسخ‌های بسیار مناسبی را ارائه می‌کند و با استفاده از یک سری تنظیمات محدود، حل مطلوبی را در اختیار کاربر قرار می‌دهد.

نوعی دیگر از نرم افزارها، نرم افزارهای متن باز مانند OpenFoam هستند. این نرم افزار شامل مجموعه‌ای از کدهای آماده است که به کاربر اجازه اجازه ایجاد تغییراتی در کد را می‌دهد علاوه بر این، کاربر می‌تواند کدی را به این نرم افزار اضافه کند. بر خلاف دو نرم افزار تجاری CFX و Fluent که کاربرد زیادی در صنعت دارند، معمولا نرم افزار OpenFoam در جوامع دانشگاهی کاربرد دارد و حل‌گرهای متنوع با استفاده از این نرم افزار روی یک پدیده فیزیکی مورد آزمایش قرار می‌گیرند.

توجه شود که اجرای درست یک حل عددی در تمام روش‌ها و نرم افزارهای دینامیک سیالات محاسباتی، نیازمند استفاده از سخت افزار مناسب، مدل سازی درست پدیده فیزیکی و همچنین داشتن دانش کافی و دقیق درباره «معادلات با مشتق‌های جزئی» (Partial Differential Equations) است. در مطالب دیگر وبلاگ فرادرس انواع روش‌های عددی موجود در دینامیک سیالات محاسباتی مانند روش تفاضل محدود و روش حجم محدود به صورت دقیق مورد بررسی قرار می‌گیرند. توجه کنید که مطالعه پایداری روش‌های مختلف عددی، نقش مهمی در انتخاب و استفاده از این روش‌ها دارد. به همین دلیل «پایداری روش تفاضل محدود » در وبلاگ فرادرس به صورت دقیق بررسی شده است.

در صورتی که به مباحث ارائه شده، علاقه‌مند هستید و قصد یادگیری در زمینه‌های مطرح شده در مکانیک سیالات را دارید، آموز‌ش‌های زیر به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
• تابع جریان در سیالات -- به زبان ساده
• آیرودینامیک (Aerodynamics) چیست؟ — از صفر تا صد
• پیوستگی و بقای جرم در سیالات — از صفر تا صد
• مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد
• جریان پوازی (Poiseuille Flow) — به زبان ساده
• جریان کوئت (Couette Flow) در مکانیک سیالات — از صفر تا صد
• توربوماشین (Turbomachinery) — به زبان ساده
• تونل باد (Wind Tunnel) در مهندسی مکانیک — از صفر تا صد
• ویسکوزیته (Viscosity) — به زبان ساده