کنترل مقاوم – مفاهیم بنیادی | به زبان ساده

نظریه کنترل رایج و متعارف به بشر این امکان را داده است تا قرن‌ها محیط خود را کنترل و خودکار کند. با گذشت زمان، تکنیک‌های کنترل مدرن به مهندسان این توانایی را داده است که سیستم‌های کنترلی را که از نظر هزینه و کارایی بهینه کنند. با این حال، الگوریتم‌های کنترل بهینه همیشه در برابر تغییرات سیستم کنترل یا محیط کارایی لازم را ندارند. نظریه «کنترل مقاوم» (Robust Control) راهکاری برای اندازه‌گیری تغییرات عملکرد یک سیستم کنترل نسبت به تغییر پارامترهای سیستم و کنترل آن است. استفاده از این تکنیک برای ساختن «سیستم‌های توکار یا تعبیه‌ای» (Embedded Systems) قابل اعتماد اهمیت فراوانی دارد. هدف کنترل مقاوم این است که امکان کاوش در فضای طراحی برای گزینه‌های غیرحساس نسبت به تغییرات در سیستم فراهم شود و بتواند پایداری و عملکرد آن‌ها را حفظ کند. یکی از نتایج مطلوب این روش، مربوط به سیستم‌هایی است که در صورت وجود تغییرات یا خطاهای سیستم، افت عملکرد شدیدی را نشان می‌دهند.

چرا کنترل مقاوم؟

برای بررسی کنترل مقاوم یک روش مفید این است که از برخی مفاهیم اساسی نظریه کنترل استفاده کنیم. نظریه کنترل از نظر تاریخی به دو بخش تقسیم می‌شود: کنترل سنتی یا کلاسیک و کنترل مدرن. کنترل کلاسیک مفاهیم و روش‌هایی را پوشش می‌دهد که تا سال ۱۹۵۰ رایج بودند. کنترل مدرن به روش‌های ارائه شده از ۱۹۵۰ تاکنون اطلاق می‌شود. در ادامه، درباره این دو دسته به اختصار بحث می‌کنیم.

فیلم آموزش طراحی کنترل مقاوم H∞/H2 با الگوریتم های تکاملی و فراابتکاری در فرادرس

کلیک کنید

کنترل کلاسیک با گسترش نظریه فیدبک مورد توجه قرار گرفت. از فیدبک برای پایدارسازی سیستم کنترل استفاده شد. یکی از اولین استفاده‌ها از کنترل فیدبک تنظیم‌گر گریز از مرکز برای پایدارسازی موتورهای بخار لوکوموتیوها بود.

نمونه دیگر استفاده از فیدبک، در سیگنال‌های تلفن در دهه ۱۹۲۰ بود. مسئله موجود، انتقال سیگنال‌ها از طریق خطوط طولانی بود. در تعداد تکرارگرها محدودیت وجود داشت که به دلیل اعوجاج، به صورت سری با خط تلفن اضافه می‌شدند. «هارولد استفن بلک» (Harold Stephen Black) سیستم فیدبکی را پیشنهاد داد که از فیدبک برای محدود کردن اعوجاج بهره می‌برد. حتی اگر فیدبک اضافه شده باعث افزایش بهره تکرارگر می‌شد، اما عملکرد کلی را ارتقا می‌بخشید.

کنترل کلاسیک مبتنی بر تشکیل یک مدل از سیستم کنترل با استفاده از معادلات دیفرانسیل است. از تبدیل لاپلاس برای بیان معادلات سیستم در فضای فرکانس استفاده می‌شود. در این فضا، می‌توان عملیات جبری را به سادگی روی معادلات انجام داد.

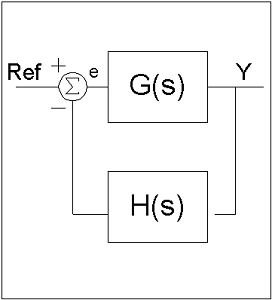
شکل ۱ یک حلقه کنترل رایج را نشان می‌دهد. ورودی سیستم سیگنال مرجع است که مقدار کنترل مطلوب را نشان می‌دهد. این مرجع به تابع تبدیل پیش‌روی $$G ( s)$$ اصطلاحاً خورانده می‌شود تا خروجی $$y$$ دستگاه تعیین شود. خروجی از طریق تابع تبدیل $$H( s)$$ بازخورانده (فیدبک) می‌شود. سیگنال فیدبک از مرجع کم شده و سیگنال خطای $$e$$ به دست می‌آید. کنترل آتی بر اساس سیگنال خطا است. بنابراین، سیستم به گونه‌ای عمل می‌کند که خروجی تا حد ممکن به ورودی مرجع مطلوب نزدیک شود. به دلیل پیچیدگی ریاضیات، روش‌های کنترل کلاسیک اغلب در سیستم‌های تک‌خروجی-تک‌ورودی (SISO) به کار می‌رفتند.

یکی از پیشرفت‌های مهم در گسترش کنترل مقاوم، روش مکان هندسی ریشه‌ها بود. در حوزه فرکانس، $$G(s)$$ و $$H(s)$$ به عنوان نسبت چندجمله‌ای‌هایی بر حسب متغیر فرکانس مختلط $$s$$ بیان شدند. «نایکوئیست» (Nyquist)، «بود» (Bode) و دیگران فهمیدند که ریشه‌های چندجمله‌ای مخرج، پایداری سیستم کنترل را مشخص می‌کنند. به این ریشه‌ها «قطب» تابع تبدیل گفته می‌شود. موقعیت این قطب‌ها برای تضمین پایداری باید در نیم‌صفحه چپ صفحه فرکانس‌ مختلط باشد. مکان ریشه روشی گرافیکی برای نشان دادن حرکت قطب‌ها در دامنه فرکانس در اثر تغییر ضرایب چندجمله‌ای $$s$$ است. حرکت به سمت نیمه راست صفحه به معنای سیستمی ناپایدار است. بنابراین سیستم‌ها را می‌توان با حساسیت آن‌ها به تغییرات کوچک در ضرایب مخرج مورد بررسی قرار داد.

روش‌های کنترل مدرن با تحقق معادلات سیستم کنترل توسعه یافتند، به گونه‌ای که کامپیوترها می‌توانستند آن‌ها را به خوبی حل کنند. نشان داده شد که هر معادله دیفرانسیل مرتبه $$n$$اُم که سیستم کنترل را توصیف می‌کرد، قابلیت تبدیل به $$n$$ معادله مرتبه اول را دارد. این معادلات را می‌توان به فرم معادلات ماتریسی نوشت. این روش اغلب یه عنوان روش متغیر حالت شناخته می‌شود. فرم کانونی معادلات حالت در ادامه نشان داده شده است که در آن، $$\overrightarrow x$$ برداری است که حالت سیستم را نشان می‌دهد، $$\dot {\overrightarrow x}$$ بردار تغییر حالت، $$u$$ بردار ورودی‌ها، $$y$$ بردار خروجی‌ها و $$A$$، $$B$$، $$C$$ و $$D$$ ماتریس‌هایی هستند که به سیستم کنترل بستگی دارند.

$$\large \begin {array} { l } \dot { \overrightarrow { x } } = A \overrightarrow { x } + B \overrightarrow { u } \\ \overrightarrow { y } = C \overrightarrow { x } + D \overrightarrow { u } \end {array}$$

روش‌های کنترل مدرن بسیار موفق بوده‌اند، زیرا به خوبی در کامپیوتر قابل پیاده‌سازی هستند، با سیستم‌های چندورودی-چندخروجی (MIMO) سازگاری دارند و می‌توان آن‌ها را بهینه کرد.

روش‌های بهینه کردن ماتریس‌های حالت ثابت توسعه یافته بود و برای مثال، یک سیستم کنترل فضاپیما برای رسیدن به مقصد در کوتاه‌ترین زمان یا با مصرف حداقل مقدار سوخت یا ترکیبی وزن‌دار از این دو بهینه شد. قابلیت طراحی برای عملکرد و هزینه مطلوب، سیستم‌های کنترل مدرن را بسیار محبوب کرده است.

تعریف کنترل مقاوم

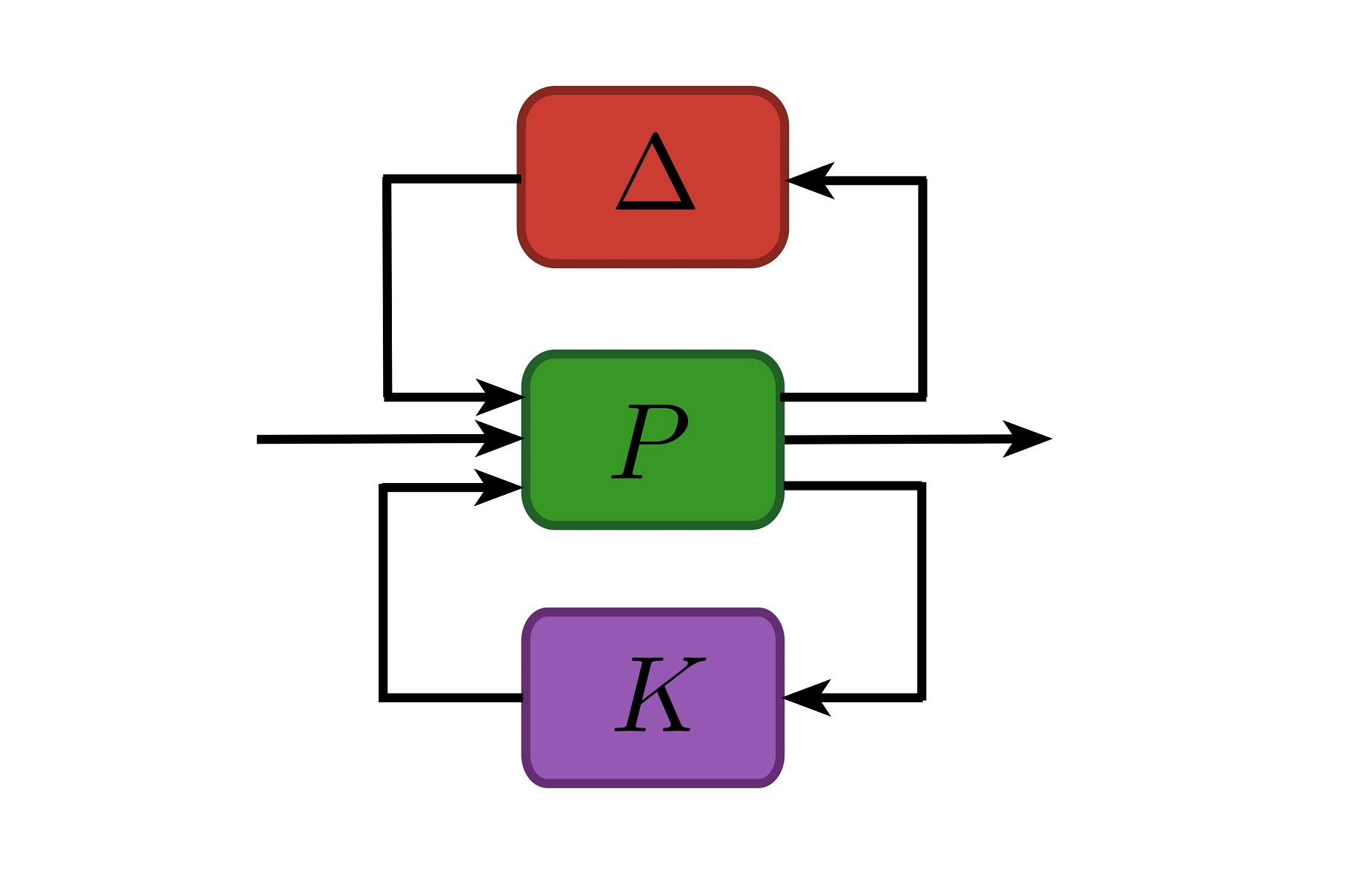
کنترل مقاوم به کنترل دستگاه‌های نامعلوم با دینامیک نامعلوم ناشی از اغتشاش‌های نامعلوم اطلاق می‌شود. واضح است که مسئله اصلی سیستم‌های کنترل مقاوم نامعینی و چگونگی برخورد سیستم کنترل با این مشکل است. شکل ۲ نمایی از حلقه کنترل ساده‌ای است که در بالا نشان دادیم.

نامعینی وارد بر سیستم در سه مکان نشان داده شده است. در مدل دستگاه، نامعینی وجود دارد. اغتشاش‌هایی وجود دارد که در سیستم رخ می‌دهد. همچنین نویزهایی وجود دارد که در ورودی‌های سنسور خوانده می‌شود. هر کدام از این نامعینی‌ها می‌توانند یک مؤلفه جمع‌شونده یا ضرب‌شونده داشته باشد.

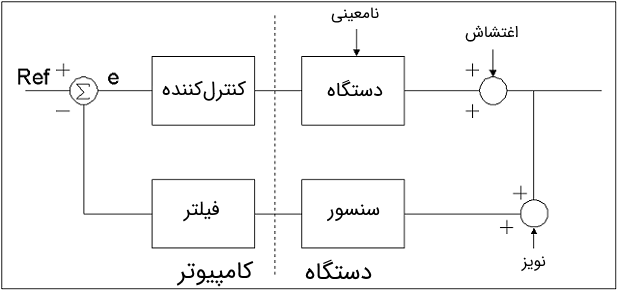
شکل بالا همچنین جدایی سیستم کنترل کامپیوتری را از دستگاه نشان می‌دهد. درک این نکته مهم است که طراح سیستم کنترل، کنترل اندکی روی نامعینی سیستم دارد. طراح، یک سیستم کنترل طراحی می‌کند که مبتنی بر مدل دستگاه است. البته سیستم کنترل پیاده شده باید با سیستم واقعی تعامل داشته باشد، نه با مدل آن.

اثر نامعینی

مهندسان سیستم‌های کنترل با سه موضوع اصلی سر و کار دارند: رؤیت‌پذیری، کنترل‌پذیری و پایداری. رؤیت‌پذیری قابلیت مشاهده همه پارامترها یا متغیرهای حالت سیستم است. کنترل‌پذیری قابلیت بردن یک سیستم از یک حالت مشخص به هر حالت دلخواه است. پایداری اغلب به عنوان پاسخ کران‌دار سیستم به هر ورودی کران‌دار بیان می‌شود. هر سیستم کنترل موفق و مناسب این سه ویژگی را دارد. نامعینی چالشی برای مهندس سیستم کنترل ایجاد می‌کند که باید این ویژگی‌ها را با اطلاعات محدود حفظ کند.

یکی از راه‌های مقابله با نامعینی کنترل تصادفی است. در کنترل تصادفی نامعینی‌های سیستم به صورت توزیع‌های احتمالاتی مدل می‌شوند. این توزیع‌ها با هم ترکیب شده و قانون کنترل را می‌سازند. این روش با امید ریاضی کنترل سر و کار دارد. موقعیت‌های غیرنرمال ممکن است منجر به نتایجی شوند که لزوماً به امید ریاضی نزدیک نیستند. این موضوع ممکن است در سیستم‌های توکار که ایمنی آن‌ها اهمیت دارد، مطلوب نباشد.

روش‌های کنترل مقاوم به دنبال بیان نامعینی به جای توزیع آماری هستند. با توجه به نامعینی، کنترل می‌تواند نتایج مطابق با الزامات سیستم کنترل را در همه موارد ارائه دهد. بنابراین، نظریه کنترل مقاوم را می‌توان به عنوان روش تحلیل بدترین حالت بیان کرد تا تضمین شود که سیستم الزامات مشخصی را برآورده می‌کند.

مدل‌سازی

یکی از متفاوت‌ترین بخش‌های طراحی یک سیستم کنترل مناسب مدل‌سازی رفتار دستگاه است. دلایل متفاوتی برای دشوار بودن مدل‌سازی وجود دارد:

• داده‌های ناقص سیستم: اغلب، مقدار کمی داده دقیق درباره دستگاه در دسترس است. بسیاری از سیستم‌های کنترل به صورت همزمان با دستگاه طراحی می‌شوند. حتی اگر دستگاه‌های مشابهی وجود داشته باشد، هر دستگاه به دلیل وجود تلرانس‌هایی که دارد، اندکی با سایرین تفاوت خواهد داشت.
• سیستم‌های متغیر با زمان: دینامیک برخی از دستگاه‌ها با زمان تغییر می‌کند. یک مدل کنترل ثابت ممکن است نتواند به صورت دقیق دستگاه را در همه زمان‌ها نشان دهد.
• دینامیک‌های مرتبه بالا: برخی دستگاه‌ها دینامیک فرکانس بالایی دارند که اغلب در مدل نامی دستگاه از آن چشم‌پوشی می‌شود. برای مثال، ارتعاش ممکن است موجب اثرات ناخواسته در فرکانس‌های بالا شود. گاهی این دینامیک نامعلوم است و گاهی عامدانه برای ساده کردن مدل در نظر گرفته نمی‌شود.
• غیرخطی بودن: اغلب سیستم‌های کنترل با فرض سیستم‌های تغییر ناپذیر با زمان خطی (LTI) طراحی می‌شوند. دلیل این کار این است که تحلیل سیستم بسیار ساده خواهد شد. با این حال، تمام سیستم‌هایی که در دنیای واقعی با آن‌ها سر و کار داریم، مؤلفه غیرخطی دارند. بنابراین مدل همیشه تقریبی از رفتار دنیای واقعی خواهد بود.
• پیچیدگی: مدل‌سازی سیستم‌های مکانیکی و الکتریکی ذاتاً دشوار است. حتی یک سیستم ساده نیازمند معادلات دیفرانسیل پیچیده برای توصیف رفتارش است.
• مهارت‌ها: مدل‌سازی نیازمند مهارت‌های متنوعی است. پدیده‌های فیزیکی مانند انتقال حرارت برای مدل‌سازی رفتار و اندازه‌گیری این رفتار به متخصص فیزیک نیاز دارند. سیستم‌هایی با اجسام یا محرک‌های صلب به مهندسان مکانیک نیاز دارند. تبدیل پارامترهای فیزیکی به سیگنال‌هایی که قابلیت پایش داشته باشند، به مهندسان برق نیاز دارد. الگوریتم‌های کنترل دستگاه مستلزم استفاده از ریاضیات کاربردی است. پیاده‌سازی الگوریتم‌های کنترلی روی سیستم‌های دیجیتال را نیز مهندسان کامپیوتر انجام می‌‌دهند.

در یک سیستم توکار، منبع محاسباتی و هزینه مسئله مهمی است. موضوع مهم برای مهندس کنترل این است که مدلی را سنتز کند که به اندازه کافی برای پیاده‌سازی ساده باشد تا بتواند محدودیت‌ها را مدیریت کند. علاوه بر این، مدل باید به اندازه کافی دقیق عمل کند تا الزامات عملکرد را برآورده سازد. مهندس کنترل مقاوم همچنین می‌خواهد که این مدل ساده نسبت به نامعینی غیرحساس باشد. این ساده‌سازی مدل دستگاه اغلب «کاهش مدل» (Model Reduction) نامیده می‌شود.

یکی از تکنیک‌های مورد استفاده برای کنترل نامعینی مدل که اغلب در فرکانس‌های بالا اتفاق می‌افتد، تعادل عملکرد و قوام (مقاوم بودن) سیستم است. بهره زیاد بدین معنی است که سیستم به سرعت به اختلاف بین حالت مطلوب و حالت واقعی دستگاه پاسخ می‌دهد. در فرکانس‌های پایین که دستگاه به طور دقیق مدل‌سازی شده باشد، این بهره بالا (نزدیک به ۱) منجر به عملکرد خوب سیستم می‌شود. این ناحیه از عملکرد، باند عملکرد نامیده می‌شود. در فرکانس‌های بالا که دستگاه به طور دقیق مدل نمی‌شود، بهره کمتر است. بهره کم در فرکانس‌های بالا منجر به یک خطای بزرگ‌تر بین خروجی اندازه‌گیری‌شده و سیگنال مرجع می‌شود. این ناحیه، باند قوام نامیده می‌شود. در این ناحیه، فیدبک از خروجی اساساً نادیده گرفته می‌شود.

روش تغییر بهره برای فرکانس‌های مختلف از طریق تابع تبدیل انجام می‌شود. این موضوع شامل تنظیم قطب‌ها و صفرهای تابع تبدیل برای دستیابی به یک فیلتر است. بین این دو ناحیه، عملکرد و قوام، یک ناحیه گذار وجود دارد. در این ناحیه، کنترل‌کننده عملکرد یا قوام خوبی ندارد. ناحیه گذار نمی‌تواند به طور دلخواه کوچک شود، زیرا به تعداد قطب‌ها و صفرهای تابع تبدیل بستگی دارد. اضافه کردن جملات به تابع تبدیل، پیچیدگی سیستم کنترل را افزایش می‌دهد. بنابراین، بین سادگی مدل و حداقل اندازه باند گذار، یک مصالحه برقرار می‌شود.

ابزارها و روش‌های کنترل مقاوم

تاکنون، تکنیک‌های مختلف و متنوعی برای کنترل مقاوم ارائه شده‌ است. درک مفاهیم این تکنیک‌ها دشوار و پیاده‌سازی‌شان خسته‌کننده است و در این آموزش نمی‌گنجد. توضیحات مفصل این تکنیک‌ها در مقالات و کتاب‌ها بر جزئیات ریاضیات آن‌ها متمرکز است و نه مفهوم کلی‌شان. در این ادامه، موارد اصلی را بیان می‌کنیم و به طور خلاصه، مفهوم اصلی پشت هر تکنیک را شرح می‌دهیم. درک دقیق یک تکنیک خاص مستلزم مطالعه گسترده است.

• کنترل تطبیقی: یک سیستم کنترل تطبیقی، رؤیت‌گرهایی را برای هر متغیر حالت مورد نظر در سیستم تشکیل می‌دهد. این سیستم می‌تواند هر رؤیت‌گری را تنظیم کند و پارامترهای مختلف سیستم را که از نظر زمان متغیر هستند در نظر بگیرد. در یک سیستم تطبیقی، همیشه نقش دوگانه در سیستم کنترل وجود دارد؛ خروجی قرار است ورودی را دنبال کند و همزمان، سیستم باید به تخمین پارامترهای متغیر با زمان سیستم ادامه دهد. این روش گاهی با مشکلاتی از جمله عدم همگرایی پارامترهای سیستم مواجه می‌شود.
• $$H_2$$ و $$H_ {infinity}$$: از «نُرم‌های هنکل» (Hankel Norms) برای سنجش خواص سیستم کنترل استفاده می‌شود. نرم، انتزاعی از مفهوم طول است. هر دو روش تکنیک‌های حوزه فرکانس هستند. کنترل $$H_ 2$$ به دنبال محدود کردن بهره توان سیستم است، در حالی که کنترل $$H_ {infinity}$$ بهره انرژی سیستم را محدود می‌کند. بهره‌های توان یا انرژی در سیستم نشانگر عملکرد سیستم در نزدیکی قطب تابع تبدیل است. این موقعیت‌ها ناپایدار هستند.
• تخمین پارامتر: تکنیک‌های تخمین پارامتر مرزهایی را در حوزه فرکانس ایجاد می‌کنند که برای حفظ پایداری نمی‌توان از آن‌ها عبور کرد. این مرزها با استفاده از بردارهای نامعینی ارزیابی می‌شوند. این تکنیک گرافیکی است و شباهت‌هایی با روش مکان هندسی ریشه‌ها دارد. پیشرفت این روش بر اساس ساده‌سازی محاسباتی در ارزیابی این موضوع است که آیا نامعینی‌های متعدد باعث می‌شوند سیستم از مرز پایداری عبور کند یا خیر. این تکنیک‌ها اطلاعاتی در مورد چگونگی تغییر سیستم برای حساسیت کمتر نسبت به نامعینی‌ها در اختیار کاربر قرار می‌دهند.
• لیاپانوف: تنها تکنیک کلی برای ارزیابی سیستم‌های غیرخطی روش لیاپانوف است. این روش بر پایداری تمرکز دارد. توابع لیاپانوف که مشابه توابع انرژی هستند، رفتار سیستم‌های واقعی را مدل می‌کنند. این توابع در طول مسیر سیستم مورد بررسی قرار می‌گیرند تا ببینیم که مشتق اول اتلاف انرژی است یا خیر. هرگونه افزایش انرژی بیانگر این است که سیستم در نزدیکی یک قطب کار می‌کند و بنابراین ناپایدار خواهد بود.
• کنترل فازی: کنترل فازی مبتنی بر ساخت مجموعه‌های فازی برای توصیف عدم قطعیت ذاتی در همه متغیرها و روشی برای ترکیب این متغیرها به نام منطق فازی است. کنترل فازی در کنترل مقاوم کاربرد دارد، زیرا روشی برای کنترل نامعینی سیستم است. کنترل فازی یک موضوع بحث برانگیز است. طرفداران آن ادعا می‌کنند که بدون نیاز به مدل‌سازی ریاضی پیچیده، می‌توانند سیستم را کنترل کنند. مواردی وجود دارد که تعداد زیادی از متغیرها کنترل می‌شوند که از نظر شهودی واضح است (اما از نظر ریاضی آشکار نیست). یک مثال رایج از کنترل فازی پارک کردن خودرو است.

در آموزش‌های بعدی، روش‌های کنترل مقاوم را معرفی خواهیم کرد.