کنترل تطبیقی — از صفر تا صد

در آموزش‌های پیشین مجله فرادرس، با روش‌های کنترل فازی و کنترل پیش‌بین آشنا شدیم. در این آموزش با یک رویکرد دیگر در مهندسی کنترل، به نام کنترل تطبیقی آشنا می‌شویم.

تاریخچه کنترل تطبیقی

پژوهش در زمینه کنترل تطبیقی تاریخچه‌ای طولانی دارد. در اوایل دهه ۱۹۵۰ میلادی، طراحی خلبان‌های خودکار برای هواپیماها موجب پیشرفت پژ‌وهش در زمینه کنترل تطبیقی شد. با تغییر نقطه کار پرواز، دینامیک هواپیما دچار تغییرات شدیدی می‌شود که نمی‌توان آن را با یک کنترل فیدبکی با بهره ثابت کنترل کرد. بنابراین، به یک کنترل پیچیده، مانند کنترل‌کننده تطبیقی، نیاز بود که بتواند تغییرات را یاد گرفته و سیستم را با آن‌ها وفق دهد. بنابراین، کنترل تطبیقی مدل رجع توسط وایتکر (Whitaker) و همکارانش برای حل مسئله کنترل خلبان خودکار ارائه شد. روش حساسیت و قانون MIT نیز برای طراحی قوانین تطبیق طرح‌های کنترل تطبیقی مختلف مورد استفاده قرار گرفت. یک طرح کنترل جایابی قطب مبتنی بر مسئله خطی مرتبه دوم بهینه نیز توسط کالمن پیشنهاد شد.

فیلم آموزش کنترل بهینه در فرادرس

کلیک کنید

کار در زمینه کنترل پرواز تطبیقی در آن زمان را می‌توان با «شور و شوق زیاد، سخت‌افزار بد و عدم وجود نظریه» توصیف کرد. عدم اثبات پایداری و عدم درک ویژگی‌های طرح‌های کنترل تطبیقی در کنار فاجعه در یک آزمایش پروازی، سبب شد علاقه به کنترل تطبیقی کاهش پیدا کند.

اما دهه ۱۹۶۰ مهم‌ترین دوره توسعه نظریه کنترل و به ویژه کنترل تطبیقی بود. روش‌های فضای حالت و نظریه پایداری مبتنی بر لیاپانوف در این دوره معرفی شدند. پیشرفت‌ها در زمینه برنامه‌ریزی پویا، کنترل دوگانه، و کنترل تصادفی و در شناسایی سیستم و تخمین پارامتر نقش مهمی در بازنویسی و بازطراحی کنترل تطبیقی داشت. در سال ۱۹۶۶، پارکس و همکارانش، با استفاده از رویکرد طراحی لیاپانوف به راهی برای بازطراحی قوانین تطبیق مبتنی بر قاعده MIT که در کنترل تطبیقی مدل مرجع استفاده شده بود، رسیدند. کار آن‌ها، با اینکه به دسته‌ خاصی از سیستم‌های LTI قابل اعمال بود، باب تازه‌ای در اثبات دقیق پایداری در کنترل تطبیقی سیستم‌های عمومی‌تر گشود.

پیشرفت‌ها در زمینه نظریه پایداری و پیشرفت در نظریه کنترل در دهه ۱۹۶۰ درک کنترل تطبیقی را بهبود دارد و منجر به زمینه‌های جدید در دهه ۱۹۷۰ شد. از طرف دیگر، پیشرفت همزمان کامپیوترها و الکترونیک که موجب امکان پیاده‌سازی کنترل‌کننده‌های پیچیده، مانند این کنترل‌کننده‌های تطبیقی، می‌شد، جذابیت کاربردهای کنترل تطبیقی را مضاعف کرد. دهه ۱۹۷۰ شاهد چندین نتیجه امیدوارکننده در طراحی کنترل تطبیقی بود. در آن سال‌ها، کنترل تطبیقی مدل مرجع مبتنی بر طراحی لیاپانوف ارائه و تحلیل شد. همچنین، مفاهیم مثبت بودن و اَبَرپایداری برای توسعه دسته وسیعی از طرح‌های کنترل تطبیقی مدل مرجع با پایداری اثبات شده مورد استفاده قرا گرفت.

همزمان، تلاش‌هایی برای سیستم‌های زمان‌گسسته در یک محیط قطعی و تصادفی انجام شد و به چندین دسته مختلف از کنترل‌کننده‌های تطبیقی با اثبات پایداری قوی انجامید.

موفقیت‌های دهه ۱97۰ با تردیدهایی درباره پیاده‌سازی عملی کنترل تطبیقی همراه شد. در اوایل سال ۱۹۷۹ این نتیجه حاصل شد که طرح‌های ارائه شده دهه ۱۹۷۰ در صورت وجود اغتشاش‌های کوتاه به ناپایداری می‌انجامند. رفتار غیرمقاوم کنترل تطبیقی در اوایل دهه ۱۹۸۰ بسیار جنجالی شد؛ به ویژه اینکه مثال‌های بیشتری از ناپایداری و مشاهده عدم قوام در حضور دینامیک‌های مدل نشده یا اغتشاش‌های محدود گزارش شده بود. این موضوع محققان را بر این داشت تا ساز و کار ناپایداری‌ها را بررسی کنند و راه‌هایی برای غلبه بر آن‌ها بیابند. در اواسط دهه ۱۹۸۰ میلادی، طرح‌های جدیدی پیشنهاد شد و مورد تجزیه و تحلیل قرار گرفت. این طرح‌ها اساس آنچه را تشکیل داد که امروزه به عنوان کنترل تطبیقی مقاوم شناخته می‌شود. بدین ترتیب، یک کنترل‌کننده تطبیقی، مقاوم تعریف می‌شد اگر کران‌داری سیگنال در حضور دسته‌هایی از دینامیک‌های مدل نشده و اغتشاش‌های کران‌دار تضمین شده بود. کار بر روی کنترل تطبیقی مقاوم در دهه ۱۹۸۰ ادامه پیدا کرد و در قالب اصلاحات مقاوم مختلف و یکپارچگی آن‌ها در چارچوب‌های عمومی‌تر بیان شد.

حل مسئله قوام در کنترل تطبیقی به حل مسئله دیرینه کنترل یک سیستم خطی که پارامترهای آن نامعلوم‌ هستند یا با زمان تغییر می‌کنند، انجامید. در پایان دهه ۱۹۸۰ چند نتیجه موفق در زمینه کنترل تطبیقی سیستم‌های خطی تغییر پذیر با زمان منتشر شد.

تمرکز تحقیقات در زمینه کنترل تطبیقی از اواخر دهه ۱۹۸۰ تا اوایل دهه ۱۹۹۰ بر مشخصه‌های عملکرد و توسعه نتایج دهه ۱۹۸۰ برای سیستم‌های غیرخطی با پارامترهای نامعلوم بود. این تلاش‌ها منجر به دسته‌های جدیدی از طرح‌های کنترل تطبیقی شد که از نظریه سیستم غیرخطی گرفته شده بود.

کنترل تطبیقی چیست؟

«تطبیق یافتن» معادل "to adapt" و به معنی «تغییر دادن به گونه‌ای که رفتار موجود با شرایط جدید مطابقت داشته باشد» است. کنترل تطبیقی نیز بر همین مطابقت با تغییر اشاره دارد. اصطلاحات «سیستم‌های تطبیقی» (Adaptive Systems) و «کنترل تطبیقی» (Adaptive Control) به اوایل دهه ۱۹۵۰ بر می‌گردند.

فیلم آموزش کنترلرهای تطبیقی خود تنظیم با متلب در فرادرس

کلیک کنید

همان‌طور که گفتیم، طراحی خلبان‌های خودکار برای هواپیماها یکی از انگیزه‌های اولیه برای تحقیقات در زمینه کنترل تطبیقی بود. هواپیماها در سرعت‌ها و ارتفاع‌های مختلفی کار می‌کنند و دینامیک آن‌ها غیرخطی و متغیر با زمان است. برای یک نقطه کار مشخص (سرعت و ارتفاع)، دینامیک پیچیده هواپیما را می‌توان با با یک مدل خطی تقریب زد. برای مثال، در نقطه کار $$i$$، مدل خطی هواپیما به فرم زیر است:

$$ \large \begin {align*}
\dot {x} & = A _ i x + B _ i u, \;\; x ( 0 ) = x _ 0 \\
y & = C _ i ^ \top x + D _ i u
\end {align*} \;\;\;\;\; (1) $$

که در آن، $$ A_i$$، $$B_i$$، $$C _ i $$ و $$ D_ i $$ تابع شرایط نقطه کار $$i$$ هستند. وقتی هواپیما در شرایط مختلف پرواز قرار گیرد، نقاط کار تغییر کرده و منجر به مقادیر مختلف $$ A_i$$، $$B_i$$، $$C_i$$ و $$ D_ i $$ خواهد شد. از آنجایی که پاسخ خروجی $$y(t)$$ اطلاعاتی درباره حالت $$x$$ و همچنین پارامترها دارد، انتظار می‌رود یک کنترل‌کننده فیدبک پیشرفته این توانایی را داشته باشد که تغییرات پارامتر را با پردازش $$y(t)$$ یاد گرفته و از بهره‌های مناسب برای سازگاری با آن‌ها استفاده کند. این گفته منجر به یک ساختار کنترل فیدبک می‌شود که کنترل تطبیقی بر آن بنا شده است. ساختار این کنترل‌کننده از یک حلقه فیدبک و یک کنترل‌کننده با بهره‌های قابل تنظیم تشکیل شده است (شکل ۱).

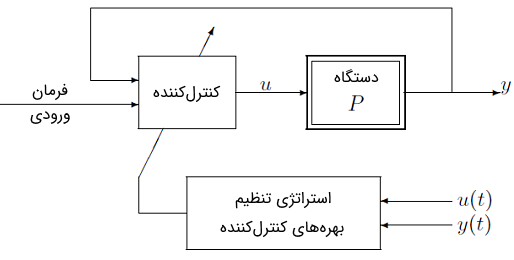
روش تغییر بهره‌های کنترل‌کننده در پاسخ به تغییرات دستگاه و دینامیک اغتشاش منجر به طرح‌های کنترلی متفاوتی می‌شود. در ادامه، طرح‌های مختلف کنترل تطبیقی را بررسی می‌کنیم.

کنترل مقاوم و کنترل تطبیقی

برای غلبه بر تغییرات پارامتر که در محدوده‌های کران‌دار قرار دارد، می‌توان یک کنترل‌کننده فیدبک با بهره ثابت طراحی کرد. نمودار بلوکی چنین کنترل‌کننده‌ای در شکل ۲ نشان داده شده است که در آن، $$ G (s)$$ تابع تبدیل دستگاه و $$ C( s) $$ تابع تبدیل کنترل‌کننده است.

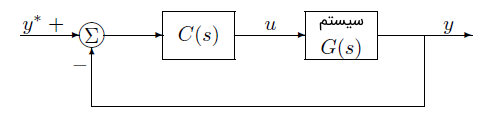
تابع تبدیل از $$ y^*$$ به $$y$$ به صورت زیر به دست می‌آید:

$$ \large \frac { y } { y ^ * } = \frac { C ( s ) G ( s ) } { 1 + C ( s ) G ( s ) } \;\;\;\;\; ( 2 ) $$

که در آن، $$ C ( s ) $$ باید به گونه‌ای انتخاب شود که سیستم حلقه‌بسته، علی‌رغم تغییرات پارامتر یا نامعینی‌های $$ G ( s)$$، پایدار بوده و در محدوده فرکانس مورد نظر، $$ y \approx y ^ * $$ باشد. این شرط آخر با انتخاب $$ C ( s) $$ به طوری که بهره حلقه $$ | C ( j \omega ) G ( j \omega)|$$، در صورت امکان، در طیف فرکانسی $$ y ^ * $$ بزرگ باشد، قابل حصول است. البته این بهره حلقه بزرگ الزامات پایداری حلقه‌بسته را نقض نمی‌کند. با طراحی $$ C ( s) $$ به گونه‌ای که تغییرات $$G(s)$$ در محدوده مشخصی باشند، می‌توان به اهداف ردیابی و پایداری دست یافت.

البته لازم به ذکر است که کنترل مقاوم به عنوان یک سیستم تطبیقی در نظر گرفته نمی‌شود؛ حتی اگر بتواند دسته‌های خاصی از نامعینی‌های پارامتری و دینامیکی را مدیریت کند.

جدول‌بندی بهره

مدل (۱) هواپیما را در نظر بگیرید که برای هر نقطه کار $$i$$ ($$i = 1 , 2 , \ldots , N $$) داده شده و پارامترهای $$ A_ i $$، $$ B_ i $$، $$ C_ i $$ و $$ D_ i $$ آن معلوم هستند. برای نقطه کار $$i$$، می‌توان یک کنترل‌کننده فیدبکی با بهره‌های ثابت $$ \theta _ i $$ طراحی کرد که الزامات عملکرد مدل خطی مربوطه را برآورده کند. این منجر به کنترل‌کننده $$ C (\theta)$$ با مجموعه بهره‌های $$\{ \theta _ 1, \theta _ 2 , \ldots , \theta _ i , \ldots , \theta _ N \}$$ برای $$N$$ نقطه کار خواهد شد.

فیلم آموزش کاربرد متلب در کنترل خطی در فرادرس

کلیک کنید

وقتی نقطه کار $$i$$ آشکار شود، بهره‌های کنترل‌کننده را می‌توان برای رسیدن به $$\theta _ i $$ مناسب تغییر داد. این مجموعه بهره‌ها از قبل محاسبه شده است. انتقال یا گذار بین نقاط کار مختلف که منجر به تغییرات پارامتر قابل توجهی می‌شود را می‌توان با درون‌یابی یا افزایش تعداد نقاط کار مدیریت کرد. دو عنصر مهم در پیاده‌سازی این روش، جدول جست‌وجو (Look-up Table) برای ذخیره مقادیر $$ \theta _ i $$ و اندازه‌گیری‌های کمکی سیستم (مرتبط با تغییرات در نقاط کار) است. این روش جدول‌بندی بهره (Gain Scheduling) نامیده می‌شود و در شکل ۳ نشان داده شده است.

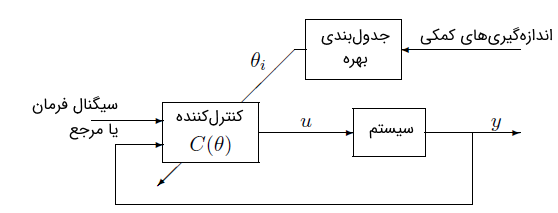
جدول‌بندی بهره از یک جدول جست‌وجو و منطق مناسب برای آشکارسازی نقطه کار و انتخاب مقدار $$ \theta _ i $$ از جدول تشکیل شده است. در مورد هواپیما، اندازه‌گیری‌های کمکی سرعت (عدد ماخ) و فشار دینامیکی هستند. در این روش، تغییرات پارامتر سیستم را می‌توان با تغییر بهره‌های کنترل‌کننده به عنوان توابعی از اندازه‌گیری‌های کمکی جبران کرد.

مزیت جدول‌بندی بهره این است که بهره‌های کنترل‌کننده را می‌توان به سرعتِ پاسخ اندازه‌گیری‌های کمکی به تغییرات پارامتر تغییر داد. البته، تغییرات مکرر و سریع بهره‌های کنترل‌کننده ممکن است به ناپایداری سیستم منجر شود. بنابراین، محدودیتی برای تعداد دفعات و سرعت تغییر بهره‌های کنترل‌کننده وجود دارد.

یکی از معایب جدول‌بندی بهره این است که ساز و کار تنظیم بهره‌های کنترل‌کننده به صورت برون‌خط (آفلاین) از قبل محاسبه شده و به همین دلیل، فیدبکی برای جبران اشتباه ندارد. همچنین، تغییرات پیش‌بینی نشده در دینامیک سیستم ممکن است منجر به زوال عملکرد و یا حتی خرابی کامل آن شوند. یک عیب دیگر این روش، هزینه‌های بالای طراحی و پیاده‌سازی است که با افزایش تعداد نقاط کار بیشتر نیز می‌شود.

علی‌رغم این محدودیت‌ها، جدول‌بندی بهره یک روش محبوب برای مدیریت تغییرات پارامتر در کنترل پرواز و سایر سیستم‌ها است.

کنترل تطبیقی مستقیم و غیرمستقیم

کنترل‌کننده تطبیقی از ترکیب یک تخمینگر پارامتر برخط (آنلاین)، که در هر لحظه پارامترهای نامعلوم را تخمین می‌زند و یک قانون کنترل با پارامتر معلوم تشکیل می‌شود. تخمینگرِ پارامتر را که قانون تطبیق (Adaptive Law) نیز نامیده می‌شود، می‌توان به دو صورت با قانون کنترل ترکیب کرد.

در روش اول، که کنترل تطبیقی غیرمستقیم (Indirect Adaptive Control) نام دارد، پارامترهای دستگاه یا سیستم به صورت آنلاین تخمین زده شده و برای محاسبه پارامترهای کنترل‌کننده مورد استفاده قرار می‌گیرند. این روش کنترل تطبیقی صریح (Explicit Adaptive Control) نیز نامیده می‌شود، زیرا طراحی براساس یک مدل صریح انجام می‌شود.

در روش دوم، که به کنترل تطبیقی مستقیم (Direct Adaptive Control) معروف است، مدل سیستم برحسب پارامترهای کنترل‌کننده به صورت پارامتری است و این پارامترها مستقیماً و بدون تخمین پارامترهای سیستم تحت کنترل تخمین زده می‌شوند. از این روش با نام کنترل تطبیقی ضمنی (Implicit Adaptive Control) نیز یاد می‌شود، زیرا طراحی آن مبتنی بر تخمین مدل ضمنی سیستم است.

کنترل تطبیقی غیرمستقیم

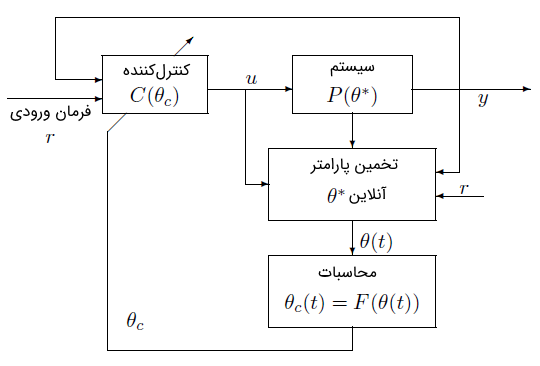
در کنترل تطبیقی غیرمستقیم، مدل $$ P ( \theta ^ * ) $$ نسبت به بردار پارامتر مجهول $$ \theta ^ * $$ پارامتری می‌شود. برای مثال، در مدل یک سیستم خطی تغییرناپذیر با زمان (LTI) تک‌ورودی-تک‌خروجی (SISO)، $$ \theta ^ * $$ نشان دهنده ضرایب نامعلوم صورت و مخرج تابع تبدیل سیستم است. یک تخمینگر پارامتر آنلاین تخمین $$ \theta ( t) $$ را از $$ \theta ^ * $$ در هر زمان $$t$$ با پردازش ورودی $$u$$ و خروجی $$y$$ سیستم تولید می‌کند. تخمین پارامتر $$ \theta ( t) $$ یک مدل تخمین زده شده را مشخص خواهد کرد که با $$ \hat { P } ( \theta ( t))$$ نشان داده شده و در طراحی کنترل به عنوان مدل «صحیح» سیستم در نظر گرفته می‌شود و برای محاسبه پارامتر کنترل‌کننده یا بردار بهره $$ \theta _ c ( t) $$ با حل معادله جبری مشخص $$ \theta _ c ( t) = F (\theta ( t))$$ در زمان $$t$$ مورد استفاده قرار می‌گیرد.

فرم قانون کنترل $$ C (\theta _ c )$$ و معادله جبری $$ \theta _ c = F ( \theta ) $$ مشابه فرم قانون کنترل $$ C ( \theta _ c ^ * )$$ و معادله $$ \theta _ c ^ * = F ( \theta ^*) $$ انتخاب می‌شود تا بتوان الزامات عملکرد مدل را برآورده کرد.

بنابراین، واضح است که با این روش، $$ C ( \theta _ c ( t))$$ در هر لحظه به گونه‌ای طراحی می‌شود که الزامات عملکرد مدل تخمین زده شده $$ \widehat {P} (\theta (t))$$ را که ممکن است نسبت به مدل نامعلوم $$ P (\theta ^*)$$ متفاوت باشد، برآورده کند.

در نتیجه، مسئله اصلی در کنترل تطبیقی غیرمستقیم انتخاب دسته‌ای از قوانین کنترل $$ C (\theta _c)$$ و دسته تخمینگرهای پارامتری $$\theta ( t) $$ و معادله جبری $$ \theta _ c ( t) = F (\theta (t))$$ به گونه‌ای است که $$ C ( \theta _ c ( t))$$ الزامات عملکرد مدل $$ P (\theta ^ * )$$ را با متغیر نامعلوم $$ \theta ^ * $$ برآورده کند. نمودار بلوکی طرح کنترل تطبیقی غیرمستقیم در شکل ۴ نشان داده شده است.

کنترل تطبیقی مستقیم

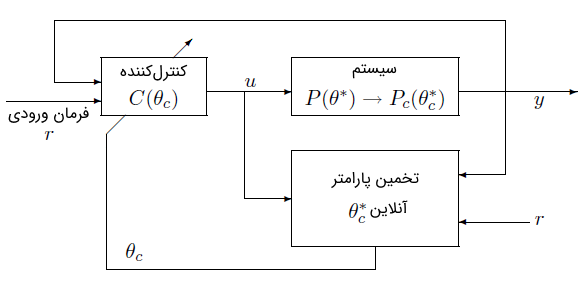
در کنترل تطبیقی مستقیم، مدل $$ P (\theta ^ * )$$ برحسب بردار پارامترهای نامعلوم $$ \theta ^ * _ c $$ کنترل‌کننده، به گونه‌ای پارامتری می‌شود که کنترل‌کننده $$ C (\theta ^ * _ c )$$ الزامات عملکرد مدل $$ P_ C ( \theta ^ * _ c ) $$ را با مشخصه دقیقاً‌ مشابه با مشخصه ورودی-خروجی $$ P ( \theta ^ * ) $$ برآورده سازد.

در این رویکرد کنترلی، تخمینگر آنلاین به جای $$P(\theta ^*)$$ براساس $$P_c(\theta _c^*)$$ طراحی شده است تا در هر لحظه، با پردازش ورودی $$u$$ و خروجی $$y$$ دستگاه، مستقیماً تخمین $$\theta _ c ( t) $$ را برای $$\theta ^*_c$$ مهیا کند. پس از آن، برای به‌روزرسانی بردار $$\theta_c$$ پارامتر کنترل‌کننده، از تخمین $$ \theta _ c ( t) $$ استفاده می‌شود. مسئله اساسی کنترل تطبیقی مستقیم، انتخاب دسته قوانین کنترل $$ C ( \theta _ c )$$ و تخمینگرهای $$\theta _ c ( t)$$ برای داشتن کنترل‌کننده $$C( \theta _ c ( t))$$ که موجب برآورده شدن الزامات عملکرد مدل $$P(\theta ^ *) $$ است.

ویژگی‌های مدل $$ P (\theta^*)$$ در به دست آوردن مدل پارامتری $$ P _ c (\theta _ c ^ *)$$ که تخمین آنلاین آن راحت باشد، بسیار مهم هستند. در نتیجه، کنترل تطبیقی مستقیم به دسته‌های مشخصی از مدل‌ها محدود می‌شود. دسته‌ای از مدل‌ها که برای کنترل تطبیقی مستقیم مناسب هستند، شامل همه مدل‌های LTI و SISO می‌شوند که کمینه فاز باشند؛ یعنی صفرهای آن‌ها در سمت چپ محور موهومی صفحه مختلط واقع شده باشد. نمودار بلوکی کنترل تطبیقی مستقیم در شکل ۵ نشان داده شده است.

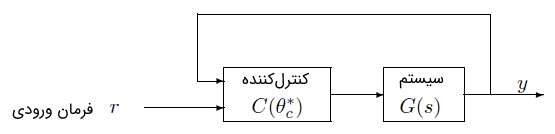
قاعده اصلی در طراحی کنترل تطبیقی مستقیم و غیرمستقیم در شکل‌های ۴ و ۵ به صورت ساده نشان داده شد. در طراحی $$ C (\theta _ c ) $$ از تخمین $$ \theta _ c ( t) $$ (در کنترل تطبیقی مستقیم) یا تخمین $$ \theta ( t) $$ (در کنترل تطبیقی غیرمستقیم) درست مانند مقادیر اصلی‌شان استفاده می‌کنیم. این روش طراحی هم‌ارزی قطعیت (Certainty Equivalence) نام دارد و می‌توان از آن برای تولید دسته وسیعی از طرح‌های کنترل تطبیقی با ترکیب تخمین‌های آنلاین با قوانین کنترلی مختلف استفاده کرد.

ایده پشت این هم‌ارزی آن است که وقتی تخمین‌های $$ \theta _ c ( t) $$ و $$ \theta (t)$$ به ترتیب به مقادیر واقعی $$ \theta _ c ^ * $$ و $$ \theta ^*$$ همگرا شوند، عملکرد کنترل‌کننده تطبیقی $$ C (\theta _ c ) $$ به عملکردی میل کند که توسط $$ C ( \theta _ c ^ * ) $$ برای پارامترهای معلوم به دست می‌آید.

کنترل تطبیقی مدل مرجع

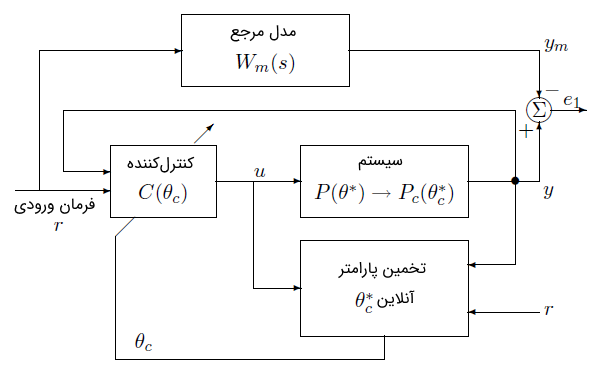
کنترل تطبیقی مدل مرجع (Model Reference Adaptive Control) یا MRAC از مسئله کنترل مدل مرجع (MRC) به دست می‌آید. در MRC، یک درک مناسب از دستگاه و الزامات عملکرد به دست می‌آید و طراح با یک مدل، که مدل مرجع (Reference Model) نامیده می‌شود، ویژگی‌های ورودی-خروجی مطلوب سیستم حلقه‌بسته مطلوب را بیان می‌کند.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

هدف کنترلِ مدل مرجع یافتن یک قانون کنترل فیدبک است که ساختار و دینامیک سیستم را به گونه‌ای تغییر دهد که مشخصه‌ ورودی-خروجی آن دقیقاً مشابه مدل مرجع باشد. ساختار کنترل مدل مرجع برای یک سیستم LTI و SISO در شکل ۶ نشان داده شده است.

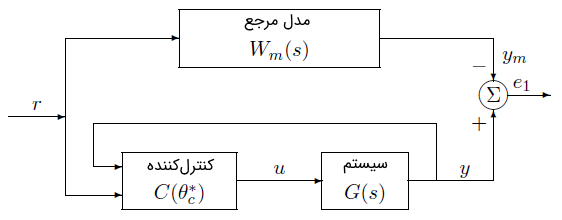
تابع تبدیل $$ W _ m ( s ) $$ مربوط به مدل مرجع به گونه‌ای طراحی شده است که برای یک سیگنال ورودی مرجع $$ r ( t) $$ خروجی $$ y _ m ( t) $$ مدل مرجع، پاسخ مطلوب خروجی $$ y ( t) $$ سیستم اصلی را نتیجه دهد. کنترل‌کننده با $$ C (\theta _ c ^ * )$$ نشان داده شده و به گونه‌ای طراحی می‌شود که همه سیگنال‌ها کران‌دار بوده و تابع تبدیل حلقه‌بسته از $$r$$ به $$y$$ برابر با $$ W _ m ( s) $$ باشد. این تطبیق تابع تبدیل تضمین می‌کند که برای هر ورودی مرجع $$ r (t)$$، خطای ردیابی $$ e _ 1 \triangleq y - y _ m $$، که انحراف خروجی سیستم را از مسیر مطلوب $$ y _ m $$ نشان می‌دهد، با گذشت زمان به صفر میل کند. تطبیق تابع تبدیل با حذف صفرهای $$ G ( s)$$ سیستم و جایگزینی آن‌ها با صفرهای $$W_m(s)$$ با استفاده از کنترل‌کننده فیدبک $$ C (\theta _ c ^ *)$$ انجام می‌شود. حذف صفرهای سیستم یک محدودیت برای سیستم تعیین می‌کند و آن این است که کمینه فاز باشد؛ یعنی صفرهای پایدار داشته باشد. اگر هر صفر سیستم ناپایدار باشد، حذف آن به سادگی منجر به نامحدود شدن سیگنال‌ها خواهد شد.

طراحی $$ C (\theta _ c ^ * )$$ مستلزم دانستن ضرایب تابع تبدیل $$ G( s) $$ سیستم است. اگر $$ \theta ^*$$ برداری شامل همه ضرایب $$ G ( s ) = G ( s , \theta ^ * ) $$ باشد، آنگاه بردار پارامتر $$\theta ^ * _ c $$ را می‌توان با حل یک معادله جبری به فرم زیر محاسبه کرد:

$$ \large \theta _ c ^ * = F ( \theta ^ * ) \;\;\;\;\; (2)$$

بنابراین، واضح است که برای رسیدن به هدف کنترل مدل مرجع، مدل سیستم کمینه فاز باشد و بردار پارامتر $$ \theta ^ * $$ آن دقیقاً‌ معلوم باشد.

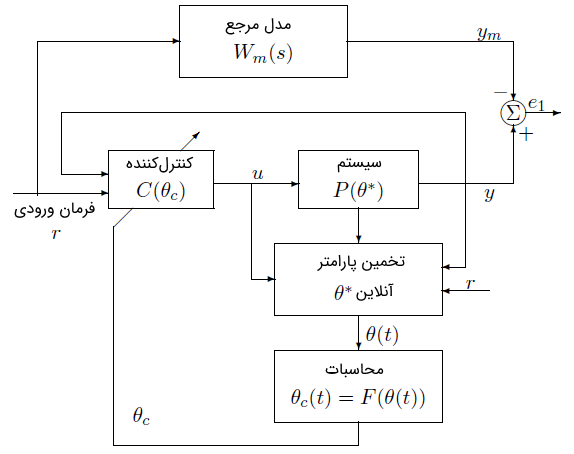
وقتی $$\theta ^ * $$ نامعلوم باشد، کنترل مدل مرجع شکل ۶ را نمی‌توان پیاده‌سازی کرد، زیرا $$\theta _ c ^ * $$ از معادله (۲) قابل محاسبه نیست و در نتیجه، نامعلوم است. یک راه برای کار در حالت نامعلوم بودن پارامتر، استفاده از روش هم‌ارزی قطعیت برای جایگزینی تخمین $$\theta _ c (t)$$ (با استفاده از روش مستقیم یا غیرمستقیم) به جای پارامتر نامعلوم $$ \theta _ c ^ * $$ در قانون کنترل است. این نوع کنترل‌‌کننده‌های تطبیقی را می‌توان در دو دسته غیرمستقیم (شکل ۷) و مستقیم (شکل ۸) دسته‌بندی کرد.

کنترل جایابی قطب تطبیقی

کنترل جایابی قطب تطبیقی (Adaptive Pole Placement Control) یا APPC مبتنی بر کنترل جایابی قطب (Pole Placement Control) یا PPC و مسائل تنظیم در سیستم‌های LTI با پارامترهای معلوم است.

در کنترل جایابی قطب، الزامات عملکرد در قالب مکان قطب‌های سیستم‌ حلقه‌بسته بیان می‌شوند. پس از آن، یک قانون کنترل فیدبک برای جایابی قطب‌های حلقه‌بسته در مکان‌های مطلوب طراحی می‌شود. ساختار رایج PPC برای یک سیستم LTI و SISO در شکل ۹ نشان داده شده است.

ساختار کنترل‌کننده $$ C (\theta ^* _ c )$$ و بردار پارامتر $$ \theta _ c ^*$$ به گونه‌ای انتخاب می‌شوند که قطب‌های تابع تبدیل سیستم حلقه‌بسته از $$r$$ به $$y$$ برابر با مقادیر مطلوب شوند. بردار $$\theta _ c ^*$$ معمولاً‌ از یک معادله جبری به فرم زیر محاسبه می‌شود:

$$ \large \theta _ c ^ * = F ( \theta ^* ) \;\;\;\; ( 3 )$$

که در آن، $$\theta ^*$$ برداری شامل ضرایب تابع تبدیل $$ G ( s ) $$ سیستم است.

اگر $$\theta ^*$$ معلوم باشد، آنگاه $$\theta _c ^*$$ از (۳) محاسبه می‌شود و در قانون کنترل مورد استفاده قرار می‌گیرد. اما اگر $$\theta ^*$$ نامعلوم باشد، $$\theta _ c ^*$$ نیز نامعلوم خواهد بود، و طرح PPC شکل ۹ قابل پیاده‌سازی نیست. مشابه MRC، می‌توانیم با استفاده از رویکرد جایگزینی، به جای بردار نامعلوم $$\theta _c^*$$ از تخمین $$\theta _ c (t)$$ آن استفاده کنیم. اگر $$\theta _ c ( t) $$ مستقیماً با استفاده از یک تخمینگر پارامتر آنلاین به‌روز شود، طرح کنترلی را APPC مستقیم می‌نامند. حال اگر $$\theta _c ( t) $$ با استفاده از معادله زیر محاسبه شود:

$$ \large \theta _ c ( t) = F ( \theta ( t) ) \;\;\;\;\; (4) $$

که در آن، $$\theta ( t) $$ تخمین $$\theta ^*$$ است که با یک تخمینگر آنلاین به دست آمده، به طرح کنترل APPC غیرمستقیم می‌گویند. ساختار APPC مستقیم و غیرمستقیم مشابه بوده و به ترتیب، در شکل‌های ۴ و ۵ در حالت کلی نشان داده شد.

طراحی APPC نسبت به انتخاب فرم کنترل‌کننده $$C(\theta _ c )$$ و تخمینگر پارامتر آنلاین بسیار انعطاف پذیر است. برای مثال، قانون کنترل ممکن است مبتنی بر تکنیک طراحی مرتبه دوم خطی، روش‌های طراحی حوزه فرکانس، یا هر روش جایابی قطب دیگری باشد که در موارد پارامتر معلوم مورد استفاده قرار می‌گیرد. ترکیبات مختلف تخمینگرهای آنلاین و قوانین کنترل منجر به طرح‌های جایابی قطب تطبیقی مختلفی خواهند شد.

این کنترل‌کننده‌ها در کنترل تطبیقی اغلب به عنوان رگولاتور خودتنظیم نیز در نظر گرفته شده و نسبت به کنترل مدل مرجع تمایز داده می‌شوند. البته این تمایز بیشتر تاریخی است تا اینکه مفهومی باشد؛ زیرا کنترل تطبیقی مدل مرجع را می‌توان به عنوان دسته‌ای از کنترل‌کننده‌های تطبیقی جایابی قطب در نظر گرفت. کنترل تطبیقی مدل مرجع ابتدا برای سیستم‌های زمان‌پیوسته و برای دنبال کردن مدل ارائه شد؛ در حالی که کنترل جایابی قطب تطبیقی در ابتدا برای سیستم‌های گسسته‌زمان در یک محیط تصادفی و با استفاده از روش‌های کمینه‌سازی توسعه یافت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترلرهای تطبیقی خود تنظیم با متلب
• مجموعه آموزش‌های مهندسی برق
• آموزش طراحی سیستم‌های تطبیقی مدل مرجع با متلب
• کنترل پیش‌بین در الکترونیک قدرت — از صفر تا صد
• کنترل بهینه در متلب — از صفر تا صد
• کنترل‌کننده PID — مفاهیم و ساختارها

^^