چرا عالم یکنواخت و تخت است؟ | به زبان ساده

در ادامه بحث سوالات بی جواب در کیهان شناسی به سومین و چهارمین سوال بی پاسخ بر اساس نظریه استاندارد انفجار بزرگ می‌پردازیم که توضیح می‌دهد چرا عالم یکنواخت و تخت است.

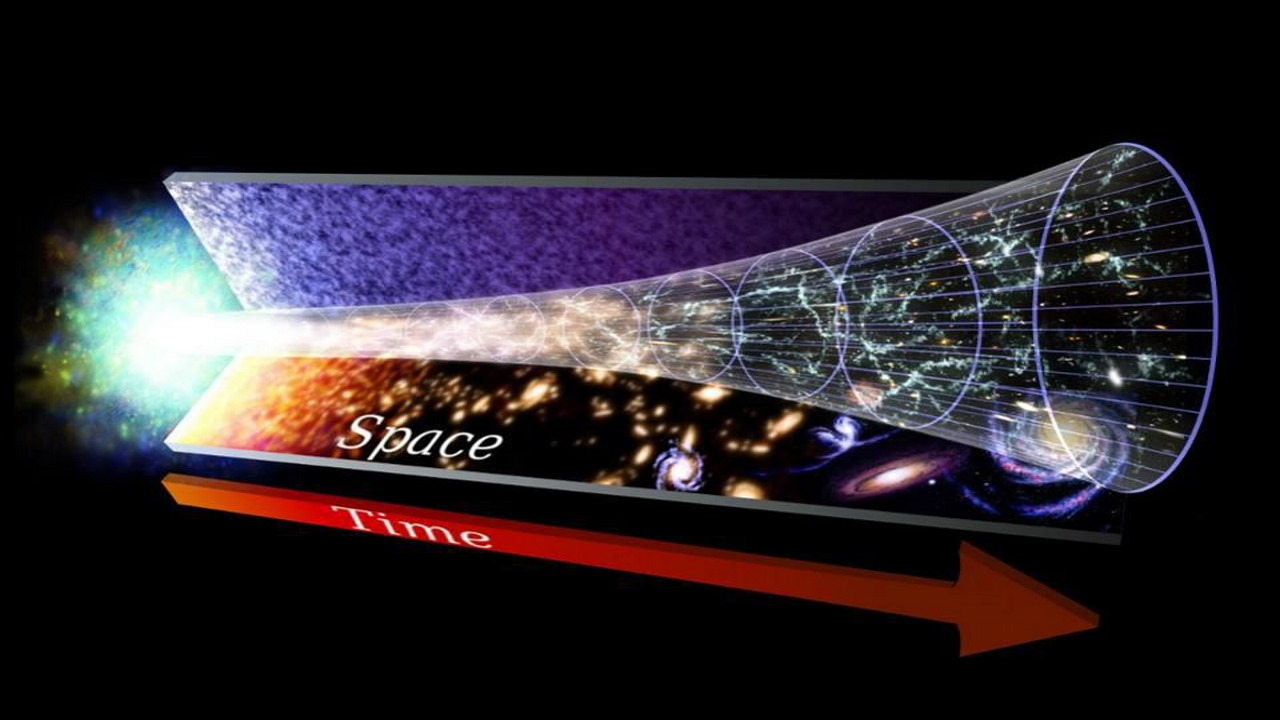
در واقع این دو سوال بی پاسخ براساس نظریه استاندارد کیهان شناسی یکنواختی و تختی عالم است که دو خصوصیت رصد شده به آن مربوط می‌شوند و هیچ یک از این دو خصوصیت نتایج طبیعی مدل انفجار بزرگ داغ نیستند. به همین دلیل است كه توضیح یکنواختی و هموار بودن فضایی عالم را به عنوان مشکل قلمداد می‌کنیم و به ترتیب به این دو پدیده رصد شده نام‌های «مشکل افق رویداد» (Horizon problem) و «مشکل همواری» (Flatness problem) می‌دهیم. بدین ترتیب در این مطلب این سوالات یعنی سومین و چهارمین سوال بی جواب کیهان شناسی را بررسی می‌کنیم.

مشکل افق رویداد

با انبساط و پیر شدن عالم یک ناظر به طور فزاینده‌ای در هر نقطه قادر به دیدن اجسام دور است زیرا با گذشت زمان نور از آن‌ها به ما می‌رسد. رسیدن نور بدین معنی است که هرچه سن عالم بیشتر می‌شود نقاط دورتری توسط ناظر قابل مشاهده خواهد بود. فاصله تا دورترین نقطه قابل مشاهده عالم را افق رویداد قابل مشاهده عالم می‌نامیم.

فیلم آموزش مقدماتی کیهان شناسی و نجوم در فرادرس

کلیک کنید

برای توضیح مشکل افق رویداد ابتدا باید کمیتی به نام فاصله افق رویداد را تعریف کنیم. این کمیت در یک زمان مشخص معرف بیشترین فاصله‌ای است که یک سیگنال فیزیکی می‌تواند در فضا و در زمان سپری شده پس از اولین لحظات انفجار بزرگ منتشر شود.

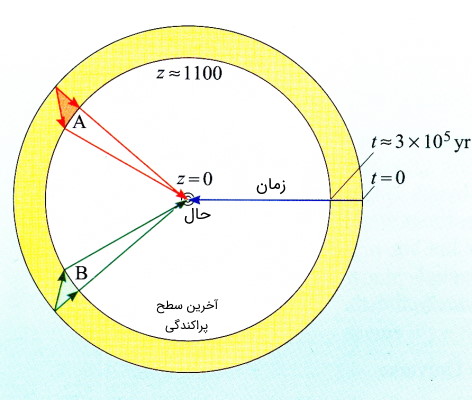
به مشکل افق رویداد زمانی برخورد می‌کنیم که تابش‌های پس زمینه کیهانی یا CMB را یکنواخت در نظر بگیریم. این مشکل در حقیقت از رصدهایی ناشی می‌شود که در آن دمای تابش‌های پس زمینه کیهانی تا حد چند بخش در $$10^{5}$$ در عرض آسمان یکنواخت است، در صورتی که نقاطی روی آسمان که با بیش از حدود دو درجه از یکدیگر جدا هستند با فاصله‏‌ای که بزرگتر از فاصله افق رویداد است، در زمان پراکندگی نهایی از هم تفکیک شده‌اند. برای درک بهتر موضوع تصویر (۲) را ببینید.

هرچند ما بر فاصله افق رویداد در زمان پراکندگی نهایی تمرکز کردیم اما می‌توان فاصله افق رویداد و یکنواختی هستی را در زمان‌های بعد نیز در نظر گرفت و به نتایج مشابهی در مورد وجود مشکل افق رویداد دست یافت. مزیت بحث در مورد فواصل افق رویداد برحسب سطح پراکندگی نهایی آن است که این فواصل به آسانی در بین رصدهای CMB قابل مشاهده هستند. بنابراین بر اساس مدل انفجار بزرگ استاندارد دلیلی ندارد که انتظار داشته باشیم CMB در مقیاس‌های بزرگتر از حدود $$2^{\circ}$$ یکنواخت باشد.

در حقیقت سوال اصلی این است که بعد از انفجار بزرگ ذرات عالم پراکنده شده‌اند و این پراکندگی حاصل از انفجار در فواصلی بزرگتر از $$2^{\circ}$$ نباید یکنواخت باشد، این چیزی است که انتظار داریم اتفاق بیفتد اما رصدها نشان می‌دهد که یکنواختی پراکندگی در فواصلی بزرگتر از ۲ درجه نیز اتفاق می‌افتد. با توجه به مدل انفجار بزرگ این یکنواختی چگونه قابل توضیح است؟

برای جواب به این مشکل یک راه ‌حل این است که برخلاف استدلال‌های پیشین که نشان می‌داد نواحی سطح پراکندگی نهایی نمی‌‏توانند با یکدیگر در ارتباط باشند آن‌ها را در ارتباط با یکدیگر ببینیم.

همان طور که می‌دانیم در مراحل ابتدایی گسترش هستی، این نواحی با یکدیگر در ارتباط بوده‌ و به حالت تعادل گرمایی رسیده‌اند. آنچه پس از آن لازم بوده تفکیک این نواحی از یکدیگر است که نتیجه آن عالم با ویژگی‌های حال حاضر است.

ایده کلیدی این است که این جداسازی به جای انتشار یک سیگنال فیزیکی در فضا، یک یکنواختی مقیاس بزرگ که با انبساط هستی همراه است تولید کند. در این حالت انبساط باید ضریب بسیار بزرگی داشته باشد تا دو ناحیه که پیش از این با یکدیگر در ارتباط بوده‌اند با فواصل افقی متعدد از یکدیگر جدا به نظر برسند.

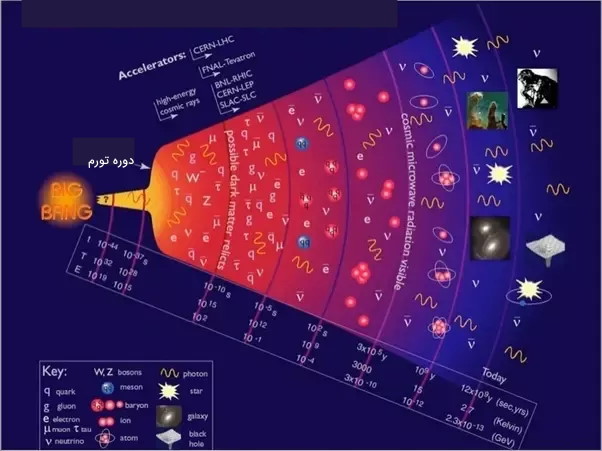
سوالی که مطرح می‌شود این است که چه فرآیندی در هستی اولیه توانسته این تاثیر را داشته باشد، یعنی انبساطی با ضریب بسیار بالا تولید کرده باشد که اجازه دهد تا یکنواختی تا نقاط گسترده عالم انتشار یابد؟ دوره تورم. در حقیقت تورم دوره کوتاهی از انبساط بسیار سریع است که باعث شده نواحی که با یکدیگر در ارتباط بوده‌اند با فاصله‌ای بیش از فاصله افق از یکدیگر جدا شوند.

ایده تورم به شکل خلاصه عبارت است از آن که نزدیک به زمان پایان «دوره اتحاد بزرگ» (Unified era)، عالم دچار انبساطی بسیار سریع اما کوتاه بوده است. نتیجه نهایی این تورم این بوده است که ناحیه‌ای از هستی که در ابتدا و پیش از تورم شانس حضور در ناحیه همگن و در تعادل گرمایی را داشته است، با رخداد تورم در فاصله‌ای طولانی‌تر قرار گرفته است که این فاصله بسیار بیشتر و بزرگتر از فاصله افق رویداد است.

بر اساس نظریات در طول دوره تورم، ضریب و آهنگ انبساط چیزی در حدود $$10^{50}$$ یا بیشتر بوده است.

بنابراین نظریه تورم می‌تواند با انبساط و دور کردن نواحی از هستی که پیش از تورم همگن شده بودند و در اثر تورم با فواصل بسیار زیاد از یکدیگر قرار گرفته‌اند، به حل مشکل افق رویداد کمک کند.

هنگامی که تابش پس زمینه کیهانی از ماده جدا شده یعنی در زمانی که عمر عالم در حدود 380,000 سال بوده است، اين تابش‌ها ضرورتاً ایزوتروپیک بوده‌اند زیرا از ماده‌ای ساطع شده‌اند که در آن زمان همگن بوده است.

درک این نکته مهم است که نظریه تورم را باید به عنوان كامل‌كننده مدل انفجار بزرگ استاندارد در نظر گرفت. پیش‌بینی‌های مدل انفجار بزرگ استاندارد از زمان حدود $$10^{-9}$$ ثانیه به بعد به شکل گسترده‌ای پذیرفته شده و با نتیجه‌های رصدی همخوانی دارد، حال آن‌ که فرضیه تورم یک فرضیه بسیار نظری است. در حقیقت مکانیزمی که باعث شده تا فرآیند تورم اتفاق افتد هنوز ناشناخته است.

با این حال جنبه جذاب نظریه تورم این است که یک راه حل واحد برای چندین مسئله کیهان شناختی ارائه می‌دهد. این نظریه نه تنها راه حلی برای مشکل افق رویداد، بلکه پاسخی برای مشکلات ساختاری و تخت بودن فضایی عالم نیز دارد.

مشکل همواری عالم

از مسائل باقی مانده از مشکلات مدل استاندارد انفجار بزرگ مشکل همواری فضایی یا تخت بودن هندسه عالم است که به رصدهایی مربوط می‌شود که چگالی متوسط هستی در آن‌ها تقریباً برابر با چگالی بحرانی یعنی $$\Omega=1$$ به دست آمده است.

چگالی بحرانی هستی برابر با مجموع چگالی تابش، چگالی ماده و پارامتر معرف خمیدگی فضایی یعنی k است و از مدل FRW در کیهان شناسی داریم:

$$\rho_{\text {crit }}=\rho+\rho_{\Lambda}-\frac{3 H^{2}}{8 \pi G} \frac{k c^{2}}{H^{2} R^{2}}$$

فیلم آموزش مبانی گرانش یا Gravitation در فرادرس

کلیک کنید

با تقسیم طرفین معادله بر چگالی بحرانی داریم:

$$\Omega=\Omega_{m}+\Omega_{\Lambda}=1+\frac{kc^2}{H^2R^2}$$

در نتیجه در مدل فریدمن-رابرتسون -واکر یا FRW، اگر رصدها نمایش‌دهنده این باشند که چگالی هستی برابر با چگالی بحرانی است، خمیدگی یا k برابر با صفر خواهد بود و نشان می‌دهد فضای سه بعدی هندسه تخت دارد، اما چرا این نتیجه‌گیری یک مشکل حساب می‌شود؟

برای نزدیک بودن پارامتر چگالی به مقدار ۱ در حال حاضر، باید مقدار آن در زمان گذشته، بیش از این به ۱ نزدیک بوده باشد. دلیل این پیش‌بینی این است که با گذشت زمان اختلاف میان $$\Omega(t)$$ و 1 افزایش می‌یابد و مقدار آن کوچکتر می‌شود. در نتیجه اگر مقدار فعلی $$\Omega(t)$$ در حال حاضر دقیقاً برابر با 1 است در زمان $$t=0$$ و در هر زمان زودتر نیز دقیقاً برابر با $$1$$ بوده است.

اگر مقدار فعلی پارامتر چگالی هستی از یک کمتر و مثلاً $$\Omega=0.9$$ باشد، مقدار آن در زمان‌های قبل‌تر و هنگامی که عمر هستی تنها کسری از  ثانیه بوده چه قدر است؟

پاسخ به این سوال به مدل FRW‌ای که برای معرفی هستی استفاده می‌شود بستگی خواهد داشت. اما در یک حالت می‌توان گفت که اختلاف چگالی با نسبتی معادل $$t^{2 / 3}$$ رشد می‌کند.

برای این حالت خاص اختلافی از مرتبه $$0.1$$ نشان می‌دهد هنگامی که عمر عالم یک سی‌اُم عمر فعلی‌اش بوده اختلاف بین $$\Omega(t)$$ و 1 به اندازه $$0.01$$ بوده است. بنابراین اگر $$\Omega(t_0)=0.9$$ باشد آنگاه $$\Omega(\frac{t_{0}}{30})=0.99$$ بوده است.

این واقعیت که هستی در حال حاضر در حدود $$10^{17}$$ ثانیه عمر دارد و پارامتر چگالی آن هم چنان نزدیک به یک است به این معنی است که در زمان‌های اولیه مثلاً $$t<10^{-6}$$ چگالی بسیار به یک نزدیک بوده است و توضیح اینکه چرا باید در زمان‌های بسیار اولیه تا این حد به یک 1 نزدیک باشد، موضوع اصلی مسئله همواری است.

البته در حال حاضر ممکن است که مجموع چگالی هستی مقدار بحرانی داشته باشد که در این حالت $$k=0$$ و $$\Omega(t)$$ همواره با یک برابر خواهد بود. این یکی از احتمالات فرضی برای حل مسئله همواری عالم است که چندان اعتماد کیهان شناسان را بر نمی‌انگیزد.

ترجیح کیهان شناسان همواره مکانیزم‌ها یا فرآیندهایی است كه پارامترهای کیهان شناختی را به مقادیر رصد شده آن‌ها متصل کند و بین این دو مطابقت وجود داشته باشد. یکی از انگیزه‌ها برای ارائه این فرضیه که ممکن است دوره‌ای از تورم در هستی بسیار اولیه وجود داشته باشد، عبارت است از اينكه این فرضیه می‌تواند مشکل همواری و نیز مشکل افق رویداد را به سادگی حل کند.

مستقیم‌ترین نتیجه تورم، افزایش بسیار زیاد ضریب مقیاس کیهانی یا $$R(t)$$ بوده است و در این دوره این ضریب با مقیاس $$10^{50}$$ یا حتی بیشتر افزایش داشته است. همانگونه که در تصویر (۴) نیز نمایش داده شده تاثیر این افزایش، کاهش خمیدگی فضا بوده که به کمیت $$\frac{k}{R^{2}}$$ بستگی دارد.

در نتیجه تورم کمیت $$\frac{k}{R^{2}}$$ کاهش یافته و مقدار موثر خمیدگی یا k صفر می‌شود و فضا بدون در نظر گرفتن مقدار حقیقی k پیش از تورم، از حیث هندسی تخت است.

ممکن است در نگاه اول این استدلال هندسی متقاعد کننده به نظر برسد، اما باید توجه داشته باشید كه چنین استدلالی چگونه چگالی هستی را تعریف می‌کند و آن را توضیح می‌دهد. تصویر (۴) می‌تواند از لحاظ هندسی فضای تخت قابل مشاهده یا k=0 را در نتیجه تورم نشان دهد اما این نظریه چگونه می‌تواند نشان دهد که در ابتدای عالم $$\Omega(t)$$ برابر با ۱ بوده است؟

برای فهم این موضوع باید بدانید که ارتباط بین خمیدگی فضا و چگالی، مستقیماً از معادله فریدمن به دست می‌آید و مشخص نمی‌شود كه منبع چگالی انرژی کیهانی ممکن است چه چیز باشد. بنابراین نزدیک به پایان دوره تورم، هنگامی که فضا تخت بوده احتمالاً عالم کاملاً سرد شده و بیشتر انرژی آن به شکل نوعی انرژی خلاء نامتعارف درآمده است، اما چگالی این انرژی خلاء دقیقاً همان چیزی بوده که برای تولید یک هندسه تخت موثر لازم است.

فرض معمول بر این اصل استوار است که در هنگام توقف دوران تورم عالم، مقداری از انرژی خلاء مجدداً به اشکال بسیار متعارف ماده و تابش تبدیل شده و عالم دوباره تا درجه حرارتی مشابه آنچه می‌توانست در غیاب تورم داشته باشد، گرم شده است. این که تمام مواد و تابش‌ها در عالم قابل مشاهده را نتیجه مستقیم تورم بدانیم، بسیار قابل توجه است اما این واقعیت را تغییر نمی‌دهد که با محاسبه تمام اشکال ماده، تابش و نیز همه انرژی تاریک مجموع چگالی عالم بسیار نزدیک به چگالی بحرانی یعنی $$\Omega(t)$$ خواهد بود و به همان نسبت به مقدار یک نیز نزدیک است.

هرچند تورم به شکل طبیعی به عالمی که دارای چگالی بحرانی است منجر می‌شود، اما مقدار چگالی را دقیقاً برابر با چگالی بحرانی قرار نمی‌دهد. در حقیقت در مدل تورمی، اگر چگالی پیش از آغاز تورم بزرگتر (یا کوچکتر) از چگالی بحرانی بوده، پس از آن نیز بزرگتر (یا کوچکتر) خواهد بود.

پرسش: با فرض اینکه پیش از تورم چگالی کمتر از چگالی بحرانی بوده است، تغییرات آن بعد از تورم اگر بخواهید آن را مشابه تصویر (۴) نمایش دهید چگونه خواهد شد؟

پاسخ: در این حالت شکلی شبیه به زين اسب خواهد داشت که پس از تورم تقریباً به شکل کامل روی بخش کوچکی که هستی قابل رویت را شکل داده تخت شده است.

تاکنون بهترین اندازه‌گیری انجام شده از مقدار فعلی پارامتر چگالی مقدار $$1.02\pm 0.02$$ را نشان داده است که نشان می‌دهد هستی حقیقتاً به چگالی بحرانی و نیز داشتن هندسه تخت بسیار نزدیک است.

هم چنین همان گونه که در مطالب ماهیت ماده تاریک و انرژی تاریک بیان شد، میزان انرژی تاریک در حدود $$73\%$$ و ميزان ماده تاریک در حدود $$23\%$$ است. بنابراین رصدها از دو عنصر غیرشناخته از هستی یعنی ماده و انرژی تاریک به اضافه چگالی بحرانی به سادگی به وسيله فرآیند تورم توجیه می‌شود و اگر بخواهیم نظریه تورم را کنار بگذاریم فهم این تطابق بسیار دشوار خواهد بود.

نظریه تورم به طور همزمان مشکل افق رویداد و تخت بودن عالم که باعث ايجاد اشكال در مدل استاندارد انفجار بزرگ است را حل می‌کند. در واقع احتمال دارد نظریه تورم کلید حل غیریکنواختی اندکی باشد که حقیقتاً رخ داده است، چه غیریکنواختی که به شروع شکل‌گیری کهکشان‌ها مربوط است و چه غیریکنواختی که خود را در تابش پس زمینه کیهانی نشان می‌دهد.

چرا عالم یکنواخت و تخت است؟

همان‌طور که دیدید دو نتیجه رصدی افق رویداد و چگالی هستی منجر به عالم یکنواخت و تخت می‌شود. هیچ یک از این دو نتیجه رصدی را نمی‌توان توسط مدل استاندارد انفجار بزرگ توضیح داد و به همین دلیل نظریه متمم تورم برای توضیح عالم یکنواخت و تخت به نظریه استاندارد اضافه می‌شود. با این حال نظریه تورم نیز نقایصی دارد که در مطالب بعدی در مورد این نظریه صحبت خواهیم کرد.

فیلم آموزش مقدماتی نجوم – نجوم باستان تا کیهان شناسی در فرادرس

کلیک کنید

جمع‌بندی

در این مطلب در مورد عالم یکنواخت و تخت صحبت کردیم. همانطور که می‌دانید در کیهان شناسی هشت سوال بی پاسخ وجود دارد که عبارتند از :

1. ماهیت ماده تاریک چیست؟
2. ماهیت انرژی تاریک چیست؟
3. چرا عالم یکنواخت است؟
4. چرا عالم هندسه تخت (k=0) دارد؟
5. ساختارها از کجا می‌آیند؟
6. چرا میزان ماده از پادماده بیشتر است؟
7. در زمان  0 =t (در ابتدای عالم) چه رخ داده است؟
8. چرا هستی به شکل فعلی آن است؟

در این مطلب در مورد سوال سوم و چهارم که در مورد عالم یکنواخت و تخت است صحبت کردیم. موضوع و مشکل اصلی در نظریه عالم یکنواخت و تخت دو نتیجه رصدی است که با مشاهدات به‌ دست آمده و توسط نظریه استاندارد انفجار بزرگ توضیحی برای آن وجود ندارد به همین دلیل برای توضیح هر دو پدیده از نظریه تورم استفاده کردیم.