پیاده سازی الگوریتم K–means++‎‏ در پایتون – راهنمای گام به گام

در آموزش‌های پیشین مجله فرادس، با پیاده سازی الگوریتم خوشه بندی K-means در پایتون آشنا شدیم. در این آموزش، روش گام به گام پیاده‌سازی نوع خاصی از این الگوریتم خوشه‌بندی، یعنی پیاده سازی الگوریتم K-means++‎ در پایتون را بیان می‌کنیم.

الگوریتم K-means++‎

همان‌طور که می‌دانیم، در مسئله K-means تابع هزینه به شکل زیر تعریف می‌شود:

$$\large J=\sum_{i=1}^{k} \sum_{x \in S_{i}}\left\|c_{i}-x\right\|^{2}$$

به عبارتی این تابع حاصل جمع فاصله اقلیدسی هر داده از مرکز خوشه مربوطه را نشان می‌دهد که به آن Within Cluster Sum of Squares گفته می‌شود.

بهینه‌سازی موقعیت خوشه‌ها برای دست یافتن به کمترین مقدار تابع هزینه، یک مسئله NP-Hard است و به‌لحاظ محاسباتی هزینه‌بر است. به این دلیل از الگوریتم‌هایی برای یافتن بهینه‌های محلی (Local Optimum) استفاده می‌شود. الگورتم لوید (Lloyd Algorithm) که در آموزش‌های قبلی پیاده‌سازی شد نیز مثالی از این روش‌ها است.

فیلم آموزش خوشه بندی با الگوریتم های تکاملی و فراابتکاری در فرادرس

کلیک کنید

همان‌طور که گفته شد، این الگوریتم‌ها اغلب به‌جای یافتن بهینه سراسری (Global Minimum)، بهینه محلی را می‌یابند. به همین دلیل، نتایج حاصل نیز به شرایط شروع (Initialization) بسیار وابسته هستند.

برای حل این مشکل، راه‌حل‌هایی ارائه شده‌اند که یکی از آن‌ها، استفاده از روش K-means++‎ است.

در این روش، اولین مرکز خوشه به صورت تصادفی از بین داده‌ها انتخاب می‌شود. سایر مراکز نیز به‌صورت تصادفی از بین داده‌ها انتخاب می‌شوند، با این تفاوت که برای داده‌هایی با فاصله بیشتر از مراکز قبلی، احتمال انتخاب بیشتری داده می‌شود. به این ترتیب، احتمال انتخاب مراکز خوشه نزدیک به هم کاهش می‌یابد.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

این الگوریتم را می‌توان در مراحل زیر توصیف کرد:

۱. مرکز خوشه اول ($$C_1$$) به‌صورت تصادفی از بین داده‌ها انتخاب می‌شود.

۲. مراحل زیر به تعداد $$k-1$$ بار تکرار می‌شود:

a. فاصله همه داده‌ها از تمامی مراکز خوشه محاسبه و کمترین آن به‌صورت زیر ذخیره می‌شود:

$$\large D_{j}=\min _{i \in\{1,2 \ldots k\}}\left\|c_{i}-x_{j}\right\|^{2}$$

b. احتمال انتخاب متناظر برای هر داده به شکل زیر تعریف می‌شود:

$$\large P_{j}=\frac{D_{j}^{2}}{\sum_{k=1}^{n} D_{k}^{2}}$$

c. یک داده با توجه به احتمال‌های محاسبه شده، انتخاب می‌شود.

۴. مراکز خوشه به نقاط شروع انتخاب می‌شوند.

۵. لگوریتم Lloyd اجرا می‌شود.

به این ترتیب، مراحل کار الگوریتم کامل بیان می‌شود.

فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش های خوشه بندی هوشمند در فرادرس

کلیک کنید

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

بررسی وابستگی الگوریتم Lloyd به شرایط اولیه

حال وارد محیط برنامه‌نویسی می‌شویم و الگوریتم نوشته‌شده در مطلب قبلی با عنوان «پیاده سازی الگوریتم خوشه بندی K-means در پایتون — راهنمای گام به گام» را که لینک آن را در ابتدای متن آوردیم، به شکل زیر بازنویسی می‌کنیم:

ابتدا داده‌ها را ایجاد و نمایش می‌دهیم:

که شکل زیر خواهیم داشت.

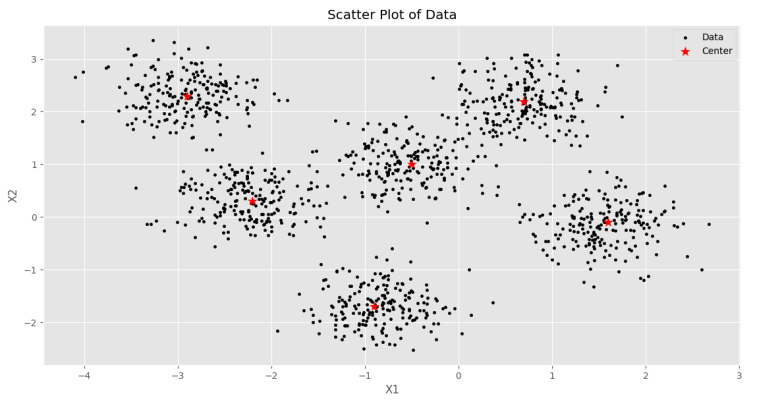
حال تابع هزینه را در قالب یک تابع تعریف می‌کنیم. در ورودی این تابع داده‌ها و مراکز خوشه‌ها را دریافت و در خروجی Within Cluster Sum of Squares را برمی‌گردانیم:

حال برنامه را ۱۰۰ بار با شرایط شروع متفاوت اجرا می‌کنیم و مقدار تابع هزینه را ذخیره می‌کنیم:

اکنون یک نمودار هیستوگرام (Histogram) برای مقدار تابع هزینه رسم می‌کنیم:

توجه داشته باشید که کم بودن تعداد bins توزیع را با جزئیات مناسب نشان نمی‌دهد و زیاد بودن آن باعث ایجاد ناپیوستگی‌هایی در نمودار می‌شود و باز هم مطلوب نیست. به همین دلیل، باید تعداد آن با توجه به اندازه داده و در بازه‌ مطلوب قرار گرفته باشد.

پس از اجرای کد فوق نمودار زیر حاصل خواهد شد.

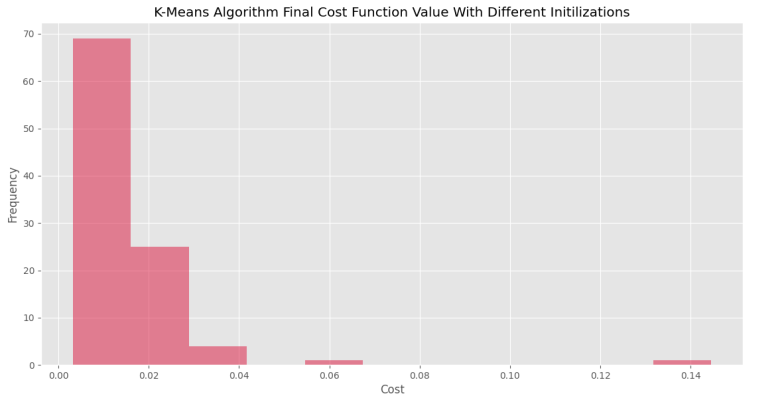
به این ترتیب، مشاهده می‌کنیم که حدود ۷۰ بار اجرا، به هزینه‌ای کمتر از ۰٫۰۲ ختم شده است. در مقابل، برای برخی اجراها، تابع هزینه به بیشتر ۰٫۱۴ رسیده است که ۳۵ برابر کمترین مقدار است. به این ترتیب، به‌سادگی وابستگی الگوریتم Lloyd به شرایط اولیه مشاهده می‌شود.

فیلم آموزش خوشه بندی سلسله مراتبی با SPSS اس پی اس اس در فرادرس

کلیک کنید

پیاده سازی الگوریتم K-means++‎ در پایتون

برای پیاده‌سازی الگوریتم K-means++‎ در پایتون یک تابع ایجاد می‌کنیم که در ورودی تعداد مرکز و مجموعه داده را دریافت می‌کند:

حال تعداد داده را استخراج و سپس ماتریسی خالی برای ذخیره مراکز دسته انتخاب شده ایجاد می‌کنیم:

حال اولین مرکز دسته را به‌صورت تصادفی از مجموعه داده انتخاب می‌کنیم:

حال یک حلقه برای $$k-1$$ بار تکرار کد می‌نویسیم:

حال باید ماتریس فاصله هر داده از نزدیک‌ترین مرکز را محاسبه و ذخیره کنیم، برای این کار، ابتدا ماتریسی خالی برای آن ایجاد می‌کنیم:

حال یه حلقه ایجاد می‌کنیم تا برای هر داده فاصله را محاسبه کنیم:

در این مرحله، یک لیست خالی ایجاد می‌کنیم تا فاصله داده از هر مرکز خوشه را به آن اضافه کنیم:

حال می‌توانیم یک حلقه برای تمامی مراکز خوشه ایجاد و فاصله را به لیست ایجادشده اضافه کنیم. توجه داشته باشید که با هر بار اجرای حلقه بیرونی، تعداد مراکز خوشه افزایش می‌یابد؛ به این دلیل، باید تعداد مراکز از متغیر $$i+1$$ تبعیت کند:

حال باید کمترین فاصله مشاهده شده را به آرایه D اضافه کنیم:

به این ترتیب، کمترین فاصله هر داده از مراکز محاسبه می‌شود. با توجه به فرمول، باید از توان دوم فاصله‌ها استفاده کنیم؛ بنابراین، به‌شکل زیر توان دوم ماتریس D را محاسبه می‌کنیم:

حال مجموع مقادیر آرایه D2 را محاسبه کرده و در نهایت احتمال متناظر با هر داده را می‌یابیم:

به این ترتیب، احتمال انتخاب هر داده به‌عنوان مرکز بعدی محاسبه شد. حال باید با استفاده از Random Choice یک داده را انتخاب کنیم:

به این ترتیب، داده مورد نظر با توجه به احتمال‌های محاسبه‌شده، انتخاب می‌شود. توجه داشته باشید که تابع np.random.choice در خروجی یک آرایه برمی‌گرداند که با توجه به اینکه تنها یک عدد در آن وجود دارد، تنها عضو اول آن را انتخاب می‌کنیم.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

در نهایت، نیز مراکز خوشه‌ها را در خروجی برمی‌گردانیم و تابع نهایی شکل زیر را به خود می‌گیرد:

حال برای استفاده از این تابع، کد قبلی را به شکل زیر تغییر می‌دهیم:

پس از اجرای این کد و رسم نمودار هیستوگرام، نمودار زیر حاصل می‌شود.

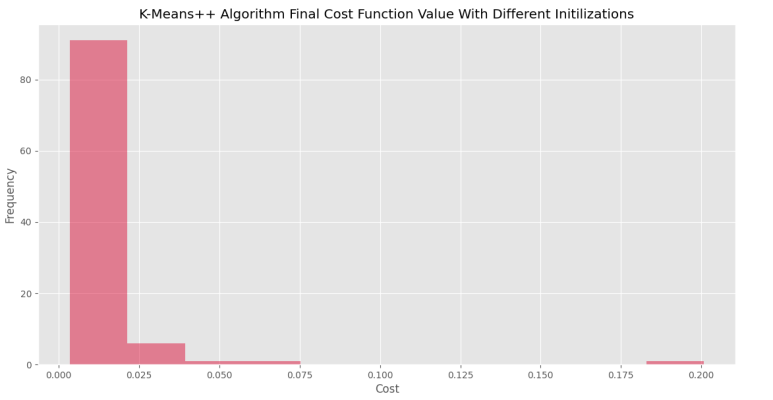
در اولین نگاه، کاملاً مشهود از که ۹۰٪ اجراها به هزینه‌ای کمتر از ۰٫۰۲ رسیده‌اند که در مقایسه با حالت معمولی (۷۰٪) بسیار بهتر است.

توجه داشته باشید که برای اثبات اثربخشی هر الگوریتم، باید تعداد دفعات اجرا بسیار بیشتر از ۱۰۰ بار باشد. از طرفی، بررسی عملکرد روی چندین مجموعه داده نیز از الزامات این کار است. برای مثال، در نمودار اخیر، برای یک اجرا مقدار تابع هزینه به ۰٫۲ رسیده که نسبت به الگوریتم معمولی افزایش یافته است. این حالت برخلاف تصور ما و غالب مشاهدات ما مبنی بر عملکرد بهتر الگوریتم K-means++‎ بوده است. به همین دلیل، می‌توان با افزایش تعداد دفعات اجرای الگوریتم، با اطمینان بهتری عمل مقایسه را انجام داد.

جمع‌بندی پیاده سازی الگوریتم K-means++‎ در پایتون

در این مطلب، تابع هزینه و وابستگی الگوریتم Lloyd به شرایط اولیه را بررسی کردیم. همچنین، به پیاده‌سازی الگوریتم K-means++‎ در پایتون پرداختیم.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای مطالعه بیشتر، می‌توان پاسخ پرسش‌های زیر را تحقیق کرد:‌

1. چرا از توان دوم فاصله به‌عنوان معیار مرتبط با احتمال انتخاب داده استفاده کردیم؟
2. آیا ممکن است در صورت استفاده از الگوریتم K-means++‎ نیز مراکز خوشه اولیه نزدیک به هم باشند؟ چه راهکاری برای حل این مشکل می‌توان ارائه داد؟
3. اگر نمودار هیستوگرام دو الگوریتم را روی هم رسم و آن‌ها را مقایسه کنیم، چه معیارهای آماری می‌توانند عملکرد بهتر الگوریتم K-means++‎ را نشان دهند؟
4. آیا الگوریم K-means++‎ می‌تواند به‌لحاظ هزینه محاسباتی، مزیتی داشته باشد؟