مثلث قائم الزاویه چیست؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده

در آموزش‌های پیشین مجله فرادرس، با مثلث و روش‌های محاسبه مساحت و محیط آن آشنا شدیم. در این آموزش، مطالبی را درباره مثلث قائم الزاویه بیان می‌کنیم.

مثلث قائم الزاویه چیست ؟

«مثلث قائم الزاویه» (Right Triangle) مثلثی است که اندازه یکی از زاویه‌های آن ۹۰ درجه (قائمه یا راست) است.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

زاویه قائمه مثلث قائم الزاویه با یک مربع کوچک ($$\Box$$) نمایش داده می‌شود.

«وَتَر» (Hypotenuse) ضلع مقابل زاویه قائمه مثلث قائم الزاویه است. دو ضلع دیگر مثلث قائم الزاویه را «ساق» (Leg) می‌نامند. شکل زیر یک مثلث قائم الزاویه را نشان می‌دهد که وتر و دو ساق آن مشخص شده‌اند.

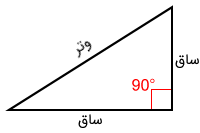
برخی از ویژگی‌های مثلث قائم الزاویه که بهتر است به خاطر داشته باشیم، عبارتند از:

• یک زاویه این مثلث همواره برابر با 90 درجه است.
• ضلع مقابلِ زاویه 90 درجه، وتر است.
• وتر همیشه طولانی‌ترین ضلع مثلث قائم الزاویه است.
• مجموع دو زاویه داخلی دیگر مثلث قائم الزاویه برابر با 90 درجه است.
• دو ضلع مجاور زاویه قائمه را قاعده و ارتفاع نیز می‌نامند.

مثلث قائم الزاویه و قضیه فیثاغورس

در مطالب دیگر مجله فرادرس در مورد قضیه فیثاغورس صحبت کردیم. این قضیه یکی از قضایای مهم هندسه است که رابطه بین اضلاع مثلث قائم الزاویه را بیان می‌کند.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

طبق قضیه فیثاغورس،‌ مربع اندازه وتر یک مثلث قائم الزاویه برابر است با مجموع مربعات دو ضلع دیگر. به عبارت دیگر، در مثلث قائم الزاویه شکل زیر، داریم:

$$\large a^2+b^2=c^2$$

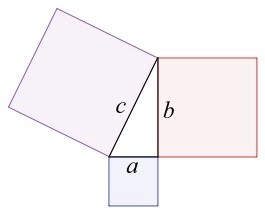
مثلث قائم الزاویه در مثلثات

مثلث‌های قائم‌الزاویه به طور گسترده‌ای در مثلثات استفاده می‌شوند. در مثلثات، از ساق‌های مثلث قائم الزاویه اغلب به عنوان «ضلع مقابل» و «ضلع مجاور» یک زاویه حاده یاد می‌شود. این موضوع در شکل زیر نشان داده شده است.

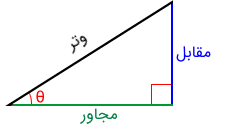
توابع مثلثاتی با استفاده از مثلث قائم الزاویه به صورت زیر تعریف می‌شوند:

مثلث قائم الزاویه محاط در دایره

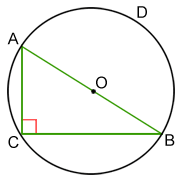
اگر مثلث قائم الزاویه در یک دایره محاط شده باشد، حتماً یکی از اضلاع آن (وتر) قطر دایره است. برعکس، اگر قطر دایره یکی از اضلاع مثلث محاطی را تشکیل دهد، این مثلث یک مثلث قائم الزاویه خواهد بود. سه رأس مثلث قائم الزاویه ABC شکل بالا روی دایره‌ای به مرکز O هستند و AB وتر مثلث را نشان می‌دهد.

مساحت مثلث قائم الزاویه

مساحت مثلث قائم الزاویه برابر است با نصف حاصل‌ضرب ضلع‌های مجاور زاویه قائمه.

فیلم آموزش محاسبه مساحت مثلث – رایگان در فرادرس

کلیک کنید

به عبارت دیگر، فرمول محاسبه مساحت مثلث قائم الزاویه برابر است با:

(قاعده × ارتفاع) ۰٫۵= مساحت مثلث قائم الزاویه

به عنوان مثال، مثلث زیر را با اضلاع قاعده $$b$$، ارتفاع $$a$$ و وتر $$c$$ در نظر بگیرید.

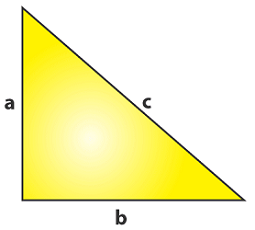
فرمول محاسبه مساحت این مثلث به صورت زیر است:

$$\large A = \frac 12 a \times b$$

محیط مثلث قائم الزاویه

برای به دست آوردن محیط مثلث قائم الزاویه کافی است اندازه اضلاع آن را با هم جمع کنیم.

مثال های مثلث قائم الزاویه

در این بخش، چند مثال را از مثلث قائم‌الزاویه بررسی می‌کنیم.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

مثال اول مثلث قائم الزاویه

مساحت مثلث قائم‌الزاویه زیر را به دست آورید.

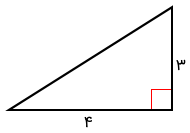
حل: از فرمول مساحت مثلث قائم‌الزاویه استفاده می‌کنیم و خواهیم داشت:

۶ = (۴ × ۳) × ۰٫۵ = (قاعده × ارتفاع) ۰٫۵= مساحت مثلث

مثال دوم مثلث قائم الزاویه

مساحت مثلث قائم الزاویه زیر برابر با $$24\; \text{cm}^2$$ است. اگر $$a=6\, \text{cm}$$‌ باشد، اندازه وتر مثلث را محاسبه کنید.

حل: با توجه به فرمول مساحت مثلث قائم الزاویه، می‌توان نوشت:

$$\large A = \frac 12 \times a \times b \Rightarrow 24 = 0.5 \times 6\times b \\ \large \Rightarrow b = \frac {24}{0.5\times 6} = 8 \; \text{cm}$$

اکنون که اندازه ضلع $$b$$ را نیز داریم، می‌توانیم به راحتی با استفاده از قضیه فیثاغورس می‌توان نوشت:

$$\large a^2+b^2 = c^ 2 \Rightarrow 6 ^2 + 8 ^ 2 = c ^2\\ \large c ^2 = 36+64 = 100 \Rightarrow c = \sqrt{100} = 10 \, \text{cm}$$

مثال سوم مثلث قائم الزاویه

اگر $$\sin (34^\circ) = 0.559$$ باشد، طول ارتفاع مثلث زیر را به دست آورید.

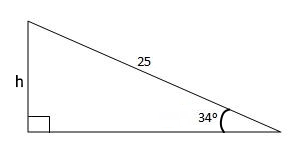
حل: با توجه به روابط ملثاتی بالا که بیان کردیم، طول ارتفاع $$h$$ را می‌توان به صورت زیر به دست آورد:

$$\large { \begin{align} \sin{\left(34^{\circ}\right)} &=\frac{h}{25} \\ 25\cdot \sin{ \left(34^{\circ}\right)} &=h\\ h &= 25\cdot \sin{ \left(34^{\circ}\right)}\\ h &= 25 \cdot \left(0.559\right)\\ h &=14 \end{align} }$$