فاصله بین دو نقطه — به زبان ساده

در این مطلب از مجله فرادرس نحوه محاسبه فاصله بین دو نقطه به صورت دقیق مورد بررسی قرار می‌گیرد. در واقع سوال اصلی که در این مطلب به دنبال پاسخ آن هستیم این است که اگر مختصات دو نقطه A و B را داشته باشیم، فاصله بین آن‌ها چگونه محاسبه می‌شود. این موضوع در شکل زیر نشان داده شده است.

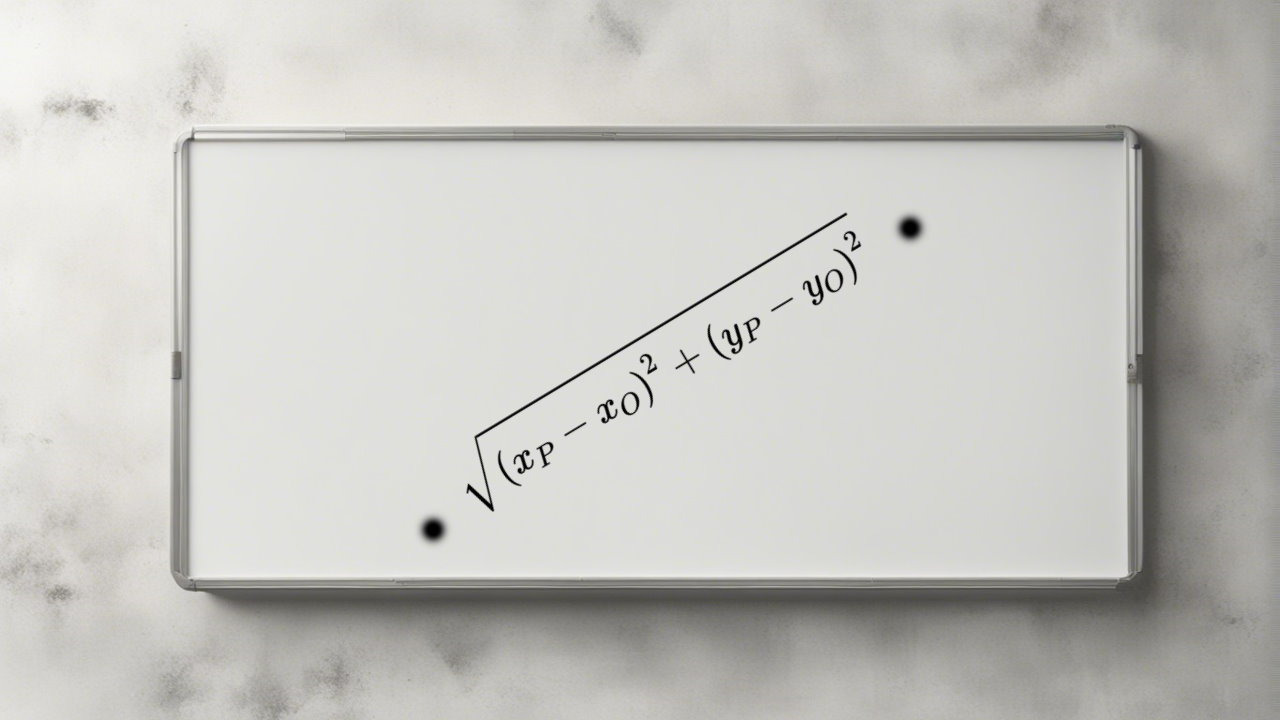
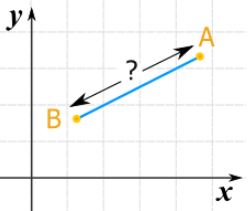
همانطور که در شکل زیر نشان داده شده، ما می‌توانیم خطوطی را بین نقاط A و B طوری رسم کنیم که یک مثلث قائم الزاویه شکل بگیرد.

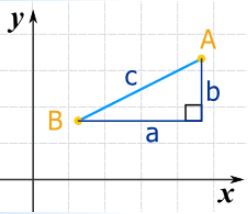
با توجه به شکل بالا می‌توان رابطه فیثاغورس را بین سه ضلع مثلث نوشت. این رابطه به شکل زیر بیان می‌شود و ارتباطی را بین سه ضلع مثلث قائم الزاویه ایجاد می‌کند.

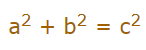
بنابراین با توجه به رابطه بالا، ایده اصلی یافتن فاصله بین دو نقطه یعنی فاصله c را متوجه شدیم. این ایده همان قضیه فیثاغورس است که در مثلثات و ریاضیات به صورت کامل مورد بررسی قرار گرفته است.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

همانطور که اشاره شد، برای یافتن فاصله بین دو نقطه نیاز به دانستن مختصات آن دو نقطه است. بنابراین در ادامه مختصات نقاط A و B را به شکل زیر مشخص می‌کنیم.

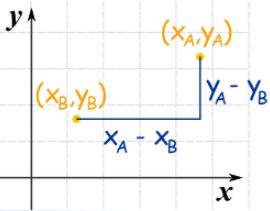
در شکل بالا، مختصات x نقطه A، با نماد x_A و مختصات y آن نقطه با نماد y_A نمایش داده شده است. همچنین مختصات نقطه B در راستای x و y به ترتیب با نماد x_B و y_B مشخص می‌شوند. توجه کنید که این نام گذاری یک نام گذاری رایج است و در اکثر مسائل ریاضی و هندسه از همین مدل نام‌گذاری برای نمایش مختصات نقاط مختلف استفاده می‌شود.

بنابراین با توجه به شکل بالا و توضیحاتی که داده شد، می‌توان نتیجه گرفت که فاصله a و b در شکل ۲ با استفاده از دو رابطه زیر محاسبه می‌شوند.

$$a = (x _ A - x _ B)$$

$$b = (y _ A - y _ B)$$

دقت کنید که a فاصله افقی را نشان می‌دهد و با استفاده از مختصات در راستای x قابل محاسبه است و b نیز فاصله عمودی را نشان می‌دهد و با استفاده از مختصات در راستای y به دست می‌آید.

در ادامه به محاسبه فاصله c که در شکل 2 نشان داده شده با استفاده از مختصات نقاط A و B می‌پردازیم. توجه کنید که فاصله c همان فاصله بین نقاط را نمایش می‌دهد و برابر با طول پاره خطی است که دو نقطه A و B دو سمت این پاره خط هستند. بنابراین در ابتدا رابطه فیثاغورس را به شکل زیر دوباره بیان می‌کنیم.

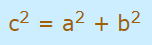
در قدم بعدی، مقادیر a و b که در قسمت قبل محاسبه شد را در رابطه بالا قرار می‌دهیم. بنابراین رابطه فوق به شکل زیر در می‌آید.

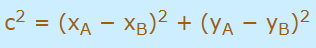
در ادامه برای به دست آوردن فاصله بین دو نقطه A و B که با نماد c نشان داده شده، کافی است که از طرفین رابطه بالا جذر بگیریم. بنابراین داریم:

رابطه بالا به صورت کلی برای محاسبه فاصله بین دو نقطه با مختصات معلوم، استفاده می‌شود. در ادامه به کمک چند مثال، کاربرد رابطه بالا را برای حل مسائل مختلف مورد ارزیابی قرار می‌دهیم.

مثال 1

فاصله بین نقاط A و B در شکل زیر را بیابید.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

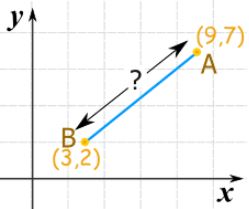
توجه کنید که در این مثال قرار است فاصله بین دو نقطه A و B محاسبه شود و این طول برابر با طول پاره خط AB نیز در نظر گرفته می‌شود. در بخش قبل بیان شد که فاصله بین دو نقطه دلخواه A و B با استفاده از رابطه زیر قابل محاسبه است.

با جایگذاری مقادیر موجود در شکل بالا (مختصات نقاط A و B)، فاصله بین دو نقطه A و B به شکل زیر به دست می‌آید.

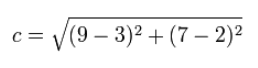
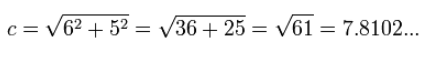
نکته بسیار مهمی که باید به آن توجه کرد این است که در محاسبه فاصله بین دو نقطه، اهمیتی ندارد که کدام نقطه را اول بنویسیم. در واقع در رابطه فوق $$x _A - x _ B$$ و $$x _B - x _ A$$ با یکدیگر تفاوتی ندارند. دلیل این موضوع این است که توان ۲ موجود در رابطه فاصله بین دو نقطه، علامت منفی را از بین می‌برد. برای اثبات این موضوع، به روابط زیر توجه کنید.

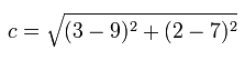
مثال 2

در این قسمت مثالی را برای مختصات منفی مورد بررسی قرار می‌دهیم. بر این اساس، فاصله بین دو نقطه نشان داده شده در شکل زیر را بیابید.

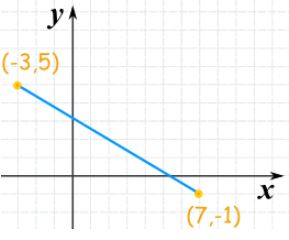
همانطور که بیان شد، فاصله بین دو نقطه، طول پاره خط بین آن دو نقطه را نشان می‌دهد. بنابراین خطی بین این دو نقطه رسم می‌کنیم. طول این خط با استفاده از رابطه زیر محاسبه می‌شود.

با جایگذاری مقادیر مختصات دو نقطه در رابطه بالا، فاصله بین دو نقطه موجود در این مثال، به شکل زیر محاسبه می‌شود.

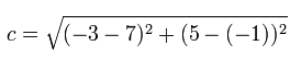
فاصله بین دو نقطه در حالت سه بعدی

توضیحاتی که در بالا برای محاسبه فاصله بین دو نقطه ارائه شد، برای حالتی که سه بعد وجود دارد نیز قابل استفاده است و رابطه آن به شکل زیر بیان می‌شود.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

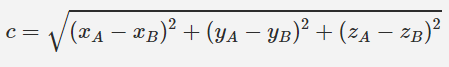
رابطه بالا نشان می‌دهد که برای محاسبه فاصله بین دو نقطه کافی است که اختلاف بین هرکدام از مولفه‌های دو نقطه را محاسبه کنیم. سپس مربع این اختلاف‌ها را با یکدیگر جمع کنیم و جذر آن را به دست آوریم. این مقدار نهایی برابر با فاصله بین دو نقطه A و B است و این فاصله، برابر با طول پاره خطی است که دو نقطه A و B، دو سمت آن هستند.

مثال 3

فاصله بین دو نقطه که در شکل زیر نشان داده شده را به دست آورید.

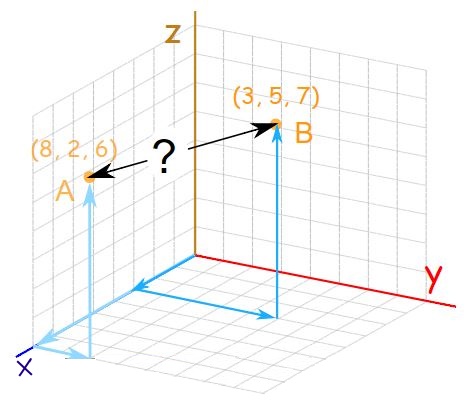
فاصله بین دو نقطه A و B که در شکل نشان فوق داده شده‌اند برابر با طول پاره خط بین آن دو است و رابطه آن به شکل زیر در نظر گرفته می‌شود.

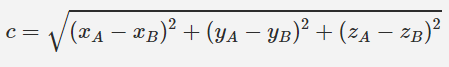
در ادامه، مختصات دو نقطه را در رابطه فوق که برای هندسه سه بعدی بیان شده، قرار می‌دهیم. بنابراین داریم:

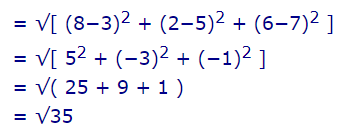
این مقدار به صورت تقریبی برابر با 5.9 است.