ضریب همبستگی پیرسون چیست؟ – نحوه محاسبه با مثال و تمرین
یکی از پرکاربردترین ضرایب همبستگی، «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) است که با r نمایش داده میشود و همبستگی خطی بین دو مجموعه داده را اندازهگیری میکند. مقدار ضریب r همواره در بازه ۱- تا ۱ است و بسته به علامت و اندازه این عدد، میتوانیم تعیین کنیم همبستگی در چه جهتی و با چه شدتی برقرار است. در این نوشته از مجله فرادرس ابتدا تعریف میکنیم که ضریب همبستگی پیرسون چیست و چه مشخصاتی دارد.
- مبانی ضریب همبستگی پیرسون و دلایل استفاده از آن را میآموزید.
- تحلیل شدت و جهت همبستگی بر اساس مقدار r را یاد خواهید گرفت.
- خواهید آموخت چگونه آزمون معناداری r را با آزمون t اجرا و تفسیر کنید.
- با تفاوتهای پیرسون، اسپیرمن و سایر ضرایب آشنا میشوید.
- شیوه ارائه و تفسیر صحیح نتایج پیرسون در گزارشهای علمی را یاد میگیرید.
- با مفهوم ضریب تعیین r² و نقش آن در تبیین واریانس دادهها آشنا میشوید.


سپس توضیح میدهیم چگونه میتوانیم انواع همبستگی را بر اساس مقدار ضریب r تعیین کنیم و شروط استفاده از ضریب همبستگی پیرسون چیست. همچنین با برخی از مفاهیم آماری مانند اندازه اثر و آزمون معناداری آشنا خواهید شد و با بررسی مثالها و تمرینهای متنوع، به روش محاسبه این ضریب نیز کاملا مسلط میشوید.
ضریب همبستگی پیرسون چیست؟
محاسبه ضریب همبستگی مرسومترین روش اندازهگیری همبستگی خطی است. مقدار این ضریب که همواره عددی بین ۱- و ۱ است، نشان میدهد رابطه خطی بین دو مجموعه داده تا چه اندازه قوی است و در چه جهتی پیش میرود. اگر هر دو گروه متغیر ما کمی باشند، رابطه بین آنها خطی باشد و توزیع نرمالی با تعداد دادههای پرت خیلی کمی داشته باشند، در این صورت میتوانیم از ضریب همبستگی پیرسون برای بررسی همبستگی این دادهها استفاده کنیم که توسط فرمول زیر محاسبه میشود:
- r: ضریب همبستگی پیرسون
- x: مقادیر اولین مجموعه دادهها
- y: مقادیر دومین مجموعه دادهها
- n: تعداد کل مقادیر یا اندازه نمونه

دقت کنید اگر در متون مختلف عبارت ضریب همبستگی بدون مشخص کردن نوع آن استفاده شد، منظور همان ضریب همبستگی پیرسون است. همچنین ممکن است این ضریب با عبارتهایی مانند Pearson’s r، همبستگی دو متغیره، یا با نماد اختصاری PPMCC به معنای «ضریب همبستگی حاصلضرب - گشتاور پیرسون» (Pearson Product-Moment Correlation Coefficient) و یا با نمادی بر گرفته از حروف اول نام لاتین آن به شکل PCC بیان شود.
ضریب همبستگی پیرسون نمونهای از یک کمیت آماری توصیفی است، چرا که توصیف کننده جهت و شدت رابطه خطی بین دو متغیر کمی است. در حقیقت این ضریب، نسبت کواریانس به حاصلضرب انحراف معیار دو مجموعه داده است. کواریانس و انحراف معیار بهصورت زیر تعریف میشوند:
- «کواریانس» (Covariance): نرخ تغییرات دو متغیر را در مقایسه با هم توصیف میکند.
- «انحراف معیار» (Standard Deviation) یا σ: نوعی شاخص پراکندگی است که نشان میدهد فاصله دادهها از مقدار میانگین چقدر است.
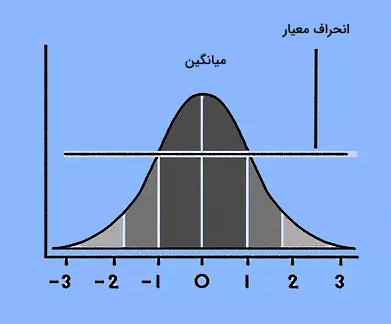
تعریف بالا همان مفهوم گشتاور حاصلضرب است که به آن اشاره شد. در واقع، اگر بخواهیم تعریف دقیقتری از ضریب همبستگی پیرسون ارائه دهیم، لازم است ابتدا ببینیم دادههای ما مربوط به یک نمونه هستند یا یک جمعیت. البته در نهایت، تفاوت فرمول ضریب همبستگی پیرسون برای این دو حالت فقط در نمادها و ورودیها است. برای مثال ضریب همبستگی پیرسون جمعیت با ρ نشان داده میشود، در حالی که برای نمایش ضریب همبستگی پیرسون نمونه حرف r بکار میرود. در ادامه این دو وضعیت را توضیح خواهیم داد.
مقدمات یادگیری ضریب همبستگی با فرادرس
پس از اینکه با کلیات ضریب همبستگی پیرسون آشنا شدیم، در این بخش قصد داریم چند دوره آموزشی با مباحث آمار و احتمال در مقطع متوسطه از مجموعه فرادرس را به شما معرفی کنیم. مشاهده این فیلمهای آموزشی به شما کمک میکند تا بهتر متوجه شوید مفهوم ضریب همبستگی پیرسون چیست. همچنین با یادگیری چند پارامتر آماری مهم مانند میانگین، انحراف معیار و واریانس به انجام محاسبات با کمک فرمول ضریب همبستگی پیرسون تسلط بیشتری خواهید داشت.
چنانچه در رشتههای ریاضی یا علوم تجربی مشغول به تحصیل در مقطع متوسطه هستید، میتوانید فیلمهای آموزشی زیر را با موضوع آمار و احتمال مشاهده کنید:
- فیلم آموزش ریاضی دهم تجربی و ریاضی فرادرس
- فیلم آموزش ریاضی یازدهم تجربی فرادرس
- فیلم آموزش ریاضی دوازدهم تجربی فرادرس
- فیلم آموزش آمار و احتمال پایه یازدهم فرادرس
اما اگر دانشآموز رشته علوم انسانی هستید، فیلمهای آموزشی زیر به شما در یادگیری مفاهیمی مانند آمار توصیفی، احتمال و توزیعهای احتمالاتی کمک میکنند:
- فیلم آموزش ریاضی و آمار دهم انسانی فرادرس
- فیلم آموزش ریاضی و آمار دهم حل سوالات کنکور فرادرس
- فیلم آموزش ریاضی و آمار دوازدهم انسانی فرادرس
- فیلم آموزش ریاضی و آمار دوازدهم حل سوالات کنکور فرادرس
ضریب همبستگی پیرسون برای جمعیت
اگر از ضریب همبستگی پیرسون در مورد یک جمعیت استفاده کنیم، در این صورت برای نشان دادن آن از حرف یونایی ρ استفاده میشود. معمولا ضریب همبستگی جمعیت، ضریب همبستگی پیرسون جمعیت نیز نامیده میشود. جفت متغیر تصادفی را در نظر بگیرید، در این صورت فرمول ضریب همبستگی پیرسون جمعیت خواهد شد:
که در آن cov نشاندهنده کواریانس، σX انحراف معیار متغیر X و σY انحراف معیار متغیر Y است.
در ادامه میتوانیم از فرمول کواریانس که بر حسب مقدار میانگین (μ) و مقدار انتظاری یا امید ریاضی (E) است، استفاده کنیم:
در رابطه بالا μX و μY بهترتیب معادل مقادیر میانگین روی متغیرهای X و Y هستند. اگر به خاطر داشته باشید، امید ریاضی برای یک مجموعه داده گسسته برابر میشود با مجموع حاصلضرب احتمال وقوع هر حالت در مقدار آن. بنابراین ضریب همبستگی پیرسون جمعیت برابر خواهد شد با:
حالا فرض کنید میخواهیم فرمول ρ را برای گشتاورهای غیرمرکزی بازنویسی کنیم. در این شرایط خواهیم داشت:
دقت کنید این رابطه خیلی شبیه به رابطهای است که در ابتدای نوشته برای ضریب همبستگی پیرسون نمونه معرفی کردیم. اما تفاوت اینجاست که در ضریب همبستگی پیرسون جمعیت، از کواریانس جمعیت بین متغیرها و انحراف معیار جمعیت استفاده میشود.
ضریب همبستگی پیرسون برای نمونه
در مورد نمونه، ضریب همبستگی پیرسون نمونه یا ضریب همبستگی نمونه داریم که با rxy یا r نشان داده میشود. پیش از اینکه به بررسی این موضوع بپردازیم، پیشنهاد میکنیم فیلم آموزشی رگرسیون خطی فرادرس را مشاهده کنید. یادگیری رگرسیون خطی و غیرخطی به شما کمک میکند رابطه بین دادهها را بهتر تشخیص دهید و در نتیجه ضریب همبستگی مناسبی را برای بررسی و محاسبه انتخاب کنید. لینک این دوره در ادامه قرار داده شده است:
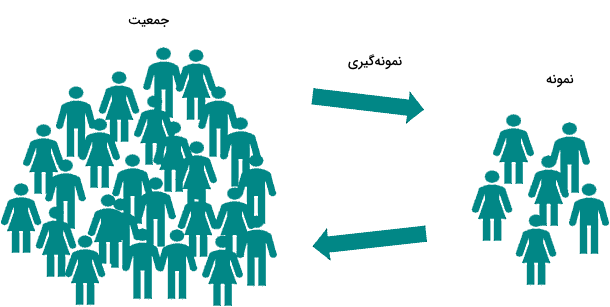
اگر n جفت داده بهصورت مجموعهای از Xها و Yها داشته باشیم، در این صورت rxy برابر است با:
که در آن n اندازه نمونه، xi و yi نقاط دادهای هستند که با اندیس i مشخص شدهاند. در رابطه بالا، یا همتای آن یعنی برابر هستند با میانگین نمونه که با فرمولهای زیر محاسبه میشوند:
اگر رابطه بالا را کمی سادهتر کنیم، میتوان آن را به شکل زیر بازنویسی کرد:
این فرمول همان فرمولی است که در این مطلب برای ضریب همبستگی پیرسون معرفی کردیم و در بخشهای بعدی با حل مثال، یاد میگیرید که چگونه با آن کار کنید.
انواع همبستگی چیست؟
در بخشهای قبل تا حدی متوجه شدیم که ضریب همبستگی پیرسون چیست و گفتیم مقدار این ضریب همواره در بازه ۱- تا ۱ قرار میگیرد. اگر این بازه را به دو قسمت ۱ تا ۰ و ۰ تا ۱- تقسیم کنیم، برای هر بخش میتوانیم نوع همبستگی مشخصی تعریف کنیم.
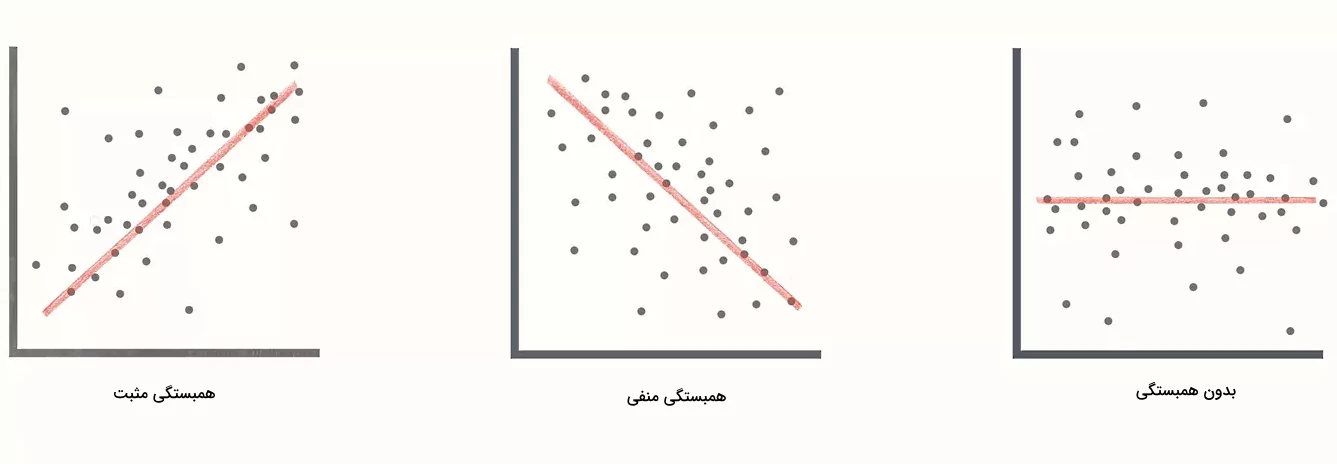
بر این اساس، سه نوع همبستگی بهصورت زیر هستند:
- همبستگی مثبت
- همبستگی صفر
- همبستگی منفی
| انواع همبستگی | همبستگی مثبت | همبستگی نداریم | همبستگی منفی |
| مقدار r | |||
| نتیجه | تغییرات متغیرها همجهت است. | متغیرها هیچ رابطهای با هم ندارند. | تغییرات متغیرها در خلاف جهت هم است. |
در ادامه انواع همبستگی را معرفی میکنیم و با بیان مثال و تحلیل هر نوع، به شما کمک میکنیم تا با مفهوم همبستگی بیشتر آشنا شوید.
همبستگی مثبت چیست؟
در این بخش یاد میگیریم رابطه بین همبستگی مثبت و ضریب همبستگی پیرسون چیست. اگر مقدار r در بازه عددی ۰ تا ۱ قرار بگیرد، در این صورت میگوییم همبستگی مثبت است. همبستگی مثبت به این معنا است که با تغییر یک متغیر، متغیر دیگر هم در همان راستا تغییر میکند.
برای مثال رابطه بین دو متغیر وزن و قد یک نوزاد را در نظر بگیرید. هر چه قد نوزاد بیشتر باشد، احتمالا وزن بیشتری هم دارد. بنابراین جهت تغییرات این دو متغیر با هم یکی است و این مسئله نشان دهنده همبستگی مثبت است.
همبستگی صفر چیست؟
حالا میخواهیم ببینیم مفهوم صفر شدن ضریب همبستگی پیرسون چیست. در تقسیمبندی بازه عددی ممکن برای ضریب همبستگی پیرسون گفتیم دو بازه در نظر میگیریم که شامل اعداد مثبت از صفر تا یک و اعداد منفی از صفر تا منفی یک میشوند.
اما اگر مقدار r صفر شود، چه نوع همبستگی داریم؟ در این شرایط همبستگی نداریم. پس همبستگی صفر معادل r = ۰ است و به معنای نداشتن همبستگی است. در چنین شرایطی هیچ نوع رابطهای بین متغیرها وجود ندارد. برای مثال بین قیمت یک خودرو و عرض برف پاککنهای آن هیچ ارتباطی وجود ندارد. بنابراین در این نمونه ضریب همبستگی پیرسون برابر با صفر است.
همبستگی منفی چیست؟
در سومین نوع همبستگی یاد میگیریم مفهوم منفی شدن ضریب همبستگی پیرسون چیست. اگر مقدار r در بازه ۰ تا ۱- قرار بگیرد، در این صورت همبستگی منفی است. در نتیجه انتظار داریم با تغییر یک متغیر، متغیر دیگر در جهت مخالف تغییر کند.
برای نمونه رابطه ارتفاع و فشار هوا را در نظر بگیرید. میدانیم با افزایش ارتفاع، فشار هوا کم میشود. بنابراین رابطه این دو متغیر عکس هم است یا میتوانیم بگوییم در جهتهای مخالف هم رشد میکنند. پس در این مثال همبستگی منفی است.
اندازه اثر چیست؟
در بخش قبل آموختیم انواع همبستگی چیست و چگونه جهت ارتباط دو متغیر با توجه به نوع همبستگی مشخص میشود. در این قسمت بازه عددی مجاز برای ضریب همبستگی پیرسون را به بخشهای بیشتری تقسیم میکنیم تا ببینیم چه ارتباطی بین مقدار ضریب r و شدت یا قدرت همبستگی وجود دارد. میزان قوی بودن همبستگی با پارامتری به نام اندازه اثر یا Effect Size مشخص میشود.
| مقدار ضریب همبستگی پیرسون (r) | شدت همبستگی | جهت همبستگی |
| کامل | همبستگی مثبت | |
| قوی | همبستگی مثبت | |
| متوسط | همبستگی مثبت | |
| ضعیف | همبستگی مثبت | |
| صفر | همبستگی نداریم. | |
| ضعیف | همبستگی منفی | |
| متوسط | همبستگی منفی | |
| قوی | همبستگی منفی | |
| کامل | همبستگی منفی |
در جدول بالا مشخص کردهایم چگونه با توجه به مقادیر مختلف r میتوانیم مشخص کنیم جهت و قدرت همبستگی به چه صورت است. بنابراین ضریب همبستگی پیرسون علاوه بر ایکه موضوع آمار توصیفی است، در شاخه آمار استنباطی نیز قرار میگیرد و در نتیجه میتوان با محاسبه این کمیت، فرضیات آماری مختلف را آزمود.
اثر ضریب همبستگی پیرسون در نمودار
در بخشهای قبل آموختیم رابطه بین جهت و شدت همبستگی با مقدار ضریب همبستگی پیرسون چیست. در این بخش قصد داریم توضیح دهیم اثر این ضریب روی نمودار نقطهای رسم شده بر اساس دادههایمان چگونه است. از مبحث رگرسیون خطی میدانیم زمانی که میخواهیم رابطه بین متغیرها را بررسی کنیم، سعی میکنیم بهترین و مناسبترین خط مستقیمی که با دادههایمان فیت شده است، رسم کنیم. این خط، «خط رگرسیون» (Regression Line) نام دارد. اگر علاقهمند به کسب اطلاعات بیشتر و حل مثال در مورد رگرسیون هستید، پیشنهاد میکنیم مطلب «رگرسیون چیست؟ – توضیح به زبان ساده» از مجله فرادرس را مطالعه کنید.
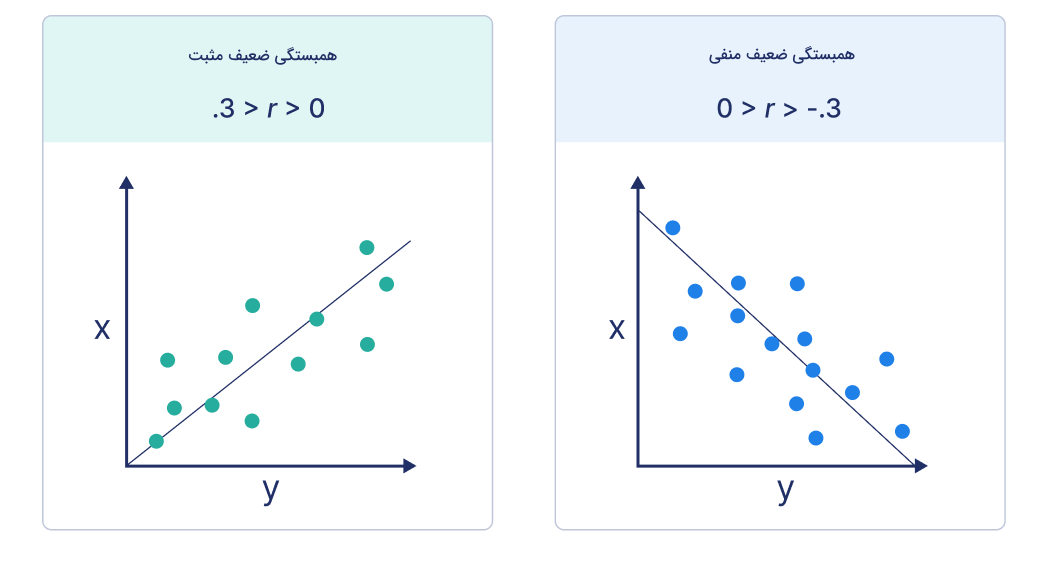
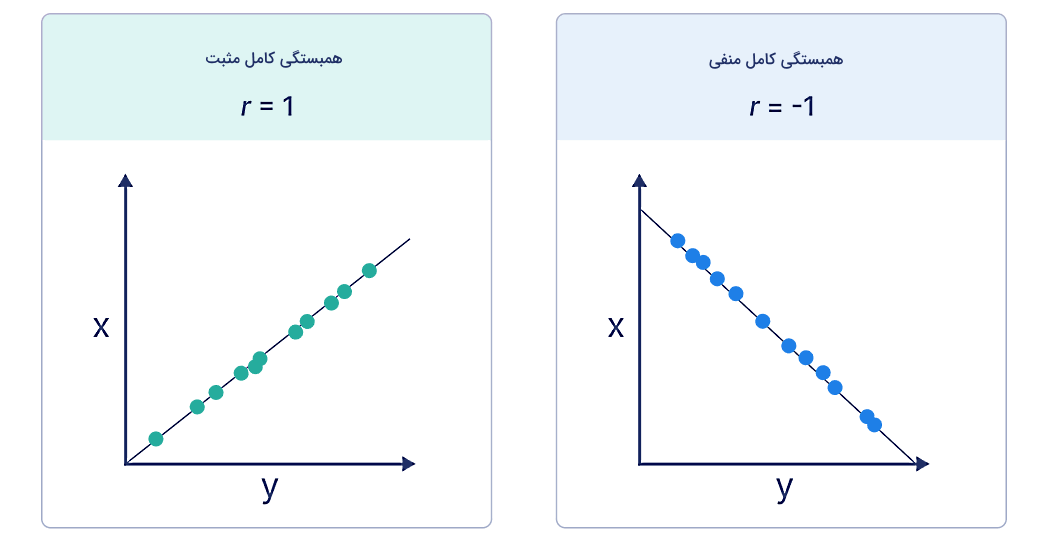
با نگاه کردن به نمودار نقطهای و خط رگرسیون باید بتوانیم حدس بزنیم همبستگی به چه صورت است. هر چه مشاهدات ما به این خط رگرسیون رسم شده نزدیکتر باشند، همبستگی قویتر و در نتیجه مقدار ضریب همبستگی پیرسون بیشتر است. یکی دیگر از نکاتی که با نگاه کردن به خط رگرسیون میتوانیم نتیجهگیری کنیم این است که اگر شیب این خط منفی باشد، مقدار r هم منفی است و اگر شیب مثبت باشد، مقدار r نیز مثبت است. همچنین در شرایطی که مقدار r کاملا با ۱- یا ۱ برابر شود، تمام نقاط مشاهدات ما کاملا روی خط رگرسیون قرار میگیرند و شرایط همبستگی کامل برقرار است.
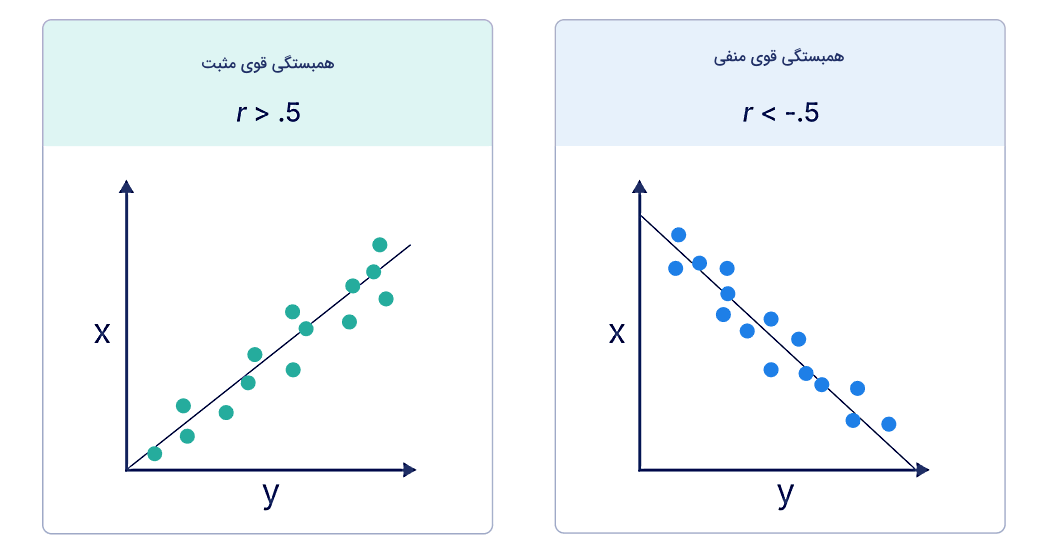
برای مثال در شکل بالا مشاهده میکنید که اگر مقدار r از ۰٫۵ بزرگتر یا از ۰٫۵- کمتر باشد، نقاط روی نمودار که معادل همان مشاهدات ما است، به خط رگرسیون خیلی نزدیک هستند، اما برخلاف حالت همبستگی کامل، دقیقا روی خط قرار نمیگیرند. در این شرایط همبستگی قوی داریم، اما کامل نیست. اگر مقدار r بین ۰ و ۰٫۳ یا بین ۰٫۳- و ۰ قرار داشته باشد، نقاط داده از خط رگرسیون دور هستند (شکل زیر). در این حالت همبستگی ضعیف است.
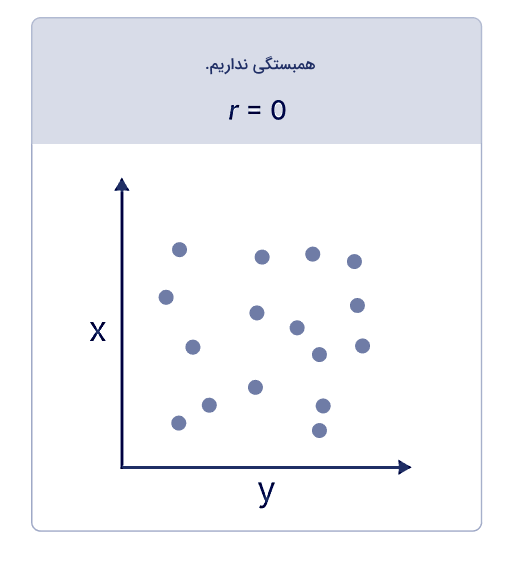
در نهایت زمانی که همبستگی وجود نداشته باشد، پراکندگی دادهها در نمودار نقطهای شکلی شبیه تصویر زیر خواهد داشت. در این شرایط مقدار ضریب همبستگی پیرسون یا r برابر با صفر است.
چه زمانی باید از ضریب همبستگی پیرسون استفاده کنیم؟
ضریب همبستگی پیرسون یکی از ابزارهایی است که جهت اندازهگیری همبستگی میتوانید از بین انواع ضرایب همبستگی دیگر انتخاب کنید. در بخشهای بعد توضیح میدهیم انواع ضرایب همبستگی چه هستند تا بهتر درک کنید که تفاوت سایر ضرایب با ضریب همبستگی پیرسون چیست. اما برای اینکه بتوانید از این ضریب استفاده کنید، لازم است شرایطی برقرار باشد که عبارتاند از:
- هر دو متغیر ما کمی هستند.
- نحوه توزیع متغیرها نرمال است.
- «دادههای پرت» (Outliers) کمی داریم.
- نوع ارتباط بین متغیرها خطی است.
دقت کنید کاربرد ضریب همبستگی پیرسون زمانی مجاز است که تمام شروط بالا برقرار باشند. در ادامه هر کدام از این موارد را بهصورت مختصر توضیح میدهیم.
کمی بودن متغیرها
میخواهیم ببینیم اولین شرط استفاده از ضریب همبستگی پیرسون چیست. کمی بودن متغیرها به این معنا است که هر دو متغیر مورد بررسی در مسئله ما باید کمی باشند و حتی اگر یکی از دو متغیر کیفی باشد، باید روش دیگری برای بررسی همبستگی دادههای خود انتخاب کنیم. بنابراین در اولین قدم باید بتوانیم نوع متغیرها را بهدرستی تشخیص دهیم.
توزیع نرمال متغیرها
پس از بررسی اولین شرط، میخواهیم ببینیم دومین شرط استفاده از ضریب همبستگی پیرسون چیست. برای اینکه بتوانیم تشخیص دهیم آیا توزیع دادههای ما نرمال است یا نه، کافی است هیستوگرام هر متغیر را رسم کنیم. البته در اینجا منظورمان از توزیع نرمال، داشتن یک توزیع دقیقا نرمال نیست. اگر نرمال بودن با تقریب هم برقرار باشد، شرط دوم را داریم.
ناچیز بودن دادههای پرت
سومین شرط این است که داده پرت نداشته باشیم یا اگر داریم، تعداد خیلی کمی باشند. داده پرت به هر دادهای گفته میشود که از روند یا الگوی سایر دادهها پیروی نمیکند. برای تشخیص دادههای پرت، باید نمودار نقطهای دادههای خود را رسم کنیم و هر نقطهای که در مقایسه با سایر نقاط در مکان دورتری قرار داشت را بهعنوان داده پرت در نظر بگیریم.
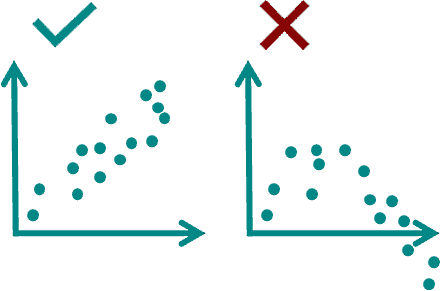
خطی بودن رابطه بین متغیرها
رابطه خطی بین متغیرها به این معنا است که بتوانیم ارتباط بین دادههای خود را توسط یک خط مستقیم توصیف کنیم. برای اینکه مشخص شود آیا رابطه بین دادههای ما خطی است یا نه، اولین قدم رسم نمودار نقطهای است.
فرمول ضریب همبستگی پیرسون چیست؟
در این بخش یاد میگیریم روش محاسبه ضریب همبستگی پیرسون چیست. فرمول ضریب همبستگی پیرسون به شکل زیر است:
که در آن r ضریب همبستگی پیرسون، x مقادیر اولین مجموعه دادههای ما، y مقادیر دومین مجموعه دادههای ما و n تعداد کل مقادیر یا اندازه نمونه ما است. اگر طبق مثال بخش بعد قدم به قدم مقادیر مختلف را محاسبه کنید، کار کردن با این فرمول بسیار راحت است. همچنین میتوانید برای محاسبه مقدار r از نرمافزارهایی مانند آر (R) یا اکسل (Microsoft Excel) نیز استفاده کنید.
برای مثال در R کافی است از تابع ()cor استفاده کنید تا ضریب همبستگی پیرسون را برای شما محاسبه کند. در اکسل تابع ()PEARSON این ضریب را به شما میدهد، به این صورت که اگر دادههای خود را در دو ستون A و B قرار داده باشید، با کلیک در یک سلول خالی و نوشتن فرمول (A:A,B:B)PEARSON ضریب r بهدست میآید.
یک نکته مهم در مورد بهدست آوردن ضریب همبستگی پیرسون با این فرمول این است که مهم نیست کدام یک از متغیرهای خود را x و کدام را y در نظر بگیرید. در نهایت جواب با هر کدام از این فرضیات، یکسان خواهد بود. این در حالی است که اگر خاطرتان باشد، برای بهدست آوردن معادله خط رگرسیون این مسئله مهم است و باید متغیر مستقل را x و متغیر وابسته را y در نظر میگرفتیم. بنابراین اگر خط رگرسیون هم جزء محاسبات شما هست، بهتر است از ابتدا متغیر وابسته و مستقل خود را مشخص کنید. اما در شرایطی که فقط میخواهید مقدار r را پیدا کنید، نوع متغیر مهم نیست.
مراحل محاسبه ضریب همبستگی پیرسون
فرض کنید شخصی میخواهد رابطه بین وزن نوزادان تازه متولد شده با قد آنها را مطالعه کند. به همین دلیل مشخصات ۱۰ نوزاد را در جدولی به شکل زیر جمعآوری میکند. میخواهیم ببینیم مقدار ضریب همبستگی پیرسون چیست و چه اطلاعاتی به ما میدهد.
| قد (cm) | وزن (kg) |
برای محاسبه r قدم به قدم با مراحل زیر پیش میرویم:
- مرحله اول: محاسبه و
- مرحله دوم: محاسبه و
- مرحله سوم: محاسبه
- مرحله چهارم: قرار دادن مقادیر بالا در فرمول r

مرحله اول
اولین قدم برای اینکه ببینیم در این سوال مقدار ضریب همبستگی پیرسون چیست، محاسبه مقادیر و است. اگر وزن نوزاد با x و قد با y مشخص شود، در این صورت خواهیم داشت:
مرحله دوم
در دومین مرحله برای محاسبه r باید مجموع مقادیر و را بهدست آوریم. برای این مرحله بهتر است جدولی رسم کنیم و توان دوم هر کدام از xها و yها را در این جدول درج کنیم:
| وزن (kg) = x | قد (cm) = y | ||
حالا مجموع مقادیر ستونهای و را بهدست میآوریم:
مرحله سوم
در این مرحله باید حاصل را پیدا کنیم. اما قبل از اینکه مجموع مقادیر xy را محاسبه کنیم، لازم است ابتدا حاصلضرب x در y را برای هر مشاهده یا هر نوزاد بهدست آوریم. مجددا جدولی مشابه جدول بالا رسم میکنیم:
| وزن (kg) = x | قد (cm) = y | |
مرحله چهارم
در آخرین مرحله محاسبه میکنیم مقدار ضریب همبستگی پیرسون چیست. فقط کافی است اعدادی که در مراحل قبل پیدا کردیم را در فرمول ضریب همبستگی پیرسون قرار دهیم. دقت کنید مقدار n در این مطالعه برابر با ۱۰ است:
ضریب همبستگی کمتر از ۰٫۵ و بیشتر از ۰٫۳ شد. بنابراین طبق آنچه که در بخشهای قبل گفتیم، همبستگی ما متوسط و مثبت است. مثبت بودن همبستگی به این معنا است که رابطه بین دو متغیر قد و وزن نوزاد در یک جهت پیش میرود. پس با افزایش قد، وزن نوزاد نیز بیشتر میشود. اما دقت داریم که چون همبستگی متوسط است، شدت این رابطه خیلی قوی نیست.
آزمون معناداری ضریب همبستگی پیرسون
پس از اینکه یاد گرفتیم فرمول محاسبه ضریب همبستگی پیرسون چیست و برای محاسبه r لازم است چه مراحلی را طی کنیم، در این قسمت قصد داریم یکی دیگر از کاربردهای ضریب همبستگی پیرسون را بیان کنیم. این ضریب را میتوان با هدف بررسی اینکه آیا رابطه بین دو متغیر معنادار است یا خیر، بکار برد. در ادامه با استفاده از مثال بخش قبل نشان میدهیم چگونه میتوان این فرآیند را انجام داد.
گفتیم همبستگی پیرسون یک نمونه را با r نشان میدهیم، اما r در حقیقت تخمینی از ρ است. ρ همبستگی پیرسون جمعیت است. بنابراین با دانستن r و n (اندازه نمونه)، میتوانیم استنباط کنیم آیا ρ خیلی با مقدار صفر متفاوت است یا خیر. ابتدا فرضیات آزمون را تعریف میکنیم:
- «فرض صفر» (Null Hypothesis) یا H0: زمانی این فرض برقرار است که باشد.
- «فرض مقابل» (Alternative Hypothesis) یا Ha: زمانی این فرض برقرار است که باشد.
جهت آزمون این فرضیات میتوانید از نرمافزارهایی مانند آر (R) با کاربرد تابع ()cor.test یا استتا (Stata) استفاده کنید، اما اجرای مراحل زیر نیز اطلاعات مشابهی به شما خواهد داد:
- مرحله اول: محاسبه t value
- مرحله دوم: پیدا کردن مقدار بحرانی t
- مرحله سوم: مقایسه t value با مقدار بحرانی t
- مرحله چهارم: تصمیمگیری در مورد اینکه فرض صفر رد شود یا نه
در ادامه هر مرحله را با توجه به دادههایی که در مثال بخش قبل داشتیم، بررسی میکنیم. دقت کنید در اکسل تابع مشخصی برای آزمودن معناداری همبستگی وجود ندارد.
مرحله اول: محاسبه t value
اولین مرحله برای اینکه بهتر متوجه شویم آزمون معناداری ضریب پیرسون چیست و چه اطلاعاتی به ما میدهد، محاسبه t value است. برای محاسبه مقدار t میتوانید از فرمول زیر استفاده کنید:
اگر به مشخصات قد و وزن نوزادان در مثال قبل مجددا بازگردیم، ضریب همبستگی پیرسون برای آن دادهها معادل ۰٫۴۷ شد. با توجه به اینکه در آن مثال اندازه نمونه برابر با ۱۰ است، پس میتوانیم با فرمول بالا t value را پیدا کنیم:
مرحله دوم: پیدا کردن مقدار بحرانی t
مقدار بحرانی t را با نشان میدهیم. برای پیدا کردن باید به جدول t مراجعه کنیم که برای استفاده از آن، لازم است سه مورد زیر را بدانیم:
- درجات آزادی یا df: در مورد آزمونهای همبستگی پیرسون فرمول درجات آزادی بهصورت است.
- سطح معناداری یا α: طبق قرارداد سطح معناداری معمولا برابر با ۰٫۰۵ است.
- یک طرفه یا دو طرفه بودن: عموما دو طرفه بودن انتخاب مناسبی برای همبستگیها است.
بنابراین در مورد مثال قد و وزن، با در نظر گرفتن دو طرفه بودن شرایط بهصورت زیر خواهد شد:
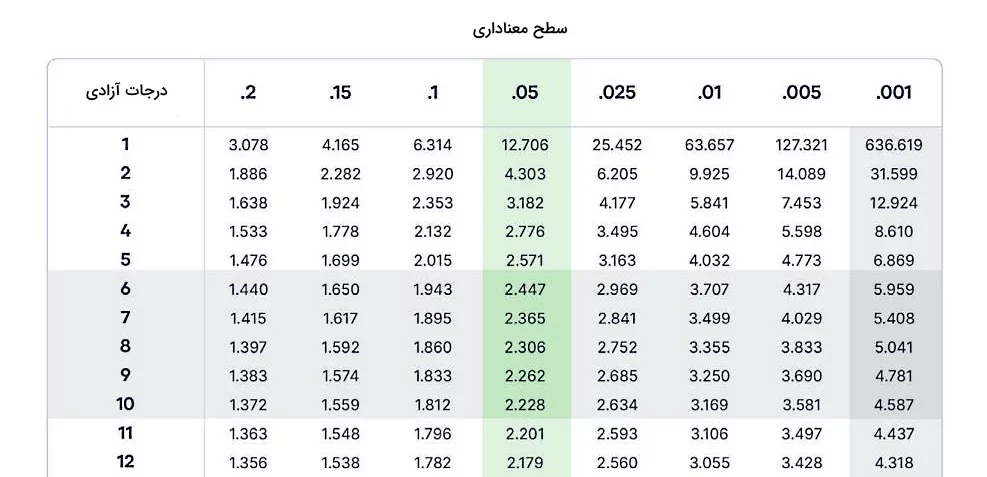
طبق تصویر بالا که از بخشی از یک جدول t در مورد آزمونهای فرضیه دو طرفه تهیه شده است، با در نظر گرفتن شرایط بالا، مقدار بحرانی t برابر میشود با ۲٫۳۰۶.
مرحله سوم: مقایسه t value با مقدار بحرانی t
در این مرحله فقط کافی است مقدار مطلق t بهدست آمده در مرحله اول را با t بحرانی حاصل از مرحله قبل مقایسه کنید. دقت کنید منظورمان از مقدار مطلق t این است که اگر در محاسبه t value عدد منفی بهدست آوردید، علامت منفی را در این مقایسه در نظر نگیرید. همانطور که مشاهده میکنید، در مثال مورد بررسی ما، t value از کمتر است:
مرحله چهارم: تصمیمگیری در مورد اینکه فرض صفر رد شود یا نه
در انتها میخواهیم ببینیم آخرین مرحله از آزمون معناداری ضریب همبستگی پیرسون چیست. در این گام به یکی از این دو نتیجه میرسیم:
- اگر مقدار t value از مقدار بحرانی t بیشتر شد، در این صورت رابطه بین دادهها از نظر آماری معنادار است، یعنی داریم .
- اگر مقدار t value از مقدار بحرانی t کمتر شد، در این صورت رابطه بین دادهها از نظر آماری معنادار نیست، یعنی داریم .
دقت کنید در روابط بالا p به معنای مقدار احتمال یا p value است که نباید با ρ اشتباه شود. رسیدن به معناداری نشان میدهد دادههای ما فرض صفر را رد کرده و فرض مقابل را پشتیبانی میکنند. اما اگر به معناداری نرسیدیم و مقدار بحرانی t از t value بیشتر شد، در این حالت دادههای ما نهتنها اجازه رد فرض صفر را نمیدهند، بلکه فرض مقابل را هم پشتیبانی نمیکنند.
در مثال قد و وزن، شرایط دوم برقرار است، یعنی رابطه بین دادههای ما از نظر آماری معنادار نیست. بنابراین فرض صفر را رد نمیکنیم، به این معنا که ضریب همبستگی پیرسون جمعیت یا ρ ممکن است صفر باشد. همچنین رابطه معناداری بین قد و وزن وجود ندارد و داریم . البته در این مثال باید دقت کنید که اندازه نمونه ۱۰ اندازه بسیار کوچکی برای بررسی همبستگی در این سطح است. بنابراین ممکن است با افزایش اندازه نمونه، به معناداری رابطه بین قد و وزن دست پیدا کنید.
مثال ضریب همبستگی پیرسون
پس از اینکه متوجه شدید فرمول و مراحل محاسبه ضریب همبستگی پیرسون چیست و چگونه میتوانیم معناداری همبستگی را بررسی کنیم، در این بخش با حل چند سوال نحوه استفاده از فرمول بالا را تمرین میکنیم تا کاملا به این مبحث مسلط شوید.
مثال ۱
طبق بررسی زیر در یک شهر، رابطه بین سن و درآمد اشخاص بهصورت جدول زیر است. بررسی کنید که آیا با افزایش سن، درآمد اشخاص نیز زیاد میشود یا خیر؟
| سن | درآمد |
پاسخ
در مسائل این چنینی که با اعداد بزرگی مانند میزان درآمد مواجهایم، برای اینکه محاسبات آسانتری داشته باشیم، میتوانیم این اعداد را بر ۱۰۰۰ تقسیم کنیم. بنابراین با در نظر گرفتن این نکته و انتخاب متغیر x بهعنوان سن و متغیر y بهعنوان میزان درآمد تقسیم بر ۱۰۰۰، مراحل محاسبه را پیش میبریم. در اولین مرحله مجموع مقادیر x و y را پیدا میکنیم:
در دومین مرحله برای محاسبه r باید مجموع مقادیر و را بهدست آوریم. طبق جدول زیر پیش میرویم:
| سن = x | ۱/۱۰۰۰ درآمد = y | ||
حالا مجموع مقادیر ستونهای و را بهدست میآوریم:
سپس باید حاصل را پیدا کنیم. اما قبل از اینکه مجموع مقادیر xy را محاسبه کنیم، لازم است ابتدا حاصلضرب x در y را برای هر مشاهده بهدست آوریم. بنابراین مجددا جدولی مشابه جدول بالا رسم میکنیم:
| سن = x | ۱/۱۰۰۰ درآمد = y | |
در نهایت اعدادی که در مراحل قبل پیدا کردیم را در فرمول ضریب همبستگی پیرسون قرار میدهیم. دقت کنید مقدار n در این مطالعه برابر با ۴ است:
ضریب همبستگی بسیار به یک نزدیک شد. این مقدار r نشان میدهد که همبستگی ما قوی و مثبت است. مثبت بودن همبستگی به این معنا است که رابطه بین دو متغیر سن و درآمد اشخاص در این مثال در یک جهت پیش میرود و با افزایش سن، درآمد هم بیشتر میشود. چون همبستگی قوی است، میتوانیم با اطمینان بیشتری در مورد چنین ارتباطی صحبت کنیم.
مثال ۲
نمرات ریاضی و هندسه ۵ دانشآموز به شرح زیر است:
| ریاضی | هندسه |
نشان دهید که همبستگی این دادهها متوسط و منفی است.
پاسخ
برای اینکه بتوانیم تعیین کنیم نوع همبستگی به چه صورت است، باید ضریب همبستگی پیرسون یا r را محاسبه کنیم. سپس با توجه به اندازه و علامت این ضریب در مورد نوع همبستگی میتوانیم نظر دهیم. برای محاسبه r مطابق مثال قبل عمل میکنیم. در این سوال نمرات ریاضی را متغیر x و نمرات هندسه را متغیر y در نظر میگیریم و جدولی به شکل زیر رسم میکنیم:
| ریاضی = x | هندسه = y | ||
پس اغلب مقادیر لازم برای فرمول ضریب همبستگی پیرسون در جدول بالا محاسبه شد. فقط باید و مجموع آن را حساب کنیم:
| ریاضی = x | هندسه = y | |
بنابراین کافی است در آخرین مرحله فرمول r را بنویسیم:
با توجه به اینکه n = ۵ است، حاصل برابر است با:
همانطور که مشاهده میکنید، علامت ضریب همبستگی پیرسون منفی شد. بنابراین همبستگی منفی است، به این معنا که اگر نمرات ریاضی زیاد شوند، نمرات هندسه کم میشوند و برعکس. همچنین مقدار این ضریب بین ۰٫۳ و ۰٫۵ قرار دارد که طبق جدول بخشهای ابتدایی این مطلب، همبستگی این سوال متوسط است.
مثال ۳
معنادار بودن همبستگی در دادههای زیر را تعیین کنید:
پاسخ
اگر خاطرتان باشد، گفتیم برای تعیین معناداری همبستگی باید از آزمون معناداری ضریب همستگی پیرسون استفاده کنیم. این آزمون چهار مرحله داشت که در اولین مرحله آن لازم است t value محاسبه شود. فرمول مقدار t به شکل زیر است:
که در آن n اندازه نمونه است که در اینجا برابر میشود با ۵ و r هم که ضریب همبستگی پیرسون است. پس برای محاسبه t در اولین مرحله آزمون معناداری نیاز داریم اول مقدار r را بدانیم. برای محاسبه r مانند مثالهای قبل از فرمول زیر استفاده میکنیم:
همچنین جدول مقادیر خود را رسم کرده و حاصل هر ستون را بهدست میآوریم:
| x | y | ||
در مرحله بعدی مقادیر حاصلجمع xy را باید بهدست آوریم:
| x | y | |
حالا با قرار دادن مقادیر بالا در فرمول r خواهیم داشت:
پس مقدار r تعیین شد که نشاندهنده همبستگی منفی و ضعیفی است (چون r بین ۰ و ۰٫۳- قرار دارد). حالا میتوانیم برویم سراغ فرمول t value:
دقت کنید نوشتن دو رقم بعد از اعشار در محاسبات برای مقدار r کافی است. همچنین درج علامت منفی r برای این مرحله ضرورتی ندارد:
مقدار t بهدست آمد. مرحله بعدی تعیین مقدار t بحرانی یا است که گفتیم روند زیر را باید برای انتخاب این مقدار طی کنیم:
- استفاده از فرمول درجات آزادی بهصورت که درجه آزادی به ما میدهد.
- سطح معناداری یا α که طبق قرارداد گفتیم سطح معناداری برابر با ۰٫۰۵ در نظر گرفته میشود.
- همچنین گفتیم در مورد همبستگیها آزمون دو طرفه است.
حالا اگر به جدول مناسب آزمون دو طرفه t مراجعه کنیم، طبق شکل زیر مقدار t بحرانی با درجه آزادی ۳ و سطح معناداری ۰٫۰۵ برابر میشود با ۳٫۱۸. پس اگر t را با t بحرانی مقایسه کنیم، مشخصا مقدار خیلی از t بزرگتر است. گفتیم اگر مقدار t value از مقدار بحرانی t کمتر شد، در این صورت رابطه بین دادهها از نظر آماری معنادار نیست.

مثال ۴
فرض کنید مقادیر ضریب همبستگی پیرسون برای چند مطالعه بهصورت زیر است. نوع همبستگی را برای هر کدام مشخص کنید:
پاسخ
- ضریب همبستگی پیرسون ۰٫۶۹ مثبت و بزرگتر از ۰٫۵ است. بنابراین همبستگی قوی و مثبت میدهد.
- ضریب همبستگی پیرسون ۰٫۴۲ مثبت و کوچکتر از ۰٫۵ است. بنابراین همبستگی متوسط و مثبت میدهد.
- ضریب همبستگی پیرسون ۰٫۲۳- منفی و بزرگتر از ۰٫۳- است. بنابراین همبستگی ضعیف و منفی میدهد.
- ضریب همبستگی پیرسون ۰٫۹۹- منفی و کوچکتر از ۰٫۵- است. بنابراین همبستگی قوی و منفی میدهد.
تمرین ۱
تمرین ۲
تفاوت ضریب همبستگی رتبهای اسپیرمن با ضریب همبستگی پیرسون چیست؟
در بخشهای گذشته یاد گرفتیم ضریب همبستگی پیرسون چیست، چه شرایط اولیهای برای کاربرد آن باید برقرار باشد و مقادیر آن چه ارتباطی با نوع همبستگی دادههای ما دارد. در این بخش میخواهیم ببینیم این ضریب با ضریب همبستگی دیگری به نام «ضریب همبستگی رتبهای اسپیرمن» (Spearman’s Rank Correlation Coefficients) چه تفاوتی دارد. ضریب همبستگی رتبهای اسپیرمن یکی دیگر از پرکاربردترین پارامترهایی است که در مطالعات همبستگی محاسبه میشود. در ادامه شرایطی را بیان میکنیم که اگر یکی یا تعداد بیشتری از این شرایط برقرار بودند، بهتر است انتخاب ما بهجای ضریب همبستگی پیرسون، ضریب همبستگی رتبهای اسپیرمن باشد:
- متغیرهای ما ترتیبی هستند.
- نحوه توزیع متغیرها نرمال نیست.
- دادههای پرت داریم.
- نوع ارتباط بین متغیرها غیرخطی و یکنوا است.
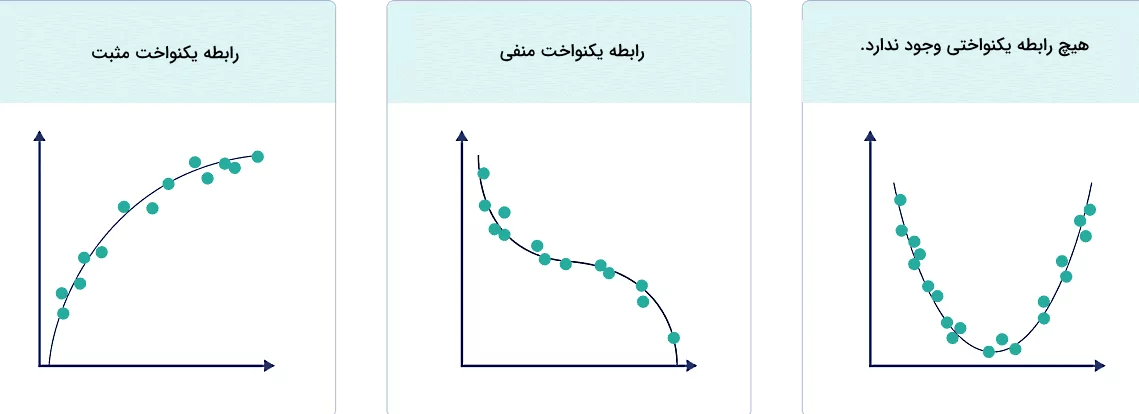
دقت کنید در آخرین شرط مهم است که علاوه بر خطی نبودن رابطه بین دادهها، با رسم نمودار نقطهای منحنی حاصل یکنوا باشد. یعنی هر دو شرط غیرخطی بودن و یکنوا بودن با هم باید درست باشند. در حالی که ضریب همبستگی پیرسون خطی بودن رابطه دادهها را اندازه میگیرد، ضریب همبستگی اسپیرمن یکنواختی رابطه بین دادهها را بررسی میکند.
در یک رابطه خطی، هر متغیر در جهت موافق یا مخالف متغیر مقابل خود تغییر میکند، اما در رابطه یکنواخت، متغیرها در یک راستا تغییر میکنند اما با نرخی متفاوت از دیگری. همین مسئله باعث میشود دو نوع یکنواختی داشته باشیم:
- یکنواختی مثبت: وقتی با افزایش یک متغیر، دیگری هم زیاد شود.
- یکنواختی منفی: وقتی با افزایش یک متغیر، دیگری کم شود.
انواع ضرایب همبستگی چه هستند؟
برای اینکه بهتر درک کنید تفاوت سایر ضرایب همبستگی با ضریب همبستگی پیرسون چیست، در این بخش میخواهیم بهصورت مختصر انواع ضرایب همبستگی را معرفی کنیم. انتخاب اینکه کدام ضریب برای بررسی دادههای شما مناسب است، در اولین قدم به این بستگی دارد که نوع ارتباط دادههای شما خطی است یا غیرخطی. همچنین نحوه توزیع دادهها به همراه سطح اندازهگیری متغیرها از نظر میزان دقت، موارد دیگری هستند که باید در نظر گرفته شوند.
همانطور که تا اینجا متوجه شدید، اگر رابطه بین دادههای شما خطی است، بهترین انتخاب استفاده از ضریب همبستگی پیرسون است. اما در صورت غیرخطی بودن، ضرایب همبستگی مانند اسپیرمن یا «کندال» (Kendall) به کار میآیند. برای دادههای رتبهای، ضریب کندال در نمونههای کوچک پایداری بیشتری دارد، اما ضریب اسپیرمن در نمونههای بزرگ محاسبه آسانتری دارد. جدول زیر انواع ضرایب همبستگی همراه با مشخصات آنها را نشان میدهد:
| ضریب همبستگی | نوع رابطه بین دادهها | سطح اندازهگیری | نحوه توزیع دادهها |
| پیرسون (r) | خطی | دو متغیر کمی | نرمال |
| اسپیرمن (ρ) | غیرخطی | دو متغیر ترتیبی | هر نوع توزیعی |
| بیسریال نقطهای | خطی | یک متغیر باینری و یک متغیر کمی | نرمال |
| کرامر (V) | غیرخطی | دو متغیر اسمی | هر نوع توزیعی |
| کندال (τ) | غیرخطی | دو متغیر ترتیبی | هر نوع توزیعی |
چند نکته در مورد ضریب همبستگی پیرسون
در این قسمت توضیح میدهیم چنانچه مقاله یا گزارشی داشتیم، روش استفاده از ضریب همبستگی پیرسون چیست، چگونه و در چه بخشی آن را وارد کنیم و چگونه اثر آن را در نتایج خود تحلیل کنیم. ضریب همبستگی پیرسون در بخش نتایج اعلام میشود و معمولا برای نشان دادن آن از نماد r ایتالیک استفاده میشود. بهتر است که مقادیر عددی با دو رقم بعد از اعشار نشان داده شوند. همچنین چون مقدار ضریب r همواره بین مقادیر ۱- و ۱ قرار میگیرد، معمولا در متون آماری پیش از علامت اعشار آن از ۰ استفاده نمیشود.
زمانی که ضریب همبستگی پیرسون را در آمار استنباطی و بررسی معناداری بکار میبرید، بهتر است r را همراه با درجات آزادی و p value یا مقدار احتمال بیان کنید. درجات آزادی داخل یک پرانتز و بلافاصله بعد از r به شکل زیر نمایش داده میشود:
رابطه بالا را بر اساس مثال قد و وزن در بخش «مراحل محاسبه ضریب همبستگی پیرسون» نوشتیم که طبق آن اگرچه بین قد و وزن نوزادان تازه متولد شده همبستگی متوسطی برقرار است، اما این رابطه از نظر آماری معنادار نیست.

ضریب تعیین چیست؟
در این بخش میخواهیم ببینیم مربع ضریب همبستگی پیرسون چیست. اگر r را به توان دوم برسانیم، «ضریب تعیین یا تشخیص» (Coefficient of Determination) بهدست خواهد آمد. مقدار ضریب تعیین همیشه بین ۰ و ۱ قرار میگیرد و معمولا در قالب درصد بیان میشود. معمولا از ضریب تعیین در مدلهای مختلف رگرسیون استفاده میکنیم تا بدانیم چه مقدار از واریانس یک متغیر توسط واریانس متغیر دیگر توضیح داده میشود.
بیشتر بودن مقدار r۲ یا ضریب تعیین، به این معنا است که مقدار زیادی از میزان تنوع در یک متغیر توسط رابطهاش با متغیر دیگر تعیین میشود. در مقابل، کمتر بودن ضریب تعیین نشان میدهد که تنها نسبت خیلی کمی از میزان تنوع در یک داده را میتوان توسط رابطهاش با داده دیگر توضیح داد.
ضریب ناهمبستگی چیست؟
اگر مقدار ضریب تعیین را از واحد یا عدد یک کم کنید، «ضریب ناهمبستگی» (Coefficient of Alienation) را بهدست میآورید. ضریب ناهمبستگی نسبتی از واریانسی است که بین متغیرها مشترک نیست یا در واقع، همان واریانس توضیح داده نشده بین متغیرها است.
اگر ضریب ناهمبستگی بزرگی داشته باشیم یعنی دو متغیر واریانس کوچکی را با هم به اشتراک گذاشتهاند. در صورتی که مقدار ضریب ناهمبستگی کوچک بیانگر این است که بخش قابلتوجهی از واریانس، توسط رابطه بین متغیرها تعیین میشود.
مسیر یادگیری آمار و احتمال در سطح دانشگاهی با فرادرس
در انتهای این مطلب و با توجه به اینکه کاملا یاد گرفتید ضریب همبستگی پیرسون چیست، در نظر داریم چند فیلم آموزشی با موضوع آمار و احتمال در سطوح دانشگاهی به شما معرفی کنیم.

- فیلم آموزش آمار و احتمال مهندسی با مثال های مختلف فرادرس
- فیلم آموزش آمار و احتمال مهندسی حل تمرین و تست کنکور ارشد فرادرس
- فیلم آموزش رایگان رگرسیون فرادرس
- فیلم آموزش رایگان رگرسیون خطی ساده فرادرس
- فیلم آموزش رگرسیون ۱ - رگرسیون خطی فرادرس
- فیلم آموزش رگرسیون ۲ فرادرس
- فیلم آموزش اقتصاد سنجی فرادرس
پس از اینکه کاملا به مباحث آمار و احتمال مسلط شدید، مشاهده فیلمهای آموزشی زیر از مجموعه فرادرس در زمینه کاربردهای آمار و احتمال یا یادگیری نرمافزارهای آماری به شما کمک خواهد کرد:
- مجموعه آموزش اس پی اس اس SPSS – مقدماتی تا پیشرفته فرادرس
- مجموعه آموزش تخمین و رگرسیون – مقدماتی تا پیشرفته فرادرس
- فیلم آموزش محاسبات آماری در اکسل Excel فرادرس
- فیلم آموزش برنامه نویسی R و نرم افزار RStudio مقدماتی فرادرس
- فیلم آموزش آمار و احتمال در پایتون Python فرادرس
- فیلم آموزش رایگان رگرسیون غیرخطی و لجستیک در تحلیل اطلاعات با SAS فرادرس
- فیلم آموزش رایگان رگرسیون خطی و شبکه عصبی MLP در پایتون برای پیش بینی چربی بدن فرادرس
- فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS فرادرس
- فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS فرادرس
جمعبندی
در این نوشته از مجله فرادرس توضیح دادیم که ضریب همبستگی پیرسون چیست و یاد گرفتیم که از آن برای بررسی همبستگی خطی بین دو مجموعه داده کمی استفاده میشود. پیش از انتخاب این ضریب برای مطالعه وضعیت همبستگی در یک بررسی، لازم است پیشفرضهایی برقرار باشند. برای مثال، هر دو گروه داده باید کمی و دارای توزیع نرمال باشند، تا حد امکان داده پرتی در بررسی وجود نداشته باشد، دادهها از یک نمونه تصادفی باشند و حتما رابطه بین آنها خطی باشد.
بنابراین اگر ارتباط بین دادههای شما غیرخطی است یا توزیع آنها دارای نوعی خمیدگی یا چولگی است، محاسبه ضریب r برای بررسی همبستگی اطلاعات دقیقی به شما نخواهد داد. همچنین زمانی که میخواهید همبستگی را پیدا کنید، لازم است در نظر داشته باشید که دادههای شما از نمونه است یا از جمعیت. در صورتی که با دادههای یک نمونه سروکار دارید، فرمول محاسبه ضریب همبستگی پیرسون یا r برای دو گروه داده x و y و اندازه نمونه n، بهصورت زیر است:













سلام، خیلی عالی؛ فقط در یک مورد که تفاوت ضریب همبستگی اسپرمن و کندال تائو برعکس عنوان نشده است! یعنی ضریب همبستگی اسپیرمن برای نمونه های کوچکتر از 300 نمونه و ضریب همبستگی کندال برای نمونه های بالا و یا هر حجم نمونه ای…
با سلام خدمت شما؛
عبارت صحیحتر این است که برای دادههای رتبهای، ضریب کندال در نمونههای کوچک پایداری بیشتری دارد، اما ضریب اسپیرمن در نمونههای بزرگ محاسبه آسانتری دارد. این اصلاح در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.