حل مساله رنگ آمیزی گراف با الگوریتم پس گرد – به زبان ساده
انواع گوناگونی از مسائل رنگآمیزی گراف وجود دارد که مساله رنگ کردن راسهای گراف، یکی از محبوبترین و متداولترین آنها به شمار میآید. در این مساله، یک گراف غیر مستقیم و عدد m داده شده است. هدف رنگ کردن راسهای گراف به صورتی است که هیچ دو راس مجاوری، دارای رنگ مشابه نباشند. m تعداد رنگهای داده شده است. باید توجه داشت که در اینجا منظور از رنگآمیزی، تخصیص رنگ به راسهای گراف است. برای حل مساله رنگ آمیزی گراف، الگوریتمهای گوناگونی ارائه شده که «الگوریتم پس گرد» (Backtracking) و «حریصانه» (Greedy) از این جمله هستند. در این مطلب، هدف حل مساله رنگ آمیزی گراف با الگوریتم پس گرد است.
تعریف مساله
تعداد m رنگ و یک گراف داده شده است. هدف رنگ کردن راسهای این گراف به صورتی است که هیچ دو راس مجاوری دارای یک رنگ مشابه نباشند. ورودی و خروجی مساله، به طور دقیق به شرح زیر هستند.
ورودی:
- یک آرایه دو بعدی، یعنی گراف [graph[V][V که در آن، V تعداد یالها در گراف را مشخص میکند و [graph[V][V نمایش ماتریس همسایگی گراف است. مقدار [graph[i][j در صورتی که یک یال مستقیم از i به j وجود داشته باشد برابر با یک، و در غیر این صورت، مقدار [graph[i][j برابر با ۰ است.
- عدد صحیح m، تعداد کل رنگهایی است که میتوان از آنها استفاده کرد.
خروجی:
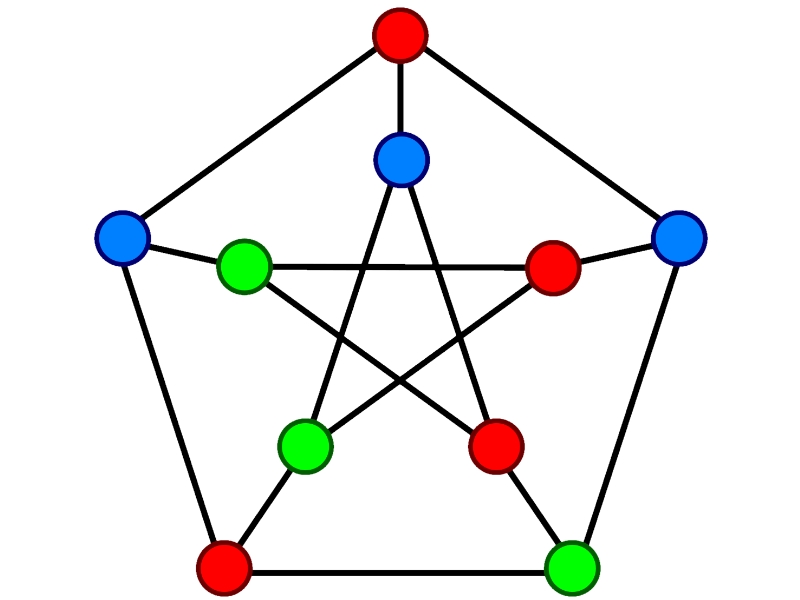
آرایه [color[V که باید حاوی اعدادی از ۱ تا m باشد. [color[i باید رنگ تخصیص یافته به iاُمین راس را نشان دهد. همچنین، در صورتی که نمیتوان گراف را با m رنگ طبق شرط موجود رنگآمیزی کرد، کد باید مقدار False را بازگرداند. در ادامه، تصویری از یک گراف داده شده که با m=3 رنگ (سفید، سبز، قرمز) رنگآمیزی شده است.

الگوریتم ساده
الگوریتم ساده ارائه شده در زیر، همه پیکربندیهای ممکن برای رنگآمیزی گراف را که شروط داده شده در آنها رعایت میشود، در خروجی چاپ میکند.
while there are untried conflagrations
{
generate the next configuration
if no adjacent vertices are colored with same color
{
print this configuration;
}
}
به تعداد Vm پیکربندی مختلف از رنگها وجود دارد.
حل مساله رنگ آمیزی گراف با الگوریتم پس گرد
ایده اساسی آن است که رنگها یکی یکی به راسهای مختلف اختصاص پیدا کنند. این کار با شروع از راس صفر (۰) آغاز میشود. پیش از تخصیص رنگ، امکانپذیری تخصیص رنگ بر اساس شرط داده شده بررسی میشود.
این کار، با در نظر گرفتن رنگهایی که در حال حاضر به راسهای همسایه تخصیص پیدا کردهاند، صورت میپذیرد. اگر الگوریتم تشخیص دهد که تخصیص یک رنگ مشخص در شرط داده شده صدق میکند، تخصیص رنگ به عنوان بخشی از راهکار انجام میشود. اگر رنگی برای یک راس مشخص پیدا نشود که در شرط مذکور صدق کند، پسگرد انجام و پیغام خطای False صادر میشود.
کد راه حل مساله رنگ آمیزی گراف در ++C/C
کد راه حل مساله رنگ آمیزی گراف در جاوا
کد راه حل مساله رنگ آمیزی گراف در پایتون
پیادهسازی و انجام عملیات مختلف مربوط به گراف در پایتون هم دارای اصول و قواعد یکسانی است. با این تفاوت که هر زبان سینتکس و قواعد گرامری مخصوص به خود را دارد. در زیر کدهای مربوط به راه حل مساله رنگ آمیزی گراف را در این زبان مشاهده میکنید.
خروجی
Solution Exists: Following are the assigned colors 1 2 3 2
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
- زبان برنامهنویسی پایتون (Python) — از صفر تا صد
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
^^













پیچیدگی زمانی این الگوریتم چیست؟
این یک الگوریتم بازگشتی است چون در تابع خودش را صدا زده.
مرتبه زمانی یک تابع بازگشتی از مرتبه n^n است که بی نهایت کند است.