نظریه حالت گذار — از صفر تا صد
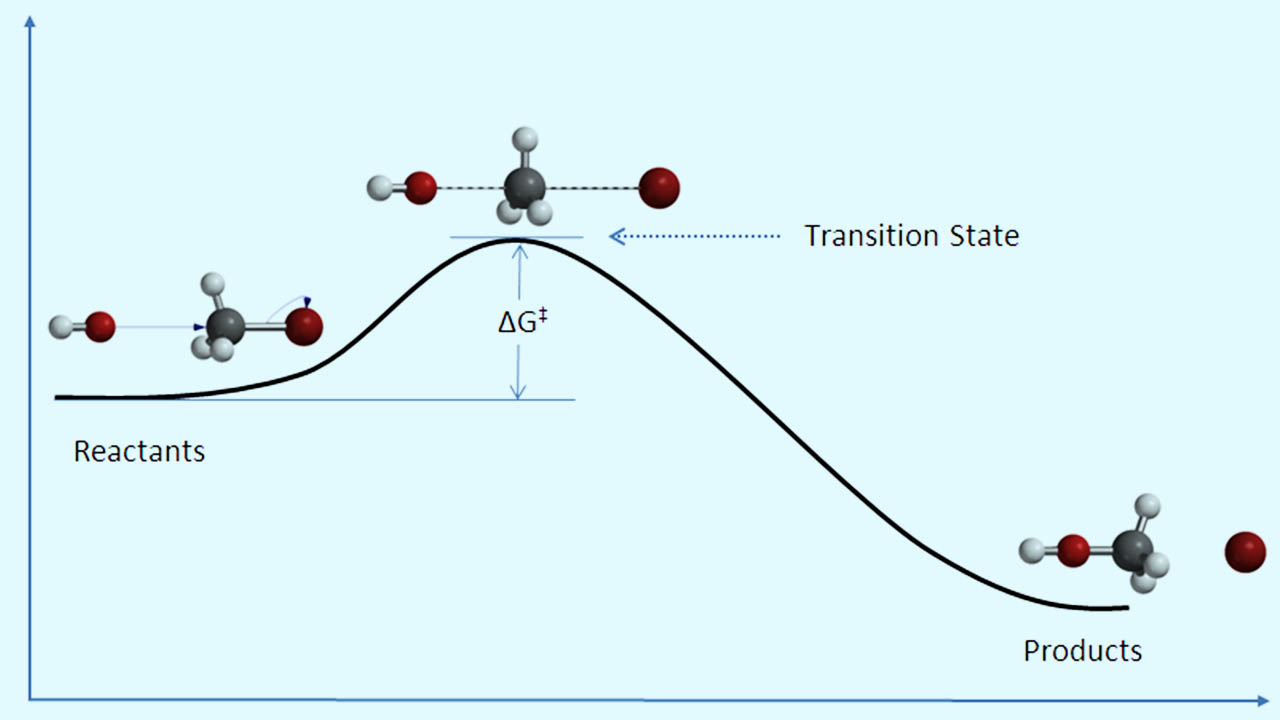
نظریه حالت گذار به عنوان توضیحی برای سرعت در واکنشهای شیمیایی در نظر گرفته میشود. این نظریه، نوعی تعادل شیمیایی را بین واکنشدهندهها و حالت گذار کمپلکس فعال فرض میکند. از نظریه حالت گذار بمنظور درک کیفی نحوه انجام یک واکنش شیمیایی بهره میگیرند. نظریه حالت گذار در محاسبه سرعت مطلق واکنشهای شیمیایی چندان موفق نبوده چراکه این امر مستلزم دانش دقیقی از سطوح انرژی پتانسیل است اما در محاسبه آنتالپی، آنتروپی و انرژی گیبس استاندارد اکتیواسیون برای یک واکنش خاص، عملکرد خوبی دارد که البته در این خصوص، به مقدار آزمایشگاهی ثابت سرعت نیاز داریم. توجه داشته باشید که از نماد «$$^‡$$» در بیان مقادیر حالت گذار استفاده میکنند. به طور مثال، $$Δ H ^ ‡$$، بیانگر اختلاف بین آنتالپی حالت گذار و آنتالپی واکنشدهندهها است.
مقدمه
«نظریه حالت گذار» (Transition State Theory) یا TST، به طور همزمان در سال 1935 در دانشگاههای پرینستون و منچستر ارائه شد. نظریه حالت گذار را همچنین با نامهای نظریه کمپلکس فعال، نظریه سرعت مطلق و نظریه سرعت مطلق واکنش نیز میشناسند. پیش از توسعه نظریه حالت گذار، از قانون سرعت آرنیوس برای تعیین انرژی واکنشها استفاده میکردند.
معادله آرنیوس از مشاهدات تجربی بدست آمده بود و مسائل مختلفی همچون تشکیل مواد واسط را به هنگام تبدیل واکنشدهنده به فرآورده در نظر نمیگرفت. به همین دلیل، مطالعات بیشتری برای فهم این معادله نیاز بود. البته مدت زمانی در حدود 46 سال طول کشید تا این مطالعات، توسعه پیدا کنند.
بیان ساده نظریه حالت گذار
بر اساس نظریه حالت گذار، بین شرایطی که در آن، مولکولها به صورت واکنشدهنده هستند و حالتی که مولکولها به شکل فرآورده دیده میشوند، حالتی موسوم به حالت گذار وجود دارد. در حالت گذار، واکنشدهنده به ذراتی به نام کمپلکس (پیچیده) فعال تبدیل میشود. نظریه حالت گذار پیشنهاد میکند سه عامل اصلی برای انجام شدن یک واکنش وجود دارند:
- غلظت کمپلکس فعال
- سرعت شکستن اجزای کمپلکس فعال
- نحوه شکستن اجزای کمپلکس فعال: یعنی حالتی که کمپلکس فعال در اثر شکسته شدن به واکنشدهنده یا فرآورده تبدیل میشود.
واکنش دو مولکولی زیر به همراه رابطه ثابت تعادل را در نظر بگیرید:
$$A + B \rightarrow C $$
$$K = \dfrac { [ C ] } { [ A ] [ B ] }$$
در نظریه حالت گذار در این واکنش، یک کمپلکس فعال به صورت $$AB ^ \ddagger$$ تشکیل میشود که واکنش و رابطه ثابت تعادل برای آن در زیر نوشته شده است:
$$\begin {equation} \begin {aligned}
A + B & \rightleftharpoons A B ^ {\ddagger} \rightarrow C \\
K ^ {\ddagger} & = \frac { [ A B ] ^ { \dagger } } { [ A ] [ B ] }
\end {aligned} \end{equation}$$
در مسیر واکنش، همانطور که در تصویر زیر هم نشان داده شده است، مانعی به نام انرژی اکتیواسیون (فعالسازی) وجود دارد که برای انجام واکنش باید بر آن غلبه کرد.
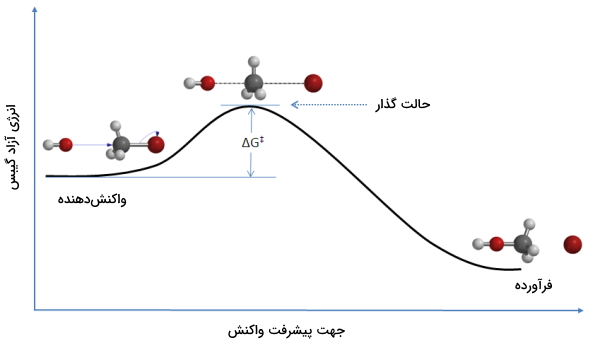
سرعت واکنش، برابر با تعداد کمپلکسهای فعالی است که برای تشکیل فرآورده تجزیه شدهاند. این مقدار را به صورت حاصلضرب غلظت کمپلکس فعال در فرکانس غلبه بر انرژی فعالسازی ذکر میکنند:
$$\begin{eqnarray} rate ~ & = & ~ v [ A B ^ \ddagger] \\ & = & ~ v [ A] [ B ] K ^ \ddagger \end{eqnarray}$$
علاوه بر این، سرعت را میتوان به شکل زیر نیز نوشت:
$$rate = k [ A ] [ B ] $$
با ترکیب دو معادله بالا، به رابطه زیر میرسیم:
$$\begin {eqnarray} k [ A ][ B ] ~ & = & ~ v [ A] [ B ] K ^ \ddagger \\ k ~ & = &~ v K ^ \ddagger \end{eqnarray}$$
در خصوص این روابط، در ادامه متن به طور دقیقتری صحبت خواهیم کرد.
بیان دقیقتر نظریه حالت گذار
ایدههای اصلی در نظریه حالت گذار به شرح زیر هستند:
- سرعتهای واکنش را میتوان به کمک بررسی کمپلکس فعال در نزدیکی «نقطه زینی» (Saddle Point) سطوح انرژی پتانسیل، مورد مطالعه قرار داد. جزییات نحوه تشکیل این کمپلکسها اهمیتی ندارند و نقطه زینی را به عنوان حالت گذار در نظر میگیرند.
- کمپلکسهای فعال در یک حالت ویژه تعادلی (شبه تعادلی) با مولکولهای واکنشدهندهها قرار دارند.
- این کمپلکسهای فعال میتوانند به فرآورده تبدیل شوند و سرعت این تبدیل توسط نظریه سینتیک، قابل محاسبه است.
توسعه نظریه حالت گذار
در توسعه TST، سه رویکرد مدنظر است که در ادامه به توضیح آنها خواهیم پرداخت:
رویکرد ترمودینامیکی
در سال 1884، «ژاکوب وانت هوف» (Jacoubus van't Hoff)، معادله وانت هوف را در توضیح وابستگی دمایی ثابت تعادل برای یک واکنش برگشتپذیر ارائه داد:
$$\begin{aligned}
& A \rightleftharpoons B \\
& \frac { d \ln K } { d T } = \frac {\Delta U } { R T ^ { 2 } }
\end {aligned}$$
- $$\Delta U$$: انرژی درونی
- $$K$$: ثابت تعادل واکنش
- $$R$$: ثابت جهانی گازها
- $$T$$: دمای ترمودینامیکی
بر اساس کارهای آزمایشگاهی، در سال 1889، آرنیوس رابطه مشابهی را برای ثابت سرعت در یک واکنش ارائه داد که در زیر آورده شده است:
$${\frac { d\ln k} {d T } } = {\frac { \Delta E } { R T ^ { 2} } }$$
با انتگرالگیری از معادله بالا، به رابطه اصلی آرنیوس میرسیم:
$$k = A e ^ { - E _ { a } / R T }$$
در رابطه بالا، $$k$$ ثابت سرعت و $$A$$، ضریب پیشنمایی یا فاکتور فرکانس است. در این رابطه، $$E_a$$ نیز به عنوان انرژی اکتیواسیون (فعالسازی) شناخته میشود. تا اوایل قرن بیستم، بسیاری از دانشمندان، رابطه آرنیوس را قبول کرده بودند اما توصیف فیزیکی برای $$A$$ و $$E_a$$ وجود نداشت. این مورد سبب شد تا بسیاری از محققان سینتیک شیمیایی، نظریههای مختلفی را پیرامون نحوه انجام واکنشهای شیمیایی ارائه دهند تا به نوعی، $$A$$ و $$E_a$$ را به طور مستقیم به دینامیک مولکولی واکنشهای شیمیایی مرتبط کنند. در سال 1910، شیمیدان فرانسوی، «رنه مارسلین» (René Marcelin)، مفهوم انرژی گیبس استاندارد فعالسازی را به صورت زیر معرفی کرد:
$$k \propto \exp \left ({ \frac { - \Delta ^ { \ddagger } G ^ { \ominus } } { R T }} \right )$$
در همان زمان که مارسلین بر روی معادله خود کار میکرد، دانشمندان هلندی نیز آنتروپی و آنتالپی استاندارد اکتیواسیون را معرفی کردند. آنها، رابطه ثابت سرعت زیر را به همین منظور معرفی کردند. گرچه طبیعت این ثابت، همچنان نامشخص بود.
$$k \propto \exp \left ( { \frac { \Delta ^ {\ddagger } S ^ { \ominus } } { R } } \right ) \exp \left({ \frac { - \Delta ^ { \ddagger } H ^ {\ominus }} { R T } } \right)$$

رویکرد نظریه سینتیکی
در اوایل قرن بیستم و سال 1900، «ماکس تراوتس» (Max Trautz) و «ویلیام لوویس» (William Lewis)، سرعت واکنش را با استفاده از نظریه برخورد مورد مطالعه قرار دادند. نظریه برخورد، مولکولهای واکنشدهنده را به صورت گویهایی سخت در نظر میگیرد که به یکدیگر برخورد میکنند. این نظریه، تغییرات آنتروپی را در لحاظ نمیکند زیرا فرض میکند که برخورد بین مولکولها به صورت کاملا الاستیک رخ میدهد. لوویس، رویکرد خود را بر روی واکنش زیر اعمال کرد و نتایج خوبی در تطابق با دادههای آزمایشگاهی بدست آورد:
$$\begin{equation} 2 \mathrm { H I } \rightarrow \mathrm { H} _ { 2 } + \mathrm { I } _ { 2 } \end {equation}$$
البته با بکارگیری این رویکرد در سایر واکنشها، اختلاف بسیاری بین دادههای آزمایشگاهی و نظری دیده شد.
رویکرد مکانیک آماری
مکانیک آماری، نقش اساسی را در توسعه نظریه حالت گذار ایفا کرد. البته سرعت توسعه این رویکرد بسیار کند بود و در اواسط قرن 19، دانشمندانی همچون ماکسول، بولتزمن و فاندلر، مقالات علمی متعددی را در توصیف سرعت و تعادل واکنش بر مبنای حرکات مولکولی و توزیع آماری سرعتهای آنها ارائه دادند. اما در سال 1912 بود که شیمیدان فرانسوی، «برتود» (A. Berthoud) از قانون توزیع ماکسول-بولتزمن استفاده کرد تا به رابطه برای ثابت سرعت دست پیدا کند. در این رابطه، $$a$$ و $$b$$، ثابتهایی بودند که به مولفههای انرژی مربوط میشدند.
$${\frac { d \ln k } { d T } } = {\frac { a - b T } { RT ^ { 2 } } }$$
دو سال بعد، رنه مارسلین، تلاشهایی اساسی را برای بررسی پیشرفت یک واکنش شیمیایی به عنوان حرکت یک نقطه در «فضای فاز» (Phase Space) انجام داد. او در ادامه، روند مکانیکی-آماری گیبس را در مطالعات خود لحاظ کرد و به رابطهای مشابه با رابطه قبل خود رسید که در آن از رویکرد ترمودینامیکی کمک گرفته بود. با فعالیتهای علمی چندین دانشمند دیگر، در نهایت، فیزیکدان اتریشی، «کارل فردیناند هرزفلد» (Karl Ferdinand Herzfeld)، مکانیک آماری را در محاسبات ثابت تعادل لحاظ کرد و به کمک بکارگیری نظریه سینتیک در ثابت سرعت برای واکنش معکوس، رابطه زیر را ارائه داد:
$$\begin {equation} k _ { 1 } = \frac { k _ {\mathrm { B } } T } { h } \left ( 1 - e ^ { - \frac { h \nu } { k _ { B } T } } \right ) \exp \left ( \frac { - E ^ {\ominus} } { R T } \right ) \end {equation}$$
- $$E ^ {\ominus}$$: انرژی تفکیک در صفر مطلق
- $${ k _ { B } }$$: ثابت بولتزمن
- $$h$$: ثابت پلانک
- $$T$$: دمای ترمودینامیکی
- $$\nu$$: فرکانس ارتعاش پیوند
این رابطه، اهمیت بسیاری دارد چراکه ضریب $$\frac { k _ {\mathrm { B } } T } { h }$$، که از اجزای اصلی در نظریه حالت گذار است، در ابتدا در این رابطه ظاهر شد.
سطوح انرژی پتانسیل
مفهوم سطوح انرژی پتانسیل، در توسعه نظریه حالت گذار اهمیت بسیاری داشت. اساس این مفهوم، همانطور که در بالا اشاره شد، توسط رنه مارسلین در سال 1913 مورد بررسی قرار گرفت. او بیان کرد که پیشرفت یک واکنش شیمیایی را میتوان به صورت یک نقطه در یک سطح انرژی پتانسیل با مختصات تکانه اتمی و فاصله توضیح داد.
در سال 1931، «هنری ایرینگ» (Henry Eyring) و «مایکل پولانی» (Michael Polanyi)، یک سطح انرژی پتانسیل را برای واکنش زیر تشکیل دادند. این سطح انرژی، یک دیاگرام سهبعدی بر اساس مکانیک کوانتوم و دادههای آزمایشگاهی فرکانسهای ارتعاش و انرژیهای پیوند بود.
$$\begin {equation} \mathrm { H } + \mathrm { H } _ { 2 } \rightarrow \mathrm { H } _ { 2 } + \mathrm { H } \end {equation}$$
یک سال بعد از ایرینگ و پولانی، دو دانشمند دیگر، تلاشهایی را برای بیان پیشرفت یک واکنش شیمیایی بر اساس سطوح انرژی پتانسیل انجام دادند. اهمیت کار آنها در این بود که برای اولین بار مفهوم نقطه زینی در سطح انرژی پتانسیل معرفی شد. این دو دانشمند بیان کردند که سرعت یک واکنش را میتوان به کمک حرکت سیستم در نقطه زینی بیان کرد. در ابتدا فرض بر این بود که نقطه زینی در همان سطح انرژی حالت پایه اولیه قرار دارد اما به تازگی دانشمندان دریافتهاند که این فرض در فرآیندهای موجود در نیمههادیها و عایقها صحیح نیست و در چنین شرایطی، حالت برانگیخته اولیه میتواند به نقطه زینی پایینتر از سطح اولیه حالت پایه برسد.
توضیحاتی در خصوص رابطه ایرینگ
از مهمترین ویژگیهایی که توسط ایرینگ و سایر دانشمندان ارائه شد این بود که کمپلکسهای فعال در حالتی «شبه تعادلی» (Quasi-equilibrium) با واکنشدهندهها قرار دارند. بنابراین، سرعت واکنش به طور مستقیم با حاصلضرب غلظت این کمپلکسها در فرکانس $$( k _ B T / h )$$ تبدیل آنها به فرآورده مرتبط است.
فرض شبه تعادلی در نظریه حالت گذار
حالت شبه تعادلی با حالت کلاسیک تعادل شیمیایی تفاوت دارد اما میتوان به کمک همان روش ترمودینامیکی آنرا توضیح داد. واکنش زیر را در نظر بگیرید که در این واکنش، تعادل کاملی بین تمامی اجزای سیستم و همچنین کمپلکس فعال $$[ A B ] ^ ‡$$ صورت گرفته است:
$${\displaystyle { {{ A } + { B } \rightleftharpoons { [ A B ] ^ {\ddagger } } \rightarrow { P } } } } $$
به کمک مکانیک آماری، غلظت $$[ A B ] ^ ‡$$ را میتوان از طریق غلظتهای $$A$$ و $$B$$ بیان کرد. نظریه حالت گذار فرض میکند که حتی در زمانی که واکنشدهندهها و فرآوردهها با یکدیگر در تعادل نیستند، کمپلکس فعال، در یک حالت شبهتعادلی با واکنشدهندهها قرار دارد. همانطور که در تصویر زیر نشان داده شده است، در هر لحظه از زمان، کمپلکسهای فعالی وجود دارند که شامل مولکولهای واکنشدهنده و فرآورده هستند و به ترتیب با $$[ A B _ l ] ^ ‡$$ و $$[ A B _ r ] ^ ‡$$ نشان داده شدهاند.
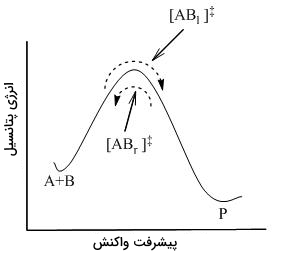
با توجه به اینکه سیستم در حالت تعادل کامل قرار دارد، غلظتهای $$[ A B _ l ] ^ ‡$$ و $$[ A B _ r ] ^ ‡$$ با یکدیگر برابرند. بنابراین، غلظت هرکدام با نیمی از غلظت کل کمپلکس فعال، طبق رابطه زیر برابر است:
$$\begin {equation} \left [ \mathrm { A B } _ { r } \right] ^ {\dagger} = \left [ \mathrm { A B } _ { l } \right ] ^ { \dagger } = \frac { 1 } { 2 } [ \mathrm { A B } ] ^ { \dagger } \end {equation}$$
در نظریه حالت گذار فرض میشود که شار کمپلکسهای فعال در هر دو جهت، مستقل از یکدیگر هستند. این امر بدان معنی است که اگر تمامی مولکولهای فرآورده، به طور ناگهانی از سیستم واکنش حذف شوند، جریان $$[ A B _ r ] ^ ‡$$ متوقف میشود اما همچنان، جریانی از سمت چپ به راست خواهیم داشت. به همین دلیل، واکنشدهندهها تنها با $$[ A B _ l ] ^ ‡$$ در تعادل هستند.
بحث در خصوص ثابت تعادل نظریه حالت گذار
کمپلکسهای فعال از توزیع انرژی بولتزمن تبعیت نمیکنند اما میتوان از توزیع این کمپلکسها، یک ثابت تعادل بدست آورد. ثابت تعادل $$( K ^ ‡)$$ برای حالبت شبهتعادلی را میتوان به شکل زیر نوشت:
$${\displaystyle K ^ { \ddagger } = { \frac { { [ A B ] ^ { \ddagger } } } { { [ A ] [ B ] } } } }$$
بنابراین، غلظت حالت گذار برابر خواهد بود با:
$${\displaystyle [ { { A B } } ] ^ { \ddagger } = K ^ { \ddagger } [ { { A } } ] [ { { B } } ] }$$
در نتیجه، معادله سرعت برای تولید فرآورده را میتوان به شکل زیر نوشت:
$$\begin {equation} \frac { d [ \mathbf { P } ] } { d t } = k ^ { \ddagger } [ \mathrm { A B } ] ^ { \ddagger } = k ^ { \ddagger } K ^ { \ddagger } [ \mathrm { A } ] [ \mathrm { B } ] = k [ \mathrm { A } ] [\mathrm { B } ] \end {equation}$$
در رابطه بالا، برای محاسبه ثابت سرعت $$(k)$$ از رابطه زیر کمک میگیریم:
$$k = k ^ { \ddagger } K ^ { \ddagger }$$
در اینجا، $$k^ ‡$$ به طور مستقیم با فرکانس حالت ارتعاشی $$(\nu)$$ دخیل در تبدیل کمپلکس فعال به فرآورده مرتبط است. لازم به ذکر است که هر ارتعاشی سبب تشکیل فرآورده نمیشود، به همین دلیل از ثابت تناسب $$ {\displaystyle \kappa }$$ موسوم به ضریب انتقال برای لحاظ کردن این تاثیر استفاده میشود. بنابراین، $$k^ ‡$$ را میتوان به صورت زیر نوشت:
$$k ^ { \ddagger } = \kappa \nu $$
به کمک مکانیک آماری، به رابطهای بر حسب دما برای محاسبه ثابت تعادل $$K^ ‡$$ میرسیم:
$$\begin {equation} K ^ { \ddagger } = \frac { k _ { B } T } { h \nu } K ^ {\ddagger ^ {\prime} } \left ( K ^ {\ddagger ^ {\prime} } = e ^ {\frac {-\Delta G ^ {\ddagger } } { R T } } \right) \end {equation}$$
با ترکیب روابطی که برای محاسبه $$k^ ‡$$ و $$K^ ‡$$ بیان شد، رابطه جدیدی برای ثابت سرعت به شکل زیر بدست میآید:
$${\displaystyle k = k ^ { \ddagger } K ^ {\ddagger } = \kappa { \frac { k _ { B } T } { h } } e ^ {\frac { - \Delta G ^ {\ddagger } } { R T } } = \kappa { \frac { k _ { B } T } { h } } K ^ { \ddagger '} }$$
با توجه به رابطه $$Δ G ^ ‡ = Δ H ^‡ – T Δ S ^‡$$، رابطه ثابت سرعت را میتوان به شکل زیر نشان داد تا شکل دیگری از رابطه ایرینگ بدست آید:
$$k = \kappa { \frac { k _ { B } T } { h } } e ^ {\frac {\Delta S ^ {\ddagger } } { R } } e ^ {\frac { - \Delta H ^ {\ddagger } }{ R T } } $$
برای اصلاح ابعاد در واکنشهایی که به صورت «تکمولکولی» نیستند، از یک ضریب استفاده میکنیم که در آن $$c^ ⊖$$، غلظت استاندارد 1 مول بر لیتر و $$m$$، مولکولاریته است.
$${\displaystyle k = \kappa { \frac { k _ { B } T } { h } } e ^ {\frac {\Delta S ^ {\ddagger } } { R } } e ^ {\frac { - \Delta H ^ {\ddagger } } { R T } } ( c ^ { \ominus } ) ^ { 1 - m } }$$
رابطه بالا در سال 1935 توسط هنری ایرینگ و بر اساس نظریه حالت گذار بیان شد که وابستگی دما را به واکنش توضیح میداد. شکل خطی رابطه ایرینگ را به صورت زیر تعریف میکنند:
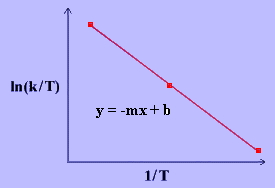
$$\ln { \dfrac { k } { T } } ~ = ~ \dfrac{ - \Delta H ^ \dagger } { R } \dfrac { 1} { T } ~ + ~ \ln{ \dfrac { k _ B } { h } } ~ + ~ \dfrac { \Delta S ^ \ddagger } { R } $$
با رسم نمودار رابطه بالا میتوان مقادیر $$Δ H ^ ‡$$ و $$\Delta S ^ \ddagger$$ را محاسبه کرد. این معادله نشان میدهد که نمودار مورد نظر، خطی مستقیم با شیب منفی برابر با $$\dfrac{ - \Delta H ^ \ddagger} { R }$$ و عرض از مبدا $$\dfrac {\Delta S ^ \ddagger } { R } + \ln {\dfrac { k _ B } { h } } $$ دارد.
جمعبندی
در این آموزش، رویکردهای مختلف در بررسی نظریه حالت گذار را بیان کردیم. روابطی که در این نظریه بیان شد، معتبرتر از معادلات آرنیوس و نظریه برخورد هستند اما نظریه حالت گذار، محدودیتهایی به خصوص برای مکانیک کوانتومی دارد. مکانیک کوانتومی بیان میکند که ممکن است «تونلزنی کوانتومی» (Quantum Tunneling) اتفاق بیافتد به گونهای که ذرات میتوانند از مانع انرژی ایجاد شده توسط حالت گذار عبور کنند. این مورد به خصوص زمانی بوقوع میپیوندد که انرژی فعالسازی کمی داشته باشیم چراکه احتمال تونلزنی کوانتومی با کاهش انرژی فعالسازی، افزایش پیدا میکند.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای نرم افزارهای مهندسی شیمی
- آموزش هایسیس HYSYS برای شبیهسازی فرآیندهای شیمیایی
- قانون هس — به زبان ساده
- اصطلاحات کروماتوگرافی گازی — به زبان ساده
^^










کامل بود