نوشتن معادله خط با دو نقطه – به زبان ساده و با مثال

خط از مبانی مهم و بنیادی در ریاضی و هندسه است. دانستن معادله خط در مهندسی و فیزیک کاربرد دارد. در این مطلب از مجله فرادرس به نوشتن معادله خط با دو نقطه با استفاده از رابطه میپردازیم و همینطور یاد میگیریم که چگونه از روی نمودار یک خط بتوانیم معادله آن را بنویسیم. چند مثال و تمرین نیز برای درک بهتر این موضوع در ادامه آمده است. همچنین اجزای مختلف خط مانند عرض از مبدا و انواع شیب خط نیز معرفی خواهند شد. اگر به این موضوع علاقهمند هستید پس این مطلب را تا انتها مطالعه کنید.
در این مطلب، ابتدا نحوه نوشتن معادله خط از روی نقطه را آموزش میدهیم. البته نیاز داریم که با اجزای مختلف خط نیز آشنا باشیم و به همین دلیل، در ادامه، این اجزا را معرفی میکنیم. نحوه نوشتن معادله خط از روی نمودار را بعد از معرفی اجزای خط به طور کامل بیان میکنیم. در انتها نیز پس از حل مثالهای مختلف، چند تمرین را برای خودآزمایی قرار دادهایم.
نوشتن معادله خط از روی نقطه
برای نوشتن معادله یک خط حداقل به دو نقطه از آن نیاز داریم و باید مراحل زیر را انجام دهیم:
- محاسبه شیب خط با دو نقطه از خط و استفاده از رابطه شیب خط.
- با داشتن شیب خط و فقط یک نقطه میتوان با استفاده از رابطه ، معادله آن خط را نوشت.
مثال اول معادله خط با دو نقطه
میخواهیم معادله خطی که شامل دو نقطه و است را بنویسیم.
پاسخ:
ابتدا باید شیب خط را حساب کنیم:
اکنون شیب و یک نقطه از خط (که در اینجا 4 و 2- را در نظر گرفتیم) را داخل معادله گفته شده جایگذاری میکنیم:
مثال دوم معادله خط با دو نقطه
معادله خطی را میخواهیم بنویسیم که شیب آن 2- است و شامل نقطه میشود.
پاسخ:
دادههای مثال فوق را در معادله خط راست جایگذاری میکنیم.
سپس معادله را مرتب میکنیم.

مثال سوم معادله خط
معادله خطی را میخواهیم بنویسیم که شامل نقاط و باشد.
پاسخ:
ابتدا باید شیب خط را حساب کنیم.
سپس از فرمول معادله خط راست استفاده میکنیم.
در آخر معادله را مرتب میکنیم.
مثال چهارم معادله خط با دو نقطه
خطی به معادله داریم که شامل نقطه است. میخواهیم عرض از مبدا را حساب کنیم.
پاسخ:
نقطه داده شده را باید درون معادله جایگذاری کنیم.
مثال پنجم معادله خط با دو نقطه
یک خط راست با شیب ۵ شامل نقطه است میخواهیم معادله آن را بنویسیم.
پاسخ:
از آنجا که نقطه داده شده دقیقا روی محور عمودی قرار دارد پس عرض از مبدا ۲ است. فقط کافی است تا مقادیر داده شده را درون معادله قرار دهیم.
مثال ششم معادله خط
میخواهیم نشان دهیم که شیب معادله خط برابر ۲ است.
پاسخ:
باید معادله فوق را به شکل استاندارد تبدیل کنیم.
طرفین معادله را تقسیم بر ۴ میکنیم:
سپس طرفین معادله را با y+ جمع میکنیم:
از طرفین ۳- کسر میکنیم:
مشاهده میشود که ضریب x یعنی شیب معادله برابر ۲ است.

مثال هفتم معادله خط با دو نقطه
یک خط با معادله داریم که شامل نقطه است. میخواهیم مقدار x را محاسبه کنیم.
پاسخ:
نقطه روی خط در معادله آن صدق میکند بنابراین باید نقطه مورد نظر را درون معادله داده شده جایگذاری کنیم تا مقدار x را بتوانیم بدست آوریم.
مثال هشتم معادله خط با دو نقطه
یک خط با معادله داریم که شامل نقطه است. میخواهیم مقدار y را محاسبه کنیم.
پاسخ:
مانند مثال قبل نقطه روی خط در معادله آن صدق میکند بنابراین باید نقطه مورد نظر را درون معادله داده شده جایگذاری کنیم تا اینبار مقدار y را بتوانیم بدست آوریم.
مثال نهم معادله خط
میخواهیم معادله خطی را بنویسیم که شامل نقطه و شیب ۲ است.
پاسخ:
ابتدا شیب و نقطه داده شده را باید در معادله استاندارد خط جایگذاری کنیم تا عرض از مبدا را بدست آوریم سپس میتوانیم با داشتن شیب و عرض از مبدا معادله خط را بنویسیم.
مثال دهم معادله خط
معادله خطی را میخواهیم بنویسیم که شامل نقاط و است.
پاسخ:
با استفاده از نقاط داده شده باید ابتدا شیب خط را محاسبه کنیم.
سپس با داشتن شیب و یکی از نقاط معادله خط را مینویسیم:
اجزای مختلف خط
در این قسمت به معرفی اجزای مختلف خط مانند معادله خط، شیب خط و عرض از مبدا میپردازیم.
معادله خط
معادله خط راست به صورت زیر است:
در معادله فوق عوامل به کار رفته به شرح زیر است:
- y: مختصه در محور عمودی
- x: مختصه در محور افقی
- m: شیب خط
- b: عرض از مبدا
برای درک بهتر به شکل زیر توجه کنید.
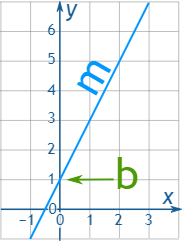
در شکل فوق خط راست شیب مثبت دارد و عرض از مبدا آن در نقطه ۱ است.
البته معادله خط راست به صورت زیر نیز وجود دارد اما در اصل همگی یکسان هستند:
میتوان به آسانی هرکدام را به دیگری تبدیل کرد.
عرض از مبدا
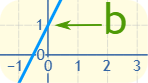
به نقطهای که خط، محور عمودی مختصات را قطع میکند عرض از مبدا میگویند. برای مثال اگر به شکل زیر توجه کنید، خط در نقطه ۱ محور عمودی را قطع کرده پس عرض از مبدا ۱ است. واضح است که عرض از مبدا میتواند مثبت، منفی یا صفر باشد.
شیب خط
نسبت تغییرات خط روی محور عمودی به تغییرات آن روی محور افقی، شیب خط میگویند. یکی از روشهای محاسبه شیب خط به وسیله دو نقطه است که در زیر نشان داده شده است:
در معادله فوق مختصات نقطه اول و مختصات نقطه دوم هستند که روی یک خط قرار دارند.
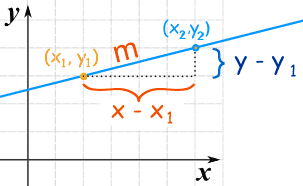
انواع شیب خط
میتوانیم شیب یک خط را براساس مقدار و علامتی که میگیرد به صورت زیر دستهبندی کنیم:
- شیب مثبت
- شیب منفی
- شیب صفر
- شیب تعریف نشده
البته باید توجه داشت که در نمودار برای شیب خط همیشه از چپ به راست آن را بررسی میکنیم.
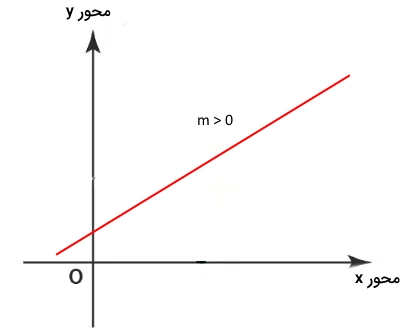
شیب مثبت
اگر شیب خط به طوری باشد که مقدار مختصه آن در محور عمودی افزایش پیدا کند به اصطلاح میگوییم شیب خط مثبت است. توجه کنید که در این حالت و علامت m نیز مثبت میشود.
شیب منفی
اگر شیب خط به طوری باشد که مقدار مختصه آن در محور عمودی کاهش پیدا کند به اصطلاح میگوییم شیب خط منفی است. توجه کنید که در این حالت و علامت m نیز منفی میشود.
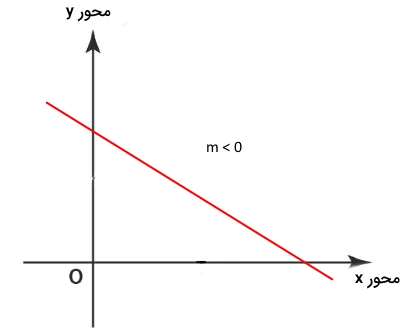
شیب صفر
هرگاه مقدار مختصه خط در محور عمودی تغییر نکند، شیب آن خط صفر است. به عبارت دیگر و است.
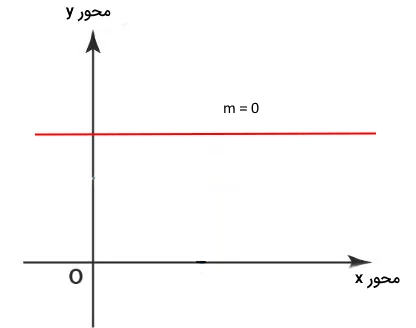
شیب تعریف نشده
هرگاه مقدار مختصه خط در محور افقی تغییر نکند، شیب آن خط تعریف نشده است. به عبارت دیگر است.
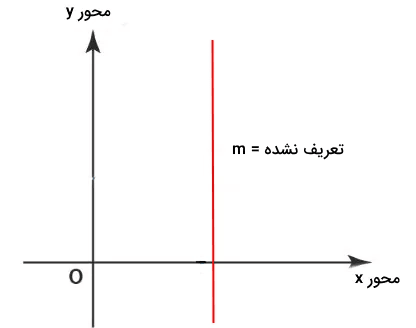
نوشتن معادله خط از روی نمودار
برای نوشتن معادله خط از روی نمودار کافی است که دو نقطه دلخواه از روی خط یا دو نقطه که در سوال مشخص شده است را انتخاب کنیم و سایر مراحل را انجام دهیم.
مثال اول معادله خط از روی نمودار
با توجه به شکل زیر میخواهیم معادله خط نشان داده شده را بنویسیم.
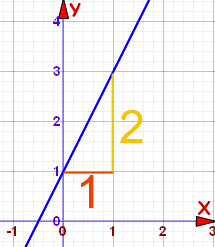
دو نقطه دلخواه و را انتخاب کرده و سپس شیب خط را حساب میکنیم:
در اینجا شیب خط مثبت شد سپس با نقطه دلخواه درون معادله جایگذاری میکنیم.
مثال دوم معادله خط از روی نمودار
با توجه به شکل زیر میخواهیم معادله خط نشان داده شده را بنویسیم.
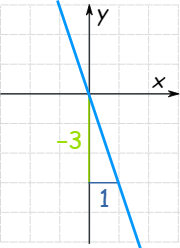
دو نقطه دلخواه و را انتخاب کرده و سپس شیب خط را حساب میکنیم:
در اینجا شیب خط منفی شد سپس با نقطه دلخواه درون معادله جایگذاری میکنیم.
مثال سوم معادله خط از روی نمودار
با توجه به شکل زیر میخواهیم معادله خط را بدست آوریم.
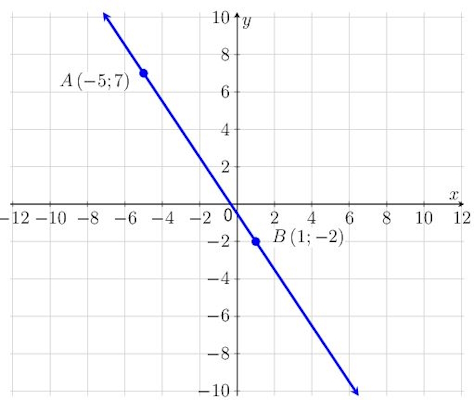
از نقاط داده شده روی شکل یعنی A و B استفاده میکنیم و در ابتدا شیب خط را حساب میکنیم.
سپس با استفاده از معادله استاندارد خط شیب و نقطه A را جایگذاری میکنیم تا عرض از مبدا را بدست آوریم.
اکنون میتوانیم با داشتن شیب و عرض از مبدا معادله خط را بنویسیم.
مثال چهارم معادله خط از روی نمودار
با توجه به شکل زیر نقطه A روی خط واقع شده است و شیب آن است. میخواهیم معادله خط را بدست آوریم.
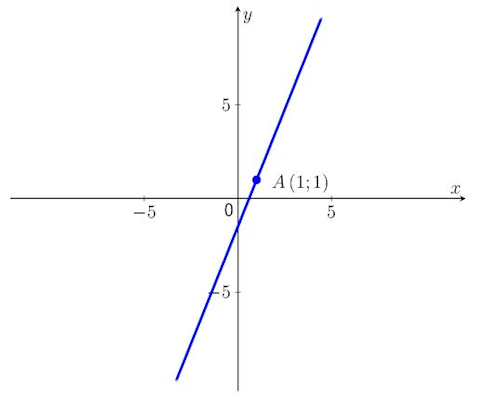
شیب و نقطه داده شده را درون معادله استاندارد جایگذاری میکنیم تا عرض از مبدا را حساب کنیم.
اکنون با داشتن شیب و عرض از مبدا میتوانیم معادله خط را بنویسیم.
مثال پنجم معادله خط از روی نمودار
در شکل زیر نقاط A و B روی خط واقع هستند میخواهیم معادله آن را بدست آوریم.
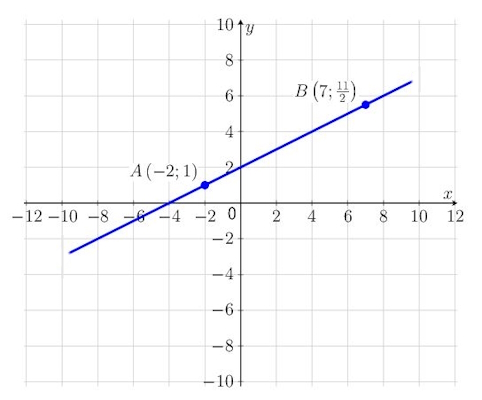
با استفاده از نقاط داده شده ابتدا شیب خط را حساب میکنیم.
اکنون نقطه A و شیب خط را در معادله استاندارد جایگذاری میکنیم تا عرض از مبدا را حساب کنیم.
بنابراین با داشتن شیب خط و عرض از مبدا میتوانیم معادله خط را بنویسیم.
تمرین معادله خط
پس از توضیحات در مورد نوشتن معادله خط با دونقطه اکنون میتوانید با تمرینهای زیر مهارت خود را در این موضوع بسنجید.
با توجه به معادله خط شیب خط و عرض از مبدا را به ترتیب تعیین کنید.
شیب ۲ و عرض از مبدا ۳-
شیب ۲- و عرض از مبدا ۳
شیب ۳ و عرض از مبدا ۲-
شیب ۳- و عرض از مبدا ۲
برای هر معادله به شکل ضریب x یعنی m شیب خط است و b عرض از مبدا میتواند باشد. پس در این سوال ۲- شیب خط و ۳ عرض از مبدا است.
با توجه به نمودار زیر معادله خط را بنویسید.
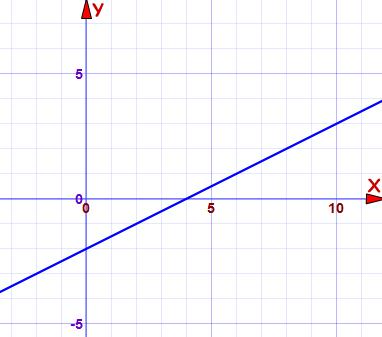
میتوانیم برای نوشتن معادله خط هر دو نقطه دلخواه که روی خط هستند را انتخاب کنیم که در اینجا نقاط و را که محورهای مختصات را قطع کردند انتخاب کردیم.
ابتدا شیب خط را با این دو نقطه حساب میکنیم:
سپس برای یافتن عرض از مبدا باید x را برابر صفر بگیریم و معادله را برحسب y حل کنیم. بنابراین عرض از مبدا برابر ۲- میشود.
بنابراین با داشتن شیب خط و عرض از مبدا میتوان معادله خط را نوشت.
با توجه به نمودار زیر معادله خط را بنویسید.
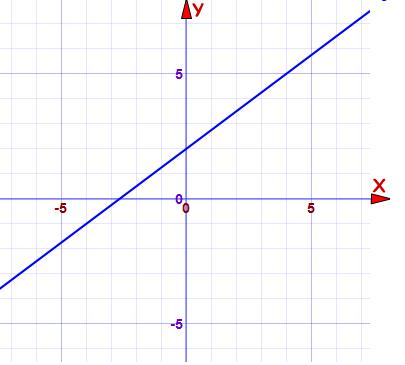
میتوانیم برای نوشتن معادله خط هر دو نقطه دلخواه که روی خط هستند را انتخاب کنیم که در اینجا نقاط و را انتخاب کردیم.
ابتدا شیب خط را با این دو نقطه حساب میکنیم:
سپس برای یافتن عرض از مبدا باید x را برابر صفر بگیریم و معادله را برحسب y حل کنیم. بنابراین عرض از مبدا برابر ۲ میشود.
بنابراین با داشتن شیب خط و عرض از مبدا میتوان معادله خط را نوشت.
با توجه به نمودار زیر معادله خط را بنویسید.
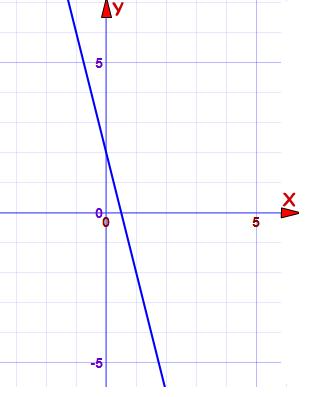
میتوانیم برای نوشتن معادله خط هر دو نقطه دلخواه که روی خط هستند را انتخاب کنیم که در اینجا نقاط و انتخاب کردیم.
ابتدا شیب خط را با این دو نقطه حساب میکنیم:
سپس برای یافتن عرض از مبدا باید x را برابر صفر بگیریم و معادله را برحسب y حل کنیم. بنابراین عرض از مبدا برابر ۲ میشود.
بنابراین با داشتن شیب خط و عرض از مبدا میتوان معادله خط را نوشت.
برای معادله مقدار شیب و عرض از مبدا را حساب کنید.
شیب و عرض از مبدا
شیب و عرض از مبدا
شیب و عرض از مبدا
شیب و عرض از مبدا
برای حل این سوال باید معادله را به شکل استاندارد آن تبدیل کنیم.
بنابراین شیب و عرض از مبدا است.
با توجه به شکل زیر معادله خط را حساب کنید.
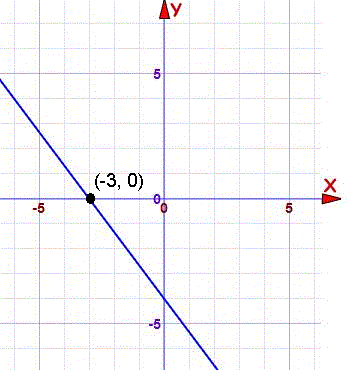
میتوانیم برای نوشتن معادله خط هر دو نقطه دلخواه که روی خط هستند را انتخاب کنیم که در اینجا نقاط و را که محورهای مختصات را قطع کردند انتخاب کردیم.
ابتدا شیب خط را با این دو نقطه حساب میکنیم:
سپس برای یافتن عرض از مبدا باید x را برابر صفر بگیریم و معادله را برحسب y حل کنیم. بنابراین عرض از مبدا برابر ۴- میشود.
بنابراین با داشتن شیب خط و عرض از مبدا میتوان معادله خط را نوشت.
با توجه به شکل زیر معادله خط را بدست آورید.
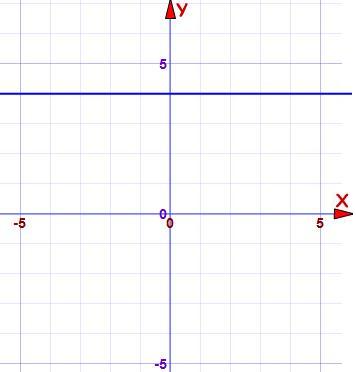
با توجه به شکل متوجه میشویم که شیب خط صفر است و خط در نفطه ۴ محور عمودی را قطع میکند. در نتیجه خواهیم داشت:
با توجه به شکل زیر معادله خط را بدست آورید.
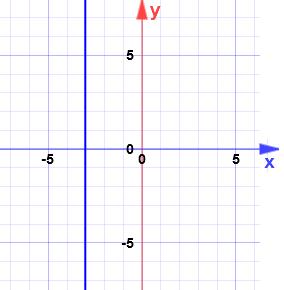
با توجه به شکل شیب خط تعریف نشده است یعنی و خط در نقطه ۳- محور افقی را قطع کرده است در نتیجه معادله خط برابر مقدار زیر است:
نتیجهگیری
معادله خط راست از اصول اولیه هندسه است و پایه یادگیری مباحث پیشرفتهتر به حساب میآید. در این مطلب از مجله فرادرس شکل معادله خط راست و روش نوشتن آن به وسیله دو نقطه با استفاده از رابطه و همچنین روش نوشتن معادله خط از روی نمودار را با مثال و تمرین آموختید همچنین اجزای مختلف خط مانند عرض از مبدا و انواع شیب خط نیز معرفی شد.













سلام ببخشید من وقتی که شیب رو پیدا میکنم برای y نمیدونم چه عددی بزارم بر اساس عدد بزرگه؟؟
سلام و وقت بخیر؛
برای y و x، نیازی به جایگذاری عدد نیست. به جای y1، عدد دوم و به جای x1، عدد اول نقطه را قرار دهید. به عنوان مثال، در (15, 4)، عدد 15 را به جای y1 و عدد 4 را به جای x1 قرار دهید؛ مگر اینکه اشاره شده باشد کدام طول و کدام عرض است. در [37]، عدد 3 (عدد بالا) x1 و عدد 7 (عدد پایین)، y1 است.
از همراهی شما با مجله فرادرس سپاسگزاریم.