در حسابان ماتریسی، «فرمول ژاکوبی» (Jacobi's formula) بیان میکند که مشتق دترمینان ماتریس A را میتوان برحسب ماتریس الحاقی A و مشتق A نوشت.
اگر A یک تصویر مشتقپذیر از اعداد حقیقی به ماتریس n×n باشد، رابطه زیر برقرار است:
dtddetA(t)=tr(adj(A(t))dtdA(t))
که در آن، tr(X) اثر ماتریس X را نشان میدهد.
در یک حالت خاص، داریم:
∂Aij∂det(A)=adjT(A)ij.
اگر dA دیفرانسیل A باشد، فرمول ژاکوبی به صورت زیر در میآید:
ddet(A)=tr(adj(A)dA).
این فرمول به نام ریاضیدان آلمانی، «کارل گوستاو یاکوب ژاکوبی» (Carl Gustav Jacob Jacobi)، نامگذاری شده است.
استخراج فرمول ژاکوبی
در این بخش، دو روش رسیدن به فرمول ژاکوبی را معرفی میکنیم.
محاسبات ماتریسی
ابتدا یک لم مقدماتی را اثبات میکنیم.
لم: فرض کنید A و B دو ماتریس مربعی با بُعد یکسان n باشند. در این صورت، داریم:
i∑j∑AijBij=tr(ATB).
اثبات لم: ضرب AB دو ماتریس دارای درایههای زیر است:
(AB)jk=i∑AjiBik.
با جایگزینی ماتریس A با ترانهادهاش، AT، اندیسها به صورت زیر تغییر میکنند:
(ATB)jk=i∑AijBik.
اگر اثر دو طرف تساوی بالا را محاسبه کنیم، داریم:
tr(ATB)=j∑(ATB)jj=j∑i∑AijBij=i∑j∑AijBij. □
قضیه (فرمول ژاکوبی): برای هر تصویر مشتقپذیر ماتریس A از اعداد حقیقی به ماتریسهای n×n، داریم:
ddet(A)=tr(adj(A)dA).
اثبات قضیه: فرمول لاپلاس برای دترمینان ماترس A را میتوان به صورت زیر نوشت:
det(A)=j∑AijadjT(A)ij.
لازم به ذکر است که مجموع برای سطر دلخواه i ماتریس انجام میشود.
دترمینان A را میتوان به عنوان تابعی از درایههای A در نظر گرفت:
det(A)=F(A11,A12,…,A21,A22,…,Ann)
بنابراین، با استفاده از قاعده زنجیرهای دیفرانسیل به صورت زیر است:
ddet(A)=i∑j∑∂Aij∂FdAij.
این مجموع روی همه n×n درایه ماتریس اعمال میشود.
برای یافتن ∂F/∂Aij، دقت کنید که در سمت راست فرمول لاپلاس، اندیس i را میتوان به صورت دلخواه انتخاب کرد (این کار برای بهینه کردن محاسبات است و هر انتخاب دیگری منجر به نتیجه یکسانی خواهد شد). به ویژه، میتوان آن را طبق اندیس اول ∂/∂Aij انتخاب کرد:
∂Aij∂det(A)=∂Aij∂∑kAikadjT(A)ik=k∑∂Aij∂(AikadjT(A)ik)
بنابراین، با استفاده از قاعده ضرب، داریم:
∂Aij∂det(A)=k∑∂Aij∂AikadjT(A)ik+k∑Aik∂Aij∂adjT(A)ik.
اکنون اگر هر درایه ماتریس Aij و کهاد adjT(A)ik درایه Aik در سطر (یا ستون) مشابه صدق میکنند، در نتیجه، کهاد تابعی از Aij نیست، زیرا کهاد Aik برحسب درایههای خود آن سطر (یا ستون) نیست. بنابراین:
∂Aij∂adjT(A)ik=0
در نتیجه:
∂Aij∂det(A)=k∑adjT(A)ik∂Aij∂Aik.
همه درایههای A مستقل از یکدیگرند، یعنی:
∂Aij∂Aik=δjk
که در آن، δ دلتای کرونکر است، بنابراین:
∂Aij∂det(A)=k∑adjT(A)ikδjk=adjT(A)ij.
در نتیجه:
d(det(A))=i∑j∑adjT(A)ijdAij
و با اعمال لم بالا، داریم:
d(det(A))=tr(adj(A)dA). □
قاعده زنجیرهای
در این روش نیز ابتدا دو لم را اثبات میکنیم.
لم ۱: رابطه det′(I)=tr برقرار است که در آن، det′ دیفرانسیل det است.
این معادله بدین معنی است که دیفرانسیل det در ماتریس یکه برابر با اثر ماتریس است. دیفرانسیل det′(I) یک عملگر خطی است که ماتریس n×n را به یک عدد حقیقی تصویر میکند.
اثبات لم ۱: با استفاده از تعریفِ مشتق جهتدار همراه با یکی از ویژگیهای اساسی توابع مشتقپذیر، داریم:
det′(I)(T)=∇Tdet(I)=ε→0limεdet(I+εT)−detI
det(I+εT) یک چندجملهای برحسب ε و از درجه n است. این، رابطه نزدیکی با چندجملهای مشخصه T دارد. جمله ثابت (ε=0) برابر با ۱ است، در حالی که جمله خطی در ε برابر با trT است.
لم ۲: برای ماتریس معکوسپذیر A، داریم: det′(A)(T)=detAtr(A−1T).
اثبات لم ۲: تابع زیر از X را در نظر بگیرید:
detX=det(AA−1X)=(detA) det(A−1X)
دیفرانسیل تابع detX را محاسبه کرده و آن را در X=A با استفاده از لم ۱، معادله بالا و قاعده زنجیرهای به دست میآوریم:
det′(A)(T)=detA det′(I)(A−1T)=detA tr(A−1T)
قضیه (فرمول ژاکوبی): dtddetA=tr(adj AdtdA)
اثبات قضیه: اگر A وارونپذیر باشد، با استفاده از لم ۲ و مقدار T=dA/dt و با استفاده از معادلهای که ماتریس الحاقی A را به A−1 مرتبط میکند، داریم:
dtddetA=detAtr(A−1dtdA)=tr(adj AdtdA)
این فرمول برای همه ماتریسها برقرار است، زیرا مجموعه ماتریسهای خطی وارونناپذیر در فضای ماتریسها فشرده است.
فرمول ژاکوبی برای نمایی ماتریسی
رابطه مفید زیر، اثر ماتریس را به دترمینان نمایی ماتریسی متناظر ربط میدهد:
detetB=etr(tB)
تساوی فوق برای ماتریسهای قطری واضح است و اثبات آن برای ماتریسهای عمومی در ادامه آمده است. برای هر ماتریس وارونپذیر A(t)، در بخش قبل (قاعده زنجیرهای)، نشان دادیم که:
dtddetA(t)=detA(t)tr(A(t)−1dtdA(t))
با توجه به A(t)=exp(tB) در این معادله، داریم:
dtddetetB=tr(B)detetB
نتیجه مطلوب با جواب این معادله دیفرانسیل معمولی حاصل میشود.
کاربردهای فرمول ژاکوبی
فرمهای مختلف فرمول ژاکوبی برای محاسبه چندجملهای مشخصه و به طور خاص در قضیه کیلی همیلتون استفاده میشود. برای مثال، با استفاده از فرمول زیر که قبلاً آن را اثبات کردیم:
dtddetA(t)=detA(t) tr(A(t)−1dtdA(t))
و با استفاده از A(t)=tI−B، خواهیم داشت:
dtddet(tI−B)=det(tI−B)tr[(tI−B)−1]=tr[adj(tI−B)]
که در آن، adj ماتریس الحاقی را نشان میدهد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^
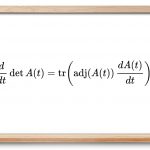
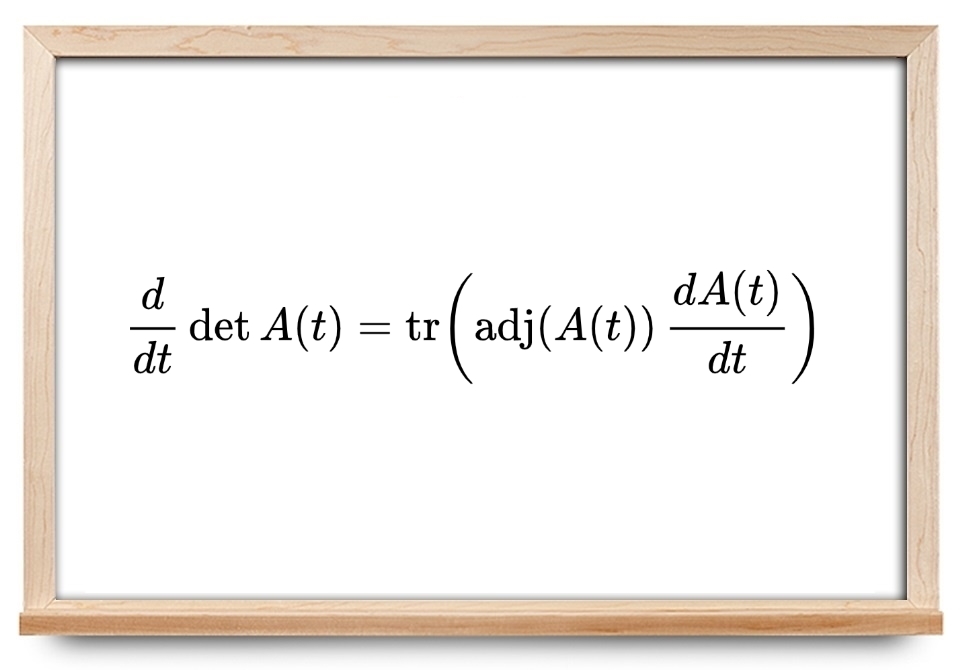













فرمول ها خیلی کلی توضیح داده شده اند و در انتها خود ماتریس ژاکوبی که در دروس کنترل مورد نیاز هستند به فرم ماتریس شرح داده نشده است. حتی اثبات ها خیلی کلی انجام شده اند و به جزییات اشاره ای نشده. لطفا فرم ماتریس ژاکوبی رو اضافه کنید
با تشکر
سلام خسته نباشید یک مثال مثل مشتق
گرفتن از یک ماتریس ۳ در ۳ با درایه های سینوس و کسینوس بیاورید تشکر از لطف شما.
سلام.
ماتریس ژاکوبی در مطلب «خطی سازی سیستم های غیرخطی — از صفر تا صد» معرفی شده است.
از همراهی شما با مجله فرادرس خوشحالیم.