همگرایی سری فوریه – از صفر تا صد

قبلاً در آموزش‌های ریاضی مجله فرادرس، با سری فوریه آشنا شدیم. در این آموزش، درباره همگرایی سری فوریه بحث می‌کنیم. ابتدا چند تعریف را ارائه می‌کنیم.

تعاریف

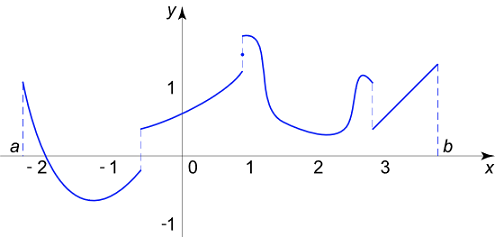
تابع تکه‌ای پیوسته (Piecewise Continuous): تابع $$f\left( x \right)$$ در بازه $$\left[ {a,b} \right]$$ تکه‌ای پیوسته نامیده می‌شود، اگر در این بازه به جز در تعدادی نقاط محدود پیوسته باشد (شکل ۱).

تابع تکه‌ای هموار (Piecewise Smooth): تابع $$f\left( x \right)$$ را در بازه $$\left[ {a,b} \right]$$ تکه‌ای هموار می‌نامیم، اگر $$f\left( x \right)$$ و مشتق آن تکه‌ای پیوسته باشند.

مجموع جزئی سری فوریه: مجموع جزئی فوریه یا سری جزئی فوریه $${f_N}\left( x \right)$$ تابع $$f\left( x \right)$$ در بازه $$\left[ {-\pi, \pi} \right]$$ به صورت زیر تعریف می‌شود:

$$\large { { f _ N } \left ( x \right ) = \frac { { { a _ 0 } } } { 2 } } + { \sum \limits _ { n = 1 } ^ N { \left ( { { a _ n } \cos n x + { b _ n } \sin n x } \right ) } . }$$

فرم مختلط مجموع جزئی $$n$$اُم تابع $${f_N}\left( x \right)$$ روی بازه $$\left[ {-\pi, \pi} \right]$$ به شکل زیر است:

$$\large { { f _ N } \left ( x \right ) = \sum \limits _ { n = – N } ^ N { { c _ n } { e^ { i n x } } } } = { \int \limits _ { – \pi } ^ \pi { \left ( { \frac { 1 } { { 2 \pi } } \sum \limits _ { n = – N } ^ N { { e ^ { i n \left ( { x – y } \right ) } } } } \right ) f \left ( y \right ) d y } }$$

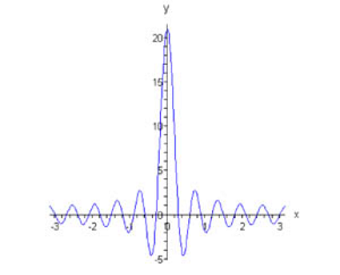
هسته دیریکله: تابعِ

$$\large { { D _ N } \left ( x \right ) = \sum \limits _ { n = – N } ^ N { { e ^ { i n x } } } } = { \frac { { \sin \left ( { N + \frac { 1 } { 2 } } \right ) x } } { { \sin \frac { x } { 2 } } } }$$

هسته دیریکله (Dirichlet Kernel) نامیده می‌شود. در شکل ۲، هسته دیریکله برای $$n = 10$$ نشان داده شده است.

مجموع جزئی فوریه $$f\left( x \right)$$ را می‌توان با هسته دیریکله بیان کرد:

$$\large { { f _ N } \left ( x \right ) } = { \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( { x – y } \right ) f \left ( y \right ) d y } } = { \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( y \right ) f \left ( { x – y } \right ) d y } . }$$

در ادامه، سه نوع همگرایی را بررسی می‌کنیم: نقطه‌ای، یکنواخت و $$L_2$$.

همگرایی نقطه‌ای سری فوریه

فرض کنید $$f\left( x \right)$$ یک تابع تکه‌ای هموار روی بازه $$\left[ {-\pi, \pi} \right]$$ باشد. آنگاه برای هر $${x_0} \in \left[ { – \pi ,\pi } \right]$$، داریم:

$$\large { \lim \limits _ { N \to \infty } { f _ N } \left ( { { x _ 0 } } \right ) \text { = } } \kern0pt { \begin {cases} f \left ( { { x _ 0 } } \right ) , \text {if} \, f \left ( x \right ) \, \; \text {is continuous on} \, \left[ { – \pi ,\pi } \right ] \\ \frac { { f \left ( { { x _ 0 } – 0 } \right ) + f \left ( { { x _ 0 } + 0 } \right ) } } { 2 } , \; \text {if} \, f \left ( x \right ) \, \text {has a jump discontinuity at} \, { { x _ 0 } } \end {cases}}$$

که در آن، $${f\left( {{x_0} – 0} \right)}$$ و $${f\left( {{x_0} + 0} \right)}$$ حد چپ و حد راست در نقطه $$x _ 0$$ را نشان می‌دهند.

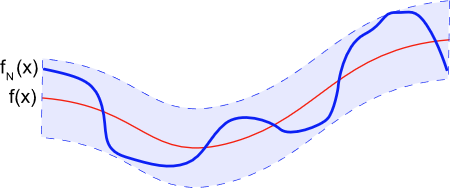
همگرایی یکنواخت سری فوریه

دنباله مجموع جزئی $$\left\{ {{f_N}\left( x \right)} \right\}$$ را همگرای یکنواخت به تابع $$f ( x)$$ می‌نامیم، اگر سرعت همگرایی مجموع جزئی $${{f_N}\left( x \right)}$$ به $$x$$ وابسته نباشد (شکل ۳).

سری فوریه تابع $$f (x)$$ را همگرای یکنواخت به این تابع می‌‌گوییم، اگر داشته باشیم:

$$\large { \lim \limits _ { N \to \infty } \left[ { \max \limits _ { x \in \left[ { – \pi , \pi } \right] } \left| { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right | } \right ] } = { 0 . }$$

قضیه: سری فوریه یک تابع پیوسته و تکه‌ای هموار با دوره تناوب $$2 \pi$$، به صورت یکنواخت همگرا می‌شود.

همگرایی سری فوریه در نرم $$\LARGE L _ 2$$

فضای $${L_2}\left( { – \pi ,\pi } \right)$$ با توابعی شکل می‌گیرد که:

$$\large \int \limits _ { – \pi } ^ \pi { { { \left | { f \left ( x \right ) } \right | } ^ 2 } d x } < \infty .$$

تابع $$f (x)$$ را انتگرال‌پذیر مربعی گوییم، اگر به فضای $$L_2$$ متعلق باشد. اگر تابع $$f(x)$$ انتگرال‌پذیر مربعی باشد، آنگاه:

$$\large { \lim \limits _ { N \to \infty } \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { { { \left | { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right | } ^ 2 } d x } } = { 0 , }$$

و مجموع جزئی $${f_N}\left( x \right)$$ در نرم $$L_2$$ به $$f (x)$$ همگراست.

همگرایی یکنواخت، همگرایی نقطه‌ای و همگرایی $$L_2$$ را نشان می‌دهد. اما، عکس آن برقرار نیست؛ یعنی همگرایی $$L_2$$ به معنای همگرایی نقطه‌ای و یکنواخت نیست. همچنین نمی‌توان از همگرایی نقطه‌ای، همگرایی یکنواخت و همگرایی $$L_2$$ را نتیجه گرفت.

پدیده گیبس

اگر یک ناپیوستگی جهشی وجود داشته باشد، مجموع جزئی سری فوریه در نزدیک جهش نوسان‌هایی دارد که ممکن است بیشینه مجموع جزئی تابع را افزایش دهد. این پدیده، پدیده گیبس (Gibbs Phenomenon) نامیده می‌شود. دامنه فراجهش در هر نقطه جهش یک تابع تکه‌ای هموار تقریباً ۱۸ درصد بزرگ‌تر از جهش تابع اصلی است (شکل ۴).

مثال‌ها

در این بخش، چند مثال را درباره همگرایی سری فوریه بررسی می‌کنیم.

مثال ۱

انتگرال $$\large \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( z \right ) d z }$$ را محاسبه کنید.

حل: می‌دانیم:

$$\large { { f _ N } \left ( x \right ) \text { = }}\kern0pt{ \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( { x – y } \right ) f \left ( y \right ) d y } . }$$

هسته دیریکله $${D_N}\left( x \right)$$ یک تابع متناوب با دوره تناوب $$2 \pi$$ و زوج است، بنابراین، می‌توان نوشت:

$$\large { { f _ N } \left ( x \right ) \text { = }}\kern0pt{ \frac { 1 } { \pi } \int \limits _ 0 ^ \pi { { D _ N } \left ( { x – y } \right ) f \left ( y \right ) d y } . }$$

فرض کنید $${f_N}\left( x \right) = f\left( x \right) = 1$$ و با قرار دادن آن در فرمول بالا، داریم:

$$\large 1 = \frac { 1 } { \pi } \int \limits _ 0 ^ \pi { { D _ N } \left ( { x – y } \right ) d y } .$$

از تغییر متغیر $$z = x – y$$ استفاده می‌کنیم. بنابراین، $$y = x - z$$ و $$dy = -dz$$. اکنون حدود جدید انتگرال را به دست می‌آوریم. وقتی $$y = 0$$، داریم: $$z = x$$ و وقتی $$y = \pi$$ داریم: $$z = x - \pi$$. در نتیجه، خواهیم داشت:

$$\large { 1 = \frac { 1 } { \pi } \int \limits _ x ^ { x – \pi } { { D _ N } \left ( z \right ) \left ( { – d z } \right ) } \; \; \text {or}\;\;}\kern-0.3pt { 1 = \frac { 1 } { \pi } \int \limits _ { x – \pi } ^ x { { D _ N } \left ( z \right ) d z } . }$$

به دلیل متناوب بودن $${{D_N}\left( x \right)}$$، می‌توان نوشت:

$$\large 1 = \frac { 1 } { \pi } \int \limits _ { – \pi } ^ 0 { { D _ N } \left ( z \right ) d z } .$$

در نتیجه:

$$\large { \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( z \right ) d z } } = { 2 \int \limits _ { – \pi } ^ 0 { { D _ N } \left ( z \right ) d z } } = { 2 \pi . }$$

راه دیگری نیز برای محاسبه این انتگرال وجود دارد. ابتدا انتگرال را به صورت زیر بازنویسی می‌کنیم:

$$\large { I = \int \limits _ { – \pi } ^ \pi { { D _ N } \left ( z \right ) d z } } = { 2 \int \limits _ 0 ^ \pi { { D _ N } \left ( z \right ) d z } . }$$

از آنجایی که داریم:

$$\large { { D _ N } \left ( z \right ) = \frac { { \sin \left ( { N + \frac { 1 } { 2 } } \right ) z } } { { \sin \frac { z } { 2 } } } } = { 2 \left ( { \frac { 1 } { 2 } + \sum \limits _ { n = 1 } ^ N { \cos n z } } \right ) , }$$

می‌توانیم از این سری به صورت جمله به جمله انتگرال بگیریم. بنابراین:

$$\large { I = 2 \int \limits _ 0 ^ \pi { { D _ N } \left ( z \right ) d z } } = { 4 \int \limits _ 0 ^ \pi { \left ( { \frac { 1 } { 2 } + \sum \limits _ { n = 1 } ^ N { \cos n z } } \right ) d z } } = { 4 \left[ {\left. { \left ( { \frac { z } { 2 } + \sum \limits _ { n = 1 } ^ N { \frac { { \sin n z } } { n } } } \right ) } \right| _ 0 ^ \pi } \right ] . }$$

در رابطه بالا، در $$z = 0 , \pi$$، مقدار $$\sin {nz} = 0$$ را داریم. در نتیجه:

$$\large I = 4 \cdot \frac { \pi } { 2 } = 2 \pi .$$

مثال ۲

تابع $$f (x)= {\frac{{\pi – x}}{2}\normalsize}$$ در بازه $$\left[ {0,2\pi } \right]$$ تعریف شده است. بسط سری فوریه تابع را در بازه داده شده به دست آورده و با استفاده از آن، مقدار تقریبی $$\pi$$ را محاسبه کنید.

حل: ابتدا ضرایب فوریه را محاسبه می‌کنیم:

$$\large { { a _ 0 } } = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { f \left ( x \right ) d x } } = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { \frac { { \pi – x } } { 2 } d x } } = { \frac { 1 } { { 2 \pi } } \left [ { \left . { \left ( { \pi x – \frac { { { x ^ 2 } } } { 2 } } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] } = { 0 . }$$

برای $$n \ge 1$$، داریم:

$$\large \begin {align*} { { a _ n } } & = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { f \left ( x \right ) \cos n x d x } } = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { \frac { { \pi – x } } { 2 } \cos n x d x } } \\ & = { \left . { \left ( { \frac { { \pi – x } } { 2 } \frac { { \sin n x } } { { n \pi } } } \right ) } \right| _ 0 ^ { 2 \pi } } + { \frac { 1 } { { 2 \pi n } } \int \limits _ 0 ^ { 2 \pi } { \sin n x d x } } \\ & = { 0 – \frac { 1 } { { 2 \pi n } } \left [ { \left . { \left ( { \frac { { \cos n x } }{ n } } \right ) } \right| _ 0 ^ { 2 \pi } } \right] } = { 0, } \end {align*}$$

$$\large \begin {align*} { { b _ n } } & = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { f \left ( x \right ) \sin n x d x } } = { \frac { 1 } { \pi } \int \limits _ 0 ^ { 2 \pi } { \frac { { \pi – x } } { 2 } \sin n x d x } } \\ & = { \left. { \left ( { – \frac { { \pi – x } } { 2 } \frac { { \cos n x } } { { n \pi } } } \right ) } \right| _ 0 ^ { 2 \pi } } - { \frac { 1 } { { 2 \pi n } } \int \limits _ 0 ^ { 2 \pi } { \cos n x d x } } \\ & = { \left ( { – \frac { { \frac { { \pi – 2 \pi } } { 2 } \cos 2 \pi n } } { { n \pi } } + \frac { { \frac { \pi } { 2 } \cos 0 } } { { n \pi } } } \right ) } - { \frac { 1 } { { 2 \pi n } } \left [ { \left . { \left ( { \frac { { \sin n x } } { n } } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] } \\ & = { \frac { 1 } { { 2 n } } + \frac { 1 } { { 2 n } } } = { \frac { 1 }{ n } . } \end {align*}$$

بنابراین، بسط سری فوریه برابر است با:‌

$$\large { \frac { { \pi – x } } { 2 } = \sum \limits _ { n = 1 } ^ \infty { \frac { { \sin n x } } { n } } \; \; } \kern-0.3pt{ \text {for}\;\;x \in \left[ { 0 , 2 \pi } \right] . }$$

با قرار دادن $$x = {\large\frac{\pi }{2}\normalsize}$$، یک سری جایگزین برای $${\large\frac{\pi }{4}\normalsize}$$ به دست می‌آوریم:

$$\large { \frac { \pi } { 4 } = \sum \limits _ { n = 1 } ^ \infty { \frac { { \sin \frac { { n \pi } } { 2 } } } { n } } } = { 1 – \frac { 1 } { 3 } + \frac { 1 } { 5 } – \frac { 1 } { 7 } + \ldots } = { \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { { 2 n – 1 } } } . }$$

با استفاده از رابطه بالا، می‌توانیم نمایش سری بی‌نهایت $$\pi$$ را به صورت زیر بنویسیم:

$$\large { \pi = 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { { 2 n – 1 } } } } = { 4 \left ( { 1 – \frac { 1 } { 3 } + \frac { 1 } { 5 } – \frac { 1 } { 7 } + \ldots } \right ) . }$$

مثال ۳

ثابت کنید سری فوریه تابع $$f (x) = x ^ 2$$ در بازه $$\left[ {-\pi, \pi} \right]$$ به صورت یکنواخت به $$f (x)$$ همگرا می‌شود.

حل: بسط سری فوریه $$f (x) = x ^ 2$$ روی بازه $$\left[ {-\pi, \pi} \right]$$ به صورت زیر است:

$$\large { f \left ( x \right ) = { x ^ 2 } } = { \frac { { { \pi ^ 2 } } } { 3 } } + { 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } . }$$

مجموع جزئی نیز به صورت زیر تعریف می‌شود:

$$\large { { f _ N } \left ( x \right ) = \frac { { { \pi ^ 2 } } } { 3 } } + { 4 \sum \limits _{ n = 1 } ^ N { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } . }$$

بنابراین:

$$\large \begin {align*} { \left| { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right| } & = { \left| { 4 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } } \right . } - { \left . { 4 \sum \limits _ { n = 1 } ^ N { \frac { { { { \left ( { – 1 } \right ) } ^ n } } }{ { { n ^ 2 } } } \cos n x } } \right| } \\ & = { \left| { 4 \sum \limits _ { n = N + 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { { { n ^ 2 } } } \cos n x } } \right | } \le { 4 \sum \limits _ { n = N + 1 } ^ \infty { \left | { \frac { { { { \left ( { – 1 } \right ) } ^ n } } } { {{ n ^ 2 } } } \cos n x } \right| } } \le { 4 \sum \limits _ { n = N + 1 } ^ \infty { \frac { 1 }{ { { n ^ 2 } } } } . } \end {align*}$$

وقتی $$N \to \infty$$، مجموع آخری به صفر میل می‌کند. در واقع، با اعمال آزمون انتگرال، داریم:

$$\large \begin {align*} { \lim \limits _ { N \to \infty } \sum \limits _ { n = N + 1 } ^ \infty { \frac { 1 } { { { n^ 2 } } } } } & = { \lim \limits _ { N \to \infty } \int \limits _ { N + 1 } ^ \infty { \frac { { d x } } { { { x ^ 2 } } } } } = { \lim \limits _ { N \to \infty } \left[ { \left . { \left ( { – \frac { 1 } { x } } \right ) } \right | _ { N + 1 } ^ \infty } \right ] }\\ & = { \lim \limits _ { N \to \infty } \frac { 1 } { { N + 1 } } } = { 0.} \end {align*}$$

بنابراین:

$$\large { \lim \limits _ { N \to \infty } \left [ { \max \limits _ { x \in \left [ { – \pi , \pi } \right ] } \left | { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right | } \right ] } = { 0 , }$$

که بدین معنی است، تابع $$f (x) = x ^ 2$$ به صورت یکنواخت همگرا می‌شود.

مثال ۴

ثابت کنید سری فوریه تابع $$f (x) = x$$ در بازه $$\left[ {-\pi, \pi} \right]$$ در نرم $$L_2$$ به $$f (x)$$ همگرا می‌شود.

حل: سری فوریه تابع $$f (x) = x$$ در بازه $$\left[ {-\pi, \pi} \right]$$، به صورت زیر است:

$$\large { f \left ( x \right ) = x } = { 2 \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } . }$$

مجموع جزئی به صورت زیر تعریف می‌شود:

$$\large { { f _ N } \left ( x \right ) } = { 2 \sum \limits _ { n = 1 } ^ N { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } . }$$

حد زیر را محاسبه می‌کنیم:

$$\large { \lim \limits _ { N \to \infty } \frac { 1 } { { 2 \pi } } \int \limits _ { – \pi } ^ \pi { { { \left| { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right| } ^ 2 } d x } } = { \lim \limits _ { N \to \infty } \left| { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right| , }$$

که در آن، $$\left\| {f\left( x \right)} \right\|$$ نرم $$L _ 2$$ تابع $$f (x)$$ است.

اکنون نرم $$\left\| {f\left( x \right) – {f_N}\left( x \right)} \right\|$$ را پیدا می‌کنیم:

$$\large \begin {align*} \left| { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right | & = \kern0pt { {\left[ { \frac { 1 } { { 2 \pi } } { { \int \limits _ { – \pi } ^ \pi { \left | { \sum \limits _ { n = 1 } ^ \infty { \frac { { 2 { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } } \right . } } } } \right . } - { \left . { { { { \left . { \sum \limits _ { n = 1 } ^ N { \frac { { 2 { { \left ( { – 1 } \right ) } ^ { n + 1 } } } }{ n } \sin n x } } \right | } } ^ 2 } d x } \right] }^{\frac{1}{2}} } \\ &= { \left | { \sum \limits _ { n = N + 1 } ^ \infty { \frac { { 2 { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } } \right|.} \end {align*}$$

اکنون از نامساوی مثلثی $$\left\| {f + g} \right\| \le \left\| f \right\| + \left\| g \right\|$$ برای توابع فضای $$L_2$$ استفاده می‌کنیم. بنابراین، داریم:

$$\large { \left| { f \left( x \right) – {f_N}\left( x \right)} \right| } = { \left | { \sum \limits _ { n = N + 1 } ^ \infty { \frac { { 2 { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } } \right | } \\ \large \le { \sum \limits _ { n = N + 1 } ^ \infty { \left | { \frac { { 2 { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { n } \sin n x } \right |} } \le { \sum \limits _ { n = N + 1 } ^ \infty { \left | { \frac { 2 } { n } } \right | } } = { \lim \limits _ { N \to \infty } \sum \limits _ { n = N + 1 } ^ \infty { { { \left ( { \frac { 2 } { n } } \right ) } ^ 2 } } }\\ \large = { \lim \limits _ { N \to \infty } \sum \limits _ { n = N + 1 } ^ \infty { \frac { 4 } { { { n ^ 2 } } } } . }$$

حد آخر برابر با صفر است:

$$\large { \lim \limits _ { N \to \infty } \left | { f \left ( x \right ) – { f _ N } \left ( x \right ) } \right | } = { \lim \limits _ { N \to \infty } \sum \limits _ { n = N + 1 } ^ \infty { \frac { 4 }{ { { n ^ 2 } } } } } = { 0 . }$$

بنابراین، ثابت کردیم که سری فوریه تابع $$f (x) = x$$ در نرم $$L_2$$ به $$f (x)$$ همگرا می‌شود.

مثال ۵

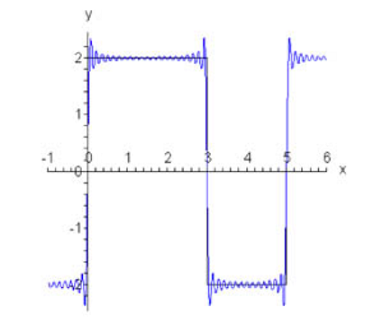
سری فوریه تابع $$f\left( x \right) ={\large\frac{{\pi – x}}{2}\normalsize}$$ که در بازه $$\left[ {0,2\pi } \right]$$ تعریف شده، با فرمول $$f \left( x \right) ={\large\frac{{\pi – x}}{2}\normalsize}= \sum\limits_{n = 1}^\infty {\large\frac{{\sin nx}}{n}\normalsize}$$ داده شده است (مثال ۲ را ببینید). رفتار مجموع جزئی $${f_N}\left( x \right)$$ سری فوریه را بررسی کنید.

حل: مجموع جزئی سری فوریه برابر است با:

$$\large { f _ N } \left ( x \right ) = \sum \limits _ { n = 1 } ^ N { \frac { { \sin n x } } { n } } .$$

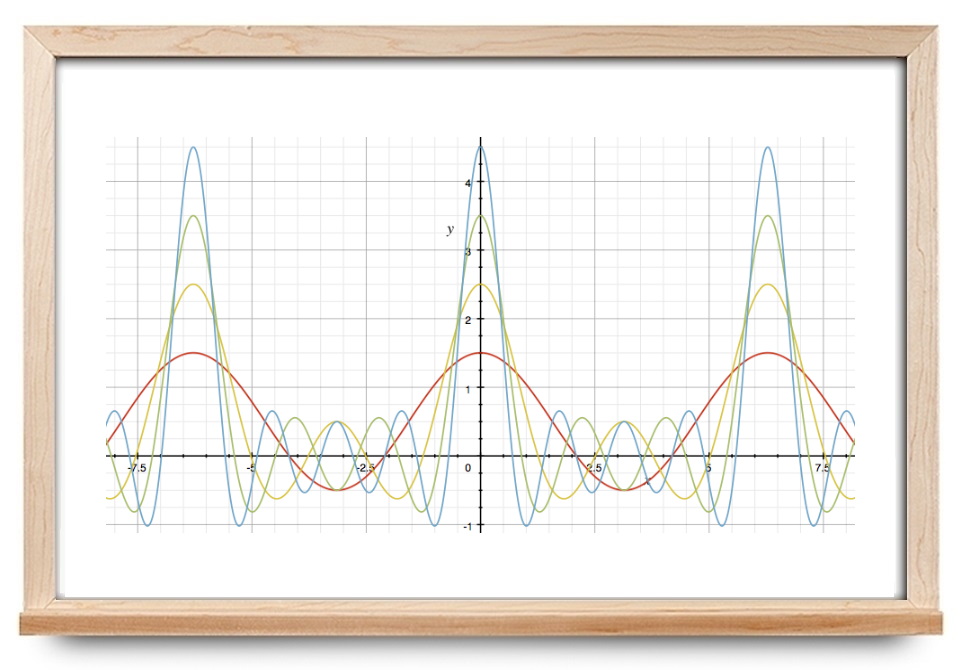
شکل ۵، مجموع جزئی تقریب زننده تابع را برای $$N$$های متفاوت نشان می‌دهد. همان‌طور که می‌بینیم، فراجهشی که توسط پدیده گیبس رخ می‌دهد، به ازای افزایش $$N$$، کوچک و کوچک‌تر می‌شود.

حال فراجهش دامنه را برای $$N \to \infty$$ بررسی می‌کنیم. با انتگرال‌گیری جمله به جمله، خواهیم داشت:

$$\large { { f _ N } \left ( x \right ) } = { \int \limits _ 0 ^ x { \left ( { \sum \limits _ { n = 1 } ^ N { \cos n t} } \right ) d t } . }$$

از رابطه زیر استفاده می‌کنیم:

$$\large { \frac { 1 } { 2 } + \sum \limits _ { n = 1 } ^ N { \cos n t } } = { \frac { 1 } { 2 } + \cos t + \cos 2 t + \ldots } +{ \cos n t } = { \frac { { \sin \frac { { 2 n + 1 } } {2 } t }} { { 2 \sin \frac { t } {2 } } } , }$$

و داریم:

$$\large { { f _ N } \left ( x \right) } = { \int \limits _ 0 ^ x { \left ( { \frac { 1 } { 2 } – \frac { { \sin \frac { { 2 n + 1 } } { 2 } t } }{ { 2 \sin \frac { t } { 2 } } } } \right ) d t } } = { – \frac { x} { 2 } + \int \limits _ 0 ^ x { \frac { { \sin \frac { { 2 n + 1 } } { 2 } t } }{ { 2 \sin \frac { t } { 2 } } } d t } . }$$

از تغییر متغیر $${\frac{{2N + 1}}{2}\normalsize} t = z$$ و در نتیجه $$dt = {\frac{2}{{2N + 1}}\normalsize} dz$$ استفاده می‌کنیم. در این تغییر متغیر، وقتی $$t = 0$$ باشد، $$z = 0$$ و وقتی $$t = {x_N}= {\frac{{2\pi }}{{2N + 1}}\normalsize}$$ باشد، $$z = {\frac{{2N + 1}}{2}\normalsize} \cdot {\frac{{2\pi }}{{2N + 1}}\normalsize}$$ است.

بنابراین، خواهیم داشت:

$$\large { { f _ N } \left ( { { x _ N } } \right ) + \frac { { { x _ N } } } { 2 } } = { \int \limits _ 0 ^ \pi { \frac { { \sin z } } { { 2 \sin \frac { z } { { 2 N + 1 } } } } \cdot \frac { { 2 d z } } { { 2 N + 1 } } } } \\ \large = { \int \limits _ 0 ^ \pi { \frac { { \sin z } } { { \sin \frac { z } { { 2 N + 1 } } \left ( { 2 N + 1 } \right ) } } d z } } = { \int \limits _ 0 ^ \pi { \frac { { \sin z } } { { \frac { { z \cdot \sin \frac { z } { { 2 N + 1 } } } } { { \frac { z } { { 2 N + 1 } } } } } } d z . } }$$

اکنون در می‌یابیم که وقتی $$N \to \infty$$، $${f_N}\left( x \right) = \int\limits_0^\pi {{\large\frac{{\sin z}}{z}\normalsize} dz}$$، زیرا:‌

$$\large { \lim \limits _ { N \to \infty } { x _ N } } = { \lim \limits _ { N \to \infty } \frac { { 2 \pi } } { { 2 N + 1 } } = 0 \; \; } \kern-0.3pt { \text {,}\;\;\;\;\;\;\;}\kern -0.3pt { \lim \limits _ { N \to \infty } \frac { { \sin \frac { z } { { 2 N + 1 } } } } { { \frac { z } { { 2 N + 1 } } } } } = { 1 . }$$

انتگرال $$\int\limits_0^x {{\large\frac{{\sin z}}{z}\normalsize} dz}$$، انتگرال سینوسی نام دارد و به صورت زیر نمایش داده می‌شود:

$$\large \text {Si} \left ( x \right ) = \int \limits _ 0 ^ x { \frac { { \sin z } } { z } d z } .$$

بنابراین، می‌توان نوشت:

$$\large { \lim \limits _ { N \to \infty } \sum \limits _ { n = 1 } ^ N { \frac { { \sin n { x _ N } } } { n } } } = { \int \limits _ 0 ^ \pi { \frac { { \sin z } } { z } d z } } = { \text {Si} \left ( \pi \right ) , }$$

که در آن، $$\text{Si}\left( \pi \right) \approx {\large\frac{\pi }{2}\normalsize} \cdot 1,17898$$.

در نتیجه، دامنه فراجهش تقریباً‌ ۱۸ درصد است.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سری فوریه مختلط — به زبان ساده
• تبدیل فوریه (Fourier Transform) — به زبان ساده
• انتگرال فوریه — به زبان ساده

^^