انرژی و توان سیگنال — از صفر تا صد

انرژی و توان سیگنال (Energy and Power of Signal) دارای تعریف متفاوتی نسبت به تعریف انرژی و توان در فیزیک هستند. در فیزیک، انرژی برابر با کار و توان برابر با کار در واحد زمان تعریف می‌شود. اما در علم پردازش سیگنال، انرژی و توان سیگنال بدون واحد فیزیکی در نظر گرفته می‌شوند؛ زیرا سیگنال‌ها ممکن است نشان‌دهنده کمیت‌های فیزیکی مختلفی باشند. می‌توان گفت انرژی و توان سیگنال را بر اساس اندازه سیگنال به دست می‌آورند. در این مطلب قصد داریم به نحوه محاسبه انرژی و توان سیگنال بپردازیم و دو گروه مهم از سیگنال‌ها، یعنی سیگنال‌های توان و سیگنال‌های انرژی را تعریف کنیم.

اندازه سیگنال

در پردازش سیگنال، یک سیگنال به صورت تابعی از زمان در نظر گرفته می‌شود. عبارت «اندازه سیگنال» برای اشاره به قدرت یک سیگنال به کار برده می‌شود. دانستن اندازه سیگنال در کاربردهای مختلف، امری ضروری محسوب می‌شود. به عنوان مثال، در اندازه گیری الکتریکی ممکن است نیاز داشته باشیم مقدار ولتاژ و جریان مورد نیاز برای روشن کردن یک نمایش‌گر LCD رابدانیم و تفاوت مقادیر به دست آمده با مقادیر لازم برای روشن کردن نمایش‌گر CRT را با هم مقایسه کنیم. این دو LCD با یکدیگر متفاوت هستند و بنابراین مقدار این مولفه‌ها نیز با یکدیگر تفاوت خواهد داشت.

فیلم آموزش مخابرات ۱ – مقدماتی در فرادرس

کلیک کنید

اندازه یک سیگنال فرضی را می‌توان از روش‌های مختلفی به دست آورد. مساحت ناحیه زیر منحنی یک سیگنال که توسط یک تابع ریاضی توصیف شده است، ممکن است روشی مناسب برای به دست آوردن اندازه سیگنال محسوب می‌شود. توجه کنید که یک سیگنال می‌تواند هم مقادیر مثبت و هم مقادیر منفی در خود داشته باشد. به همین دلیل است که مساحت برخی نواحی در یک سیگنال، منفی می‌شود. در نتیجه، ممکن است مقادیر مساحت‌های محاسبه شده گاهی به صورت کامل و یا قسمتی از یکدیگر را خنثی کنند و منجر به نتایج نادرست شوند.

پس می‌توان گفت که مساحت زیر منحنی، روشی مناسب برای محاسبه اندازه سیگنال نیست. حال دو روش برای محاسبه این مقدار داریم. در روش اول، می‌توان مساحت زیر منحنی قدر مطلق سیگنال را به دست آورد و در روش دوم، مساحت زیر مجذور نمودار سیگنال را برای محاسبه اندازه سیگنال مورد استفاده قرار می‌دهیم.

در حالت کلی، روش دوم از محبوبیت بالاتری برخوردار است؛ زیرا این روش از لحاظ ریاضی معقول‌تر است و علاوه بر این، شباهت زیادی به نرم اقلیدسی یا نرم L2 دارد که در تکنیک‌های شناسایی سیگنال مورد استفاده قرار می‌گیرد. نرم اقلیدسی به این دلیل بسیار مورد استفاده قرار می‌گیرد که اندازه‌گیری بهتری از فاصله بین دو نقطه در سیگنال را فراهم می‌آورد. این فاصله را در اصطلاح، فاصله اقلیدسی می‌گویند.

انرژی سیگنال

بنابراین، با در نظر گرفتن روش دوم، اندازه سیگنال را می‌توان به صورت مساحت ناحیه زیر مجذور سیگنال تعریف کرد. در نتیجه، انرژی سیگنال پیوسته با زمان و مختلط $$x(t)$$ نیز به صورت زیر محاسبه می‌شود:

$$E_x=\int_{-\infty }^{\infty }\left | x(t) \right |^{2} dt$$

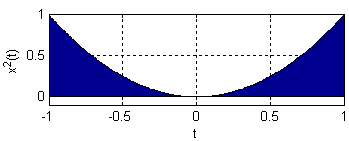
در تصویر زیر نحوه به دست آوردن انرژی سیگنال با استفاده از سطح زیر نمودار مجذور سیگنال $$x(t)$$ نشان داده شده است.

$$x(t)$$" width="349" height="141">

اگر سیگنال $$x(t)$$ حقیقی باشد، بر خلاف سیگنال‌های مختلط به عملگر قدر مطلق (برای به دست آوردن اندازه سیگنال) نیازی نیست. در پردازش سیگنال، فرمول به دست آمده در بالا را انرژی سیگنال می‌نامند. این کمیت در واقع بیانی از قدرت (Strength) یک سیگنال محسوب می شود. موضوع مهم دیگر این است که فرمول انرژی سیگنال بالا را می‌توان به هر سیگنالی اعمال کرد و اهمیتی ندارد که آیا کمیت انرژی تعریف شده برای آن سیگنال، با مفهوم فیزیکی انرژی سازگار است یا خیر. اگر سیگنال متناظر با یک کمیت فیزیکی باشد، آن‌گاه تعریف بالا برابر با انرژی نهفته در آن کمیت خواهد بود. اگر سیگنال، از نوع الکتریکی باشد، آن‌گاه تعریف بالا، مجموع انرژی سیگنال بر حسب ژول را نشان می‌دهد که در یک مقاومت ۱ اهمی تلف می‌شود.

محاسبه انرژی فیزیکی سیگنال‌های جریان و ولتاژ

برای دانستن انرژی واقعی سیگنال الکتریکی ($$E$$)، باید از مقدار بار $$Z$$ که سیگنال درایو می‌کند و نیز ذات سیگنال (ولتاژ یا جریان) مطلع بود. برای یک سیگنال ولتاژ، معادله بالا را باید توسط یک فاکتور $$1/Z$$ مقیاس‌بندی کرد.

$$E=\frac{E_x}{Z}=\frac{1}{Z}\int_{-\infty }^{\infty }\left | x(t) \right |^{2} dt$$

اما برای سیگنال جریان، معادله را باید توسط فاکتور $$Z$$ مقیاس‌بندی کرد.

$$E=Z E_x=Z\int_{-\infty }^{\infty }\left | x(t) \right |^{2} dt$$

در این فرمول‌ها، $$Z$$ برابر با مقدار امپدانسی است که توسط سیگنال $$x(t)$$ درایو می‌شود و $$E_x$$، انرژی سیگنال (عبارت پردازش سیگنال) و $$E$$ برابر با انرژی سیگنال به صورت یک کمیت فیزیکی در نظر گرفته می‌شود.

انرژی سیگنال‌های گسسته در زمان

در فضای گسسته، انرژی یک سیگنال را می‌توان توسط عبارت ریاضی زیر محاسبه کرد:

$$E_x=\sum_{n=-\infty }^{\infty }\left | x(n) \right |^2$$

واضح است که انرژی یک سیگنال فقط زمانی محدود می‌ماند که مقدار مجموع محاسبه شده توسط فرمول بالا، به مقدار محدودی همگرا شود. محدود ماندن سیگنال نشان دهنده جمع‌پذیر بودن مربعات آن سیگنال در نظر گرفته می‌شود. سیگنالی که در این شرایط صدق کند، سیگنال انرژی محدود نامیده می‌شود. اما اگر مقدار یک سیگنال نسبت به زمان کاهش نیابد چه اتفاقی می‌افتد؟ به عبارت دیگر اگر سیگنال مانند یک موج سینوسی پیوسته به صورت متناوب تا بی‌نهایت تکرار شود، چه شرایطی پیش می‌آید؟

در این شرایط می‌توان گفت که انرژی سیگنال برابر با بی‌نهایت می‌شود و مربع چنین سیگنالی دیگر جمع‌پذیر نخواهد بود. در نتیجه به کمیت قابل اندازه‌گیری دیگری برای غلبه بر این مشکل نیاز داریم. این کمیت توان (Power) نام دارد.

توان سیگنال

توان یک سیگنال به صورت مقدار انرژی مصرف شده در واحد زمان تعریف می‌شود. این کمیت، زمانی که انرژی یک سیگنال به بی‌نهایت برود و یا مربع آن جمع‌پذیر نباشد، مفید خواهد بود. برای سیگنالی که مجذور آن جمع‌پذیر نباشد، توان را با در نظر گرفتن سیگنال در بازه‌های زمانی مشخصی محاسبه می‌کنند. مراحل انجام این کار به صورت زیر خواهد بود:

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

1. سیگنال را در بازه مشخص و محدودی از زمان در نظر بگیرد.
2. انرژی سیگنال $$E_x$$ را در طول این بازه محدود محاسبه کنید.
3. مقدار انرژی به دست آمده را بر تعداد نمونه‌های در نظر گرفته شده ($$N$$) تقسیم کنید.
4. حد (Limit) نمونه‌های سیگنال را به سمت بی‌نهایت میل دهید ($$N\rightarrow \infty$$). در این شرایط توان کلی سیگنال به دست می‌آید.

در حوزه زمان گسسته، توان کلی سیگنال توسط فرمول زیر محاسبه می‌شود:

$$P_x=\lim_{N\rightarrow \infty }\frac{1}{2N+1}\sum_{n=-N}^{n=+N}\left | x(n) \right |^2$$

معادلات زیر هر کدام بیان دیگری از معادله بالا هستند که گاهی در کتب مختلف به آن‌ها اشاره می‌شود:

$$\begin{array}{ccc} P_x=\lim_{N\rightarrow \infty }\frac{1}{2N}\sum_{n=-N}^{n=N-1}\left | x(n) \right |^2 \\ P_x=\lim_{N\rightarrow \infty }\frac{1}{N}\sum_{n=0}^{n=N-1}\left | x(n) \right |^2 \\ P_x=\lim_{N\rightarrow \infty }\frac{1}{N_1-N_0+1}\sum_{n=N_0}^{n=N_1}\left | x(n) \right |^2 \end{array}$$

تنها تفاوت این فرمول‌ها با فرمول قبلی در تعداد نمونه‌های در نظر گرفته‌ شده برای محاسبه است. در این فرمول‌ها مخرج کسر متناسب با تعداد نمونه‌ها تغییر می‌کند.

توان در سیگنال‌های متناوب

یک سیگنال متناوب پیوسته با زمان $$x(t)$$ با دوره تناوب $$T_0$$ را در نظر بگیرید. نمونه‌ای از چنین سیگنالی در تصویر زیر نشان داده شده است.

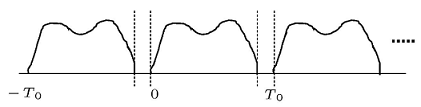
برای این سیگنال، انرژی که توسط فرمول $$\int_{-\infty}^{\infty} |x(t)|^2 dt$$ محاسبه می‌شود، دارای مقدار بی‌نهایت است. از آن‌جا که توان یک سیگنال نیز از میانگین انرژی سیگنال در واحد زمان به دست می‌آید، در نتیجه توان به صورت زیر خواهد بود:

$$P_{x}=\frac{1}{T_0} \int_{t_0}^{t_0+T_0} |x(t)|^2 dt.$$

در فرمول بالا، $$t_0$$ هر زمان تصادفی است که از آن لحظه دوره تناوب را محاسبه می‌کنیم. چون سیگنال متناوب است، $$t_0$$ می‌تواند به صورت تصادفی و دلخواه انتخاب شود. علی رغم این‌که کدام بازه زمانی را برای اندازه‌گیری انرژی سیگنال انتخاب می‌کنیم، مادامی که انرژی را در یک بازه برابر با دوره تناوب سیگنال اندازه بگیریم، نتیجه یکسانی به دست خواهد آمد؛ زیرا سیگنال متناوب است.

اگر سیگنال مورد نظر، گسسته با زمان و متناوب با دوره تناوب $$N_0$$ باشد، آن‌گاه توان سیگنال به صورت زیر محاسبه می‌شود:

$$P_x=\frac{1}{N_0} \sum_{n_0}^{n_0+N_0-1} |x[n]|^2$$

دقیقا همانند سیگنال پیوسته با زمان، انتخاب $$n_0$$ به صورت تصادفی بوده و هیچ تاثیری در نتیجه نهایی نخواهد داشت.

طبقه‌بندی سیگنال‌های مختلف بر اساس انرژی و توان سیگنال

سیگنال‌ها را می‌توان بر اساس توان و انرژی آن‌ها به دو گروه اساسی طبقه‌بندی کرد. سیگنال‌هایی که دارای انرژی محدود باشند را سیگنال انرژی و سیگنال‌هایی که دارای توان محدود و غیر صفر باشند را سیگنال توان می‌نامند.

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

سیگنال انرژی

برای یک سیگنال نوع انرژی $$x(t)$$، تابع خودهمبستگی (Autocorrelation) را به صورت زیر تعریف می‌کنیم:

$$\begin{aligned} R_{x}(\tau) &=x(\tau) \star x^{*}(-\tau) \\ &=\int_{-\infty}^{\infty} x(t) x^{*}(t-\tau) d t \\ &=\int_{-\infty}^{\infty} x(t+\tau) x^{*}(t) d t \end{aligned}$$

در تابع خودهمبستگی، مقدار $$\tau$$ را برابر با صفر در نظر می‌گیریم. در این صورت مقدار انرژی سیگنال را به صورت زیر به دست می‌آوریم:

$$E_x = \int_{-\infty}^{\infty} {|x(t)|}^2 d t = R_x(0)$$

حال با استفاده از قضیه خودهمبستگی در تبدیل فوریه، می‌توان تبدیل فوریه سیگنال $$R_X({\tau})$$ یعنی $${|x(f)|}^2$$ را به دست آورد و با توجه به آن رابطه زیر را نوشت:

$$E_x = \int_{-\infty}^{\infty} {|x(t)|}^2 d t = = \int_{-\infty}^{\infty} {|x(f)|}^2 d f$$

این رابطه، دو روش اساسی برای یافتن مقدار انرژی در یک سیگنال را نشان می‌دهد. یک روش از سیگنال در حوزه زمان استفاده می‌کند و روش دیگر از تبدیل سیگنال در حوزه فرکانس بهره می‌برد. مقدار عبارت $$\mathscr{F}[R_x(\tau) ]= {|X(f)|}^2$$، چگالی طیف انرژی (Energy Spectral Density) نام دارد و مقدار انرژی هر هرتز از پهنای باند یا فرکانس‌های مختلف موجود در سیگنال را نشان می‌دهد.

سیگنال توان

برای سیگنال‌هایی که در گروه سیگنال توان طبقه‌بندی می‌شوند نیز می‌توان از بسطی مشابه با سیگنال انرژی استفاده کرد. در این حالت، تابع خودهمبستگی میانگین زمانی (Time-Average Autocorrelation Function) برای سیگنال نوع توان $$x(t)$$ به صورت زیر به دست می‌آید:

$$R_{x}(\tau) =\lim_{T \rightarrow \infty}\int_{-\frac{T} {2}}^{\frac{T} {2}} x(t) x^{*}(t-\tau) d t$$

حال توان سیگنال را به سادگی با استفاده از فرمول زیر به دست می‌آوریم:

$$P_{x} =\frac 1 T\lim_{T \rightarrow \infty}\int_{-\frac{T} {2}}^{\frac{T} {2}} {|x(t)|}^2 d t = R_X(0)$$

سپس متغیر $$S_x(f)$$ را تعریف می‌کنیم و آن را چگالی طیف توان (Power Spectral Density) سیگنال $$x(t)$$ نام می‌گذاریم. چگالی طیف توان برابر با تبدیل فوریه تابع خودهمبستگی و به صورت زیر خواهد بود:

$$S_x(f)=\mathscr{F}[R_x(\tau) ]$$

در ادامه باز به این رابطه باز خواهیم گشت. اکنون می‌توانیم توان سیگنال $$x(t)$$ را بر حسب $$S_x(f)$$ بسط دهیم. با توجه به $$R_x(0)=\int_{-\infty}^{\infty}S_x(f)df$$، داریم:

$$P_x = R_x(0)=\int_{-\infty}^{\infty}S_x(f)df$$

عبور سیگنال توان از فیلتر LTI

اگر یک سیگنال نوع توان را از یک فیلتر با پاسخ ضربه $$h(t)$$ عبور دهیم، خروجی به صورت زیر خواهد بود:

$$y(t) = \int_{-\infty}^{\infty} x(\tau)h(t-\tau)d \tau$$

تابع خودهمبستگی میانگین زمانی برای این سیگنال خروجی برابر است با:

$$R_y(\tau)= \lim_{T \rightarrow \infty} \frac {1} {T}\int_{- \frac {T} {2}}^{ \frac {T} {2}} y(t)y^*(t-\tau)d t$$

با جای‌گذاری $$y(t)$$ داریم:

$$R_y(\tau)=\frac 1 T \lim_{T \rightarrow \infty} [\int_{- \infty}^{ \infty} h(u)x(t-\tau)d u] [\int_{- \infty}^{ \infty} h^*(v) x^*(t-\tau-v)d v] d t$$

با تغییر متغیر $$w=t-u$$ و تغییر مرتبه انتگرال‌گیری، داریم:

$$\begin{aligned} R_{y}(\tau)=& \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} h(u) h^{*}(v) \\ & \times \lim _{T \rightarrow \infty} \frac{1}{T} \int_{-\frac{T}{2}-u}^{\frac{T}{2}+u}\left[x(w) x^{*}(u+w-\tau-v) d w\right] d u d v \\=& \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} R_{x}(\tau+v-u) h(u) h^{*}(v) d u d v \\ \quad=& \int_{-\infty}^{\infty}\left[R_{x}(\tau+v) \star h(\tau+v)\right] h^{*}(v) d v \\ \quad=& R_{x}(\tau) \star h(\tau) \star h^{*}(-\tau) \end{aligned}$$

در به دست آوردن رابطه بالا، از تعریف $$R_x$$ و نیز از تعریف انتگرال کانولوشن استفاده کرده‌ایم. با گرفتن تبدیل فوریه از هر دو طرف رابطه بالا داریم:

$$S_y(f) = S_x(f) H(f) H^*(f) \\ = S_x(f) |H(f)|^2$$

سیگنال‌های متناوب از نوع سیگنال‌های توان در نظر گرفته می‌شوند. در مورد سیگنال‌های متناوب، تابع خودهمبستگی میانگین زمانی و چگالی طیف توان تا حد قابل توجهی ساده‌سازی می‌شوند. فرض کنید که سیگنال $$x(t)$$ یک سیگنال متناوب با دوره تناوب $$T_0$$ باشد و ضرایب سری فوریه آن برابر با $${x_n}$$ در نظر گرفته شوند. برای به دست آوردن تابع خودهمبستگی میانگین زمانی این سیگنال داریم:

$$\begin{aligned} R_{x}(\tau) &=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} x(t) x^{*}(t-\tau) d t \\ &=\lim _{k \rightarrow \infty} \frac{1}{k T_{0}} \int_{-\frac{k T_{0}}{2}}^{\frac{k T_{0}}{2}} x(t) x^{*}(t-\tau) d t \\ &=\lim _{k \rightarrow \infty} \frac{k}{k T_{0}} \int_{-\frac{T_{0}}{2}}^{\frac{T_{0}}{2}} x(t) x^{*}(t-\tau) d t \\ &=\frac{1}{T_{0}} \int_{-\frac{T_{0}}{2}}^{\frac{T_{0}}{2}} x(t) x^{*}(t-\tau) d t \end{aligned}$$

این رابطه می‌تواند تابع خودهمبستگی میانگین زمانی برای یک سیگنال متناوب را محاسبه کند. اگر بسط سری فوریه یک تابع متناوب را در فرمول بالا جایگذاری کنیم، به رابطه زیر می‌رسیم:

$$R_x(\tau) = \frac {1} {T} \int_{- \frac {T_0} {2}}^{\frac {T_0} {2}} \sum_{n = - \infty}^{\infty}\sum_{m = - \infty}^{\infty} \;x_n x_m^* e^{ j 2 \pi \frac {m} {T_0} \tau }\;e^{ j 2 \pi \frac {n-m} {T_0} t } dt$$

حال اگر از رابطه زیر استفاده کنیم:

$$\frac {1} {T_0} \int_{- \frac {T_0} {2}}^{\frac {T_0} {2}}e^{ j 2 \pi \frac {n-m} {T_0} t } dt = \delta _{m,n}$$

آن‌گاه به رابطه زیر می‌رسیم:

$$R_x(\tau) =\sum_{n = - \infty}^{\infty} |x_n|^ 2 e^{j 2 \pi \frac {n} {T_0} \tau}$$

با استفاده از این رابطه می‌توان به این نتیجه رسید که تابع خودهمبستگی میانگین زمانی مربوط به یک سیگنال متاوب، خود متناوب بوده و دوره تناوب آن نیز با دوره تناوب سیگنال اصلی برابر است و همچنین ضرایب سری فوریه آن، برابر با مجذور دامنه ضرایب سری فوریه سیگنال اصلی خواهند بود.

برای به دست آوردن چگالی طیف توان یک سیگنال، کافی است که تبدیل فوریه $$R_x(\tau)$$ را به دست آوریم. از آن‌جا که ما با یک تابع متناوب روبه‌رو هستیم، تبدیل فوریه از مجموعه‌ای از ضربه‌ها (Impulses) در حوزه فرکانس تشکیل شده است. این دقیقا همان چیزی است که از قبل انتظار آن را داشتیم؛ زیرا یک سیگنال متناوب، از مجموع سیگنال‌های سینوسی یا توابع نمایی تشکیل شده است و بنابراین توان در فرکانس‌های خاص گسسته‌ای (هارمونیک‌ها) متمرکز شده است. پس می‌توان گفت که چگالی طیف توان در یک سیگنال متناوب، توسط رابطه زیر داده می‌شود:

$$S_x(f) = \sum_{n = - \infty}^{\infty} |x_n|^ 2 \delta (f - \frac {n} {T_0})$$

برای به دست آوردن توان یک سیگنال متناوب، باید از رابطه بالا در تمام طیف فرکانسی انتگرال بگیریم. پس از انجام این کار، به رابطه زیر می‌رسیم:

$$P_x = \sum_{n = - \infty}^{\infty} |x_n|^ 2$$

این رابطه، رابطه رایلی (Rayleigh’s Relation) برای توابع متناوب نام دارد. اگر این تابع متناوب از یک سیستم LTI یا خطی نامتغیر با زمان عبور داده شود که پاسخ فرکانسی سیستم برابر با $$H(f)$$ باشد، آن‌گاه خروجی این سیستم نیز یک سیگنال متناوب خواهد بود. چگالی طیف توان سیگنال خروجی این سیستم را می‌توان با اعمال رابطه رایلی بین چگالی طیف توان سیگنال ورودی و خروجی یک فیلتر به دست آورد. بنابراین داریم:

$$S_y(f) = |H(f)|^2 \sum_{n = - \infty}^{\infty} |x_n|^ 2 \delta (f - \frac {n} {T_0}) \\ = \sum_{n = - \infty}^{\infty} |x_n|^ 2 |H(\frac {n} {T_0})|^2 \delta (f - \frac {n} {T_0})$$

در نتیجه مقدار توان سیگنال خروجی به صورت زیر به دست می‌آید:

$$P_y = \sum_{n = - \infty}^{\infty} |x_n|^ 2 |H(\frac {n} {T_0})|^2$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌های مهندسی برق
• آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎
• خواص تبدیل لاپلاس — به زبان ساده
• تبدیل فوریه (Fourier Transform) — به زبان ساده
• انتگرال فوریه — به زبان ساده

^^