امواج چیست؟ – به زبان ساده
هنگامی که در مورد کلمه موج میاندیشید ممکن است امواج دریا به ذهنتان خطور کند. با کمی دقت به اطرافتان امواج زیادی را مشاهده میکنید. ولی آیا واقعا با مفهوم امواج چیست آشنا هستند. به عنوان مثال، صوت نوعی موج است که از میان ماده حرکت میکند و پس از به ارتعاش درآوردن پرده گوش، فرد صدا را میشنود. نور نیز نوعی موج است که از فوتونها تشکیل شده است. هنگامی که سنگی را داخل نهر آبی میاندازید تشکیل امواج را داخل نهر میبینید. حتی از امواج برای پختن سریع غذا استفاده میکنید. در این مطلب به زبان ساده به مبحث امواج چیست با بیان جزییات مانند انواع موج، موجهای طولی و عرضی، تداخل امواج و معادله موج میپردازیم.


امواج چیست ؟
امواج همهجا هستند. ولی باید بدانیم به چه پدیدهای و با چه ویژگیهایی موج میگویند. به انتقال اختلال از مکانی به مکان دیگر در محیط، موج گفته میشود. این انتقال اختلال بدون انتقال ماده، انرژی را از نقطه اول (منبع) به نقطه دیگر منتقل میکند. هر نقطه در محیطِ انتقالدهنده موج به طور موقت جابجا میشود و سپس به موقعیت تعادلی اصلی خود بازمیگردد.
به عنوان مثال فنری را در نظر بگیرید که در حالت طبیعی خود قرار دارد. به این حالت طبیعی، موقعیت تعادلی گفته میشود که در آن حقلههای فنر به فاصله مساوی از یکدیگر قرار گرفتهاند. به منظور ایجاد موج در فنر، اولین حلقه از موقعیت تعادلی خود به سمت بالا، پایین، چپ یا راست جابجا میشود. حلقه پس از جایجایی از موقعیت تعادلی، به این مکان بازمیگردد. این جابجاییِ اولین حلقه از موقعیت تعادلی و بازگشت آن به این نقطه باعث ایجاد اختلال در فنر میشود. سپس اختلال ایجاد شده در سراسر فنر حرکت میکند.
موج چیست ؟
اگر به اولین حلقه فنر ارتعاش رفت و برگشتی بدهیم، به گسترش اختلال ایجاد شده در فنر، پالس فنر میگوییم. پالس، اختلالی است که در محیط از مکانی به مکان دیگر حرکت میکند. هنگامی که اولین حلقه فنر به طور متناوب و پیوسته به عقب و جلو ارتعاش کند، اختلال تکرار شوندهای در سراسر فنر برای مدت زمان مشخصی حرکت میکند. در نتیجه به جابجایی اختلال تکرار شونده و متناوب از نقطهای به نقطه دیگری در محیط موج گفته میشود.
در توضیحات بالا به جابجایی اختلال در محیط اشاره کردیم. برای درک پرسش امواج چیست باید با مفاهیمی مانند محیط و برهمکنش ذره با ذره آشنا شوید.
محیط چیست ؟
محیط مادهای است که موج را منتقل میکند. برای مثال در رابطه با فنر، محیط انتقالدهنده موج، حلقههای فنر است. برای موج آب در اقیانوس، محیط انتقالدهنده موج، آب اقیانوس است.
برهمکنش ذره با ذره
به منظور درک عمیق طبیعت امواج و پاسخ به سوال امواج چیست باید محیط انتقالدهنده موج را به صورت مجموعهای از ذرات در حال برهمکنش در نظر بگیریم. برهمکنش ذرهای از محیط با ذره کناری باعث انتقال اختلال میشود. برای فنر، برهمکنش ذرات در محیطِ حلقههای فنر هستند. در حالت امواج صوت در هوا، این ذرات، مولکولهای هوا خواهند بود.
انتقال موج در فنر را در نظر بگیرید. حلقه اول پس از مختل شدن سبب فشردن یا کشیدن حلقه دوم میشود. این فشار یا کشش در حلقه دوم آن را از موقعیت تعادلی جابجا میکند. حلقه دوم پس از جابجایی موجب کشیدن یا فشردن حلقه سوم میشود و آن را نیز از موقعیت تعادلی جابجا میکند. این روند به صورت متوالی ادامه مییابد. در نتیجه، اختلال در محیط منتقل میشود.
محیط انتقالدهنده موج را به صورت ذرات متصل شده توسط فنرها در نظر میگیریم. به هنگام حرکت یک ذره، فنری که آن را به ذره کناری وصل کرده است نیروی کششی به همسایه کناری وارد میکند. این همسایه شروع به حرکت میکند و به طور مشابه فنر متصل به آن نیرویی به همسایه کناری وارد خواهد کرد.

موج انرژی را منتقل میکند
به هنگام وجود موج در محیط ذرات محیط به طور موقت از مکان تعادلی جابجا میشوند. به هنگام جابجایی ذرات، همواره نیرویی آنها را به مکان اولیهشان بازمیگرداند. به این دلیل، امواج شامل حرکت اختلال هستند و در آنها مادهای منتقل نمیشود. از این روِ، در حالیکه ذرات محیط منتقل کننده موج در محدوده نقطه ثابتی ارتعاش میکنند الگوی اختلال (موج) از مکانی به مکان دیگر منتقل میشود.
امواج پدیده انتقال انرژی هستند. وقتی اختلال در محیط از ذرهای به ذره دیگر حرکت میکند انرژی از یک طرف محیط به طرف دیگر منتقل میشود. هنگام ایجاد اختلال در فنر، به اولین حلقه آن انرژی زیادی وارد میشود. این حلقه انرژی دریافتی را به حلقه دوم منتقل میکند. حلقه اول پس از بازگشت به مکان اولیهاش، دارای مقدار انرژی یکسان قبل از جابجایی است. حلقه دوم پس از دریافت انرژی، آن را به حلقه سوم منتقل میکند. روند انتقال انرژی به صورت برهمکنش هر حلقه با حلقه همسایه ادامه مییابد. در این حالت، انرژی از انتهای فنر به انتهای دیگر منتقل میشود.
موج و انواع آن
امواج در حالتها و شکلهای مختلفی وجود دارند. یک راه برای دستهبندی امواج، جهت حرکت ذرات محیط نسبت به جهت انتقال موج است. بر این اساس، امواج به سه دسته کلی زیر تقسیم میشوند.
- امواج عرضی
- امواج طولی
- امواج سطحی
امواج عرضی چیست ؟
در موج عرضی ذرات محیط در امتداد عمود بر جهت حرکت موج منتقل میشوند. امواح سطح آب یا امواج الکترومغناطیسی (مانند نور و امواج رادیویی) امواج عرضی هستند. تصویر زیر انتشار موج عرضی را از چپ به راست نشان میدهد. ذرات به سادگی به بالا و پایین در محدوده موقعیت تعادلی نوسان میکنند.
امواج طولی چیست ؟
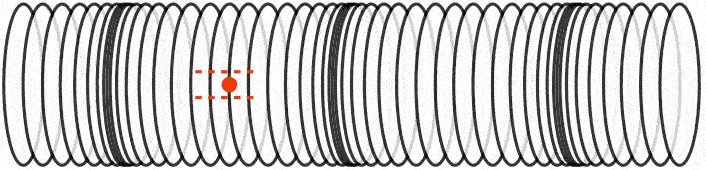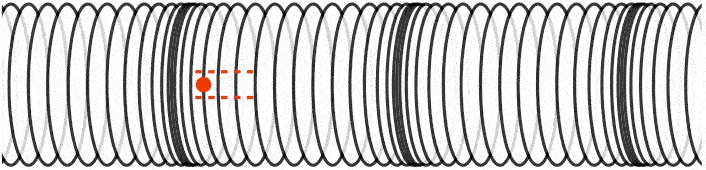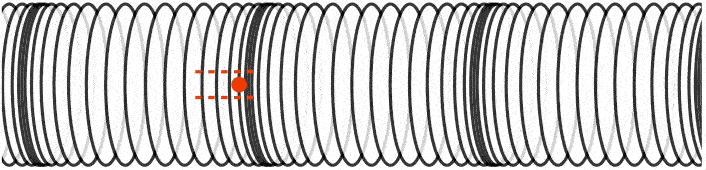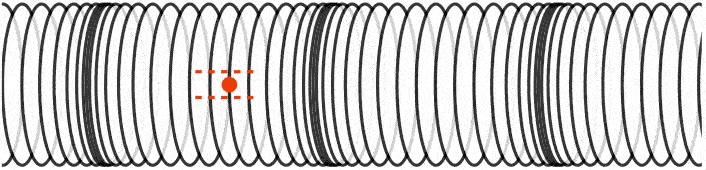
در موج طولی جابجایی «ذرات» (Particles) موازی با جهت انتشار «موج» (wave) است. تصویر زیر انتشار موج را در لوله نشان میدهد. ذرات به همراه موج به پایین لوله حرکت نمیکنند. بلکه هماگونه که مشاهده میشود آنها به جلو و عقب در محدوده نقطه تعادلی خود نوسان میکنند.

امواج منتقل شده در محیط جامد میتوانند به دو صورت امواج طولی یا امواج عرضی باشند. در حالیکه امواج منتقل شونده در سیالات (مانند گاز یا مایع) اغلب به صورت امواج طولی هستند.
امواج سطحی
در اعماق اقیانوسها امواج به صورت طولی منتقل میشوند. درحالیکه امواج منتقل شده در سطح آنها به عنوان امواج سطحی شناخته شدهاند. در یک موج سطحی ذرات محیط دارای حرکت دایرهای هستند. امواج سطحی، امواج طولی یا عرضی نیستند. در امواج سطحی تنها ذرات سطحی حرکت دایرهای انجام میدهند و با دور شدن از سطح، حرکت ذرات کاهش مییابد.
علاوه بر جهت حرکت ذرات محیط نسبت به جهت انتقال موج، توانایی یا عدم توانایی امواج در انتقال انرژی در محیط خلا نیز راه دیگری برای دستهبندی امواج است.
امواج الکترومغناطیسی
امواج الکترومغناطیسی قادر به انتقال انرژی در محیط خلأ هستند. این امواج از طریق نوسان ذرات باردار تولید میشوند. امواج الکترومغناطیسی تولید شده بر روی خورشید از طریق محیط خلأ خارج از جو به زمین منتقل میشوند.
امواج مکانیکی
موج مکانیکی قادر به انتقال انرژی در خلأ نیست. امواج مکانیکی برای انتقال انرژی از مکانی به مکان دیگر به محیط انتقال نیاز دارند. موج صوتی مثالی از موج مکانیکی است. امواج صوت در محیط خلأ منتقل نمیشوند.
پس از آشنایی با طبیعت موج و دستهبندی امواج، خواص امواج در ادامه توضیح داده میشود.
خواص امواج چیست ؟
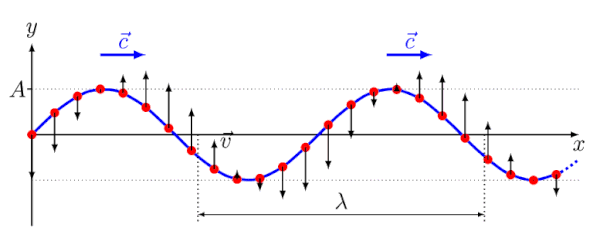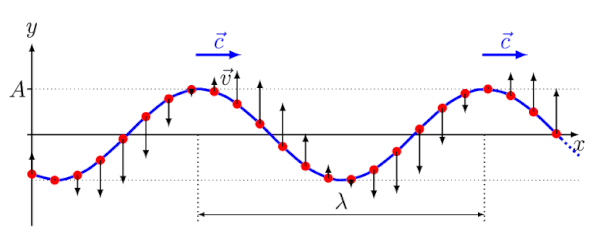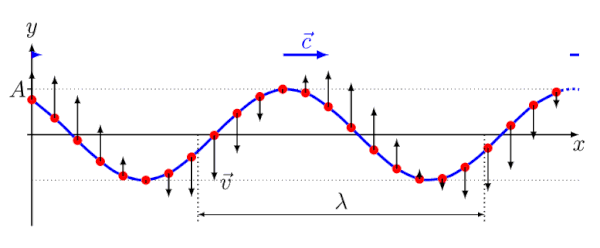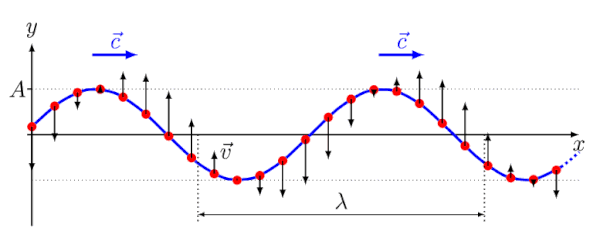
کشیدن طناب به صورت افقی و ارتعاش انتهای آن به سمت بالا و پایین باعث انتقال موج عرضی در طناب میشود. با گرفتن عکسی از طناب در زمان t، تصویر زیر را خواهیم داشت.
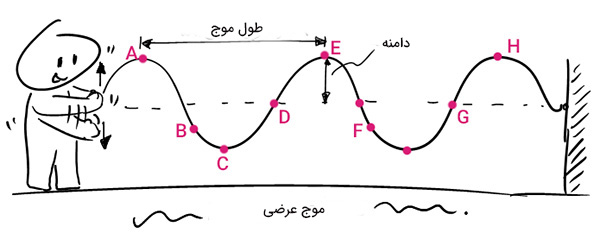
خط نقطهچین نشاندهنده موقعیت تعادلی طناب است. پس از ایجاد اختلال در طناب، ذرات طناب شروع به ارتعاش به سمت بالا و پایین میکنند. در هر زمان دلخواه ذره موجود در طناب ممکن است بالا یا پایین موقعیت تعادلی باشد. نقاط A و E و H در تصویر، نشاندهنده قلهها یا نقاط ماکزیمم این موج هستند. این نقاط مقدار ماکزیمم جابجایی را در جهت مثبت موقعیت تعادلی نشان میدهند. به نقطه C، نقطه مینیموم گفته میشود. این نقطه حداکثر جابجایی به سمت پایین و در جهت منفی نقطه تعادلی است.
موج نشان داده شده در تصویر بالا با چهار مشخصه اصلی زیر شناسایی میشود.
- دامنه
- طول موج
- فرکانس
- دوره تناوب
دامنه موج چیست ؟
به حداکثر جابجایی ذره محیط از نقطه تعادل، دامنه موج گفته میشود. در واقع دامنه فاصله نقطه تعادل از نقاط قله (ماکزیمم) یا فرورفتگی (مینیموم) است.
طول موج چیست ؟
طول موج در تصویر بالا نشان داده شده است. طول موج به زبان ساده به طول دوره کامل موج و شروع تکرار دوره بعدی گفته میشود. اگر انگشتتان را بر روی موج در تصویر بالا بگذارید و در امتداد آن حرکت کنید مسیر تکراری حرکت انگشت را خواهید دید. در واقع موج الگویی تکرار شونده است و رفتارش را در فضا و زمان تکرار میکند. طول موج میتواند فاصله یک قله از قله بعدی (فاصله A تا E) یا دره تا دره بعدی باشد.
تعریف فرکانس
فرض کنید هنگامی که حلقه اول فنر را در دست گرفتهاید در یک ثانیه، دو دوره کامل، آن را به عقب و جلو حرکت دهید. در این هنگام نرخ حرکت دست برابر ۲ دوره در یک ثانیه است. بدین شکل همه حلقهها با نرخ دو سیکل در ثانیه ارتعاش خواهند کرد. در نتیجه، فرکانس (frequency) موج برابر با تعداد ارتعاشات ذره به هنگام عبور موج از آن است. بُعد فرکانس «دوره بر ثانیه» یا «ارتعاش بر ثانیه» است که به آن هرتز (Hertz با Hz) گفته میشود.
دوره تناوب
در اغلب اوقات فرکانس با دوره تناوب (T) اشتباه گرفته میشود. دوره تناوب به مدت زمانی میگویند که در آن زمان، طرح موج تکرار میشود. فرکانس و دوره تناوب با اینکه دو مفهوم کاملا متفاوت هستند ولی به یکدیگر مربوط میشوند. به عنوان مثال، اگر دارکوبی هر ثانیه دو مرتبه به درختی ضربه بزند، فرکانس برابر ۲ هرتز خواهد بود. دوره تناوب آن نیز برابر با 0/5 ثانیه است. در نتیجه رابطه زیر بین فرکانس و دوره تناوب برقرار خواهد بود.
همانگونه که در بالا اشاره شد موج پدیدهای است که در آن انرژی در محیط بدون انتقال ماده منتقل میشود. برای ایجاد نوسان فنر یا طناب نیاز به وارد آوردن انرژی به آنها است. این انرژی در امتداد فنر یا طناب حرکت میکند و به انتهای آن میرسد. بنابراین اگر انتهای فنر یا طناب را در دست داشته باشید به محض رسیدن انرژی به انتها، آن را احساس میکنید. تا اینجا یاد گرفتیم که امواج چیست و در ادامه به انرژی موج و رابطه آن با دامنه نوسان میپردازیم.
انتقال انرژی و دامنه موج
مقدار انرژی حمل شده توسط موج با دامنه آن موج رابطه دارد. موج با انرژي بالا دامنه بزرگی خواهد داشت و برعکس این حالت، موج با انرژی پایین دامنه کوچکی دارد. رابطه میان دامنه و انرژی را میتوان با استفاده از مثال فنر نوسانی شرح داد.
با وارد آوردن پالس عرضی به فنر، نخستین حلقه آن به اندازه معینی جابجا میشود. این جابجایی به دلیل نیروی وارد شده از طرف شخص به حلقه به منظور جابجایی آن به اندازه معینی از نقطه تعادل است. هر اندازه فرد انرژی بیشتری به حلقه اول فنر وارد کند میزان کار بیشتری بر روی آن انجام میشود. از اینرو حلقه جابجایی بزرگتری نسبت به نقطه تعادل و در نتیجه دامنه بزرگتری خواهد داشت. بنابراین، دامنه موج عرضی با انرژی وارد شده نسبت مستقیم دارد. وارد آوردن مقدار زیاد انرژی بر طول موج، فرکانس یا سرعت موج تاثیر نخواهد داشت.
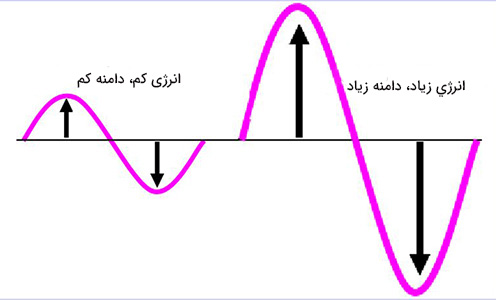
دو فنر یکسان را در نظر بگیرید که پالسی به هر دوی آنها وارد میشود. اگر میزان انرژی وارد شده به هر دو فنر یکسان باشد، هر پالس دارای دامنه یکسانی است. ولی هنگامی که دو فنر متفاوت باشند چه اتفاقی میافتد؟ اگر یکی از فنرها از فلز روی و دیگری از مس ساخته شده باشند آیا به هنگام نوسان دامنههای یکسانی خواهند داشت؟ اگر به دو فنر متفاوت پالسی با انرژی یکسان وارد کنیم، دامنه پالسها لزوما یکسان نخواهند بود. آیا میدانید وقتی انرژی یکسانی به دو فنر سبک و سنگین وارد کنید دامنه کدامیک بزرگتر خواهد بود؟
رابطه ریاضی بین انرژی و دامنه
انرژی منتقل شده توسط موج با مجذور دامنه موج رابطه مستقیم دارد.
رابطه بالا بدان معنا است که دو برابر شدن دامنه موج متناسب با چهار برابر شدن انرژی منتقل شده توسط آن است.
سرعت امواج چیست ؟
به هنگام تماشای امواج دریا مشاهده میکنید که قله موج در فاصله زمانی مشخصی از یک نقطه به نقطه دیگر حرکت میکند. با تعریف سرعت در حرکت بر روی خط راست آشنا شدید. برای موج، سرعت فاصلهای است که نقطه معینی از موج در فاصله زمانی مشخصی طی میکند. اگر قله موج اقیانوس فاصله ۲۰ متری را در مدت زمان ۱۰ ثانیه طی کند، آنگاه سرعت آن برابر خواهد بود.
گاهی موج به انتهای محیط انتقال میرسد یا از یک محیط به محیط دیگری میرود. به طور مثال، طنابی را در نظر بگیرید که یک سر آن در دست شما و سر دیگر آن به دیوار اتاق بسته شده است، موج پس از رسیدن به انتهای طناب و برخورد آن با دیوار منعکس میشود. موج به هنگام بازتاب، تغییر محیط نمیدهد و تنها جهت انتشارش برعکس میشود.
پدیده بازتاب به طور معمول برای امواج صوتی مشاهده میشود. به هنگام فریاد زدن در کوهستان بازتاب فریاد خود را میشنوید. امواج صوتی پس از انتقال در هوا و برخورد به کوه منعکس میشوند و به مبدا صدا بازمیگردند.
عوامل موثر بر سرعت امواج چیست ؟
فرض کنید با استفاده از مولد موج، در طنابی با کشش قابل اندازهگیری، امواج مختلفی ایجاد میکنید. طول موج، فرکانس و سرعت تعیین شدهاند. با تغییر فرکانس ارتعاش مولد، اثر فرکانس بر سرعت موج بررسی میشود. در پایان، با تغییر کشش طناب، اثر آن بر روی سرعت موج بررسی میشود. دادههای آزمایش در جدول زیر نشان داده شده است.
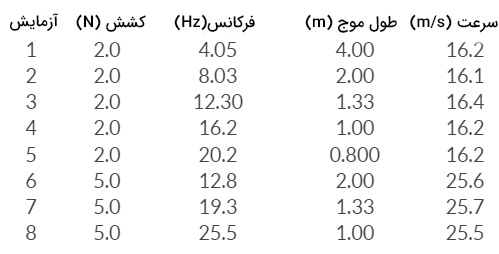
با ثابت نگه داشتن کشش نخ در پنج آزمایش، فرکانس به صورت سیستماتیک تغییر کرده است. طبق دادههای اندازیگیری شده در پنج آزمایش اول، تغییر در فرکانس، سرعت موج را تغییر نداده است و اندازه سرعت در محدوده تغییر بسیار جزئی میکند که ناشی از خطای آزمایش است. دادههای اندازیگیری شده نشان میدهند که فرکانس موج بر سرعت موج تاثیری ندارد. همچنین، افزایش فرکانس موج، سبب کاهش طول موج میشود.
سه آزمایش آخر روند یکسانی را نشان میدهند با این تفاوت که کشش نخ تغییر کرده است. با افزایش مقدار کشش نخ، سرعت موج نیز افزایش یافته است. در نتیجه، سرعت موج به ویژگیهای موج وابسته نیست بلکه مقدار آن به ویژگیهای محیط انتقال موج مانند کشش طناب بستگی دارد.
با توجه به ویژگیهای بیان شده در بالا معادله موج در حالت کلی به صورت زیر نوشته میشود.
در ادامه معادلات ریاضی حاکم بر موج سینوسی یکبعدی را به دست میآوریم.
معادله موج سینوسی یک بعدی در امواج چیست ؟
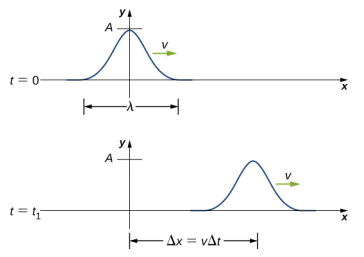
در تصویر زیر انتشار پالسی در دو زمان صفر و نشان داده شده است. در زمان صفر، پالس با دامنه A در مکان x=0 قرار دارد.
پالس بدون تغییر شکل با سرعت ثابت v به اندازه در فاصله زمانی حرکت میکند. فاصله طی شده میتواند با دنبال کردن هر نقطه دلخواهی بر روی پالس اندازه گرفته شود.
طنابی با کشش با یک انتهای ثابت، از سمت انتهای آزاد بین y=+A و y=-A با فرکانس ثابتی نوسان میکند. شکل زیر عکسهای مختلف را از نوسان طناب با فاصله زمانی یکهشتم () دوره تناوب نشان میدهد.
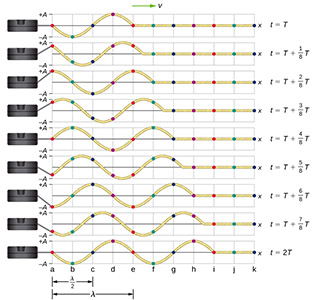
توجه به این نکته مهم است که هر نقطه رنگی روی طناب با حرکت هارمونیک ساده به سمت بالا و پایین بین y=+A و y=-A با دوره تناوب T نوسان میکند. موج منتشر شده در طناب سینوسی است و در جهت مثبت محور x منتشر میشود. هدف ما در این بخش به دست آوردن معادله موج است که برای هر مکان x و زمان t موقعیت y هر بخش از طناب به دست بیاید.
با نگاه کردن به تصویر طناب در زمان T، موقعیت y طناب بین x=0 و میتواند به صورت تابع سینوسی مدلسازی شود. این موج در امتداد طناب به اندازه یک طول موج در یک دوره تناوب حرکت میکند. بنابراین، موج با سرعت ثابت حرکت میکند.
از مثلثات به یاد داریم که تابع سینوسی بین دو مقدار 1- تا 1+ نوسان میکند و هر رادیان تکرار میشود. در این حالت موقعیت تابع موج بین بین y=+A و y=-A نوسان میکند و پس از هر طول موج تکرار میشود.
برای نوشتن تابع موج، نسبت زاویه و موقعیت را به صورت زیر در نظر بگیرید.
با استفاده از و ضرب تابع سینوس در دامنه میتوانیم موقعیت مکانی y طناب را بر حست تابعی از x به دست آوریم.
موج در طناب در جهت مثبت محور x با سرعت ثابت v منتقل میشود. پس از گذشت زمان t این موج به اندازه vt جابجا شده است. در نتیجه تابع موج میتواند به صورت زیر نوشته شود.
در اغلب مواقع نوشتن تابع موج به صورت فشردهتر استفاده از آن را راحتتر میکند.
مقدار به عنوان عدد موج (k) تعریف میشود. همچنین فرکانس زاویهای نیز به صورت بیان میشود. بنابراین عبارت دوم در معادله بالا به صورت زیر نوشته میشود.
در نتیجه معادله موج برای موج سینوسی ساده در طناب به عبارت زیر ساده میشود.
علامت منفی و مثبت به ترتیب برای موج پیشرو در جهت مثبت محور x و جهت منفی محور x است. سرعت موج نیز به صورت زیر بیان میشود.
معادله موج سینوسی با تغییر فاز
اکنون جرمی بر روی طناب با موقعیت در نظر بگیرید. در این عبارت، تغییر فاز است. اضافه شدن به عبارت به دلیل در نظر گرفتن شرایط اولیه جرم است. بنا به دلایل مشابه فاز اولیه به تابع موج اضافه میشود. از اینرو تابع موج سینوسی با تغییر فاز اولیه به صورت زیر نوشته میشود.
که مقدار فاز موج گفته میشود.
مثال معادله موج سینوسی
موج عرضی در طنابی کشیده به صورت زیر است
مقادیر دامنه، طول موج، دوره تناوب و سرعت موج را به دست آورید.
پاسخ
۱. دامنه، عدد موج و فرکانس زاویهای از معادله داده شده به طور مستقیم به دست میآید.
2. برای به دست آوردن طول موج از عدد موج استفاده میشود.
3. با استفاده از فرکانس زاویهای دوره تناوب به دست میآید.
4. با استفاده از مقادیر عدد موج و فرکانس زاویهای سرعت موج به دست میآید. جهت انتشار موج با علامت عبارت تعیین میشود. علامت منفی نشاندهنده انتشار موج در جهت مثبت محور xها است.
پس از آشنایی با ویژگیهای موج و به دست آوردن معادله موج سینوسی در یک بعد به رفتار مرزی امواج میپردازیم.
رفتار مرزی امواج چیست ؟
موج به هنگام انتشار میتواند به انتهای محیط انتشار برسد یا به مانع برخورد کند. آیا بازتاب موج بر سرعت انتشار ، طول موج، دامنه، فرکانس و دیگر ویژگیهای آن تاثیر میگذارد؟
بازتاب موج از نقطه ثابت
طناب کشسانی را در نظر بگیرید که یک انتهای آن به میلهای ثابت شده است. موج در طناب منتشر میشود. پس از برخورد موج به میله دو حالت اتفاق میفتد.
- قسمتی از انرژی موج منعکس میشود.
- قسمتی از انرژی به میله منتقل میشود و سبب نوسان آن خواهد شد.
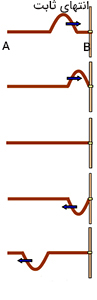
همانطور که در تصویر بالا مشاهده میکنید موج منعکس شده از انتهای ثابت، نسبت به محور افق قرینه میشود. هنگامی که قله به انتهای محیط A میرسد، آخرین ذره از محیط A به سمت بالا جابجا میشود. این ذره به اولین ذره محیط B (میله) وصل شده است. طبق قانون سوم نیوتن هنگامی که آخرین ذره محیط A اولین ذره محیط B را به سمت بالا میکشد، اولین ذره محیط B آخرین ذره محیط A را به سمت پایین میکشد. در نتیجه، اثر کشش رو به پایین بر آخرین ذره محیط A، بر دیگر ذرات این محیط اثر میگذارد. بنابراین، موج به صورت قرینه بازتاب مییابد. موج بازتاب یافته دارای مشخصات زیر است.
- سرعت آن با موج فرودی یکسان است.
- طول موج آن با طول موج موج فرودی برابر است.
- دامنه آن کمتر از دامنه موج فرودی است.
بازتاب موج از نقطه آزاد
اکنون حالتی را در نظر بگیرید که انتهای طناب به حلقه متصل به میلهای وصل شده است و آزادانه حرکت میکند.
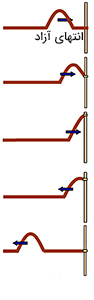
همانطور که در تصویر مشاهده میکنید موج پس از رسیدن به نقطه آزاد بدون تغییر جهت انتشار، منعکس میشود.
انتقال موج از محیط با چگالی کمتر به محیط با چگالی بیشتر
طناب نازکی را در نظر بگیرید که به طناب ضخیمی متصل شده است. در این هنگام موجی در طناب نازک ایجاد و منتشر میشود. به هنگام رسیدن موج به مرز طنابها قسمتی از آن منعکس میشود و قسمت دیگر به طناب ضخیم منتقل خواهد شد.
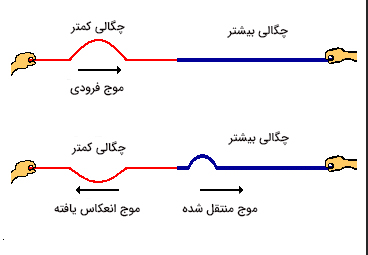
مطابق با تصویر بالا دیده میشود موج منتقل شده در همان جهت موج فرودی حرکت میکند. ولی موج منعکس شده مانند حالت بازتاب از انتهای ثابت قرینه شده است. همچنین برای امواج بازتابی و انتقالی اتفاقات زیر رخ میدهد.
- موج انتقالی (در محیط با چگالی بیشتر) با سرعت کمتری نسبت به موج بازتابی (در محیط با چگالی کمتر) حرکت میکند.
- موج انتقالی طول موج کوتاهتری نسبت به موج منعکس شده دارد.
- طول موج و سرعت موج منعکس شده با طول موج و سرعت موج فرودی برابر است.
انتقال موج از محیط با چگالی بیشتر به محیط با چگالی کمتر
طناب ضخیمی را در نظر بگیرید که به طناب نازکی متصل شده است. قسمتی از موج ایجاد شده در طناب ضخیم پس از رسیدن به مرز دو طناب، به طناب نازک منتقل میشود و قسمت دیگر از مرز دو طناب بازتاب مییابد. همانگونه که در تصویر زیر مشاهده میشود جهت موج بازتاب یافته، همانند بازتاب موج از انتهای آزاد، تغییر نمیکند.
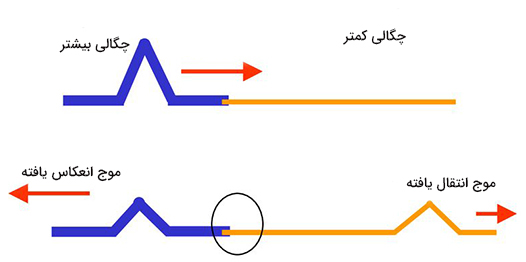
براساس مشاهدات صورت گرفته برای امواج انتقالی و بازتابی نتایج زیر به دست میآید.
- موج انتقال یافته (در محیط با چگالی کمتر) نسبت به موج بازتاب یافته (در محیط با چگالی بیشتر) با سرعت بیشتری حرکت میکند.
- موج انتقال یافته نسبت به موج منعکس شده دارای طول موج بزرگتری است.
- طول موج و سرعت موج بازتاب یافته برابر با طول موج و سرعت موج فرودی است.
با توجه به توضیحات بالا، رفتار مرزی موجها به صورت زیر خلاصه میشود.
- سرعت موج در محیط با چگالی کمتر، بیشتر است.
- طول موج همواره در محیط با چگالی کمتر، بیشتر است.
- فرکانس موج پس از عبور از مرز تغییر نمیکند.
- موج بازتاب یافته به هنگام بازتاب از محیط با چگالی بیشتر قرینه میشود.
- دامنه موج فرودی همواره از دامنه موج بازتاب شده بیشتر است.
رفتار امواج در محیطهای با ابعاد بالاتر
همانطور که در توضیحات بالا اشاره شد، قسمتی از امواج هنگام رسیدن به مرز دو محیط منتقل میشوند و قسمتی نیز بازتاب مییابند. حال این سوال مطرح میشود که موج به هنگام انتقال در محیطی دوبعدی مانند اقیانوس یا محیطی سهبعدی مانند نور چگونه رفتار میکند. در ادامه به رفتار امواج در محیطهای دوبعدی و سهبعدی میپردازیم.
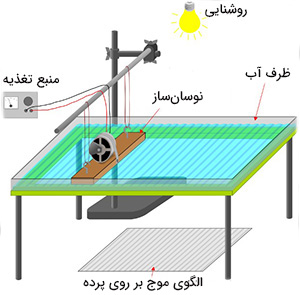
بازتاب امواج چیست ؟
تصویر زیر دستگاهی را نشان میدهد که در آن به وسیله نوسانساز، امواج مستقیمی بر روی سطح آب ایجاد میشود. این امواج مستقیم، دارای قلهها و درههایی هستند که به ترتیب به صورت خطوط تاریک و روشن بر روی صفحه زیر ظرف آب مشاهده میشوند.
امواج ایجاد شده روی سطح آب پس از برخورد به مانعی که با دیواره ظرف آب زاویه ساخته است به صورت زیر منعکس میشوند.
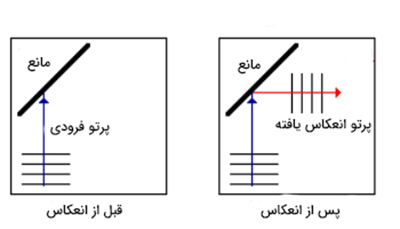
مستقل از زاویه موج فرودی، امواج به گونهای منعکس میشوند که زاویه فرود برابر با زاویه بازتاب باشد. این قانون به قانون بازتاب معروف است. این قانون در بازتاب از صفحه تخت مشاهده میشود. به هنگام بازتاب از سطحی دایرهای یا سهمیشکل چه اتفاقی میافتد؟ به هنگام بازتاب از این سطوح، امواج منعکس شده پس از تغییر جهت در یک نقطه به یکدیگر میرسند. به عبارت دیگر تمام انرژی انتقال یافته توسط امواج، در در یک نقطه موسوم به نقطه کانونی جمع میشوند. پس از گذر از نقطه کانونی، امواج در سطح آب پخش خواهد شد.
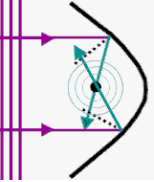
انکسار امواج چیست ؟
بازتاب به معنای تغییر جهت امواج به هنگام انعکاس از مانع است. به تغییر جهت امواج در زمان عبور از محیطی به محیط دیگر انکسار میگویند. انکسار با تغییر طول موج و سرعت امواج به هنگام عبور از دو محیط همراه است. سرعت امواج به عمق آب بستگی دارد و با عمیقتر شدن سطح آب، امواج سریعتر حرکت میکنند. در نتیجه به هنگام عبور از سطوح عمیقتر به سطوح کمعمقتر، امواج آب با سرعت کمتری حرکت میکنند.
پراش امواج چیست ؟
پراش امواج به هنگام عبور از حفره یا در اطراف مانع اتفاق میافتد. با قرار دادن مانعهای کوچک در ظرف آب مشاهده میشود که امواج آب پس از برخورد با این موانع با تغییر مسیر از آنها عبور میکنند. اگر اندازه طول موج از مانع کوچکتر باشد پراش قابل ملاحظهای رخ نمیدهد. پراش امواج صوت از موانع موجب شنیدن صحبت افراد در اتاق کناری میشود.
پس از توضیحات در مورد رفتار مرزی امواج، به مبحث تداخل یا برهمنهی امواج میپردازیم.
تداخل امواج چیست ؟
به هنگام عبور دو موج در یک محیط تداخل اتفاق میافتد. دو موج سینوسی را با دامنه یکسان A در نظر بگیرید که در جهتهای مختلف در یک محیط حرکت میکنند.
به هنگام رسیدن این دو موج به یکدیگر و همپوشانی کامل آنها با هم، موج حاصل موجی سینوسی با دامنه 2A خواهد بود. به این پدیده «تداخل سازنده» (Constructive Interference) گفته میشود.
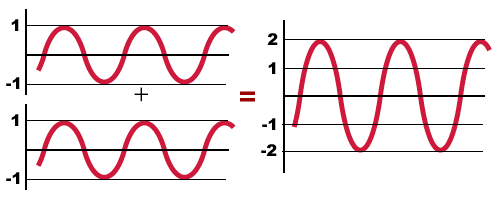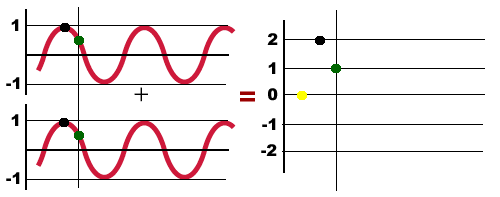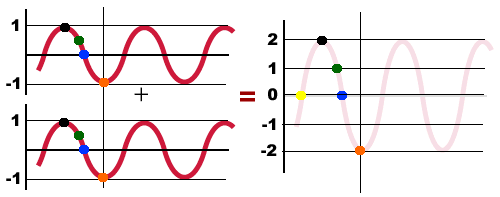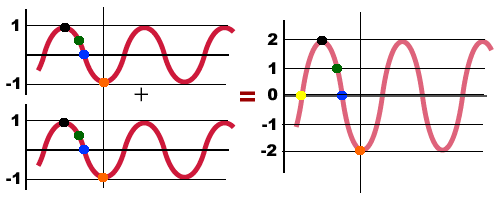
هنگامی که دو موج در جهتهای مخالف یکدیگر در یک محیط حرکت کنند تداخل ویرانگر رخ میدهد. به طور مثال، به هنگام همپوشانی کامل دو موج سینوسی با دامنه A، دامنه موج حاصل صفر میشود.

ذکر این نکته مهم است که به هنگام تداخل دو موج دامنه آنها همیشه یکسان نیست یا همفاز با یکدیگر حرکت نمیکنند.
اکنون دو منبع موج را در نظر بگیرید. منبع دوl را به اندازه یک طول موج نسبت به منبع یکم جلو میبریم. از اینرو منبع موج ۱ نسبت به منبع موج ۲ باید به اندازه یک طول موج بیشتر حرکت کند تا به آشکارساز برسد. اکنون این دو موج نسبت به یکدیگر همفاز هستند و تداخل سازنده اتفاق میافتد.
ولی این تنها حالتی نیست که رخ میدهد. اگر منبع موج ۲ را به اندازه دو طول موج نسبت به منبع موج ۱ جلوتر ببریم باز هم تداخل سازنده رخ میدهد. در واقع تا هنگامی که به اندازه مضرب صحیح و مثبتی از طول موج () منبع موج ۲ را به جلو حرکت دهیم تداخل سازنده اتفاق میافتد. اکنون به دنبال فرمولبندی نتیجه بهدستآمده هستیم.
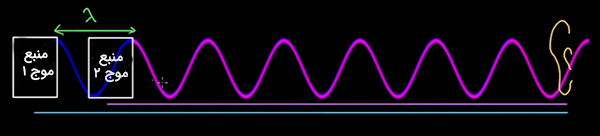
اگر فاصله منبع موج ۱ ومنبع موج ۲ از آشکار ساز به ترتیب برابر و باشد هنگامی که اختلاف این دو منبع به صورت زیر باشد تداخل سازنده رخ میدهد.
حال این سوال پیش میآید که به هنگام تداخل ویرانگر چه اتفاقی میافتد. منبع موج ۲ را چه اندازه نسبت به منبع موج ۱ جلوتر بیاوریم تا امواج اثر یکدیگر را از بین ببرند؟ همانگونه که در تصویر مشاهده میشود اگر منبع موج ۲ را به اندازه نسبت به منبع موج ۱ جابجا کنیم تداخل ویرانگر رخ میدهد.
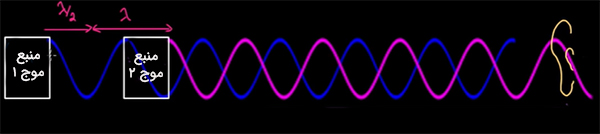
در نتیجه به منظور داشتن تداخل ویرانگر، فاصله دو منبع موج باید به صورت زیر نوشته شود.
دو معادله بالا برای حالتی به دست آمد که دو موج همفاز بودند. حال حالتی را در نظر میگیریم که دو موج به اندازه زاویه نسبت به یکدیگر اختلاف فاز داشته باشند. در این حالت وقتی فاصله دو منبع موج صفر است، تداخل ویرانگر اتفاق میافتد. هنگامی که به اندازه یک طول موج منبع ۲ را جلوتر میبریم باز هم دو موج با یکدیگر تداخل ویرانگر دارند. در نتیجه برعکس حالت دو موج همفاز، در این حالت هنگامی که فاصله دو منبع مضرب صحیحی از طول باشد تداخل ویرانگر اتفاق میافتد. برای تداخل سازنده نیز فاصله دو منبع باید مضرب صحیحی از نصف طول موج باشد.
شکاف یانگ در
شکاف یانگ یکی از مثالهای بسیار مهم در تداخل امواج است. برای آشنایی بیشتر با این آزمایش در اینجا به حل مثالی در این زمینه اکتفا میکنیم.
مثال شکاف یانگ
نوری با طول موج 700 نانومتر به دو شکاف که اندازه هر کدام 200 نانومتر است و به فاصله 1300 نانومتر از هم قرار گرفتهاند میتابد. اگر پردهای به فاصله ۳ متر از دو شکاف قرار بگیرد، فاصله نقطه روشن مرکزی بر روی پرده از نقطه روشن بعدی چقدر است؟
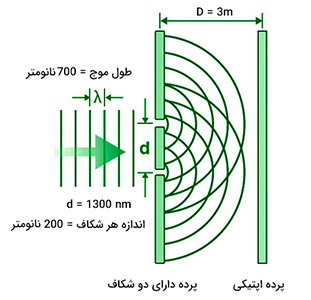
پاسخ
طبق معادله به دست آمده برای آزمایش یانگ داریم.
در رابطه بالا d فاصله دو شکاف و برابر با 1300 نانومتر است. زاویه در شکل زیر نشان داده شده است.
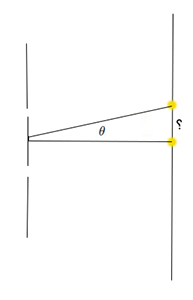
با قرار دادن m = ۱ و مقادیر داده شده برای d و در معادله بالا داریم.
حال برای به دست آوردن فاصله بین دو نقطه روشن مجاور داریم.
در نتیجه فاصله نقطه روشن مرکزی از نقطه روشن کناری برابر 1/92 متر است. در این سوال فاصله دو شکاف برابر 200 متر داده شد ولی جایی در محاسبات از آن استفاده نکردیم. فاصله دو شکاف تنها در این مورد استفاده میشود که بدانیم فاصله به اندازهای کوچک است که پراش به اندازه کافی داشته باشیم.
در آزمایش دو شکاف یانگ گاهی یافتن نقطههای روشن و اندازهگیری فاصله بین آنها بسیار سخت است. آیا راه حلی برای حل این مشکل وجود دارد؟ بله، با ایجاد شکافهای بیشتر میتوان این مشکل را حل کرد. به طور مثال میتوان هزاران شکاف با فاصله یکسان d از یکدیگر درست کرد. پس از عبور نور از این شکافها، بر روی پرده اپتیکی به جای الگوهای پراش، نقاط روشنی را مشاهده میکنیم.

اثر دوپلر
فرض کنید حشره خوشحالی در استخر آبی قرار دارد و به صورت متناوب پاهای خود را برای شنا کردن حرکت میدهد و اختلالی را بر سطح آب ایجاد میکند. الگوی ایجاد شده توسط حشره، دایرههای هممرکزی هستند که در همه جهتها حرکت میکنند. حال دو ناظر A و B را در نظر بگیرید. ناظر A مشاهده میکند امواجی که از سمت حشره میآیند با فرکانس f به لبه استخر برخورد میکنند. همچنین فرد B نیز امواج را با فرکانس مشابهی میبیند.
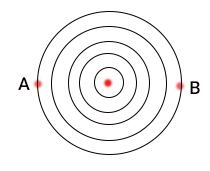
حال حالتی را در نظر بگیرید که حشره به هنگام ایجاد اختلال به سمت راست استخر حرکت میکند و امواجی با فرکانس مشابه حالت قبل ایجاد میکند. در این حالت اختلال دایرهای ایجاد شده از نقطهای میآید که به ناظر B نسبت به ناظر A نزدیکتر است. در نتیجه این امواج دایرهای در مدت زمان کمتری به ناظر میرسند. از این رو، فرد B مشاهده میکند که امواج با فرکانس بزرگتری نسبت به فرکانس امواج ایجاد شده به او میرسند. برعکس این حالت، فرد A امواج را با فرکانس کمتری نسبت به فرکانس امواج اولیه دریافت میکند.
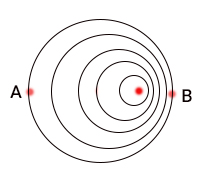
از مباحث بالا به این نتیجه میرسیم فردی که حشره به سمت او حرکت میکند فرکانس بزرگتر و فردی که حشره از او دور میشود فرکانس کمتری را نسبت به موج اولیه مشاهده میکند. این اثر به اثر دوپلر معروف است.
برای آشنایی بیشتر با معادلات اثر دوپلر، مطالعه مطلب زیر پیشنهاد میشود.
مثال اثر دوپلر
ماشین آتشنشانی با سرعت به سمت دوندهای در حرکت است. دونده نیز با سرعت به سمت ماشین آتشنشانی در حال دویدن است. اگر فرکانس آژیر 1000 هرتز باشد، دونده آن را با چه فرکانسی دریافت میکند؟ (سرعت صوت را در نظر بگیرید).
پاسخ
به منظور حل این مساله از فرمول دوپلر استفاده میکنیم.
عبارات داده شده در فرمول بالا به صورت زیر است.
- سرعت ناظر است.
- سرعت منبع موج است.
توجه به این نکته لازم است که به هنگام نزدیک شدن ناظر و منبع موج به یکدیگر فرکانس افزایش مییابد. بنابراین، علامت مثبت در صورت کسر و علامت منفی در مخرج کسر استفاده میشوند. در مثال بالا میبینیم که منبع موج یعنی ماشین آتشنشانی با سرعت حرکت میکند و دونده که ناظر است با سرعت حرکت میکند. با قرار دادن مقادیر فوق در معادله بالا داریم.
در نتیجه دونده آژیر را با فرکانس 1166 هرتز میشنود.
مثال دوم اثر دوپلر
دوچرخهسواری به هنگام نزدیک شدن به دیوار متوجه میشود فرکانس بوق دوچرخهاش پس از بازتاب از دیوار از مقدار 440 هرتز به مقدار 480 هرتز تغییر میکند. اگر سرعت صوت برابر باشد، سرعت دوچرخهسوار را بیابید.
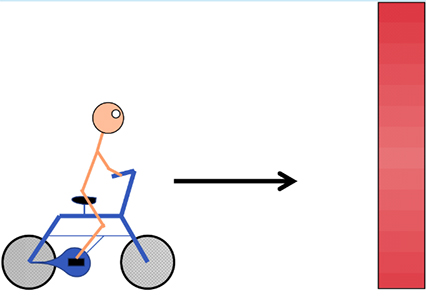
پاسخ
فرض کنید دوچرخهسوار با سرعت به دیوار نزدیک میشود. از اینرو فرکانس ظاهری دریافتی توسط دیوار به صورت زیر محاسبه میشود.
رابطه (۱):
رابطه (۲) برای موج بازتاب یافته به صورت زیر است.
با قرار دادن معادله ۱ در معادله ۲، خواهیم داشت.
پس از ساده سازی رابطه زیر به دست میآید.
با جایگزین کردن مقادیر داده شده در مثال، سرعت دوچرخه سوار به دست میآید.
کاربرد اثر دوپلر
افراد بسیاری فکر میکنند که اثر دوپلر فقط برای امواج صوت کاربرد دارد. در حالیکه این اثر برای تمامی امواج از جمله نور کاربرد دارد. در زیر کاربردهایی از اثر دوپلر را مشاهده میکنید.
- آژیرها
- رادار
- نجوم
- تصویربرداری پزشکی
- اندازهگیری جریان خون
- ارتباطات ماهوارهای
- اندازهگیری ارتعاش
- توسعه زیستشناسی
امواج ایستاده
در مطالب بالا به این نکته اشاره شد که موج مکانیکی اختلالی است که توسط یک جسم مرتعش به وجود میآید و انرژی را در محیط از یک نقطه به نقطه دیگر منتقل میکند. به این موج گاهی موج رونده نیز گفته میشود. اگر به طناب کشسانی با طول ۳ متر موجی وارد شود، این موج در ناحیه کوچکی محبوس میشود. موج به سرعت به انتهای طناب میرسد و پس از بازتاب در جهت مخالف شروع به حرکت میکند. قسمتی از موج بازتابی با قسمتی از موج فرودی تداخل خواهد کرد و به سمت نقاط ثابت پیش میرود.
گره و شکم در امواج چیست ؟
این تداخل شکل جدیدی ایجاد میکند که با شکل موج سینوسی بسیار متفاوت است. به این موج، موج ایستاده میگویند. امواج ایستاده دارای نقاطی هستند که اختلال موج در آنها بسیار کوچک و حتی صفر است. به این نقاط گره گفته میشود. همچنین نقاطی وجود دارند که اختلال بسیار قوی است که به آنها شکم میگویند.
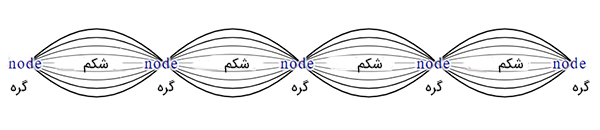
سیم گیتار، طبل، هوای داخل اتاق، آب دریاچه یا سطح زمین مثالهایی از امواج ایستاده هستند. امواج ایستاده تحت هر شرایطی ایجاد نمیشوند. اگر هنگامی که فرکانس پیشرو به سیستمی اعمال میشود، با فرکانس طبیعی آن برابر باشد شرط تولید موج ایستاده برآورده میشود. به این شرط، تشدید گفته میشود.
هر سیستمی که امواج ایستاده در آن شکل میگیرد دارای فرکانسهای طبیعی زیادی است. مجموعه تمام امواج ایستاده ممکن، به عنوان هارمونیک سیستم شناخته میشوند. سادهترین هارمونیک، هارمونیک اول یا اصلی نام دارد. در تئوری موسیقی به هارمونیکهای بالاتر از هارمونیک اول نت همساز میگویند.
امواج ایستاده در یکبعد: دو نقطه ثابت
اگر محیطی در دو انتها ثابت باشد، به این دو نقطه گره گفته میشود. سادهترین موج ایستادهای که میتواند در این محیط ایجاد شود دارای یک شکم در وسط است. به منظور ساختن موج ایستاده بعدی، گرهای را در مرکز قرار میدهیم. برای موج ایستاده سوم، با اضافه کردن گرهای دیگر محیط را به سه قسمت تقسیم میکنیم. این کار به ما طول میدهد. در نتیجه به منظور ایجاد امواج ایستاده بعدی باید گرههای بیشتری اضافه کنیم و محیط را به چهار، پنج، شش قسمت و بیشتر تقسیم کنیم. این سیستم، هارمونیکهای بیشماری دارد. ذکر این نکته مهم است که طول سیستم همواره ضریب صحیحی از نصف طول موج است.
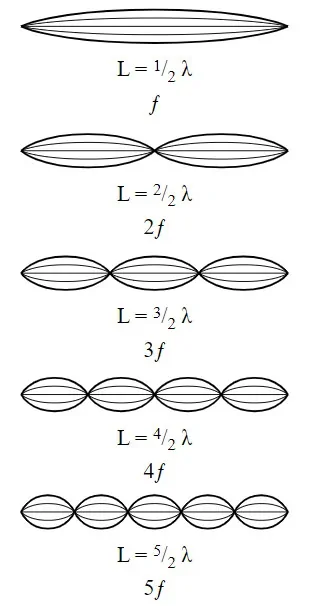
طول موجهای هارمونیکهای مختلف کسر سادهای از طول موج بنیادی است. به جدول زیر دقت کنید.
| طول موج-مقدار | فرکانس | مقدار فرکانس-هرتز |
| طول موج بنیادی = یک متر | فرکانس بنیادی | ۱ |
| هارمونیک دوم = | هارمونیک دوم | ۲ |
| هارمونیک سوم = | هارمونیک سوم | ۳ |
| هارمونیک چهارم = | هارمونیک چهارم | ۴ |
امواج ایستاده در یکبعد: دو نقطه آزاد
اگر محیطی در دو انتها آزاد باشد، به این دو نقطه، شکم گفته میشود. سادهترین موج ایستادهای که در این حالت تشکیل میشود دارای یک گره در وسط است. این موج ایستاده نصف طول موج خواهد بود. به منظور ساختن موج ایستاده بعدی، یک شکم در مرکز قرار میدهیم. در این هنگام موج ایستاده یک طول موج است. برای ساختن سومین موج ایستاده طول L را با اضافه کردن یک شکم دیگر یه سه قسمت تقسیم میکنیم. برای این حالت طول برابر خواهد شد. با مقایسه دو انتهای آزاد با حالتی که دو انتهای محیط ثابت بودند به روابط یکسانی برای امواج ایستاده خواهیم رسید. تنها تفاوت این دو حالت آن است که شکمها با گرهها و برعکس جایگزین شدهاند.
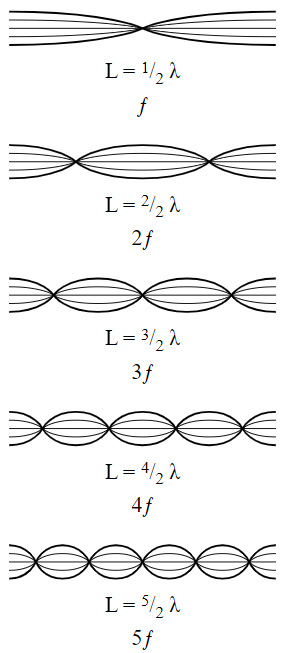
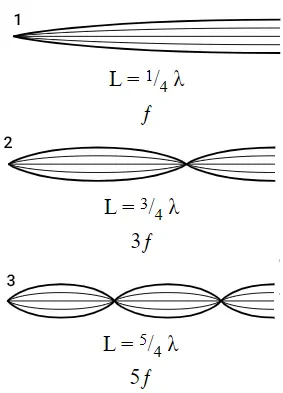
امواج ایستاده در یکبعد: یک نقطه ثابت و یک نقطه آزاد
در این حالت، یک گره در انتهای ثابت و یک شکم در انتهای آزاد تشکیل میشود. سادهترین موج ایستادهای که میتواند تحت این شرایط تشکیل شود یکچهارم طول موج است (تصویر شماره ۱). برای درست کردن موج ایستاده بعدی یک گره و یک شکم اضافه میکنیم (تصویر شماره ۲). در این حالت سهچهارم یک طول موج را داریم. با تکرار روند بالا پنجچهارم یک طول موج را خواهیم داشت (تصویر شماره ۳). از اینرو، طول موجهای هارمونیک همیشه کسری از طول موج بنیادی و مخرج کسر اعداد فرد هستند. به طور مشابه، فرکانسهای هارمونیکها همواره ضریب فردی از فرکانس بنیادی خواهند بود.
امواج ایستاده در دو بعد
توصیف امواج ایستاده در ابعاد بالاتر کمی پیچیدهتر است. امواج ایستاده در دو بعد کاربردهای بسیاری در موسیقی خواهند داشت. درامز سیستم سادهای است که امواج ایستاده بر روی آن مطالعه میشود. برخلاف گیتار و پیانو که دارای گره در دو انتهای مخالف هستند، تمام لبه طبل یک گره محسوب میشود. گرههای دیگر خطوط مستقیم و دایرهها هستند. همچنین فرکانسهای هارمونیک مضرب سادهای از فرکانس بنیادی نیستند.
امواج ایستاده در سه بعد
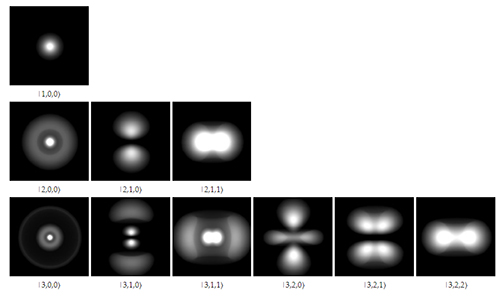
در یکبعد گرهها نقاط صفربعدی هستند. در دوبعد گرهها نمودارهای یکبعدی هستند. ابعاد گرهها همواره از بعد سیستم یک واحد کمتر است. بنابراین در سه بعد گرهها صفحات دوبعدی به شمار میآیند. مهمترین مثال امواج ایستاده در سهبعد اوربیتالهای الکترونی در اتم است. در مقیاس اتمی، توصیف الکترون به عنوان موج بسیار مناسبتر از توصیف آن به عنوان ذره است. مربع تابع موج الکترون، تابع احتمال حضور الکترون را در یک مکان خاص میدهد.
اوربیتالها توصیفکننده شکل ناحیهای هستند که احتمال حضور الکترون در آنجا بسیار بالا است. الکترونها به فضای دور هسته محدود شدهاند. این حالت بسیار شبیه امواج ایستاده در سیم گیتار است. محدودیت سیم در گیتار باعث نوسان سیم با فرکانسهای خاصی میشود. به طور مشابه، الکترون فقط با فرکانسهای خاصی نوسان میکند. تصویر زیر چگالی احتمال الکترونها را در اتم هیدروژن را نشان میدهد.
معرفی فیلم آموزش امواج و ارتعاشات
مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش امواج و ارتعاشات برای دانشجویان رشته فیزیک و فنی مهندسی کرده که این مجموعه آموزشی از شش درس تشکیل شده است.
درس یکم در مورد حرکت نوسانی ساده و و معادلههای حاکم بر این حرکتها است. با معادله موج در یک بعد و امواج طولی و عرضی در درس دوم آشنا میشوید. همچنین، برای آشنایی بیشتر با تداخل امواج و آزمایش یانگ میتوانید به درس چهارم مراجعه کنید.
- برای دیدن فیلم آموزش امواج و ارتعاشات + اینجا کلیک کنید.
مثال دیگری از امواج ایستاده
مبحث امواج چیست را با حل یک مثال در مورد امواج ایستاده به پایان میبریم.
تعدادی دانشآموز در تلاشند عمق چاهی را اندازهگیری کنند. آنها سنگی را از حالت سکون رها کردند و مدت زمانی را که سنگ به ته چاه رسید اندازه گرفتند. مدت زمان به دست آمده برابر بود. برای اندازهگیری عمق چاه با دقت بیشتر آنها موج صوتی را در بالای چاه ایجاد و تشدیدی را در فرکانس 285 هرتز دریافت کردند. اگر سرعت صوت برابر باشد عمق چاه چقدر است؟
پاسخ
در ابتدا محدوده عمقهایی را تعیین میکنیم که از آزمایش اول دانشآموزان به دست میآید. با در نظر گرفتن مقدار خطای آزمایش بیشترین زمان به دست آمده برابر است با
و کوتاهترین زمان سقوط سنگ برابر است با
با استفاده از دو زمان به دست آمده max و min عمق چاه را به دست میآوریم.
به منظور به دست آوردن جواب دقیقتر از اطلاعات موج صوتی استفاده میکنیم. چاه در یک انتها بسته و در انتهای دیگر باز است، بنابراین فرکانس تشدید به صورت زیر داده میشود.
که در رابطه بالا است. با استفاده از معادله موج طول موج را به صورت زیر به دست میآوریم.
از آنجایی که نمیدانیم دانشآموزان کدام هارمونیکها را شنیدهاند مقادیر m را تا جایی که طول تشدید بین 3/2 متر تا 4/8 متر بشود امتحان میکنیم. برای m=0 داریم.
مقدار به دست آمده برای m=0 بسیار کوچک است، بنابراین دیگر مقادیر m را امتحان میکنیم.
تنها مقداری که با آزمایش دانشآموزان همخوانی دارد مقدار 3.9 متر است.
جمعبندی
در مبحث امواج چیست با نکات زیر آشنا شدیم.
- مفهوم موج و چگونگی انتقال موج در محیط
- دسته بندی امواج
- با ویژگیهای امواج
- رفتار مرزی امواج
- تداخل امواج
- امواج ایستاده
- اثر دوپلر
اکنون انتظار میرود بتوانیم به پرسش امواج چیست پاسخ مناسبی دهیم.













بفرمایید جنس یک موج چی هست ووابسته به چی میتواند باشد،؟میتوان برای موج جرمی تعریف کرد؟
درمعادلات میتوان به رسید
با سلام خدمت شما؛
موج یک نوع اختلال یا آشفتگی است که توسط یک منیع ایجاد شده و در محیط منتشر میشود و انرژی را منتقل میکند. برخی پارامترهای موج مانند سرعت یا طولموج آن به عواملی مانند جنس و ویژگیهای محیط، فرکانس و دامنه منبع تولید موج بستگی دارند. نوع خاصی از امواج به نام امواج مکانیکی به دلیل ارتعاش ذرات محیط، میتوانند حامل انرژی و تکانه باشند، اما حتی این نوع از امواج نیز جرم سکون ندارند. فوتونها که جزء امواج الکترومغناطیسی محسوب میشوند نیز جرم سکون ندارند، اما انرژی و تکانه دارند. پس مفهوم جرم برای امواج به معنای جرم سکون ذرات مادی نیست. اما در فیزیک نسبیتی، مفهومی به نام جرم نسبیتی مطرح میشود که به انرژی و تکانه یک جسم در حال حرکت بستگی دارد. فوتونها با اینکه جرم سکون ندارند، به دلیل سرعت بسیار بالای خود، جرم نسبیتی دارند. در زمینه معادلات امواج میتوانید به مطلب «معادله موج – از صفر تا صد» از مجله فرادرس مراجعه کنید.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام خانم دکتر آموزش شما بینظیره ایا جایی بصورت حضوری آموزش نمیدید
ممنون از شما ، همونطور که فرمودید موج حرکت نداره اما میبنیم در دریا وقتی موج به ساحل میرسه اب پیش میاد و دوباره بر میگرده دلیلش چی هست ممنون
متوسط بود معلومات شما