آینه محدب (Convex Mirror) – به زبان ساده

پیشتر در مقاله «آینه مقعر در فیزیک — به زبان ساده» با اصول و تعاریف اولیه آینه‌‌های منحنی، به خصوص آینه‌های کروی (Spherical Mirrors) آشنا شدیم. ناگفته نماند که مطالعه مطلب ذکر شده، پیش از خواندن مطلبی که در ادامه آمده است توصیه می‌شود. دیدیم که آینه‌های کروی به دو دسته تقسیم می‌شوند؛ آینه‌های محدب یا کوژ (Convex Mirrors) و آینه‌های مقعر یا کاو (Concave Mirrors). در این مقاله سعی داریم تا با آینه محدب و همچنین با ویژگی‌ و کاربردهای آن آشنا شویم. با ما در ادامه مقاله همراه باشید.

تعریف و ویژگی‌های آینه محدب

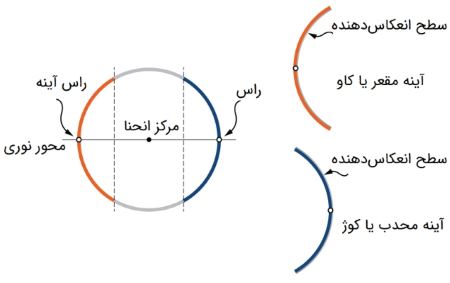
برشی از یک کره شیشه‌ای را در نظر بگیرید. با جیوه‌ اندود کردن سطح داخلی می‌توانیم یک آینه محدب یا کوژ بسازیم. درواقع در یک آینه محدب، سطح خارجی کره انعکاس‌دهنده نور است (شکل ۱).

شکل (۱)با توجه به شکل (۲) یک آینه محدب دارای ۴ ویژگی کلی زیر است:

• مرکز انحنا (C) پشت آینه است.
• میدان دید زیاد (فضای بیشتری قابل رویت است)
• تصویر جسم نزدیک به آینه تشکیل می‌شود (فاصله تصویر تا آینه از فاصله جسم تا آینه کمتر است).
• اندازه تصویر، کوچکتر از ابعاد اصلی جسم و نسبت به آن مستقیم است.

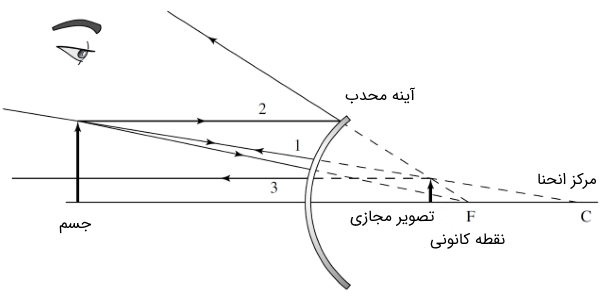
پرتوهایی که با اعداد در شکل (۲) مشخص شده‌اند را در نظر بگیرید. با توجه به شکل، می‌توان موارد زیر را نتیجه گرفت:

• پرتو شماره ۱: هرگاه پرتویی به طور عمود (زاویه تابش ۹۰ درجه)، بر سطح آینه کروی محدب بتابد، مطابق با قانون بازتاب (زاویه تابش $$i$$ = زاویه بازتابش $$r$$)، پرتو بازتاب شده روی پرتو فرودی منطبق شده و امتداد آن‌ از مرکز انحنا ($$C$$) عبور می‌کند.
• پرتو شماره ۲: هرگاه پرتویی موازی با محور آینه یا «محور نوری» (Optical Axis) بر سطح آینه محدب بتابد و بازتاب پیدا کند، امتداد پرتو بازتابیده شده از نقطه کانونی ($$F$$) می‌گذرد.
• پرتو شماره ۳: اگر پرتو تابش تحت زاویه‌ای بر سطح آینه محدب بتابد که بازتابش آن با محور نوری آینه موازی شود، امتداد پرتو تابش از نقطه کانونی ($$F$$) عبور می‌کند.

از آنجایی که امتداد پرتوهای بازتاب (نه خود پرتوهای تابش) یکدیگر را قطع می‌کنند (شکل ۲)، لذا کانون یک آینه کروی محدب، مجازی بوده و منفی در نظر گرفته‌ می‌شود. فاصله مرکز انحنا ($$C$$) تا سطح آینه، در واقع شعاع آینه را با $$r$$ تعریف می‌کنیم. فاصله کانونی برابر است با:

$$f=-\frac{r}{2}$$

در رابطه فوق علامت منفی بیانگر مجازی بودن نقطه کانونی است. همچنین این رابطه در صورتی صحیح است که ابعاد آینه در مقایسه با شعاع آن کوچک باشد.

رسم تصویر در آینه محدب

حداقل با رسم دو پرتو تابش طبق قواعدی که در بالا گفته شد و امتداد دادن بازتاب آن‌ها می‌توان به مکان تصویر پی برد. محل تلاقی امتداد پرتوهای بازتاب، مکان تصویر را مشخص می‌کند. از آن‌جا که تصویر، حاصل امتداد پرتوهای بازتابش بوده، نوع آن مجازی محسوب می‌شود. همچنین این تصویر نسبت به جسم اصلی مستقیم و کوچکتر بوده و داخل فاصله کانونی آینه دیده می‌شود. به هنگام رسم پرتوهای تابش و بازتابش، توجه کنید که قانون بازتاب همیشه و به هنگام بازتاب از هر سطحی برقرار است (زاویه تابش $$i$$ = زاویه بازتابش $$r$$).

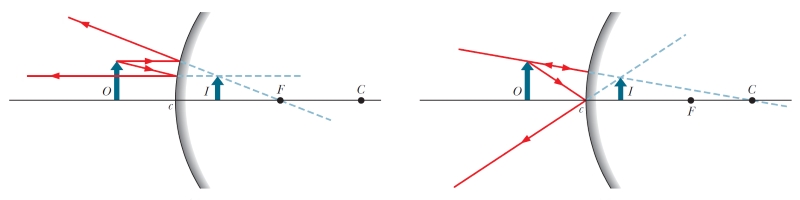
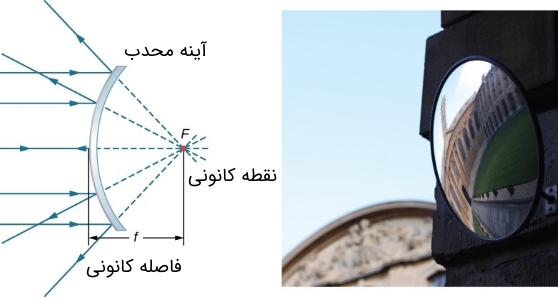
با توجه به اینکه در آینه محدب پرتوهای بازتابیده از یکدیگر باز شده (شکل۴)، می‌توان نتیجه گرفت که زاویه دید یا میدان دید بزرگی را پوشش می‌دهد. دلیل استفاده از آینه‌های محدب در سر پیچ‌ها یا آینه بغل خودروها نیز همین مطلب است.

معادله آینه

در مقاله «آینه مقعر در فیزیک — به زبان ساده» با معادله اصلی آینه‌های کروی آشنا شدیم. در واقع این معادله برای هر دو آینه محدب (کوژ) و مقعر (کاو) به کار می‌رود. تنها نکته‌ای که به هنگام استفاده از آن باید دقت کرد، صحیح قرار دادن علامت‌های + یا - در آن با توجه به موقعیت تصویر و نقطه کانونی است. این معادله به فرم کلی زیر است:

$$\frac{1}{p}+\frac{1}{q}=\frac{1}{f}$$

در رابطه فوق $$p$$ فاصله جسم با آینه و $$q$$ فاصله تصویر تا آینه است. از آنجا که فاصله کانونی و تصویر در آینه محدب همیشه مجازی است، لذا علامت $$f$$ و $$q$$ همیشه منفی در نظر قرار گرفته می‌شود. پس برای آینه محدب داریم:

$$\frac{1}{p}-\frac{1}{q}=-\frac{1}{f}$$

در صورت استفاده از رابطه فوق، دقت شود که مقدار مثبت $$f$$ و $$q$$ را در رابطه جایگذاری کنید. زیرا علامت منفی که به منزله مجازی بودن آن‌ها است، در معادله لحاظ شده است. می‌دانیم که بزرگ‌نمایی یک آینه از تقسیم اندازه تصویر ($$h^{°}$$) بر اندازه اصلی جسم ($$h$$) به دست می‌آید. یعنی:

$$m=\frac{h^{°}}{h}$$

همچنین از تقسیم فاصله تصویر تا آینه ($$q$$) بر فاصله جسم تا آینه ($$p$$) به همراه علامت منفی می‌توان بزرگ نمایی را تعیین کرد. علامت منفی بیانگر معکوس شدن تصویر است. از آنجا که تصویر در آینه محدب همیشه نسبت به جسم مستقیم بوده، علامت منفی به کار نمی‌رود.

$$m=-\frac{q}{p}$$

آینه محدب در عمل

فرض کنید در حال رانندگی هستید و جلوی خود آینه محدب بزرگی به شعاع 16 متر می‌بینید. خودروی پشت سر شما در فاصله 10 متری از این آینه است. با توجه به روابط گفته شده تصویر خودرو پشت سری، با محاسبات زیر در فاصله 4.4 متری از آینه و به صورت مجازی تشکیل می‌شود.

$$\frac{1}{p}+\frac{1}{q}=\frac{1}{f}$$

توجه شود که علامت منفی، به معنی مجازی بودن نقطه کانونی است. با استفاده از معادله کلی آینه‌های کروی داریم:

$$\frac{1}{10}+\frac{1}{q}=-\frac{1}{8}\Rightarrow q=-4.4m$$

در اینجا باز هم علامت منفی برای مقدار $$q$$ به منزله مجازی بودن تصویر است. در این آینه طبق رابطه ($$m=-\frac{q}{p}$$) اندازه تصویر مجازی 0.44 اندازه واقعی خودرو و به دلیل علامت مثبت، مستقیم با آن است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش جامع فیزیک دبیرستان
• آینه مقعر در فیزیک — به زبان ساده
• آینه تخت در فیزیک — به زبان ساده
• دوگانگی موج و ذره — به زبان ساده

^^