آشنایی با فرمول اویلر هندسی

«فرمول اویلر» بیشتر به عنوان فرمولی در رابطه با اعداد مختلط شناخته شده است، اما این متن درباره ی فرمولی است که در هندسه و شکل های هندسی کاربرد دارد.

فرمول اویلر

برای هر جسم چند وجهی که خودش را قطع نمی‌کند، اگر تعداد وجه‌ها (Faces) را با تعداد رأس‌ها (Vertices) جمع کنیم و از حاصل، تعداد اضلاع (Edges) را کم کنیم، همواره نتیجه مساوی 2 می‌باشد.

این فرمول را به شکل F + V – E = 2 می‌توان نوشت: به عنوان مثال این فرمول را برای مکعب زیر امتحان می‌کنیم.

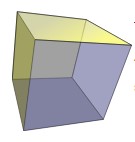
این مکعب 6 وجه، 8 رأس و 12 ضلع دارد. لذا خواهیم داشت: 2 = 12 – 8 + 6

مثالی در مورد اجسام افلاطونی

حال فرمول اویلر را در مورد 5 جسم افلاطونی به کار می‌بریم (با استفاده از فرمول اویلر می‌توان نشان داد تنها 5 جسم افلاطونی وجود دارد).

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

نام		وجه ها	رأس ها	اضلاع	فرمول اویلر
چهاروجهی (Tetrahedron)		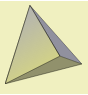4	4	6	2
مکعب		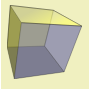6	8	12	2
هشت‌وجهی (Octahedron)		8	6	12	2
دوازده‌وجهی (Dodecahedron)		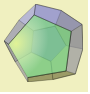12	20	30	2
بیست‌وجهی (Icosahedron)		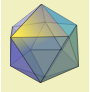20	12	30	2

برای اینکه عملکرد این فرمول را بهتر متوجه شویم، تصور کنید به مکعب یک ضلع دیگر اضافه کنیم (مانند شکل روبرو، از یک گوشه به گوشه‌ی دیگری از یک وجه رسم می‌کنیم) حال ما یک ضلع و یک وجه بیشتر خواهیم داشت. داریم: 2 = 13- 8 + 7
به همین ترتیب اگر رأس دیگری به مکعب اضافه کنیم (مانند شکل روبرو، این رأس را در وسط یک خط قرار می‌دهیم) یک ضلع بیشتر نیز خواهیم داشت: 2 = 13- 9 + 6 فرقی نمی‌کند چه عملیاتی انجام دهیم، در هر صورت به جواب "2" خواهیم رسید.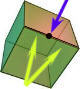

کره

تمامی اجسام افلاطونی (و بسیاری از اجسام دیگر) مانند یک کره هستند. به عبارت دیگر می‌توان به گونه‌ای آنها را تغییر شکل داد که شبیه کره شوند. برای این کار ابتدا گوشه ها را جابجا کرده و سپس مقداری وجه ها را خم می‌کنیم. به همین دلیل فرمول F + V − E = 2 را برای یک کره می‌دانیم.

نتایجی غیر از 2

حال که به‌خوبی با مثال‌هایی از صحت فرمول اویلر آشنا شده‌اید، بهتر است مثال‌هایی را بررسی کنیم که این فرمول برای آنها صدق نمی‌کند.

اگر دو گوشه‌ی مخالف یک بیست‌وجهی (icosahedron) را به هم وصل کنیم، شکل زیر به دست می‌آید: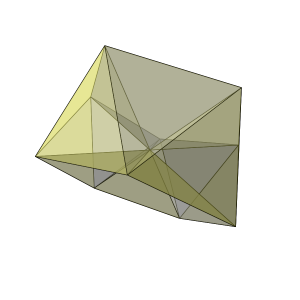

این شکل هنوز هم یک بیست‌وجهی است، اما غیر‌ محدب. در حقیقت این شکل به‌گونه‌ای است که به نظر می‌رسد بالا و پایین یک طبل را به هم گره زده‌ایم. در شکل جدید به همان تعداد وجه و ضلع خواهیم داشت، اما تعداد رأس‌ها یکی کم شده است. لذا داریم: F + V − E = 1

می‌بینیم که نتیجه همواره برابر 2 نخواهد بود. از آن جایی که اساساً این شکل با شکل قبلی متفاوت است، فرمول اولیه کارآیی خود را از دست می‌دهد. زیرا عملی که انجام دادیم به این معنی است که تعداد رأس‌ها یک عدد کاهش یافته است.

مشخصه‌ی اویلر

دیدیم که F+V−E می تواند مساوی 2، 1 یا مقادیر دیگری باشد. لذا فرمول کلی‌تر به شکل زیر خواهد بود: F + V − E = χ

فیلم آموزش ریاضیات گسسته – جامع و به زبان ساده در فرادرس

کلیک کنید

که χ «مشخصه‌ی اویلر» نامیده می‌شود. برای مثال در جدول زیر مشخصه‌ی اویلر چند شکل آورده شده است:

شکل		χ
کره		2
چنبره (Torus)		0
نوار موبیوس (Mobius Strip)		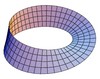0

مشخصه‌ی اویلر می‌تواند مقداری کمتر از صفر نیز داشته باشد.

به عنوان مثال جسم بالا یک «کوبا‌هِمی‌اُکتاهدرا» (Cubohemioctahedron) نام دارد. این جسم شامل 10 وجه، 24 ضلع و 12 رأس می‌باشد (شاید تعداد وجه‌های داخلی بیشتر به نظر برسد، اما در حقیقت بعضی از وجوه داخلی، یک وجه هستند). لذا خواهیم داشت: F + V − E = −2

مشخصه‌ی اویلر ایده‌ای پایه‌ای در علم توپولوژی (دانش مطالعه‌ی طبیعت فضا) می‌باشد.

دونات و فنجان قهوه

در پایان این بحث می‌خواهیم نشان دهیم که دونات و فنجان قهوه در حقیقت یکی هستند! به عبارتی آنها می‌توانند به یکدیگر تغییر شکل بدهند.

در چنین حالتی می‌گوییم که به اصطلاح دو شئ «همسان‌ریخت» (homeomorphic) هستند (برگرفته از لغت یونانی homoios به معنای یکسان و morphe به معنای شکل). دقیقاً مانند اجسام افلاطونی که نسبت به کره همسان‌ریخت هستند. همچنین اگر بینی خود را به سمت پاهای خود کشیده و ببندید متوجه خواهید شد که بدن ما نیز نسبت به یک چنبره همسان‌ریخت است!

امیدواریم این مقاله مورد توجه شما قرار گرفته باشد. اگر به مطالعه بیشتر در زمینه هندسه علاقه‌مند هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• آموزش جامع هندسه دبیرستان
• چندضلعی ها در هندسه — به زبان ساده
• هندسه فضایی و تعاریف آن — به زبان ساده
• مکعب در هندسه – مبانی، مفاهیم و محاسبات

#