مساحت بیضی چیست؟ – به زبان ساده + حل تمرین
مساحت بیضی، سطح درون این شکل هندسی است که از رابطه «نصف محور اصلی × نصف محور فرعی × عدد پی» یا «شعاع کوچک × شعاع بزرگ × عدد پی» به دست میآید. محورهای اصلی و فرعی بیضی، با عنوان قطرهای بزرگ و کوچک نیز شناخته میشوند. در این آموزش، به معرفی فرمول محاسبه مساحت بیضی به عنوان یکی از شکلهای مهم هندسه تحلیلی به همراه حل چند مثال میپردازیم. به علاوه، ضمن اثبات این فرمول، ابزارهای محاسبه آنلاین مساحت را نیز ارائه میکنیم.


بیضی چیست؟
بیضی، شکلی متشکل از یک منحنی بسته است. مجموع فاصله تمام نقاط روی بیضی، از دو نقطه ثابت در درون آن، به یک اندازه است.
تصویر زیر، محیط بیضی و کانونهای آن را نمایش میدهد.

اجزای بیضی چه هستند؟
از مهمترین اجزای بیضی میتوان به موارد زیر اشاره کرد:
- قطر: پارهخط اتصالدهنده دو نقطه مقابل بر روی محیط بیضی
- محور بزرگ یا محور اصلی: بزرگترین قطر بیضی
- محور کوچک یا محور فرعی: کوچکترین قطر بیضی
- مرکز: محل برخورد قطرهای بیضی
- کانونها: دو نقطه ثابت بر روی محور بزرگ (مجموع فاصله تمام نقاط از کانونها به یک اندازه است.)
- گوشه: محل برخورد محورهای بزرگ و کوچک با محیط بیضی
- شعاع: فاصله هر نقطه از محیط بیضی تا مرکز آن (شعاع، نصف قطر متناظر است.)
- شعاع بزرگ: نصف محور اصلی
- شعاع کوچک: نصف محور فرعی
محورهای اصلی و فرعی، مبنای محاسبه محاسبه مساحت بیضی هستند.
مساحت بیضی چیست؟
مساحت بیضی، اندازه سطح درون این شکل است. شکل زیر را در نظر بگیرید. ناحیه رنگی، مساحت یک بیضی را نمایش میدهد.

مساحت بیضی چگونه بدست می آید؟
مساحت بیضی، از رابطه «نصف محور فرعی × نصف محور اصلی × عدد پی» به دست میآید. بیضی زیر را در نظر بگیرید.
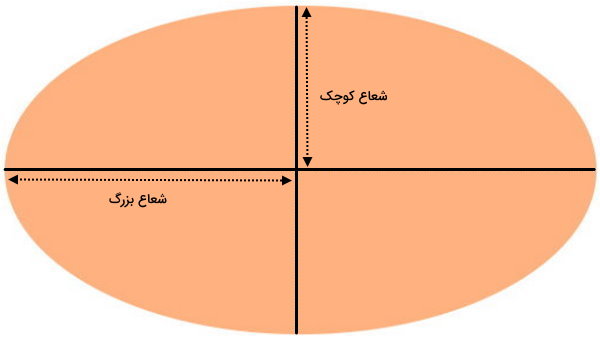
عدد پی، همواره برابر 3/14 است. نصف محورهای اصلی و فرعی را نیز میتوان به عنوان شعاعهای بزرگ و کوچک در نظر گرفت. بنابراین، فرمول مساحت بیضی به صورت زیر نوشته میشود:
شعاع کوچک × شعاع بزرگ × 3/14 = مساحت بیضی
مثال 1: محاسبه مساحت بیضی با قطر
تصویر زیر، اندازه محورهای اصلی و فرعی یک بیضی را نمایش میدهد. مساحت بیضی را به دست بیاورید.
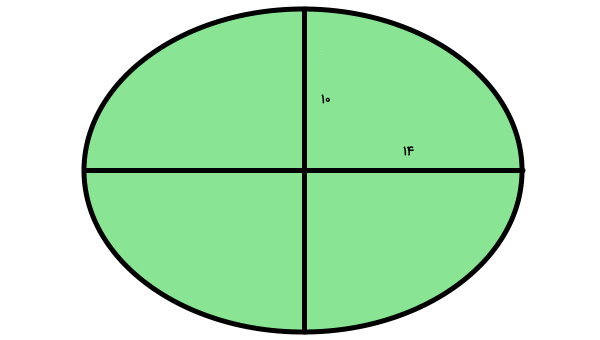
محور بزرگ بیضی برابر 14 و محور کوچک آن برابر 10 است. به منظور محاسبه مساحت، به اندازه شعاعهای بزرگ و کوچک نیاز داریم. این اندازهها، نصف محورهای اصلی و فرعی هستند. بنابراین، داریم:
۷ = ۲ ÷ ۱۴ = شعاع بزرگ
۵ = ۲ ÷ ۱۰ = شعاع کوچک
شعاعها را درون فرمول مساحت بیضی قرار میدهیم:
شعاع کوچک × شعاع بزرگ × 3/14 = مساحت بیضی
5 × 7 × 3/14 = مساحت بیضی
35 × 3/14 = مساحت بیضی
109/9 = مساحت بیضی
در نتیجه، مساحت بیضی برابر 109/9 واحد سطح است.
مساحت بیضی به صورت جبری چیست؟
عبارتهای جبری، مجموعهای از اعداد، متغیرها و علائم ریاضی هستند که به منظور نمایش روابط و فرمولهای مختلف مورد استفاده قرار میگیرند. عبارت جبری مساحت بیضی به صورت زیر نوشته میشود:
- S: مساحت بیضی
- π: عدد ثابت 3/14
- a: شعاع بزرگ یا نصف محور اصلی
- b: شعاع کوچک یا نصف محور فرعی
بیان هندسی مساحت بیضی از روی مساحت دایره
دایره، یکی از حالتهای خاص بیضی است که در آن، محورهای طولی، محورهای عرضی، قطرها و تمام شعاعها با یکدیگر برابر هستند. فرمولهای مساحت دایره و مساحت بیضی شباهت بسیار زیادی به یکدیگر دارند. فرمول مساحت دایره به صورت زیر نوشته میشود:
شعاع × شعاع × عدد پی = مساحت دایره
این فرمول را با فرمول زیر مقایسه کنید:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
در واقع، فرمول مساحت دایره از روی فرمول مساحت بیضی نوشته میشود. دایرهای به شعاع a را در نظر بگیرید.
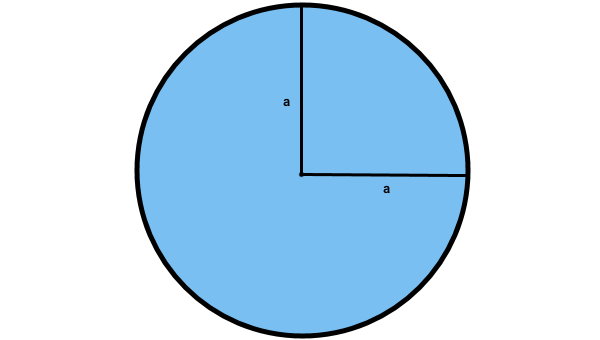
مساحت دایره بالا از ضرب دو شعاع در عدد پی به دست میآید:
π × a × a = مساحت دایره
اکنون دایره را بدون تغییر در محیط (اندازه طول منحنی بسته آن)، از بالا و پایین فشرده میکنیم. با این کار، دایره به یک بیضی تبدیل میشود. نقطهچین تصویر پایین، شکل این بیضی را نمایش میدهد.
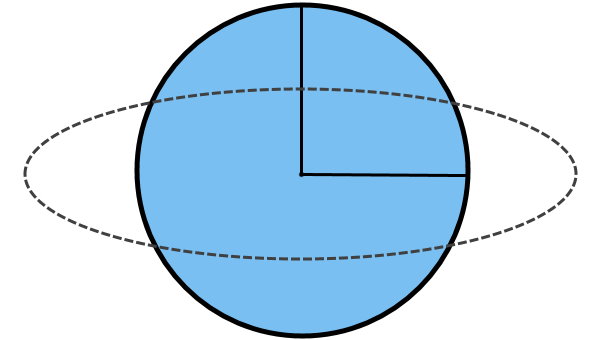
با فشرده کردن دایره، اندازه یکی از شعاعها، کاهش یافته و اندازه شعاع دیگر، افزایش مییابد.
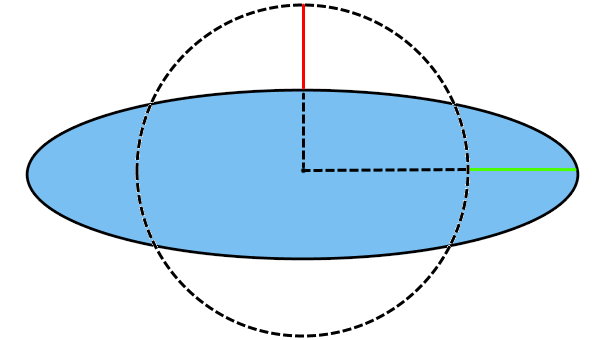
مساحت بیضی بالا با مساحت دایره (محدوده درون نقطهچین) یکسان است؛ چراکه افزایش و کاهش شعاعها همدیگر را خنثی میکنند.
حل تمرین و مثال مساحت بیضی
در این بخش، به منظور آشنایی بیشتر با فرمول مساحت بیضی و محاسبه اندازههای مختلف بیضی با استفاده از این فرمول، به حل چند مثال میپردازیم.
مثال 2: محاسبه مساحت بیضی به صورت جبری
مساحت یک بیضی با محور اصلی 10 سانتیمتر و شعاع کوچک 4 سانتیمتر را به دست بیاورید.
به منظور تعیین مساحت، به اندازه شعاعهای بزرگ و کوچک نیاز داریم. بر اساس اطلاعات سوال داریم:
۵ = ۲ ÷ ۱۰ = شعاع بزرگ
۴ = شعاع کوچک
فرمول مساحت بیضی عبارت است از:
- S: مساحت بیضی
- π: عدد ثابت 3/14
- a: شعاع بزرگ برابر ۵ سانتیمتر
- b: شعاع کوچک برابر ۴ سانتیمتر
اندازههای معلوم را درون فرمول بالا قرار میدهیم و آن را حل میکنیم:
در نتیجه، مساحت بیضی برابر با ۶۲/۸ سانتیمتر مربع است.
مثال 3: محاسبه قطر بزرگ بیضی
مساحت یک بیضی برابر 628 متر مربع و شعاع کوچک آن برابر 10 متر است. اندازه قطر بزرگ بیضی را حساب کنید.
منظور از قطر بزرگ، محور اصلی بیضی است. این اندازه، از ضرب شعاع بزرگ در عدد 2 به دست میآید. بنابراین، با محاسبه شعاع بزرگ، امکان تعیین قطر بزرگ فراهم میشود. بر اساس فرمول مساحت داریم:
- S: مساحت بیضی برابر 628 متر مربع
- π: عدد ثابت 3/14
- a: شعاع بزرگ
- b: شعاع کوچک برابر 10 متر
اندازههای معلوم را درون فرمول جایگذاری میکنیم و آن را برای به دست آوردن a (شعاع بزرگ) حل میکنیم:
شعاع بزرگ بیضی برابر 20 متر است. بنابراین، قطر بزرگ یا محور اصلی آن برابر است با:
۴۰ = ۲۰ × ۲ = قطر بزرگ
مثال 4: محاسبه شعاع های بیضی
مساحت یک بیضی برابر با 50/24 سانتیمتر مربع است. اگر شعاع بزرگ، به اندازه شش واحد برابر شعاع کوچک باشد، اندازه هر شعاع چقدر خواهد بود؟
در این مثال، به جای بیان مقادیر عددی هر شعاع، رابطه ریاضی بین آنها بیان شده است. فرمول مساحت بیضیها به صورت زیر نوشته میشود:
بر اساس اطلاعات مسئله، فقط اندازه مساحت (S) را داریم. در طرف دیگر فرمول، دو مجهول وجود دارد. اگر این دو مجهول را به کمک رابطه بین آنها، به یک مجهول تبدیل کنیم، امکان محاسبه شعاعهای بیضی فراهم میشود. مطابق با صورت مسئله داریم:
۶ + شعاع کوچک = شعاع بزرگ
عبارت جبری این رابطه به صورت زیر نوشته میشود:
به این ترتیب، به جای a در فرمول مساحت، عبارت بالا را قرار میدهیم:
عبارتهای سمت راست فرمول را بر اساس قواعد ضرب چند جملهایها در یکدیگر ضرب میکنیم و مقدار عددی مساحت را مینویسیم:
برای سادهسازی، طرفین رابطه را بر 3/14 تقسیم میکنیم:
اگر عدد 16 را به سمت دیگر رابطه ببریم، شکل استاندارد یک معادله درجه دو به وجود میآید:
چندین روش برای حل معادله درجه دو وجود دارد. از این روشها میتوان به روش دلتا و روش تجزیه معادله اشاره کرد. در روش تجزیه، معادله بالا به شکل زیر در میآید:
ضرب دو عبارت، تنها زمانی صفر میشود که یکی از آن عبارتها برابر صفر باشد. بنابراین:
یا
اندازه شعاع، نمیتواند منفی باشد. بنابراین، شعاع کوچک برابر 2 سانتیمتر است. مطابق با فرض مسئله، شعاع بزرگ نیز از رابطه زیر به دست میآید:
در نتیجه، شعاع بزرگ برابر ۸ سانتیمتر است.
مثال 5: محاسبه قطرهای بیضی
مساحت یک بیضی برابر 157 متر مربع و نسبت شعاع بزرگ به کوچک آن برابر 2 است. اندازه قطرهای بیضی را به دست بیاورید.
برای شروع حل مسئله، رابطه بین شعاع بزرگ به شعاع کوچک بیضی را مینویسیم:
در فرمول مساحت بیضی، به جای عبارت معرف شعاع بزرگ (a)، رابطه بالا را قرار میدهیم:
- S: مساحت بیضی برابر 157 متر مربع
- π: عدد ثابت 3/14
- a: شعاع بزرگ برابر 2b
- b: شعاع کوچک
به این ترتیب، شعاع کوچک بیضی برابر با 5 متر است. بر اساس اطلاعات مسئله، شعاع بزرگ از رابطه زیر به دست میآید:
شعاع بزرگ بیضی برابر 10 متر است. سوال، قطرهای بیضی را از ما خواسته بود. اکنون میتوانیم این اندازهها را حساب کنیم:
20 = 10 × 2 = قطر بزرگ یا محور اصلی
10 = 5 × 2 = قطر کوچک یا محور فرعی
در نتیجه، قطر بزرگ بیضی برابر 20 متر و قطر کوچک آن برابر 10 متر است.
مثال 6: مساحت بیضی داخل مربع
بیضی محاطی زیر را در نظر بگیرید. اگر طول ضلع مربع برابر با 7 سانتیمتر باشد، مساحت ناحیه رنگی چقدر است؟

مساحت قسمت رنگی شکل بالا برابر است با:
مساحت بیضی - مساحت مربع = مساحت رنگی
مساحت مربع از رابطه زیر به دست میآید:
خودش × یک ضلع = مساحت مربع
۷ × ۷ = مساحت مربع
۴۹ = مساحت مربع
به منظور تعیین مساحت بیضی، به اندازه شعاعهای بزرگ و کوچک آن نیاز داریم. از اینرو، محورهای بیضی را بر روی شکل رسم میکنیم.
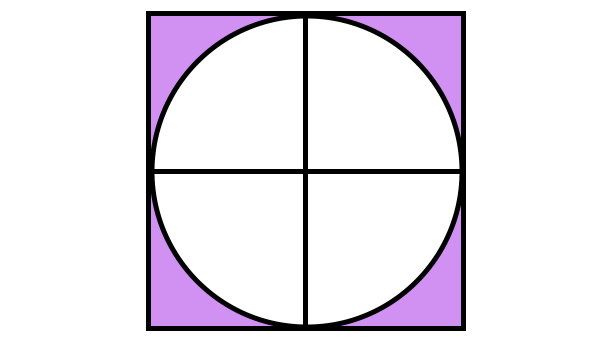
با توجه به تصویر بالا، محورهای بیضی، برابر با ضلعهای مربع هستند. به عبارت دیگر:
7 = محور بزرگ بیضی
7 = محور کوچک بیضی
شعاعهای بزرگ و کوچک، از تقسیم اندازه محورها بر عدد 2 به دست میآیند:
3/5 = شعاع بزرگ بیضی
3/5 = شعاع کوچک بیضی
به این ترتیب، مساحت بیضی از رابطه زیر محاسبه میشود:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
3/5 × 3/5 × 3/14 = مساحت بیضی
38/46 = مساحت بیضی
اکنون میتوانیم مساحت قسمت رنگی را محاسبه کنیم:
مساحت بیضی - مساحت مربع = مساحت رنگی
38/46 - 49 = مساحت رنگی
10/54 = مساحت رنگی
در نتیجه، مساحت قسمت رنگی برابر با 10/54 است. در صورت تمایل به یادگیری در مورد نحوه رسم بیضی، مطالعه مطلب «رسم بیضی — آموزش تصویری و گام به گام هفت روش — به زبان ساده» را به شما پیشنهاد میکنیم.
اثبات مساحت بیضی با انتگرال
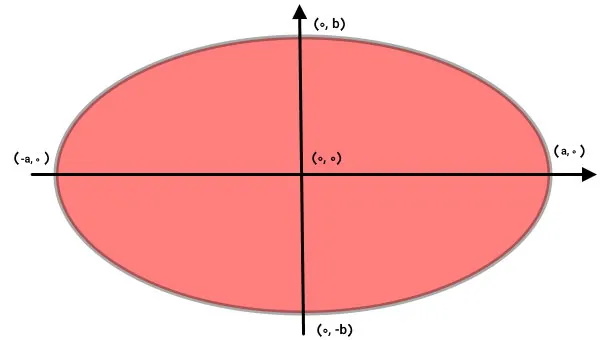
انتگرال، یکی از مهمترین ابزارهای ریاضی است که به منظور محاسبه اندازههای مختلف شکلهای هندسی، مانند محاسبه مساحت بیضی، مورد استفاده قرار میگیرد. معادله بیضی به صورت زیر نوشته میشود:
- a: شعاع بزرگ
- b: شعاع کوچک
- x: مختصات طولی یک نقطه روی بیضی
- y: مختصات عرضی یک نقطه روی بیضی
انتگرال یک منحنی، سطح زیر آن را نمایش میدهد. برای گرفتن انتگرال، باید معادله منحنی و بازه انتگرالگیری را داشته باشیم. از اینرو، برای شروع، معادله منحنی بیضی را بر حسب y مینویسیم:
محورها، بیضی را به چهار منحنی مساوی تقسیم میکنند. با محاسبه سطح زیر یکی از این منحنیها و ضرب نتیجه به دست آمده در عدد 4، مساحت بیضی به دست میآید. در تصویر بالا، منحنی موجود در ربع اول را در نظر بگیرید. این منحنی در بازه (۰ و ۰) تا (a و 0) قرار گرفته است. در نتیجه، برای محاسبه مساحت بیضی داریم:
به منظور اثبات مساحت بیضی، معادله منحنی بیضی را درون رابطه بالا قرار میدهیم و از آن انتگرال میگیریم:
بر اساس قواعد انتگرال رادیکالی، متغیرهای x و dx را به شکل زیر تغییر میدهیم:
به این ترتیب، بازه انتگرالگیری از 0 تا a به 0 تا π/2 تغییر میکند:
در مرحله بعد، از عبارت a فاکتور میگیریم و حل انتگرال را ادامه میدهیم:
به این ترتیب، فرمول محاسبه سطح درون بیضی به دست میآید. در صورت تمایل به یادگیری بیشتر در مورد مبحث مساحت بیضی با انتگرال، + اینجا کلیک کنید.
اثبات فرمول مساحت بیضی از روی معادله دایره
یکی دیگر از روشهای اثبات فرمول مساحت بیضی، استفاده از معادله دایره و مساحت آن است. فرم کلی معادله بیضی به صورت زیر نوشته میشود:
معادله دایرهای به شعاع a که مرکز آن بر روی مبدا مختصات (۰ و ۰) قرار دارد، عبارت است از:
معادله منحنی این دایره را نیز بر حسب y بازنویسی میکنیم:
روابط y در دایره و بیضی را با هم مقایسه کنید:
با توجه به روابط بالا، مختصات هر نقطه از بیضی، b/a مختصات دایره است. مساحت دایره و بیضی نیز از همین نسبت پیروی میکنند. به عبارت دیگر:
- Ae: مساحت بیضی
- b: شعاع بزرگ بیضی
- a: شعاع کوچک بیضی
- Ac: شعاع دایره
شعاع دایره برابر a است. بنابراین، داریم:
رابطه بالا، فرمول مساحت بیضی است.
محاسبه آنلاین مساحت بیضی چگونه است؟
امروزه، ماشینحسابهای آنلاین، محاسبه مساحت شکلهای هندسی مختلف را ساده کردهآند. از بهترین و متداولترین سایتهای محاسبه آنلاین مساحت بیضی میتوان به موتور جستجوی گوگل (+)، سایت Omni Calculator (+) و سایت Keisan (+) اشاره کرد.
از میان این موارد، محاسبهگر آنلاین گوگل، سادهتر بوده و دسترسی به آن سریعتر است. تصویر زیر این ابزار محاسباتی را نمایش میدهد.
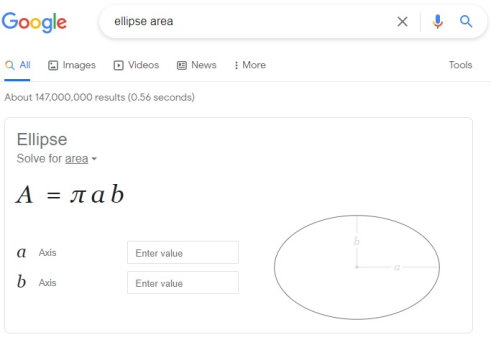
به منظور تعیین مساحت بیضی با ماشینحساب گوگل، کافی است اندازه یکی از محورهای بیضی را در کادر مقابل «a Axis» و اندازه محور دیگر را در کادر «b Axis» وارد کنید. با این کار، مساحت بیضی محاسبه میشود و نتیجه آن به همراه روند حل به نمایش در میآید. به عنوان مثال، تصویر زیر، خروجی محاسبه آنلاین مساحت یک بیضی با محورهای 27 و 31 است.
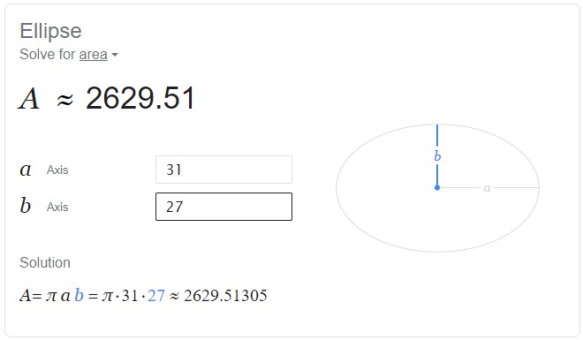
محاسبه آنلاین مساحت بیضی با استفاده از ابزار سایت Omni Calculator (+) نیز مشابه ماشینحساب گوگل است. البته در سایت Omni Calculator، امکان تنظیم یکای محاسبات وجود دارد. سایت Keisan (+)، علاوه بر محاسبه مساحت، اندازه محیط بیضی و مختصات کانونها آن را نیز تعیین میکند. به طور کلی، سایتهای مذکور، گزینههای مناسبی برای تمرین و بررسی نحوه محاسبات انواع شکلهای هندسی از جمله بیضی هستند. در رابطه با نحوه محاسبه محیط بیضی، مطالب زیر در مجله فرادرس تهیه شدهاند. مطالعه این مطالب را به شما پیشنهاد میکنیم.
سوالات متداول در رابطه با مساحت بیضی
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت بیضی به طور خلاصه پاسخ میدهیم.
مساحت بیضی چیست؟
مساحت بیضی، اندازه محدوده درون محیط آن است.
مساحت بیضی چگونه محاسبه میشود؟
مساحت بیضی با ضرب شعاع کوچک در شعاع بزرگ در عدد 3/14 محاسبه میشود.
فرمول مساحت بیضی به صورت جبری چیست؟
عبارت جبری مساحت بیضی، معمولا به صورت S=πab نوشته میشود.
محاسبه مساحت بیضی با انتگرال چگونه است؟
در روش انتگرالی محاسبه مساحت بیضی، انتگرال معادله منحنی بیضی در ربع اول (بازه 0 تا π/2) محاسبه شده و در عدد 4 ضرب میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت بیضی — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- بیضی چیست ؟ | تعریف و مفاهیم به زبان ساده
- محیط بیضی چیست ؟ — تقریبها، سریها و انتگرالها
- مساحت بیضی چیست ؟ — به زبان ساده + حل تمرین(همین مطلب)
- مساحت بیضی با انتگرال — اثبات فرمول به زبان ساده
- قطر بیضی چیست و بیضی چند قطر دارد ؟ — به زبان ساده
- رسم بیضی — آموزش تصویری و گام به گام هفت روش — به زبان ساده
- محاسبه آنلاین مساحت بیضی — معرفی بهترین سایتها + مثال
- فرمول مساحت بیضی — به زبان ساده + حل تمرین و مثال
- محاسبه آنلاین محیط بیضی — معرفی بهترین سایتها + مثال
- فرمول محیط بیضی چیست ؟ — معرفی 9 فرمول پرکاربرد
- بیضی چند قطر دارد ؟ — تعداد ضلع، گوشه و دیگر اجزای بیضی — به زبان ساده












