در آموزشهای پیشین مجله فرادرس ، با مفاهیم مربوط به چگالی آشنا شدیم. در این آموزش با محاسبه جرم با چگالی با انتگرال آشنا میشویم.
جرم یک میله نازک
میتوانیم از انتگرالگیری یک تابع چگالی برای محاسبه جرم استفاده کنیم.
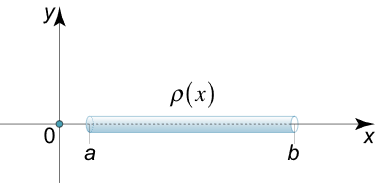
یک سیم یا میله نازک را در نظر بگیرید که در بازه [ a , b ] [a, b ] [ a , b ]
شکل ۱ چگالی میله در هر نقطه x x x ρ ( x ) \rho \left( x \right) ρ ( x ) ρ ( x ) \rho \left( x \right) ρ ( x )
m = ∫ a b ρ ( x ) d x . \large m = \int \limits _ a ^ b { \rho \left ( x \right ) d x } . m = a ∫ b ρ ( x ) d x .
جرم یک قرص (دیسک) نازک
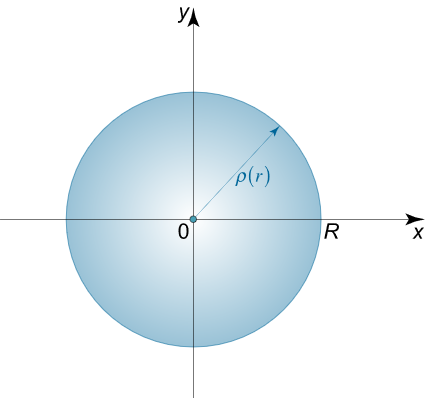
فرض کنید ρ ( r ) \rho \left( r \right) ρ ( r ) R R R
شکل ۲ جرم این قرص به صورت زیر قابل محاسبه است:
m = 2 π ∫ 0 R r ρ ( r ) d r . \large m = 2 \pi \int \limits _ 0 ^ R { r \rho \left ( r \right ) d r } . m = 2 π 0 ∫ R r ρ ( r ) d r .
جرم ناحیه محصور بین دو منحنی
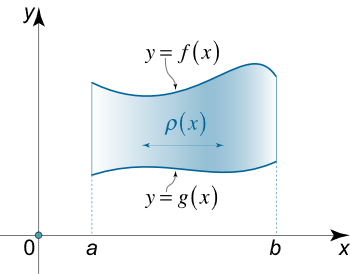
ناحیه محصور بین دو منحنی y = f ( x ) y = f\left( x \right) y = f ( x ) y = g ( x ) y = g\left( x \right) y = g ( x ) x = a x = a x = a x = b x = b x = b
شکل ۳ اگر چگالی لایهای که این ناحیه را در بر گرفته فقط به مختصات x x x
m = ∫ a b ρ ( x ) [ f ( x ) – g ( x ) ] d x \large m = \int \limits _ a ^ b { \rho \left ( x \right ) \left [ { f \left ( x \right ) – g \left ( x \right ) } \right ] d x } m = a ∫ b ρ ( x ) [ f ( x ) – g ( x ) ] d x
که در آن، رابطه f ( x ) ≥ g ( x ) f\left( x \right) \ge g\left( x \right) f ( x ) ≥ g ( x ) [ a , b ] [a , b ] [ a , b ] ρ ( x ) \rho ( x ) ρ ( x ) x x x
جرم یک جسم با تابع چگالی یک بعدی
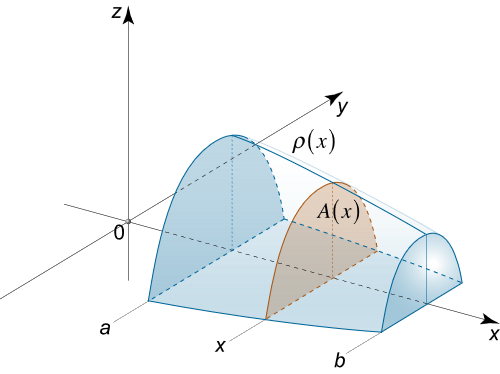
جسم S S S x x x x = a x = a x = a x = b x = b x = b A ( x ) A(x) A ( x )
شکل ۴ فرض کنید تابع چگالی ρ ( x ) \rho \left( x \right) ρ ( x ) x x x A ( x ) A ( x ) A ( x )
جرم این جسم برابر است با:
m = ∫ a b ρ ( x ) A ( x ) d x . \large m = \int \limits _ a ^ b { \rho \left ( x \right ) A \left ( x \right ) d x } . m = a ∫ b ρ ( x ) A ( x ) d x .
جرم جسم حاصل از دوران
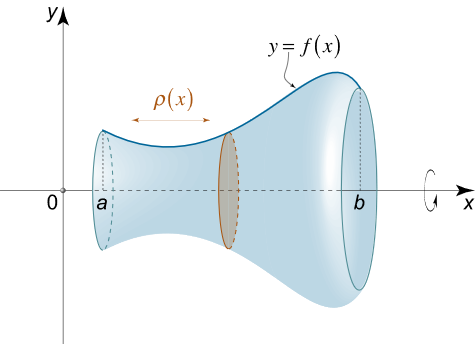
فرض کنید S S S y = f ( x ) y = f ( x ) y = f ( x ) [ a , b ] [a , b ] [ a , b ] x x x
شکل ۵ اگر ρ ( x ) \rho \left( x \right) ρ ( x ) x x x
m = π ∫ a b ρ ( x ) f 2 ( x ) d x . \large m = \pi \int \limits _ a ^ b { \rho \left ( x \right ){ f ^ 2 } \left ( x \right ) d x } . m = π a ∫ b ρ ( x ) f 2 ( x ) d x .
مثالهای محاسبه جرم با چگالی
در این بخش، مثالهای مختلفی از محاسبه جرم با چگالی را بررسی میکنیم.
مثال ۱
میلهای با با چگالی خطی ρ ( x ) = x 3 + x \rho \left( x \right) = {x^3} + x ρ ( x ) = x 3 + x x x x x = 0 x = 0 x = 0 x = 2 x = 2 x = 2
حل: با استفاده از انتگرالگیری، داریم:
m = ∫ a b ρ ( x ) d x = ∫ 0 2 ( x 3 + x ) d x = ( x 4 4 + x 2 2 ) ∣ 0 2 = 6. \large { m = \int \limits _ a ^ b { \rho \left ( x \right ) d x } } = { \int \limits _ 0 ^ 2 { \left ( { { x ^ 3 } + x } \right ) d x } } = { \left . { \left ( { \frac { { { x ^ 4 } } } { 4 } + \frac { { { x ^ 2 } } } {2 } } \right ) } \right | _ 0 ^ 2 } = { 6 . } m = a ∫ b ρ ( x ) d x = 0 ∫ 2 ( x 3 + x ) d x = ( 4 x 4 + 2 x 2 ) 0 2 = 6.
اگر ρ \rho ρ x x x m = 6 kg m = 6\,\text{kg} m = 6 kg
مثال ۲
میلهای به طول L = 10 cm L = 10\,\text{cm} L = 10 cm ρ ( x ) = 50 e – x 10 \rho \left( x \right) = 50{e^{ – \frac{x}{{10}}}} ρ ( x ) = 50 e – 10 x g cm \large{\frac{\text{g}}{\text{cm}}}\normalsize cm g x x x cm \text{cm} cm
حل: برای یافتن جرم میله، از تابع چگالی انتگرال میگیریم:
m = ∫ a b ρ ( x ) d x = ∫ 0 10 50 e – x 10 d x = – 500 e – x 10 ∣ 0 10 = 500 ( 1 – 1 e ) = 500 ( e – 1 ) e ≈ 316 g . \large \begin {align*} m & = \int \limits _ a ^ b { \rho \left ( x \right ) d x } = { \int \limits _ 0 ^ { 1 0 } { 5 0 { e ^ { – \frac { x } { { 1 0 } } } } d x } } = { – 5 0 0 \left . { { e ^ { – \frac { x } { { 1 0 } } } } } \right | _ 0 ^ { 1 0 } }\\ & = { 5 0 0 \left ( { 1 – \frac { 1 } { e } } \right ) } = { \frac { { 5 0 0 \left ( { e – 1 } \right ) } } { e } }\approx { 3 1 6 \, \text {g} . } \end {align*} m = a ∫ b ρ ( x ) d x = 0 ∫ 10 50 e – 10 x d x = –500 e – 10 x 0 10 = 500 ( 1– e 1 ) = e 500 ( e –1 ) ≈ 316 g .
مثال ۳
فرض کنید تراکم خودروها در ازدحام ترافیک یک بزرگراه، به طور خطی از ۳۰ تا ۱۵۰ خودرو در کیلومتر بر خط تغییر کند. طول هر خط ۵ کیلومتر است. اگر ۴ خط وجود داشته باشد، تعداد کل خودروهای مسیر بزرگراه را محاسبه کنید.
شکل ۶ حل: ابتدا معادلهای برای تابع چگالی ρ ( x ) \rho \left( x \right) ρ ( x )
ρ ( 0 ) = 30 , ρ ( 5 ) = 150. \large { \rho \left ( 0 \right ) = 3 0 , \; \; } \kern0pt { \rho \left ( 5 \right ) = 1 5 0 . } ρ ( 0 ) = 30 , ρ ( 5 ) = 150.
با استفاده از این دو نقطه، میتوان معادله خط را به دست آورد:
ρ – 30 150 – 30 = x – 0 5 – 0 , ⇒ ρ – 30 120 = x 5 , ⇒ ρ – 30 = 24 x , ⇒ ρ ( x ) = 24 x + 30. \large \begin {align*} & \frac { { \rho – 3 0 } } { { 1 5 0 – 3 0 } } = \frac { { x – 0 } } { { 5 – 0 } } , \; \; \Rightarrow { \frac { { \rho – 3 0 } } {{ 1 2 0 } } = \frac { x } { 5 } , } \; \; \\ & \Rightarrow { \rho – 30 = 2 4 x , } \; \; \Rightarrow { \rho \left ( x \right ) = 2 4 x + 3 0 . } \end {align*} 150–30 ρ –30 = 5–0 x –0 , ⇒ 120 ρ –30 = 5 x , ⇒ ρ –30 = 24 x , ⇒ ρ ( x ) = 24 x + 30.
اکنون تعداد خودروهای بزرگراه را به دست میآوریم. برای این کار، از تابع چگالی انتگرال گرفته و نتیجه را در ۴ ضرب میکنیم:
N = 4 ∫ a b ρ ( x ) d x = 4 ∫ 0 5 ( 24 x + 30 ) d x = 4 ( 12 x 2 + 30 x ) ∣ 0 5 = 4 ( 300 + 150 ) = 1800 cars . \large \begin {align*} N & = 4 \int \limits _ a ^ b { \rho \left ( x \right ) d x } = { 4 \int \limits _ 0 ^ 5 { \left ( { 2 4 x + 3 0 } \right ) d x } }\\ & = { \left . { 4 \left ( { 1 2 { x ^ 2 } + 3 0 x } \right ) } \right | _ 0 ^ 5 } = { 4 \left ( { 3 0 0 + 1 5 0 } \right ) } = { 1 8 0 0 \, \text {cars}}. \end {align*} N = 4 a ∫ b ρ ( x ) d x = 4 0 ∫ 5 ( 24 x + 30 ) d x = 4 ( 12 x 2 + 30 x ) 0 5 = 4 ( 300 + 150 ) = 1800 cars .
مثال ۴
مقدار باکتری موجود در یک پتری دیش به شعاع R R R ρ 0 \rho _ 0 ρ 0
شکل ۷ حل: چگالی باکتری با قانون زیر تغییر میکند:
ρ ( r ) = ρ 0 ( 1 – r R ) \large \rho \left ( r \right ) = { \rho _ 0 } \left ( { 1 – \frac { r } { R } } \right ) ρ ( r ) = ρ 0 ( 1– R r )
که در آن، 0 ≤ r ≤ R 0 \le r \le R 0 ≤ r ≤ R
برای یافتن تعداد کل باکتری درون پتری دیش، از فرمول زیر استفاده میکنیم:
N = 2 π ∫ 0 R r ρ ( r ) d r . \large N = 2 \pi \int \limits _ 0 ^ R { r \rho \left ( r \right ) d r } . N = 2 π 0 ∫ R r ρ ( r ) d r .
این انتگرال به صورت زیر محاسبه میشود:
N = 2 π ρ 0 ∫ 0 R r ( 1 – r R ) d r = 2 π ρ 0 ∫ 0 R ( r – r 2 R ) d r = 2 π ρ 0 ( r 2 2 – r 3 3 R ) ∣ 0 R = 2 π ρ 0 ( R 2 2 – R 2 3 ) = 2 π ρ 0 R 2 6 = π ρ 0 R 2 3 . \large \begin {align*} N & = 2 \pi { \rho _ 0 } \int \limits _ 0 ^ R { r \left ( { 1 – \frac { r } { R } } \right ) d r } = { 2 \pi { \rho _ 0 } \int \limits _ 0 ^ R { \left ( { r – \frac { {{ r ^ 2 } } } { R } } \right ) d r } } \\ & = { 2 \pi { \rho _ 0 } \left . { \left ( { \frac { { { r ^ 2 } } } { 2 } – \frac { { {r ^ 3 } } } { { 3 R } } } \right ) } \right | _ 0 ^ R } = { 2 \pi { \rho _ 0 } \left ( { \frac { { { R ^2 } }} { 2 } – \frac { { { R^ 2 } } } { 3} } \right ) } \\ & = { \frac { { 2 \pi { \rho _ 0 }{ R ^ 2} } } { 6 } } = { \frac { { \pi { \rho _ 0 } { R ^ 2 } } } { 3 } . } \end{align*} N = 2 π ρ 0 0 ∫ R r ( 1– R r ) d r = 2 π ρ 0 0 ∫ R ( r – R r 2 ) d r = 2 π ρ 0 ( 2 r 2 – 3 R r 3 ) 0 R = 2 π ρ 0 ( 2 R 2 – 3 R 2 ) = 6 2 π ρ 0 R 2 = 3 π ρ 0 R 2 .
مثال ۵
فرض کنید توزیع ستارهای در یک کهکشان از قانون نمایی زیر تبعیت کند:
ρ ( r ) = ρ 0 e – r h \large \rho \left ( r \right ) = { \rho _ 0 } { e ^ { – \frac { r } { h } } } ρ ( r ) = ρ 0 e – h r
جرم کهکشان را با پارامترهای ρ 0 = 1 0 3 M ⊙ kpc 2 {\rho _0} = {10^3}\large{\frac{{{M_{\odot}}}}{{{\text{kpc}^2}}}}\normalsize ρ 0 = 1 0 3 kpc 2 M ⊙ h = 1 0 4 kpc h = {10^4}\,\text{kpc} h = 1 0 4 kpc M ⊙ {M_{\odot}} M ⊙ kpc \text{kpc} kpc kpc \text{kpc} kpc سال نوری ) است.
شکل ۸ حل: فرض میکنیم کهکشان به فرم یک قرص باشد و در نتیجه، میتوان از فرمول زیر استفاده کرد:
m = 2 π ∫ 0 R r ρ ( r ) d r . \large m = 2 \pi \int \limits _ 0 ^ R r \rho \left ( r \right ) d r . m = 2 π 0 ∫ R r ρ ( r ) d r .
از آنجایی که مقدار دقیق شعاع R R R انتگرال ناسره زیر را محاسبه میکنیم:
m = 2 π ∫ 0 ∞ r ρ ( r ) d r = 2 π ρ 0 ∫ 0 ∞ r e – r h d r = 2 π ρ 0 lim b → ∞ ∫ 0 b r e – r h d r . \large { m = 2 \pi \int \limits _ 0 ^ \infty { r \rho \left ( r \right ) d r } } = { 2 \pi { \rho _ 0 } \int \limits _ 0 ^ \infty { r { e ^ { – \frac { r } { h } } } d r } } = { 2 \pi { \rho _ 0 } \lim \limits _ { b \to \infty } \int \limits _ 0 ^ b { r { e ^ { – \frac { r } { h } } } d r } . } m = 2 π 0 ∫ ∞ r ρ ( r ) d r = 2 π ρ 0 0 ∫ ∞ r e – h r d r = 2 π ρ 0 b → ∞ lim 0 ∫ b r e – h r d r .
با استفاده از انتگرالگیری جزء به جزء داریم:
$$ \large \begin {align*}<br />
\int { \underbrace r _ u \underbrace { { e ^ { – \frac { r }{ h } } } d r } _ { d v } } & = { \left [ { \begin {array} { * { 2 0 }{ l } } { u = r } \\ { d v = { e ^ { – \frac { r } { h } } } d r } \\ { d u = d r } \\ { v = – h { e ^ { – \frac { r } { h } } } } \end {array} } \right ] } = { – h r { e ^ { – \frac { r } { h } } } – \int { \left ( { – h { e ^ { – \frac { r } { h } } } } \right ) d r } } \\ & = { – h r { e ^ { – \frac { r } { h } } } + h \int { { e ^ { – \frac { r } { h } } } d r } } = { – h r { e ^ { – \frac { r } { h } } } – { h ^ 2 } { e ^ { – \frac { r } { h } } } } \\ & = { – h \left ( { r + h } \right ) { e ^ { – \frac { r } { h } } } . }<br />
\end {align*} $$
با حدگیری، خواهیم داشت:
m = 2 π ρ 0 lim b → ∞ ∫ 0 b r e – r h d r = 2 π ρ 0 h lim b → ∞ [ ( – ( r + h ) e – r h ) ∣ 0 b ] = 2 π ρ 0 h lim b → ∞ [ h – b + h e b h ] . \large \begin {align*} m & = 2 \pi { \rho _ 0 } \lim \limits _ { b \to \infty } \int \limits _ 0 ^ b { r { e ^ { – \frac { r } { h } } } d r } \\ & = { 2 \pi { \rho _ 0 } h \lim \limits _ { b \to \infty } \left [ { \left . { \left ( { – \left ( { r + h } \right ) { e ^ { – \frac { r } { h } } } } \right ) } \right | _ 0 ^ b } \right ] } \\ & = { 2 \pi { \rho _ 0 } h \lim \limits _ { b \to \infty } \left [ { h – \frac { { b + h } }{ { { e ^ { \frac { b } { h } } } } } } \right ] . } \end {align*} m = 2 π ρ 0 b → ∞ lim 0 ∫ b r e – h r d r = 2 π ρ 0 h b → ∞ lim [ ( – ( r + h ) e – h r ) 0 b ] = 2 π ρ 0 h b → ∞ lim [ h – e h b b + h ] .
حال از قاعده هوپیتال استفاده میکنیم:
lim b → ∞ [ h – b + h e b h ] = h – lim b → ∞ ( b + h ) ′ ( e b h ) ′ = h – lim b → ∞ 0 1 h e b h = h . \large { \lim \limits _ { b \to \infty } \left [ { h – \frac { { b + h } } { { { e ^ { \frac { b } { h } } }} } } \right ] } = { h – \lim \limits _ { b \to \infty } \frac { { \left ( { b + h } \right ) ^ \prime } } { { \left ( { { e ^ { \frac { b } { h } } } } \right ) ^ \prime } } } = { h – \lim \limits _ { b \to \infty } \frac { 0 } { { \frac { 1 } { h } { e ^ { \frac { b } { h } } } } } } = { h . } b → ∞ lim [ h – e h b b + h ] = h – b → ∞ lim ( e h b ) ′ ( b + h ) ′ = h – b → ∞ lim h 1 e h b 0 = h .
در نتیجه، جرم کهکشان از معادله زیر به دست خواهد آمد:
m = 2 π ρ 0 h 2 . \large m = 2\pi {\rho _0}{h^2}. m = 2 π ρ 0 h 2 .
با جایگذاری مقادیر داده شده اندازه جرم به دست میآید:
m = 2 π × 1 0 3 × ( 10 4 ) 2 = 2 π × 1 0 11 ≈ 6.28 × 1 0 11 M ⊙ \large { m = 2 \pi \times { 1 0 ^ 3 } \times { \left ( { { { 1 0 } ^ 4 } } \right ) ^ 2 } } = { 2 \pi \times { 10 ^ { 1 1 } } } \approx { 6 . 2 8 \times { 1 0 ^ { 1 1} } \, { M _ \odot } } m = 2 π × 1 0 3 × ( 10 4 ) 2 = 2 π × 1 0 11 ≈ 6.28 × 1 0 11 M ⊙
که تقریباً نصف جرم کهکشان راه شیری است.
مثال ۶
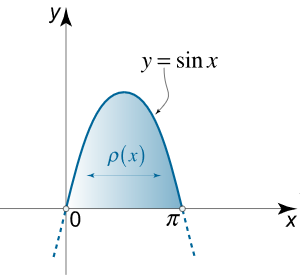
یک لایه، ناحیه محدود به یک کمان سینوسی و محور x x x y y y
شکل ۹ حل: فرمول کلی جرم یک ناحیه بین دو نمودار به صورت زیر است:
m = ∫ a b ρ ( x ) [ f ( x ) – g ( x ) ] d x . \large m = \int \limits _ a ^ b { \rho \left ( x \right ) \left [ { f \left ( x \right ) – g \left ( x \right ) } \right ] d x } . m = a ∫ b ρ ( x ) [ f ( x ) – g ( x ) ] d x .
با قرار دادن تابع و حدود انتگرال، خواهیم داشت:
m = ∫ 0 π x sin x d x . \large m = \int \limits _ 0 ^ \pi { x \sin x d x } . m = 0 ∫ π x sin x d x .
برای محاسبه این انتگرال، از انتگرالگیری جزء به جزء استفاده میکنیم:
$$ \large \begin {align*}<br />
m & = \int \limits _ 0 ^ \pi { \underbrace x _ u \underbrace { \sin x d x } _ { d v } } = { \left [ { \begin {array} { * { 2 0 } { l } }<br />
{ u = x } \\<br />
{ d v = \sin x d x } \\<br />
{ d u = d x } \\<br />
{ v = – \cos x }<br />
\end {array} } \right ] } = { \left . { \left ( { – x \cos x } \right ) } \right | _ 0 ^ \pi – \int \limits _ 0 ^ \pi { \left ( { – \cos x } \right ) d x } } \\ & = { \left . { \left ( { – x \cos x } \right ) } \right | _ 0 ^ \pi + \int \limits _ 0 ^ \pi { \cos x d x } } = { \left . { \left ( { \sin x – x \cos x } \right ) } \right | _ 0 ^ \pi } = { \pi . }<br />
\end {align*} $$
اگر چگالی ρ ( x ) {\rho \left( x \right)} ρ ( x ) kg m \large{\frac{\text{kg}}{\text{m}}}\normalsize m kg x x x m \text{m} m m = π kg m = \pi\,\text{kg} m = π kg
مثال ۷
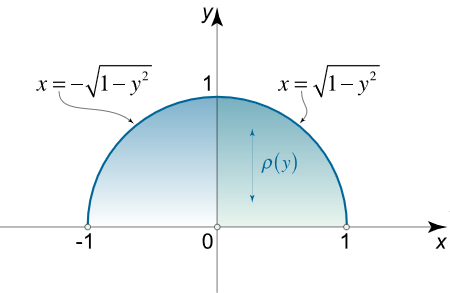
لایهای یک نیمدایره بالایی به شعاع ۱ و به مرکز مبدأ را در بر گرفته است. چگالی این لایه با تابع ρ ( y ) = y 3 \rho \left( y \right) = {y^3} ρ ( y ) = y 3
حل: تابع چگالی در طول محور y y y
m = ∫ c d ρ ( y ) [ f ( y ) – g ( y ) ] d y . \large m = \int \limits _ c ^ d { \rho \left ( y \right ) \left [ { f \left ( y \right ) – g \left ( y \right ) } \right ] d y } . m = c ∫ d ρ ( y ) [ f ( y ) – g ( y ) ] d y .
به دلیل تقارن نسبت به محور y y y
شکل ۱۰ معادله دایره در ربع اول x = f ( y ) = 1 – y 2 x = f\left( y \right) = \sqrt {1 – {y^2}} x = f ( y ) = 1– y 2
m = 2 ∫ 0 1 y 3 1 – y 2 d y . \large m = 2 \int \limits _ 0 ^ 1 { { y ^ 3 } \sqrt { 1 – { y ^ 2 } } d y } . m = 2 0 ∫ 1 y 3 1– y 2 d y .
برای محاسبه انتگرال، از تغییر متغیر زیر استفاده میکنیم:
1 – y 2 = z 2 , ⇒ y 2 = 1 – z 2 , y d y = – z d z , y 3 d y = ( 1 – z 2 ) ( – z d z ) = ( z 3 – z ) d z . \large \begin {align*} 1 – { y ^ 2 } & = { z ^2 } , \; \; \Rightarrow { { y ^ 2 } = 1 – { z ^ 2 } , \; \; } \kern0pt { y d y = – z d z , \; \; } \kern0pt \\ { y ^ 3 } d y & = \left ( { 1 – { z ^ 2 } } \right ) \left ( { – z d z } \right ) = { \left ( { { z ^ 3 } – z } \right ) d z . } \end {align*} 1– y 2 y 3 d y = z 2 , ⇒ y 2 = 1– z 2 , y d y = – z d z , = ( 1– z 2 ) ( – z d z ) = ( z 3 – z ) d z .
وقتی y = 0 y=0 y = 0 z = 1 z = 1 z = 1 y = 1 y = 1 y = 1 z = 0 z = 0 z = 0 z z z
m = 2 ∫ 1 0 ( z 3 – z ) z d z = 2 ∫ 1 0 ( z 4 – z 2 ) d z = 2 [ z 5 5 – z 3 3 ] ∣ 1 0 = 2 [ 0 – ( 1 5 – 1 3 ) ] = 2 ( 1 3 – 1 5 ) = 4 15 . \large \begin {align*} m & = 2 \int \limits _ 1 ^ 0 { \left ( { { z ^ 3 } – z } \right ) z d z } = { 2 \int \limits _ 1 ^ 0 { \left ( { { z ^ 4 } – { z ^ 2 } } \right ) d z } } = { 2 \left . { \left [ { \frac { { { z ^ 5 } } } { 5 } – \frac { {{ z ^ 3 } } } { 3 } } \right ] } \right | _ 1 ^ 0 } \\ & = { 2 \left [ { 0 – \left ( { \frac { 1 } { 5 } – \frac { 1 } { 3 } } \right ) } \right ] } = { 2 \left ( { \frac { 1 } { 3 } – \frac { 1 } { 5 } } \right ) } = { \frac { 4 } { { 1 5 } } . } \end {align*} m = 2 1 ∫ 0 ( z 3 – z ) z d z = 2 1 ∫ 0 ( z 4 – z 2 ) d z = 2 [ 5 z 5 – 3 z 3 ] 1 0 = 2 [ 0– ( 5 1 – 3 1 ) ] = 2 ( 3 1 – 5 1 ) = 15 4 .
مثال ۸
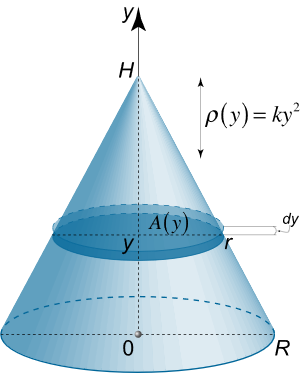
یک مخروط دایرهای قائم با شعاع قاعده R R R H H H ρ ( y ) = k y 2 \rho \left( y \right) = k{y^2} ρ ( y ) = k y 2
شکل ۱۱ حل: یک برش نازک را در ارتفاع y y y r r r
r R = H – y H , ⇒ r = R H ( H – y ) . \large { \frac { r } { R } = \frac { { H – y } } { H } , } \; \; \Rightarrow { r = \frac { R } { H } \left ( { H – y } \right ) . } R r = H H – y , ⇒ r = H R ( H – y ) .
جرم برش به ضخامت d y dy d y
d m = ρ ( y ) d V = π r 2 ρ ( y ) d y = π R 2 ρ ( y ) ( H – y ) 2 H 2 d y = π k R 2 y 2 ( H – y ) 2 H 2 d y . \large \begin {align*} d m & = \rho \left ( y \right ) d V = \pi { r ^ 2 } \rho \left ( y \right ) d y \\ & = { \frac { { \pi { R ^ 2 } \rho \left ( y \right ) { { \left ( { H – y } \right ) } ^ 2 } } } { { { H ^ 2 } } } d y } = { \frac { { \pi k { R ^ 2 } { y ^ 2 } { { \left ( { H – y } \right ) } ^ 2 } } } { { { H ^ 2 } } } d y . } \end {align*} d m = ρ ( y ) d V = π r 2 ρ ( y ) d y = H 2 π R 2 ρ ( y ) ( H – y ) 2 d y = H 2 πk R 2 y 2 ( H – y ) 2 d y .
برای محاسبه کل جرم مخروط، از y = 0 y= 0 y = 0 y = H y = H y = H
m = π k R 2 H 2 ∫ 0 H y 2 ( H – y ) 2 d y = π k R 2 H 2 ∫ 0 H y 2 ( H 2 – 2 H y + y 2 ) d y = π k R 2 H 2 ∫ 0 H ( H 2 y 2 – 2 H y 3 + y 4 ) d y = π k R 2 H 2 ( H 2 y 3 3 – H y 4 2 + y 5 5 ) ∣ 0 H = π k R 2 H 3 ( 1 3 – 1 2 + 1 5 ) = π k R 2 H 3 30 . \large \begin {align*} m & = \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \int \limits _ 0 ^ H { { y ^ 2 } { { \left ( { H – y } \right ) } ^ 2 } d y } \\ & = { \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \int \limits _ 0 ^ H { { y ^ 2 } \left ( { { H ^ 2 } – 2 H y + { y ^ 2 } } \right ) d y } } \\ & = { \frac { { \pi k { R ^ 2 } } }{ { { H ^ 2 } } } \int \limits _ 0 ^ H { \left ( { { H ^ 2 } { y ^ 2 } – 2 H { y ^ 3 } + { y ^ 4 } } \right ) d y } } \\ & = { \frac { { \pi k { R ^ 2 } } } {{ { H ^ 2 } } } \left . { \left ( { \frac { { { H ^ 2 } { y ^ 3 }} } { 3 } – \frac { { H { y ^ 4 } } } { 2 } + \frac { { { y ^ 5 } } } { 5 } } \right ) } \right | _ 0 ^ H } \\ & = { \pi k { R ^ 2 } { H ^ 3 } \left ( { \frac { 1 } { 3 } – \frac { 1 }{ 2 } + \frac { 1 } { 5 } } \right ) } = { \frac { { \pi k { R ^ 2 } { H ^ 3 } } } { { 3 0 } } . } \end {align*} m = H 2 πk R 2 0 ∫ H y 2 ( H – y ) 2 d y = H 2 πk R 2 0 ∫ H y 2 ( H 2 –2 Hy + y 2 ) d y = H 2 πk R 2 0 ∫ H ( H 2 y 2 –2 H y 3 + y 4 ) d y = H 2 πk R 2 ( 3 H 2 y 3 – 2 H y 4 + 5 y 5 ) 0 H = πk R 2 H 3 ( 3 1 – 2 1 + 5 1 ) = 30 πk R 2 H 3 .
صحت جواب را با تحلیل واحدها بررسی میکنیم. چگالی با تابع ρ ( y ) = k y 2 \rho \left( y \right) = k{y^2} ρ ( y ) = k y 2 y y y k k k kg m 5 \large{\frac{\text{kg}}{\text{m}^5}}\normalsize m 5 kg
$$ \large \require {cancel} { { m } = { \frac { { \pi k { R ^ 2 } { H ^ 3 } } } { { 3 0 } } } } = { \left [ { \frac { { k g } } { { { m ^ 5 } } } } \right ] \left [ { { m ^ 2 } } \right ] \left [ { { m ^ 3 } } \right ] } = { \frac { { \left [ { k g } \right ] \cancel { \left [ { { m ^ 5 } } \right ] } } } { { \cancel { \left [ { { m ^ 5 } } \right ] } } } } = { \left [ { k g } \right ] . } $$
مثال ۹
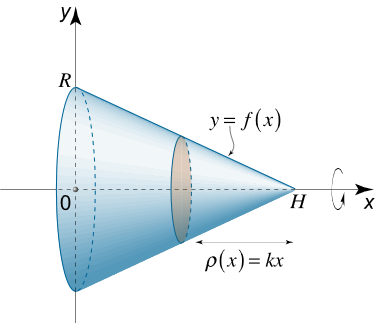
یک مخروط دایرهای را به شعاع قاعده R R R H H H x x x ρ ( x ) = k x \rho \left( x \right) = kx ρ ( x ) = k x
شکل ۱۲ حل: جرم مخروط از فرمول زیر به دست میآید:
m = π ∫ a b ρ ( x ) f 2 ( x ) d x . \large m = \pi \int \limits _ a ^ b { \rho \left ( x \right ){ f ^ 2 } \left ( x \right ) d x } . m = π a ∫ b ρ ( x ) f 2 ( x ) d x .
معادله خط راست y = f ( x ) y = f\left( x \right) y = f ( x )
y = f ( x ) = R – R H x = R H ( H – x ) . \large { y = f \left ( x \right ) } = { R – \frac { R } { H } x } = { \frac { R } { H } \left ( { H – x } \right ) . } y = f ( x ) = R – H R x = H R ( H – x ) .
با جایگذاری تابع چگالی ρ ( x ) = k x \rho \left( x \right) = kx ρ ( x ) = k x x = 0 x = 0 x = 0 x = H x = H x = H
m = π ∫ 0 H k x R 2 H 2 ( H – x ) 2 d x = π k R 2 H 2 ∫ 0 H x ( H – x ) 2 d x = π k R 2 H 2 ∫ 0 H x ( H 2 – 2 H x + x 2 ) d x = π k R 2 H 2 ∫ 0 H ( H 2 x – 2 H x 2 + x 3 ) d x = π k R 2 H 2 ( H 2 x 2 2 – 2 H x 3 3 + x 4 4 ) ∣ 0 H = π k R 2 H 2 ( 1 2 – 2 3 + 1 4 ) = 5 π k R 2 H 2 12 . \large \begin {align*} m & = \pi \int \limits _ 0 ^ H { k x \frac { {{ R ^ 2 } } } { { { H ^ 2 } } } { { \left ( { H – x } \right ) } ^ 2 } d x } \\ & = { \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \int \limits _ 0 ^ H { x { { \left ( { H – x } \right ) } ^ 2 } d x } } \\ & = { \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \int \limits _ 0 ^ H { x \left ( { { H ^ 2 } – 2 H x + { x ^ 2 } } \right ) d x } } \\ &= { \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \int \limits _ 0 ^ H { \left ( { { H ^ 2 } x – 2 H { x ^ 2 } + { x ^ 3 } } \right ) d x } } \\ & = { \frac { { \pi k { R ^ 2 } } } { { { H ^ 2 } } } \left . { \left ( { \frac { { { H ^ 2 } { x ^ 2 } } }{ 2 } – \frac { { 2 H { x ^ 3 } } } { 3 } + \frac { { { x ^ 4 } } } {4 } } \right ) } \right | _ 0 ^ H } \\ & = { \pi k { R ^ 2 } { H ^ 2 } \left ( { \frac { 1 } { 2 } – \frac { 2 } { 3 } + \frac { 1 } { 4 } } \right ) } = { \frac { { 5 \pi k { R ^ 2 } { H ^ 2 } } } { { 1 2 } } . } \end {align*} m = π 0 ∫ H k x H 2 R 2 ( H – x ) 2 d x = H 2 πk R 2 0 ∫ H x ( H – x ) 2 d x = H 2 πk R 2 0 ∫ H x ( H 2 –2 H x + x 2 ) d x = H 2 πk R 2 0 ∫ H ( H 2 x –2 H x 2 + x 3 ) d x = H 2 πk R 2 ( 2 H 2 x 2 – 3 2 H x 3 + 4 x 4 ) 0 H = πk R 2 H 2 ( 2 1 – 3 2 + 4 1 ) = 12 5 πk R 2 H 2 .
لازم به ذکر است که اگر شعاع و ارتفاع مخروط برحسب متر، و جرم برحسب کیلوگرم اندازهگیری شوند، ضریب k k k kg m 4 {\large{\frac{{\text{kg}}}{{{\text{m}^4}}}}\normalsize} m 4 kg
مثال ۱۰
چگالی هسته درونی زمین تقریباً 13000 kg m 3 13000\,\large{\frac{\text{kg}}{\text{m}^3}}\normalsize 13000 m 3 kg 1000 kg m 3 1000\,\large{\frac{\text{kg}}{\text{m}^3}}\normalsize 1000 m 3 kg 6200 km 6200\,\text{km} 6200 km
شکل ۱۳ حل: ابتدا معادله مربوط به محاسبه جرم یک گوی با توزیع چگالی خطی را به دست میآوریم. اگر یک لایه دلخواه با ضخامت d r d r d r r r r
d V = 4 π r 2 d r . \large d V = 4 \pi { r ^ 2 } d r . d V = 4 π r 2 d r .
جرم لایه نیز برابر است با:
d m = ρ ( r ) d V = 4 π ρ ( r ) r 2 d r . \large { d m = \rho \left ( r \right ) d V } = { 4 \pi \rho \left ( r \right ) { r ^ 2 } d r . } d m = ρ ( r ) d V = 4 π ρ ( r ) r 2 d r .
بنابراین، جرم کل گوی با فرمول زیر محاسبه خواهد شد:
m = 4 π ∫ 0 R ρ ( r ) r 2 d r . \large m = 4 \pi \int \limits _ 0 ^ R { \rho \left ( r \right ){ r ^ 2 } d r } . m = 4 π 0 ∫ R ρ ( r ) r 2 d r .
با فرض اینکه چگالی به صورت خطی کاهش پیدا کند، آن را به فرم ρ ( r ) = a – b r \rho \left( r \right) = a – br ρ ( r ) = a – b r a a a b b b
m = 4 π ∫ 0 R ( a – b r ) r 2 d r = 4 π ∫ 0 R ( a r 2 – b r 3 ) d r = 4 π ( a r 3 3 – b r 4 4 ) ∣ 0 R = 4 π ( a R 3 3 – b R 4 4 ) . \large \begin {align*} m & = 4 \pi \int \limits _ 0 ^ R { \left ( { a – b r } \right ){ r ^ 2 } d r } = { 4 \pi \int \limits _ 0 ^ R { \left ( { a { r ^ 2 } – b { r ^ 3 } } \right ) d r } } \\ & = { 4 \pi \left . { \left ( { \frac { { a { r ^ 3 } } } { 3 } – \frac { { b { r ^ 4 } } } { 4 } } \right ) } \right | _ 0 ^ R } = { 4 \pi \left ( { \frac { { a { R ^ 3 } } } { 3 } – \frac { { b { R ^ 4 } } } { 4 } } \right ) . } \end {align*} m = 4 π 0 ∫ R ( a – b r ) r 2 d r = 4 π 0 ∫ R ( a r 2 – b r 3 ) d r = 4 π ( 3 a r 3 – 4 b r 4 ) 0 R = 4 π ( 3 a R 3 – 4 b R 4 ) .
اکنون، با استفاده از شرایط مسئله، ضرایب a a a b b b
ρ ( 0 ) = 13000 kg m 3 , ρ ( R ) = 1000 kg m 3 , R = 6200 km = 6.2 × 1 0 6 m, \large { \rho \left ( 0 \right ) = 1 3 0 0 0 \frac { { \text {kg} } } { { { \text {m} ^ 3 } } } , \; \; } \kern0pt { \rho \left ( R \right ) = 1 0 0 0 \frac { { \text {kg} } } { { { \text{m} ^ 3 } } } , \; \; } \kern0pt { R = 6 2 0 0 \, \text {km} = 6 . 2 \times 1 0 ^ 6 \, \text {m,} } ρ ( 0 ) = 13000 m 3 kg , ρ ( R ) = 1000 m 3 kg , R = 6200 km = 6.2 × 1 0 6 m,
با استفاده از فرمول دونقطهای یک خط راست، داریم:
ρ ( r ) – ρ ( 0 ) ρ ( R ) – ρ ( 0 ) = r – 0 R – 0 , ⇒ ρ ( r ) = ρ ( 0 ) + ρ ( R ) – ρ ( 0 ) R r = 13000 + 1000 – 13000 6.2 × 10 6 r = 13000 – 1.935 × 1 0 – 3 r . \large \begin{align*} & \frac { { \rho \left ( r \right ) – \rho \left ( 0 \right ) } } { { \rho \left ( R \right ) – \rho \left( 0 \right ) } } = \frac { { r – 0 } } { { R – 0 } } , \; \; \Rightarrow { \rho \left ( r \right ) = \rho \left ( 0 \right ) + \frac { { \rho \left ( R \right ) – \rho \left ( 0 \right ) } } { R } r } \\ &= { 1 3 0 0 0 + \frac { { 1 0 0 0 – 1 3 0 0 0 } } { { 6 . 2 \times { { 1 0 } ^ 6 } } } r } = { 1 3 0 0 0 – 1 . 9 3 5 \times { 1 0 ^ { – 3 } } r . } \end {align*} ρ ( R ) – ρ ( 0 ) ρ ( r ) – ρ ( 0 ) = R –0 r –0 , ⇒ ρ ( r ) = ρ ( 0 ) + R ρ ( R ) – ρ ( 0 ) r = 13000 + 6.2 × 10 6 1000–13000 r = 13000–1.935 × 1 0 –3 r .
بنابراین، a = 13000 a = 13000 a = 13000 b = 1.935 × 1 0 − 3 b = 1.935\times{10^{-3}} b = 1.935 × 1 0 − 3
اکنون میتوانیم کل جرم زمین را محاسبه کنیم:
m = 4 π ( a R 3 3 – b R 4 4 ) = 4 π [ 1.3 × 10 4 × ( 6.2 × 10 6 ) 3 3 − 1.935 × 10 – 3 × ( 6.2 × 10 6 ) 4 4 ] = 4 π [ 103.28 × 10 22 – 714.81 × 10 21 ] ≈ 4 × 1 0 24 kg . \large \begin{align*} m & = 4 \pi \left ( { \frac { { a { R ^ 3 } } } { 3 } – \frac { { b { R ^ 4 } } } { 4 } } \right ) \\ & = { 4 \pi \left [ { \frac { { 1 . 3 \times { { 1 0 } ^ 4 } \times { { \left ( { 6 . 2 \times { { 1 0 } ^ 6 } } \right ) } ^ 3 } } } { 3 } } \right . } - { \left . { \frac { { 1 . 9 3 5 \times { { 1 0 } ^ { – 3 } } \times { { \left ( { 6 . 2 \times { { 1 0 } ^ 6 } } \right ) } ^ 4 } } } { 4 } } \right ] } \\ & = { 4 \pi \left [ { 1 0 3 . 2 8 \times { { 1 0 } ^ { 2 2 } } – 7 1 4 . 8 1 \times { { 1 0 } ^ { 2 1 } } } \right ] } \approx { 4 \times { 1 0 ^ { 2 4 } } \, \text {kg} . } \end {align*} m = 4 π ( 3 a R 3 – 4 b R 4 ) = 4 π 3 1.3 × 10 4 × ( 6.2 × 10 6 ) 3 − 4 1.935 × 10 –3 × ( 6.2 × 10 6 ) 4 = 4 π [ 103.28 × 10 22 –714.81 × 10 21 ] ≈ 4 × 1 0 24 kg .
این نتیجه، تقریباً ۳۰ درصد کمتر از جرم واقعی زمین (6 × 1 0 24 kg 6 \times {10^{24}}\,\text{kg} 6 × 1 0 24 kg
اگر به یادگیری مباحث مشابه مطلب بالا علاقهمند هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^