در آموزشهای قبلی مجله فرادرس، انتگرال خطی را معرفی کردیم. انتگرال خطی کاربردهای مختلفی در ریاضیات، فیزیک و مهندسی دارد. در این آموزش، کاربردهای انتگرال خطی در هندسه را بررسی میکنیم. به طور خاص، کاربرد انتگرال خطی را در موارد زیر معرفی میکنیم:
طول منحنی
مساحت ناحیه محدود به یک منحنی بسته
حجم حاصل از دوران یک منحنی بسته حول یک خط
در ادامه، هر یک از این موارد را توضیح خواهیم داد.
طول یک منحنی
فرض کنید C C C α ≤ t ≤ β \alpha \le t \le \beta α ≤ t ≤ β r ( t ) \mathbf{r}\left( t \right) r ( t ) انتگرال زیر محاسبه کرد:
L = ∫ C d s = ∫ α β ∣ d r d t ( t ) ∣ d t = ∫ α β ( d x d t ) 2 + ( d y d t ) 2 + ( d z d t ) 2 d t \large { L = \int\limits _ C { d s } } = { \int \limits _ \alpha ^ \beta { \left | { \frac { { d \mathbf { r } } } { { d t } } \left ( t \right ) } \right | d t } \text { = } } \kern0pt { \int \limits _ \alpha ^ \beta { \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d z } } { { d t } } } \right ) } ^ 2 } } d t } } L = C ∫ d s = α ∫ β d t d r ( t ) d t = α ∫ β ( d t d x ) 2 + ( d t d y ) 2 + ( d t d z ) 2 d t
که در آن d r d t \large\frac{{d\mathbf{r}}}{{dt}}\normalsize d t d r مشتق و x ( t ) x (t) x ( t ) y ( t ) y(t) y ( t ) z ( t ) z (t) z ( t ) بردار موقعیت r ( t ) \mathbf{r}\left( t \right) r ( t )
اگر منحنی C C C
L = ∫ C d s = ∫ α β ∣ d r d t ( t ) ∣ d t = ∫ α β ( d x d t ) 2 + ( d y d t ) 2 d t . \large { L = \int \limits _ C { d s} } = { \int \limits _ \alpha ^ \beta { \left | { \frac { { d \mathbf { r } } } { { d t } } \left ( t \right ) } \right | d t } } = { \int \limits _ \alpha ^ \beta { \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2} + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } d t } . } L = C ∫ d s = α ∫ β d t d r ( t ) d t = α ∫ β ( d t d x ) 2 + ( d t d y ) 2 d t .
اگر منحنی C C C y = f ( x ) y = f (x ) y = f ( x ) x y xy x y
L = ∫ a b 1 + ( d y d x ) 2 d x . \large L = \int \limits _ a ^ b { \sqrt { 1 + { { \left ( { \frac { { d y } } { { d x } } } \right ) } ^ 2 } } d x } . L = a ∫ b 1 + ( d x d y ) 2 d x .
در نهایت، اگر منحنی C C C r = r ( θ ) r = r\left( \theta \right) r = r ( θ ) α ≤ θ ≤ β \alpha \le \theta \le \beta α ≤ θ ≤ β مختصات قطبی تعریف شده و r ( θ ) r (\theta ) r ( θ ) [ α , β ] \left[ {\alpha ,\beta } \right] [ α , β ] پیوسته و مشتقپذیر باشد، طول منحنی با فرمول زیر قابل محاسبه است:
L = ∫ α β ( d r d θ ) 2 + r 2 d θ . \large L = \int \limits _ \alpha ^ \beta { \sqrt { { { \left ( { \frac { { d r } } { { d \theta } } } \right ) } ^ 2 } + { r ^ 2 } } d \theta } . L = α ∫ β ( d θ d r ) 2 + r 2 d θ .
مساحت ناحیه محصور در یک منحنی بسته
اگر C C C صفحه x y xy x y باشد (شکل ۱)، مساحت ناحیه R R R
S = ∮ C x d y = – ∮ C y d x = 1 2 ∫ C x d y – y d x . \large { S = \oint \limits _ C { x d y } } = { – \oint \limits _ C { y d x } } = { \frac { 1 } { 2 } \int \limits _ C { x d y – y d x } . } S = C ∮ x d y = – C ∮ y d x = 2 1 C ∫ x d y – y d x .
شکل ۱ در اینجا فرض شده که کانتور C C C
اگر منحنی بسته C C C r ( t ) = ( x ( t ) , y ( t ) ) \mathbf { r } \left ( t \right ) = \left ( { x \left ( t \right ) , y \left ( t \right ) } \right ) r ( t ) = ( x ( t ) , y ( t ) )
S = ∫ α β x ( t ) d y d t d t = – ∫ α β y ( t ) d x d t d t = 1 2 ∫ α β [ x ( t ) d y d t − y ( t ) d x d t ] d t . \large \begin {align*}\large S & = \int \limits _ \alpha ^ \beta { x \left ( t \right ) \frac { { d y } } { { d t } } d t } = { – \int \limits _ \alpha ^ \beta { y \left ( t \right ) \frac { { d x } } { { d t } } d t } } \\ & = { \frac { 1 } { 2 } \int \limits _ \alpha ^ \beta { \left [ { x \left ( t \right ) \frac { { d y } } { { d t } } } \right . } - { \left . { y \left ( t \right ) \frac { { d x } } { { d t } } } \right ] d t . } } \end {align*} S = α ∫ β x ( t ) d t d y d t = – α ∫ β y ( t ) d t d x d t = 2 1 α ∫ β [ x ( t ) d t d y − y ( t ) d t d x ] d t .
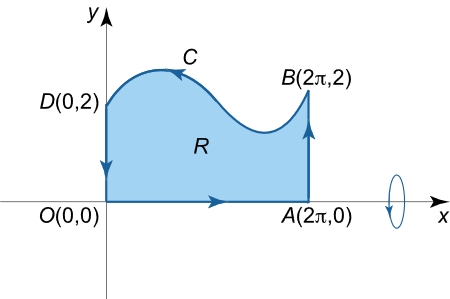
حجم حاصل از دوران یک منحنی بسته حول محور x \LARGE{x} x
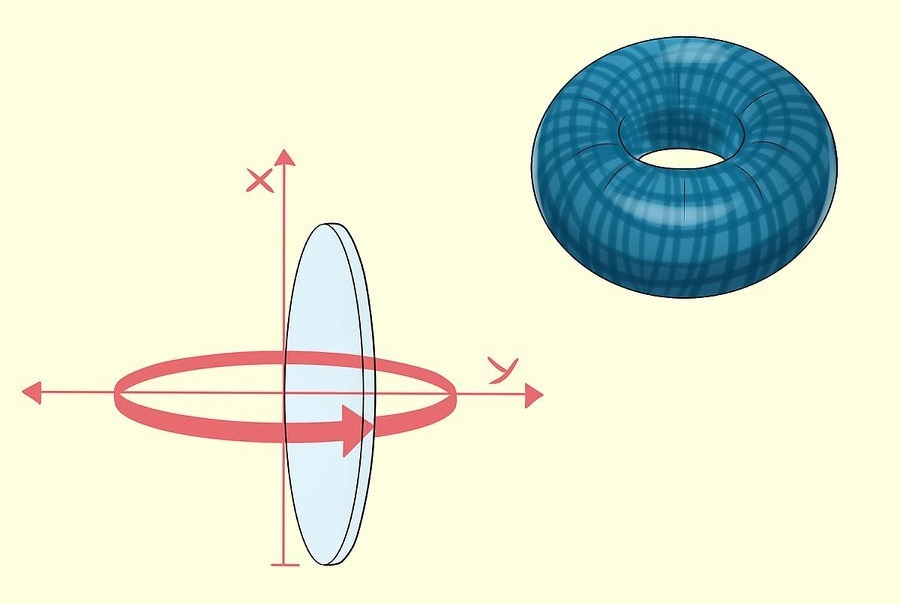
فرض کنید R R R y ≥ 0 y \ge 0 y ≥ 0 C C C
همچنین فرض کنید حجم Ω \Omega Ω R R R x x x
شکل ۲ در نتیجه، حجم به صورت زیر خواهد بود:
V = – π ∮ C y 2 d x = – 2 π ∮ C x y d y = – π 2 ∮ C 2 x y d y + y 2 d x . \large { V = – \pi \oint \limits _ C { { y ^ 2 } d x } } = { – 2 \pi \oint \limits _ C { x y d y} } = { – \frac { \pi }{ 2 } \oint \limits _ C { 2 x y d y + { y ^ 2 } d x } . } V = – π C ∮ y 2 d x = –2 π C ∮ x y d y = – 2 π C ∮ 2 x y d y + y 2 d x .
مثالهای حل شده کاربردهای انتگرال خطی
در ادامه، چند مثال حل شده را بررسی میکنیم.
مثال ۱
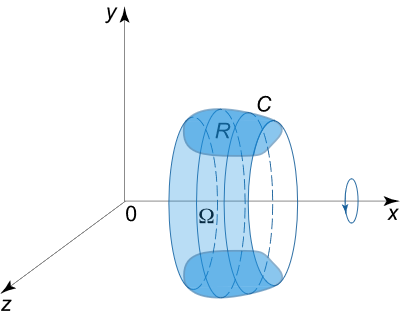
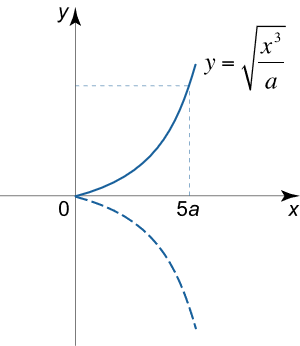
طول کمان منحنی a y 2 = x 3 a{y^2} = {x^3} a y 2 = x 3 0 ≤ x ≤ 5 a 0 \le x \le 5a 0 ≤ x ≤ 5 a y ≥ 0 y \ge 0 y ≥ 0
حل: میتوانیم تابع را به صورت y 2 = x 3 a {y^2} = {\large\frac{{{x^3}}}{a}\normalsize} y 2 = a x 3 y = ± x 3 a y = \pm \sqrt {\large\frac{{{x^3}}}{a}\normalsize} y = ± a x 3 y ≥ 0 y \ge 0 y ≥ 0
شکل ۳ بنابراین، طول کمان به صورت زیر محاسبه میشود:
L = ∫ 0 5 a 1 + [ f ’ ( x ) ] 2 d x = ∫ 0 5 a 1 + [ d d x ( x 3 a ) ] 2 d x = ∫ 0 5 a 1 + [ 3 x 2 a 2 x 3 a ] 2 d x = ∫ 0 5 a 1 + [ 3 x 2 a ] 2 d x = ∫ 0 5 a 1 + 9 x 4 a d x = 1 2 a ∫ 0 5 a 4 a + 9 x d x = 1 18 a [ ( ( 9 x + 4 a ) 3 2 3 2 ) ∣ x = 0 5 a ] = 1 27 a [ ( 45 a + 4 a ) 3 2 – ( 4 a ) 3 2 ] = 1 27 a [ ( 49 a ) 3 – ( 4 a ) 3 ] = a 27 ( 49 3 – 4 3 ) = a 27 ( 7 3 – 2 3 ) = 335 27 . \large \begin {align*} L & = \int \limits _ 0 ^ { 5 a } { \sqrt { 1 + { { \left [ { f ’ \left ( x \right ) } \right ] } ^ 2 } } d x } = { \int \limits _ 0 ^ { 5 a } { \sqrt { 1 + { { \left [ { \frac { d } { { d x } } \left ( { \sqrt { \frac { { { x ^ 3 } } } { a } } } \right ) } \right ] } ^ 2 } } d x } } \\ &= { \int \limits _ 0 ^ { 5 a } { \sqrt { 1 + { { \left [ { \frac { { \frac { { 3 { x ^ 2 } } } { a } } } { { 2 \sqrt { \frac { { { x ^ 3 } } } { a } } } } } \right ] } ^ 2 } } d x } } = { \int \limits _ 0 ^ { 5 a } { \sqrt { 1 + { { \left [ { \frac { { 3 \sqrt x } } { { 2 \sqrt a } } } \right ] } ^ 2 } } d x } } \\ &= { \int \limits _ 0 ^ { 5 a } { \sqrt { 1 + \frac { { 9 x } } { { 4 a } } } d x } } = { \frac { 1 } { { 2 \sqrt a } } \int \limits _ 0 ^ { 5 a } { \sqrt { 4 a + 9 x } d x } } \\ & = { \frac { 1 } { { 1 8 \sqrt a } } \left [ { \left . { \left ( { \frac { { { { \left ( { 9 x + 4 a } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 3 } { 2 } } } } \right ) } \right | _ { x = 0 } ^ { 5 a } } \right ] } \\ &= { \frac { 1 } { { 2 7 \sqrt a } } \left [ { { { \left ( { 4 5 a + 4 a } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } – { { \left ( { 4 a } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } \right ] } \\ & = { \frac { 1 } { { 2 7 \sqrt a } } \left [ { \sqrt { { { \left ( { 4 9 a } \right ) } ^ 3 } } – \sqrt { { { \left ( { 4 a } \right ) } ^ 3 } } } \right] } \\ & = { \frac { a } {{ 2 7 } } \left ( { \sqrt { {{ 4 9 } ^ 3 } } – \sqrt { { 4 ^ 3 } } } \right ) } = { \frac { a } { { 2 7 } } \left ( { { 7 ^ 3 } – { 2 ^ 3 } } \right ) } = { \frac { { 3 3 5 } } { { 2 7 } } . } \end {align*} L = 0 ∫ 5 a 1 + [ f ’ ( x ) ] 2 d x = 0 ∫ 5 a 1 + d x d a x 3 2 d x = 0 ∫ 5 a 1 + 2 a x 3 a 3 x 2 2 d x = 0 ∫ 5 a 1 + [ 2 a 3 x ] 2 d x = 0 ∫ 5 a 1 + 4 a 9 x d x = 2 a 1 0 ∫ 5 a 4 a + 9 x d x = 18 a 1 2 3 ( 9 x + 4 a ) 2 3 x = 0 5 a = 27 a 1 [ ( 45 a + 4 a ) 2 3 – ( 4 a ) 2 3 ] = 27 a 1 [ ( 49 a ) 3 – ( 4 a ) 3 ] = 27 a ( 49 3 – 4 3 ) = 27 a ( 7 3 – 2 3 ) = 27 335 .
مثال ۲
طول ستارهگون x 2 3 + y 2 3 = a 2 3 { x ^ { \large \frac { 2 } { 3 } \normalsize } } + { y ^ { \large \frac { 2 }{ 3 } \normalsize } } = { a ^ { \large \frac { 2 } { 3 } \normalsize } } x 3 2 + y 3 2 = a 3 2
حل: ستارهگون در شکل ۴ نشان داده شده است.
شکل ۴ با توجه به تقارن ستارهگون، میتوانیم طول کمان ربع اول را محاسبه کرده و نتیجه را در 4 4 4
y = ( a 2 3 – x 2 3 ) 3 2 , x ∈ [ 0 , a ] . \large { y = { \left ( { { a ^ { \large \frac { 2 } { 3 } \normalsize } } – { x ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) ^ { \large \frac { 3 } { 2 } \normalsize } } , \; \; } \kern-0.3pt \, \, \, \, \kern-0.3pt { x \in \left [ { 0 , a } \right ] . \; } y = ( a 3 2 – x 3 2 ) 2 3 , x ∈ [ 0 , a ] .
بنابراین، داریم:
d y d x = 3 2 ( a 2 3 – x 2 3 ) 1 2 ( – 2 3 x – 1 3 ) = – ( a 2 3 – x 2 3 ) 1 2 x 1 3 \large { \frac { { d y } } { { d x } } \text { = } } \kern0pt { \frac { 3 } { 2 } { \left ( { { a ^ { \large \frac { 2 } { 3 } \normalsize } } – { x ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } \left ( { – \frac { 2 } { 3 } { x^ { – \large \frac { 1 } { 3 } \normalsize } } } \right ) } = { – \frac { { { { \left ( { { a ^ { \large \frac { 2 }{ 3 } \normalsize } } – { x ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } } {{ { x ^ { \large \frac { 1 } { 3 } \normalsize } } } } } d x d y = 2 3 ( a 3 2 – x 3 2 ) 2 1 ( – 3 2 x – 3 1 ) = – x 3 1 ( a 3 2 – x 3 2 ) 2 1
همچنین خواهیم داشت:
( d y d x ) 2 = [ – ( a 2 3 – x 2 3 ) 1 2 x 1 3 ] 2 = a 2 3 – x 2 3 x 2 3 = a 2 3 x 2 3 – 1. \large { { \left ( { \frac { { d y } } {{ d x } } } \right ) ^ 2 } \text { = } } \kern0pt { { \left [ { – \frac { { { { \left ( { { a ^ { \large \frac { 2 } { 3 } \normalsize } } – { x ^ { \large \frac { 2 } { 3 } \normalsize } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } }{ { { x ^ { \large \frac { 1 } { 3 } \normalsize } } } } } \right ] ^ 2 } } = { \frac { { { a ^ { \large \frac { 2 } { 3 } \normalsize } } – { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } { { { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } } = { \frac { { { a ^ { \large \frac { 2 } { 3 } \normalsize } } } } { { { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } – 1 . } ( d x d y ) 2 = – x 3 1 ( a 3 2 – x 3 2 ) 2 1 2 = x 3 2 a 3 2 – x 3 2 = x 3 2 a 3 2 –1.
در نتیجه، طول ستارهگون برابر است با:
L = 4 ∫ 0 a 1 + a 2 3 x 2 3 – 1 d x = 4 ∫ 0 a a 1 3 x 1 3 d x = 4 a 1 3 ∫ 0 a x – 1 3 d x = 4 a 1 3 [ ( x 2 3 2 3 ) ∣ 0 a ] = 4 a 1 3 ⋅ 3 2 a 2 3 = 6 a . \large \begin {align*} L & = 4 \int \limits _ 0 ^ a { \sqrt { 1 + \frac { { { a ^ { \large \frac { 2 }{ 3 } \normalsize } } } } { { { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } – 1 } \, d x } = { 4 \int \limits _ 0 ^ a { \frac { { { a ^ { \large \frac { 1 } { 3 } \normalsize } } } } { { { x ^ { \large \frac { 1 }{ 3 } \normalsize } } } } d x } } = { 4 { a ^ { \large \frac { 1 } { 3 } \normalsize } } \int \limits _ 0 ^ a { { x ^ { – \large \frac { 1 } { 3 } \normalsize } } d x } } \\ & = { 4 { a ^ { \large \frac { 1 } { 3 } \normalsize } } \left [ { \left . { \left ( { \frac { { { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } { { \frac { 2 } { 3 } } } } \right ) } \right | _ 0 ^ a } \right ] } = { 4 { a ^ { \large \frac { 1 } { 3 } \normalsize } } \cdot \frac { 3 } { 2 } { a ^ { \large \frac { 2 } { 3 } \normalsize } } } = { 6 a . } \end {align*} L = 4 0 ∫ a 1 + x 3 2 a 3 2 –1 d x = 4 0 ∫ a x 3 1 a 3 1 d x = 4 a 3 1 0 ∫ a x – 3 1 d x = 4 a 3 1 3 2 x 3 2 0 a = 4 a 3 1 ⋅ 2 3 a 3 2 = 6 a .
مثال ۳
طول یک منحنی فضایی را که با معادله پارامتری r ( t ) = ( 3 t , 3 t 2 , 2 t 3 ) \mathbf { r } \left ( t \right ) = \left ( { 3 t , 3 { t ^ 2 } , 2 { t ^ 3 } } \right ) r ( t ) = ( 3 t , 3 t 2 , 2 t 3 ) 0 ≤ t ≤ 1 0 \le t \le 1 0 ≤ t ≤ 1
حل: از فرمول زیر استفاده میکنیم:
L = ∫ C d s = ∫ α β ( d x d t ) 2 + ( d y d t ) 2 + ( d z d t ) 2 d t \large { L = \int \limits _ C { d s } \text { = } } \kern0pt { \int \limits _ \alpha ^ \beta { \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d z } } { { d t } } } \right ) } ^ 2 } } d t } } L = C ∫ d s = α ∫ β ( d t d x ) 2 + ( d t d y ) 2 + ( d t d z ) 2 d t
بنابراین، داریم:
L = ∫ C d s = ∫ 0 1 3 2 + ( 6 t ) 2 + ( 6 t 2 ) 2 d t = ∫ 0 1 9 + 36 t 2 + 36 t 4 d t = ∫ 0 1 ( 3 + 6 t 2 ) 2 d t = ∫ 0 1 ( 3 + 6 t 2 ) d t = ( 3 t + 2 t 3 ) ∣ 0 1 = 5. \large \begin {align*} L & = \int \limits _ C { d s } = { \int \limits _ 0 ^ 1 { \sqrt { { 3 ^ 2 } + { { \left ( { 6 t } \right ) } ^ 2 } + { { \left ( { 6 { t ^ 2 } } \right ) } ^ 2 } } d t } } \\ & = { \int \limits _ 0 ^ 1 { \sqrt { 9 + 3 6 { t ^ 2 } + 3 6 { t ^ 4 } } d t } } = { \int \limits _ 0 ^ 1 { \sqrt { { { \left ( { 3 + 6 { t ^ 2 } } \right ) } ^ 2 } } d t } } \\ & = { \int \limits _ 0 ^ 1 { \left ( { 3 + 6 { t ^ 2 } } \right ) d t } } = { \left . { \left ( { 3 t + 2 { t ^ 3 } } \right ) } \right | _ 0 ^ 1 } = { 5 . } \end {align*} L = C ∫ d s = 0 ∫ 1 3 2 + ( 6 t ) 2 + ( 6 t 2 ) 2 d t = 0 ∫ 1 9 + 36 t 2 + 36 t 4 d t = 0 ∫ 1 ( 3 + 6 t 2 ) 2 d t = 0 ∫ 1 ( 3 + 6 t 2 ) d t = ( 3 t + 2 t 3 ) 0 1 = 5.
مثال ۴
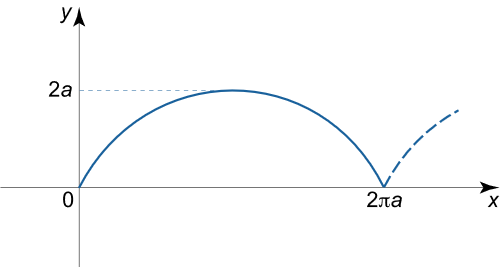
طول کمان یک چرخزاد را با معادله پارامتری r ( t ) = ( a ( t – sin t ) , a ( 1 – cos t ) ) \mathbf{r}\left( t \right) = \big( {a\left( {t – \sin t} \right),} {a\left( {1 – \cos t} \right)} \big) r ( t ) = ( a ( t – sin t ) , a ( 1– cos t ) ) 0 ≤ t ≤ 2 π 0 \le t \le 2\pi 0 ≤ t ≤ 2 π
شکل ۵ حل: از فرمول زیر استفاده میکنیم:
L = ∫ C d s = ∫ α β ( d x d t ) 2 + ( d y d t ) 2 d t . \large { L = \int \limits _ C { d s } } = { \int \limits _ \alpha ^ \beta { \sqrt { { { \left ( { \frac { { d x } } { { d t } } } \right ) } ^ 2 } + { { \left ( { \frac { { d y } } { { d t } } } \right ) } ^ 2 } } d t } . } L = C ∫ d s = α ∫ β ( d t d x ) 2 + ( d t d y ) 2 d t .
مشتقهای معادله بالا به صورت زیر هستند:
d x d t = d ( a ( t – sin t ) ) d t = a ( 1 – cos t ) , d y d t = d ( a ( 1 – cos t ) ) d t = a sin t . \large \begin {align*} \frac { { d x } } { { d t } } & = \frac { { d \left ( { a \left ( { t – \sin t } \right ) } \right ) } } { { d t } } = { a \left ( { 1 – \cos t } \right ) , } \\ \frac { { d y } } { { d t } } & = \frac { { d \left ( { a \left ( { 1 – \cos t } \right ) } \right ) } } { { d t } } = { a \sin t . } \end {align*} d t d x d t d y = d t d ( a ( t – sin t ) ) = a ( 1– cos t ) , = d t d ( a ( 1– cos t ) ) = a sin t .
بنابراین، طول چرخزاد برابر است با:
L = ∫ 0 2 ( a ( 1 – cos t ) ) 2 + ( a sin t ) 2 d t = ∫ 0 2 1 – 2 cos t + cos 2 t + sin 2 t d t = ∫ 0 2 2 – 2 cos t d t = a 2 ∫ 0 2 1 – cos t d t = a 2 ∫ 0 2 2 sin 2 ( t 2 ) d t = 2 a ∫ 0 2 sin t 2 d t = 2 a [ ( – cos t 2 1 2 ) ∣ t = 0 2 π ] = 4 a ( – cos π + cos 0 ) = 8 a . \large \begin {align*} L & = \kern0pt { \int \limits _ 0 ^ 2 { \sqrt { { { \left ( { a \left ( { 1 – \cos t } \right ) } \right ) } ^ 2 } + { { \left ( { a \sin t } \right ) } ^ 2 } } d t } } \\ & = { \int \limits _ 0 ^ 2 { \sqrt { 1 – 2 \cos t + { { \cos } ^ 2 } t + { { \sin } ^ 2 } t } \, d t } } = { \int \limits _ 0 ^ 2 { \sqrt { 2 – 2 \cos t } \, d t} } \\ & = { a \sqrt 2 \int \limits _ 0 ^ 2 { \sqrt { 1 – \cos t } \, d t } } = { a \sqrt 2 \int \limits _ 0 ^ 2 { \sqrt { 2 { { \sin } ^ 2 } \left ( { \frac { t } { 2 } } \right ) } d t } } = { 2 a \int \limits _ 0 ^ 2 { \sin \frac { t } { 2 } d t } } \\ & = { 2 a \left [ { \left . { \left ( { – \frac { { \cos \frac { t } { 2 } } } { { \frac { 1 } { 2 } } } } \right ) } \right | _ { t = 0 } ^ { 2 \pi } } \right ] } = { 4 a \left ( { – \cos \pi + \cos 0 } \right ) } = { 8 a . } \end {align*} L = 0 ∫ 2 ( a ( 1– cos t ) ) 2 + ( a sin t ) 2 d t = 0 ∫ 2 1–2 cos t + cos 2 t + sin 2 t d t = 0 ∫ 2 2–2 cos t d t = a 2 0 ∫ 2 1– cos t d t = a 2 0 ∫ 2 2 sin 2 ( 2 t ) d t = 2 a 0 ∫ 2 sin 2 t d t = 2 a ( – 2 1 cos 2 t ) t = 0 2 π = 4 a ( – cos π + cos 0 ) = 8 a .
مثال ۵
طول سهمی y = x 2 y = {x^2} y = x 2 0 ≤ x ≤ 1 0 \le x \le 1 0 ≤ x ≤ 1
حل: از فرمول زیر استفاده میکنیم:
L = ∫ a b 1 + [ f ’ ( x ) ] 2 d x \large L = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f ’ \left ( x \right ) } \right ] } ^ 2 } } d x } L = a ∫ b 1 + [ f ’ ( x ) ] 2 d x
بنابراین، داریم:
L = ∫ 0 1 1 + [ d ( x 2 ) d x ] 2 d x = ∫ 0 1 1 + ( 2 x ) 2 d x = ∫ 0 1 1 + 4 x 2 d x . \large { L } = { \int \limits _ 0 ^ 1 { \sqrt { 1 + { { \left [ { \frac { { d \left ( { { x ^ 2 } } \right ) } } { { d x } } } \right ] } ^ 2 } } d x } } = { \int \limits _ 0 ^ 1 { \sqrt { 1 + { { \left ( { 2 x } \right ) } ^ 2 } } d x } } = { \int \limits _ 0 ^ 1 { \sqrt { 1 + 4 { x ^ 2 } } d x } . } L = 0 ∫ 1 1 + [ d x d ( x 2 ) ] 2 d x = 0 ∫ 1 1 + ( 2 x ) 2 d x = 0 ∫ 1 1 + 4 x 2 d x .
برای محاسبه انتگرال، از تغییر متغیر x = 1 2 tan t x = {\large\frac{1}{2}\normalsize}\tan t x = 2 1 tan t d x = 1 2 d t cos 2 t dx = {\large\frac{1}{2}\normalsize} {\large\frac{{dt}}{{{{\cos }^2}t}}\normalsize} d x = 2 1 cos 2 t d t 2 x = tan t 2x = \tan t 2 x = tan t t = arctan ( 2 x ) t = \arctan \left( {2x} \right) t = arctan ( 2 x ) x = 0 x = 0 x = 0 t = arctan 0 = 0 t = \arctan 0 = 0 t = arctan 0 = 0 x = 1 x = 1 x = 1 t = arctan 2 t = \arctan 2 t = arctan 2
بنابراین، طول سهمی برابر است با:
L = ∫ 0 arctan 2 1 + tan 2 t ⋅ d t 2 cos 2 t − 1 2 ∫ 0 arctan 2 d t cos 3 t = 1 2 ∫ 0 arctan 2 cos t d t cos 4 t = 1 2 ∫ 0 arctan 2 d ( sin t ) ( 1 – sin 2 t ) 2 . \large \begin {align*} L & = { \int \limits _ 0 ^ { \arctan 2 } { \sqrt { 1 + { { \tan } ^ 2 } t } \cdot \frac { { d t } } { { 2 { { \cos } ^ 2 } t } } } } - { \frac { 1 } { 2 } \int \limits _ 0 ^ { \arctan 2 } { \frac { { d t } } { { { { \cos } ^ 3 } t } } } } \\ & = { \frac { 1 } { 2 } \int \limits _ 0 ^ { \arctan 2 } { \frac { { \cos t d t } } { { { { \cos } ^ 4 } t } } } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ { \arctan 2 } { \frac { { d \left ( { \sin t } \right ) } } { { { { \left ( { 1 – { \sin ^ 2 } t } \right ) } ^ 2 } } } } . } \end {align*} L = 0 ∫ a r c t a n 2 1 + tan 2 t ⋅ 2 cos 2 t d t − 2 1 0 ∫ a r c t a n 2 cos 3 t d t = 2 1 0 ∫ a r c t a n 2 cos 4 t cos t d t = 2 1 0 ∫ a r c t a n 2 ( 1– sin 2 t ) 2 d ( sin t ) .
از یک تغییر متغیر دیگر نیز استفاده میکنیم. بنابراین، sin t = z \sin t = z sin t = z t = 0 t = 0 t = 0 z = 0 z = 0 z = 0 t = arctan 2 t = \arctan 2 t = arctan 2
z = sin ( arctan 2 ) = [ tan ( arctan 2 ) ] 2 [ tan ( arctan 2 ) ] 2 + 1 = 2 2 2 2 + 1 = 2 5 . \large { z = \sin \left ( { \arctan 2 } \right ) } = { \sqrt { \frac { { { { \left [ { \tan \left ( { \arctan 2 } \right ) } \right ] } ^ 2 } } } { { { { \left [ { \tan \left ( { \arctan 2 } \right ) } \right ] } ^ 2 } + 1 } } } } = { \sqrt { \frac {{ { 2 ^ 2 } } } { { { 2 ^ 2 } + 1 } } } } = { \frac { 2 } { { \sqrt 5 } } . } z = sin ( arctan 2 ) = [ tan ( arctan 2 ) ] 2 + 1 [ tan ( arctan 2 ) ] 2 = 2 2 + 1 2 2 = 5 2 .
از اتحاد مثلثاتی زیر استفاده میکنیم:
sin α = tan 2 α tan 2 α + 1 . \large { \sin \alpha } = { \sqrt { \frac { { { { \tan } ^ 2 } \alpha } } { { { { \tan } ^ 2 } \alpha + 1 } } } . } sin α = tan 2 α + 1 tan 2 α .
در نتیجه، فرمول محاسبه طول منحنی به صورت زیر در خواهد آمد:
L = 1 2 ∫ 0 2 5 d z ( 1 – z 2 ) 2 = 1 2 ∫ 0 2 5 d z ( 1 – z ) 2 ( 1 + z ) 2 . \large { L = \frac { 1 } { 2 } \int \limits _ 0 ^ { \frac { 2 } { { \sqrt 5 } } } { \frac { { d z } } { { { { \left ( { 1 – { z ^ 2 } } \right ) } ^ 2 } } } } } = { \frac { 1 } { 2 } \int \limits _ 0 ^ { \frac { 2 } { { \sqrt 5 } } } { \frac { { d z } } { { { { \left ( { 1 – z } \right ) } ^ 2 } { { \left ( { 1 + z } \right ) } ^ 2 } } } } . } L = 2 1 0 ∫ 5 2 ( 1– z 2 ) 2 d z = 2 1 0 ∫ 5 2 ( 1– z ) 2 ( 1 + z ) 2 d z .
اکنون انتگرالده اخیر را به کسرهای جزئی بسط میدهیم:
1 ( 1 – z ) 2 ( 1 + z ) 2 = A ( 1 – z ) 2 + B 1 – z + C ( 1 + z ) 2 + D 1 + z { \frac { 1 } { { { { \left ( { 1 – z } \right ) } ^ 2 } { { \left ( { 1 + z } \right ) } ^ 2 } } } } = { \frac { A } { { { { \left ( { 1 – z } \right ) } ^ 2 } } } + \frac { B } { { 1 – z } } } + { \frac {C } { { { { \left ( { 1 + z } \right ) } ^ 2 } } } } + { \frac { D } { { 1 + z } } } ( 1– z ) 2 ( 1 + z ) 2 1 = ( 1– z ) 2 A + 1– z B + ( 1 + z ) 2 C + 1 + z D
1 = A ( 1 + z ) 2 + B ( 1 – z ) ( 1 + z ) 2 + C ( 1 – z ) 2 + D ( 1 + z ) ( 1 – z ) 2 , 1 = A ( 1 + 2 z + z 2 ) + ( B – B z ) ( 1 + 2 z + z 2 ) + C ( 1 – 2 z + z 2 ) + ( D + D z ) ( 1 – 2 z + z 2 ) , 1 = A + 2 A z + A z 2 + B – B z + 2 B z – 2 B z 2 + B z 2 – B z 3 + C – 2 C z + C z 2 + D + D z – 2 D z – 2 D z 2 + D z 2 + D z 3 . \large \begin {align*} 1 & = A { \left ( { 1 + z } \right ) } ^ 2 + { B { \left ( { 1 – z } \right ) } { \left ( { 1 + z } \right ) } ^ 2 } + { { C { \left ( { 1 – z } \right ) } ^ 2 } } + { D { \left ( { 1 + z } \right ) } { \left ( { 1 – z } \right ) } ^ 2 , } \\ 1 & = A \left ( { 1 + 2 z + { z ^ 2 } } \right ) + \left ( { B – B z } \right ) \left ( { 1 + 2 z + { z ^ 2 } } \right ) + { C \left ( { 1 – 2 z + { z ^ 2 } } \right ) } \\ & \, \,\,\,\,\,\,\, + { \left ( { D + D z } \right ) \left ( { 1 – 2 z + { z ^ 2 } } \right ) , } \\ 1 & = A + 2 A z + A { z ^ 2 } + { B – B z + 2 B z – 2 B { z ^ 2 } + B { z ^ 2 } – B { z ^ 3 } } \\ & \,\,\,\,\,\,\,+ { C – 2 C z + C { z ^ 2 } } + { D + D z – 2 D z – 2 D { z ^ 2 } + D { z ^ 2 } + D { z ^ 3 } . } \end {align*} 1 1 1 = A ( 1 + z ) 2 + B ( 1– z ) ( 1 + z ) 2 + C ( 1– z ) 2 + D ( 1 + z ) ( 1– z ) 2 , = A ( 1 + 2 z + z 2 ) + ( B – B z ) ( 1 + 2 z + z 2 ) + C ( 1–2 z + z 2 ) + ( D + Dz ) ( 1–2 z + z 2 ) , = A + 2 A z + A z 2 + B – B z + 2 B z –2 B z 2 + B z 2 – B z 3 + C –2 C z + C z 2 + D + Dz –2 Dz –2 D z 2 + D z 2 + D z 3 .
از روابط بالا، به دستگاه معادلات زیر میرسیم:
{ A + B + C + D = 1 2 A + B – 2 C – 2 D = 0 A – B + C – D = 0 – B + D = 0 . \large \left \{ \begin {array} { l } A + B + C + D = 1 \\ 2 A + B – 2 C – 2 D = 0 \\ A – B + C – D = 0 \\ – B + D = 0 \end{array} \right . . ⎩ ⎨ ⎧ A + B + C + D = 1 2 A + B –2 C –2 D = 0 A – B + C – D = 0 – B + D = 0 .
با حل دستگاه معادلات بالا، ضرایب به دست میآید:
A = B = C = D = 1 4 . \large {A = B = C = D }={ \frac{1}{4}.} A = B = C = D = 4 1 .
بنابراین، طول منحنی برابر است با:
L = 1 2 ∫ 0 2 5 d z ( 1 – z ) 2 ( 1 + z ) 2 = 1 8 [ ∫ 0 2 5 d z ( 1 – z ) 2 + ∫ 0 2 5 d z 1 – z + ∫ 0 2 5 d z ( 1 + z ) 2 + ∫ 0 2 5 d z 1 + z ] = 1 8 [ ( 1 1 – z – ln ∣ 1 – z ∣ − 1 1 + z + ln ∣ 1 + z ∣ ) ∣ 0 2 5 ] = 1 8 [ ( 2 z 1 – z 2 – ln ∣ 1 + z 1 – z ∣ ) ∣ 0 2 5 ] = 1 8 [ 2 ⋅ 2 5 1 – ( 2 5 ) 2 – ln ∣ 1 + 2 5 1 – 2 5 ∣ ] = 1 8 ( 4 5 + ln 5 + 2 5 – 2 ) = 5 2 + 1 8 ln ( 5 + 2 ) 2 5 – 4 = 5 2 + 1 4 ln ( 5 + 2 ) ≈ 1 , 48. \large \begin {align*} L & = { \frac { 1 } { 2 } \int \limits _ 0 ^ { \large \frac { 2 }{ { \sqrt 5 } } \normalsize } { \frac { { d z } } { { { { \left ( { 1 – z } \right ) } ^ 2 } { { \left ( { 1 + z } \right ) } ^ 2 } } } } } \\ & = { { \frac { 1 } { 8 } \left [ { \int \limits _ 0 ^ { \large \frac { 2 } { { \sqrt 5 } } \normalsize } { \frac { { d z } } { { { { \left ( { 1 – z } \right ) } ^ 2 } } } } } \right . } + { \left . { \int \limits _ 0 ^ { \large \frac { 2 } { { \sqrt 5 } } \normalsize } { \frac { { d z } } { { 1 – z } } } } \right . } + { \left . { \int \limits _ 0 ^ { \large \frac { 2 } { { \sqrt 5 } } \normalsize } { \frac { { d z } } { { { { \left ( { 1 + z } \right ) } ^ 2 } } } } } \right . } + { \left . { \int \limits _ 0 ^ { \large \frac { 2 }{ { \sqrt 5 } } \normalsize } { \frac { { d z } } { { 1 + z } } } } \right ] } } \\ & = { \frac { 1 } { 8 } \left [ { \left . {\left( {\frac{1}{{1 – z}} – \ln \left| {1 – z} \right| }\right.}\right.}-{\left.{\left.{ \frac{1}{{1 + z}} }\right.}\right.}+{\left.{\left.{ \ln \left| {1 + z} \right|} \right)} \right|_0^{\large\frac{2}{{\sqrt 5 }}\normalsize}} \right] } \\ & = {\frac{1}{8}\left[ {\left. {\left( {\frac{{2z}}{{1 – {z^2}}} – \ln \left| {\frac{{1 + z}}{{1 – z}}} \right|} \right)} \right|_0^{\large\frac{2}{{\sqrt 5 }}\normalsize}} \right] } \\ & = {\frac{1}{8}\left[ {\frac{{2 \cdot \frac{2}{{\sqrt 5 }}}}{{1 – {{\left( {\frac{2}{{\sqrt 5 }}} \right)}^2}}} – \ln \left| {\frac{{1 + \frac{2}{{\sqrt 5 }}}}{{1 – \frac{2}{{\sqrt 5 }}}}} \right|}\right] } = {\frac{1}{8}\left( {4\sqrt 5 + \ln \frac{{\sqrt 5 + 2}}{{\sqrt 5 – 2}}} \right) }\\ & = {\frac{{\sqrt 5 }}{2} + \frac{1}{8}\ln \frac{{{{\left( {\sqrt 5 + 2} \right)}^2}}}{{5 – 4}} } = {\frac{{\sqrt 5 }}{2} + \frac{1}{4}\ln \left( {\sqrt 5 + 2} \right) }\approx{ 1,48.} \end {align*} L = 2 1 0 ∫ 5 2 ( 1– z ) 2 ( 1 + z ) 2 d z = 8 1 0 ∫ 5 2 ( 1– z ) 2 d z + 0 ∫ 5 2 1– z d z + 0 ∫ 5 2 ( 1 + z ) 2 d z + 0 ∫ 5 2 1 + z d z = 8 1 ( 1– z 1 – ln ∣ 1– z ∣ − 1 + z 1 + ln ∣ 1 + z ∣ ) ∣ 0 5 2 = 8 1 ( 1– z 2 2 z – ln 1– z 1 + z ) 0 5 2 = 8 1 1– ( 5 2 ) 2 2 ⋅ 5 2 – ln 1– 5 2 1 + 5 2 = 8 1 ( 4 5 + ln 5 –2 5 + 2 ) = 2 5 + 8 1 ln 5–4 ( 5 + 2 ) 2 = 2 5 + 4 1 ln ( 5 + 2 ) ≈ 1 , 48.
مثال ۶
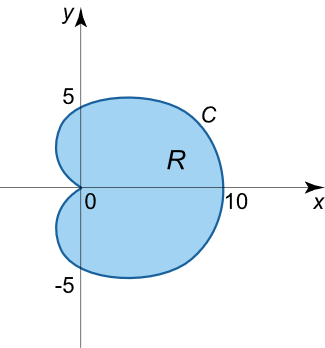
طول دلگونی را محاسبه کنید که معادله آن در مختصات قطبی به صورت زیر است:
r = 5 ( 1 + cos θ ) \large r = 5 \left ( { 1 + \cos \theta } \right ) r = 5 ( 1 + cos θ )
شکل ۶ حل: از فرمول زیر استفاده میکنیم:
L = ∫ α β r 2 + ( d r d θ ) 2 d θ . \large L = \int \limits _ \alpha ^ \beta { \sqrt { { r ^ 2 } + { { \left ( { \frac { { d r } } { { d \theta } } } \right ) } ^ 2 } } d \theta } . L = α ∫ β r 2 + ( d θ d r ) 2 d θ .
بنابراین، طول دلگون را میتوان به صورت زیر محاسبه کرد:
L = ∫ 0 2 π [ ( 5 ( 1 + cos θ ) ) 2 + ( d ( 5 ( 1 + cos θ ) ) d θ ) 2 ] 1 2 d θ = 5 2 ∫ 0 2 π 1 + cos θ d θ = 5 2 ∫ 0 2 π 2 ( cos θ 2 ) 2 d θ = 10 ∫ 0 2 π ( cos θ 2 ) 2 d θ . \large \begin {align*} L & = \kern0pt { \int \limits _ 0 ^ { 2 \pi } { \Big [ { { { \left ( { 5 \left ( { 1 + \cos \theta } \right ) } \right ) } ^ 2 } + } } } \kern0pt { { { { { \left ( { \frac { { d \left ( { 5 \left ( { 1 + \cos \theta } \right ) } \right ) } } { { d \theta } } } \right ) } ^ 2 } } \Big ] ^ { \frac { 1 } { 2 } } d \theta } } \\ & = { 5 \sqrt 2 \int \limits _ 0 ^ { 2 \pi } { \sqrt { 1 + \cos \theta } d \theta } } = { 5 \sqrt 2 \int \limits _ 0 ^ { 2 \pi } { \sqrt { 2 { { \left ( { \cos \frac { \theta } { 2 } } \right ) } ^ 2 } } d \theta } } \\ & = { 1 0 \int \limits _ 0 ^ { 2 \pi } { \sqrt { { { \left ( { \cos \frac { \theta } { 2 } } \right ) } ^ 2 } } d \theta } . } \end {align*} L = 0 ∫ 2 π [ ( 5 ( 1 + cos θ ) ) 2 + ( d θ d ( 5 ( 1 + cos θ ) ) ) 2 ] 2 1 d θ = 5 2 0 ∫ 2 π 1 + cos θ d θ = 5 2 0 ∫ 2 π 2 ( cos 2 θ ) 2 d θ = 10 0 ∫ 2 π ( cos 2 θ ) 2 d θ .
توجه کنید که وقتی 0 ≤ θ ≤ π 0 \le \theta \le \pi 0 ≤ θ ≤ π cos θ 2 ≥ 0 {\cos {\large\frac{\theta }{2}\normalsize}} \ge 0 cos 2 θ ≥ 0 π ≤ θ ≤ 2 π \pi \le \theta \le 2\pi π ≤ θ ≤ 2 π cos θ 2 ≤ 0 {\cos {\large\frac{\theta }{2}\normalsize}} \le 0 cos 2 θ ≤ 0
( cos θ 2 ) 2 = cos θ 2 , 0 ≤ θ ≤ π , ( cos θ 2 ) 2 = − cos θ 2 , π ≤ θ ≤ 2 π . \large \begin {align*} { \sqrt { { { \left ( { \cos \frac { \theta } { 2 } } \right ) } ^ 2 } } } & = { \cos \frac { \theta } { 2 }, \; \; \; } \kern-0.3pt {\;\;0 \le \theta \le \pi ,} \\ { \sqrt { { { \left ( { \cos \frac { \theta } { 2 } } \right ) } ^ 2 } } } & = { - \cos \frac { \theta } { 2 }, \; \; \; } \kern-0.3pt \; \;\pi \le \theta \le 2\pi . \end {align*} ( cos 2 θ ) 2 ( cos 2 θ ) 2 = cos 2 θ , 0 ≤ θ ≤ π , = − cos 2 θ , π ≤ θ ≤ 2 π .
بنابراین، انتگرال را به دو انتگرال تفکیک میکنیم و طول دلگون را به دست میآوریم:
L = 10 ∫ 0 2 π ( cos θ 2 ) 2 d θ = 10 [ ∫ 0 π cos θ 2 d θ + ∫ π 2 π ( – cos θ 2 ) d θ ] = 10 [ ( sin θ 2 1 2 ) ∣ θ = 0 π − ( sin θ 2 1 2 ) ∣ θ = π 2 π ] = 20 [ ( sin π 2 – sin 0 ) − ( sin π – sin π 2 ) ] = 20 [ ( 1 – 0 ) – ( 0 – 1 ) ] = 40. \large \begin {align*} L & = 1 0 \int \limits _ 0 ^ { 2 \pi } { \sqrt { { { \left ( { \cos \frac { \theta } { 2 } } \right ) } ^ 2 } } d \theta } = { { 1 0 \left [ { \int \limits _ 0 ^ \pi { \cos \frac { \theta }{ 2 } d \theta } } \right . } + { \left . { \int \limits _ \pi ^ { 2 \pi } { \left ( { – \cos \frac { \theta } { 2 } } \right ) d \theta } } \right ] } } \\ & = { { 1 0 \left [ { \left . { \left ( { \frac { { \sin \frac { \theta } { 2 } } } { { \frac { 1 } { 2 } } } } \right ) } \right | _ { \theta = 0 } ^ \pi } \right . } - { \left . { \left . { \left ( { \frac { { \sin \frac { \theta } { 2 } } } { { \frac { 1 } { 2 } } } } \right ) } \right | _ { \theta = \pi } ^ { 2 \pi } } \right ] } } = { 2 0 \left [ { \left ( { \sin \frac { \pi } { 2 } – \sin 0 } \right ) } \right . } - { \left . { \left ( { \sin \pi – \sin \frac { \pi } { 2 } } \right ) } \right ] } \\ & = { 2 0 \left [ { \left ( { 1 – 0 } \right ) – \left ( { 0 – 1 } \right ) } \right ] } = { 4 0 . } \end {align*} L = 10 0 ∫ 2 π ( cos 2 θ ) 2 d θ = 10 0 ∫ π cos 2 θ d θ + π ∫ 2 π ( – cos 2 θ ) d θ = 10 ( 2 1 sin 2 θ ) θ = 0 π − ( 2 1 sin 2 θ ) θ = π 2 π = 20 [ ( sin 2 π – sin 0 ) − ( sin π – sin 2 π ) ] = 20 [ ( 1–0 ) – ( 0–1 ) ] = 40.
مثال ۷
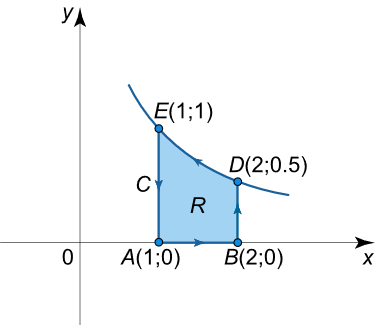
مساحت ناحیه محدود به سهمی y = 1 x y = {\large\frac{1}{x}\normalsize} y = x 1 x x x x = 1 x = 1 x = 1 x = 2 x= 2 x = 2
شکل ۷ حل: میتوانیم مساحت را با استفاده از انتگرال خطی زیر محاسبه کنیم:
S = – ∮ C y d x = – ∫ A B y d x – ∫ B D y d x − ∫ D E y d x − ∫ E A y d x . \large { S = – \oint \limits _ C { y d x } } = { – \int \limits _ { A B } { y d x } – \int \limits _ { B D } { y dx } } - { \int \limits _ { D E } { y d x } } - { \int \limits _ { E A } { y d x } . } S = – C ∮ y d x = – A B ∫ y d x – B D ∫ y d x − D E ∫ y d x − E A ∫ y d x .
حاصل هر یک از انتگرالها را جداگانه به دست میآوریم:
− ∫ A B y d x = – ∫ 1 2 0 ⋅ d x = 0 , − ∫ B D y d x = – ∫ 0 0 y d x = 0 , − ∫ D E y d x = – ∫ 2 1 d x x = ( – ln x ) ∣ 2 1 = – ln 1 + ln 2 = ln 2 , − ∫ E A y d x = – ∫ 0 0 y d x = 0. \large \begin {align*} - \int \limits _ { A B } { y d x } & = – \int \limits _ 1 ^ 2 { 0 \cdot d x } = { 0 , } \\ - \int \limits _ { B D } { y d x } & = – \int \limits _ 0 ^ 0 { y d x } = { 0 , } \\ - \int \limits _ { D E } { y d x } & = – \int \limits _ 2 ^ 1 { \frac { { d x } } { x } } = { \left . { \left ( { – \ln x } \right ) } \right | _ 2 ^ 1 } = { – \ln 1 + \ln 2 } = { \ln 2 , } \\ - \int \limits _ { E A } { y d x } & = – \int \limits _ 0 ^ 0 { y d x } = { 0 . } \end {align*} − A B ∫ y d x − B D ∫ y d x − D E ∫ y d x − E A ∫ y d x = – 1 ∫ 2 0 ⋅ d x = 0 , = – 0 ∫ 0 y d x = 0 , = – 2 ∫ 1 x d x = ( – ln x ) ∣ 2 1 = – ln 1 + ln 2 = ln 2 , = – 0 ∫ 0 y d x = 0.
بنابراین، مساحت ناحیه، برابر است با:
S = ln 2. \large S = \ln 2 . S = ln 2.
مثال ۸
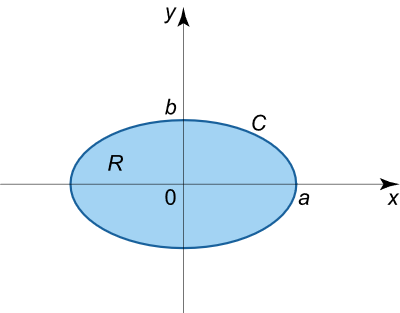
مساحت ناحیه محدود به بیضی زیر را به دست آورید:
x = a cos t , y = b sin t , 0 ≤ t ≤ 2 π \large x = a \cos t , y = b \sin t , 0 \le t \le 2 \pi x = a cos t , y = b sin t , 0 ≤ t ≤ 2 π
شکل ۸ حل: ابتدا از فرمول S = ∮ C x d y = ∫ α β x ( t ) d y d t d t . { S = \oint \limits _ C { x d y } } { = \int \limits _ \alpha ^ \beta { x \left ( t \right ) { \large \frac { { d y } }{ { d t } } \normalsize } d t } . } S = C ∮ x d y = α ∫ β x ( t ) d t d y d t .
S = ∫ 0 2 π a cos t d ( b sin t ) d t d t = a b ∫ 0 2 π cos 2 t d t = a b ∫ 0 2 π 1 + cos 2 t 2 d t = a b 2 [ ( t + sin 2 t 2 ) ∣ 0 2 π ] = a b 2 [ ( 2 π + 0 ) – 0 ] = π a b . \large \begin {align*} S & = \int \limits _ 0 ^ { 2 \pi } { a \cos t \frac { { d \left ( { b \sin t } \right ) }} { { d t } } d t } = { a b \int \limits _ 0 ^ { 2 \pi } { { { \cos } ^ 2 } t d t } } \\ & = { a b \int \limits _ 0 ^ { 2 \pi } { \frac { { 1 + \cos 2 t } } { 2 } d t } } = { \frac { { a b } }{ 2 } \left [ { \left . { \left ( { t + \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] } \\ & = { \frac { { a b } } { 2 } \left [ { \left ( { 2 \pi + 0 } \right ) – 0 } \right ] } = { \pi a b . } \end {align*} S = 0 ∫ 2 π a cos t d t d ( b sin t ) d t = ab 0 ∫ 2 π cos 2 t d t = ab 0 ∫ 2 π 2 1 + cos 2 t d t = 2 ab [ ( t + 2 sin 2 t ) 0 2 π ] = 2 ab [ ( 2 π + 0 ) –0 ] = πab .
علاوه بر فرمول بالا، میتوانیم از دو فرمول زیر نیز برای محاسبه مساحت مورد نظر استفاده کنیم:
S = – ∮ C y d x = – ∫ 0 2 π y ( t ) d x d t d t = – ∫ 0 2 π b sin t d ( a cos t ) d t d t = – a b ∫ 0 2 π ( – sin 2 t ) d t = a b ∫ 0 2 π 1 – cos 2 t 2 d t = a b 2 [ ( t – sin 2 t 2 ) ∣ 0 2 π ] = a b 2 [ ( 2 π – 0 ) – 0 ] = π a b . \large \begin {align*} S & = – \oint \limits _ C { y d x } = { – \int \limits _ 0 ^ { 2 \pi } { y \left ( t \right ) \frac { { d x } } { { d t } } d t } } = { – \int \limits _ 0 ^ { 2 \pi } { b \sin t \frac { { d \left ( { a \cos t } \right ) } } { { d t } } d t } } \\ & = { – a b \int \limits _ 0 ^ { 2 \pi } { \left ( { – { { \sin } ^ 2 } t } \right ) d t } } = { a b \int \limits _ 0 ^ { 2 \pi } { \frac { { 1 – \cos 2 t } } { 2 } d t } } \\ & = { \frac { { a b } } { 2 } \left [ { \left . { \left ( { t – \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] } = { \frac { { a b } } { 2 } \left [ { \left ( { 2 \pi – 0 } \right ) – 0 } \right ] } = { \pi a b . } \end {align*} S = – C ∮ y d x = – 0 ∫ 2 π y ( t ) d t d x d t = – 0 ∫ 2 π b sin t d t d ( a cos t ) d t = – ab 0 ∫ 2 π ( – sin 2 t ) d t = ab 0 ∫ 2 π 2 1– cos 2 t d t = 2 ab [ ( t – 2 sin 2 t ) 0 2 π ] = 2 ab [ ( 2 π –0 ) –0 ] = πab .
S = 1 2 ∮ C x d y – y d x = 1 2 ∫ 0 2 π [ x ( t ) d y d t – y ( t ) d x d t ] d t = 1 2 ∫ 0 2 π [ a cos t d ( b sin t ) d t − b sin t d ( a cos t ) d t ] d t = a b 2 ∫ 0 2 π ( cos 2 t + sin 2 t ) d t = a b 2 ∫ 0 2 π d t = a b 2 ⋅ 2 π = π a b . \large \begin {align*} S & = \frac { 1 } { 2 } \oint \limits _ C { x d y – y d x } = { \frac { 1 } { 2 } \int \limits _ 0 ^ { 2 \pi } { \left [ { x \left ( t \right ) \frac { { d y } } { { d t } } – y \left ( t \right ) \frac { { d x } } { { d t } } } \right ] d t } } \\ & = { { \frac { 1 } { 2 } \int \limits _ 0 ^ { 2 \pi } { \left [ { a \cos t \frac { { d \left ( { b \sin t } \right ) } } { { d t } } } \right . } } - { { \left . { b \sin t \frac { { d \left ( { a \cos t } \right) } } { {d t } }} \right ] d t} } } \\ & = { \frac { { a b } } { 2 } \int \limits _ 0 ^ { 2 \pi } {\left( {{{\cos } ^ 2 } t + { \sin ^ 2 } t } \right ) d t} } = { \frac { { a b }} { 2 } \int \limits _ 0 ^ { 2 \pi } { d t } } = {\frac { { a b } }{ 2 } \cdot 2 \pi } = {\pi ab.} \end {align*} S = 2 1 C ∮ x d y – y d x = 2 1 0 ∫ 2 π [ x ( t ) d t d y – y ( t ) d t d x ] d t = 2 1 0 ∫ 2 π [ a cos t d t d ( b sin t ) − b sin t d t d ( a cos t ) ] d t = 2 ab 0 ∫ 2 π ( cos 2 t + sin 2 t ) d t = 2 ab 0 ∫ 2 π d t = 2 ab ⋅ 2 π = πab .
مثال ۹
حجمی را که از دوران ناحیه محصور منحنی y = 2 – sin x y = 2 – \sin x y = 2– sin x x = 0 x = 0 x = 0 x = 2 π x = 2\pi x = 2 π y = 0 y = 0 y = 0 x x x
حل: ناحیه R R R
شکل ۹ با فرمول زیر میتوان حجم مورد نظر را به دست آورد:
V = – π ∮ C y 2 d x = – π [ ∫ O A y 2 d x + ∫ A B y 2 d x + ∫ B D y 2 d x + ∫ D O y 2 d x ] . \large { V = – \pi \oint \limits _ C { { y ^ 2 } d x } } = { – \pi \left [ { \int \limits _ { O A } { { y ^ 2 } d x } } \right . } +{ \left . { \int \limits _ { A B } { { y ^ 2 } d x } } \right . } +{ \left . { \int \limits _ { B D } { { y ^ 2 } d x } } \right . } +{ \left . { \int \limits _ { D O } { { y ^ 2 } d x } } \right ] . } V = – π C ∮ y 2 d x = – π O A ∫ y 2 d x + A B ∫ y 2 d x + B D ∫ y 2 d x + D O ∫ y 2 d x .
محاسبه تک تک انتگرالها به صورت زیر است:
∫ O A y 2 d x = ∫ 0 2 π 0 d x = 0 , ∫ A B y 2 d x = ∫ 2 π 2 π y 2 d x = 0 , ∫ B D y 2 d x = ∫ 2 π 0 ( 2 – sin x ) 2 d x = – ∫ 0 2 π ( 2 – sin x ) 2 d x = – ∫ 0 2 π ( 4 – 4 sin x + sin 2 x ) d x = – ∫ 0 2 π ( 4 – 4 sin x + 1 – cos 2 x 2 ) d x = ∫ 0 2 π ( 4 sin x – 9 2 + cos 2 x 2 ) d x = ( – 4 cos x – 9 2 x + sin 2 x 2 ) ∣ 0 2 π = ( – 4 – 9 π + 0 ) − ( – 4 – 0 + 0 ) = – 9 π , ∫ D O y 2 d x = ∫ 0 0 y 2 d x = 0. \large \begin {align*} \int \limits _ { O A } { { y ^ 2 } d x } & = \int \limits _ 0 ^ { 2 \pi } { 0 d x } = 0 , \\ \int \limits _ { A B } { { y ^ 2 } d x } & = \int \limits _ { 2 \pi } ^ { 2 \pi } { { y ^ 2 } d x } = 0 , \\ { \int \limits _ { B D } { { y ^ 2 } d x } } & = { \int \limits _ { 2 \pi } ^ 0 { { { \left ( { 2 – \sin x } \right ) } ^ 2 } d x } } = { – \int \limits _ 0 ^ { 2 \pi } { { { \left ( { 2 – \sin x } \right ) } ^ 2 } d x } } \\ & = { – \int \limits _ 0 ^ { 2 \pi } { \left ( { 4 – 4 \sin x + { { \sin } ^ 2 } x } \right ) d x } } = { – \int \limits _ 0 ^ { 2 \pi } { \left ( { 4 – 4 \sin x } \right . } + { \left . { \frac { { 1 – \cos 2 x } } { 2 } } \right ) d x } } \\ &= { \int \limits _ 0 ^ { 2 \pi } { \left ( { 4 \sin x – \frac { 9 } { 2 } + \frac { { \cos 2 x } } { 2 } } \right ) d x } } = { \left . { \left ( { – 4 \cos x – \frac { 9 } { 2 } x + \frac { { \sin 2 x } } { 2} } \right ) } \right | _ 0 ^ { 2 \pi } } \\ & = { \left ( { – 4 – 9 \pi + 0 } \right ) } - { \left ( { – 4 – 0 + 0 } \right ) } = { – 9 \pi , } \\ \int \limits_{DO} {y^2}dx & = \int \limits_0^0 {{y^2}dx} = 0. \end {align*} O A ∫ y 2 d x A B ∫ y 2 d x B D ∫ y 2 d x D O ∫ y 2 d x = 0 ∫ 2 π 0 d x = 0 , = 2 π ∫ 2 π y 2 d x = 0 , = 2 π ∫ 0 ( 2– sin x ) 2 d x = – 0 ∫ 2 π ( 2– sin x ) 2 d x = – 0 ∫ 2 π ( 4–4 sin x + sin 2 x ) d x = – 0 ∫ 2 π ( 4–4 sin x + 2 1– cos 2 x ) d x = 0 ∫ 2 π ( 4 sin x – 2 9 + 2 cos 2 x ) d x = ( –4 cos x – 2 9 x + 2 sin 2 x ) 0 2 π = ( –4–9 π + 0 ) − ( –4–0 + 0 ) = –9 π , = 0 ∫ 0 y 2 d x = 0.
بنابراین، حجم مورد نظر برابر است با:
V = – π ( 0 + 0 – 9 π + 0 ) = 9 π 2 . \large {V = – \pi \left( {0 + 0 – 9\pi + 0} \right) }={ 9{\pi ^2}.} V = – π ( 0 + 0–9 π + 0 ) = 9 π 2 .
مثال ۱۰
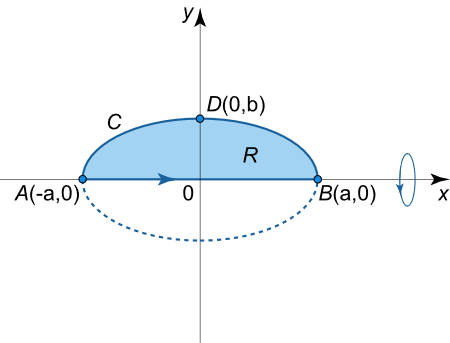
حجم بیضیواری را به دست آورید که با دوران بیضی با نیممحورهای a a a b b b x x x
شکل ۱۰ حل: معادلات پارامتری بیضی به صورت زیر هستند:
x = a cos t , y = b sin t . \large { x = a \cos t , \; \; \; } \kern-0.3pt { y = b \sin t . } x = a cos t , y = b sin t .
میتوانیم نیمه بالایی بیضی را برای y ≥ 0 y \ge 0 y ≥ 0 a a a b b b
V = – π ∫ C y 2 d x = – π ∫ A O B y 2 d x – π ∫ B O A y 2 d x = – π ∫ – a a 0 2 d x – π ∫ a – a y 2 d x = – π ∫ a – a y 2 d x , \large \begin {align*} V & = – \pi \int \limits _ C { { y ^ 2 } d x } = { – \pi \int \limits _ { A O B } { { y ^ 2 } d x } – \pi \int \limits _ { B O A } { { y ^ 2} d x } } \\ & = { – \pi \int \limits _ { – a } ^ a { { 0 ^ 2 } d x } – \pi \int \limits _ a ^ { – a } { { y ^ 2 } d x } } = { – \pi \int \limits _ a ^ { – a } { { y ^ 2 } d x } , } \end {align*} V = – π C ∫ y 2 d x = – π A OB ∫ y 2 d x – π BO A ∫ y 2 d x = – π – a ∫ a 0 2 d x – π a ∫ – a y 2 d x = – π a ∫ – a y 2 d x ,
که در آن، y ( x ) y (x) y ( x )
V = – π ∫ 0 π ( y ( t ) ) 2 d x d t d t = – π ∫ 0 π ( b sin t ) 2 d ( a cos t ) d t d t = – π a b 2 ∫ 0 π sin 2 t ( – sin t ) d t = – π a b 2 ∫ 0 π sin 2 t d ( cos t ) = π a b 2 ∫ 0 π ( cos 2 t – 1 ) d ( cos t ) = π a b 2 [ ( cos 3 t 3 – cos t ) ∣ 0 π ] = π a b 2 [ ( cos 3 π 3 – cos π ) − ( cos 3 0 3 – cos 0 ) ] = π a b 2 [ ( – 1 3 + 1 ) − ( 1 3 – 1 ) ] = 4 π a b 2 3 . \large \begin {align*} V & = – \pi \int \limits _ 0 ^ \pi { { { \left ( { y \left ( t \right ) } \right ) } ^ 2 } \frac { { d x } } { { d t} } d t } = { – \pi \int \limits _ 0 ^ \pi { { { \left ( { b \sin t } \right ) } ^ 2 } \frac { { d \left ( { a \cos t } \right ) } } { { d t } } d t } } \\ & = { – \pi a { b ^ 2 } \int \limits _ 0 ^ \pi { { { \sin } ^ 2 } t \left ( { – \sin t } \right ) d t } } = { – \pi a { b ^ 2 } \int \limits _ 0 ^ \pi { { { \sin } ^ 2 } t \, d \left ( { \cos t } \right ) } } \\ & = { \pi a { b ^ 2 } \int \limits _ 0 ^ \pi { \left ( { { \cos ^ 2 } t – 1 } \right ) d \left ( { \cos t } \right ) } } = { \pi a { b ^ 2 } \left [ { \left . { \left ( { \frac { { { { \cos } ^ 3 } t } } { 3 } – \cos t } \right ) } \right | _0 ^ \pi } \right ] } \\ & = { { \pi a { b ^ 2 } \left [ { \left ( { \frac { { { { \cos } ^ 3 } \pi } } { 3 } – \cos \pi } \right ) } \right . } - { \left . { \left ( { \frac { { { { \cos } ^ 3 } 0 } } { 3 } – \cos 0 } \right ) } \right ] } } \\ & = {{\pi a{b^2}\left[ {\left( { – \frac{1}{3} + 1} \right) }\right.} - { \left.{ \left( {\frac{1}{3} – 1} \right)} \right] }} = {\frac{{4\pi a{b^2}}}{3}.} \end {align*} V = – π 0 ∫ π ( y ( t ) ) 2 d t d x d t = – π 0 ∫ π ( b sin t ) 2 d t d ( a cos t ) d t = – πa b 2 0 ∫ π sin 2 t ( – sin t ) d t = – πa b 2 0 ∫ π sin 2 t d ( cos t ) = πa b 2 0 ∫ π ( cos 2 t –1 ) d ( cos t ) = πa b 2 [ ( 3 cos 3 t – cos t ) 0 π ] = πa b 2 [ ( 3 cos 3 π – cos π ) − ( 3 cos 3 0 – cos 0 ) ] = πa b 2 [ ( – 3 1 + 1 ) − ( 3 1 –1 ) ] = 3 4 πa b 2 .