قانون دوم نیوتن چیست؟ – به زبان ساده با مثال و تمرین
اگر بخواهید یک ماشین و یک کامیون را با نیروی مساوی هل دهید، واضح است که حرکت دادن ماشین آسانتر است. علت این ماجرا با پاسخ دادن به این سوال که «قانون دوم نیوتن چیست»، مشخص میشود. قانون دوم نیوتون به زبان ساده این است که اگر نیروی خالص و مخالف صفری به جسم وارد شود، حرکت آن شتابدار میشود. اندازه این شتاب همیشه با اندازه نیروی کل وارد بر جسم نسبت مستقیم و با جرم آن نسبت عکس دارد. پس چون جرم ماشین از جرم کامیون کمتر است، شتاب ماشین از شتاب کامیون بیشتر است و راحتتر حرکت میکند.
- خواهید آموخت چگونه رابطه نیرو، جرم و شتاب را در فرمول مربوطه به کار ببرید.
- میآموزید چطور با ترسیم نمودار جسم آزاد نیروهای مؤثر بر اجسام را تحلیل کنید.
- با روش حل گامبهگام مسائل دینامیکی شامل اصطکاک و سطح شیبدار آشنا میشوید.
- نحوه محاسبه و تفسیر وزن ظاهری در سناریوهایی مانند آسانسور را یاد خواهید گرفت.
- یاد میگیرید کشش طناب و توزیع شتاب را در سیستمهای چندجسمی بررسی کنید.
- فرمولهای اساسی حرکت دایرهای و نقش نیروی مرکزگرا را خواهید آموخت.
در این مطلب سعی میکنیم پس از توضیح قوانین نیوتن، با حل مثال به شما کمک کنیم تا درک عمیقتری از قانون دوم نیوتن بدست آورید. همچنین کاربرد قانون دوم نیوتن را در حل مسائلی مانند بررسی وزن در آسانسور، حرکت دایرهای، حرکت روی سطح شیبدار و بررسی نیروی کشش نخ (طناب) متصل به قرقره بررسی میکنیم.
قانون دوم نیوتن چیست؟
در قانون دوم نیوتن، وارد شدن نیرو باعث تغییر در وضعیت حرکتی جسم خواهد شد. در نتیجه جسم شتابی بدست میآورد که با جرم آن نسبت عکس دارد. یعنی هر چه جرم جسم کمتر باشد، نیروی کمتری برای حرکت دادن آن لازم داریم و در نتیجه جسم شتاب بیشتری خواهد داشت. بنابراین میتوانیم ارتباط بین جرم m، شتاب a و نیروی وارد شده F را در یک فرمول خلاصه کنیم که در آن واحد m کیلوگرم، واحد a متر بر مجذور ثانیه و واحد F نیوتن است:
در واقع ما از قوانین نیوتن استفاده میکنیم تا بتوانیم آثار تمام نیروهای وارد بر یک جسم را بررسی کنیم و در نهایت، در مورد نحوه حرکت جسم نتیجهگیری کنیم. در ادامه مطلب، خواهیم دید که فرمول به ظاهر ساده قانون دوم نیوتن چگونه میتواند کلید حل مسائل خیلی پیچیده باشد.

بررسی مسائل قانون دوم نیوتن
بخشی از فیزیک کلاسیک که به بررسی علت تغییر حرکت یک جسم میپردازد، «دینامیک» (Dynamics) نامیده میشود. فیزیک دینامیک توسط دانشمندی به نام «آیزاک نیوتن» (Isaac Newton) در قالب «سه قانون حرکت نیوتن» (Newton's Three Laws of Motion) پایهگذاری شد. قدم اول در بررسی مسائل دینامیکی، آشنایی با نوع کمیتهایی است که با آنها کار داریم.
در این مطلب با سه کمیت مهم نیرو (F)، شتاب (a) و جرم (m) کار میکنیم. برخلاف جرم که یک «کمیت اسکالر» (Scalar Quantity) است، نیرو و شتاب «کمیتهای برداری» (Vector Quantities) محسوب میشوند. پس دارای اندازه و جهت هستند و جمع آنها بر اساس قوانین جمع برداری محاسبه میشود.

مراحل حل مسائل قانون دوم نیوتن
همچنین پیش از شروع حل مسائل دینامیکی بهتر است با نسبتهای مثلثاتی، قضیه فیثاغورس و مفهوم حرکت نسبی آشنا باشیم تا بتوانیم از آنها بهعنوان ابزاری در جهت حل آسانتر مسائل استفاده کنیم. در نهایت، با بررسی دادههای صورت مسئله و انجام مراحل زیر به محاسبه کمیتهای خواسته شده میپردازیم:
- رسم شماتیک سادهای از وضعیت جسم یا «نمودار جسم آزاد» (Free-body Diagram)
- تشخیص شکل برداری تمام نیروهای وارد بر جسم
- انتخاب دستگاه مختصات مناسب با توجه به توزیع نیروها
- تجزیه بردارهای نیرو در راستای محورهای مختصات
- جمع برداری نیروها و تعیین نیروی برآیند
- کاربرد قانون دوم نیوتن برای هر محور مختصات
دقت شود در رسم نمودار جسم آزاد، جسم را بهصورت یک شکل هندسی ساده در نظر میگیریم و برای سادهسازی بیشتر، فرض میکنیم نیروها به نقطهای در وسط جسم (مرکز جرم) وارد شوند. همچنین در این مطلب تمام واحدها بر اساس سیستم بینالمللی SI نوشته شده است. در مرحله ششم، بسته به اینکه در محاسبات جمع برداری مجموع نیروهای وارد بر جسم صفر شود یا خیر، با قانون اول یا دوم روبرو میشویم.
در ادامه بهتر است ابتدا با انواع نیروهای مهمی که در اکثر مسائل دینامیکی به جسم وارد میشوند، آشنا شویم. برای تفکیک بهتر این نیروها از سایر نیروها، آنها را بهجای F با حروف مخصوصی نشان میدهیم.
نیروی وزن چیست؟
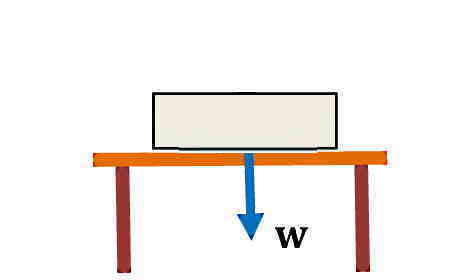
این نیرو همان نیروی گرانش زمین است که همیشه به تمام اجسام روی زمین وارد میشود. جهت این نیرو به سمت زمین است که معمولا در مسائل به سمت پایین در نظر گرفته میشود. نیروی وزن (Weight) را با W نشان میدهیم و بهصورت زیر محاسبه میشود:
- W نیروی وزن که واحد آن نیوتن (N) است.
- m جرم جسم که واحد آن کیلوگرم (kg) است.
- g شتاب جاذبه زمین که واحد آن متر بر مجذور ثانیه (m/s2) است. مقدار g در تمام مسائل این مطلب برابر با 9.8 m/s2 در نظر گرفته میشود.
نیروی عمودی سطح چیست؟
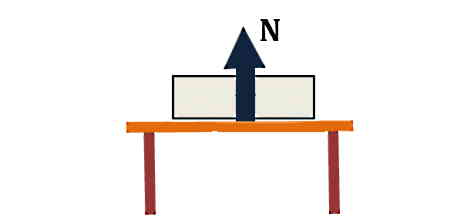
هرگاه جسمی روی یک سطح قرار داشته باشد، همواره از طرف سطح نیرویی به جسم وارد میشود. نیروی عمودی سطح (Normal Force) را با N نشان میدهیم. برای محاسبه این نیرو فرمول مشخصی وجود ندارد، اما میتوانیم اندازه آن را با کاربرد قانون دوم نیوتن و در تعامل با سایر نیروهای وارد بر جسم پیدا کنیم. جهت این نیرو همیشه عمود بر سطح است.
نیروی اصطکاک چیست؟
وقتی جسمی روی یک سطح حرکت میکند، از طرف سطح نیرویی در خلاف جهت حرکت جسم به آن وارد میشود. این نیرو اصطکاک (Frictional Force) نام دارد. اگر جسم در «آستانه حرکت» باشد، نیروی اصطکاک از نوع ایستایی (Static Friction) است و آن را با fs نشان میدهیم. در واقع ضریب اصطکاک ایستایی μs در شرایطی در فرمول نیروی اصطکاک استفاده میشود که میخواهیم بیشینه نیروی اصطکاک ایستایی را محاسبه کنیم. پس از این حالت، جسم شروع به حرکت میکند و برای جسم در حال حرکت اصطکاک جنبشی یا لغزشی (Kinetic Friction) را در نظر میگیریم که با fk نمایش داده میشود.
نیروی اصطکاک در هر دو حالت خود توسط رابطه زیر بدست میآید و بسته به نوع اصطکاک در مسئله، از ضریب s یا k برای f و μ استفاده میشود:
- f نیروی اصطکاک که واحد آن نیوتن (N) است.
- μ ضریب اصطکاک که مقدار ثابتی است و واحدی ندارد.
- N نیروی عمودی سطح که واحد آن نیوتن (N) است.
فرمول قانون دوم نیوتن
اگر نیروی برآیند وارد بر جسم صفر نشود، حرکت جسم دیگر مثل حرکت آن قبل از اعمال نیروها نیست. در این حالت، نیروی خالصی بر جسم وارد میشود، به آن شتاب میدهد و حرکت جسم شتابدار میشود. پس در این حالت عامل اصلی تغییر حرکت جسم، تغییرات در سرعت آن یا ایجاد شتاب است. اگر بخواهیم این شتاب را محاسبه کنیم، از فرمول قانون دوم نیوتن بهصورت زیر استفاده میکنیم:
- F∑ جمع برداری تمام نیروهای وارد بر جسم که واحد آن نیوتن (N) است.
- m جرم جسم که واحد آن کیلوگرم (kg) است.
- a شتاب جسم که واحد آن متر بر مجذور ثانیه (m/s2) است.
برای نمونه فرض کنید جسمی تحت تاثیر نیروی F روی سطح بدون اصطکاکی حرکت کند. اگر بخواهیم مراحل گفته شده برای این شکل را پیاده کنیم، ابتدا شماتیک ساده ای از سیستم جسم و میز همراه تمام نیروهای وارد بر جسم را رسم میکنیم. جهت سیستم مختصات انتخابی را بهصورت استاندارد (جهت مثبت محور y به سمت بالا و جهت مثبت محور x به سمت راست) تعیین میکنیم.
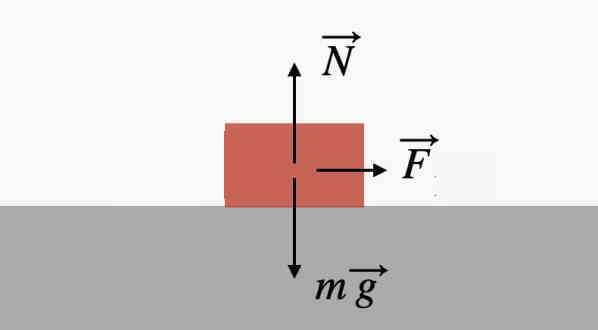
حال بهراحتی میتوانیم نیروهای در راستای x را با هم و نیروهای در راستای y را با هم جمع کنیم. برای مجموع نیروها در هر راستا، قانون دوم نیوتن را مینویسیم و شتاب را محاسبه میکنیم.
دیدیم در این سیستم نسبتا ساده تمام نیروها در راستای محورها هستند و نیازی به تجزیه بردار نیرو نداریم. در مثالهای بعدی خواهیم دید در موارد بسیاری لازم است نیروها در راستای محورهای مختصات تجزیه شوند. همچنین گاهی لازم است سیستم مختصات انتخابی شکل دیگری داشته باشد تا مسئله راحتتر حل شود.
حل مثال در مورد قانون دوم نیوتن
تا اینجا متوجه شدیم قانون دوم نیوتن چیست و چگونه در تعیین شتاب حرکت جسم موثر است. در این بخش گام به گام با بررسی چند مثال، نحوه استفاده از قانون دوم را خواهیم دید.
مثال ۱
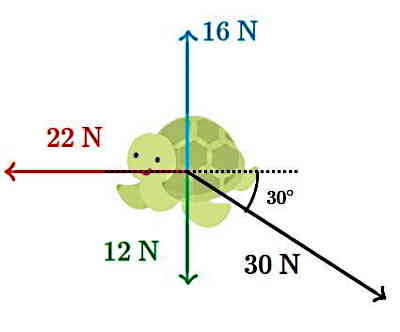
مطابق شکل زیر به لاکپشتی به جرم 1.2 kg، چهار نیروی مختلف وارد میشود. شتاب لاکپشت چقدر خواهد بود؟
پاسخ
قدم اول اجرای مراحل گفته شده است. اگر دقت کنیم نیروی 12 N احتمالا نیروی وزن است. با توجه به اینکه لاکپشت روی سطح خاصی قرار نگرفته است، بنابراین نیروی عمودی سطح نداریم. فقط میدانیم سه نیروی دیگر به لاکپشت وارد میشوند و احتمالا توسط این نیروها نگه داشته شده است. فرض میکنیم F3=16 N، F2=22 N، F1=12 N و F4=30 N است.
لازم است نیروی چهارم در راستای محورهای x و y تصویر شود. یک مولفه این نیرو در راستای افقی برابر است با F4cos30 و مولفه دیگر در راستای منفی محور y میشود F4sin30. حالا میتوانیم قانون دوم را برای هر محور بنویسیم، اعداد را جایگذاری کنیم و شتاب در راستای هر محور را بدست آوریم:
تا اینجا دو مولفه شتاب در راستای دو محور مختصات بدست آمدند. برای محاسبه اندازه شتاب کل باید از قضیه فیثاغورس استفاده کنیم:
مثال ۲
جعبهای به جرم 20 kg ابتدا در حالت سکون قرار دارد. ضریب اصطکاک ایستایی بین جعبه و زمین 0.7 و ضریب اصطکاک لغزشی 0.6 است. اگر نیروی افقی P توسط فردی به جعبه وارد شود، مقدار شتاب جعبه و نیروی اصطکاک را در حالتهای زیر برای مقادیر مختلف نیروی P بدست آورید:
- P=20 N
- P=30 N
- P=120 N
- P=180 N
پاسخ
ابتدا به بررسی حالت اول یعنی P=20 N میپردازیم. با توجه به اینکه جعبه روی سطح زمین است، همواره نیروی عمودی سطح و نیروی وزن به جعبه وارد میشوند که در شکل نیز مشخص است. انتظار داریم با اعمال نیروی P به جعبه و تلاش برای حرکت دادن آن، نیروی اصطکاک f خلاف جهت P وجود داشته باشد.
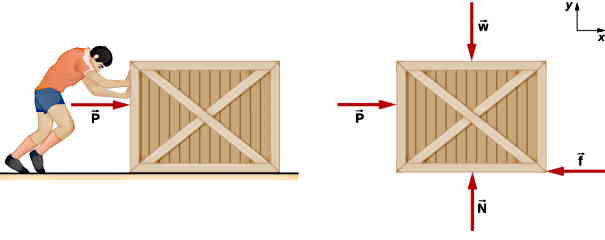
همچنین واضح است که با اعمال نیروی افقی P جعبه در راستای y حرکتی ندارد. بنابراین ay مساوی صفر است و میتوانیم مقدار نیروی عمودی سطح را از نوشتن قانون دوم برای محور y محاسبه کنیم:
حالا سوال مهمی که مطرح است این است که آیا با اعمال نیروی P=20 N جعبه حرکت میکند؟ برای پاسخ به این سوال، ابتدا بیشترین مقدار نیروی اصطکاک ایستایی را محاسبه میکنیم:
پس تا زمانی که مقدار نیروی P وارد شده به جعبه از 137.2 N کمتر باشد، جعبه همچنان ساکن باقی میماند و شتاب آن در هر دو راستای x و y صفر است. در ادامه برای مقدار نیروی اصطکاک در این حالت خواهیم داشت:
برای حالتهای دوم و سوم نیز شرایط حالت اول برقرار است. در تمام حالتهای اول تا سوم مقدار نیروی P از بیشترین مقداری نیروی اصطکاک ایستایی، کوچکتر است. در نتیجه جسم ساکن میماند و a=0. مقدار نیروی اصطکاک ایستایی در هر حالت با مقدار نیروی P وارد شده به جسم برابر است. بنابراین برای حالت P=30 N نیروی fs=30 N و برای P=120 N نیروی fs=120 N خواهد شد.
برای حالت چهارم، نیروی اعمال شده به جعبه از بیشینه نیروی اصطکاک ایستایی بیشتر است (fsmax=137.2 N < P=180 N). پس جعبه دیگر ساکن نمیماند و با اعمال نیروی P شروع به حرکت خواهد کرد. حالا با حرکت جعبه، نیروی اصطکاک جنبشی یا لغزشی در خلاف جهت حرکت به آن وارد خواهد شد و جعبه در راستای محور x شتاب میگیرد. مجددا قانون دوم را برای هر دو راستا مینویسیم:
پس در این مثال یاد گرفتیم که نیروی اصطکاک ایستایی تا جایی که به بیشترین مقدار خود نرسید، با نیروی وارد شده به جسم مقدار برابری داشت. زمانی که نیروی اعمال شده به جسم با بیشینه نیروی اصطکاک ایستایی برابر شد، همچنان حرکت نداشتیم. ولی دیدیم اگر نیروی اعمالی از این میزان کمی بیشتر شود، جسم شروع به حرکت کرده و اصطکاک جنبشی خواهیم داشت.
مثال ۳
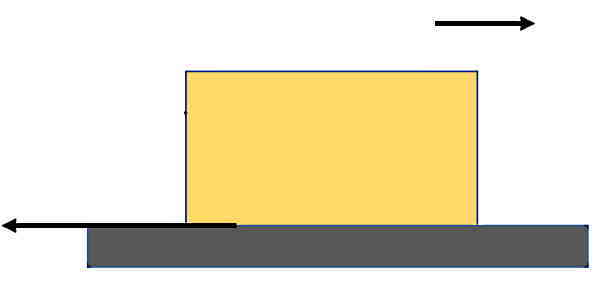
یک جعبه 50 kg را که روی سطح یک کامیون قرار دارد، در نظر بگیرید. ضرایب اصطکاک بین سطوح بهصورت μk = 0.3 و μs = 0.4 است. نیروی اصطکاک جعبه را زمانی که کامیون نسبت به زمین با شتاب 2 m/s2 یا 5 m/s2 حرکت میکند، پیدا کنید:
پاسخ
اگر نمودار جسم آزاد جعبه را رسم کنیم، نیروهای وارد بر آن شامل نیروی وزن، نیروی عمودی از سمت سطح کامیون و نیروی اصطکاک خواهد بود. نکته مهم این است که با شتاب گرفتن کامیون رو به جلو (در راستای مثبت محور xها) جعبه به سمت عقب (منفی) حرکت میکند. پس جهت نیروی اصطکاکی که جعبه با سطح کامیون دارد، در راستای مثبت محور است. در این مثال هم دستگاه مختصات به شکل استاندارد در نظر گرفته میشود.
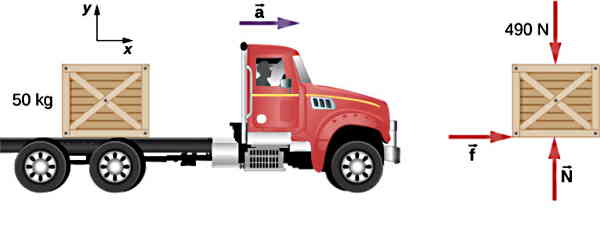
بررسی حالت اول: a=2 m/s2
فرض میکنیم جعبه روی کامیون سر نخورد، در این شرایط نیروی اصطکاک ایستایی fs روی جعبه اثر خواهد داشت و شتاب آن با شتاب کامیون یعنی 2 m/s2 برابر است. قانون دوم را در هر دو راستای مختصات مینویسیم:
حالا میخواهیم فرضمان مبنی بر لیز نخوردن یا سر نخوردن جعبه روی کامیون را بررسی کنیم. بیشترین مقدار نیروی اصطکاک ایستایی یا نیروی اصطکاکی که در آن جعبه در آستانه حرکت است، را بهدست میآوریم:
با توجه به اینکه مقدار نیروی f بدست آمده از مرحله قبل از بیشینه اصطکاک در آستانه حرکت کمتر شد (100<196)، پس فرض ما درست بوده است.
در واقع اگر بخواهیم دقیقتر حرکت جعبه را بررسی کنیم، لازم است حرکت آن را نسبت به کامیون و نسبت به زمین تفکیک کنیم. حرکت جعبه نسبت به زمین، با شتاب 2 m/s2 و به سمت راست خواهد بود، ولی در این حالت جعبه نسبت به کامیون حرکتی ندارد و نیروی بین این دو بهصورت اصطکاک ایستایی و معادل 100 N است. پس نیروی اصطکاک برای حالت اول 100 N و از نوع ایستایی شد.
بررسی حالت دوم: a=5 m/s2
با این شتاب مجددا قانون دوم را مینویسیم:
واضح است که با این شتاب، مقدار نیروی اصطکاک بر اساس قانون دوم از بیشینه اصطکاک در آستانه حرکت (196 N) بیشتر است. بنابراین جعبه به آسانی همزمان با حرکت شتابدار کامیون به سمت راست، به سمت چپ روی کامیون سر میخورد. نیروی اصطکاک جنبشی یا لغزشی که بین جعبه و کامیون وجود دارد، به شکل زیر حاصل میشود:
پس نیروی اصطکاک حالت دوم 147 N و از نوع لغزشی شد. اگر بخواهیم حرکت جعبه را دقیقتر تحلیل کنیم، میدانیم در اینجا جعبه همزمان با حرکتاش نسبت به زمین، نسبت به کامیون هم حرکت دارد:
شتاب حرکت جعبه نسبت به زمین (؟) = شتاب حرکت جعبه نسبت به کامیون (؟) + شتاب حرکت کامیون نسبت به زمین (5 m/s2)
برای محاسبه شتاب حرکت جعبه نسبت به کامیون، کافی است که از نیروی اصطکاک لغزشی بدست آمده برای جعبه استفاده کنیم و شتاب را محاسبه کنیم:
نکته مهم در اینجا این است که با توجه حرکت جعبه به سمت چپ، لازم است علامت منفی برای این شتاب در نظر گرفته شود. بنابراین برای شتاب حرکت جعبه نسبت به زمین خواهیم داشت:
مثال ۴
فرض کنید شخصی با جرم 70 kg روی طنابی که از هر دو طرف به دیواری متصل شده است، ایستاده است. اگر زاویه طناب با افق از هر سمت ۵ درجه باشد، نیروی کشش طناب را حساب کنید:
پاسخ
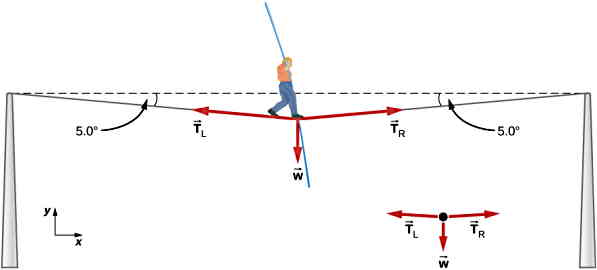
همانطور که مشخص است، دو نیروی کشش طناب از دو سمت همراه نیروی وزن به شخص وارد میشوند. آنچه که باعث حفظ تعادل فرد میشود، تعادل ایجاد شده بین این نیروها است. پس لازم است با توجه به دستگاه مختصات انتخابی، نیروهای TR و TL را در راستای محورها تجزیه کنیم و قانون دوم را بنویسیم.
دقت کنید خطی موازی خط افق که از نقطه اثر نیروها عبور میکند، رسم میکنیم. در این صورت با رسم خط مورب بین دو خط موازی، زاویه بین نیروی T و خط رسم شده جدید نیز معادل 5 درجه است.
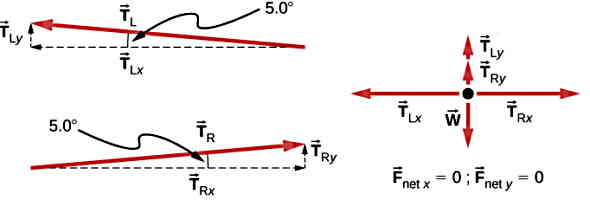
بنابراین اندازه نیروی کشش طناب بدست آمد. میبینیم که برای حفط تعادل شخص لازم است این نیرو عدد بزرگی باشد.
ترازو در آسانسور
مثالهای حرکت آسانسور و حضور شخص در آن، بهترین موقعیت برای یادگیری عمیقتر نیروی عمودی سطح و نیروی وزن هستند. با مفهوم وزن ظاهری در این بخش آشنا خواهیم شد و با حل مثال، مفهوم آن را بهتر درک میکنیم.
مثال محاسبه وزن شخص در آسانسور
فرض کنید شخصی داخل یک آسانسور روی یک ترازوی آبی رنگ ایستاده است. در حالتهای زیر، ترازو وزن شخص را چقدر نشان میدهد؟
- حالت اول: شتاب آسانسور صفر است.
- حالت دوم: آسانسور با شتاب مثبت a به سمت بالا میرود.
- حالت سوم: آسانسور با شتاب منفی a به سمت بالا میرود.
- حالت چهارم: آسانسور با شتاب مثبت a به سمت پایین میرود.
- حالت پنجم: آسانسور با شتاب منفی a به سمت پایین میرود.
- حالت ششم: کابل آسانسور پاره شود.
پاسخ
ابتدا به بررسی حالت اول میپردازیم. میدانیم که ترازو مقدار نیروی FN را نشان میدهد. در این شرایط چون شتاب آسانسور صفر است، دو سناریو خواهیم داشت. اگر آسانسور ساکن باشد، ساکن میماند و اگر در حال حرکت با سرعت ثابتی باشد، به حرکت خود با همان سرعت ادامه میدهد.
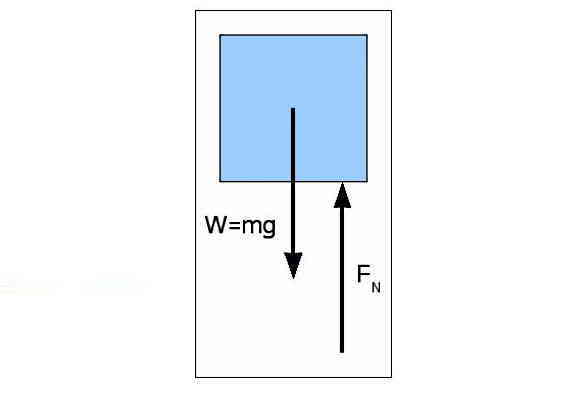
در واقع نیروی وزن به ترازو وارد میشود و از سمت ترازو، نیروی عمودی سطح (که در اینجا با FN نشان داده شده است) به شخص وارد میشود. پس در این شرایط نیروها یکدیگر را خنثی خواهند کرد و ترازو وزن واقعی (True Weight) شخص را نشان میدهد.
در حالت دوم با شتاب گرفتن آسانسور، اینرسی شخص باعث میشود که به حفظ حالت سکون خود متمایل باشد. اما کف آسانسور و ترازو، شخص را به سمت بالا هل میدهند. همین مسئله باعث میشود که ترازو نیروی بیشتری به شخص وارد کند تا او را به سمت بالا همراه آسانسور شتاب دهد. پس نیروی FN در این حالت بزرگتر از حالت اول خواهد شد و ترازو مقدار بیشتری برای وزن نشان میدهد.
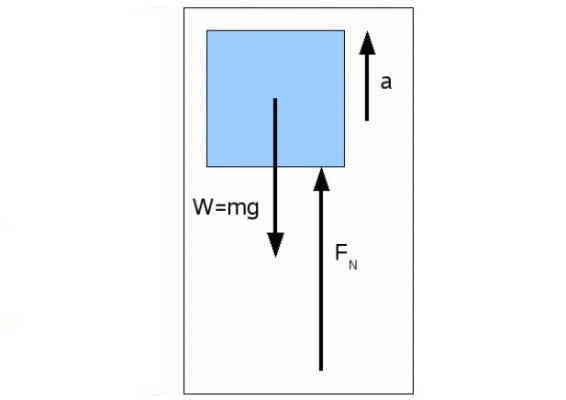
با در نظر گرفتن جهت مثبت به سمت بالا و همجهت بودن نیروی عمودی با شتاب، قانون دوم را مینویسم:
بنابراین ترازو در این حالت «وزن ظاهری» (Apparent Weight) شخص را میخواند که از وزن واقعی او بیشتر است.
وقتی آسانسور با شتاب منفی a به سمت بالا میرود، اینرسی شخص تمایل دارد وضعیت حرکت به سمت بالا با سرعت ثابت را حفظ کند. اما با وارد شدن شتاب منفی، ترازو نیروی کمتری به شخص وارد خواهد کرد. پس با نوشتن قانون دوم و اعمال علامت منفی برای شتاب داریم:
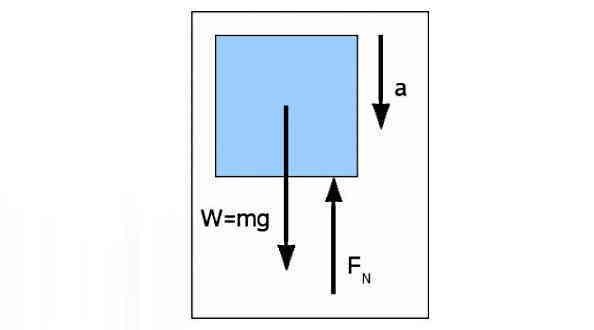
پس دیدیم که ترازو در این حالت هم وزن ظاهری شخص را میخواند، اما اینجا وزن ظاهری از وزن واقعی کمتر است.
در حالت چهارم شکل مسئله با شکل حالت دوم مشابه است. اما دقت شود در این حالت حرکت آسانسور به سمت پایین است، در حالی که برای حالت دوم حرکت به سمت بالا بود. در حالی که شخص تمایل دارد حرکت با سرعت ثابت به سمت پایین خود را حفظ کند، با وارد شدن شتاب به سمت بالا نیروی عمودی سطح بیشتری به شخص وارد خواهد شد.

پس ترازو در این حالت مشابه حالت دوم وزن ظاهری شخص را میخواند که از وزن واقعی او بیشتر است.
شکل مسئله حالت پنجم با شکل حالت سوم مشابه است. اما دقت شود در این حالت حرکت آسانسور به سمت پایین است، در حالی که برای حالت سوم حرکت به سمت بالا بود. در حالی که شخص تمایل دارد حرکت با سرعت ثابت به سمت پایین خود را حفظ کند، با وارد شدن شتاب به سمت پایین نیروی عمودی سطح کمتری به شخص وارد خواهد شد.

پس ترازو در این حالت مشابه حالت سوم وزن ظاهری شخص را میخواند که از وزن واقعی او کمتر است.
در حالتی که کابل پاره شود، شتاب حرکت آسانسور و تمام اجزای داخل آن، معادل شتاب جاذبه زمین است. در واقع آسانسور، شخص و ترازو سقوط آزاد خواهند داشت. بنابراین هیچ نیروی عمودی سطحی به شخص وارد نمیشود، چون ترازو دیگر زیر پای شخص نخواهد ماند و تماسی با هم ندارند. پس وزن ظاهری در این حالت معادل صفر است.
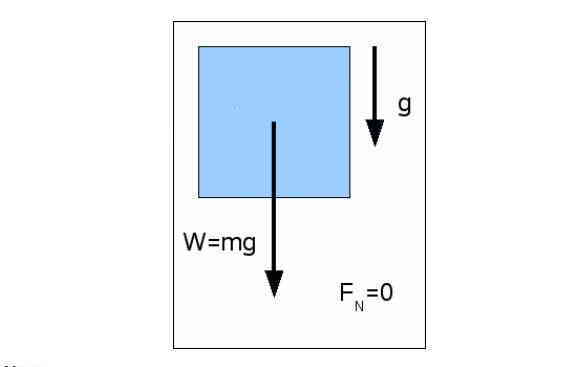
حرکت دایرهای
در «حرکت دایرهای» (Circular Motion) حرکت جسم در یک مسیر دایرهای انجام میشود. در این حالت حتی اگر اندازه سرعت تغییر نکند، چون جهت آن تغییر میکند، پس شتاب داریم. بنابراین حرکت دایرهای یک حرکت شتابدار محسوب میشود. این شتاب طبق قانون دوم نیوتن باید توسط یک نیرویی ایجاد شود. در حالت کلی هر نیرویی که حرکت دایرهای را ایجاد کند، «نیروی مرکزگرا» ( Centripetal Force) مینامیم و آن را با Fc نشان میدهیم. جهت این نیرو همیشه به سمت مرکز مسیر دایرهای است.
این نیرو در مسائل مختلف برابر با نیروی کشش طناب، نیروی اصطکاک یا .. است. پس معمولا در مسائل حرکت دایرهای هدف این است که ببینیم کدام نیرو نقش نیروی مرکزگرا را دارد. سپس با توجه به فرمول مخصوص این نیرو، میتوانیم در حل مسئله با ابزارهای بیشتری جلو رویم. اگر بخواهیم اندازه نیروی مرکزگرا را بدست آوریم، طبق قانون دوم نیوتن داریم:
برای محاسبه شتاب مرکزگرا (ac) از شکل زیر استفاده میکنیم. اگر جسم روی مسیر دایرهای با سرعت v1 و v2 و ... حرکت کند، همواره فاصله جسم از مرکز اندازه شعاع r است و اندازه سرعتها هم با یکدیگر برابر و مساوی v است. همچنین مشخص است که مثلثهای ABC و PRQ مشابهاند. طبق قوانین تشابه مثلث برای این دو خواهیم داشت:
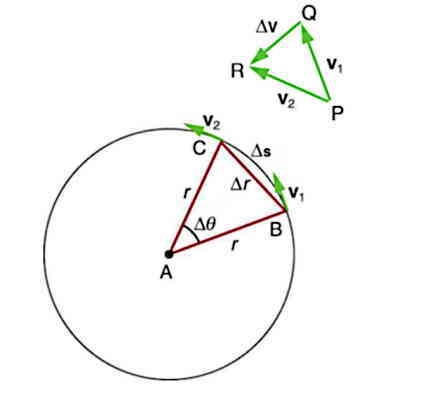
از رابطه بین شتاب و سرعت، در نهایت شتاب مرکزگرا بدست میآید:
پس اندازه نیروی مرکزگرا خواهد شد:
مثال در مورد حرکت دایرهای
اگر جرم اتومبیلی 900 kgباشد و مسیر دایرهای شکل به شعاع 500 m را با سرعت 25 m/sطی کند، نیروی مرکرگزا را بدست آورید. سپس حداقل ضریب اصطکاک ایستایی بین تایرهای اتومبیل و جاده را محاسبه کنید.
پاسخ
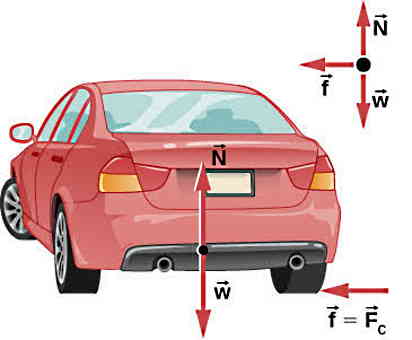
در این مسئله اصطکاک ایستایی عاملی است که از سر خوردن اتومبیل جلوگیری میکند. برای محاسبه نیروی مرکزگرا با توجه به در اختیار داشتن سرعت و شعاع حرکت، خواهیم داشت:
در مرحله بعدی لازم است نمودار جسم آزاد را برای اتومبیل رسم کنیم. نیروهای وارد بر آن شامل وزن، نیروی عمودی سطح و نیروی مرکزگرا هستند. نکته مهم در این مسئله این است که نیروی مرکزگرا برابر با نیروی اصطکاک است و از لیز خوردن اتومبیل به سمت مرکز مسیر جلوگیری میکند. بنابراین میتوانیم با داشتن نیروی مرکزگرا و محاسبه نیروی عمودی سطح، ضریب اصطکاک را محاسبه کنیم:
نکته جالب در این مثال این است که اگر عددگذاری نکنیم و با کمیت ها پیش رویم، برای مقدار ضریب اصطکاک خواهیم داشت:
میبینیم که در این رابطه جرم اتومبیل حدف شده است. پس جرم اتومبیل در اینکه آیا اتومبیل میتواند مستقل از میزان سنگینیاش مسیر دایرهای را بدون واژگونی دور بزند یا خیر، اثری ندارد.
حرکت روی سطح شیبدار
یکی از سیستمهای مرسوم و پر تکرار جهت بررسی مسائل دینامیکی «سطح شیبدار» (Inclined Plane) است. در مثالهای قبلی حرکت جسم روی سطح صاف را بررسی کردیم. تفاوت حل مسئله برای سطح شیبدار و سطح صاف، در نحوه انتخاب دستگاه مختصات مناسب است. خواهیم دید که با انتخاب دستگاه مختصات مناسب میتوانیم حل چنین مسائلی را چقدر سادهتر کنیم.
مثال ۱ در مورد سطح شیبدار
فرض کنید شخصی با جرم 62 kg روی یک شیب برفی در حال اسکی کردن به سمت پایین است. اگر مقدار نیروی اصطکاک 45 N و زاویه شیب با سطح افقی °25 باشد، ضریب اصطکاک جنبشی و شتاب شخص را محاسبه کنید:
پاسخ
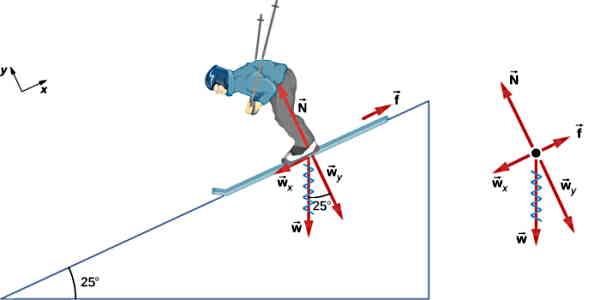
طبق رابطه و با توجه به داشتن مقدار نیروی اصطکاک در صورت مسئله، اگر نیروی عمودی سطح را پیدا کنیم میتوانیم ضریب اصطکاک را محاسبه کنیم. برای حل مسئله اولین کار ترسیم نمودار جسم آزاد است. سپس رسم تمام نیروهای وارد بر شخص، که در اینجا شامل نیروی وزن، نیروی عمودی سطح و نیروی اصطکاک جنبشی است.
حالا اگر دستگاه مختصات خود را مشابه مثالهای قبل بصورت استاندارد (جهت مثبت محور y به سمت شمال و جهت مثبت محور x به سمت شرق) در نظر بگیریم، نیروی عمودی سطح در راستای محور y قرار ندارند. نیروی اصطکاک نیز در راستای محور x نیست. فقط نیروی وزن است که در راستای محور y قرار دارد. پس با این انتخاب باید دو نیرو را تجزیه کنیم.
اما اگر دستگاه مختصات خود را به شکل بالا در نظر بگیریم، فقط لازم است نیروی وزن را تجزیه کنیم و حل مسئله سادهتر خواهد شد. نکته مهم بعدی تعیین زاویه نیروی وزن با محورهای x و y جدید است. طبق شکل، زاویه بردار نیروی وزن با سطح شیبدار °65 است که همان زاویه W با Wx است. پس زاویه W با Wy خواهد شد °25. با توجه به روابط مثلثاتی میدانیم .
با نوشتن قانون دوم برای هر راستا داریم:
پس طبق انتظارمان برای محاسبه نیروی اصطکاک به نیروی عمودی سطح نیاز داشتیم. اما تفاوت این مسئله با مسائل روی سطح افقی این بود که در اینجا نیروی عمودی سطح با نیروی وزن برابر نبود، بلکه با مولفهای از نیروی وزن برابر شد.
مثال ۲ در مورد سطح شیبدار
اگر اتومبیلی در یک «مسیر دایرهای شکل و شیبدار» (Banked Curves) با شیب θ در حال حرکت در مسیر دایرهای باشد، زاویه θ را به گونهای تعیین کنید که اتومبیل بدون نیاز به نیروی نگهدارنده اصطکاک بین تایرها و سطح، در مسیر دایرهای خود حرکت کند. سپس سرعتی را محاسبه کنید که در آن با شعاع مسیر 100 m و زاویه شیب ،31° شرایط اتومبیل در حالت ایدهآل بخش قبل باشد:
پاسخ
این مثال تلفیقی از حرکت دایرهای و سطح شیبدار است. ابتدا نمودار جسم آزاد را برای این موقعیت مطابق شکل زیر رسم میکنیم. نیروی عمودی سطح و نیروی وزن مشابه مسائلی که در بخش سطح شیبدار دیدیم، در یک راستا نیستند. با انتخاب دستگاه مختصات در راستای نیروی وزن یعنی در حالت استاندارد و معمول، لازم است نیروی N را تجزیه کنیم. اگر مثلث ساخته شده توسط زاویه θ با نیروی وزن را در نظر بگیریم، زاویه W با سطح شیبدار 90-θ است.
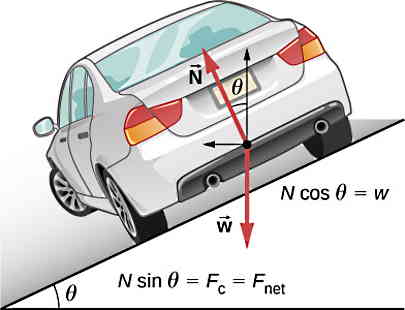
به همین ترتیب در نهایت زاویه N با مولفه عمودیاش معادل θ خواهد شد. حالا قانون دوم را اعمال میکنیم:
گفتیم میخواهیم نیروی اصطکاک در نگهداشتن اتومبیل کمک نکند، پس لازم بود مولفه افقی عمودی سطح نقش نیروی مرکزگرا را داشته باشد. با تقسیم دو عبارت بالا بر هم، زاویه مناسب برای شیب را بدست خواهیم آورد:
این عبارت نشان میدهد باز هم مستقل از میزان جرم اتومبیل، تا چه اندازه سرعت و شعاع حرکت در حفظ تعادل اتومبیل موثر است. هر چه مقدار سرعت بیشتر و شعاع کوچکتر شود، زاویه شیب برای حفظ این شرایط باید بیشتر شود. حالا برای محاسبه بخش دوم لازم است فقط از رابطه بالا استفاده کنیم:
اگر نیروی اصطکاک در نظر گرفته شود، قطعا میتوان از سرعتهای بالاتری نیز استفاده کرد.
سیستم طناب و قرقره
در خیلی از مسائل دینامیکی اجسام توسط «طناب» (Rope) (یا نخ) و «قرقره» (Pulley) بهم متصل شده و سیستمی را میسازند که در حال حرکت روی یک سطح یا در حالت سکون است. نکته مهم در این سوالات در نظر گرفتن «نیروی کشش طناب یا نخ» (Tension) در محاسبات است. معمولا این نیرو را با T نشان میدهیم. همچنین در این مسائل چون معمولا با دو یا چند جسم سروکار داریم، لازم است قانون دوم برای هر جسم جداگانه نوشته شود. در مثالهای زیر چند نمونه از سیستمهای طناب و قرقره را بررسی میکنیم.
مثال ۱ در مورد سیستم طناب و قرقره
در شکل زیر فرض کنید دو جسم m1=16.5 kg و m2=15 kg توسط یک طناب بدون جرم و یک قرقره به هم متصل شدهاند. همچنین سطحی که جسم اول روی آن قرار داده شده است را یک سطح بدون اصطکاک در نظر بگیرید. مقدار کشش طناب و شتاب سیستم را محاسبه کنید.
پاسخ
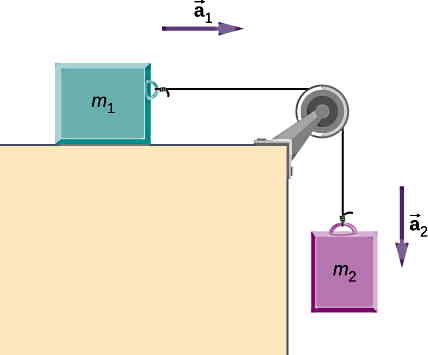
با توجه به اینکه دو جسم با یک طناب بهم متصل شدهاند، شتاب برای کل سیستم مقدار یکسانی خواهد داشت. نیروهای وارد بر اجسام با توجه به نبود اصطکاک برابر با کشش طناب یکسان برای دو جسم و نیروی وزن است. نکات مهم در حل این مسئله اول این است که شتاب جسم اول در راستای محور x و جسم دوم در راستای محور y است. این دو شتاب به هم تبدیل شده و بهعنوان شتاب a سیستم در نظر گرفته میشوند.
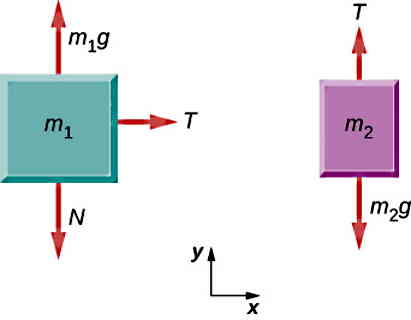
نکته بعدی انتخاب دستگاه مختصات است. برای راحتی جهت مثبت محور x را به سمت راست و جهت مثبت محور y را به سمت پایین در نظر میگیریم. حالا با نوشتن قانون دوم نیوتن برای هر جسم ابتدا شتاب و سپس نیروی کشش را برای سیستم بدست خواهیم آورد:
در نهایت مسئله بهصورت یک دستگاه دو معادله دو مجهول خواهد شد که با حل آن، مقدار T برابر با 77 N و شتاب 4.6 m/s2 بدست می آید.
مثال ۲ در مورد سیستم طناب و قرقره
دو بلوک متصل به یک طناب بدون جرم و یک قرقره بدون اصطکاک، روی هم قرار دارند و قرقره نیز از سمت راست به دیواری متصل است. زمانی که بلوک پایینی به جرم 4 kg با نیروی ثابت P به چپ کشیده میشود، بلوک بالایی با جرم 2 kg روی آن به سمت راست میلغزد. اندازه نیروی لازم برای حرکت دادن بلوکها با سرعت ثابت را بدست آورید (ضریب اصطکاک جنبشی بین تمام سطوح را 0.4 در نظر بگیرید):
پاسخ
ابتدا نمودار جسم آزاد برای هر دو بلوک بهصورت مجزا رسم میشود. چون هر دو بلوک با یک طناب بهم وصل شدهاند، پس برای هر دو بلوک مقدار نیروی کشش طناب T یکسان است. برای بلوک پایینی نیروی P طبق صورت سوال آن را به سمت چپ میکشد و نیروی کشش طناب T از سمت راست بلوک را میکشد. برای این بلوک دو نیروی عمودی سطح داریم. از سطح زمین نیروی عمودی N2 و از سطح بلوک بالایی نیروی عمودی N1 به آن وارد میشود. پس نیروی عمودی سطح بین دو بلوک با N1 مشخص می شود. با توجه به حضور دو نیروی عمودی سطح برای بلوک پایینی، نیروی اصطکاک جنبشی این بلوک نیز دارای دو مقدار μN1 و μN2 است.
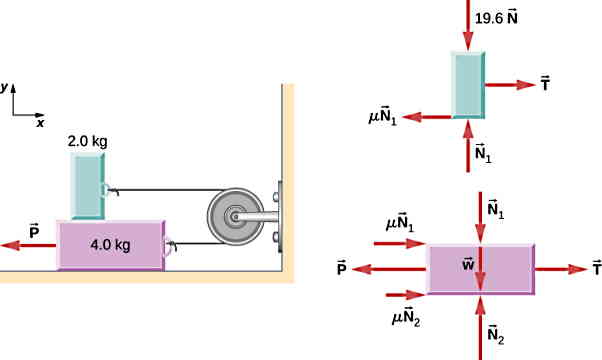
نمودار بلوک بالایی نیز به همین شکل رسم میشود. دقت کنید که نیروی P فقط به بلوک پایینی وارد میشود. پس در نمودار بلوک بالایی رسم نمیشود. فقط نیروی کشش T و اصطکاک جنبشی ناشی از عمودی سطح N1 را برای این بلوک در راستای افقی داریم. در واقع اثر نیروی P روی بلوک بالایی، توسط نیروی عمودی سطح N1 و به دنبال آن μN1 منتقل میشود. دستگاه مختصات انتخابی هم به شکل استاندارد همیشگی در نظر گرفته شده است.
فرض میکنیم بلوک بالایی شماره 1 و بلوک پایینی شماره 2 است. همچنین چون در راستای y حرکتی نداریم، پس ay برای هر دو بلوک صفر در نظر گرفته شده است. جهت نیروهای اصطکاک نیز برای هر بلوک همیشه در خلاف جهت حرکت بلوک است. نکته مهم دیگر این است که در صورت سوال خواسته شده حرکت نهایی سیستم با سرعت ثابت باشد. پس شتاب در راستای محور x یعنی ax نیز باید در معادلات برای هر دو بلوک صفر در نظر گرفته شود.
حالا قانون دوم نیوتن را در هر راستا برای هر بلوک جداگانه مینویسیم:
برای بلوک بالایی خیلی راحت میتوانیم ابتدا N1 را حساب کنیم و سپس با استفاده از آن مقدار T را نیز بدست آوریم:
با داشتن N1 و T از معادلات مربوط به بلوک پایینی، میتوانیم N2 و نیروی خواسته شده در صورت سوال یعنی P را محاسبه کنیم:
سایر قوانین نیوتن
در انتهای این مطلب، به توضیح دو قانون دیگر از سه قانون نیوتن میپردازیم تا در مجموع، درک عمیقتری از اثر کلیه نیروهای وارد بر یک جسم بدست آوریم.
قانون اول نیوتن
اگر در جمع برداری نیروها مجموع نیروهای وارد بر جسم صفر شود، یعنی توزیع نیروهای وارد بر جسم به گونهای بوده که نیروها اثر همدیگر را خنثی کردهاند. از نظر دینامیکی، این جسم با شرایطی که به آن هیچ نیرویی وارد نشود، تفاوتی ندارد. در هر دو مورد نیروی خالص وارد بر جسم که به آن «نیروی برآیند» یا Fnet گفته میشود، صفر است. بنابراین این جسم شرایط حرکتی قبلی خود را حفظ میکند.

پس موضوع قانون اول نیوتن این است که اگر برآیند نیروهای وارد بر جسم صفر شد، جسم حرکت قبلی خود را حفظ میکند. یعنی اگر جسم ساکن بوده است، ساکن میماند و اگر در حال حرکت با سرعت ثابت (حرکت یکنواخت) بوده است، به حرکت خود مثل قبل ادامه میدهد. برای مثال اگر جسم در حال حرکت به سمت شرق با اندازه و جهت ثابت سرعت (m/s) ۵ است، پس از وارد شدن نیرو نیز همچنان به حرکت خود در همان راستا با سرعت ثابت (m/s) ۵ ادامه میدهد.
برای نمونه، اگر در شکل زیر جسمی را در نظر بگیرید که روی یک میز در حالت سکون قرار دارد. دو نیروی وارد شده به آن عبارتند از:
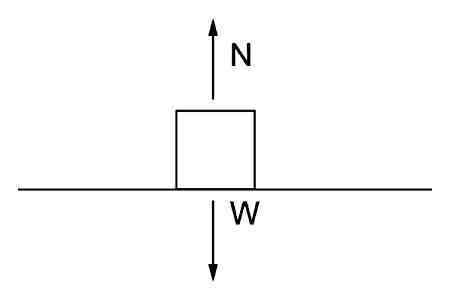
- نیروی عمودی سطح (N) که از سمت میز به جسم وارد میشود و جهت آن رو به بالا است.
- نیروی وزن (W) که از سمت زمین به جسم وارد میشود و جهت آن رو به پایین است.
با توجه به اینکه جسم در وضعیت ساکن خود روی میز باقی میماند، بنابراین مجموع اثر این دو نیرو روی آن صفر است. به عبارتی این دو نیرو هم را خنثی میکنند. پس میتوانیم بگوییم وضعیت این جسم از لحاظ رسم نمودار نیروها مشابه شکل زیر است، گویا هیچ نیرویی به آن وارد نشده است.
از آنجایی که در این قانون جسم تمایل دارد شرایط حرکتی قبلی خود را حفظ کند، به آن «قانون لختی»، «قانون اینرسی» (Law of Inertia) یا «ماند» نیز گفته می شود. اینرسی به معنای تمایل جسم برای حفظ حالت قبلی خود است.
مثال عینی این پدیده زمانی است که در یک اتومبیل در حال حرکت نشستهاید. اگر ناگهان ترمز گرفته شود، شتاب ترمز در خلاف جهت حرکت اتومبیل است و باعث میشود ماشین متوقف شود. اما با توجه قانون اول یا لختی، بدن شما همچنان تمایل دارد حالت حرکت قبلی خود را که رو به جلو بوده است، حفظ کند. در نتیجه به جلو پرت میشوید.
قانون سوم نیوتن
هر دو جسم در تماس با هم به یکدیگر نیروهایی مساوی اما خلاف جهت هم وارد میکنند. در بیشتر مواقع این نیروها هم را خنثی میکنند و به همین دلیل است که در زندگی واقعی اثر آنها مشهود نیست. دیدیم که در مسائل دینامیک مهم است زمانی که میخواهیم کلیه نیروهای وارد بر یک جسم مشخص را تعیین کنیم، این نیروها را فراموش نکنیم. بهخصوص در شرایطی که جسم موردنظرمان در تماس با جسم دیگری است.
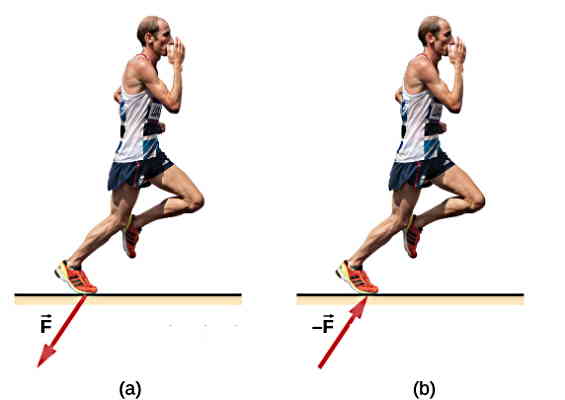
مثلا یک کتاب روی میز را در نظر بگیرید. در این مثال میدانیم طبق قانون سوم، از سمت کتاب به میز نیرویی وارد میشود که مساوی و در خلاف جهت نیروی وارد شده از سمت میز به کتاب است. اگر بررسی «سیستم کتاب و میز» مدنظر ما باشد، لازم نیست اثر این دو نیرو را بررسی کنیم چون هم را خنثی میکنند. اما اگر بخواهیم تمام نیروهای وارد بر «کتاب» را بررسی کنیم، لازم است حتما نیرویی که از سمت میز بر کتاب وارد می شود، را در محاسبات برداری لحاظ کنیم.
آزمون قانون دوم نیوتن
در این بخش به منظور ارزیابی بهتر مطالبی که یاد گرفتیم، تعدادی سوال چهار گزینهای را در قالب یک آزمون قرار دادهایم. پس از انتخاب گزینه صحیح، میتوانید نتیجه آزمون را با کلیک روی دکمه «دریافت نتیجه آزمون» مشاهده کنید.
تمرین و آزمون
مطابق شکل زیر، یک جسم 400 گرمی روی یک سطح قرار دارد و توسط یک طناب به یک قرقره متصل است. به انتهای دیگر طناب متصل به قرقره، وزنهای به جرم 200 گرم متصل شده است و مطابق شکل آویزان است. اگر کل مجموعه در آستانه حرکت باشد، مقدار ضریب اصطکاک سطح کدام است؟
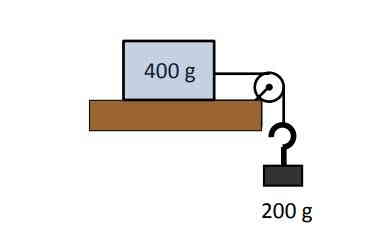
0.4
0.2
0.5
0.6
اگر نیروهای وارد بر جسم روی سطح را رسم کنیم، نیروی کشش طناب و نیروی اصطکاک در راستای افق بر این جسم وارد میشوند. از طرفی چون در صورت سوال گفته شده مجموعه در آستانه حرکت است، پس هنوز شتاب نداریم، چون حرکت انجام نشده است. بنابراین این دو نیرو در راستای افق با هم برابر هستند.
از طرفی برای جسم آویزان از قرقره، نیروی کشش طناب با نیروی وزن برابر است. جرم هر دو جسم به گرم است و باید به کیلوگرم تبدیل شود.
بنابراین چون T برای هر دو جسم یکسان است، خواهیم داشت:
در شکل زیر اگر °θ=25 و P=750 N باشد، اندازه نیروی اصطکاک و اینکه آیا بلوک روی سطح در حال تعادل است یا خیر، در کدام گزینه به درستی بیان شده است؟
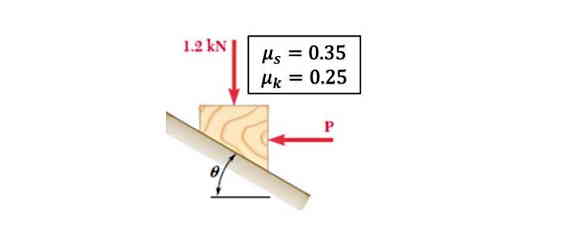
نیروی اصطکاک 171 N است و بلوک در حالت تعادل است.
نیروی اصطکاک 171 N است و بلوک در حال حرکت است.
نیروی اصطکاک 351.1 N است و بلوک در حالت تعادل است.
نیروی اصطکاک 351.1 N است و بلوک در حال حرکت است.
دقت کنید در این سوال نیروی 1200 N همان نیروی وزن است. اگر راستای محور قائم را در راستای نیروی عمودی سطح در نظر بگیریم، لازم است نیروهای وزن و P هر دو تجزیه شوند. با فرض اینکه بلوک در حالت تعادل است جلو می رویم:
حال اگر مجموع نیروها در راستای قائم را بنویسیم، داریم:
بنابراین اگر بخواهیم با داشتن مقدار نیروی عمودی سطح و ضریب اصطکاک، ماکزیمم نیروی اصطکاک برای آستانه حرکت را محاسبه کنیم، میتوانیم بنویسیم:
چون نیروی اصطکاکی که بالاتر بدست آمد، از این مقدار کمتر شد، پس جسم در حالت تعادل قرار دارد و حرکتی ندارد. یعنی فرض اولیه ما درست بوده است. پس گزینه اول صحیح است.
فرض کنید در داخل آسانسوری روی یک ترازو ایستادهاید. اگر وزن واقعی شما 610 N باشد اما ترازوی داخل آسانسور وزن شما را 730 N نشان دهد، شتاب آسانسور کدام گزینه است؟
شتاب 1.92 متر بر مجذور ثانیه و به سمت پایین است.
شتاب 1.92 متر بر مجذور ثانیه و به سمت بالا است.
شتاب صفر است.
شتاب 2 متر بر مجذور ثانیه و به سمت بالا است.
میدانیم به شخص ایستاده در داخل آسانسور روی ترازو، فقط دو نیرو در راستای قائم وارد میشود. نیروی وزن و نیروی عمودی سطح از سمت ترازو. با توجه به مطالب گفته شده، زمانی وزن ظاهری (وزنی که ترازو میخواند) از وزن واقعی بیشتر میشود که شتاب به سمت بالا باشد. پس اگر قانون دوم را بنویسیم، داریم:
اگر یک توپ بیلیارد 0.53 کیلوگرمی ساکنی با سرعت 12 m/s حرکت کند، در طول مدت زمان 4 ms چه نیروی متوسطی به آن اعمال شده است؟
15 kN
159 N
15900 N
1.59 kN
توپ بیلیارد در این مسئله از حالت سکون شروع به حرکت کرده است و لازم است شتاب متوسط را برای آن محاسبه کنیم. از مسائل حرکت به یاد داریم فرمول شتاب متوسط به صورت زیر بود:
مطابق شکل فردی در حال خرید، سبد خرید 7.5 کیلوگرمی خود را 13 درجه رو به بالا هل میدهد. اندازه نیروی لازم برای ایجاد شتابی به اندازه 1.41 m/s2 چقدر است؟
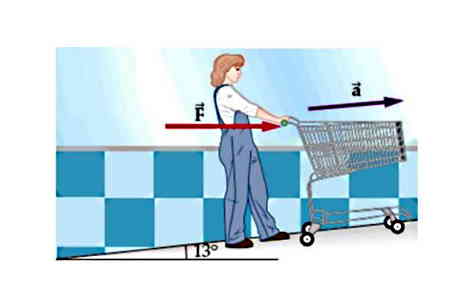
23 N
24 N
20 N
27.5 N
اگر شتاب اولیه یک موشک چهار راکتی 47.309 متر بر مجذور ثانیه، جرم کل آن 2100 kg و نیروی اصطکاک وارد بر آن 650 N باشد، میزان نیروی پیشرانی که توسط هر راکت وارد میشود، چقدر است؟
250 N
250000 N
2500 N
25000 N
در شکل زیر یک نیروی 10 N از سمت راست به بلوک شماره یک وارد میشود. اگر سطح را بدون اصطکاک در نظر بگیریم، با داشتن جرم بلوکها بهصورت m1 = 3 kg و m2 = 1 kg، نیروی کشش طناب وصلکننده دو بلوک چقدر است؟

2.3 N
2.5 N
2.4 N
2 N
فرض کنیم دو جرم m1 و m2 از دو طرف یک قرقره بدون اصطکاک آویزان شدهاند. چنانچه جرم m2 رها شود، نیروی کشش طناب کدام است؟ (m1 = 2 kg و m2 = 4 kg)
27.5 N
30 N
26.1 N
26.4 N
شخصی روی یک سطح که با افق زاویه θ = 13° دارد، با سرعت ثابتی در حال اسکی کردن به سمت پایین است. اگر ضریب اصطکاک جنبشی بین شخص و سطح 0.2 باشد، شتاب شخص چقدر است؟
فرض کنید دو جسم توسط یک سیستم طناب و قرقره بهم متصل شدهاند. اگر جسم 6.7 kg روی یک سطح شیبدار با زاویه شیب ۴۲ درجه با سطح افق قرار داشته باشد و جسم دیگر به جرم m از ضلع عمودی سطح شیبدار آویزان باشد، جرم m باید چقدر باشد تا به سمت پایین نیفتد؟
4.6 kg
4.7 kg
5.4 kg
4.5 kg













سلام خانم داستان،
سوالم اینه که در مطالبی من دیدم که گفته شده(هرچه سرعت جسم بیشتر باشد جرم آن نیز بیشتر است) اما آیا این جمله درست هست؟
من در محاسباتی که کردم با جاگذاری اعداد در قانون دوم نیوتن کهm=F/a؛
این معادله میگه که هرچه شتاب(a)جسم بیشتر باشه جرم آن جسم کمتر است.
اما آن جمله این معادله را نقص میکند.
لطفا اگه میتونید راهنماییم کنید.
با تشکر.
سلام و روز شما به خیر؛
در فیزیک کلاسیک که میزان سرعت جسم بسیار کوچکتر از سرعت نور است از وابستگی جرم به سرعت صرف نظر میشود زیرا مقدار تغییرات آن بسیار ناچیز است، اما برای سرعتهای نزدیک به سرعت نور این موضوع وجود دارد.
از اینکه با فرادرس همراه هستید خرسندیم.
واقعا فرادرس عالیه.ولی ای کاش اثبات این قضایا رو هم اورده بودین…..
واقعا عالی بود – نمره امتحانم رو مدیون توضیحات سایت شما بودم
♥♥♥☺ مرسی از زحماتتون
سلام خسته نباشید ببخشید من یک سوال درباره ی قانون دوم نیوتن داشتم در حل مسائل در رابطه با قانون دوم ما همیشه از نیروی وزن صرف نظر می کنیم میخواستم بدونم که چه دلیل برای این وجود دارد ؟
سلام و روز شما به خیر؛
لزوماً این اتفاق رخ نمیدهد و نیروی وزن در بسیاری از محاسبات وارد میشود مگر اینکه نیروی وزن با نیروی عمود بر سطح یا نیروهای دیگری خنثی شود.
از همراهی شما با فرادرس خرسندیم.