سینوس در ریاضی چیست و چگونه محاسبه می شود؟ – به زبان ساده و با مثال
به طور حتم نام سینوس یا تابع سینوس در ریاضی به گوشتان خورده است در غیر اینصورت به این صفحه از مجله فرادرس نمیرسیدید. سینوس و توابع مثلثاتی دیگر در ریاضیات برای پیدا کردن نسبت طولهای یک زاویه به کار میروند. در این نوشتار میخواهیم بدانیم که سینوس در ریاضی چیست و به چه کار میآید. از طرفی با نحوه محاسبه آن برای زاویهها نیز آشنا خواهیم شد. هر چند در دبیرستان با سینوس آشنا شدهاید ولی تا آخرین گامهای تحصیلی در دانشگاه نیز با تابع سینوس و توابع دیگر مثلثاتی مانند کسینوس و تانژانت و کتانژانت سروکار خواهید داشت. توابع مثلثاتی علاوه بر ریاضی، در فیزیک و شیمی و حتی علوم اقتصادی نیز نقش دارند.
به عنوان پیشزمینه در معرفی توابع مثلثاتی بهتر است نوشتارهای جدول دایره مثلثاتی چیست؟ – روش محاسبه + حل مثال و تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده را مطالعه کنید. همچنین خواندن مطالب سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده و روابط مثلثاتی — فرمول های مثلثاتی و روابط مهم | به زبان ساده نیز خالی از لطف نیست.
سینوس در ریاضی چیست؟
یکی از مهمترین اشکال در ریاضی و هندسه، مثلث است. یک مثلث دارای سه ضلع و سه زاویه است. تنها شکلی که محدب بوده و از کمترین زاویه تشکیل شده است، مثلث است. به همین دلیل سادهترین و در عین حال پایه شکلهای دیگر هندسی را میتوان مثلث در نظر گرفت. بررسی رابطه بین ضلعها و زاویههای یک مثلث و همینطور اشکال هندسی دیگر، علم مثلثات را بوجود آورده است.
دانشمندان زیادی در جهان علوم و قضیههای مثلثات را توسعه دادند. البته در این میان، ریاضیدانان ایرانی نقش مهمی داشته و بسیاری از اصطلاحات و عبارتهای مورد استفاده در مثلثات از طریق زبان عربی به لاتین ترجمه و به کار بسته شده. برای مثال جِیب و جیب تمام دو عبارتی هستند که دانشمندان ایرانی به کار برده و به ترتیب به اشتباه توسط مترجمها برای سینوس و کسینوس زاویه به کار برده شدند. بعدها این عبارتها به لاتین ترجمه و در علوم ریاضی گنجانده و مورد استفاده قرار گرفت.
نکته: گاهی در متنهای قدیمی ریاضی، تانژانت زاویه را به صورت ظل زاویه (سایه زاویه) به کار میبردند.
در تصویر زیر یک مثلث را مشاهده میکنید که دو ضلع آن با هم برابرند.
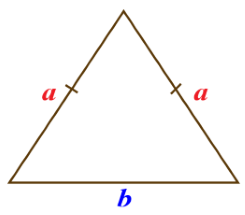
چنین مثلثی، متساویالساقین نامیده میشود. ویژگیهای اصلی این مثلث و همچنین اقسام دیگر مثلث را میتوانید در نوشتارهای دیگر مجله فرادرس مانند «مثلث قائمالزاویه» (Right-angled Triangle)، مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده مشاهده کرده و اطلاعات مفیدی بدست آورید. ولی چیزی که ما را به مثلث نزدیک میکند، زاویههایی آن و همچنین نسبت اضلاع یک مثلث و توابعی است که از زاویهها برحسب طول اضلاع آن پدید میآید.
هر یک از اضلاع مثلث با برخورد با ضلع دیگر، یک زاویه میسازد. مجموع زاویههای مثلث برابر با ۱۸۰ درجه است. به همین ترتیب با دانستن دو زاویه از مثلث میتوان، زاویه بعدی را مشخص کرد. این خصوصیات کمک میکند که براساس نسبتهای مثلثاتی که به کمک همین اضلاع ساخته میشوند، رابطههای مثلثاتی جالبی کشف و به کار گرفته شود.
در تصویر زیر یک مثلث قائمالزاویه را مشاهده میکنید که یکی از زاویههای آن ۹۰ درجه است. بنابراین مجموع دو زاویه دیگر نیز باید ۹۰ درجه باشد تا مجموع زاویههای داخلی مثلث ۱۸۰ درجه بدست آید. مشخص است که زاویه C قائمه (راست) و زاویههای B و A حاده (تند) هستند.
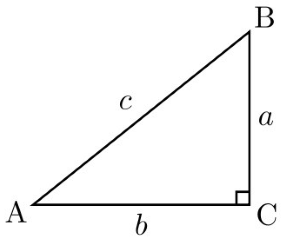
در ریاضیات، سینوس یک تابع مثلثاتی برای زاویهها است. سینوس یک زاویه حاده (تُند) در مثلث قائم الزاویه به صورت زیر تعریف میشود: برای زاویه مشخص شده، نسبت طول ضلعی مقابل به زاویه به طول طولانیترین ضلع مثلث (وتر) را سینوس آن زاویه میگویند. اگر زاویه را با نماد نشان دهیم، تابع سینوس را به صورت زیر خواهیم نوشت و میخوانیم، سینوس زاویه ایکس.
در این حالت اگر طول وتر یک مثلث قائمالزاویه برابر با واحد یا ۱ باشد، آنگاه سینوس زاویه با طول ضلع روبرو به زاویه برابر است.
به طور کلی، تعریف سینوس (و سایر توابع مثلثاتی) را میتوان از نظری به جای طول یک قطعه خط خاص در یک دایره واحد، به هر مقدار حقیقی گسترش داد. تعاریف مدرنتر، سینوس را به عنوان یک سری بینهایت یا به عنوان حل معادلات دیفرانسیل خاص بیان میکنند که حتی میتوان مفهوم آن را به صورت بسط یا دنبالهای از مقادیر مثبت و منفی و حتی اعداد مختلط گسترش داد.
از تابع سینوس معمولاً برای مدلسازی پدیدههای تناوبی مانند امواج صوتی و نوری، موقعیت و سرعت نوسانگرهای هارمونیک، شدت نور خورشید و طول روز و تغییرات دمای متوسط در طول سال استفاده میشود.
ریشه تابع سینوس را میتوان در محاسبات مربوط به نجوم در هند دوره «گوپتا» (Gupta)، جستجو کرد. از طریق ترجمه از «سانسکریت» (Sanskrit) به عربی و سپس از عربی به لاتین دنیای غرب با مفهوم توابع مثلثاتی و سینوس آشنا شد. کلمه «sine» که به لاتین «sinus» نوشته و خوانده میشود، از ترجمه اشتباه لاتین توسط رابرت چستر از عربی جِیب که ترجمه کلمه سانسکریت به معنای نصف وتر، است، گرفته شده.
نکته: نام عملگر یا تابع جیب زاویه از واژه سانسکریت جیوا گرفته شدهاست. این واژه در عربی، به صورت جیب نوشته شد که به معنی کنار است. ولی با توجه به ترجمه اشتباه و خواندن آن به صورت جَیب (به معنی سینه) به لاتین به صورت سینوس (فضای سینه) ترجمه گردید که تا به امروز نیز به همین نام خوانده میشود.
در ادامه تعریف سینوس را به دو شکل و براساس مثلث قائمالزاویه و دایره مثلثاتی مرور خواهیم کرد.
تعریف سینوس براساس مثلث قائم الزاویه
برای زاویه ، تابع سینوس، نسبت طول ضلع مقابل به زاویه مورد نظر به طول وتر است. برای تعریف تابع سینوس یک زاویه تند یا حاده مثل ، را به عنوان یکی از زاویههای مثلث قائم الزاویه در نظر بگیرید. واضح است که زاویه دیگر این مثلث باید باشد تا جمع زاویههای چنین مثلثی برابر با ۱۸۰ درجه بدست آید. در تصویر زیر این زاویه در مثلث قائمالزاویه مشخص شده است.
نکته: در یک مثلث قائمالزاویه، هیچ زاویه باز (منفرجه) وجود ندارد. زیرا در این صورت مجموع زاویهها بزرگتر از ۱۸۰ درجه خواهد شد.
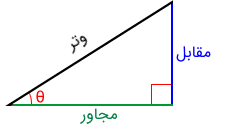
با توجه به محل قرارگیری این زاویه در مثلث، ضلعهای دیگر را مشخص و نامگذاری میکنیم.
- ضلع رو به رو به زاویه که از این به بعد آن را ضلع مقابل مینامیم.
- طولانی ترین طول از اضلاع مثلث که آن را در این متن، وتر مثلث قائمالزاویه نامگذاری خواهیم کرد. این ضلع مجاور به زاویه نیز هست.
- ضلعی که یکی از بازوهای زاویه را میسازد و مشخص است مجاور به آن زاویه نیز خواهد بود و به همین دلیل نیز ضلع مجاور نامیده میشود.
به محض انتخاب چنین مثلثی و با تعیین اضلاع آن طبق روال بالا، میتوان سینوس زاویه را برابر با طول ضلع مقابل به زاویه، تقسیم بر طول وتر تعریف کرد. در این صورت عبارت زیر را مینویسیم.
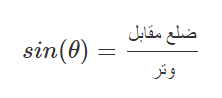
توابع مثلثاتی دیگر زاویه را میتوان به همین ترتیب نیز تعریف کرد. به عنوان مثال، کسینوس زاویه نسبت بین ضلع مجاور به وتر خواهد بود. در حالی که تانژانت این زاویه همان نسبت بین دو ضلع مقابل و مجاور به زاویه در مثلث قائمالزاویه محسوب میشود.
همانطور که بیان شد، به نظر میرسد مقدار به انتخاب مثلث قائم الزاویه و همچنین زاویه تندی که در نظر میگیریم بستگی دارد. ولی باید به این نکته نیز توجه داشت که اغلب مثلثها بخصوص مثلثهای قائمالزاویه تا حدودی با یکدیگر مشابه هستند زیرا حداقل در یک زاویه مشترک بوده و رابطه بین دو زاویه دیگر نیز معلوم است. به همین علت نسبتهای مثلثاتی برای زاویههای برابر که با طولهای متفاوت ایجاد میشوند، باز هم یکسان است.
روش دیگر برای تعریف توابع مثلثاتی، بخصوص سینوس زاویه، بهرهگیری از دایره مثلثاتی و پیادهسازی یک مثلث قائمالزاویه درون آن است. در بخش بعدی به این موضوع خواهیم پرداخت.
تعریف دایره مثلثاتی
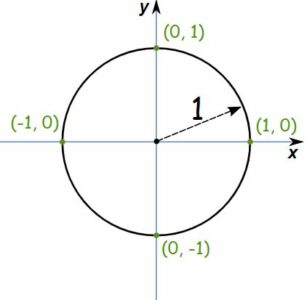
در مثلثات، دایره مثلثاتی، دایره با شعاع واحد و یک مرکز در مبدا (0 ، 0) در سیستم مختصات دکارتی است. توجه داشته باشید که منظور از دایره با شعاع واحد، دایرهاست که شعاع آن طولی برابر با ۱ دارد.
ممکن است این ۱، براساس واحد متر، کیلومتر، میلیمتر یا سانتیمتر و حتی یارد یا اینچ باشد. مهم آن است که چنین دایرههایی، در تعریف نسبتهای مثلثاتی، نقش یکسانی خواهند داشت.
فرض کنید که یک خط از طریق مبدا مختصات رسم شده و دایره را در یک نقطه قطع کرده است. زاویهای که این خط با قسمت مثبت محور افقی ایجاد میکند را مینامیم. به کمک این خط و زاویهای که ایجاد شده، نسبتهای مثلثاتی مانند سینوس و کسینوس تعریف میشوند.
از محل برخورد این خط با دایره مثلثاتی، خطی عمود بر محور افقی ایجاد کنید. طول این پاره خط که در تصویر زیر با مشخص شده، سینوس زاویه را نمایش میدهد.
از طرفی میتوانیم این خط را بوسیله ترسیم یک خط افقی از محل برخورد با دایره نیز ایجاد کنیم به طوری که محور عمودی را قطع کند. فاصله مبدا مختصات تا محل برخورد خط افقی با محور عمودی را باز هم سینوس زاویه مینامیم. به همین علت معمولا، محور عمودی در دایره مثلثاتی را محور سینوسها نیز میگویند.
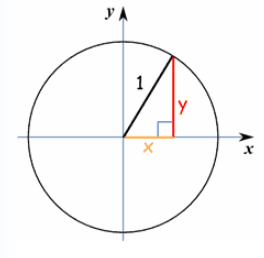
این بار فاصله خط عمودی با محور افقی را تا مبدا مختصات در نظر بگیرید. این طول را که در تصویر بالا با مشخص شده، کسینوس زاویه میخوانیم. براساس قضیه فیثاغورس میتوان در مثلث قائمالزاویه ایجاد شده به رابطه زیر رسید.
که با جاگزینی با و با به تساوی زیر دست پیدا کرد که مهمترین اتحاد مثلثاتی محسوب میشود.
به این ترتیب بین دو نسبت سینوس و کسینوس زاویه، رابطههای زیر برقرار خواهد بود.
نکته: از آنجایی که دایره با شعاع واحد است، مقدار سینوس و کسینوس هرگز از ۱ بزرگتر نخواهد شد. واضح است که اگر زاویه صفر درجه باشد، سینوس آن نیز صفر بوده ولی کسینوس آن برابر با ۱ خواهد بود.
همانطور که در تصویر بالا دیده میشود، یک مثلث قائمالزاویه نیز در داخل دایره مثلثاتی ساخته شده. با استفاده از این مثلث و مطالب قبلی باز هم میتوان نسبتهای مثللثاتی را تعریف و به کار گرفت. ولی استفاده از تعریف دایره واحد این مزیت را دارد که میتوان زاویه را به هر استدلال واقعی تعمیم داد.
این امر همچنین میتواند با نیاز به تقارنهای خاص حاصل شود و اینکه سینوس یک تابع متناوب است. یعنی با چرخش روی دایره مثلثاتی و ایجاد زاویههای مختلف، با یک بار چرخش به زاویه قبلی رسیده و باید انتظار داشته باشید که مقدار سینوس (یا حتی کسینوس) زاویه تکرار شود.
در تصویر زیر، موقعیت زاویهها و همچنین علامت نسبتهای مثلثاتی سینوس و کسینوس را مشاهده میکنید. بخشهای رنگی در تصویر زیر، ربعهای مثلثاتی هستند. قسمت صورتی رنگ، ربع اول، سبز رنگ، ربع دوم، آبی کمرنگ، ربع سوم و آبی پررنگ، ربع چهارم را تشکیل میدهند.
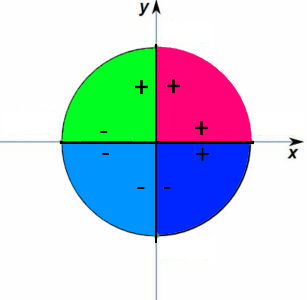
علامتهای + و - که در کنار محورهای سینوس و کسینوس در تصویر بالا دیده میشود، نواحی مختلفی را مشخص کرده است. برای مثال، ناحیه اول که با رنگ صورتی مشخص شده، دارای مقدار سینوس و کسینوس مثبت است. از طرفی ناحیه دوم یا سبز رنگ، دارای مقدار سینوس مثبت ولی کسینوس منفی است. در ناحیه آبی کمرنگ، هر دو نسبت مثلثاتی سینوس و کسینوس، منفی بوده ولی در قسمت آبی پرنگ، سینوس منفی و کسینوس مثبت است.
دقت داشته باشید که علامت + و - که در کنار محور افقی (کسینوس) کشیده شده، علامت کسینوس و علامتهایی که در کنار محور عمودی (سینوس) قرار دارند، علامت سینوس را مشخص کردهاند. در ادامه مقدار سینوس زاویههای معرف و پر کاربرد را مشاهده میکنید.
جدول مقدار سینوس برای زاویههای پرکاربرد
با توجه به تناوبی بودن تابع سینوس و کسینوس، میتوان یک نمودار برای آنها در مختصات دکارتی رسم کرده و متناسب با آن زاویه و نسبتهای مثلثاتی را روی دایره مثلثاتی مشاهده کرد. در تصویر زیر این کار صورت گرفته است.
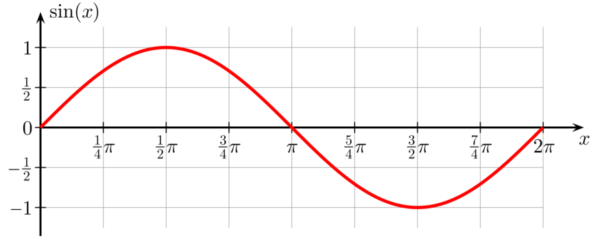
این با مقدار سینوس و کسینوس زاویهها را همزمان با نمایش آن روی دایره مثلثاتی نشان خواهیم داد.
با توجه به پویانمایی ارائه شده، تناوبی بودن تابع سینوس به خوبی نمایش داده شده.
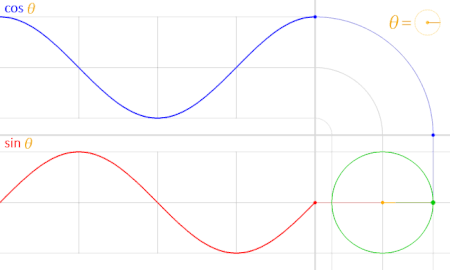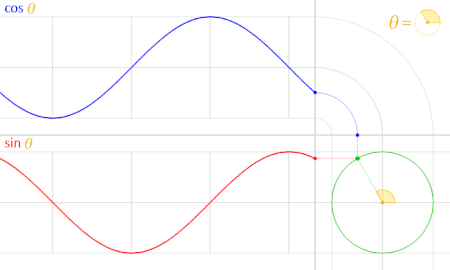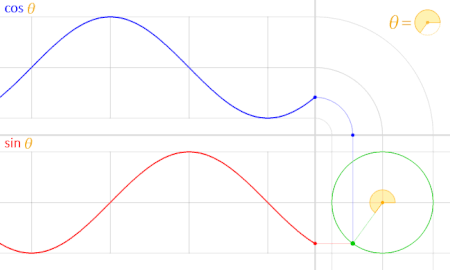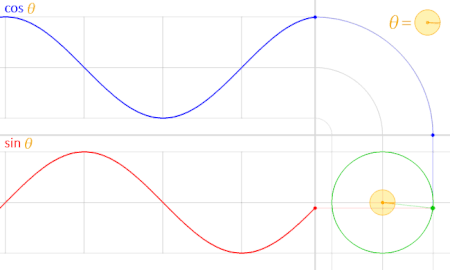
همانطور که در تصویر متحرک بالا مشاهده میکنید، تابع سینوس با رنگ قرمز تابع کسینوس با رنگ آبی ترسیم شده. دایره مثلثاتی نیز با رنگ سبز و نقطهای که به رنگ سبز درون دایره چرخش دارد، زاویه را نشان میدهد. رنگ زرد نیز برای نمایش زاویه مورد نظر (با نماد ) به کار رفته است.
محاسبه مقدار سینوس نیز در تصویر زیر صورت گرفته است. البته این مقادیر روی دایره مثلثاتی براساس دو مولفه مشخص شدهاند. در این تصویر مولفه اول از زوج مرتب، نشانگر کسینوس و مولفه دوم نشانگر سینوس است. درست به مانند زوج مرتب که برای نمایش مختصات نقطهها در مختصات دکارتی استفاده میشوند.

واضح است که با افزایش مقدار زاویه در ربع اول، کسینوس کاهش یافته ولی سینوس افزایش مییابد. در زاویه ۹۰ درجه (که در نمودار با مشخص شده) به بعد یعنی ربع دوم، این وضعیت برعکس میشود و سینوس کاهشی بوده ولی قدر مطلق کسینوس افزایشی است.
در ربع سوم یا زاویه ۱۸۰ درجه (یا ) به بعد، باز هم قدر مطلق سینوس، افزایشی ولی قدرمطلق کسینوس کاهشی است. در زاویه ۲۷۰ درجه به بعد () یا همان ربع چهار، قدر مطلق سینوس کاهشی ولی کسینوس افزایشی خواهد بود. البته میتوانید این تغییرات را در جدول سینوس کسینوس یا تصویر بالا به خوبی مشاهده کنید.
جدول زیر نیز به معرفی مقدار سینوس و کسینوس برای زاویهها مختلف پرداخته است. فاصله بین زاویهها در این جدول ۱۵ درجه در نظر گرفته شده. از طرفی علاوه بر درجه از رادیان نیز برای نمایش اندازه زاویه استفاده شده است.
| زاویه به درجه | زاویه به رادیان | مقدار سینوس | مقدار کسینوس |
| 0.00 | 0.00 | 0.00 | 1.00 |
| 15.00 | 0.26 | 0.26 | 0.97 |
| 30.00 | 0.52 | 0.50 | 0.87 |
| 45.00 | 0.79 | 0.71 | 0.71 |
| 60.00 | 1.05 | 0.87 | 0.50 |
| 75.00 | 1.31 | 0.97 | 0.26 |
| 90.00 | 1.57 | 1.00 | 0.00 |
| 105.00 | 1.83 | 0.97 | -0.26 |
| 120.00 | 2.09 | 0.87 | -0.50 |
| 135.00 | 2.36 | 0.71 | -0.71 |
| 150.00 | 2.62 | 0.50 | -0.87 |
| 165.00 | 2.88 | 0.26 | -0.97 |
| 180.00 | 3.14 | 0.00 | -1.00 |
| 195.00 | 3.40 | -0.26 | -0.97 |
| 210.00 | 3.67 | -0.50 | -0.87 |
| 225.00 | 3.93 | -0.71 | -0.71 |
| 240.00 | 4.19 | -0.87 | -0.50 |
| 255.00 | 4.45 | -0.97 | -0.26 |
| 270.00 | 4.71 | -1.00 | 0.00 |
| 285.00 | 4.97 | -0.97 | 0.26 |
| 300.00 | 5.24 | -0.87 | 0.50 |
| 315.00 | 5.50 | -0.71 | 0.71 |
| 330.00 | 5.76 | -0.50 | 0.87 |
| 345.00 | 6.02 | -0.26 | 0.97 |
| 360.00 | 6.28 | 0.00 | 1.00 |
خلاصه و جمعبندی
توابع مثلثاتی هر چند در ریاضی مطرح شده ولی کاربردهای زیادی در فیزیک و رشتههای مهندسی دارد. در این بین تابع سینوس در بسیاری از محاسبات فیزیکی به کار میرود. محاسبه مسافت پرتابهها، در شیمی فضایی، زاویه بین ملکولها، همه و همه به مثلثات و محاسبه نسبتهای مثلثاتی وابسته هستند. بنابراین آگاهی از این توابع ریاضی، کمک شایانی در درک بهتر این مبحثها خواهد کرد. نسبتهای دیگر مثلثاتی مانند کسینوس، تانژانت یا کتانژانت نیز در مسائل رشتههای مختلف به کار رفته و اهمیت ویژهای دارند.
در بسیاری از محاسبات یادگیری ماشین نیز استفاده از توابع مثلثاتی برای اندازهگیری شباهت یا فاصله به کار میرود. برای مثال یکی از روشهای اندازهگیری شباهت بین دو بردار، بدست آوردن کسینوس زاویه بین بردارها است. مشخص است که اگر دو بردار مطابق یا موازی یکدیگر باشند، کسینوس برابر با ۱ بوده و میزان یا درصد شباهت بین آنها حداکثر مقدار خواهد بود. در صورتی که دو بردار متعامد باشند، کسینوس زاویه بین آنها صفر بوده و کمترین شباهت را دارند.













سلام خدا قوت.خیلی زیبا و شیوا.
عالی بود ممنون.
بسیار عالی خداوند به شما پاداش مناسب دهد
سلام،
عالی بود.
بعد از ۵۰ سال مجدد به دانستن و فهم سینوس و کسینوس برگشتم. خیلی شیرین است.
عالی بود، فوق العاده ساده و شیوا بیان کرده بودید مطلب رو!!
ممنون از زحماتتون.