جدول دایره مثلثاتی چیست؟ – روش محاسبه + حل مثال

یکی از مهم‌ترین مباحث درس ریاضی یادگیری روش به‌ دست آوردن توابع مثلثاتی است. جدول دایره مثلثاتی به ما کمک می‌کند تا با استفاده از یک سری روابط هندسی بتوانیم سینوس، کسینوس و تانژانت یک زاویه مشخص را پیدا کنیم. در این مطلب از مجله فرادرس پس از توضیح ویژگی‌های دایره مثلثاتی، مرحله به مرحله نشان می‌دهیم بخش‌های مختلف جدول دایره مثلثاتی چگونه محاسبه می‌شود.

جدول دایره مثلثاتی

جدول دایره مثلثاتی جدولی است که نشان می‌دهد مقادیر توابع مثلثاتی از جمله سینوس، کسینوس و تانژانت برای برخی از مهم‌ترین زاویه‌ها چقدر است:

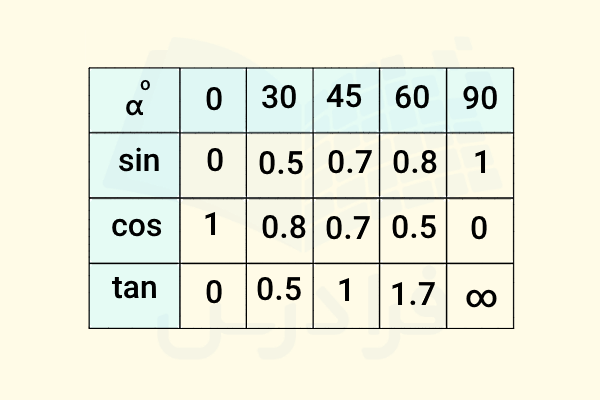
نمونه کامل‌تر این جدول را در ادامه ملاحظه می‌کنید:

دقت کنید در این جدول می‌توانیم زاویه را بر حسب درجه یا رادیان بنویسیم. همچنین با توجه به اینکه رابطه تانژانت و کتانژانت به شکل $$\tan \theta = \frac{1}{cot \theta}$$ است، گاهی در این جدول مقادیر تابع مثلثاتی کتانژانت ذکر نمی‌شود، چون می‌توان به راحتی با معکوس کردن مقادیر تانژانت هر زاویه کتانژانت آن را نیز پیدا کرد.

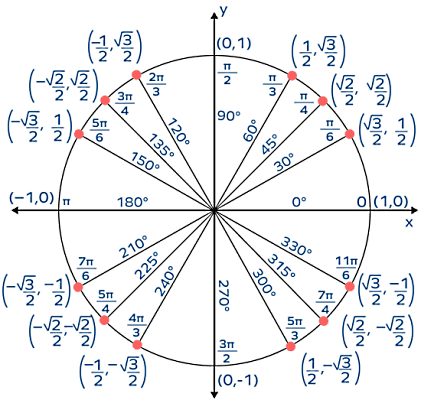
برای اینکه بتوانید این جدول را بهتر به خاطر بسپارید، لازم است ابتدا بدانید دایره واحد یا دایره مثلثاتی چیست و چگونه با بررسی آن می‌توانیم به جدول بالا برسیم. بخش بعد به این موضوع اختصاص دارد.

دایره مثلثاتی چیست؟

دایره واحد یا دایره مثلثاتی دایره‌ای است با شعاع واحد که مرکز آن در مبدا مختصات قرار می‌گیرد. می‌دانیم دایره یک شکل هندسی بسته است، به گونه‌ای که تمام نقاط روی محیط آن از مرکز آن فاصله‌ای برابر دارند. برای یک دایره مثلثاتی، این فاصله برابر با واحد یا عدد یک است، یعنی شعاع آن یک واحد است.

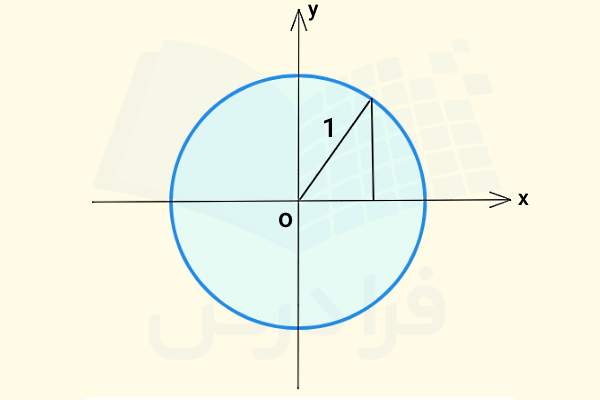
دایره واحد با مفاهیم مثلثات مرتبط است و به همین علت آن را دایره مثلثاتی هم می‌نامند. در واقع توابع مثلثاتی را می‌توانیم با کمک گرفتن از این دایره تعریف کنیم. شکل بالا یک دایره مثلثاتی در دستگاه مختصات دکارتی را نشان می‌دهد که مرکز آن در مبدا قرار دارد و تمام نقاط روی محیط آن فاصله‌ای برابر با یک واحد از مرکز دارند.

چهار ربع دایره مثلثاتی

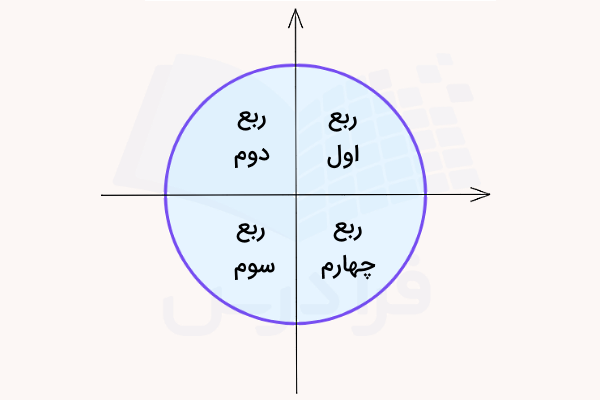
کل دایره مثلثاتی معادل است با $$2 \pi$$ رادیان یا $$360$$ درجه. در واقع با حرکت در جهت پادساعتگرد روی این دایره، زاویه‌ها افزایش می‌‌یابند و یک دور کامل روی این دایره برابر است با $$2 \pi$$ رادیان یا $$360$$ درجه. همچنین در این نمودار دایره واحد بر اساس تقاطع محورهای x و y به چهار قسمت تقسیم می‌شود که هر کدام را یک ربع می‌نامیم:

• ربع اول: از $$0$$ تا $$\frac{ \pi }{2}$$ رادیان یا از $$0$$ تا $$90$$ درجه
• ربع دوم: از $$\frac{ \pi }{2}$$ تا $$\pi$$ رادیان یا از $$90$$ تا $$180$$ درجه
• ربع سوم: از $$\pi$$ تا $$\frac{ 3\pi }{2}$$ رادیان یا از $$180$$ تا $$270$$ درجه
• ربع چهارم: از $$\frac{ 3\pi }{2}$$ تا $$2\pi$$ رادیان یا از $$270$$ تا $$360$$ درجه

نکته: برای اینکه در زمینه تبدیل واحدهای زاویه یعنی درجه و رادیان مشکلی نداشته باشید، در ادامه فرمول‌های تبدیل این دو را نیز آورده‌ایم:

$$2 \pi = 360^{\circ}$$

زاویه بر حسب رادیان = زاویه بر حسب درجه $$\frac{\pi}{180} \times$$

حالا می‌توان برای زاویه مشخصی مانند $$\theta$$ مقادیر استاندارد نسبت‌های مثلثاتی $$\sin$$ و $$\cos$$ را تعریف کرد. در واقع می‌توانیم مختصات هر نقطه روی محیط دایره را به‌جای $$(x,y)$$ توسط این دو تابع مثلثاتی تعریف کنیم. پس هر نقطه روی دایره واحد مختصاتی به شکل $$(\cos \theta , \sin\theta)$$ دارد. همچنین باید بدانیم دو مقدار سینوس و کسینوس (و به تبع آن تانژانت و کتانژانت) در ربع‌های مختلف ویژگی‌های زیر را دارند:

• در ربع اول هر دو مثبت‌اند.
• در ربع دوم $$\sin$$ مثبت و $$\cos$$ منفی است.
• در ربع سوم هر دو منفی‌اند.
• در ربع چهارم $$\sin$$ منفی و $$\cos$$ مثبت است.

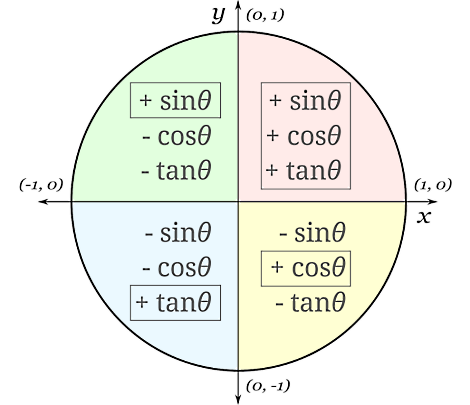
دقت کنید علامت کتانژانت دقیقا مانند علامت تانژانت است و به همین علت در تصویر قرار نگرفته است. همچنین با توجه به تعریف تانژانت که برابر است با سینوس یک زاویه تقسیم بر کسینوس آن، تعیین علامت تانژانت به راحتی با تقسیم علامت سینوس بر کسینوس در هر ربع به‌دست می‌آید. برای مثال، در ربع سوم می‌دانیم هم سینوس و هم کسینوس منفی هستند. بنابراین منفی تقسیم بر منفی مثبت می‌شود و تانژانت مثبت است. در ادامه ابتدا معادله‌ دایره مثلثاتی را می‌آموزیم و سپس روش‌های نمایش هر یک از نقاط روی محیط این دایره را به کمک نسبت‌های مثلثاتی بررسی می‌کنیم.

معادله دایره مثلثاتی

می‌دانیم معادله یک دایره به صورت زیر است:

$$( x- a) ^ 2 + (y - b)^ 2 = r^2$$

که در آن $$( a , b)$$ مختصات نقطه‌ای است که مرکز دایره در آن واقع شده و $$r$$ شعاع دایره است. به این ترتیب دایره واحد یا دایره مثلثاتی در صفحه $$xy$$ با قرار گرفتن نقطه مرکزی دایره بالا در مبدا یا $$( 0 , 0)$$ و شعاعی برابر با یک ($$r =1$$) ایجاد می‌شود. با این فرض‌ها معادله دایره بالا به شکل زیر خواهد شد:

$$( x- 0) ^ 2 + (y - 0)^ 2 = 1^2$$

$$\Rightarrow x ^ 2 + y ^ 2 = 1$$

بنابراین معادله دایره واحد در صفحه $$xy$$ برابر است با $$\Rightarrow x ^ 2 + y ^ 2 = 1$$. این معادله شروع نوشتن جدول دایره مثلثاتی است.

یادگیری توابع مثلثاتی با فرادرس

با درک عمیق‌تر مفاهیمی مانند سینوس، کسینوس و تانژانت یک زاویه و روش به دست آوردن آن‌ها بر اساس جدول دایره مثلثاتی، می‌توانید به راحتی مسائل پیچیده‌تر را حل کنید. توابع مثلثاتی نه تنها در هندسه، بلکه در علومی مانند فیزیک و مهندسی نیز کاربرد گسترده‌ای دارند. برای مثال مدل‌سازی پدیده‌های تناوبی در فیزیک با استفاده از این توابع انجام می‌شود و علت آن ماهیت تناوبی این توابع است که در فواصل منظم تکرار می‌شوند. در همین زمینه، مشاهده فیلم‌های آموزشی زیر از مجموعه فرادرس راهنمای جامعی برای یادگیری مثلثات محسوب می‌شود:

• فیلم آموزش رایگان سینوس، کسینوس و تانژانت + محاسبه نسبت‌ های مثلثاتی فرادرس
• فیلم آموزش رایگان محاسبه نسبت های مثلثاتی + ۸ رابطه مهم فرادرس
• فیلم آموزش رایگان معادلات مثلثاتی ریاضی (دوازدهم) + روش حل با مثال فرادرس
• فیلم آموزش رایگان توابع مثلثاتی در ریاضی ۲ – پایه یازدهم علوم تجربی فرادرس
• فیلم آموزش رایگان روابط مثلثاتی در مثلث قائم الزاویه + مثال فرادرس

یافتن مقادیر sin و cos با استفاده از دایره مثلثاتی

پس از اینکه با معادله دایره واحد آشنا شدیم، قدم بعدی برای اینکه بتوانیم جدول دایره مثلثاتی را تکمیل کنیم این است که ببینیم چگونه می‌توان توابع مثلثاتی را با استفاده از این دایره به دست آورد. توابع یا نسبت‌های مثلثاتی همان توابع سینوس $$\sin \theta$$، کسینوس $$\cos \theta$$، تانژانت $$\tan \theta$$ و کتانژانت $$\cot \theta$$ هستند که همگی برای یک زاویه مشخصی مانند $$\theta$$ تعریف می‌شوند.

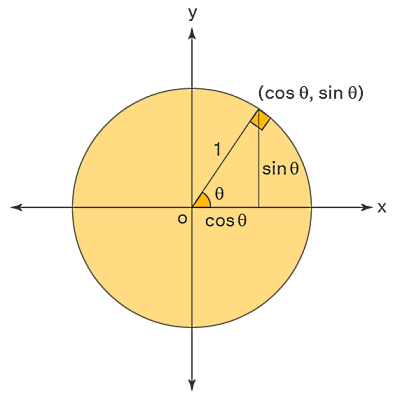
دایره مثلثاتی به ما کمک می‌کند تا با در نظر گرفتن این زاویه در یک مثلث قائم‌الزاویه و به کمک روابط ریاضیاتی حاکم بر هندسه مسئله بتوانیم سینوس، کسینوس، تانژانت و کتانژانت آن را پیدا کنیم. فرض کنید یک مثلث قائم‌الزاویه‌ در داخل دایره مثلثاتی واحد قرار دارد. حالا $$P (x,y)$$ را نقطه‌ای روی محیط دایره در نظر می‌گیریم که خط متصل کننده آن به مرکز دایره با محور افقی (در راستای مثبت) زاویه‌ تندی مطابق شکل زیر بسازد:

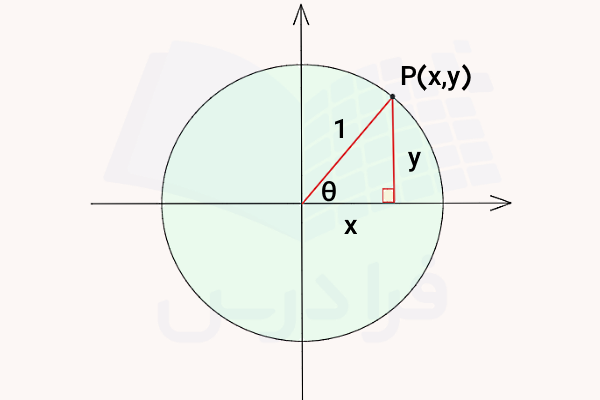
این زاویه را همان زاویه $$\theta$$ در نظر می‌گیریم که می‌خواهیم توابع مثلثاتی را برای آن تعیین کنیم. از طرفی طول این خط متصل کننده همان شعاع دایره مثلثاتی و برابر با واحد است که طبق تصویر معادل می‌شود با وتر مثلث قائم‌الزاویه. بنابراین اضلاع مثلث قائم‌الزاویه بالا به ترتیب برابراند با ضلع $$x$$، ضلع $$y$$ و $$1$$. حالا برای اینکه بتوانیم توابع مثلثاتی را استخراج کنیم، کافی است تعاریف زیر را برای هر تابع در نظر بگیریم:

وتر / ضلع روبرو به زاویه = سینوس زاویه

وتر / ضلع مجاور به زاویه = کسینوس زاویه

ضلع مجاور به زاویه / ضلع روبرو به زاویه = تانژانت زاویه

ضلع روبرو به زاویه / ضلع مجاور به زاویه = کتانژانت زاویه

دقت کنید این تعریف‌ها برای سینوس، کسینوس، تانژانت و کتانژانت هر زاویه حاده یا تند در یک مثلث قائم‌الزاویه همواره برقراراند. از این روابط در حل مسائل بسیار استفاده می‌شود. با استفاده از روابط بالا می‌توانیم سینوس، کسینوس، تانژانت و کتانژانت زاویه $$\theta$$ را به شکل زیر تعیین کنیم:

$$\sin \theta = \frac{y}{ 1} = y$$

$$\cos \theta = \frac{x}{ 1} = x$$

$$\tan \theta = \frac{y}{ x}$$

$$\cot \theta = \frac{x}{ y}$$

بنابراین $$P (x,y)$$ یا مختصات هر نقطه روی دایره واحد به جای $$(x,y)$$ معادل می‌شود با $$P = (\cos \theta , \sin\theta)$$. حالا برای اینکه بتوانیم به جدول دایره مثلثاتی برسیم، کافی است مقادیر مختلفی از زاویه را در نظر بگیریم و ببینیم $$x$$ و $$y$$ متناظر با آن‌ها چه می‌شود.

برای شروع بهتر است زاویه‌های سرراستی مانند $$0$$، $$\frac{3 \pi }{2}$$ ،$$\pi$$ ،$$\frac{ \pi }{2}$$ و $$2\pi$$ رادیان را امتحان کنیم:

• $$\theta = 0^ {\circ}$$: در این حالت نقطه $$P (x,y)$$ هیچ زاویه‌ای با محور افق ندارد و $$x$$ و $$y$$ متناظر با آن‌ عبارت‌اند از $$1$$ و $$0$$:

$$\sin \theta = y \Rightarrow \sin 0 = 0$$

$$\cos \theta = x \Rightarrow \cos 0 = 1$$

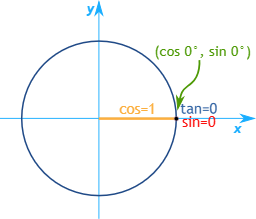
• $$\theta = \frac{ \pi }{2}$$: در این حالت زاویه نقطه $$P (x,y)$$ با محور افقی نود درجه است و $$x$$ و $$y$$ متناظر با آن‌ عبارت‌اند از $$0$$ و $$1$$:

$$\sin \theta = y \Rightarrow \sin \frac{ \pi }{2} = 1$$

$$\cos \theta = x \Rightarrow \cos \frac{ \pi }{2}= 0$$

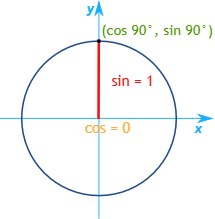
• $$\theta = \pi$$: در این حالت زاویه نقطه $$P (x,y)$$ با محور افقی صد و هشتاد درجه است و $$x$$ و $$y$$ متناظر با آن‌ عبارت‌اند از $$-1$$ و $$0$$:

$$\sin \theta = y \Rightarrow \sin \pi = 0$$

$$\cos \theta = x \Rightarrow \cos \pi = -1$$

• $$\theta = \frac{ 3\pi }{2}$$: در این حالت زاویه نقطه $$P (x,y)$$ با محور افقی دویست و هفتاد درجه است و $$x$$ و $$y$$ متناظر با آن‌ عبارت‌اند از $$0$$ و $$-1$$:

$$\sin \theta = y \Rightarrow \sin \frac{3 \pi }{2} = -1$$

$$\cos \theta = x \Rightarrow \cos \frac{3 \pi }{2} = 0$$

• $$\theta = 2\pi$$: در این حالت زاویه نقطه $$P (x,y)$$ با محور افقی سیصد و شصت درجه است و $$x$$ و $$y$$ متناظر با آن‌ عبارت‌اند از $$1$$ و $$0$$:

$$\sin \theta = y \Rightarrow \sin 2 \pi = 0$$

$$\cos \theta = x \Rightarrow \cos 2\pi = 1$$

از محاسبات بالا به نتایج زیر می‌رسیم:

پس بخشی از جدول دایره مثلثاتی به دست آمد. مرسوم است سینوس و کسینوس چند زاویه کلیدی دیگر مانند $$\frac{ \pi }{6}$$ ،$$\frac{ \pi }{3}$$ ،$$\frac{ \pi }{4}$$ را نیز بدانیم:

با دقت در این دو بخش از جدول دایره مثلثاتی می‌توانیم نکات زیر را استخراج کنیم:

• با توجه به اینکه دو زاویه $$\theta = 0^ {\circ}$$ و $$\theta = 2\pi$$ هر دو منطبق بر یک نقطه هستند، پس سینوس و کسینوس این دو زاویه نیز با هم برابر است، یعنی داریم:

$$\sin 0 = \sin 2\pi = 0$$

$$\cos 0 = \cos 2\pi = 1$$

• هرگاه سینوس زاویه‌ای صفر شود، کسینوس آن مخالف صفر است و هر جا که کسینوس زاویه‌ای صفر شود، سینوس آن مخالف صفر است.
• بیشترین مقدار سینوس یا کسینوس یک زاویه همواره برابر است با $$1$$.
• کمترین مقدار سینوس یا کسینوس یک زاویه همواره برابر است با $$-1$$.
• مقادیر سینوس و کسینوس برای زاویه $$\frac{ \pi }{4}$$ یا $$\theta = 45^ {\circ}$$ با هم برابر هستند.
• سینوس زاویه‌ $$\frac{ \pi }{3}$$ و $$\frac{ \pi }{6}$$ به ترتیب برابر هستند با کسینوس زاویه $$\frac{ \pi }{6}$$ و $$\frac{ \pi }{3}$$.

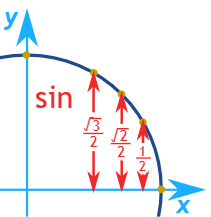
همچنین تصاویر بالا و پایین به خوبی نشان می‌دهند که تغییرات مقادیر سینوس (مختصه y) و کسینوس (مختصه x) هر نقطه روی دایره مثلثاتی برای سه زاویه $$\frac{ \pi }{6}$$ ،$$\frac{ \pi }{3}$$ ،$$\frac{ \pi }{4}$$ به چه صورت است:

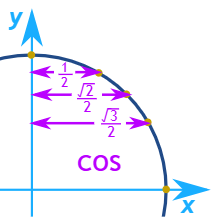
یافتن مقادیر tan و cot با استفاده از دایره مثلثاتی

در بخش‌‌ قبل با روند استخراج بخشی از جدول دایره مثلثاتی آشنا شدیم. در این بخش نشان می‌‌دهیم که چگونه می‌توان از این جدول، سایر توابع مثلثاتی از جمله تانژانت و کتانژانت را نیز به‌ دست آورد. ابتدا به کمک روابط بخش قبل تانژانت و کتانژانت زاویه $$\theta$$ را به شکل زیر تعریف می‌کنیم:

$$\tan \theta = \frac {y}{x} = \frac {\sin\theta}{\cos\theta}$$

$$\cot \theta = \frac {x}{y} = \frac {\cos\theta}{\sin\theta}$$

برای شروع بهتر است ابتدا مقادیر تانژانت و کتانژانت زاویه‌های سرراستی مانند $$0$$، $$\frac{3 \pi }{2}$$ ،$$\pi$$ ،$$\frac{ \pi }{2}$$ و $$2\pi$$ رادیان را برای نقطه فرضی $$P (x,y)$$ در بخش قبل در نظر بگیریم:

• $$\theta = 0^ {\circ}$$: می‌دانیم $$\sin 0 = 0$$ و $$\cos 0 = 1$$ است. پس برای تانژانت و کتانژانت این زاویه خواهیم داشت:

$$\tan 0 = \frac {\sin 0}{\cos 0} = \frac { 0}{1} = 0$$

$$\cot 0 = \frac {\cos 0}{\sin 0} = \frac { 1}{0} = \infty$$

• $$\theta = \frac{ \pi }{2}$$: می‌دانیم $$\sin \frac{ \pi }{2} = 1$$ و $$\cos \frac{ \pi }{2} = 0$$ است. پس برای تانژانت و کتانژانت این زاویه خواهیم داشت:

$$\tan \frac{ \pi }{2} = \frac {\sin \frac{ \pi }{2}}{\cos \frac{ \pi }{2}} = \frac {1}{0} = \infty$$

$$\cot \frac{ \pi }{2} = \frac {\cos \frac{ \pi }{2}}{\sin \frac{ \pi }{2}} = \frac {0}{1} = 0$$

• $$\theta = \pi$$: می‌دانیم $$\sin \pi = 0$$ و $$\cos \pi = -1$$ است. پس برای تانژانت و کتانژانت این زاویه خواهیم داشت:

$$\tan \pi = \frac {\sin \pi }{\cos \pi } = \frac {0}{-1} = 0$$

$$\cot \pi = \frac {\cos \pi }{\sin \pi } = \frac {-1}{0} = -\infty$$

• $$\theta = \frac{ 3\pi }{2}$$: می‌دانیم $$\sin \frac{ 3\pi }{2} = -1$$ و $$\cos \frac{ 3\pi }{2} = 0$$ است. پس برای تانژانت و کتانژانت این زاویه خواهیم داشت:

  $$\tan \frac{ 3\pi }{2} = \frac {\sin \frac{ 3\pi }{2}}{\cos \frac{ 3\pi }{2}} = \frac {-1}{0} = -\infty$$

  $$\cot \frac{ 3\pi }{2} = \frac {\cos \frac{ 3\pi }{2}}{\sin \frac{ 3\pi }{2}} = \frac {0}{-1} = 0$$

• $$\theta = 2\pi$$: می‌دانیم $$\sin 2\pi = 0$$ و $$\cos 2\pi = 1$$ است. پس برای تانژانت و کتانژانت این زاویه خواهیم داشت:

  $$\tan 2\pi = \frac {\sin 2\pi }{\cos 2\pi } = \frac {0}{1} =0$$

  $$\cot 2\pi = \frac {\cos 2\pi }{\sin 2\pi } = \frac {1}{0} =\infty$$

به همین شکل فرض کنید می‌خواهیم $$\tan \frac{ \pi }{3}$$ یا $$\tan 60^ {{\circ}}$$ را پیدا کنیم. ابتدا $$\tan \frac{ \pi }{3}$$ را به شکل زیر می‌نویسم:

$$\tan \frac{ \pi }{3} = \frac {\sin\frac{ \pi }{3}}{\cos\frac{ \pi }{3}}$$

با کمک گرفتن از جدول دایره مثلثاتی مقادیر $$\sin \frac{ \pi }{3}$$ و $$\cos \frac{ \pi }{3}$$ را به شکل زیر داریم:

$$\sin \frac{ \pi }{3} = \frac {\sqrt{3}}{2}$$

$$\cos \frac{ \pi }{3} = \frac {1}{2}$$

بنابراین تانژانت این زاویه برابر می‌شود با:

$$\Rightarrow \tan \frac{ \pi }{3} = \frac {\frac {\sqrt{3}}{2}}{\frac {1}{2}}$$

$$\Rightarrow \tan \frac{ \pi }{3} = \sqrt{3}$$

به همین شکل برای پیدا کردن $$\tan \frac{ \pi }{6}$$ یا $$\tan 30^ {{\circ}}$$ به شکل زیر عمل می‌کنیم:

$$\tan \frac{ \pi }{6} = \frac {\sin\frac{ \pi }{6}}{\cos\frac{ \pi }{6}}$$

حالا با استفاده از جدول دایره مثلثاتی مقادیر $$\sin \frac{ \pi }{6}$$ و $$\cos \frac{ \pi }{6}$$ را جایگزین می‌کنیم:

$$\sin \frac{ \pi }{6} = \frac {1}{2}$$

$$\cos \frac{ \pi }{6} = \frac {\sqrt{3}}{2}$$

بنابراین تانژانت این زاویه برابر می‌شود با:

$$\Rightarrow \tan \frac{ \pi }{6} = \frac {\frac {1}{2}}{\frac{\sqrt{3}}{2}}$$

$$\Rightarrow \tan \frac{ \pi }{3} = \frac{1}{ \sqrt{3}}= \frac{\sqrt{3}}{3}$$

در آخرین مرحله کسر رادیکالی را به روش گویا کردن ساده کردیم. اگر در زمینه ساده‌سازی رادیکال‌ها نیاز به مهارت بیشتری دارید، پیشنهاد می‌کنیم مطلب «ساده کردن رادیکال ها – به زبان ساده با مثال و تمرین» از مجله فرادرس را مطالعه کنید. به شکل مشابهی برای $$\tan \frac{ \pi }{4}$$ یا $$\tan 45^ {{\circ}}$$ خواهیم داشت:

$$\tan \frac{ \pi }{4} = \frac {\sin\frac{ \pi }{4}}{\cos\frac{ \pi }{4}}$$

طبق جدول مقادیر $$\sin \frac{ \pi }{4}$$ و $$\cos \frac{ \pi }{4}$$ عبارت‌اند از:

$$\sin \frac{ \pi }{4} = \frac {\sqrt{2}}{2}$$

$$\cos \frac{ \pi }{4} = \frac {\sqrt{2}}{2}$$

بنابراین تانژانت این زاویه برابر می‌شود با:

$$\Rightarrow \tan \frac{ \pi }{4} = \frac { \frac {\sqrt{2}}{2}}{ \frac {\sqrt{2}}{2}}$$

$$\Rightarrow \tan \frac{ \pi }{4} = 1$$

کتانژانت این سه زاویه نیز عکس مقادیر تانژانت خواهد شد:

$$\cot \frac{ \pi }{3} = \frac{\sqrt{3}}{3}$$

$$\cot \frac{ \pi }{6} = \sqrt{3}$$

$$\cot \frac{ \pi }{4} = 1$$

یافتن مقادیر sec و csc با استفاده از دایره مثلثاتی

عموما مقادیر سکانت و کسکانت زاویه‌‌هایی که تا اینجا بررسی کردیم، در جدول دایره مثلثاتی ذکر نمی‌شوند. با این وجود برای اینکه اطلاعات کامل‌تری داشته باشید، در این بخش نحوه محاسبه این دو تابع مثلثاتی نه چندان معروف را نیز بررسی می‌کنیم. سکانت و کسکانت به شکل زیر تعریف می‌شوند:

$$\sec \theta = \frac{1 }{\ cos \theta}$$

$$\csc \theta = \frac{1 }{\ sin \theta}$$

بنابراین با دانستن مقادیر سینوس و کسینوس هر زاویه، سکانت و کسکانت آن نیر توسط فرمول‌های بالا قابل محاسبه است. برای مثال سکانت زاویه $$\theta = \frac{ \pi }{3}$$ برابر است با:

$$\sec \frac{ \pi }{3} = \frac{1 }{\ cos \frac{ \pi }{3}} = \frac{1 }{\frac{ 1}{2}} = 2$$

بنابراین با دانستن مقادیر سینوس و کسینوس هر زاویه، پیدا کردن تانژانت، کتانژانت، سکانت و کسکانت آن نیز به کمک روابط مثلثاتی که تا اینجا معرفی کردیم، به راحتی انجام می‌شود. همچنین علاوه‌بر زاویه‌هایی که تا اینجا بررسی کردیم، می‌توان سینوس و کسینوس زاویه‌های دیگر را حساب کرد. برای مثال، در فیلم آموزش رایگان حل سینوس و کسینوس ۱۵ درجه – روش‌ دایره و توابع مثلثاتی فرادرس محاسبه این توابع برای زاویه پانزده درجه توضیح داده شده است.

فرمول های کوتاه جدول دایره مثلثاتی

تا اینجا آموختیم که چگونه می‌توانیم مقادیر سینوس و کسینوس چند زاویه اصلی ($$0$$، $$\frac{3 \pi }{2}$$ ،$$\pi$$ ،$$\frac{ \pi }{2}$$ و $$2\pi$$ رادیان) را به همراه سه زاویه کوچکتر از نود درجه ($$\frac{ \pi }{6}$$ ،$$\frac{ \pi }{3}$$ ،$$\frac{ \pi }{4}$$ رادیان) پیدا کنیم. در این قسمت توضیح می‌دهیم با چه روشی می‌توان برای مثال $$\sin 150^ {{\circ}}$$ یا $$\cos 150^ {{\circ}}$$ را محاسبه کرد. ابتدا به فرمول‌های زیر توجه کنید:

$$\sin ( \pi - \theta) = \sin \theta$$

$$\cos ( \pi - \theta) = -\cos \theta$$

می‌دانیم زاویه $$150^ {{\circ}}$$ معادل است با $$180^ {{\circ}} - 30^ {{\circ}}$$. بنابراین کافی است این مقادیر را بر حسب رادیان بنویسیم و فرمول‌های بالا را بکار بگیریم:

$$\sin 150^ {{\circ}} = \sin ( \pi - \frac{ \pi }{6}) = \sin \frac{ \pi }{6} = \frac{ 1}{2} = 0.5$$

$$\cos 150^ {{\circ}} = \cos ( \pi - \frac{ \pi }{6}) = -\cos \frac{ \pi }{6} = - \frac{ \sqrt3}{2}$$

به این ترتیب اگر بخواهیم سینوس، کسینوس و تانژانت زاویه‌هایی که در ربع اول قرار می‌گیرند را توسط یک فرمول میانبر پیدا کنیم، بهتر است روابط زیر را به‌ خاطر بسپاریم:

همچنین برای سینوس، کسینوس و تانژانت زاویه‌هایی که در ربع دوم قرار می‌گیرند، روابط زیر را داریم:

سینوس، کسینوس و تانژانت زاویه‌هایی که در ربع سوم قرار می‌گیرند نیز به شکل زیر محاسبه می‌شود:

و در نهایت برای چهارمین ربع داریم:

همچنین بهتر است روابط زیر را در مورد سینوس و کسینوس مقادیر منفی به خاطر بسپاریم:

$$\sin (-\theta) = - \sin \theta$$

$$\cos (-\theta) = \cos \theta$$

$$\ tan (-\theta) = - \tan \theta$$

سایر روابط مثلثاتی

در بخش‌های قبل دیدیم که یک نقطه روی دایره واحد را می‌توان با مختصات زیر نمایش داد:

$$(\cos\theta, \sin\theta)$$

همچنین گفتیم معادله دایره واحد یا دایره مثلثاتی به شکل زیر است:

$$x ^ 2 + y ^ 2 = 1$$

حالا با جایگذاری توابع مثلثاتی به جای مقادیر $$x$$ و $$y$$ این معادله می‌شود:

$$\sin^2\theta + \cos^2\theta = 1$$

رابطه بالا یکی از مهم‌ترین روابط مثلثاتی است که در حل مسائل بسیار پرکاربرد است. با دانستن این رابطه قادریم فقط با داشتن سینوس (یا کسینوس) یک زاویه، به راحتی کسینوس (یا سینوس) آن را پیدا کنیم:

$$\cos \theta = \pm \sqrt{ 1- \sin^2 \theta }$$

$$\sin \theta = \pm \sqrt{ 1- \cos^2 \theta }$$

همچنین اگر طرفین این رابطه را بر $$\sin^2\theta$$ یا $$\cos^2\theta$$ تقسیم کنیم، به روابط دیگری به شکل زیر می‌رسیم:

$$\Rightarrow \frac{\sin^2\theta}{\cos^2\theta } + \ \frac{\cos^2\theta}{\cos^2\theta } = \frac{1}{\cos^2\theta }$$

$$\Rightarrow \tan^2\theta + 1 = \frac{1}{\cos^2\theta } = sec^2\theta$$

$$\Rightarrow \frac{\sin^2\theta}{\sin^2\theta } + \ \frac{\cos^2\theta}{\sin^2\theta } = \frac{1}{\sin^2\theta }$$

$$\Rightarrow 1 + \cot^2\theta = \frac{1}{\sin^2\theta } = csc^2\theta$$

یادگیری مثلثات در حسابان با فرادرس

در ریاضیات متوسطه دوم از توابع مثلثاتی در عملیاتی مانند بررسی آهنگ تغییرات، مشتق‌گیری و محاسبه انتگرال بسیار استفاده می‌شود. به همین دلیل در این قسمت قصد داریم چند فیلم‌‌ آموزشی در مورد این کتاب درسی به شما معرفی کنیم که در مجموعه فرادرس تهیه شده‌اند. مشاهده این فیلم‌ها به شما کمک می‌کند تا با بهره‌گیری از آموزش تصویری و حل مثال‌ها و تمرین‌های متنوع به مباحثی مانند مشتق توابع مثلثاتی یا توابع معکوس مثلثاتی و ... کاملا مسلط شوید:

• فیلم آموزش حسابان پایه یازدهم – حل تمرین فرادرس
• فیلم آموزش رایگان قضیه اساسی حسابان در حساب دیفرانسیل و انتگرال فرادرس
• فیلم آموزش حسابان پیشرفته فرادرس

حل مثال و تمرین از جدول دایره مثلثاتی

در این بخش با توجه به آنچه که در مورد جدول دایره مثلثاتی آموختیم، چند سوال متنوع حل می‌کنیم تا با کاربرد این جدول بهتر آشنا شوید.

مثال ۱

مقدار عددی عبارت زیر را با استفاده از جدول دایره مثلثاتی و بدون استفاده از ماشین حساب پیدا کنید:

$$\frac{ \cos 420 ^\circ - \sin 225 ^\circ \cos (-45^\circ)}{\tan 315 ^\circ}$$

پاسخ

با توجه به روابطی که در بخش‌‌های قبل معرفی شد، اولین قدم برای حساب کردن پاسخ عبارت بالا این است که از فرمول‌های کوتاه شده توابع مثلثاتی استفاده کنیم. برای مثال می‌توانیم $$\cos 420 ^\circ$$ را به شکل $$\cos (360 ^\circ + 60 ^\circ )$$ در نظر بگیریم. به همین صورت برای سایر زاویه‌ها نیز از عبارت‌های زیر استفاده کنیم:

$$\sin 225 ^\circ = \sin (180 ^\circ + 45 ^\circ )$$

$$\tan 315 ^\circ = \tan (360 ^\circ - 45 ^\circ )$$

به این ترتیب خواهیم داشت:

$$= \frac{ \cos (360 ^\circ + 60 ^\circ) - \sin (180 ^\circ + 45 ^\circ) \cos (-45^\circ)}{\tan (360 ^\circ - 45 ^\circ)}$$

همچنین با توجه به فرمول‌های زیر عبارت بالا ساده‌تر می‌شود:

$$\cos ( 2\pi + \theta) = \cos \theta$$

$$\sin ( \pi + \theta) = -\sin \theta$$

$$\tan ( 2\pi - \theta) = -\tan \theta$$

$$\Rightarrow \frac{ \cos 60 ^\circ + \sin 45 ^\circ \cos 45^\circ}{-\tan 45 ^\circ}$$

حالا کافی است با کمک گرفتن از جدول دایره مثلثاتی مقادیر هر کدام از این توابع را در عبارت بالا قرار دهیم:

$$\Rightarrow \frac{ \frac{1}{2} + \frac{1}{\sqrt{2}} \times\frac{1}{\sqrt{2}}}{-1} =\frac{1}{-1}=-1$$

مثال ۲

کدام یک از نقاط $$(\frac{1}{4},\frac{1}{4})$$ و $$(\frac{1}{8},\frac{1}{8})$$ روی دایره مثلثاتی قرار می‌گیرند؟

پاسخ

گفتیم معادله دایره واحد یا دایره مثلثاتی $$x ^ 2 + y ^ 2 = 1$$ است. با جایگزین کردن مختصات هر کدام از این دو نقطه به جای $$x$$ و $$y$$ در سمت چپ این معادله خواهیم داشت:

$$\Rightarrow x ^ 2 + y ^ 2 = (\frac{1}{4})^2 +(\frac{1}{4})^2 = \frac{1}{8}$$

$$\Rightarrow x ^ 2 + y ^ 2 = (\frac{1}{8})^2 +(\frac{1}{8})^2 = \frac{1}{32}$$

برای اینکه این نقاط روی دایره مثلثاتی قرار بگیرند، باید حاصل عبارت‌های بالا برابر با یک شود. چون این عدد به‌دست نیامد، پس می‌توانیم بگوییم هیچ‌کدام روی دایره مثلثاتی قرار ندارند.

مثال ۳

اگر $$\sin \theta = \frac{4}{5}$$ باشد، $$\cos \theta$$ چقدر است؟

پاسخ

برای اینکه بتوانیم با داشتن سینوس یک زاویه کسینوس آن را پیدا کنیم، بهترین راه استفاده از معادله زیر است:

$$\sin^2\theta + \cos^2\theta = 1$$

$$\Rightarrow \cos^2\theta = 1 - \sin^2\theta = 1 - (\frac{4}{5})^2 = \frac{9}{25}$$

$$\Rightarrow \cos\theta = \sqrt { \frac{9}{25}} = \frac{3}{5}$$

مثال ۴

حاصل عبارت مثلثاتی $$- \ \frac{\cos328^ \circ \times \tan^2 212 ^ \circ}{\tan148^ \circ } + \sin 148^ \circ$$ را بر حسب $$\sin 32^ \circ$$ پیدا کنید:

پاسخ

با بکارگیری فرمول‌های مثلثاتی کوتاه شده زیر، عبارت صورت سوال به شکل زیر ساده می‌شود:

$$- \ \frac{\cos(360^ \circ - 32^ \circ )\times \tan^2 (180^ \circ + 32^ \circ )}{\tan(180^ \circ - 32^ \circ ) } + \sin (180^ \circ - 32^ \circ )$$

$$- \ \frac{\cos32^ \circ \times \tan^2 32^ \circ }{-\tan 32^ \circ } + \sin 32^ \circ = \cos32^ \circ \times \tan32^ \circ + \sin 32^ \circ$$

در نهایت با نوشتن تانژانت به شکل سینوس تقسیم بر کسینوس خواهیم داشت:

$$\cos32^ \circ \times \frac{ \sin 32 ^ \circ}{ \cos 32 ^ \circ} + \sin 32^ \circ = 2 \sin 32^ \circ$$