مرتب سازی ادغامی (Merge Sort) در جاوا — به زبان ساده

در این راهنما نگاهی به الگوریتم مرتب سازی ادغامی و پیاده‌سازی آن در جاوا خواهیم داشت. مرتب‌سازی ادغامی یکی از مؤثرترین تکنیک‌های مرتب‌سازی بر مبنای پارادایم «تقسیم و حل» (divide and conquer) است.

الگوریتم مرتب سازی ادغامی

مرتب‌سازی ادغامی یک الگوریتم «تقسیم و حل» است که در آن ابتدا مسئله به مسائل فرعی تقسیم می‌شود. زمانی که راه‌حل‌ها برای مسائل فرعی آماده شد، مجدداً آن‌ها را با هم ترکیب می‌کنیم تا راه‌حل نهایی برای مسئله اصلی به دست آید.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

این یکی از الگوریتم‌هایی است که با استفاده از «بازگشت» (recursion) به سادگی پیاده‌سازی می‌شود، چون به جای مسئله اصلی با مسائل فرعی سر و کار داریم.

الگوریتم آن را می‌توان به صورت فرایند 2 مرحله‌ای زیر توصیف کرد:

• تقسیم: در این مرحله آرایه ورودی به دو نیمه تقسیم می‌شود. محور تقسیم نقطه میانی آرایه است. این مرحله به صورت بازگشتی روی همه آرایه‌های نیمه انجام می‌یابد تا این که دیگر نیمه آرایه‌ای برای تقسیم وجود نداشته باشد.
• حل: در این مرحله باید آرایه‌های تقسیم‌شده را مرتب‌سازی و ادغام کنیم و این کار از بخش زیرین به سمت بالا برای به دست آوردن آرایه مرتب انجام می‌یابد.

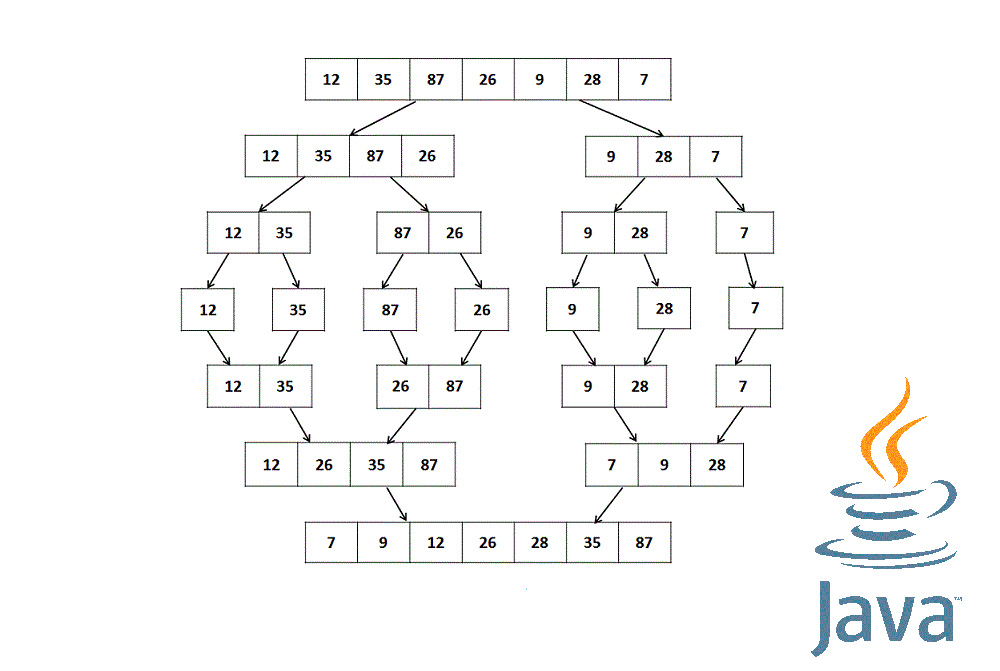
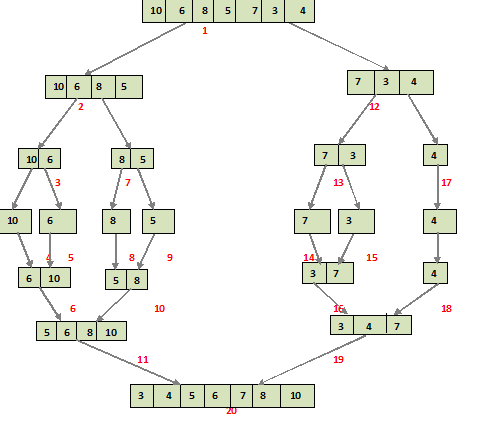
نمودار زیر فرایند کامل مرتب‌سازی ادغامی را برای آرایه نمونه {10, 6, 8, 5, 7, 3, 4} نمایش می‌دهد.

اگر نگاهی دقیق‌تر به الگوریتم داشته باشیم، می‌بینیم که آرایه به صورت بازگشتی به نیمه‌های متوالی تقسیم می‌شود تا این که اندازه آن برابر با 1 شود. زمانی که اندازه آن برابر با 1 شد، فرایندهای ادغام وارد عمل می‌شوند و شروع به ادغام آرایه‌ها برای رسیدن به آرایه مرتب می‌کنند.

پیاده‌سازی

برای پیاده‌سازی الگوریتم فوق، یک تابع مرتب‌سازی ادغامی می‌نویسیم که یک آرایه ورودی و طولانی را به عنوان پارامتر می‌گیرد. این یک تابع بازگشتی خواهد بود، بنابراین به یک شرایط پایه و بازگشت نیاز داریم.

شرایط پایه در صورتی بررسی می‌شوند که طول آرایه برابر با 1 باشد، و فقط در این حالت بازگشت می‌یابد. در بقیه موارد فراخوانی بازگشتی اجرا خواهد شد.

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

برای حالت بازگشتی اندیس میانه را پیدا کرده و دو آرایه موقت []l و []r را ایجاد می‌کنیم. سپس تابع mergeSort به صورت بازگشتی برای هر دو آرایه فرعی فراخوانی می‌شود:

1public static void mergeSort(int[] a, int n) {
2    if (n < 2) {
3        return;
4    }
5    int mid = n / 2;
6    int[] l = new int[mid];
7    int[] r = new int[n - mid];
8 
9    for (int i = 0; i < mid; i++) {
10        l[i] = a[i];
11    }
12    for (int i = mid; i < n; i++) {
13        r[i - mid] = a[i];
14    }
15    mergeSort(l, mid);
16    mergeSort(r, n - mid);
17 
18    merge(a, l, r, mid, n - mid);
19}

بعد تابع merge را فراخوانی می‌کنیم که در ورودی خود هر دو آرایه فرعی و اندیس‌های آغاز و پایان هر دو آرایه فرعی را می‌گیرد. تابع merge عناصر هر دو آرایه فرعی را یک به یک مقایسه می‌کند و عنصر کوچک‌تر را درون آرایه ورودی قرار می‌دهد.

زمانی که به انتهای یک آرایه فرعی برسید، بقیه عناصر از آرایه دیگر درون آرایه کپی می‌شوند و بدین ترتیب آرایه مرتب‌شده نهایی به دست می‌آید:

1public static void merge(
2  int[] a, int[] l, int[] r, int left, int right) {
3  
4    int i = 0, j = 0, k = 0;
5    while (i < left && j < right) {
6        if (l[i] <= r[j]) {
7            a[k++] = l[i++];
8        }
9        else {
10            a[k++] = r[j++];
11        }
12    }
13    while (i < left) {
14        a[k++] = l[i++];
15    }
16    while (j < right) {
17        a[k++] = r[j++];
18    }
19}

تست unit برنامه به صورت زیر است:

1@Test
2public void positiveTest() {
3    int[] actual = { 5, 1, 6, 2, 3, 4 };
4    int[] expected = { 1, 2, 3, 4, 5, 6 };
5    MergeSort.mergeSort(actual, actual.length);
6    assertArrayEquals(expected, actual);
7}

پیچیدگی

از آنجا که مرتب‌سازی ادغامی یک الگوریتم بازگشتی است، پیچیدگی زمانی آن را می‌توان به صورت رابطه بازگشتی زیر بیان کرد:

1T(n) = 2T(n/2) + O(n)

(2T(n/2 متناظر با زمان مورد نیاز برای مرتب‌سازی آرایه‌های فرعی و زمان (O(n برای ادغام آرایه کلی است. زمانی که مسئله حل شود، پیچیدگی زمانی به (O(nLogn می‌رسد.

این پیچیدگی برای بدترین حالت، حالت میانگین و بهترین حالت درست است زیرا همواره آرایه را به دو نیمه تقسیم کرده و سپس ادغام می‌کند. پیچیدگی فضایی الگوریتم نیز (O(n است، چون آرایه‌های موقتی در هر فراخوانی بازگشتی ایجاد می‌شوند.

سخن پایانی

در این راهنمای کوتاه، با طرز کار الگوریتم مرتب‌سازی ادغامی و روش پیاده‌سازی آن در جاوا آشنا شدیم. همه کدهای این راهنما را می‌توانید در این صفحه گیت‌هاب (+) ملاحظه کنید.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های جاوا (Java)
• مجموعه آموزش‌های برنامه‌‌نویسی
• گنجینه آموزش های جاوا (Java)
• زبان برنامه‌نویسی جاوا (Java) — از صفر تا صد
• 1۰ مفهوم اصلی زبان جاوا که هر فرد مبتدی باید بداند
• توضیح الگوریتم مرتب سازی تعویضی و پیاده سازی آن در زبان های مختلف

==