الگوریتم حل ماز (Maze) در جاوا — از صفر تا صد

در این مقاله به بررسی روش‌های ممکن برای ناوبری در یک ماز یا هزارتو (maze) با استفاده از جاوا می‌پردازیم. اگر ماز را یک تصویر سیاه‌ و سفید تصور کنیم که پیکسل‌های سیاه نماینده دیوار و پیکسل‌های سفید نشان‌دهنده مسیر هستند، دو پیکسل سفید مورد توجه ویژه هستند که یکی ورودی و دیگری خروجی ماز است. با فرض وجود چنین نیازی می‌خواهیم مسیری از ورودی به خروجی ماز پیدا می‌کنیم.

مدل‌سازی ماز

ماز را به صورت یک آرایه 2-بُعدی از اعداد صحیح تصور می‌کنیم. معنای مقادیر عددی در آرایه بر اساس قرارداد زیر تفسیر می‌شود:

• 0: مسیر
• 1: دیوار
• 2: ورودی ماز
• 3: خروجی ماز
• 4: سلول‌های مسیر از ورودی تا خروجی

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

بدین ترتیب می‌توانیم ماز را به صورت یک گراف مدل‌سازی کنیم. ورودی و خروجی دو گره خاص هستند که بین آن‌ها مسیر را پیدا می‌کنیم. گراف به طور معمول دو مشخصه دارد که گره‌ها و یال‌های آن هستند. یال وجود اتصال بین گره‌های گراف را نشان می‌دهد. از این رو فرض خواهیم کرد که یال‌های ضمنی از هر گره، گره مفروض را به گره‌های راست، چپ، بالا و پایین آن وصل می‌کنند.

در ادامه امضای متد را به صورت زیر تعریف می‌کنیم:

1public List<Coordinate> solve(Maze maze) {
2
3}

ورودی متد یک ماز است که شامل آرایه 2-بُعدی است که بر مبنای قراردادی که در بخش فوق توصیف کردیم تنظیم شده است. پاسخ متد فهرستی از گره‌ها است که یک مسیر از گره ورودی به گره خروجی تشکیل می‌دهند.

الگوریتم پس‌گرد بازگشتی (DFT)

در این بخش الگوریتم «پس‌گرد بازگشتی» (Recursive Backtracker) را برای تشکیل ماز بررسی می‌کنیم.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

الگوریتم

یکی از رویکردهای نسبتاً بدیهی این است که همه مسیرهای ممکن را بررسی کنیم تا در نهایت در صورت وجود مسیر را پیدا کنیم. اما چنین رویکردی پیچیدگی نمایی دارد و مقیاس‌پذیری مناسبی ندارد.

با این حال می‌توان یک راه‌حل «تهاجم کور» (brute force) سفارشی مانند آنچه در بخش فوق توصیف کردیم به وسیله الگوریتم پس‌گرد و علامت‌گذاری گره‌های بازدید شده برای رسیدن به مسیر مورد نظر در طی زمان معقول طراحی کرد. این الگوریتم به نام الگوریتم «جستجوی عمق-اول» (Depth-first search) نیز شناخته می‌شود.

این الگوریتم را می‌توان به صورت زیر مشخص ساخت:

1. اگر روی دیوار یا روی گره قبلاً بازدید شده باشید، یک شکست بازگشت می‌یابد.
2. در غیر این صورت اگر روی گره خروجی باشیم، در این صورت موفقیت بازگشت می‌یابد.
3. در غیر این صورت، گره به فهرست مسیر اضافه می‌شود و به صورت بازگشتی در همه جهت‌ها پیمایش می‌شود. اگر شکست بازگشت یابد، گره از مسیر حذف می‌شود و شکست بازگشت می‌یابد. فهرست مسیر شامل یک مسیر یکتا است که خروجی را پیدا می‌کند.

در ادامه این الگوریتم روی ماز نمایش یافته در شکل 1(a) به کار می‌گیریم که S نقطه شروع و E خروجی است. برای هر گره همه جهت‌های راست، پایین، چپ و بالا را به ترتیب پیمایش می‌کنیم.

در شکل 1(b) یک مسیر را بررسی می‌کنیم و به دیوار برخورد می‌کنیم. سپس به عقب باز می‌گردیم تا این که گرهی را پیدا کنیم که همسایه‌های غیر دیوار داشته باشد و مسیر دیگری را که در شکل 1(c) نمایش یافته است بپیماییم.

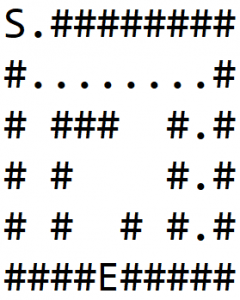
پیاده‌سازی

اکنون به بررسی پیاده‌سازی کد جاوای الگوریتم فوق می‌پردازیم. ابتدا باید چهار جهت را تعریف کنیم. این جهت‌ها را می‌توانیم بر حسب مختصات تعریف کنیم. این مختصات وقتی به هر مختصه مفروض اضافه شوند یکی از مختصات همسایه را بازگشت می‌دهند.

1private static int[][] DIRECTIONS 
2  = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };

همچنین باید یک متد کاربردی داشته باشیم که دو مختصات را با هم جمع کند:

1private Coordinate getNextCoordinate(
2  int row, int col, int i, int j) {
3    return new Coordinate(row + i, col + j);
4}

اکنون می‌توانیم امضای متد solve را تعریف کنیم. منطق کار ساده است: اگر یک مسیر از ورودی به خروجی باشد، در این صورت بازگشتی مسیر است، در غیر این صورت بازگشتی یک فهرست خالی است.

1public List<Coordinate> solve(Maze maze) {
2    List<Coordinate> path = new ArrayList<>();
3    if (
4      explore(
5        maze, 
6        maze.getEntry().getX(),
7        maze.getEntry().getY(),
8        path
9      )
10      ) {
11        return path;
12    }
13    return Collections.emptyList();
14}

در ادامه متد explore را که قبلاً اشاره کردیم تعریف می‌کنیم. اگر مسیری وجود داشته باشد، مقدار true بازگشت می‌یابد و لیستی از مختصات در آرگومان path ارائه می‌شود. این متد سه بلوک عمده دارد. در بلوک اول گره‌های نامعتبر یعنی گره‌هایی که خارج از ماز هستند یا بخشی از دیوار هستند را حذف می‌کنیم. گره کنونی را به عنوان گره بازدید شده علامت‌گذاری می‌کنیم تا بار دیگر آن را بازدید نکنیم.

در نهایت تا زمانی که خروجی را نیافته باشیم، به صورت بازگشتی در همه جهات حرکت می‌کنیم:

1private boolean explore(
2  Maze maze, int row, int col, List<Coordinate> path) {
3    if (
4      !maze.isValidLocation(row, col) 
5      || maze.isWall(row, col) 
6      || maze.isExplored(row, col)
7    ) {
8        return false;
9    }
10 
11    path.add(new Coordinate(row, col));
12    maze.setVisited(row, col, true);
13 
14    if (maze.isExit(row, col)) {
15        return true;
16    }
17 
18    for (int[] direction : DIRECTIONS) {
19        Coordinate coordinate = getNextCoordinate(
20          row, col, direction[0], direction[1]);
21        if (
22          explore(
23            maze, 
24            coordinate.getX(), 
25            coordinate.getY(), 
26            path
27          )
28        ) {
29            return true;
30        }
31    }
32 
33    path.remove(path.size() - 1);
34    return false;
35}

این راه‌حل، از پشته‌ای به اندازه حداکثر بزرگی ماز استفاده می‌کند.

الگوریتم کوتاه‌ترین مسیر

در این بخش تلاش خواهیم کرد جواب بهینه را پیدا کنیم.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

الگوریتم

الگوریتم بازگشتی توصیف شده فوق، مسیر مورد نظر از ورودی تا خروجی را می‌یابد؛ اما این مسیر لزوماً کوتاه‌ترین مسیر نیست. برای یافتن کوتاه‌ترین مسیر می‌توانیم از رویکرد دیگری برای پیمایش گراف استفاده کنیم که به نام «جستجوی سطح-اول» (Breadth-first search) به اختصار BFS شناخته می‌شود.

در روش عمق-اول (DFS) یک فرزند و همه نوادگانش ابتدا و قبل از رفتن به فرزند دیگر کاوش می‌شوند. در حالی که در روش BFS ابتدا همه فرزندان بی‌واسطه کاوش می‌شوند و سپس به نوادگان انتقال می‌یابد. این وضعیت تضمین می‌کند که همه گره‌هایی که در مسافت معینی از گره والد قرار دارند، در زمان واحدی کاوش شده‌اند.

این الگوریتم را می‌توان به صورت زیر خلاصه کرد:

1. گره ابتدایی به صف اضافه می‌شود.
2. زمانی که صف خالی نباشد، یک گره برداشته شده و کارهای زیر اجرا می‌شوند:
   1. اگر به دیوار برسیم یا گره قبلاً بازدید شده باشد، به تکرار بعدی حلقه می‌رویم.
   2. اگر به گره خروجی برسیم، از گره فعلی پس‌گرد می‌کنیم تا به گره آغازین برسیم و کوتاه‌ترین مسیر را می‌یابیم.
   3. در غیر این صورت همه همسایه‌های بی‌واسطه در چهار جهت در صف اضافه می‌شوند.

یک نکته مهم در این الگوریتم آن است که گره‌ها باید رد والد خود را داشته باشند یعنی از جایی که به صف اضافه شده‌اند آگاه باشند. این نکته مهمی است تا زمانی که به گره خروجی رسیدیم بتوانیم مسیری که آمده‌ایم را در دست داشته باشیم.

انیمیشن زیر همه مراحلی را که یک ماز با استفاده از این الگوریتم کاوش می‌شود نمایش می‌دهد. می‌توان مشاهده کرد که همه گره‌ها در مسافت یکسان از گره آغازین ابتدا بررسی می‌شوند و سپس به سراغ گره بعدی می‌رویم.

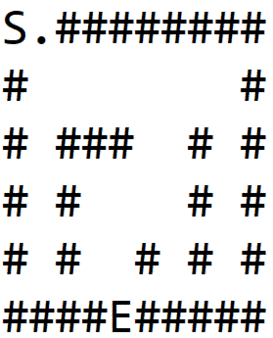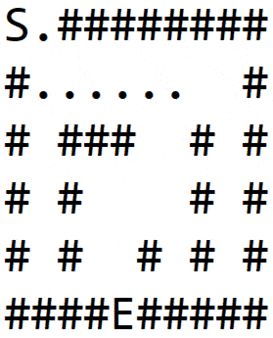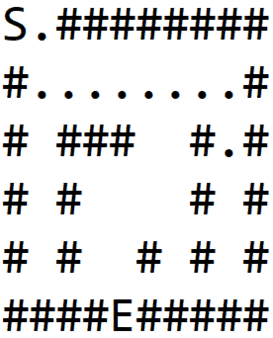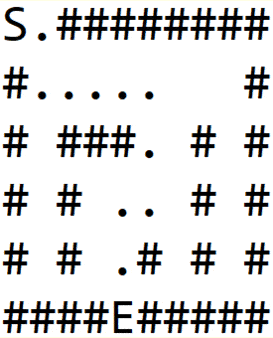
پیاده‌سازی

اینک به پیاده‌سازی این الگوریتم در جاوا می‌پردازیم. ما از متغیر DIRECTIONS که در بخش قبل تعریف کردیم مجدداً استفاده می‌کنیم.

ابتدا یک متد کاربردی تعریف می‌کنیم که از گره مفروض به ریشه آن پس‌گرد می‌کند. این متد برای ردگیری مسیر در زمان یافتن گره خروجی استفاده خواهد شد:

1private List<Coordinate> backtrackPath(
2  Coordinate cur) {
3    List<Coordinate> path = new ArrayList<>();
4    Coordinate iter = cur;
5 
6    while (iter != null) {
7        path.add(iter);
8        iter = iter.parent;
9    }
10 
11    return path;
12}

اکنون متد اصلی solve را تعریف می‌کنیم. ما سه بلوک کدی که در پیاده‌سازی DFS استفاده کردیم را در اینجا مجدداً مورد استفاده قرار می‌دهیم. این بلوک‌ها شامل اعتبارسنجی گره، علامت‌گذاری گره بازدید شده و پیمایش گره‌های همسایه هستند.

ما صرفاً یک تغییر کوچک ایجاد می‌کنیم. به جای پیمایش بازگشتی از ساختار داده FIFO برای ردگیری همسایه‌ها استفاده می‌کنیم و حلقه تکرار را روی آن‌ها تعریف می‌کنیم:

1public List<Coordinate> solve(Maze maze) {
2    LinkedList<Coordinate> nextToVisit 
3      = new LinkedList<>();
4    Coordinate start = maze.getEntry();
5    nextToVisit.add(start);
6 
7    while (!nextToVisit.isEmpty()) {
8        Coordinate cur = nextToVisit.remove();
9 
10        if (!maze.isValidLocation(cur.getX(), cur.getY()) 
11          || maze.isExplored(cur.getX(), cur.getY())
12        ) {
13            continue;
14        }
15 
16        if (maze.isWall(cur.getX(), cur.getY())) {
17            maze.setVisited(cur.getX(), cur.getY(), true);
18            continue;
19        }
20 
21        if (maze.isExit(cur.getX(), cur.getY())) {
22            return backtrackPath(cur);
23        }
24 
25        for (int[] direction : DIRECTIONS) {
26            Coordinate coordinate 
27              = new Coordinate(
28                cur.getX() + direction[0], 
29                cur.getY() + direction[1], 
30                cur
31              );
32            nextToVisit.add(coordinate);
33            maze.setVisited(cur.getX(), cur.getY(), true);
34        }
35    }
36    return Collections.emptyList();
37}

در این راهنما به بررسی دو الگوریتم گراف یعنی جستجوی عمق-اول و جستجوی سطح-اول برای حل یک ماز پرداختیم. همچنین به بررسی روش یافتن کوتاه‌ترین مسیر از ورودی به خروجی از طریق الگوریتم BFS پرداختیم. کد کامل این الگوریتم‌ها را می‌توانید در این صفحه گیت‌هاب (+) مشاهده کنید.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های جاوا (Java)
• مجموعه آموزش‌های برنامه‌‌نویسی
• گنجینه آموزش‌های جاوا (Java)
• آموزش جامع برنامه نویسی جاوا به زبان ساده
• 1۰ مفهوم اصلی زبان جاوا که هر فرد مبتدی باید بداند

==