توابع زیان (Loss Function) در یادگیری ماشین – به همراه کدهای پایتون
بیشتر الگوریتمها در «یادگیری ماشین» (Machine learning)، برمبنای کمینه یا بیشینهسازی «تابع هدف» (Objective Function)، عمل میکنند. گروهی از توابع هدف که قرار است کمینه شوند به نام «توابع زیان» (Loss Function) معروفند. البته به این توابع در مباحث هوش مصنوعی گاهی «توابع هزینه» (Cost Function) نیز میگویند.


تابع زیان، معیاری برای سنجش مناسب بودن مدل از نظر قابلیت و توانایی در پیشگویی مقدارهای جدید است. یکی از روشهای معمول برای پیدا کردن کمینه تابع زیان، استفاده از مشتق و الگوریتم «گرادیان کاهشی» (Gradient Descent) است. زیرا در بیشتر مسائل مربوط به هوش مصنوعی، توابع زیان به صورت «محدب» (Convex) هستند. متاسفانه نمیتوان برای همه نوع دادهای از یک تابع زیان استفاده کرد. انتخاب تابع زیان مناسب به عوامل متعددی نظیر وجود نقاط یا دادههای پرت، نوع الگوریتم یادگیری ماشین، هزینه زمانی اجرای الگوریتم و سادگی محاسبه مشتق و ... بستگی دارد.
هدف از این نوشتار، آشنایی با توابع زیان و کاربردهای آنها در حل مسائل یادگیری ماشین بخصوص رگرسیون است. برای اطلاع از مباحث یادگیری ماشین مطلب مقدمهای بر یادگیری ماشین و برای آگاهی بیشتر از مباحث رگرسیون به مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده مراجعه کنید.
توابع زیان
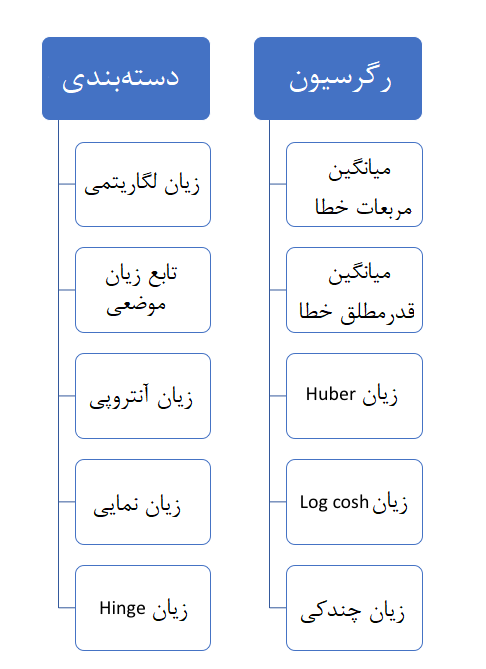
به طور کلی میتوان توابع زیان در زمینه یادگیری ماشین را به دو گروه عمده تقسیم کرد:
- توابع زیان مربوط به الگوریتمهای دستهبندی (Classification)
- توابع زیان مربوط به رگرسیون (Regression)
با توجه به کاربرد و اهمیت بیشتر روشهای رگرسیونی، در این مطلب به بررسی توابع زیان مرتبط با آن میپردازیم.
نکته: در «روشهای رگرسیونی» (Regression Methods)، مدل قادر به پیشبینی مقدارهای کمی است در حالیکه در «مدلهای دستهبندی» (Classification Models)، «برچسبها» (labels) یا «دستهها» (Groups)، پیشبینی میشوند.
باید توجه داشت که یکی از خصوصیات تابع زیان نامنفی بودن آن است. در نتیجه توابعی را میتوان به عنوان تابع زیان معرفی کرد که برد آنها حتما اعداد نامنفی باشد، زیرا اغلب به دنبال میزان خطا هستیم و نه جهت آن.
زیانهای مدلهای رگرسیونی
در این قسمت با توابع زیانی که برای برآورد پارامترهای مدل رگرسیونی به کار میروند آشنا میشویم. منظور از برآورد پارامترهای مدل رگرسیونی، محاسبه ضرایبی است که مدل رگرسیونی را میسازند.
برای مثال اگر مدل رگرسیونی به صورت زیر باشد، به کمک کمینهسازی تابع زیان، پارامترهای مدل یعنی برآورد میشوند.
مشخص است که در اینجا خطا همان است. در نتیجه تابع زیان به صورت تابعی از این خطا نوشته میشود. به شکل دیگر میتوان خطا را به صورت فاصله بین مقدار پیشبینی و مقدار واقعی برای متغیر پاسخ (y) در نظر گرفت. به این ترتیب پارامترهای مدل به شکلی انتخاب شدهاند که تابع زیان کمینه شود.
1- تابع زیان میانگین مربعات (Means Square Error)
یکی از معروفترین و معمولترین توابع زیان در تحلیل رگرسیونی، میانگین مربعات خطا (Means Square Error) است که به اختصار MSE نامیده میشود. این تابع زیان، میانگین مربعات فاصله بین مقدار پیشبینی و واقعی را محاسبه میکند. شیوه و نحوه محاسبه آن در زیر دیده میشود:
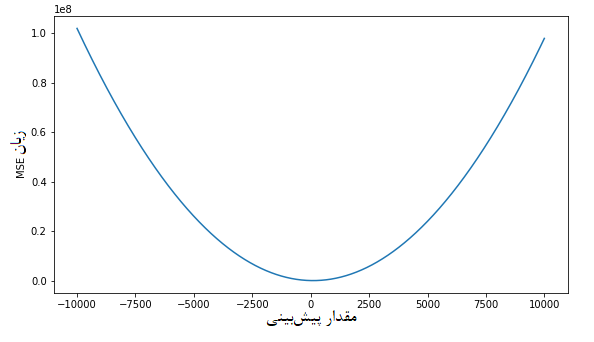
در مباحث آماری، معمولا به چنین تابعی، زیان گفته میشود. با توجه به استفاده از توان ۲ در محاسبه MSE، شکل این تابع زیان برحسب مقدارهای پیشبینی (یا خطا) به صورت سهمی خواهد بود. فرض کنید که مقدار واقعی برای متغیر پاسخ (y) برابر است با صفر، در نتیجه نمودار تابع زیان MSE را براساس مقدارهای پیشبینی در محدوده ۱۰۰۰۰- تا ۱۰۰۰۰ میتوان به صورت زیر رسم کرد.
2- میانگین قدرمطلق خطا (Mean Absolute Error)
یکی دیگر از توابع زیان که خواص جالبی دارد، میانگین قدرمطلق خطا (Mean Absolute Error) است که به اختصار MAE نیز نامیده میشود. این تابع زیان، به مانند MSE از فاصله بین مقدار پیشبینی و واقعی به عنوان معیار استفاده کرده ولی جهت این تفاضل را در نظر نمیگیرد. بنابراین در محاسبه خطا MAE فقط میزان فاصله و نه جهت فاصله به کار میرود. البته گاهی در مباحث آماری، به این تابع، زیان نیز گفته میشود.
بنابراین MAE، میانگین قدرمطلق تفاضل بین مقدار پیشبینی و واقعی را محاسبه میکند. شیوه بدست آوردن MAE در رابطه زیر نوشته شده است.
در تصویر زیر، شکل تابع زیان MAE ترسیم شده است. در این نمودار فرض بر این است که مقدار واقعی متغیر پاسخ برابر با صفر است.
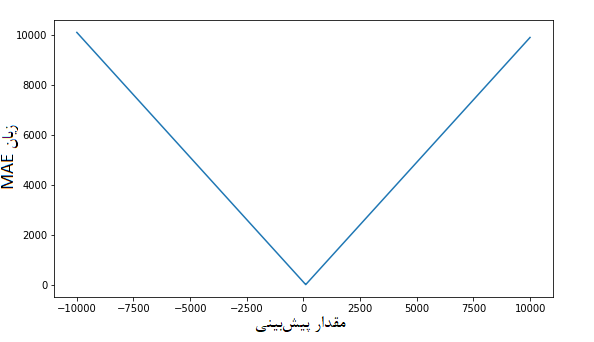
مقایسه زیان میانگین مربعات و قدر مطلق خطا (مقایسه زیان و )
معمولا محاسبات و حل معادلات با مرتبه یا توان ۲ نسبت به توابعی که در آن از قدرمطلق استفاده شده، سادهتر است. به این ترتیب شاید به نظر برسد که استفاده از تابع زیان MSE ارجح باشد. ولی زیان قدرمطلق نسبت به وجود «دادههای پرت» (Outlier) مقاومتر است. بنابراین بهتر است در این مورد بیشتر بحث کنیم. زمانی که یک مدل یادگیری ماشین را «آموزش» (Train) میدهیم، هدف پیدا کردن نقطهای است که تابع زیان در آن کمینه میشود. البته مسلم است که هر دو تابع زیان MAE و MSE زمانی که برآورد با مقدار واقعی برابر باشد، حداقل مقدار (صفر) خواهند بود. در ادامه به با استفاده از کد پایتون به مقایسه این دو تابع زیان میپردازیم.
البته محاسبه این دو تابع زیان را میتوان به کمک توابع کتابخانهای sklearn به نامهای mean_squared_error و mean_absolute_error انجام داد. برای این کار، کافی است کدهای زیر را در پایتون وارد کنید.
نکته: اگر از زیان MSE جذر گرفته شود، تابع زیان دیگری به نام «ریشه میانگین مربعات خطا» (Root Means Square Error) ساخته میشود که به اختصار با RMSE نشان داده میشود. مقایسه MSE و MAE با توجه به تغییر مقیاس مقدار خطا در MSE صحیح نیست، زیرا:
- اگر مقدار پیشبینی به مقدار واقعی نزدیک باشد (فاصله کمتر از ۱ باشد) MSE میزان خطا را منقبض میکند و در خطا فشردگی به وجود میآورد.
- اگر در دادهها، مقدار پرت وجود داشته باشد، زیان MSE، بزرگ و منبسط شده و خطا را بزرگتر از مقدار واقعی نشان میدهد.
نکته: به همین علت، برای بررسی و تشخیص تغییرات، مقایسه را بین MAE و RMSE انجام میدهیم. تا واحد اندازهگیری دادهها برای مقایسه یکسان شود. برای مثال اگر دادهها مربوط به وزن برحسب کیلوگرم باشند، واحد اندازهگیری خطا برای MSE برحسب کیلوگرم مربع (توان ۲) خواهد بود در حالی که برای MAE همان واحد اندازهگیری مشاهدات یعنی کیلوگرم است. با جذر گرفتن از MSE و محاسبه RMSE واحد اندازهگیری خطا برحسب کیلوگرم شده و با زیان MAE قابل مقایسه است.
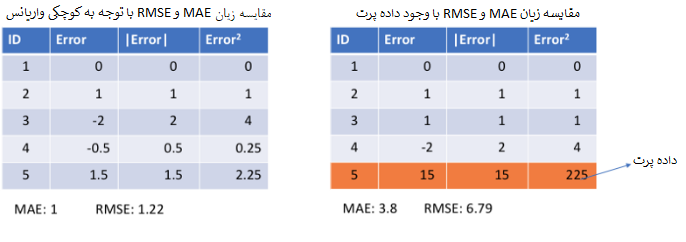
همانطور که دیده میشود در سمت چپ، با توجه به نزدیکی دادههای به یکدیگر زیان MAE و RMSE تقریبا با هم برابرند. در حالیکه در جدول سمت راست به علت وجود داده پرت RMSE تقریبا دوبرابر MAE محاسبه شده است.
مزایای استفاده از MAE
از آنجایی که در محاسبه زیان MSE از مربع خطا استفاده میشود، اگر میزان خطا بزرگتر از ۱ باشد، MSE بزرگ میشود. با وجود داده پرت خطا افزایش یافته و زیان MSE، خطا را بسیار بزرگتر نشان میدهد. بنابراین به نظر میرسد که دادههای پرت در محاسبه MSE وزن بیشتری نسبت به MAE دارند. بنابراین هنگامی که دادههای پرت یا دورافتاده در مشاهدات وجود دارد، استفاده از تابع زیان MAE میتواند کارایی مدل را بالا ببرد.
اگر بخواهیم به طوری شهودی دو تابع زیان MSE و MAE را مقایسه کنیم، میتوان این طور تصور کرد که: «اگر بخواهیم برای همه مقدارهای متغیر مستقل، یک مقدار به عنوان متغیر پاسخ پیدا کنیم که تابع زیان MSE را کمینه کند، این نقطه میانگین مقدارهای متغیر پاسخ خواهد بود. در مقابل، مقداری که تابع زیان MAE را به ازاء همه مقدارهای متغیر مستقل کمینه میکند، میانه مقدارهای متغیر پاسخ است.
میدانیم که میانه در مقابل دادههای پرت مقاوم است و نسبت به میانگین بسیار کمتر تحت تاثیر قرار میگیرد. بنابراین MAE نسبت به MSE کمتر تحت تاثیر دادههای پرت بوده و میتواند برآورد بهتری برای پارامترهای مدل یا پیشبینی متغیر پاسخ ارائه دهد.
معایب استفاده از MAE
استفاده از تابع زیان MAE، بخصوص در شبکههای عصبی، با یک مشکل بزرگ روبرو است. هنگام استفاده از MAE، مقدار گرادیان تابع زیان، برای مقدارهای کوچک خطا نیز بزرگ است. این وضعیت در الگوریتمهای یادگیری ماشین مناسب نیست. برای حل این مشکل بهتر است از «نرخ یادگیری پویا» (Dynamic Learning Rate)استفاده شود که هنگام نزدیک شدن به نقطه کمینه، مقدارش کاهش مییابد. ولی گرادیان تابع زیان MSE، زمانی که مقدار خطا، بزرگ باشد، زیاد و هنگامی که خطا کم شود، کاهش خواهد یافت. نمودارهایی که در تصاویر زیر دیده میشوند، این مطلب را بهتر نشان میدهند. در هر دو نمودار، فرض بر این است که مقدار واقعی متغیر پاسخ برابر با صفر است.
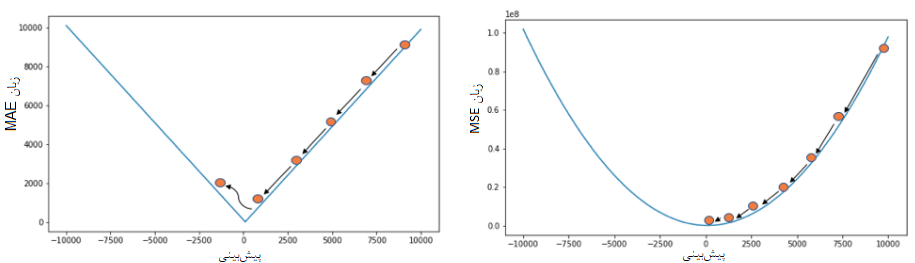
همانطور که در تصویر سمت چپ دیده میشود، برای مقدارهای پیشبینی شده با خطاهای بزرگ یا کوچک، شیب خط تابع زیان MAE ثابت است. در حالیکه در تصویر سمت راست، مقدار تابع زیان MSE، شیب منحنی برای خطاهای بزرگ، زیاد بوده و هنگامی که مقدار پیشبینی به مقدار واقعی نزدیک میشود (کاهش خطا)، شیب منحی تابع زیان MSE نیز کاهش مییابد.
نکته: مقدارهای مربوط به محور عمودی را برای هر دو نمودار مقایسه کنید. محور عمودی برای تابع زیان MSE شامل مقدارهای بسیار بزرگ است ولی با کاهش فاصله بین مقدار پیشبینی و واقعی شیب منحنی کم میشود. در عوض در نمودار سمت چپ که مربوط به تابع زیان MAE است، مقدارهای محور عمودی خیلی بزرگ نیست ولی روند کاهش ثابت است به این معنی که شیب کاهش خطا برای این تابع، یکنواخت است.
قاعده تصمیمگیری برای انتخاب تابع زیان MSE یا MAE
اگر دادههای پرت، بیانگر مقدارهای غیرمعمول (که با احتمال قوی در دادههای کسب و کار مشاهده میشوند) بوده و باید حتما برای مدلسازی شناسایی شوند، استفاده از تابع زیان MSE میتواند مفید باشد. ولی اگر دادههای پرت، حاصل مشاهدات مخدوش باشد، بهتر است از MAE استفاده کنیم تا اثر آنها را در برآورد پارامترهای مدل از بین ببریم. بنابراین اگر تابع زیان MAE را متعلق به گروه توابع زیان در فضای و MSE را نماینده توابع زیان در فضای در نظر بگیریم، به عنوان یک راهنمایی کلی میتوان گفت: «توابع زیان نسبت به دادههای پرت مقاوم بوده ولی مشتق آنها پیوسته نیست. در نتیجه برای پیدا کردن کمینه به راحتی از روشهای مشتقگیری نمیتوان استفاده کرد. در مقابل توابع زیان نسبت به دادههای پرت حساس بوده ولی محاسبات مربوط به پیدا کردن نقاط کمینه آن سادهتر است و به به کمک روشهای تحلیلی بدست میآیند.»
یک مسئله در به کارگیری توابع زیان MAE و MSE
در اینجا به وضعیتی میپردازیم که دادههای به شکلی هستند که هر دو تابع زیان MAE و MSE در برآورد پارامترها و پیشبینی متغیر پاسخ، دچار مشکل میشوند. فرض کنید که برای ۹۰٪ دادهها، مقدار واقعی متغیر پاسخ برابر با ۱۵۰ یا حدود ۱۵۰ هستند و برای ۱۰٪ باقیمانده، مقدار واقعی متغیر پاسخ در حدود ۰ تا ۳۰ تغییر میکند. در این حالت استفاده از تابع زیان MAE باعث میشود مقدار ۱۵۰ به عنوان پیشبینی برای همه مشاهدات باشد. این کار باعث میشود آن جزئی که ۱۰٪ مشاهدات را شامل میشد اصلا در محاسبه مقدارهای پیشبینی نقشی نداشته باشند. زیرا میانه برای چنین دادههایی برابر با همان ۱۵۰ خواهد بود.
همینطور استفاده از MSE باعث میشود مقدار پیشبینی برای بیشتر مشاهدات به ۰ تا ۳۰ نزدیک باشد. به این ترتیب مقدارهای پیشبینی به سمت مقدارهای پرت، تمایل پیدا کرده و به اصطلاح چوله میشوند. در نتیجه استفاده از هر یک از دو تابع زیان MSE یا MAE در پیشبینی متغیر پاسخ چنین مسئلهای، ناکارآمد هستند.
چگونه بر این مسئله غلبه کنیم
یکی از روشهایی که میتواند چنین مشکلی را کند، استفاده از «تبدیلات» (Transformation) روی متغیر پاسخ است. همچنین ممکن است به کارگیری تابع زیان دیگر، به حل این مشکل کمک کند. در ادامه به بررسی چند تابع زیان میپردازیم که به حل این مشکل کمک میکنند و در چنین مواردی کاربرد دارند.
3- تابع زیان هوبر (Huber Loss) یا میانگین خطای قدرمطلق هموار شده (Smooth Mean Absolute Error)
تابع زیان هوبر نسبت به MSE کمتر تحت تاثیر دادههای پرت است. همچنین، برعکس تابع زیان MAE، مشتقپذیر بوده و کمینهسازی آن به راحتی امکان پذیر است.
شیوه محاسبه آن مطابق با رابطه زیر صورت میپذیرد:
در نظر اول، شاید این تابع، همان MSE به نظر برسد ولی با دقت بیشتر، متوجه میشویم که با کوچک بودن خطا یا فاصله بین y و از مقدار تابع زیان شبیه تابع زیان MSE است و در غیر اینصورت شبیه تابع زیان MAE خواهد شد.
در نتیجه همانطور که مشخص است، شکل تابع زیان هوبر برحسب مقدار تغییر میکند. در تصویر زیر، نمودار مربوط به تابع زیان هوبر براساس مقدارهای مختلف نشان داده شده است.
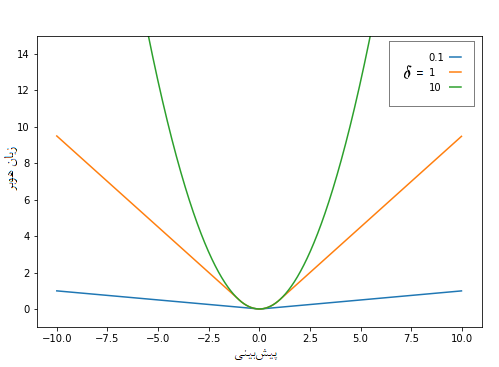
در این نمودار، محور افقی مقدارهای پیشبینی شده برای متغیر پاسخ و محور عمودی نیز مقدار تابع زیان هوبر را نشان میدهد. در اینجا فرض کردهایم که مقدار واقعی متغیر پاسخ برابر با صفر است.
نکته: اگر (به سمت صفر نزدیک شود) تابع زیان هوبر به تابع زیان MAE نزدیک میشود. در صورتی که (مقدار آن بزرگ باشد) این تابع زیان، تبدیل به تابع زیان MSE خواهد شد.
از آنجایی که مقدارهای مختلف شکل تابع زیان را تغییر میدهد، انتخاب مقدار مناسب برای آن کاری حساس و مشکل است. زیرا انتخاب مقدار بزرگ برای آن، تابع زیان را برای بیشتر مواقع MSE در نظر گرفته و انتخاب مقدار کوچک باعث استفاده از تابع زیان MAE برای بیشتر مشاهدات میشود.
چرا از تابع زیان هوبر استفاده کنیم؟
یکی از مشکلات عمده، هنگام استفاده از تابع زیان MAE در یادگیری شبکه عصبی، بزرگ بودن مشتق است که ممکن است باعث شود، کمینه مقدار تابع زیان در پایان مراحل یادگیری بوسیله الگوریتم گرادیان کاهشی حاصل نشود. در عوض استفاده از تابع زیان هوبر باعث میشود، زمانی که میزان خطا کاهش مییابد، مشتق کاهش یافته و دسترسی به کمیته مقدار تابع زیان هوبر میسر شود.
بنابراین تابع زیان هوبر از مزایای هر دو تابع زیان MSE و MAE بهره برده و معایب آنها را هم ندارد. به این ترتیب این تابع زیان، زمانی که دادههای پرت وجود داشته باشد، اثر آنها را در محاسبات کم میکند و زمانی که خطا کاهش یابد، امکان کمینهسازی تابع زیان هوبر به راحتی امکان پذیر است.
البته مسئله اصلی در به کاریگیری این تابع زیان، انتخاب مناسب پارامتر آن یعنی است که معمولا به وسیله یک فرآیند تکراری یادگیری، تعیین میشود. شاید تنظیم این پارامتر به کمک روشهای اعتبارسنجی متقابل (Cross Validation)، ما را به مقدار مناسب برای برساند.
4- تابع زیان لگاریتم کسینوس هذلولوی (Log-Cosh)
یکی دیگر از توابع زیان که بخصوص در رگرسیون به کار میرود، زیان «کسینوس هذلولی» (Logarithm of Hyperbolic Cosine) است که آن را به اختصار Log-Cosh نیز میگویند. برای محاسبه آن کافی است از کسینوس هذلولوی اختلاف یا خطای بین مقدار پیشبینی و واقعی متغیر پاسخ، لگاریتم بگیریم. شیوه محاسبه در زیر دیده میشود.
نمودار این تابع زیان برای مقدارهای مختلف پیشبینی در تصویر زیر دیده میشود. در اینجا فرض شده که مقدار واقعی برای متغیر پاسخ برابر است با صفر.
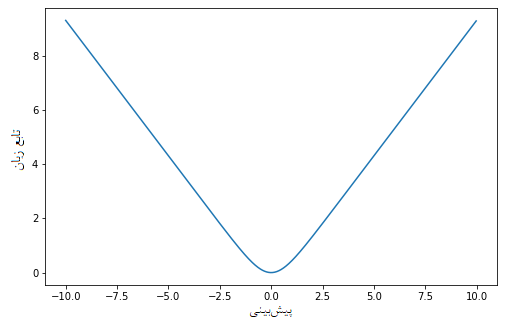
مزایای استفاده از تابع زیان Log-Cosh
میدانیم برای مقدارهای کوچک x تابع تقریبا با و برای مقدارهای بزرگ x تقریبا با برابر است. بنابراین این تابع زیان، تحت تاثیر دادههای پرت قرار نمیگیرد و از طرف دیگر مشتق دوم آن نیز وجود دارد. وجود مشتق دوم، از مزایای این تابع زیان است که در تابع زیان هوبر از آن محروم بودیم.
در بسیاری از الگوریتمهای پیادهسازی شده برای محاسبات بیشنیهسازی تابع درستنمایی، مانند کنابخانه XGBoost در پایتون، از روش بهینهسازی نیوتن استفاده میشود. در این روشها، محاسبه ماتریس مشتقات دوم که به آن ماتریس «هسین» یا «هشین» (Hessian) نیز میگویند، اهمیت پیدا میکند.
بنابراین استفاده از تابع زیان Log-Cosh، هم ما را از مزایای تابع زیان هوبر بهرمند میسازد و هم استفاده از روشهایی که برای بهینهسازی احتیاج به مشتق دوم دارند را میسر میسازد.
در کتابخانه XGBoost که در پایتون وجود دارد، تابع هدف (Obj) برای دسترسی به کمینه تابع درستنمایی به صورت زیر نوشته شده است:
باید دقت داشت که منظور از و محاسباتی هستند که برحسب مشتق دوم انجام میشوند.
کد پایتون مربوط محاسبه تابع زیان هوبر و Log-Cosh در زیر نوشته شده است. توابع به کار رفته با استفاده از کتابخانه XGBoost در دسترس قرار میگیرد.
با توجه به خصوصیاتی که تابع زیان Log-Cosh دارد باز هم نمیتوان آن را به عنوان تابع زیان کامل در نظر گرفت. مشخص است که برای خطاها یا فاصلههای زیاد بین مقدار پیشبینی و واقعی، مشتق و ماتریس هسین به راحتی قابل محاسبه نیستند.
5- تابع زیان چندکی (Quantile Loss)
در بیشتر مسائل مدلسازی با دادههای واقعی، احتیاج به تعیین قطعیت با عدم قطعیت در پیشبینیها داریم. دانستن دامنه تغییرات برای مقدارهای پیشبینی شده قطعا در تصمیمات مربوط به مسائل دنیای واقعی، اهمیت زیادی دارد.
استفاده از تابع زیان چندکی، این خاصیت را دارد که به جای مشخص کردن یک مقدار به عنوان پیشبینی، یک فاصله برای متغیر پاسخ ارائه میکند. به این ترتیب میتوان روشهای قبلی را به عنوان برآوردگرهای نقطهای و روش تابع زیان چندکی را به عنوان یک روش برآوردگر فاصلهای در نظر گرفت.
در روشهای رگرسیونی، برآورد فاصلهای براساس مربعات خطا با فرض ثابت بودن واریانس متغیر پاسخ در سطوح مختلف متغیرهای مستقل، انجام میشود. به بیان دیگر میزان خطا دارای واریانس ثابت است. اگر درستی این شرط در مدل رگرسیون احراز نشود، از مدل بدست آمده، نمیتوان برای پیشبینی صحیح و با دقت مقدارهای متغیر پاسخ استفاده کرد و در عمل، مدل مناسبی به دست نیامده است.
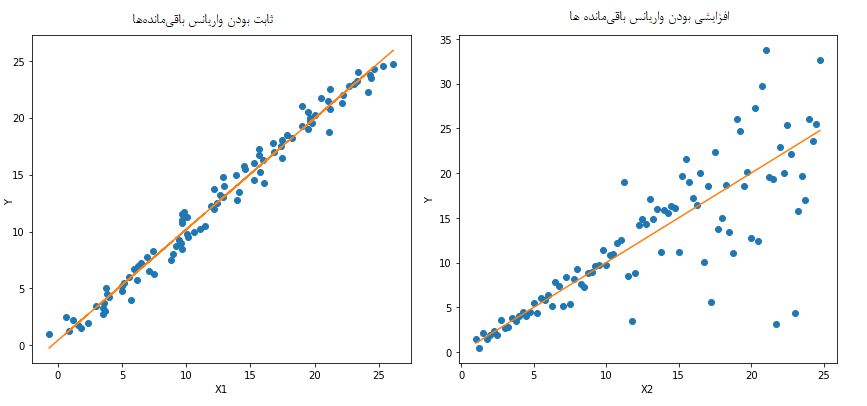
در تصویر زیر تفاوت بین حالتی که متغیر پاسخ دارای واریانس ثابت یا متغیر باشد به خوبی دیده میشود.
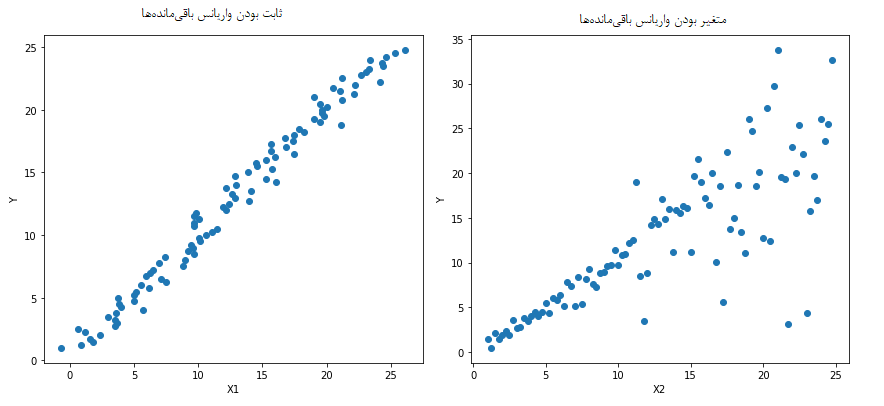
در مقام مقایسه با مدلهای غیرخطی در چنین حالتی، ممکن است کارایی چنین مدلهای از مدل خطی بسیار بهتر باشد. بنابراین وجود چنین شرطی از مهمترین شرطهای سنجش صحت مدل رگرسیونی است. در تصویر زیر خط رگرسیونی که برای دو حالت متفاوت از نظر ثابت یا متغیر بودن واریانس ایجاد شده با رنگ نارنجی دیده میشود. مشخص است هر چه واریانس افزایش مییابد، مقدار پیشبینی شده با واقعی تفاوت بیشتری پیدا میکند و در عمل برآورد متغیر پاسخ با چنین مدلی مناسب نخواهد بود.
رگرسیون چندکی میتواند راه حلی برای رفع چنین مشکلی باشد. بنابراین اگر شرط ثابت بودن واریانس یا نرمال بودن باقیماندهها (خطاها) در روشهای رگرسیونی محقق نشود، استفاده از رگرسیون چندکی مفید است.
در رگرسیون چندکی به جای برآورد یک خط به عنوان مقدار پیشبینی، از یک فاصله به عنوان برآورد فاصلهای استفاده میشود. بنابراین نتیجه اجرای رگرسیونی چندکی برای یک سری داده فرضی میتواند به صورت زیر باشد.
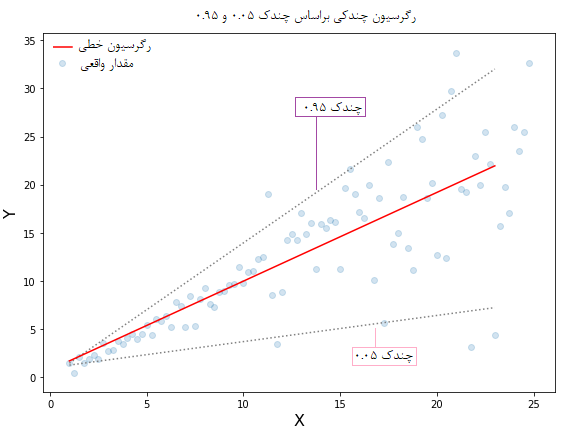
برای دسترسی به کدهای پایتون مربوط به محاسبات رگرسیون چندکی میتوانید به این لینک (+) مراجعه کنید.
شناخت تابع زیان چندکی
رگرسیون برمبنای چندکها، امکان برآورد چندکهای متغیر پاسخ را به شرط بعضی از مقدارهای متغیرهای مستقل (پیشگو) فراهم میسازد. به تعبیر دیگر میتوان تابع زیان چندکی را به عنوان نسخه توسعه یافته تابع زیان MAE در نظر گرفت. زیرا میدانیم که میانه، همان صدک ۵۰ ام است.
ایده اصلی در این تابع زیان، انتخاب مقداری برای از چندکها است که برمبنای آنها مقدار خطا، مثبت یا منفی میشود. تابع خطا چندکی، به خطاهایی که حاصل بیشبرآورد و یا کمبرآورد، هستند جریمههای (Penalty) مختلفی برحسب مقدار () نسبت میدهد. برای مثال اگر تابع زیان چندکی با جریمه ، به کار رود، جریمههای بزرگتری برای بیشبرآورد در نظر گرفته میشود و مقدارهای بیشبینی اکثرا کمتر از میانه خواهند بود.
رابطه مربوط به محاسبه تابع زیان چندکی به صورت زیر است:
مشخص است که اگر برابر با 0.25 باشد عبارت برابر با 0.75 است، در نتیجه وزن مربوط به بیشبرآوردها زیاد خواهد شد. در مقابل وزن مربوط به کمبرآوردها کاهش خواهد یافت. از آنجایی که هدف کمینهسازی تابع زیان است، مقدارهای متغیر پاسخ به مقدارهای کمتر از میانه تمایل پیدا خواهند کرد.
نکته: مقدار برای محاسبه تابع زیان چندکی لازم است. این مقدار در بین ۰ تا ۱ تغییر میکند. همانطور که دیده میشود این تابع زیان، به شکل میانگین وزنی محدب از خطاهای مثبت و منفی نوشته شده است.
نمودار زیر مقایسه تابع زیان چندکی را برای مقدارهای مختلف نشان میدهد. مشخص است که با افزایش این مقدار، شیب این تابع برای خطاهای منفی (کمبرازش) افزایش یافته و برای خطاهای مثبت (بیشبرازش) کاهش مییابد.
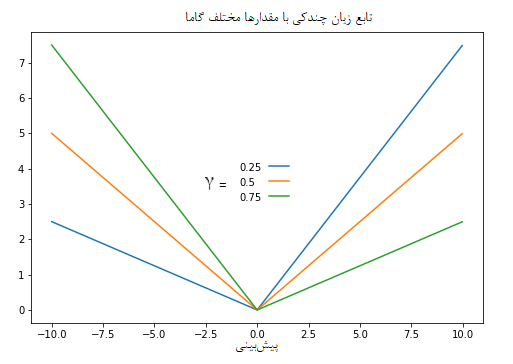
از این تابع زیان همچنین برای محاسبه فاصلههای پیشبینی در شبکه عصبی و مدلهای درخت تصمیم استفاده میشود. در مثال زیر، پیادهسازی مدل رگرسیونی «درخت تقویت شده توسط گرادیان» (Gradient Boosted Tree) با استفاده از کتابخانه SKlearn انجام شده است.
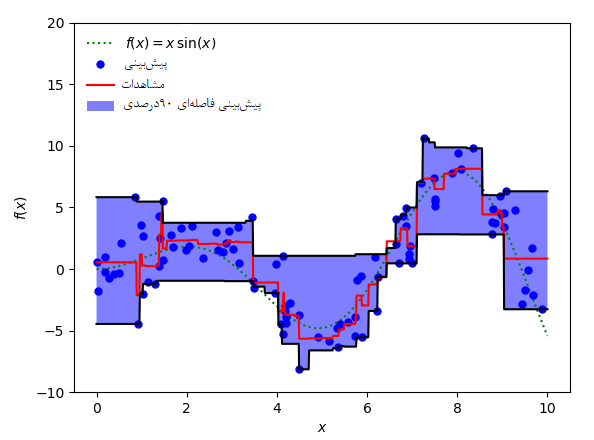
در تصویر بالا برای تابع ، پیشبینی فاصلهای ۹۰ درصدی براساس تابع زیان چندکی انجام شده است. کران بالا براساس و کران پایین با محاسبه شده است. کد پایتون برای به ترسیم این نمودار در زیر دیده میشود:
ناحیههایی که با رنگ آبی در نمودار مشخص شدهاند، حدود اطمینان برای متغیر پاسخ براساس رگرسیون چندکی هستند. خطوط قرمز نیز مقدار پیشبینی توسط رگرسیون ساده را نشان میدهند. نقطهچینها نیز مقدار تابع اصلی را ترسیم کردهاند. نقاط توپری که با رنگ آبی تیره در نمودار قرار دارند همان مشاهدات هستند که توسط اضافه کردن مقدار تابع با خطای تصادفی در شبیهسازی تولید شدهاند.
تابع اصلی در این کد مربوط به GradientBoostingRegressor است که محاسبات پیشبینی برای متغیر وابسته را براساس مشاهدات و رگرسیون چندکی انجام میدهد. در این دستور به کمک پارامتر تابع زیان چندکی برای برآورد انتخاب شده است. همینطور از آنجایی که پارامتر alpha برابر با 0.95 است، در محاسبات مربوط به رگرسیون چندکی مقدار در نظر گرفته شده.
مقایسه توابع زیان و بررسی نهایی
اگر میخواهید نمودار مربوط به هر یک از توابع زیان را با یکدیگر مقایسه کنید، تصویر زیر کمک مناسبی است.
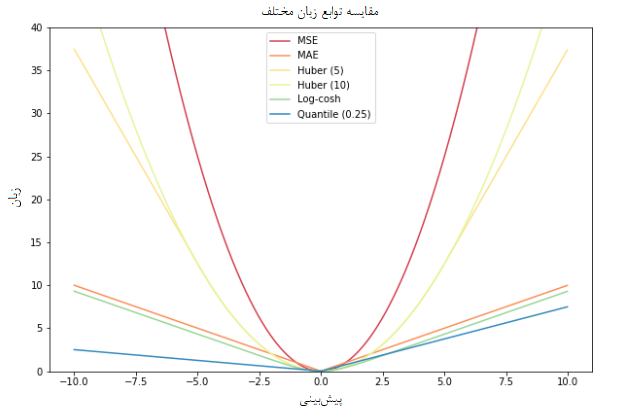
مقایسه توابع زیان در حالتهای مختلف در لینک (+) به خوبی توضیح داده شده است. ولی در ادامه برای مقایسه بین تابع زیانهایی که در بالا به آنها اشاره شد، به بررسی تابع میپردازیم. به این ترتیب براساس دادههای شبیهسازی شده روی این تابع، پیشبینی مقدار تابع را به کمک توابع زیان یاد شده انجام می دهیم.
این تابع در حقیقت با رابطه محاسبه میشود. در شبیهسازی، به این تابع دو گونه نوفه (Noise) اضافه شده است. ابتدا نوفه با توزیع نرمال با میانگین صفر و واریانس اضافه شده () سپس نوفه دیگری با توزیع برنولی با پارامتر p با آن جمع شده است ().
در تصاویر زیر نتایج مربوط به خطای رگرسیون ماشین تقویت شده با گرادیان (Gradient Boosted Machine) یا GBM به ازاء توابع زیان مختلف ترسیم شده است.
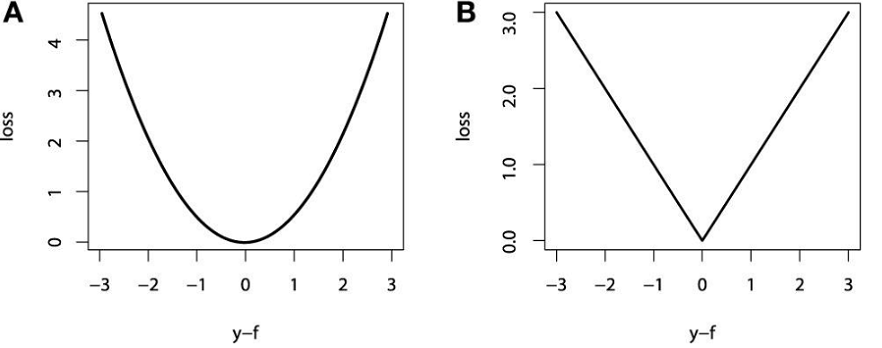
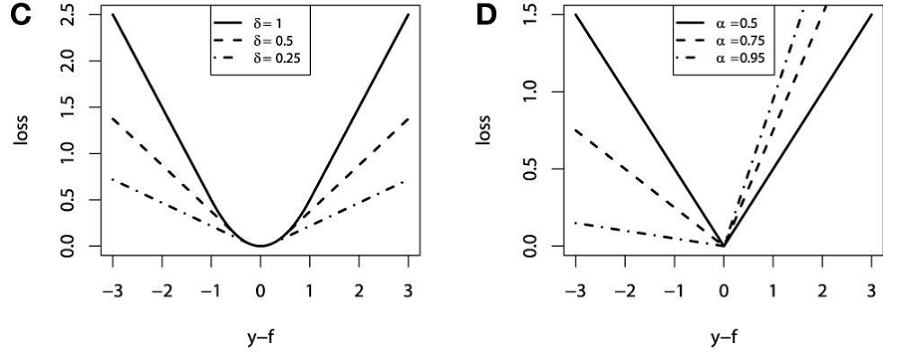
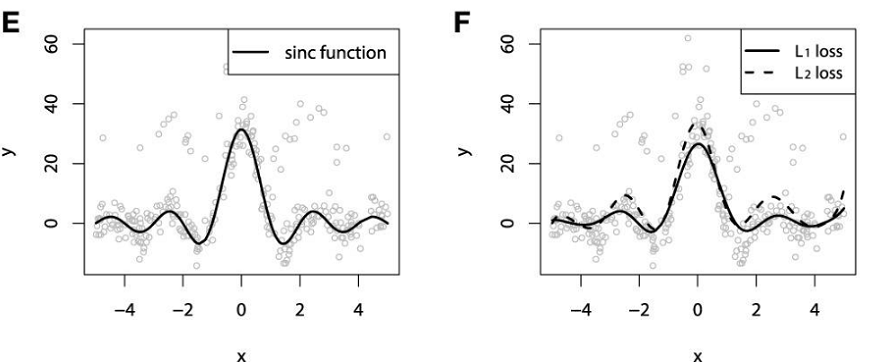
در تصویر E نیز نمودار تابع Sinc دیده میشود. همچنین نقاط روی نمودار، مربوط به نوفههایی است که به این تابع اضافه شده است. این نقاط کل مشاهدات را تشکیل میدهند.
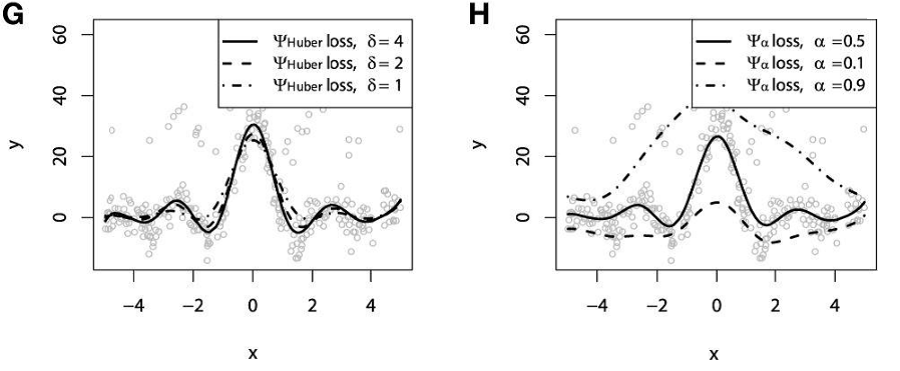
در تصویرهای F تا H با استفاده از روش GBM مقدارهای متغیر پاسخ، پیشبینی و نمایش داده شده و در تصویر F نیز کار نتایج مربوط به پیشبینی مقدار متغیر پاسخ با استفاده از تابع زیان MSE و MAE محاسبه و ترسیم شده است. در تصویرهای G و H نیز به ترتیب براساس تابع زیان هوبر و تابع زیان چندکی عمل پیشبینی صورت گرفته و نمودارهای مربوطه نمایش داده شدهاند.
نکته: لازم به ذکر است که پارامترها در نمودار G برابر با در نمودار H نیز برابر با هستند.
نتایج حاصل از شبیهسازی
با توجه به نمودارها میتوان به نتایج زیر رسید:
- با مشاهده نمودار F، دیده میشود که نتایج پیشبینی براساس تابع زیان MAE بهتر از MSE هستند و کمتر نسبت به نوفههای اعمال شده تحت تاثیر قرار گرفتهاند. در حالیکه استفاده از تابع زیان MSE باعث شده کمی اریبی (Bias) در نتایج بوجود آید.
- مقایسه نمودارهای ترسیم شده در تصویر G، نشان میدهد که تغییر پارامتر تابع زیان هوبر تاثیر کمی در بهبود پیشبینیها دارد.
- در تصویر H، برآورد فاصلهای مناسبی براساس سطح اطمینان مورد نظر صورت گرفته است. با انتخاب مقدار 0.5 برای (البته در نمودار با علامت مشخص شده است) منحنی ترسیم شده با تابع sinc بیشتر از بقیه مقادیر، مطابقت دارد.
- مجموعه آموزشهای مرتبط با یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای داده کاوی یا Data Mining در متلب
- مجموعه آموزشهای مدل سازی، برازش و تخمین
- آموزش همبستگی و رگرسیون خطی در SPSS
- آموزش انتخاب ویژگی یا Feature Selection
- فاصله اطمینان (Confidence Interval) — به زبان ساده
- تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
- الگوریتم عامل دورافتاده محلی (Local Outlier Factor) جهت شناسایی داده های پرت — به زبان ساده
^^













سلام
ممنون از لطف و اموزش کامل شما.
امکان داره در مورد توابع زیان مربوط به الگوریتمهای دستهبندی (Classification) هم توضیح بدید؟