الگوریتم شمارش اعداد اول در جاوا اسکریپت — از صفر تا صد

پیش از آن که در مورد شیوه نوشتن الگوریتم شمارش اعداد اول در جاوا اسکریپت صحبت کنیم، بهتر است توضیح کوتاهی در مورد خود اعداد اول بدهیم. اعداد اول اعدادی بزرگ‌تر از یک هستند که تنها بر خودشان و عدد یک بخش‌پذیر هستند. شما احتمالاً در طول دوران تحصیل با مفهوم اعداد اول آشنا شده‌اید، اما شاید ندانید کاربرد این اعداد چیست. یکی از کاربردهای اعداد اول به خصوص اعداد اول بسیار بزرگ، در رمزنگاری است. در این مقاله قصد داریم به بررسی یک مسئله در مورد اعداد اول بپردازیم.

در مسئله فوق خواسته شده است که تعداد اعداد اول کمتر از عدد غیر منفی n محاسبه شود. چندین روش برای حل مسئله فوق وجود دارد. ما در این نوشته تلاش می‌کنیم از غربال «اراتوستن» (Eratosthenes) برای حل آن کمک بگیریم.

اراتوستن (Eratosthenes) یک ریاضیدان، فیلسوف، تاریخدان، ورزشکار، شاعر و مخترع یونانی است که در سال 276 پیش از میلاد به دنیا آمده است. بخش عمده شهرت اراتوستن به خاطر محاسبه محیط کره زمین بر مبنای مشاهده سایه اجسام در شهرهای مختلف در روز یکسانی از سال بوده است. گفته می‌شود که واژه جغرافیا را وی ابداع کرده است. شاگردان وی در اسکندریه مصر او را Pentathlos به نام پهلوانی که پنج رویداد مختلف را به پایان برده است نامیده‌اند.

غربال اراتوستن

وی یک الگوریتم عالی برای یافتن همه اعداد اول بین 1 و هر عدد مفروض ابداع کرده است. برای مثال عدد 120 را در نظر بگیرید.

فیلم آموزش جاوا اسکریپت JavaScript در فرادرس

کلیک کنید

1. ابتدا همه اعداد بین 1 و 120 را بنویسید.
2. از عدد 2 شروع می‌کنیم و همه اعداد بزرگ‌تر را که مضربی از 2 باشد، حذف می‌کنیم.
3. عدد بعدی که حذف نشده را پیدا می‌کنیم، آن را به لیست اعداد اول اضافه می‌کنیم و گام 1 را تکرار می‌کنیم.

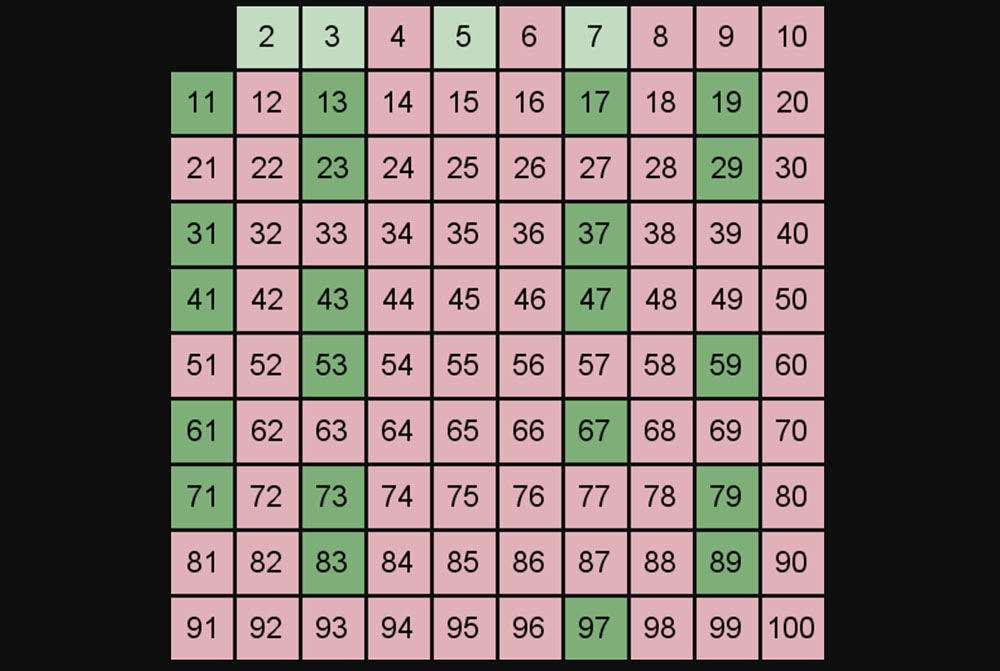
در تصویر زیر طرز کار این غربال را می‌بینید.

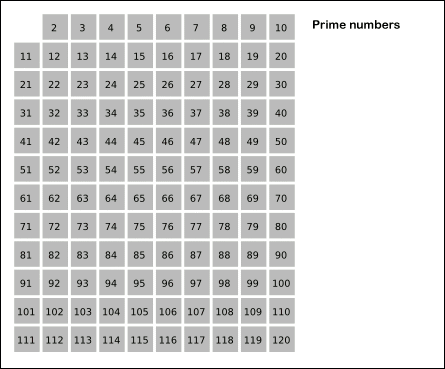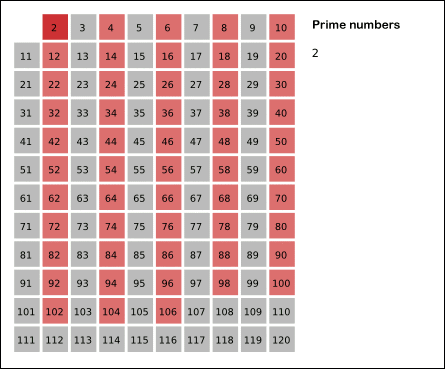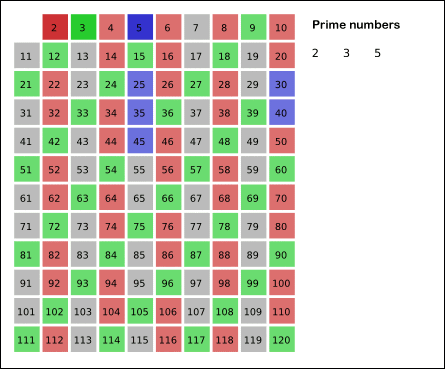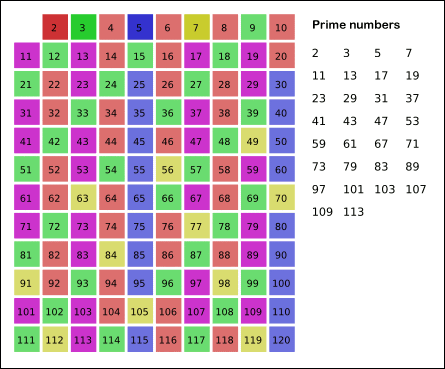
نکته: هر بار که عدد n را پیدا می‌کنیم که حذف نشده است، نخستین مضرب آن عدد که حذف نشده باشد عدد n*n خواهد بود.

زمانی که عدد n را پیدا کنیم که n*n بزرگ‌تر از عدد مورد نظر ما در لیست باشد، به پایان کار خود رسیده‌ایم.

کدنویسی غربال اراتوستن

در این بخش مراحل مختلف برای کدنویسی غربال اراتوستن در جاوا اسکریپت را بررسی می‌کنیم.

گام 1: نوشتن همه اعداد تا n

فرض کنید n=10 است. به یاد داشته باشید که ما به دنبال تعداد اعداد اول کمتر از 10 هستیم و از این رو در 9 متوقف می‌شویم.

این کار با استفاده از متد ()key جاوا اسکریپت امکان‌پذیر است. بر مبنای مستندات جاوا اسکریپت می‌دانیم که متد ()key یک شیء جدید Array Iterator بازگشت می‌دهد که شامل کلیدهایی برای هر اندیس در آرایه است.

1let nums = [...Array(n).keys()]
2=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

شاید کنجکاو باشید که چرا کار خود را از صفر آغاز کردیم، در حالی که باید از 2 آغاز می‌کردیم. چون در گام بعدی می‌خواهیم روی این اعداد حلقه تکرار تعریف کنیم و می‌خواهیم اندیسی که برای حلقه تکرار استفاده می‌کنیم با مقدار آن اندیس برابر باشد.

گام 2: آغاز از عدد 2 و حذف همه مضارب بعدی 2

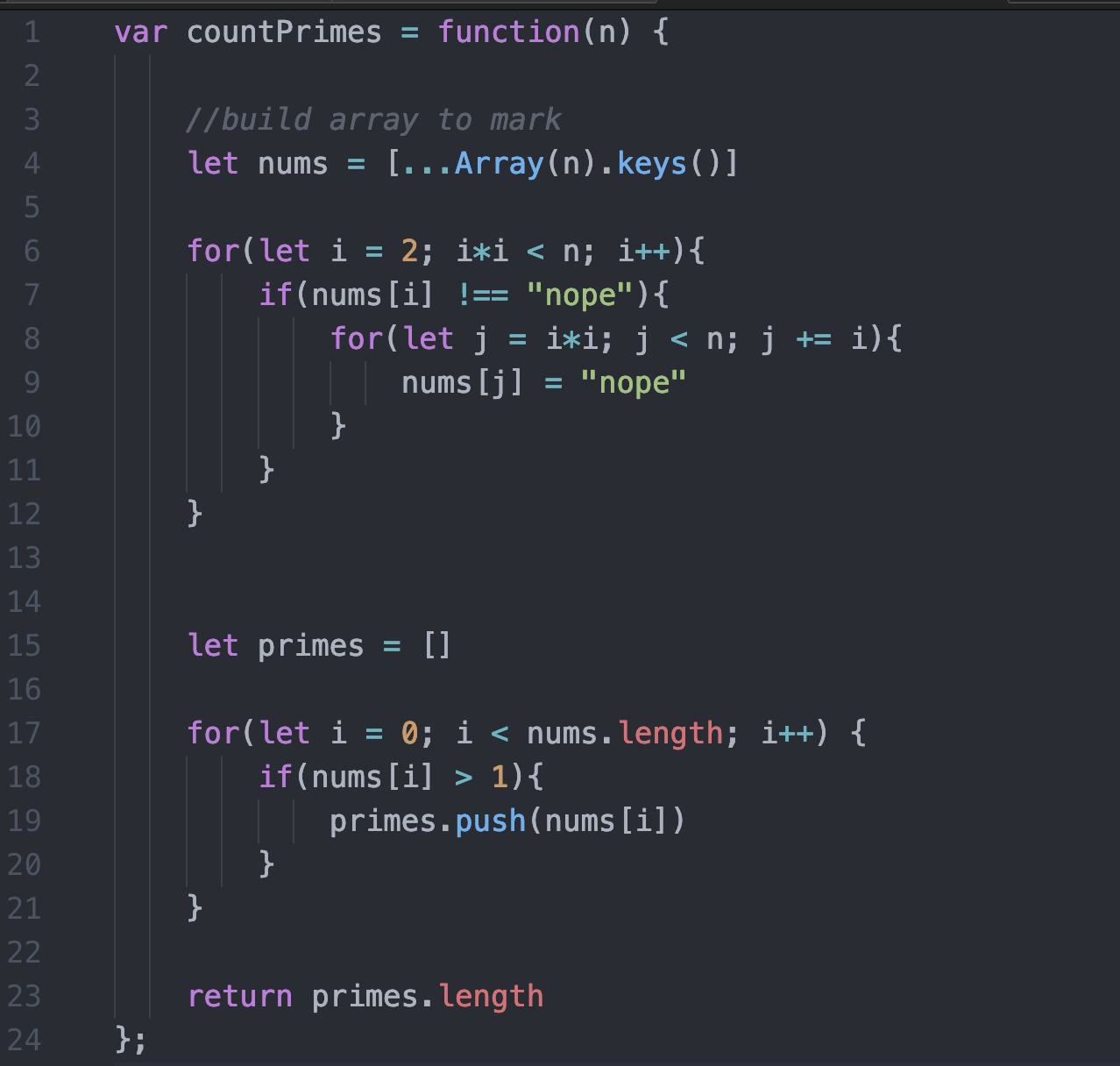
در کد به جای حذف اعداد، می‌توانیم مقادیرشان را تغییر دهیم تا بهتر ببینیم چه اتفاقاتی رخ می‌دهد. زمانی که عددی حذف می‌شود، می‌توانیم مقدار رشته‌ای آن را به nope تغییر دهیم و بدین ترتیب معنی nope این است که عدد غیر اول است.

1let n = 10
2let nums = [...Array(n).keys()]
3=> [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]
4for(let i = 2; i*i < n; i++){
5        if(nums[i] !== "nope"){
6            for(let j = i*i; j < n; j += i){
7                nums[j] = "nope"
8            }
9        }        
10    }

در این بخش کد فوق را خط به خط توضیح می‌دهیم.

در حلقه for کد زیر را داریم:

1let i =2;

به طور معمول هنگامی که روی یک آرایه می‌چرخیم، می‌خواهیم کل آرایه را بررسی کنیم و از اندیس 0 آغاز می‌کنیم. در این مورد می‌خواهیم از عدد 2 آغاز کنیم و لذا از اندیس 2 شروع کرده‌ایم:

1i*i < n;

هنگامی که عدد n را پیدا کنیم که n*n بزرگ‌تر از آخرین عدد در آرایه باشد، دیگر عددی برای حذف کردن نخواهیم داشت. بنابراین می‌توانیم حلقه را متوقف کنیم.

حذف اعداد

کد حذف اعداد به صورت زیر است:

1if(nums[i]!== “nope”)

به خاطر داشته باشید که ما تصمیم گرفتیم اعداد را به صوت تغییر مقدارشان به nope حذف کنیم. در خط فوق به عدد nums[i] نگاه می‌کنیم تا ببینیم آیا حذف شده یا نه. اگر حذف نشده باشد، ادامه می‌دهیم.

1for(let j = i*i; j < n; j += i){
2                nums[j] = "nope"
3            }

در کد فوق فرض کنید i = 2 باشد. یک تکرارکننده جدید به نام j با مقدر اولیه i*i تعیین می‌کنیم. در نخستین تکرار حلقه عنصر موجود در num[j] را حذف می‌کنیم، یعنی مقدار آن را nope تنظیم می‌کنیم. سپس j را دو واحد افزایش می‌دهیم و با تعیین آن عدد به صورت nope آن را نیز حذف می‌کنیم. این کار را تا زمانی که به انتهای آرایه برسیم تکرار می‌کنیم.

بنابراین زمانی که i=2 باشد، نخستین بار که در حلقه وارد می‌شویم، آرایه مانند زیر خواهد بود:

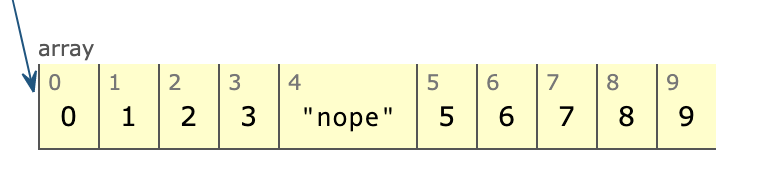
بار دوم به شکل زیر درمی‌آید:

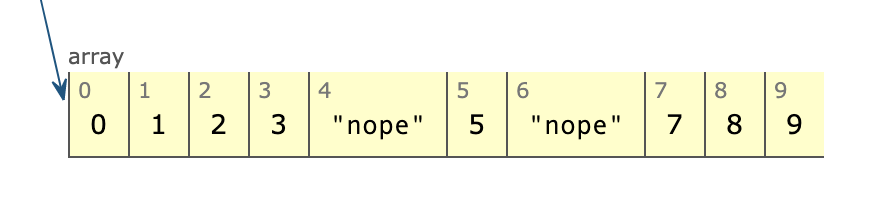
و بار سوم به صورت زیر خواهد بود:

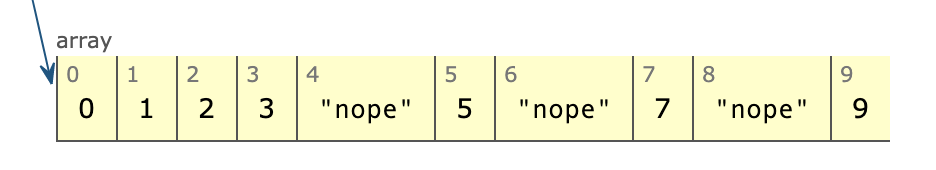
دفعه بعد که افزایش یابد، برابر با 10 خواهد بود که خارج از دامنه حلقه است. بنابراین به حلقه i بعدی می‌رویم که این بار i=3 است. مقدار j را روی مقدار اولیه i^2 یعنی 9 تعیین می‌کنیم و آن عدد را حذف می‌کنیم.

سپس حلقه j همه مضارب بعدی را حذف می‌کند، اما مضرب بعدی 12 است که خارج از آرایه است و از این رو به حلقه i بعدی می‌رویم. عدد بعدی 5 است. دوباره به حلقه j می‌رسیم و تلاش می‌کنیم تا i*i یعنی 25 را حذف کنیم که چنان که می‌بینید، خارج از دامنه آرایه است.

اگر به حلقه i بازگردیم به عدد i=7 رسیده‌ایم و با بررسی i*i می‌بینیم که عدد 49 خارج از حلقه قرار دارد. بنابراین به انتهای آرایه رسیده‌ایم.

گام 3: تبدیل آرایه اعداد به لیستی از اعداد اول

اینک باید آرایه ما به صورت زیر در آمده باشد:

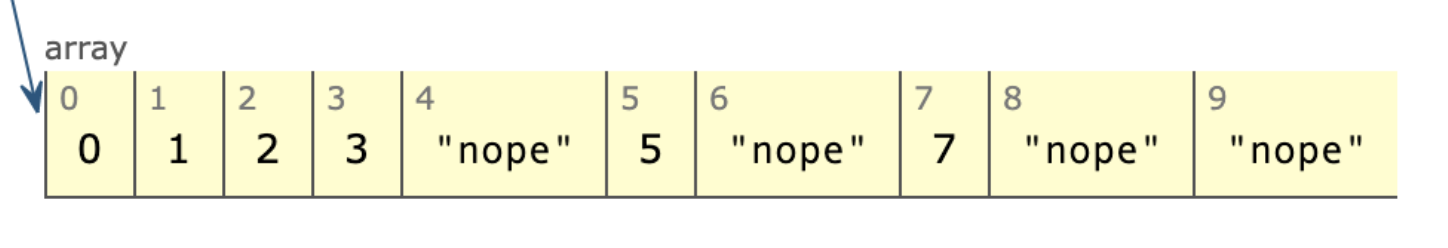
آن را به صورت زیر درمی‌آوریم:

[2,3,5,7]

به این منظور می‌توانیم روی آرایه حلقه‌ای تعریف کنیم و هر عنصری که بزرگ‌تر از 1 است را برداریم:

1for(let i = 0; i < nums.length; i++) {
2        if(nums[i] > 1){
3            primes.push(nums[i])
4        }
5    }

گام 4: بازگشت طول آرایه

در صورت مسئله آمده بود که باید تعداد اعداد اول بین 1 و n را بازگشت دهیم و نه خود اعداد را. بنابراین از متد ()length. در جاوا اسکریپت استفاده می‌کنیم:

1return primes.length()

اینک در مجموع کدهای زیر را داریم:

افزایش سرعت الگوریتم

بر اساس گزارش LeetCode، کد فوق برای اجرا به 200 میلی‌ثانیه زمان نیاز دارید که کاملاً کند است. با تغییر دادن روش حذف اعداد می‌توانیم سرعت اجرای الگوریتم را افزایش دهیم. بدین ترتیب اعداد حذف شده را به عدد 1 تغییر می‌دهیم.

اینک می‌بینیم که کد سریع‌تر اجرا می‌شود:

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های JavaScript (جاوا اسکریپت)
• آموزش JavaScript ES6 (جاوا اسکریپت)
• مجموعه آموزش‌های برنامه‌‌نویسی
• جاوا اسکریپت چیست؟ — به زبان ساده
• مثلث پاسکال در جاوا اسکریپت — به زبان ساده

==