مقایسه کسرها – آموزش ریاضی به زبان ساده + مثال و تمرین
در آموزشهای پیشین مجله فرادرس، با کسرها و جمع و ضرب و تقسیم آنها آشنا شدیم. در این آموزش، با روش مقایسه کسرها آشنا میشویم و مثالهای متنوعی را حل خواهیم کرد. مقایسه کسرها به معنای تعیین کسر بزرگتر و کوچکتر بین دو یا چند کسر است. از آنجا که کسرها از دو بخش صورت و مخرج تشکیل شدهاند، میتوان آنها را با استفاده از مجموعهای از قوانین مقایسه کرد. در ادامه، درباره این مو درباره مقایسه کسرها بیشتر بیاموزیم.


مقایسه کسر چیست؟
منظور از مقایسه کسرها، در واقع، این موضوع است که تعیین کنیم که از بین دو یا چند کسر کدمیک بزرگتر و کدامیک کوچکتر است و کدام کسرها با هم برابر هستند. مقایسه کسرها شامل مجموعهای از قوانین مربوط به صورت و مخرج است. همانطور که گفتیم، هنگامی که دو کسر با هم مقایسه میشوند، درواقع، کسر بزرگتر و کوچکتر را تعیین میکنیم. البته ممکن است دو کسر مساوی باشند.
در زندگی روزمره بسیار پیش میآید که کسرها را مقایسه کنیم. به عنوان مثال، زمانی که نیاز به مقایسه نسبت مواد در حین دستور غذایی یا مقایسه نمرات امتحانات و غیره داریم، باید کسرها را با هم مقایسه کنیم.
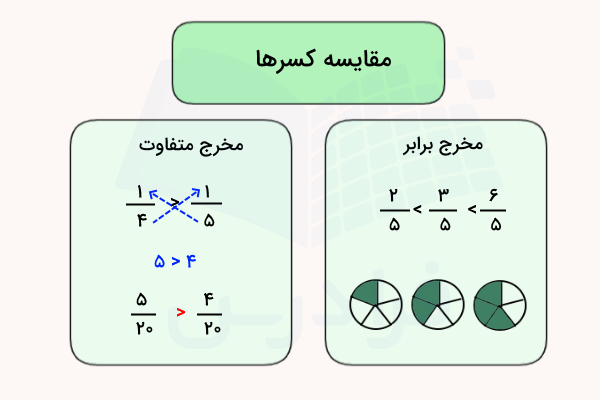
در ادامه، روشهای مختلف مقایسه کسرها را مرور میکنیم. برای مقایسه کسرها راههای متفاوتی وجود دارد که در همه آنها صورتها و مخرجهای دو کسر دخیل هستند. روشهای مقایسه کسرها معمولاً به دستههایی تقسیم میشوند که در ادامه هریک را توضیح خواهیم داد.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
کسر چیست؟
قبل از بررسی مفهوم مقایسه کسرها، بهتر است مفاهیم مربوط به کسرها و ویژگیهای آنها را مرور کنیم. کسر یک نسبت و جزئی از یک کل است و از دو قسمت صورت و مخرج تشکیل شده است. در واقع، کسرها اعدادی هستند که با تقسیم تعریف میشوند و برای نشان دادن هر تعداد از قسمتهای مساوی یک چیز بهکار میروند. آنها اعدادی حقیقی بهفرم هستند که در آنها و اعدادی صحیحاند. عدد صورت کسر و عدد مخرج کسر نامیده میشود. بنابراین، در کسر عدد ۲ صورت و عدد ۳ مخرج کسر است و آن را «دو سوم» میخوانیم.
در گامهای زیر میتوان برای کسر یک شکل رسم کرد.
۱. ابتدا کل شکل که ۱ واحد است را رسم میکنیم.

۲. این یک واحد را طبق مخرج (عدد ۳) به سه قسمت مساوی تقسیم میکنیم (یعنی ).
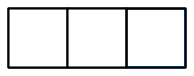
۳. بهاندازه عدد صورت، یعنی ۲، را رنگ میزنیم و به کسر میرسیم.
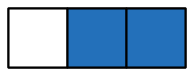
کسرها را میتوان به سه دسته تقسیم کرد:
- کسرهای سره که در آنها صورت از مخرج کوچکتر است، مثل
- کسرهای ناسره که در آنها صورت کسر از مخرج آن بزرگتر است، مانند .
- عدد مخلوط که بخشی از آن یک عدد صحیح و بخشی از آن یک کسر است. بخش کسری این عدد همواره یک کسر سره است.
برای آشنایی با اعداد مخلوط، میتوانید به آموزش «عدد مخلوط چیست و به چه اعدادی می گویند؟ — به زبان ساده» از مجله فرادرس مراجعه کنید.
مقایسه کسرها با مخرج مساوی
در مقایسه کسرها با مخرج یکسان، تعیین کسر بزرگتر یا کوچکتر یا مساوی آسانتر است. پس از بررسی یکسان بودن مخرجها، میتوانیم بهسادگی صورتهای آنها را مقایسه کنیم. کسری با صورت بزرگتر، بزرگتر است. همچنین، وقتی مخرجهای دو کسر برابر باشند، اگر صورت یکی کوچکتر از دیگری باشد، آن کسر کوچکتر است. اگر هم صورت و مخرج دو کسر مساوی باشند، کسرها نیز برابر هستند.
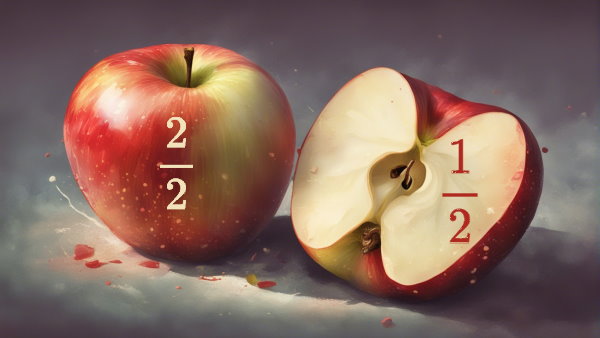
به عنوان مثال، دو کسر و را با هم مقایسه میکنیم.
- گام ۱: مخرج کسرهای دادهشده را مشاهده میکنیم. میبینیم که مخرج هر دو کسر برابر با ۱۷ است. بنابراین، مخرجها مساوی هستند و برای مقایسه باید سراغ صورتها برویم.
- گام ۲: اکنون، صورتها را با هم مقایسه میکنیم. میبینیم که ببینیم که از بزرگتر است. یعنی .
- گام ۳: کسری با صورت بزرگتر کسر بزرگتر است. بنابراین، .
مقایسه کسرها با مخرج متفاوت
برای مقایسه کسرها با مخرجهای غیرمشابه، باید آنها را به کسرهایی با مخرج مساوی تبدیل کنیم. برای این کار، باید مخرج مشترک بگیریم. برای گرفتن مخرج مشترک نیز باید کوچکترین مضرب مشترک یا ک.م.م. دو مخرج را پیدا کنیم. وقتی مخرجها را برابر کردیم، میتوانیم کسرها را بهراحتی با هم مقایسه کنیم.
در این آموزش، روش برابر کردن دو مخرج را بیان میکنیم. اگر میخواهید با مخرج مشترک گرفتن و نحوه بهدست آوردن ک.م.م. بیشتر آشنا شوید، به آموزشهای «مخرج مشترک چیست، چگونه مخرج مشترک بگیریم؟ — به زبان ساده» و «ک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» از مجله فرادرس مراجعه کنید.
بهعنوان مثال، دو کسر و را با هم مقایسه میکنیم. بدین منظور، گامهای زیر را طی میکنیم.
گام ۱: ابتدا مخرج کسرهای دادهشده را مشاهده میکنیم. میبینیم که این دو مخرج اعداد و هستند و برابر نیز نیستند و متفاوتاند. بنابراین، باید دو کسر را بهگونهای بازنویسی کنیم که مخرج آنها برابر شود. بدین منظور، باید ک.م.م. دو عدد را پیدا کنیم.
گام ۲: اکنون ک.م.م. را پیدا میکنیم. ک. م. م. دو عدد است که کوچکترین مضرب مشترک دو عدد است. حال باید صورت و مخرج کسر را در عددهای مناسبی ضرب کنیم تا مخرجها برابر با ک.م.م. و یکسان شوند.
ابتدا، صورت و مخرج کسر نخست را در عدد ۵ ضرب میکنیم. بنابراین، خواهیم داشت:
اکنون، صورت و مخرج کسر دوم را در ۲ ضرب میکنیم:
گام ۳: اکنون دو کسر و داریم که مخرجهای آنها برابر است. از آنجا که مخرجها یکسان هستند، صورتها را با هم مقایسه میکنیم و میبینیم که بزرگتر از است.
گام ۴: کسری با صورت بزرگتر، کسر بزرگتر است، یعنی بزرگتر از است. بنابراین، میتوان چنین نتیجه گرفت که بزرگتر از است و اینگونه نوشت:
مقایسه کسرها با صورت مساوی
لازم به ذکر است که اگر مخرجها متفاوت باشند و صورتها یکسان باشند، بهراحتی میتوان با مشاهده مخرجها کسرها را با هم مقایسه کرد. در اینجا با چیزی عکس حالت برابر بودن مخرجها مواجه هستیم. بدین شکل که کسری بزرگتر است که مخرج آن کوچکتر باشد. همچنین، کسری کوچکتر است که مخرج آن بزرگتر باشد. برای مثال، بزرگتر از است.
مقایسه کسرها با شکل
برای تجسم کسرهای بزرگتر و کوچکتر میتوانیم از روشها و مدلهای گرافیکی مختلف استفاده کنیم. به تصویر زیر توجه کنید که شکلهای الف و ب را نشان میدهد که دو کسر را نمایش دادهاند. بهراحتی میتوانیم بگوییم که است، زیرا ناحیه رنگ شده بزرگتری نسبت به دارد. توجه داشته باشید که کسر کوچکتر مساحت کمتری از همان شکل را اشغال میکند. نکتهای که در اینجا باید مورد توجه قرار گیرد این است که اندازه شکلهای الف و ب باید دقیقاً یکسان باشد تا مقایسه قسمتهای رنگ شده معتبر باشد.
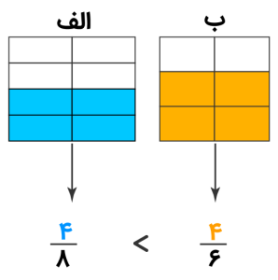
اگر به دو کسر دقت کنیم، صورت آنها برابر است. بنابراین، مطابق آنچه در بخش مقایسه کسرها با صورت مساوی گفتیم، چون مخرج کسر بزرگتر است، بنابراین این کسر کوچکتر است.
مقایسه دو کسر منفی
مقایسه کسرهای منفی کار آسانی است. کافی است بدانیم که چگونه دو کسر مثبت با هم مقایسه میشوند. همانطور که میدانیم، عدد بزرگتر از است. بنابراین، اگر دو عدد منفی را مقایسه کنیم، آن عددی بزرگتر است که قدرمطلق آن کوچکتر باشد. اعداد کسری نیز از این قاعده مستثنا نیستند.
برای مثال، فرض کنید میخواهیم دو کسر منفی و را با هم مقایسه کنیم. در گامهای زیر این موضوع را شرح میدهیم.
گام ۱: ابتدا قدرمطلق دو کسر را مینویسیم. قدرمطلق دو عدد و است.
گام ۲: اکنون قدرمطلق دو کسر را با هم مقایسه میکنیم. با توجه به اینکه دو صورت برابر هستند، باید مخرجها را مقایسه کنیم. با توجه به اینکه بزرگتر از است، پس نتیجه میگیریم که کوچکتر از است یا .
گام ۳: رابطهای که برای قدرمطلق دو عدد به آن رسیدیم، برای خود آن دو عدد منفی برعکس است. یعنی اگر کوچکتر از باشد، آنگاه بزرگتر از است.
گام ۴: بنابراین، نتیجه مقایسه .
مقایسه دو کسر با محور
برای مقایسه کسرها روی محور، کافی است آنها را روی محور اعداد رسم کنیم، سپس ببینیم وضعیت آنها نسبت به هم چگونه است. برای مثال، فرض کنید میخواهیم دو عدد کسری و را با هم مقایسه کنیم. برای این منظور، کافی است دو عدد را روی محور مشخص کنیم و ببینیم از نظر ظاهری کدامیک بزرگتر است. همانطور که در شکل زیر میبینیم، بزرگتر است و اگر آنها را روی یک محور رسم کنیم، این نقطه در سمت راست قرار میگیرد که نشاندهنده بزرگتر بودن آن است.
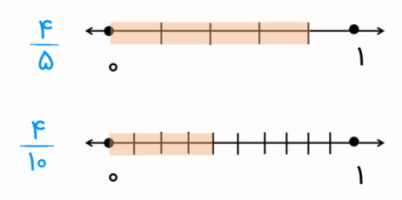
روش اعشاری مقایسه کسرها
در این روش مقادیر اعشاری کسرها را با هم مقایسه میکنیم. برای این کار، صورت بر مخرج تقسیم میشود و عدد کسری به عدد اعشاری تبدیل میشود. سپس، مقادیر اعشاری با هم مقایسه میشوند. به عنوان مثال، فرض کنید میخواهیم دو عدد و را با هم مقایسه کنیم. بدین منظور، گامهای زیر را طی میکنیم.
گام ۱: ابتدا دو کسر را به اعشار تبدیل میکنیم. برای آشنایی بیشتر با تبدیل کسر به اعشار، به آموزش «تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال» از مجله فرادرس مراجعه کنید. کسر معادل عدد اعشاری است. همچنین، کسر معادل عدد اعشاری است.
گام ۲: اعداد اعشاری را مقایسه میکنیم. میبینیم که است.
گام ۳: کسری که عدد اعشاری معادلش از عدد اعشاری معادل کسر دیگر بزرگتر باشد، بزرگتر است. بنابراین، میتوان نتیجه گرفت که .
مقایسه کسرها با ضرب متقاطع
برای مقایسه کسرها با استفاده از ضرب متقاطع، صورت یک کسر را در مخرج کسر دیگر ضرب میکنیم. این روش را با کمک یک مثال توضیح میدهیم. فرض کنید میخواهیم دو کسر و را مقایسه کنیم. به شکل زیر توجه کنید که این موضوع را بهتر توضیح می دهد.
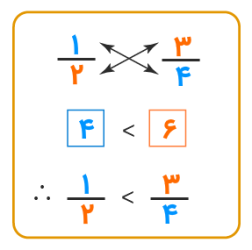
گام ۱: وقتی کسرهای دادهشده را بهصورت متقاطع ضرب میکنیم تا آنها را با هم مقایسه کنیم، باید در نظر داشته باشیم که اگر صورت کسر اول را در مخرج کسر دوم ضرب میکنیم، باید حاصلضرب را در کنار کسر اول بنویسیم. در اینجا ، و ما را در کنار کسر اول مینویسیم
گام ۲: به همین ترتیب، هنگامی که صورت کسر دوم را در مخرج کسر اول ضرب میکنیم، باید حاصلضرب را در کنار کسر دوم بنویسیم. در اینجا ، و را نزدیک کسر دوم مینویسیم.
گام ۳: اکنون، دو حاصلضرب و را با هم مقایسه میکنیم. از آنجا که ، کسرهای مربوطه را میتوان بهراحتی مقایسه کرد، یعنی . بنابراین، .
مثالهای مقایسه کسرها
در این بخش، مثالهایی را از مقایسه کسرها بررسی میکنیم.
مثال اول
دو کسر و را مقایسه کنید.
جواب: میبینیم که مخرج دو کسر با هم برابر است. بنابراین، برای مقایسه دو کسر کافی است صورتها را با هم مقایسه کنیم. چون کوچکتر از است، بنابراین، کسر کوچکتر از است و میتوان نوشت:
مثال دوم
دو عدد و را مقایسه کنید.
جواب: ابتدا دو عدد مخلوط را به کسر تبدیل میکنیم:
اکنون دو کسر و را باید مقایسه کنیم. میبینیم که دو کسر صورت یکسانی دارند. بنابراین، باید مخرجهای آنها را مقایسه کنیم. چون مخرج کسر بزرگتر است، پس این کسر کوچکتر از کسر خواهد بود، یعنی . در نتیجه، میتوان نوشت:

مثال سوم
دو کسر و را مقایسه کنید.
جواب: عدد منفی همواره از عدد مثبت کوچکتر است و نیازی به کار اضافهای نیست. بنابراین، میتوان نوشت:
مثال چهارم
دو کسر و را مقایسه کنید.
جواب: همانطور که میبینیم، نه مخرجها و نه صورتها با هم مساوی هستند. بنابراین، باید کاری کنیم که مخرج دو کسر برابر شود تا مقایسه را بهآسانی انجام دهیم. بدین منظور، بین دو کسر مخرج مشترک میگیریم. ب.م.م. دو عدد و ، عدد است. بنابراین، بهشکل زیر دو کسر را بازنویسی میکنیم:
بنابراین، دو کسر و را داریم که مخرج آنها برابر است. اکنون کافی است صورت کسرها را با هم مقایسه کنیم. میبینیم کوچکتر از است. پس میتوان نوشت: . در نتیجه، خواهیم داشت:
آزمون سنجش یادگیری مقایسه کسرها
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث مقایسه کسرها را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
تمرین و آزمون
کدامیک از گزینههای زیر در مقایسه کسرهای و درست است؟
بزرگتر از است.
و برابر هستند.
بزرگتر از است.
امکان مقایسه این دو کسر وجود ندارد.
برای مقایسه کسرها، ابتدا به علامت (مثبت و منفی بودن) و سپس به مخرج آنها توجه میکنیم. اگر کسرها، دارای علامت مشابه و مخرج مشترک باشند، مقایسه آنها توسط مقادیر صورت انجام میگیرد. در این سوال، دو کسر مثبت با مخرج ۱۱ داریم. از اینرو، کسری بزرگتر خواهد بود که صورت بزرگتری داشته باشد. بنابراین، بزرگتر از است.
کدامیک از گزینههای زیر صحیح است؟
برای مقایسه کسرها، به علامت و مخرج آنها دقت میکنیم. مخرج تمام کسرها برابر با عدد ۴۵ است اما برخی از کسرها علامت مثبت و برخی دیگر علامت منفی دارند. گزینه اول، مقایسه دو کسر با مخرج مشترک و علامت منفی را نمایش میدهد. در صورت منفی بودن دو کسر با مخرج مشترک، کسری بزرگتر خواهد بود که صورت کوچکتری داشته باشد. بنابرین، گزینه اول گزینه صحیح است.
توجه داشته باشید که اعداد کسری مثبت در هر شرایطی از اعداد کسری منفی بزرگتر هستند. در کسرهای منفی نیز هر کسری که به عدد ۰ نزدیکتر باشد، بزرگتر در نظر گرفته میشود.
کدام مقایسه بین کسرهای و صحیح است؟
برای مقایسه کسرهای و ، باید آنها به گونهای بنویسیم که مخرجشان یکسان باشد. برای این کار، معمولا از کوچکترین مضرب مشترک (ک م م) اعداد مخرجها استفاده میشود. ک م م دو عدد ۳ و ۹، عدد ۹ است. بنابراین، به منظور شروع مقایسه کسرها، مخرج آنها به این عدد تبدیل میکنیم:
همانطور که مشاهده میکنید، کسرهای و با یکدیگر برابر هستند. بنابراین گزینه صحیح است.
کدامیک از گزینههای زیر صحیح است؟
برای مقایسه دو کسر و ، ابتدا آنها را هممخرج میکنیم. این کار به صورت زیر انجام میشود:
از میان کسرهای بالا، کسری بزرگتر از که صورت بزرگتری دارد. بنابراین، کسر یا همان بزرگتر بوده و گزینه صحیح است.
بزرگترین کسر در میان کسرهای زیر کدام است؟
کدامیک از کسرهای زیر بزرگتر است؟
کدام یک از گزینههای زیر درست است؟
کدامیک از کسرهای زیر کوچکتر است؟
از میان گزینههای زیر، کوچکترین کسر کدام است؟
جمعبندی
در این آموزش، با روشهای متنوع مقایسه کسرها برای حالتهای مختلف آشنا شدیم. همچنین، مثالهای متنوعی را از مقایسه کسرها بیان کردیم.













سلام ببخشین میخوام بدونم دوچهارم بزرک است یاچعارچعارم کدام بزرک است ممنون میشم جواب بدین
خیلی ساده و روان و قابل فهم و مفید بود .
خیلی خیلی ممنون .خدا قوت
بسیار عالی توضیح دادید