نسبت در ریاضی — به زبان ساده + مثال

نسبت در ریاضی اصطلاحی است که برای مقایسه دو یا چند عدد به کار می‌رود. همچنین، از نسبت برای نشان دادن اینکه یک مقدار در مقایسه با مقدار دیگر چقدر بزرگ یا کوچک است استفاده می‌شود. در این مطلب از مجله فرادرس در مورد نسبت ها در ریاضی صحبت می‌کنیم. در یک نسبت، دو کمیت یا مقدار با استفاده از تقسیم مقایسه می‌شوند. در اینجا مقسوم را «صورت» و مقسوم‌علیه را «مخرج» می‌نامیم. در این آموزش، با نسبت در ریاضی آشنا می‌شویم.

به عنوان مثال، فرض کنید در یک گروه ۳۰ نفره، ۱۷ نفر از آن‌ها پیاده‌روی و ۱۳ نفر از آن‌ها دوچرخه‌سواری را ترجیح می‌دهند. برای نشان دادن این اطلاعات به‌عنوان نسبت تعداد افرد پیاده‌رو به تعداد افراد دوچرخه‌سوار، آن را به‌صورت $$17:13$$ می‌نویسیم. در اینجا، نماد ":" به‌عنوان «به» خوانده می‌شود و آن را از چپ می‌خوانیم، یعنی $$17$$ به $$ 13 $$. یک نمایش رایج دیگر، کسر $$ \frac {17}{13} $$ است که آن را نیز $$ 17 $$ به $$ 13$$ می‌خوانیم. بنابراین، نسبت افرادی که پیاده‌روی را ترجیح می‌دهند به افرادی که دوچرخه‌سواری را ترجیح می‌دهند، $$17$$ به $$13$$ خوانده می‌شود. در ادامه، بیشتر با نسبت در ریاضی آشنا می‌شویم.

نسبت در ریاضی چیست؟

«نسبت» (Ratio) به‌عنوان مقایسه دو کمیت با واحدهای مشابه تعریف می‌شود که نشان می‌دهد چه مقدار از یک کمیت در کمیت دیگر وجود دارد. نسبت‌ها را می‌توان به دو نوع طبقه‌بندی کرد. یکی نسبت جزء به جزء و دیگری نسبت جزء به کل.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

نسبت جزء به جزء نشان می‌دهد که چگونه دو گروه مجزا و جدا از هم مرتبط هستند. به عنوان مثال، وقتی می‌گوییم نسبت پسر به دختر در یک کلاس $$ 15 $$ به $$ 12$$ است، یعنی هم گروه دختر‌ها و هم پسرها جزئی از کلاس هستند و نسبتشان به هم را بیان کرده‌ایم.

نسبت جزء به کل نشان‌دهنده رابطه بین یک گروه خاص به یک کل است. مثلاً اگر بگوییم نسبت تعداد دخترها به کل کلاس $$ 12$$ به $$27 $$ است، نسبت جزء به کل را بیان کرده‌ایم. یا به‌عنوان یک مثال دیگر، فرض کنید از هر $$10$$ نفر $$5$$ نفر دوست دارند کتاب بخوانند. بنابراین، نسبت جزء به کل $$\frac 5 {10}$$ یا همان $$5$$ به $$10$$ است.

نکته: دقت کنید که دانستن اینکه نسبت جزء به جزء یا جزء به کل است، اهمیت چندانی ندارد و آشنایی با مفهوم نسبت در اولویت قرار دارد.

به‌عنوان یک مثال ساده از نسبت، فرض کنید یک مستطیل را به $$50 $$ قسمت مساوی تقسیم کرده‌ایم. از این $$50$$ قسمت، $$ 9 $$ قسمت را رنگ زده‌ایم. اکنون، می‌خواهیم بدانیم نسبت قسمت رنگ‌شده به کل مستطیل چقدر است.

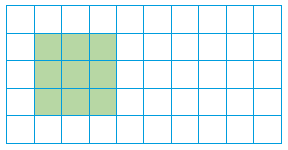
نسبت تعداد بخش‌های رنگ‌شده به کل بخش‌ها $$ 9 $$ به $$ 50 $$ است و آن را با کسر $$ \frac 9  { 50 } $$ نشان می‌دهیم.

نمایش نسبت در ریاضی

هنگام مقایسه رابطه بین دو عدد یا کمیت از فرمول نسبت استفاده می‌کنیم. شکل کلی نشان دادن نسبت بین دو کمیت "a" و "b" به‌صورت a:b است که به‌عنوان «نسبت a به b» خوانده می‌شود. البته یک شکل رایج‌تر نمایش نسبت، استفاده از کسر است. برای مثال، برای نسبت $$ a $$ به $$b$$، کسر $$ \frac  a b $$ را بیان می‌کنیم. در کتاب‌های درسی از $$ \frac a b $$ استفاده می‌شود.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

یک مثال را بیان می‌کنیم. فرض کنید از یک کلاس $$50$$ نفری، $$23$$ نفر دختر و بقیه پسر هستند. می‌خواهیم نسبت تعداد پسر به تعداد دختر را به‌صورت ریاضی بنویسیم. همان‌طور که گفته شد، تعداد کل دانش‌آموزان $$50$$ است و تعداد دخترها $$23$$. برای به‌دست آوردن تعداد پسرها، به‌صورت زیر عمل می‌کنیم:

۲۷ = ۲۳ - ۵۰ = تعداد دخترها - تعداد کل دانش‌آموزان = تعداد پسرها

بنابراین، نسبت مورد نظر (تعداد پسر به تعداد دختر) به‌صورت $$\frac {27}{23}$$ است.

نحوه نوشتن نسبت

برای نوشتن نسبت دو کمیت می‌توان از مراحل ساده‌ای استفاده کرد. با یک مثال این مراحل را بیان می‌کنیم. به‌عنوان مثال، فرض کنید برای درست کردن کیک به $$15$$ فنجان آرد و $$20$$ فنجان شکر نیاز داشته باشیم. می‌خواهیم نسبت آرد به شکر در دستور پخت را محاسبه کنیم. بدین منظور، مراحل زیر را انجام می‌دهیم:

1. ابتدا اندازه هر دو ماده را که نسبت را برای آن‌ها تعیین می‌کنیم، تعیین می‌کنیم. در این مثال، این دو مقدار برای آرد و شکر، به‌ترتیب، $$15$$ و $$20$$ فنجان هستند.
2. آن را به‌شکل کسر می‌نویسیم. بنابراین، برای این مثال، کسر $$\frac {15}{20}$$ را داریم.
3. در صورت امکان، کسر را بیشتر ساده می‌کنیم. در اینجا، کسر $$ \frac {15}{20} $$ را می‌توانیم به‌شکل $$ \frac { 15 } { 20 } = \frac { 3 \times 5 }{4 \times 5 } = \frac 34 $$ ساده کنیم.
4. کسر ساده‌شده نسبت نهایی را نشان می‌دهد. بنابراین، نسبت مقدار آرد به شکر $$ \frac 34 $$ یا $$3$$ به $$4$$ است.

چگونه نسبت‌ها را ساده کنیم؟

یک نسبت بیان می‌کند که چه مقدار از یک کمیت در مقایسه با کمیت دیگر وجود دارد. دو بخش در نسبت (صورت و مخرج) را می‌توان ساده و در پایین‌ترین شکل خود بیان کرد. وقتی نسبت‌ها با کمترین عباراتشان بیان می‌شوند، به‌راحتی قابل درک هستند. نسبت‌ها را می‌توان به همان روشی که کسرها را ساده می‌کنیم، ساده کرد. برای ساده کردن یک نسبت لازم است مراحلی را طی کنیم که در قالب یک مثال با آن‌ها آشنا می‌شویم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

برای مثال، فرض کنید می‌خواهیم نسبت $$ 18 $$ به $$ 10 $$ را ساده کنیم. برای این کار، مراحل زیر را طی می‌کنیم:

1. نسبتِ داده‌شده را به‌صورت کسر می‌نویسیم. در این مثال، با نوشتن نسبت به شکل کسری، $$ \frac { 18 } { 10 } $$ را خواهیم داشت.
2. بزرگ‌ترین مقسوم‌علیه مشترک یا همان ب.م.م. صورت رو مخرج را پیدا می‌کنیم. برای دو عدد $$ 10 $$ و $$18$$، ب.م.م. برابر با $$ 2$$ است.
3. برای به‌دست آوردن کسرِ ساده‌شده، صورت و مخرج کسر را بر ب.م.م. تقسیم می‌کنیم. در اینجا، با تقسیم صورت و مخرج بر $$2$$، کسر $$ \frac { 18÷2 } { 10÷2 } = \frac { 9 }{ 5 } $$ به‌دست می‌آید.
4. این کسر را به‌فرم نسبت بیان می‌کنیم. در این مثال، نسبت $$9 $$ به $$ 5 $$ است.

به‌عنوان یک مثال دیگر، فرض کنید می‌خواهیم نسبت $$ 9 $$ به $$ 24 $$ را ساده کنیم. بدین منظور، ابتدا نسبت را با کسر $$ \frac {9}{24} $$ نمایش می‌دهیم. ابتدا ب.م.م. دو عدد را محاسبه می‌کنیم. برای این کار، کافی است مقسوم‌علیه‌های دو عدد را بنویسیم:

• مقسوم‌علیه‌های عدد ۹: $$ 3 $$ و $$ 3 $$، یعنی $$ 9 = 3 \times 3 $$
• مقسوم‌علیه‌های عدد ۲۴: $$ 3 $$ و $$ 2 $$ و $$ 2 $$ و $$ 2 $$، یعنی $$ 24 = 2 \times 2 \times 2 \times 3 $$

می‌بینیم که $$ 3 $$ بین دو عدد مشترک است. بنابراین، می‌توانیم دو عدد صورت و مخرج را بر $$ 3 $$ تقسیم کنیم:

$$ \frac 9 { 24 } = \frac {9 \div 3 } { 24 \div 3 } = \frac { 3 }{8} $$

بنابراین، نسبت $$ \frac 9 { 24 } $$، معادل نسبت $$ \frac 3 8 $$ است. درباره نسبت‌های مساوی در بخش‌های بعدی بحث می‌کنیم.

نکته: اغلب پیش می‌آید که می‌دانیم دو عدد صورت و مخرج بر چه عدد یا عددهایی بخش‌پذیر هستند و به‌سادگی می‌توانیم آن‌ها را ساده کنیم. در این مواقع نیازی نیست گام‌هایی را که گفتیم نیست، خط به خط طی کنید. البته آنچه انجام می‌دهیم، شکل ساده‌ای از همین چند گام است.

چند نکته درباره نسبت در ریاضی

در این بخش، به چند نکته درباره نسبت در ریاضی اشاره می‌کنیم که دانستنشان خالی از لطف نیست.

فیلم آموزش محاسبات سریع ریاضی در فرادرس

کلیک کنید

• در صورتی که هر دو عدد نسبت با هم برابر باشند، نسبت برابر با ۱ است.
• در نسبت $$ \frac a b $$، اگر $$ a > b $$، آنگاه نسبت بزرگ‌تر از یک خواهد بود.
• در نسبت $$ \frac a b $$، اگر $$ a < b $$، آنگاه نسبت کوچک‌تر از یک خواهد بود.

نکته: قبل از مقایسه، باید از مشابه بودن واحدهای دو کمیت اطمینان حاصل کنید. مثلاً در بالا، آرد و شیر، هردو، با واحد فنجان مقایسه شدند یا برای دخترها و پسرهای کلاس، واحد نفر بود و تعداد چند نفر پسر را با تعداد چند نفر دختر مقایسه کردیم.

نسبت های مساوی

نسبت‌های مساوی یا معادل مشابه کسر‌های مساوی هستند. اگر صورت و مخرج کسر مربوط به یک نسبت معین، همزمان در یک عدد غیرصفر ضرب یا تقسیم شوند، نسبت معادل به‌دست می‌آید. به عنوان مثال، نسبت $$ 3 $$ بر $$ 1 $$ را در نظر بگیرید که به‌شکل کسری $$ \frac 3 1 $$ نوشته می‌شود. اگر صورت و مخرج این کسر را در $$ 3 $$ ضرب کنیم، نسبت $$\frac 3 9 $$ را خواهیم داشت که معادل هستند. به همین ترتیب، دو نسبت $$ \frac {10}{20} $$ و $$ \frac 1 2 $$ با هم معادل هستند، زیرا دومی را می‌توان با ضرب صورت و مخرج در $$ 10 $$ به‌دست آورد. با ضرب صورت و مخرج یک نسبت در یک عدد صحیح، می‌توان بی‌نهایت معادل برای آن نوشت.

به‌عنوان یک مثال برای نسبت‌های معادل، اگر قطاری $$100$$ کیلومتر را در $$1$$ ساعت بپیماید، مسافت $$500$$ کیلومتری را در $$5$$ ساعت طی می‌کند.

تناسب

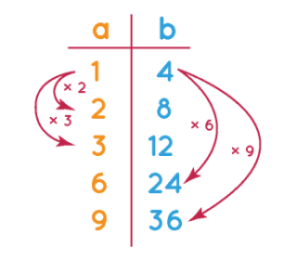
به زبان ساده، دو نسبت مساوی یک تناسب را تشکیل می‌دهند. جدول تناسب فهرستی است که شامل نسبت‌های معادل هر نسبت به‌شیوه‌ای ساختاریافته است. جدول تناسب زیر رابطه بین نسبت $$ 1 $$ به $$4$$ یا همان $$ \frac 1 4 $$ و چهار نسبت معادل آن را نشان می‌دهد. نسبت‌های معادل از ضرب یا تقسیم صورت و مخرج یک نسبت در یک عدد به‌دست می‌آیند. در مثال نشان داده شده در شکل زیر، نسبت $$1$$ به $$4$$ نشان داده شده است که با ضرب صورت و مخرج نسبت در $$ 2 $$ و $$ 3 $$ و $$ 6 $$ و $$9 $$ نسبت‌های معادل به‌دست آمده‌اند.

درصد چیست؟

درصد نوعی نسبت است که در آن، مخرج برابر با $$ 100$$ است. به عبارت دیگر، درصد یک نسبت جزء به کل است و می‌توان آن را معادل با نسبت‌های دیگر بیان کرد. برای مثال، اگر نسبت $$ \frac 1 { 1 0} $$ را داشته باشیم، با ضرب صورت و مخرج در $$ 10 $$، به نسبت معادل $$ \frac { 10 } { 100 } $$ می‌رسیم و آن را $$10$$ درصد می‌خوانیم و به‌شکل $$ 10 % $$ نمایش می‌دهیم.

در ادامه، مثال‌هایی آورده شده است که نشان می‌دهد چگونه درصد به نسبت کسری تبدیل می‌شود.

• $$25%$$ یعنی $$25$$ قسمت از $$100$$ قسمت یا $$\frac 14 = \frac {25}{100}$$ از کل. بنابراین، نسبت به‌صورت $$25$$ به $$100$$ یا $$ 1 $$ به $$ 4 $$ خوانده می‌شود.
• $$40%$$ یعنی $$40$$ قسمت از $$100$$ قسمت یا $$\frac 25 = \frac {40}{100}$$ از کل. بنابراین، نسبت به‌صورت $$40$$ به $$100$$ یا $$ 2 $$ به $$ 5 $$ خوانده می‌شود.
• $$75%$$ یعنی $$75$$ قسمت از $$100$$ قسمت یا $$\frac 34 = \frac {75}{100}$$ از کل. بنابراین، نسبت به‌صورت $$75$$ به $$100$$ یا $$ 3 $$ به $$ 4 $$ خوانده می‌شود.

مثال‌های نسبت در ریاضی

در این بخش، چند مثال از نسبت در ریاضی را بررسی می‌کنیم.

مثال اول نسبت در ریاضی

مستطیل زیر را در نظر بگیرید که به $$ 8 $$ قسمت مساوی تقسیم شده است و $$ 4 $$ قسمت از آن را رنگ کرده‌ایم. نسبت قسمت رنگ‌شده به رنگ‌نشده و قسمت رنگ‌شده به کل شکل را بنویسید و تا حد امکان آن را ساده کنید.

حل: این اطلاعات را داریم:

• تعداد کل بخش‌ها: $$ 8 $$
• تعداد بخش‌های رنگ‌شده: $$ 4 $$
• تعداد بخش‌های رنگ‌نشده: $$ 4 $$

بنابراین، نسبت تعداد بخش‌های رنگ‌شده به تعداد بخش‌های رنگ‌نشده $$ 4 $$ به $$ 4 $$ یا $$ \frac 4 4 = \frac 1 1 $$ است. این یعنی تعداد بخش‌های رنگ‌شده و رنگ‌نشده با هم برابرند. همچنین، قسمت رنگ‌شده به کل شکل $$ 4 $$ به $$ 8 $$ است که می‌توانیم آن را به‌صورت کسر $$ \frac 4 8 $$ بنویسیم. این کسر را می‌توان ساده کرد. با تقسیم صورت و مخرج بر $$4$$، این کسر به‌صورت $$ \frac 4 8 = \frac { 4 \div 4 } { 8 \div 4} = \frac 1 2 $$ است. همان‌طور که از ظاهر شکل نیز مشخص است، نصف آن رنگ شده است.

مثال دوم نسبت در ریاضی

در شکل زیر، نسب تعداد سیب‌ها به کل میوه‌ها، همچنین نسبت تعداد کل میوه‌ها به تعداد پرتقال‌ها را بنویسید.

حل: ابتدا اطلاعات مسئله را می‌نویسیم:

• تعداد پرتقال‌ها: $$3$$
• تعداد سیب‌ها: $$5$$
• تعداد کل میوه‌ها: $$11$$

بنابراین، نسبت تعداد سیب‌ها به کل میوه‌ها $$5$$ به $$11$$ است که‌ به‌شکل کسری $$ \frac 5 { 11 } $$ آن را می‌نویسیم. همچنین، نسبت تعداد کل میوه‌ها به تعداد پرتقال‌ها $$ 11 $$ به $$ 3 $$ است که آن را به‌شکل کسر $$ \frac { 11 } 3 $$ می‌نویسیم.

مثال سوم نسبت در ریاضی

خودرویی $$ 400 $$ کیلومتر را در $$ 5 $$ ساعت می‌پیماید. نسبت مسافت طی‌شده به مدت زمان صرف‌شده را بنویسید. همچنین، محاسبه کنید که این خودرو در $$1$$ ساعت چند کیلومتر را طی می‌کند.

حل: ابتدا اطلاعات مسئله را می‌نویسیم:

• مدت زمان: $$5 $$‌ساعت
• مسافت: $$ 400 $$ کیلومتر

نسبت مسافت طی‌شده به مدت زمان صرف‌شده $$ 400$$ کیلومتر بر $$ 5 $$ ساعت است که به‌شکل کسری $$ \frac { 400 } { 5 } $$ نوشته می‌شود.

بخش دوم مثال، از ما خواسته محاسبه کنیم که خودرو در $$1$$ ساعت چقدر را می‌پیماید. ما میزان مسافت مربوط به $$ 5 $$ ساعت را داریم. برای به‌دست آوردن مسافت طی‌شده در $$ 1$$ ساعت، باید صورت رو مخرج کسر را بر $$ 5 $$ تقسیم کنیم:

$$ \frac { 400 } { 5 } = \frac {400 \div 5 } { 5 \div 5 } = \frac {80}{1 }$$

می‌بینیم که نسبت $$ 400$$ به $$ 5 $$ معادل نسبت $$ 80 $$ به $$ 1 $$ است. بنابراین، مسافت طی‌شده در $$ 1 $$ ساعت، $$ 80 $$ کیلومتر است.

مثال چهارم نسبت در ریاضی

احمد و نرگس خواهر و برادر دوقلو هستند و در اوقات فراغتشان درس‌ها را به‌صورت بازی یاد می‌گیرند. آن‌ها به درس نسبت در ریاضی رسیده‌اند و یکی از بازی‌های آن‌ها این است که مقدار پولی را که دارند روی کاغذ بنویسند و نسبت آن را به‌دست آورند و اگر ممکن بود، آن را ساده کنند. در این بازی، احمد مبلغ ۵ هزار تومان و نرگس ۱۰۰ هزار ریال را روی برگه نوشته‌اند. به نظرتان، نسبت مقدار پول نرگس به پول احمد چقدر است؟‌

حل: چنان‌که در ابتدای متن گفتیم، نکته مهمی که باید به آن دقت کنیم، این است که وقتی نسبت دو چیز را می‌نویسیم، واحدهای آن‌ها باید با هم برابر باشند. همان‌طور که می‌بینیم، احمد با تومان و نرگس با ریال مقدار پول خود را بیان کرده‌اند. بنابراین، باید هر دو واحد را به‌صورت ریال یا تومان بنویسیم. در اینجا، ما دو واحد را برحسب تومان می‌نویسیم:‌

• پول احمد: ۵ هزار تومان.
• پول نرگس: ۱۰۰ هزار ریال که معادل ۱۰ هزار تومان است.

اکنون می‌توانیم نسبت پول احمد به نرگس را حساب کنیم که $$ 10 $$ به $$ 5 $$ است و به‌شکل کسری $$ \frac {10} { 5 } $$ بنویسیم. همان‌طور که احتمالاً پی برده‌اید، دو عدد صورت و مخرج بر $$ 5 $$ بخش‌پذیر هستند و می‌توان این نسبت را ساده کرد:

دامداری با گوسفند و بز$$ \frac {10}{5 }= \frac { 1 0 \div 5 }{ 5 \div 5 } = \frac { 2 } { 1 } = 2 $$

بنابراین، می‌توان گفت که نسبت پول نرگس به احمد ۲ به ۱ است، یا ساده‌تر اینکه نرگس دو برابر احمد پول دارد.

مثال پنجم نسبت در ریاضی

دامداری ۶ بز و ۴ گوسفند دارد. چند درصد از کل دام‌های او گوسفند هستند؟

حل: ابتدا اطلاعات مثال را می‌نویسیم:

• تعداد بزها: ۶
• تعداد گوسفندها: ۴
• تعداد کل دام‌ها: ۱۰ = ۴ + ۶

برای محاسبه درصد گوسفندها، ابتدا باید نسبت تعداد گوسفندها به کل دام‌ها را بیابیم. همان‌طور که از اطلاعات مسئله می‌دانیم، نسبت تعداد گوسفندها به کل دام‌ها، $$ 4 $$ به $$ 10 $$ است که به‌شکل کسری $$ \frac 4 { 10 } $$ نوشته می‌شود. برای تبدیل این نسبت به درصد، باید با یک ضریب عدد مخرج را به $$ 100$$ تبدیل کنیم. با توجه به اینکه عدد مخرج $$ 10 $$ است، باید آن را در $$ 10 $$ ضرب کنیم. اما صورت را نیز باید در $$ 10 $$ ضرب کنیم تا اصل نسبت تغییری نکند. بنابراین، با ضرب صورت و مخرج در عدد $$ 10$$، خواهیم داشت:

$$ \frac { 4 } { 10 } = \frac {4 \times 10}{10 \times 10} = \frac {40} {100} $$

مشاهده می‌کنیم که به نسبت معادل $$ \frac {40}{100} $$ رسیده‌ایم که مخرج آن $$100$$ و صورتش $$ 40 $$ است. بنابراین، گوسفندها $$40%$$ از همه دام‌ها را تشکیل می‌دهند.

مثال ششم نسبت در ریاضی

مستطیل شکل زیر را در نظر بگیرید. ابتدا نسبت عرض به طول مستطیل زیر را به‌صورت کسر بنویسید و آن را ساده کنید.

حل: می‌بینیم که طول $$6$$ و عرض $$2$$ است. بنابراین، نسبت عرض به طول $$2$$ به $$6$$ یا $$ \frac 26 $$ است که به‌شکل زیر ساده می‌شود:

$$ \frac {2} { 6 } = \frac { 2 \div 2 } { 6 \div 2 } = \frac 13 $$

مثال هفتم نسبت در ریاضی

آیا دو نسبت $$ \frac 2 3 $$ و $$ \frac 2 6 $$ یک تناسب را تشکیل می‌دهند؟

حل: برای بررسی این موضوع، ابتدا دو نسبت را تا حد ممکن ساده، سپس آن‌ها را مقایسه می‌کنیم. نسبت $$ \frac 23 $$ را نمی‌توان ساده کرد. اما نسبت $$ \frac 2 6 $$ به‌صورت $$ \frac 13 $$ ساده می‌شود. همان‌طور که می‌بینیم، این نسبت‌ها مساوی نیستند، زیرا با وجود اینکه مخرج آن‌ها یکسان است، صورتشان متفاوت است. بنابراین، این دو نسبت مساوی نیستند و در نتیجه، یک تناسب را تشکیل نمی‌دهند.

جمع‌بندی

در این آموزش از مجله فرادرس، با نسبت در ریاضی آشنا شدیم و مثال‌های متنوعی را بررسی کردیم.