معادله نوسان ماشین سنکرون — از صفر تا صد

برای کنترل فرکانس و بررسی پاسخ فرکانسی، داشتن مدل سیستم قدرت ضروری است. در این آموزش، معادله مهم ژنراتور سنکرون، موسوم به معادله نوسان ماشین سنکرون (Swing Equation) را به دست می‌آوریم. بدین منظور، از قانون دوم نیوتن برای یک جسم چرخان جهت استخراج معادله نوسان یک ژنراتور سنکرون و از فرضیاتی برای ساده‌سازی معادله استفاده خواهیم کرد. علاوه بر این، معادله خطی شده را برای آشفتگی‌های سیگنال‌کوچک به دست خواهیم آورد. همچنین، با داشتن معادله نوسان، پاسخ فرکانسی دو سیستم مختلف را به تغییر بار یا تغییر توان مکانیکی بررسی می‌کنیم.

قانون نیوتن برای یک جسم چرخان

همان‌طور که گفتیم، معادله نوسان از قانون دوم نیوتن برای یک جسم چرخان به دست می‌آید. در یک ژنراتور سنکرون، جسم چرخان همان روتور است. قانون نیوتن بیان می‌کند که شتاب زاویه‌ای متناسب با گشتاور خالص است:

$$ \large J \frac { d \omega } { d t } = T _ m - T _ e \;\;\;\;\; ( 1 ) $$

که در آن، $$J$$ لَختی روتور برحسب کیلوگرم در متر مربع ($$\mathrm{kg  \cdot m^ 2 } $$) یا ژول در ثانیه مربع ($$\mathrm { J \cdot s ^ 2 } $$) است. پارامتر $$\omega$$ سرعت چرخان برحسب $$\text{rad/s}$$، و گشتاورها برحسب واحد استاندارد نیوتن در متر ($$\mathrm{N \cdot m } $$) هستند. $$T_m$$ گشتاور مکانیکی بار و $$T_e$$ گشتاور الکترومغناطیسی تولیدی میدان الکترومغناطیسی است.

مهندسان سیستم قدرت، اغلب از توان به جای گشتاور استفاده می‌کنند. بنابراین، رابطه بالا را برحسب توان مکانیکی $$P_m$$ و توان الکتریکی $$P_e$$ تولیدی میدان الکترومغناطیسی می‌نویسیم.

همان‌طور که می‌دانیم، $$P_m=T_m\omega _m$$ که در آن، $$\omega _m$$ سرعت مکانیکی، و $$P_e=T_e \frac{2}{P}\omega _e$$ که در آن، $$\omega _e$$ فرکانس مدار استاتور و $$P$$ تعداد قطب‌های ماشین است. برای ماشین‌هایی با دو قطب، رابطه $$P_e=T_e\omega _e$$ برقرار است.

در یک ژنراتور سنکرون با دو قطب، سرعت مکانیکی $$\omega _m$$ و فرکانس الکتریکی $$\omega _e$$ استاتور با هم برابرند. بنابراین، از $$\omega$$ برای نمایش هر دو سرعت چرخش و فرکانس برق استفاده می‌کنیم. در نتیجه، معادله نوسان (۱) به صورت زیر در می‌آید:

$$ \large J \frac { d \omega } { d t } = \frac { P _ m } {\omega} - \frac { P _e} { \omega } . \;\;\;\;\; ( 2 ) $$

توجه کنید که این معادله تنها به ماشین‌های سنکرون قابل اعمال است. در ماشین‌های القایی، $$T_m=P_m/\omega _m$$، و $$T_e=P_e/\omega_e$$، که در آن‌ها، $$\omega _m$$ سرعت چرخش و $$\omega _e$$ فرکانس الکتریکی در مدار استاتور است. در ماشین‌های القایی، سرعت چرخش و فرکانس الکتریکی برابر نیستند. فرکانس الکتریکی $$\omega _e$$ برابر با سرعت چرخش میدان مغناطیسی گردان یک ماشین دوقطب است و سرعت میدان برابر با مجموع سرعت مکانیکی $$\omega _m$$ و فرکانس $$\omega _r$$ جریان مدار روتور خواهد بود: $$\omega _e = \omega _m + \omega _ r$$.

اگر اصطکاک و گشتاور اصطکاکِ متناسب با سرعت را در سیستم مکانیکی در نظر بگیریم، معادلات بالا به صورت زیر اصلاح خواهند شد:

$$ \large J \frac { d \omega } { d t } = T _ m - T _ e - k \omega \;\;\;\;\; ( 3) $$

$$ \large J \omega \frac { d \omega } { d t } = P _ m - P _ e - k \omega ^ 2 \; \; \; \; \; ( 4 ) $$

که در آن‌ها، $$k$$ ضریب اصطکاک است.

معادله (۴) نسبت به عبارت $$\omega $$ غیرخطی است. هر دو $$J\omega \frac{d\omega}{dt}$$ و $$k\omega ^2$$ غیرخطی هستند. بسط تیلور کاربرد فراوانی در به دست آوردن یک فرم خطی دارد. برای به دست آوردن یک بسط خطی، باید یک شرایط اولیه یا یک شرایط کار حالت مانا را در نظر بگیریم. در دینامیک و کنترل، شرایط حالت مانای اولیه و شرایط حالت مانای نهاییِ بعد از حالت گذار به عنوان نقاط تعادل شناخته می‌شوند.

معادله نوسان ماشین سنکرون حول سرعت نامی

اگر ژنراتور در شرایط نامی با سرعت $$\omega _0$$ کار کند، می‌توانیم معادله بالا را با استفاده از بسط تیلور حول شرایط نامی خطی‌سازی کنیم. مدل خطی شده برای دینامیک سیگنال‌کوچک در حول شرایط نامی کاربرد دارد.

$$ \large \require{cancel}
\begin {align*}
\omega \frac {d \omega } { dt} & = (\omega _ 0+ \Delta \omega ) \left ( \cancel { \frac { d \omega _ 0 } {dt} } ^0+\frac {d \Delta \omega }{d t} \right ) = \omega _ 0 \frac {d \Delta \omega } { d t } + \Delta \omega \frac { d \Delta \omega } { d t} \\
& \approx \omega _ 0 \frac { d \Delta \omega} { d t} \\
& = \omega _ 0 \frac { d \omega } { d t } \end {align*}
\; \; \; \; \; ( 5 ) $$

از آنجایی که $$\omega _0$$ ثابت است، $$\frac{d\omega_0}{dt}=0$$ و $$\Delta \omega \frac{d\Delta \omega}{dt}$$ حاصل‌ضرب دو تغییر کوچک است که از آن چشم‌پوشی می‌کنیم.

خطی‌سازی جمله $$k\omega ^2$$ مطابق روند کلی خطی‌سازی انجام شده است. برای تابع $$ f(x)$$، انحراف یا تغییر کوچک در نقطه $$x_0$$ به صورت زیر بیان می‌شود:

$$ \large \Delta f \approx \frac { \partial f } { \partial x } \Bigg | _ {x _ 0 } \Delta x \; \; \; \; \; ( 6 ) $$

بنابراین:

$$ \large k \omega ^ 2 = k \omega _ 0 ^ 2 + \Delta ( k \omega ^ 2 ) \approx k \omega _ 0 ^2 + 2 k \omega _ 0 \Delta \omega . \;\;\;\;\; (7)$$

که در آن، $$\Delta \omega = \omega - \omega _0$$.
قانون نیوتن برای شرایط حول نقطه کار نامی به صورت زیر در می‌آید:

$$ \large J \omega _ 0 \frac { d \omega } { d t } = \widetilde {P _ m } - P _ e - 2 k \omega _ 0 \Delta \omega \;\;\;\;\; (8) $$

که در آن، $$\widetilde{P_m}=P_m-k\omega_0 ^2$$.

پریونیت معادله نوسان

در معادله بالا،‌ از واحدهای فیزیکی استفاده کردیم. برای مثال، $$\omega$$ برحسب رادیان بر ثانیه و توان برحسب وات بود. مهندسان سیستم قدرت، برای سادگی محاسبات، ترجیح می‌دهند از مقادیر پریونیت استفاده کنند. بنابراین، دو طرف معادله (۸) را بر توان مبنای سیستم ($$S_b$$) تقسیم می‌کنیم. در نتیجه، داریم:

$$ \large \frac {J \omega _ 0 } { S _ b } \frac {d \omega} {dt} = \widetilde {P _ m ^ { p u } } - P _ e ^ { p u } - \frac {2 k \omega _ 0 } { S _ b } \Delta \omega .
\;\;\;\;\; (9) $$

همچنین، اگر از $$\omega ^{pu}=\frac{\omega}{\omega_0}$$ استفاده کنیم، معادله بالا با جایگزینی $$\omega = \omega _0 \omega ^ {pu}$$ و $$\Delta \omega = \omega _0 \Delta \omega ^{pu}$$ به صورت زیر خواهد بود:

$$ \large \frac {J \omega _ 0 ^ 2} { S _ b } \frac {d \omega ^ { p u }} {dt} = \widetilde {P _ m ^ { p u } } - P _ e ^ { p u } - \frac {2 k \omega _ 0 ^ 2 } { S _ b } \Delta \omega ^ { p u }
\;\;\;\;\; ( 10 ) $$

پارامتر زیر را تعریف می‌کنیم:

$$ \large H \triangleq \frac { J \omega _ 0 ^ 2 } { 2 S _ b } \; \; \; \; \; (11)$$

$$H$$ نسبت انرژی جنبشی در سرعت نامی روتور بر توان مبنا است. واحد $$H$$ ثانیه است.

در ادامه، برای سادگی، بالانویس $$pu$$ را نمی‌نویسیم. قانون نیوتن به صورت زیر خواهد بود:

$$ \large 2 H \frac { d \omega } { d t } = \widetilde {P _ m } - P _ e - D _ 1 \Delta \omega . \;\;\;\;\; ( 12 ) $$

که در آن، $$ D_1 = \frac {2k\omega _0 ^2}{S_b}$$، و $$\omega$$، $$\widetilde{P_m}$$ و $$ P _ e $$ مقادیری پریونیت هستند. توجه کنید که در شرایط نامی حالت مانا، وقتی $$\omega = \omega _0$$، آنگاه $$\widetilde{P_m}=P_e$$.

معادله نوسان سیگنال‌کوچک

برای آشفتگی‌های کوچک از شرایط نامی اولیه (که با پایین‌نویس 0‌ آن را نشان می‌دهیم)، داریم:

$$ \large \omega = \omega _ 0 + \Delta \omega \;\;\;\;\; (13) $$

$$ \large \widetilde {P _ m } = \widetilde {P _ { m 0 } } + \Delta P _ m \;\;\;\;\; (14) $$

$$ \large P _ m = {P _ { m 0 } } + \Delta P _ m \;\;\;\;\; (15) $$

$$ \large P _ e = {P _ { e 0 } } + \Delta P _ e \;\;\;\;\; (16) $$

که در آن، $$ \widetilde{P_{m0}}=P_{m0}-k\omega_0^2=P_{e0}$$.

با توجه به (۱۲)، رابطه زیر را خواهیم داشت:

$$ \large LHS = 2 H \frac { d \Delta \omega } { d t } \;\;\;\;\; (17) $$

$$ \large RHS = \underbrace{ \widetilde { P _ { m 0 } } - P _ { e 0 } }_{ = 0 } + \Delta P _ m - \Delta P _ e - D _ 1 \Delta \omega = \Delta P _ m - \Delta P _ e - D_ 1 \Delta \omega \;\;\;\;\; (18) $$

معادله نوسان خطی شده به صورت زیر است:

$$ \large 2 H \frac { d \Delta \omega } { d t } = \Delta P _ m - \Delta P _ e - D _ 1 \Delta \omega . \; \; \; \; \; (19) $$

در حوزه لاپلاس، (۱۹) به فرم (۲۰) در می‌آید:

$$ \large ( 2 H s + D _ 1 ) \Delta \omega   = \Delta P _ m- \Delta P _ e . \;\;\;\;\; (20)$$

اکنون با داشتن معادله نوسان، می‌توانیم پاسخ فرکانسی را برای دو سناریو بررسی کنیم. در سناریوی اول، باری با یک ژنراتور تغذیه می‌شود. در سناریوی دوم، یک ژنراتور به یک شبکه فشار قوی متصل می‌گردد.

ژنراتور متصل به یک بار

برای سیستمی با یک ژنراتور که باری را با مصرف توان حقیقیِ $$P _L$$ تغذیه می‌کند، می‌توانیم از (۱9) برای بررسی پاسخ فرکانسی سیستم به افزایش بار استفاده کنیم. از تلفات توان در سیستم الکتریکی صرف‌نظر کرده و تغییر توان مکانیکی را بسیار کُند در نظر می‌گیریم.

در مقیاس زمانی سیستم مورد بررسی، مثلاً ۱۰ ثانیه، توان مکانیکی تغییر نمی‌کند؛ یعنی $$\Delta P _ m = 0 $$. اکنون پاسخ پله $$\Delta P _L$$ را در نظر می‌گیریم. ابتدا، باید توجه کنیم که در این سیستم، $$P _ e = P _ L $$.

معادله (۱۹) به صورت زیر در خواهد آمد:

$$ \large 2 H \frac {d \Delta \omega } { d t } = - \Delta P _ L - D _ 1 \Delta \omega. \;\;\;\;\; (21) $$

پاسخ حالت مانا

پاسخ حالت مانای $$\Delta \omega $$ را می‌توان با صفر قرار دادن مشتق تغییر سرعت ($$\Delta \dot{\omega}$$) یافت. بنابراین، معادله (۲۱) به صورت زیر در خواهد آمد:

$$ \large - \Delta P _ L - D_ 1 \Delta \omega = 0 . \;\;\;\;\; (22) $$

اگر $$\Delta P _L =1$$، آنگاه در حالت مانا، تغییر سرعت $$-\frac {1}{D_1}$$ است.

مقدار تغییرات فرکانس حالت مانا را نیز می‌توان از تابع تبدیل به دست آورد. از رابطه (۲۱)، تابع تبدیل از بار $$ \Delta P _ L $$ به سرعت $$ \Delta \omega $$ به صورت زیر خواهد بود:

$$ \large \frac { \Delta \omega } { \Delta P _ L } = - \frac { 1 } { 2 H s +D_1 } \;\;\;\;\; (23) $$

پاسخ حالت مانای زمانی را می‌توان با استفاده از قضیه مقدار نهایی به دست آورد:

$$ \large \lim _ { t \to \infty} {f ( t) } = \lim _ {s \to 0} s F ( s ) \;\;\;\;\; ( 2 4 ) $$

که در آن، $$ f ( t)$$ یک تابع زمانی و $$F(s)$$ تبدیل لاپلاس آن است. بنابراین، داریم:

$$ \large \Delta \omega ( t \to \infty ) = \lim _ { s \to 0 } s \Delta \omega (s ) = \lim _ {s \to 0 } \left ( - \frac { 1 } { 2 H s + D _ 1} \right ) s \Delta P _ L \;\;\;\;\; ( 2 5 ) $$

اگر $$\Delta P _ L = 1 / s $$ را برای پاسخ پله در نظر بگیریم، آنگاه تنها کافی است مقدار تابع تبدیل (۲۳) را در $$ s = 0 $$ محاسبه کنیم.

در نتیجه، می‌توانیم تغییرات فرکانس حالت مانای $$ - \frac {1}{D_1}$$ را نیز به دست آوریم.

همان‌طور که می‌بینیم، افزایش بار سبب کاهش فرکانس خواهد شد. همچنین، $$D_1$$ بسیار کوچک است که افزایش بسیار فرکانس را نشان می‌دهد. بنابراین، لازم است یک سیستم کنترل برای کاهش تغییرات فرکانس حالت مانا ارائه کنیم. کنترل فرکانس اولیه یا کنترل افت این کار را انجام می‌دهند.

پاسخ دینامیکی

پاسخ دینامیکی $$\Delta \omega (t)$$ را می‌توان با حل معادله دیفرانسیل مرتبه اول (۲۱) به دست آورد. به طور خلاصه، برای $$ \Delta P _ L =1$$، داریم:

$$ \large \Delta \omega ( t) = - \frac { 1 } { D _ 1 } \left (1 - e ^ {- \frac {D_1}{2H}t} \right ) . \;\;\;\;\; ( 2 6 ) $$

پاسخ دینامیکی را می‌توان از تبدیل لاپلاس نیز به دست آورد:

$$ \large \begin {align*}
\Delta \omega (s) & = - \frac { 1 } { 2 H s + D _ 1 } \Delta P _ L ( s) = - \frac { 1 } { 2 H s + D_ 1 s } \frac { 1 } { s } \\
& = - \frac { 1 } { D _ 1 } \left ( \frac { 1 } { s } - \frac { 1 } { s + D_ 1 / (2 H)} \right )
\end {align*} \;\;\;\;\; (27) $$

تبدیل لاپلاس معکوس عبارت حوزه زمان $$ \Delta \omega (t)$$ را نتیجه خواهد داد:

$$ \large \Delta \omega ( t) = - \frac { 1 } { D _ 1 } \left ( 1 - e ^ { - \frac {D_1} { 2 H} t} \right )
\;\;\;\;\; (28) $$

سیستم ژنراتور-شین بینهایت (SMIB)

اکنون مدل یک سیستم ژنراتور-شین بینهایت یا SMIB را تشکیل می‌دهیم. یک ژنراتور را در نظر می‌گیریم که از طریق یک خط انتقال به یک باس بینهایت متصل شده است. منظور از شین بینهایت، یک شبکه بزرگ است. این شبکه لختی بینهایتی دارد. شبکه با یک منبع ولتاژ با اندازه ولتاژ ثابت و فرکانس ثابت نمایش داده می‌شود. تغییر بار اثری بر فرکانس نخواهد داشت، زیرا لختی بینهایت است ($$J \to \infty$$ و $$\dot{\omega } = 0 $$). فازور ولتاژ شین بینهایت $$ V_ \infty \angle 0 $$ است. خط انتقال با راکتانس خالص $$ X _L$$ نمایش داده می‌شود.

با فرض اینکه ژنراتور با ساده‌ترین مدل به عنوان یک منبع ولتاژ ($$ E \angle \delta$$) سری با راکتانس $$ X _ s $$ نمایش داده می‌شود و از همه دینامیک‌های الکترومغناطیسی چشم‌پوشی شود، توان الکتریکی که از ژنراتور به شین بینهایت فرستاده می‌شود، برابر است با:

$$ \large P _ e = \frac { E V _ \infty } { X } \sin ( \delta ) \;\;\;\;\; (29)$$

که $$ X = X _ s + X _ L $$ راکتانس کل، شامل راکتانس ژنراتور سنکرون و راکتانس خط است.

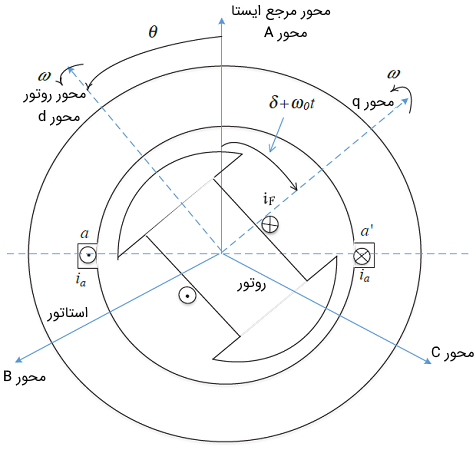
$$ E$$ مقدار ریشه میانگین مجذور (RMS) ولتاژ داخلی متناسب با جریان تحریک $$ i _ F $$ در روتور است. $$ \delta $$ به صورت زیر با موقعیت $$ \theta $$ مرتبط است:

$$ \large \theta = \omega t + \theta _ 0 = \omega _ 0 t + \delta + \frac { \pi} { 2 } \;\;\;\;\; (30)$$

که در آن، $$ \theta _ 0 $$ موقعیت اولیه روتور نسبت به یک مرجع ساکن است.

$$ \delta $$ موقعیت محور قائم روتور (محور $$q$$ در موقعیت $$ \theta - \frac {\pi}{2}$$) نسبت به یک قاب مرجع گردان (در موقعیت $$\omega _ 0 $$) است. این قاب مرجع گردان یک سرعت نامی ثابت $$ \omega _ 0 $$ دارد و به همنی دلیل، قاب مرجع گردان سنکرون نامیده می‌شود. اگر ماشین با سرعت $$ \omega $$ بچرخد، با فرض اینکه محور مستقیم (محور $$d$$) محور روتور بوده (جهت میدان تولیدی با جریان تحریک $$ i _ F $$) و محور $$q$$ به اندازه ۹۰ درجه نسبت به محور $$d$$ پس‌فاز باشد، آنگاه موقعیت محور $$q$$ نسبت به مرجع ایستا $$\theta - \frac{\pi}{2} = \omega t + \theta _ 0 - \frac {\pi}{2} $$ است.

در این حالت، داریم:

$$ \large \delta = \theta - \frac { \pi} { 2 } - \omega _ 0 t = ( \omega - \omega _0 ) t + \theta _ 0 - \frac { \pi} { 2 } \;\;\;\;\; (31) $$

$$ \large \dot { \delta } = \omega - \omega _ 0 \;\;\;\;\; (32) $$

که در آن، $$\delta$$ برحسب رادیان و $$\omega$$ برحسب رادیان بر ثانیه است.

محورهای $$dq$$، $$ \theta $$ و $$ \delta$$ در شکل ۱ نشان داده شده‌اند.

اگر از مقدار پریونیت برای $$ \omega $$ استفاده کنیم، داریم:

$$ \large \dot { \delta } = \omega _ 0 (\omega - 1 ) \;\;\;\;\; (33)$$

که در آن، $$\delta$$ برحسب رادیان و $$\omega$$ پریونیت است.

مدل سیگنال کوچک (۳۳) را می‌توان برحسب $$ \Delta \delta$$ و $$ \Delta \omega$$ نوشت:

$$ \large \Delta \dot {\delta} = \omega _ 0 \Delta \omega . \;\;\;\;\; (34)$$

معادلات نوسان برای یک سیستم SMIB به صورت زیر هستند:

$$ \large \frac {d \delta } { d t } = \omega _ 0 ( \omega - 1 ) \\
\large 2 H \frac { d \omega }{ d t } = \widetilde { P _ m } - P _ e - D_ 1 \Delta \omega \;\;\;\;\; (35)$$

که در آن، $$ P _ e = \frac { E V _ \infty } { X } \sin (\delta) $$.

مدل خطی شده

مجموعه معادله نوسان بالا را می‌توان در یک نقطه تعادل یا شرایط اولیه $$(\omega_0, \delta _ 0 , P_{m0} , P_{e0} )$$ خطی کرد.

$$ \large \frac { d \Delta \delta } { d t } = \omega _ 0 \Delta \omega \\
\large 2 H \frac { d \Delta \omega } { d t } = \Delta P _ m - \Delta P _ e - D_ 1 \Delta \omega \;\;\;\;\; (36)$$

با اعمال یک آشفتگی کوچک برای $$P_e$$ با استفاده از معادله (۶)، داریم:

$$ \large \Delta P _ e =\underbrace { \frac {E V _ \infty} { X } \cos ( \delta _ 0 )}_ T \Delta \delta . \;\;\;\;\; (37) $$

با جایگذاری $$\Delta \dot{\delta} / \omega _ 0 $$ به جای $$\Delta \omega $$ در معادله دوم (۳۶)، می‌توانیم یک معادله دیفرانسیل مرتبه دوم برحسب متغیر $$ \Delta \delta $$ به دست آوریم:

$$ \large \frac { 2 H } { \omega _ 0 } \Delta \ddot {\delta} + \frac { D_ 1 } { \omega _ 0 } \Delta \dot{\delta } + T \Delta \delta = \Delta P _ m . \;\;\;\;\; (38) $$

دو پارامتر جدید را به صورت زیر تعریف می‌کنیم:

$$ \large M \triangleq \frac { 2 H } { \omega _ 0 } \;\;\;\;\; (39) $$

$$ \large D \triangleq \frac { D _ 1 } { \omega _ 0 }. \;\;\;\;\; (40) $$

در نهایت، معادله دیفرانسیل مرتبه دوم تک متغیره به صورت زیر خواهد بود:

$$ \large M \Delta \ddot{\delta} + D \Delta \dot{\delta} + T \Delta \delta = \Delta P _ m . \;\;\;\;\; (41) $$

اگر از این معادله تبدیل لاپلاس بگیریم، خواهیم داشت:

$$ \large (M s ^ 2 + D s + T ) \Delta \delta = \Delta P _ m . \;\;\;\;\; (42) $$

تغییرات فرکانس حالت مانا و تغییرات زاویه روتور

براساس معادلات نوسان (۳۵)، از آنجایی که در حالت مانا $$\dot{\delta} = 0$$، مقدار حالت مانای سرعت باید $$\omega t \to \infty ) = 1 $$ باشد. زاویه حالت مانا باید در شرط $$ P _ m - k \omega _0^2 = P_e = \frac {EV_ \infty } { X } \sin \delta $$ صدق کند. اگر خروجی $$P_m$$ محرک اولیه ژنراتور افزایش یابد، آنگاه افزایش زاویه $$\delta$$ روتور را خواهیم دید.

اگر افزایش قابل توجه نباشد، هنوز می‌توانیم از مدل خطی شده برای بررسی $$ \Delta  \delta $$ استفاده کنیم. بر اساس رابطه $$ \Delta P _ m = \Delta P _ e = T \Delta \delta $$ در حالت مانا، داریم: $$ \Delta \delta = \frac { \Delta P _ m } { T } $$.

توابع تبدیل از $$ \Delta P _ m $$ به $$ \Delta \delta $$ و $$ \Delta \omega $$ به صورت زیر هستند:

$$ \large \frac { \Delta \delta } { \Delta P _ m } = \frac { 1 } { M s ^ 2 + D s + T } \;\;\;\;\; (43) $$

$$ \large \frac { \Delta \omega } { \Delta P _ m } = \frac { s } { \omega _ 0 ( M s ^ 2 + D s + T ) } \;\;\;\;\; (44) $$

اگر $$s$$ را برابر با صفر قرار دهیم، دو مقدار $$ 1 / T $$ و $$0$$ برای دو تابع تبدیل به دست می‌آید. اگر توان مکانیکی دارای یک پاسخ پله باشد، زاویه نهایی به اندازه $$1 / T $$ افزایش خواهد یافت، در حالی که تغییرات فرکانس صفر خواهد بود، یا فرکانس بعد از دینامیک به مقدار نامی‌اش بر خواهد گشت.

نکته: بررسی سیستم SMIB بالا نشان می‌دهد که برای یک سیستم با شبکه قوی، مسائل کنترل فرکانس وجود نخواهد داشت. پاسخ فرکانسی SMIB همچنین این نکته را تأیید می‌کند که در حالت مانا، فرکانس یا سرعت بدون تغییر است. از آنجایی که باس یا شین بینهایت یک فرکانس نامی را حفظ می‌کند، سرعت ژنراتور در حالت مانا برابر با مقدار نامی خواهد بود.

در موارد عملی مدل‌سازی سیستم قدرت، باید با احتیاط از شین بینهایت استفاده کنیم. برای بررسی اثر کنترل فرکانس، نباید از شین بینهایت در مدل‌سازی یک ژنراتور یا شبکه استفاده کرد. در این صورت، بررسی پاسخ فرکانسی واقعی خواهد بود.

در ریزشبکه‌ها، از مبدل‌های الکترونیک قدرت به عنوان واسط بین منابع انرژی پراکنده و شبکه استفاده می‌شود. مبدل‌ها اصلی‌ترین تجهیزات کنترلی هستند. ریزشبکه‌ها دو مد عملکردی دارند: متصل به شبکه و خودگردان. در مد متصل به شبکه، یک ریزشبکه به شبکه قوی متصل می‌گردد. در حالی که در مد خودگردان یا جزیره‌ای، ریزشبکه یک سیستم مستقل خواهد بود. در مد متصل به شبکه، مبدل‌ها معمولاً در مد کنترل PQ تنظیم می‌شوند. برای مثال، وقتی ریزشبکه به شبکه اصلی وصل می‌شود، شارژ یا تخلیه سطح توان باتری تنظیم می‌گردد.

در مد خودگردان، برای مثال وقتی باتری باری را تغذیه می‌کند، مبدل باید کنترل فرکانس را در نظر بگیرد. برخلاف ژنراتورهای سنکرون، که در آن‌ها کنترل فرکانس از طریق گاورنرها انجام می‌شود، کنترل فرکانس مبدل‌های الکترونیک قدرت از طریق کنترل و مدولاسیون مبدل انجام خواهد شد. مزیت این مورد آن است که مبدل‌ها کنترل را سریع‌تر انجام می‌دهند، در حالی که گاورنرها پاسخ‌های کندتری دارند. البته این مورد را می‌توان به عنوان یکی از معایب مبدل‌ها نیز در نظر گرفت که ریزشبکه‌های بدون ژنراتورهای سنکرون رایج، به دلیل نداشتن لختی، تغییرات فرکانس قابل توجهی دارند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مدل خط سه فاز — به زبان ساده
• انواع خطا در سیستم قدرت — به زبان ساده
• معادلات ژنراتور سنکرون — به زبان ساده

^^