ثابت پلانک – هر آنچه باید بدانید
«ماکس کارل ارنست لودویگ پلانک» (Max Karl Ernst Ludwig Planck) یک فیزیکدان نظری آلمانی بود که بین سالهای ۱۸۵۸-۱۹۴۷ میزیست. اکتشافات پلانک و معرفی ثابت پلانک در زمینه مکانیک کوانتومی موجب شد که او در سال ۱۹۱۸ جایزه نوبل را از آن خود کند.


پلانک کمکهای بسیاری به فیزیک نظری کرد اما شهرت وی به عنوان یک فیزیکدان در درجه اول به نقش وی در بنیانگذاری نظریه کوانتومی استوار است. در سال 1948 موسسه علمی آلمانی «كایزر ویلهلم» (Kaiser Wilhelm) كه پلانك دو دوره ریاست آن را بر عهده داشت به «انجمن ماكس پلانك» (Max Planck Society) (MPS) تغییر نام داد. این پژوهشکده در حال حاضر شامل 83 موسسه است و طیف گستردهای از فعالیتهای علمی را جهتدهی میکند. در این مطلب قصد داریم با ثابت پلانک و کاربرد آن در فیزیک آشنا شویم.
ثابت پلانک چیست؟
ثابت پلانک با نماد یک ثابت فیزیکی و شاخصه اصلی فرمولهای ریاضی مکانیک کوانتومی است. این ثابت رفتار ذرات و امواج در مقیاس اتمی و جنبه ذرهای نور را توصیف میکند.
ماکس پلانک در سال 1900 در فرمول دقیقی که برای توزیع تابش ساطع شده توسط یک جسم سیاه یا جذب کننده کامل انرژی تابشی ارائه داد این ثابت را معرفی کرد.
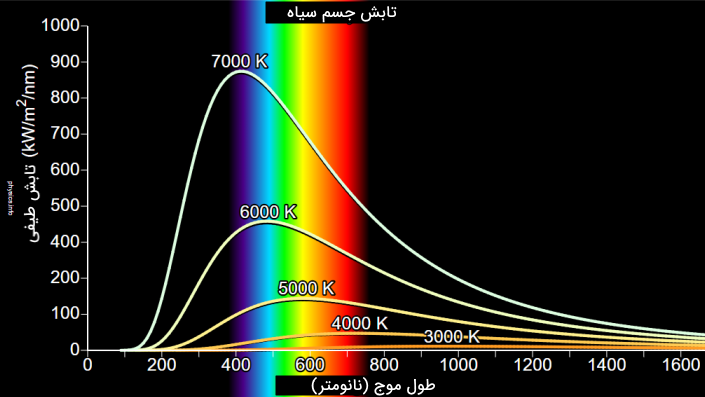
اهمیت ثابت پلانک در این است که نشان میدهد، تابشی مانند نور در بستههای انرژی گسسته یا کوانتومی تابش، منتقل و یا جذب میشود و میزان انرژی بستههای تابش به فرکانس و مقدار ثابت پلانک بستگی دارد.
انرژی هر کوانتوم یا هر فوتون برابر با ثابت پلانک ضربدر فرکانس تابشی است که با حرف یونانی یا نمایش داده میشود، به عبارت ساده است.
یک شکل اصلاح شده از ثابت پلانک به نام «اچبار» (h-bar) یا ثابت پلانک کاهش یافته است که برابر با بوده و کوانتیده تکانه زاویه ای است. به عنوان مثال، تکانه زاویه ای یک الکترون متصل به هسته برابر با کوانتومها یا ضرایبی از است.
بُعد ثابت پلانک حاصلضرب انرژی در زمان است که متناسب با کمیتی به نام عملگر است. ثابت پلانک اغلب به عنوان عملگر کوانتوم بنیادی تعریف میشود و مقدار آن در دستگاه متر- کیلوگرم- ثانیه یا MKS دقیقاً برابر با ژول در ثانیه تعریف میشود.
پیدایش ثابت پلانک
در اواخر دهه 1800 فیزیک با یک بحران روبرو شد. فیزیکدانان در تلاش بودند تا ارتعاشات اتمی را مدل کنند اما چیزی که به دست میآمد با واقعیت سازگاری نداشت. تمام چیزی که در آن زمان میدانستند این بود که مدل کردن ارتعاشات اتمی باید شکل خاصی داشته باشد.
این مشکلی بود که ماکس پلانک حل کرد. فیزیکدانان قبل از او تصور میکردند که ارتعاشات اتمی پیوسته است، یعنی این ارتعاشات میتواند در هر فرکانسی رخ دهد. ولی پلانک فرض کرد كه اتمها فقط در فرکانسهای خاصی كه مضربی از فرکانسهای پایه هستند ارتعاش میکنند که او این فرکانسهای پایه را نامید. به عبارت دیگر اتمها میتوانند در فرکانس ، یا ارتعاش کنند اما این موضوع برای فرکانس صادق نیست.
به بیانی دیگر در مکانیک کلاسیک زمانی که یک کودک در حال تاب سواری است می تواند در هر دامنه (ارتفاع) در مسیر نوسان قرار گیرد و انرژی موجود در سیستم متناسب با مربع دامنه است. از این رو کودک میتواند در هر محدوده پیوسته انرژی از صفر تا یک نقطه معین تاب سواری کند.
اما وقتی از دید کوانتومی به مسئله نگاه کنید رفتار سیستم متفاوت میشود. در این حالت مقدار انرژی که یک نوسانگر میتواند داشته باشد مانند پلههای روی نردبان گسسته است. سطوح انرژی از مرتبه با یکدیگر تفاوت دارند که فرکانس فوتون است. یک الکترون با آزاد کردن یا جذب انرژی میتواند از یک سطح به سطح دیگر انرژی برود.
فرض پلانک واقعاً عجیب بود ولی در مورد مسئله او کار کرد. با توجه به این مدل به نظر میرسد که اتمها (و بسیاری از موارد دیگر) فقط میتوانند مقادیر خاصی را به خود اختصاص دهند. به این ویژگی در فیزیک کوانتیدگی کمیت میگوییم.
اکتشاف پلانک باعث شروع تحقیقات در زمینه جدیدی از فیزیک به نام مکانیک کوانتومی شد. این ثابت بعدها به نام خود او نامگذاری شد و به معنای واقعی بیانگر کلمه کوانتوم در مکانیک کوانتومی است.
اثبات فرمول ثابت پلانک
از لحاظ ریاضی با دانستن طول موج و انرژی نوری که جسم ساطع میکند میتوانیم ثابت پلانک را محاسبه کنیم. طبق قانون پلانک انرژی کوانتیده است و از رابطه زیر پیروی میکند:
از طرف دیگر فرکانس برابر است با سرعت نور بر طول موج نور ساطع شده، یعنی داریم:
بدین ترتیب ثابت پلانک برابر است با:
از نظر تجربی نیز میتوانیم ثابت پلانک را به راحتی و با یک آزمایش ساده محاسبه کنیم. برای انجام این آزمایش به ابزار زیر نیاز داریم:
- منبع تغذیه ۰-۱۰ ولتی
- یک کلید یک طرفه
- ولت متر دیجیتال
- آمپر متر دیجیتال
- یک مقاومت یک کیلواهمی
- چند چراغ LED که نور رنگی ساطع کند و طول موج آنها را بدانیم (رنگ از خود دستگاه باشد نه از پوشش رنگی آن)
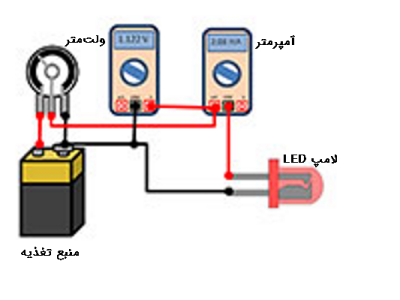
روش انجام آزمایش: LED یک منبع نور نیمههادی با دو خروجی است. در شرایط بایاس غیرمستقیم یک سد پتانسیل در محل پیوندP-N LED ایجاد میشود. هنگامی که LED را به یک ولتاژ خارجی در جهت مستقیم متصل میکنیم ارتفاع سد پتانسیل در طول اتصال P-N کاهش مییابد. در یک ولتاژ خاص ارتفاع سد پتانسیل بسیار کم میشود و LED شروع به تابیدن میکند. یعنی در شرایط بایاس مستقیم الکترونهایی که از محل اتصال P-N عبور میکنند برانگیخته میشوند و هنگام بازگشت به حالت عادی انرژی ساطع میکنند. به این ولتاژ خاص ولتاژ آستانه میگوییم، پس از رسیدن سیستم به ولتاژ آستانه ممکن است جریان افزایش یابد اما ولتاژ تغییر نمیکند. انرژی نور ساطع شده در هنگام بایاس مستقیم به صورت زیر است:
که سرعت نور، ثابت پلانک و طول موج نور است. اگر ولتاژ مستقیم که در آن لامپ شروع به تابش میکند برابر با باشد، انرژی داده شده به الکترونها در عبور از پیوند P-N برابر است با:
با برابر قرار دادن دو رابطه بالا داریم:
که شیب نمودار برحسب است و آن را مینامیم و داریم:
با انجام آزمایش و ثبت مقادیر ولتاژ آستانه بر حسب طول موج با رنگهای مختلف نموداری به صورت زیر به دست میآید.
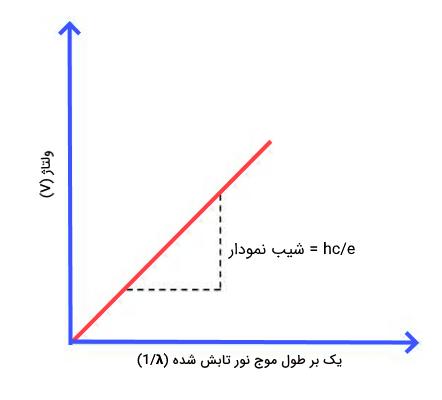
از طرفی با توجه به رابطه بالا میدانیم است، بدین ترتیب با محاسبه شیب نمودار و قرار دادن مقادیر بار الکترون و سرعت نور در معادله، ثابت محاسبه میشود.
ثابت پلانک و اثرفوتوالکتریک
استفاده از اثر فوتوالکتریک روش دیگري برای محاسبه ثابت پلانک است. طبق اثر فوتوالکتریک الکترونها بعد از تاباندن نور به ورقه فلزی از ورقه فلزی خارج میشوند. با برخورد یک فوتون به سطح فلز فوتون جذب می شود این فوتون باعث میشود که یک الکترون از فلز آزاد شود و یک فوتوالکترون به بیرون فرستاده شود. فلزاتی که تحت تاثیر اثر فوتوالکتریک قرار میگیرند را «حساس به نور» (PhotoSensitive) مینامیم. برای اثر فوتوالکتریک یک فرکانس آستانه وجود دارد که از آن فرکانس پایینتر الکترونی از سطح فلز خارج نمیشود.
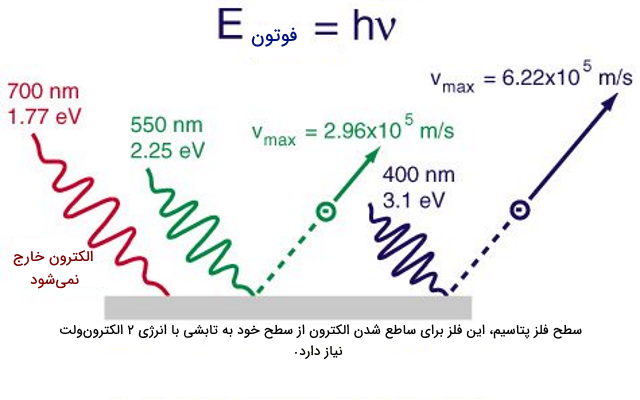
در سال ۱۹۱۶ میلیکان چندین آزمایش طراحی کرد و متوجه شد با تغییر پتانسیل بین صفحه جمعآوری الکترون و صفحه فلزی، جریان الکترونهای خروجی تغییر میکند.
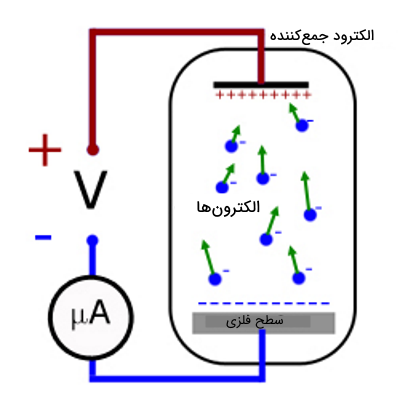
بر اساس این آزمایش هنگامی که یک پتانسیل مثبت کوچک بر روی فلز اعمال شد فقط الکترونهای کمی با انرژی به اندازه کافی بالای توانستند خود را به صفحه جمعکننده الکترون برسانند و تنها یک جریان الکتریکی کوچک در الکترود شناسایی شد. با افزایش پتانسیل مثبت جریان الکترون کاهش یافت. سرانجام در حین آزمایش ولتاژی به دست آمد که جریان الکترونها صفر شد. میلیکان این پتانسیل را پتانسیل توقف نامید. بدین ترتیب میتوان گفت کاری که الکترون برای غلبه بر پتانسیل توقف انجام میدهد ماکزیمم است، یعنی داریم:
از طرفی از اثر فوتوالکتریک معادله زیر به دست میآید:
با ترکیب اثر فوتوالکتریک و آزمایش میلیکان داریم:
و بدین ترتیب خواهیم داشت:
برای مواد مختلف نمودار پتانسیل برحسب فرکانس را رسم میکنیم، این نمودار یک خط راست به شکل زیر است.
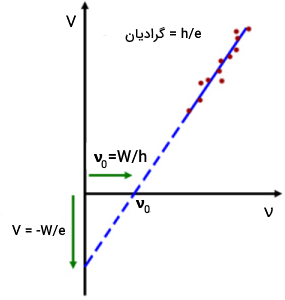
با امتداد نمودار میتوان پتانسیل به ازای فرکانس صفر و فرکانس به ازای پتانسیل صفر را به دست آورد، در حقیقت نقطه برخورد نمودار روی محور افقی و عمودی برابر است با:
که در شکل نیز نمایش داده شده است. با توجه به معادله خط، شیب نمودار نیز برابر با که با توجه به شیب خط و مقدار بار الکتریکی الکترون میتوان ثابت پلانک را محاسبه کرد.
ثابت پلانک بر حسب الکترون ولت
همانطور که گفته شد مقدار ثابت پلانک در دستگاه متر-کیلوگرم-ثانیه برابر است با:
این ثابت در دستگاه «سانتیمتر-گرم-ثانیه» (cgs) برابر با:
و بر حسب واحد الکترونولت مقدار را دارد. ثابت پلانک کاهش یافته نیز در دستگاه cgs و الکترونولت به ترتیب مقادیر زیر را دارد.
زمان پلانک و طول پلانک
طول پلانک مقیاسی است که در آن نظریههای کلاسیکی گرانش و فضا-زمان دیگر صادق نیستند و اثرات و قوانین کوانتومی حاکم میشوند. این کوانتومهای طول کوچکترین طول بامعنی در عالم هستند و برابر با متر یا تقریباً برابر اندازه پروتون هستند.
زمان پلانک مدت زمانی است که یک فوتون با سرعت نور مسافتی برابر با طول پلانک را طی میکند. این کوانتوم زمان، کمترین اندازه برای زمان است که معنی دارد. زمان پلانک برابر با ثانیه است. هر زمانی کوچکتر از این مقدار از لحاظ فیزیکی بیمعنی است. در چارچوب قوانین فیزیک که امروزه آن را درک میکنیم میتوان گفت که عالم زمانی به وجود آمده است که طول عمر آن تنها بوده است.
رابطه بین ثابت پلانک و سرعت نور
اگر فرض کنیم که جسمی که تابش را انجام میدهد یک پروتون است و آن را با نماد نمایش دهیم، باید گفت که میزان تابش ساطع شده از این پروتون برابر با مجموع انرژی فوتونهای تابشی است و داریم:
تنها فرکانس ویژه برای پروتون فرکانس اسپین ذره است که در زمان دور ذره را طی میکند و برابر با است. بدین ترتیب فرکانس پروتون به صورت زیر به دست میآید:
اگر فرض کنیم که تک پروتون از طریق تابش به فوتون تبدیل شده است همه آنها دارای همان فرکانس پروتون هستند، پس معادله (۱) به شکل زیر میشود:
از طرف دیگر طبق معادله همارزی جرم و انرژی اینشتین داریم:
با برابر قرار دادن این دو معادله خواهیم داشت:
و بدین ترتیب رابطه بین سرعت نور و ثابت پلانک به دست میآید:
با جایگذاری مقادیر مربوط به شعاع و جرم یک پروتون، سرعت نور و ثابت پلانک تعداد فوتونهای ساطع شده برابر با به دست میآید که میتوان آن را برابر با ۴ در نظر گرفت.با قرار دادن این مقدار در رابطه بالا و در نظر گرفتن این نکته که است، رابطه بین سرعت نور و ثابت پلانک به صورت زیر خواهد شد:
بدین ترتیب باید گفت و ثابتهای فیزیکی مستقل از یکدیگر نیستند.
آیا ثابت پلانک کاهش یافته است؟
یکی از مسائلی که در زمینه ثابت پلانک منتشر شده، این است که مقدار آن کاهش پیدا کرده است. این مقدار در سال ۱۹۸۵ ژول بر ثانیه اندازهگیری شد، با این حال اندازهگیریهای اخیر در سال ۲۰۱۸ نشان داد ثابت پلانک برابر با ژول بر ثانیه است.
دانشمندان در توضیح این تفاوت بیان میکنند، در حالی که این ثابتهای اساسی در بافت جهان مقدار ثابتی دارند ولی ما انسانها از ارزش دقیق آنها خبر نداریم، به همین دلیل آزمایشاتی میسازیم که هر چه بیشتر به مقدار واقعی این ثابتها نزدیک شویم. دانش ما از ثابت پلانک نیز محصور به چند آزمایش است که برای اندازهگیری ثابت پلانک طراحی شدهاند.
در اندازهگیری اخیر ثابت پلانک دانشمندان از دو آزمایش مختلف استفاده کردهاند، آزمایش تعادل Kibble و روش تراکم کریستال اشعه ایکس یا XRCD. با گذشت زمان دانشمندان متوجه شدند که چهطور میتوانند به اندازهگیری دقیقتری بر اساس این روشها دست یابند.

وقتی مقدار جدیدی از ثابتهای فیزیکی منتشر میشود باید امیدوار باشیم که روش اندازهگیری ما به قدری دقیق بوده است که از مقدار واقعی ثابت خیلی دور نباشد و با در نظر گرفتن خطاهای مطلق و نسبی اندازهگیری به مقدار واقعی دست پیدا خواهیم کرد.
با اینحال از آنجا که نمیتوان از مقدار به دست آمده برای ثابتها به طور کامل مطمئن بود باید این نکته را بیان کرد که مقدار کوچک تغییر برای ثابت پلانک یا ثابتهای فیزیکی دیگر تاثیر زیادی بر روی دنیای اطراف ما نخواهد گذاشت. ولی اگر این مقدار به صورت قابل توجهی بالاتر یا پایینتر باشد همه دنیای اطراف ما كاملاً متفاوت خواهد شد. برای مثال اگر مقدار ثابت پلانک افزایش یابد بدین معنی خواهد بود که اتمهای پایدار ممکن است چندین برابر بزرگتر از ستارگان باشند. با این حال اندازه و مقیاس جدید برای کمیت اصلی یک کیلوگرم که توسط دفتر بین المللی وزن و اندازهگیری در ماه می سال ۲۰۱۹ تایید شد بر پایه مقدار ثابت پلانکی است که اخیرا مورد اندازهگیری قرار گرفته است.













با سلام من معادله درجه سه ای یافته ام که دارای ضرایب ثابت پلانک است و عدد پی را میدهد ایا این معادله کاربردی دارد ؟
با سلام من با استفاده از ثابت پلانک معادله در جه ۳ ای پیدا کرد ه ام که به ازای عدد نامتناهی عدد پی را می دهد ایا این معادله می تواند کاربردی داشته باشد ؟
با سلام.
در واقع این معادله توسط انیشتین ارائه شده و معادله ی پلانک فقط در مورد تابش جسم سیاه بوده است. در وافع در1900 پلانک با فرض گسسته بودن انرژی معادله ای برای توجیه نمودار تجربی جسم سیاه ارائه داد و پنج سال بعد در 1905 معادله گفته شده در متن توسط انیشتین ارائه شد.
سلام و روز شما به خیر؛
طبق منابع معتبر این ثابت توسط ماکس پلانک و در توضیح تابش جسم سیاه معرفی شد و به همین دلیل به نام پلانک نیز نامگذاری شده است. اینشتین بعدها از این رابطه انرژی که پلانک تعریف کرده بود استفاده کرد تا نور را به صورت کوانتیده انرژی یا فوتونها تعریف کند. این موضوعی است که در مطالب و منابع پیشرفته علمی مورد تایید است.
تز اینکه با فرادرس همراه هستید خرسندیم.
باسلام مطلب شما خيلى مفيد بود يك سوال داشتم ايا ثابت پلانك كوچك ترين واحد انتقال انرژى نيست؟
نه، انرژی پلانک کوچکترین واحد انرژی نیست. برخلاف فاصله یا زمان پلانک، انرژی پلانک را می توان به واحدهای بسیار کوچکتری تقسیم کرد که واحد کوچکتر انرژی، کوانتا، برابر با مقدار انرژی حمل شده توسط یک فوتون است.
سلام آیا رابطه ای بین جرم و ثابت پلانک وجود دارد؟ و اگر وجود دارد چگونه تعریف میشود
با سلام
در راستای استانداردسازی مراجع ملی نیاز به اجرای پیمان متر است که در کشور به آن توجه نشده چرا که هفت ثابت بنیادی اساس استانداردسازی استانداردهای مرجع جهانی در مترولوژی است و ثابت پلانک یکی از آن هفت کمیت بنیادی است
و پس از سال ۲۰۱۹ واحد جرم از ثابت پلانک منتج میشود وبا دستگاه کیبل بالانس دقت آن در آزمایشگاه دانش بنیان با نه رقم اعشار بدست میآید تا با مقایسه آزمایشگاهی واحد یک کیلوگرم استاندارد جهانی در سیستم متریک پیمان مترملاک عملی باشد
سلام و وقت به خیر؛
رابطه بین ثابت پلانک و جرم را به راحتی میتوانید از رابطه E=hν تعریف کنید. اگر به جای E رابطه mc2 را قرار دهید رابطه جرم و ثابت پلانک به دست میآید. در رابطه به دست آمده دو ثابت سرعت نور و پلانک وجود دارد که با استفاده از مقادیر اعلام شده این دو ثابت در سال 2019 میتوانید پارامترهای دیگر این معادله را به دست آورید.
از اینکه با مجله فرادرس همراه هستید خرسندیم.