تندی لحظه ای چیست؟ – به زبان ساده + فرمول و مثال

تندی لحظه‌ ای یا «Instantaneous Speed» نشان می‌دهد یک جسم در هر لحظه از زمان با چه سرعتی حرکت می‌کند. این کمیت یک کمیت نرده‌‌ای است و همواره مقادیر مثبت یا صفر را می‌پذیرد. در این نوشته از مجله فرادرس همراه با حل مثال نشان می‌دهیم مفهوم تندی لحظه‌ ای چیست و چه فرمولی دارد. همچنین تفاوت این کمیت را با سایر کمیت‌‌های مشابه در سینماتیک مانند سرعت لحظه‌ای، سرعت متوسط و تندی متوسط توضیح می‌دهیم.

تندی لحظه ای چیست؟

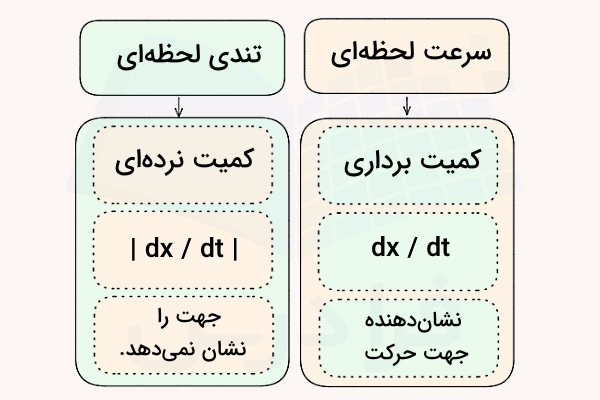
تندی لحظه ای یا تندی آنی نوعی کمیت سینماتیکی است که نشان می‌دهد در یک لحظه‌ بسیار کوتاه و بدون توجه به جهت حرکت، مقدار یا اندازه سرعت یک جسم چیست. در واقع تندی لحظه‌ ای همان قدر مطلق یا اندازه سرعت لحظه‌ای است، بنابراین یک کمیت نرده‌ای یا اسکالر است که همیشه مقداری مثبت یا صفر دارد.

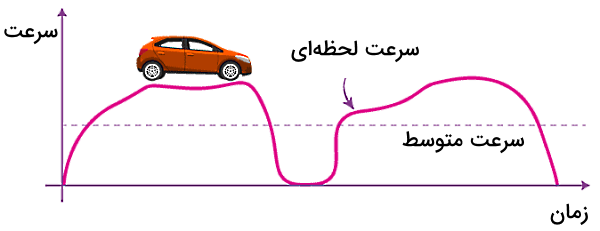
همچنین بهتر است نکات زیر را در مورد تندی لحظه ‌ای به خاطر داشته باشید:

• تندی لحظه ای یک کمیت نرده‌ای، عددی یا اسکالر است، پس جهت ندارد.
• تندی لحظه ای همواره مقداری مثبت یا صفر دارد، پس هیچ‌گاه منفی نیست.
• تندی لحظه ای به صورت قدر مطلق یا اندازه سرعت لحظه‌‌ای تعریف می‌شود.
• در نمودار مکان - زمان، تندی لحظه‌ ای برابر است با شیب خط مماس بر نمودار در آن لحظه.
• اگر حرکت با سرعت ثابت باشد، تندی لحظه‌ای در تمام لحظات ثابت و برابر با تندی متوسط است.
• اگر حرکت با شتاب ثابت باشد، تندی لحظه‌ای در طول زمان تغییر می‌کند و باید برای محاسبه آن از معادله مکان بر حسب زمان مشتق‌گیری کنیم.

تفاوت تندی و سرعت چیست؟

در حالت کلی اغلب از واژه‌های «سرعت» (Velocity) و «تندی» (Speed) به جای یکدیگر استفاده می‌شود. اما در حرکت‌‌شناسی این دو کلمه معنا و کاربردهای کاملا متفاوتی دارند. یکی از تفاوت‌های اصلی تندی و سرعت این است که تندی جهت ندارد، چون یک کمیت نرده‌ای است. در واقع تفاوت این کمیت از تفاوت مسافت و جابجایی ناشی می‌شود. به همین دلیل برای محاسبه تندی لازم است مسافت را بر زمان تقسیم کنیم:

زمان / مسافت = تندی

در مقایسه با تندی، سرعت یک کمیت برداری است و از تقسیم کردن جابجایی بر زمان به دست می‌آید:

زمان / جابجایی = سرعت

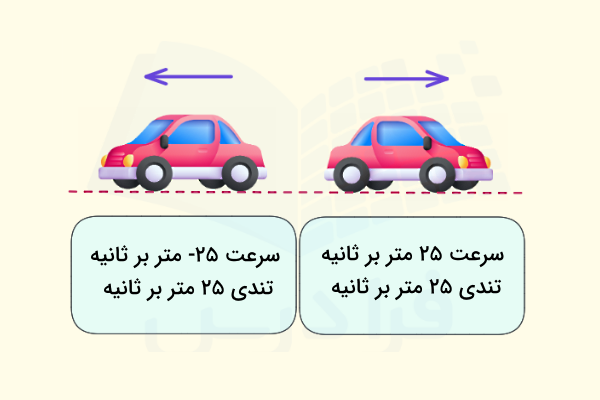
برای مثال اگر حرکتی از یک نقطه آغاز شود و در همان نقطه به پایان برسد، جابجایی صفر است و سرعت نیز صفر می‌شود. با این وجود تندی صفر نیست، چون مسافت پیموده‌ شده مخالف صفر است. می‌دانیم برای مفاهیمی مانند سرعت، تندی و شتاب می‌توانیم دو حالت مختلف لحظه‌ای (یا آنی) و متوسط را در نظر بگیریم. تندی لحظه‌ ای را با قدر مطلق گرفتن از مقدار سرعت لحظه‌ای می‌توان به دست آورد:

| سرعت لحظه‌ ای | = اندازه سرعت لحظه‌‌ ای = تندی لحظه ای

برای نمونه، فرض کنید ذره‌ای در راستای محور افقی و با سرعت ‎$$+ 0.7 \ \frac{m}{s}$$ حرکت می‌کند و ذره‌ دیگری نیز در همان راستا اما با سرعت $$- 0.7 \ \frac{m}{s}$$‎ حرکت کند. با اینکه این دو ذره سرعت‌های متفاوتی دارند، اما تندی آن‌ها یکسان و برابر با ‎$$0.7 \ \frac{m}{s}$$‎ است.

نکته مهم: با اینکه تندی لحظه‌ ای برابر است با اندازه سرعت لحظه‌ای، اما تندی متوسط لزوما با اندازه‌ سرعت متوسط برابر نیست.

در حالت کلی چه در مورد سرعت و تندی لحظه‌ ای و چه در مورد سرعت و تندی متوسط، تفاوت‌های تندی و سرعت به شکل زیر فهرست می‌شوند:

• تندی همواره یک کمیت نرده‌ای است و فقط بزرگی یا اندازه سرعت را نشان می‌دهد، اما سرعت یک کمیت برداری است و علاوه‌بر اندازه، جهت حرکت را نیز مشخص می‌کند.
• تندی همیشه مثبت است ولی سرعت می‌تواند بسته به جهت حرکت منفی هم باشد.
• تندی بر اساس طول مسیر طی‌ شده یا مسافت تعریف می‌شود، در حالی که سرعت بر اساس جابجایی که یک بردار است، محاسبه می‌شود.

فرمول تندی لحظه ای چیست؟

گفتیم تندی لحظه ای معادل است با قدر مطلق یا اندازه سرعت لحظه‌ای. پس اگر فرمول سرعت لحظه‌ای را بدانیم، مشخص است که فرمول تندی لحظه‌ای چیست. فرمول سرعت لحظه‌ای به شکل $$v = \frac{d x}{d t}$$ یا مشتق تابع مکان نسبت به زمان تعریف می‌شود، بنابراین فرمول تندی لحظه ای برابر است با:

$$|\vec{v}| = |\frac{d \vec{x}}{d t} |$$ = تندی لحظه ای

در ادامه نشان می‌دهیم چگونه می‌توان این فرمول را با کمک گرفتن از مفاهیمی مانند حدگیری و مشتق به دست آورد.

می‌دانیم سرعت متوسط یا $$\bar v$$ به شکل جابجایی تقسیم بر زمان تعریف می‌شود:

$$\bar v = \frac{\Delta x}{\Delta t}$$

• $$\bar v$$: سرعت متوسط بر حسب متر بر ثانیه ($$\frac {m}{s}$$)
• $$\Delta x$$: جابجایی بر حسب متر ($$m$$)
• $$\Delta t$$: زمان لازم برای جابجایی بر حسب ثانیه ($$s$$)

با توجه به اینکه جابجایی یک کمیت برداری است، پس سرعت متوسط نیز یک کمیت برداری است، به این معنا که اندازه و جهت سرعت را نشان می‌دهد. سرعت لحظه‌ای به صورت حد سرعت متوسط تعریف می‌شود، زمانی که بازه‌ زمانی  $$\Delta t$$ بسیار کوچک شده یا به سمت صفر میل کند:

$$v = \lim_{\Delta t \rightarrow 0} \bar v = \lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}$$

در ریاضیات $$\lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}$$ برابر است با مشتق مکان نسبت به زمان که با $$\frac{d x}{d t}$$ نشان داده می‌شود. پس سرعت لحظه‌‌ای برابر شد با مشتق معادله مکان نسبت به زمان:

$$v = \frac{d x}{d t}$$

دقت کنید سرعت لحظه‌ای نیز مانند سرعت متوسط یک کمیت برداری است. حالا کافی است از فرمول بالا قدر مطلق بگیریم تا متوجه شویم تندی لحظه ای چیست:

$$|v| = \frac{d x}{d t}$$ = تندی لحظه ای

همچنین واحد تندی لحظه‌ ای در سیستم SI مانند واحد سرعت متوسط یا سرعت لحظه‌ای متر بر ثانیه یا $$\frac {m}{s}$$ است.

چگونه تندی لحظه ای را با فرادرس بهتر یاد بگیریم؟

در بخش قبل یاد گرفتیم تندی لحظه ای چیست و با تفاوت تندی و سرعت نیز آشنا شدیم. گفتیم تندی لحظه‌ای، همان قدر مطلق یا اندازه سرعت متوسط جسم با در نظر گرفتن یک بازه زمانی خیلی خیلی کوچک است، به گونه‌ای که این بازه زمانی عملا به سمت صفر میل‌ می‌کند. در واقع برای داشتن اندازه سرعت در هر نقطه از زمان و مکان، باید تندی لحظه‌ای را محاسبه کنیم. در این بخش قصد داریم چند فیلم آموزشی تهیه شده در مجموعه فرادرس را به شما معرفی کنیم تا با مشاهده آن‌ها، درک بهتری نسبت به مفهوم انواع سرعت، از جمله تندی لحظه‌ای و تندی متوسط به‌ دست آورید.

در کتاب علوم تجربی پایه نهم (بخش فیزیک) مفاهیمی مانند «حرکت، تندی و سرعت» برای اولین بار مطرح و تعریف می‌شوند. سپس در کتاب فیزیک دوازدهم، انواع حرکت توضیح داده می‌شود. به‌طور کلی در حرکت‌شناسی دو نوع حرکت داریم که عبارت‌اند از حرکت با سرعت ثابت و حرکت با شتاب ثابت. اغلب اگر حرکت با سرعت ثابت روی یک خط راست انجام شود، به آن حرکت یکنواخت نیز گفته می‌شود. بنابراین یادگیری تندی لحظه‌ای، یکی از مهم‌ترین نکات تشخیص نوع حرکت و به دنبال آن تشخیص فرمول‌های سینماتیک مناسب برای حل مسئله به‌شمار می‌رود:

1. فیلم آموزش علوم تجربی نهم بخش فیزیک فرادرس
2. فیلم آموزش فیزیک دوازدهم فرادرس
3. فیلم آموزش فیزیک دوازدهم سوالات امتحانات نهایی با حل تشریحی فرادرس
4. فیلم آموزش فیزیک دوازدهم مرور و حل تمرین فرادرس
5. فیلم آموزش فیزیک دوازدهم نکته و حل تست کنکور فرادرس
6. فیلم آموزش رایگان دینامیک و حرکت دایره ای فرادرس
7. فیلم آموزش رایگان نمودار سرعت زمان در فیزیک فرادرس

نمودار تندی زمان چه اطلاعاتی به ما می دهد؟

یکی از روش‌های درک بهتر تغییرات در کمیت‌هایی مانند مکان، سرعت و شتاب این است که نمودار این کمیت‌ها را بر حسب زمان رسم کنیم. برای مثال، اگر تابع مکان بر حسب زمان به شکل یک چند جمله‌ای مانند $$x(t) = at^n +bt +c$$ داده شده باشد که در آن $$a$$ و $$b$$ و $$c$$ اعداد ثابتی هستند، در این صورت برای پیدا کردن نمودار مکان زمان کافی است به $$t$$ عدد بدهیم و $$x$$های متناظر را به دست آوریم.

سپس با مشخص کردن نقاط حاصل شده نمودار $$x$$ بر حسب $$t$$ را رسم می‌کنیم. به همین شکل نمودار تندی - زمان نیز برای توصیف تندی یک جسم و محاسبه شتاب آن بکار می‌رود. اگر مقادیر تندی لحظه‌ای متناظر با هر مقدار زمانی $$t$$ِ مشخص شوند، می‌توانیم این نمودار را رسم کنیم. در ادامه این بخش نکاتی را بیان می‌کنیم که در تحلیل این نمودار در شرایط مختلف به شما کمک می‌کند.

نمودار تندی زمان در حرکت با شتاب ثابت

در اولین بخش ویژگی‌های حرکت با شتاب ثابت را با در نظر گرفتن نکات زیر روی نمودار تندی - زمان بررسی می‌کنیم:

• اگر جسمی با شتاب ثابتی در حال حرکت باشد، نمودار تندی - زمان آن به شکل یک خط مستقیم خواهد بود:
  • در صورتی که مقدار شتاب ثابت برابر با صفر باشد، این خط حتما موازی با محور زمان است.
  • در صورتی که شتاب ثابت ما مخالف صفر باشد، این خط مستقیم با شیب مشخصی از مبدا عبور می‌کند.

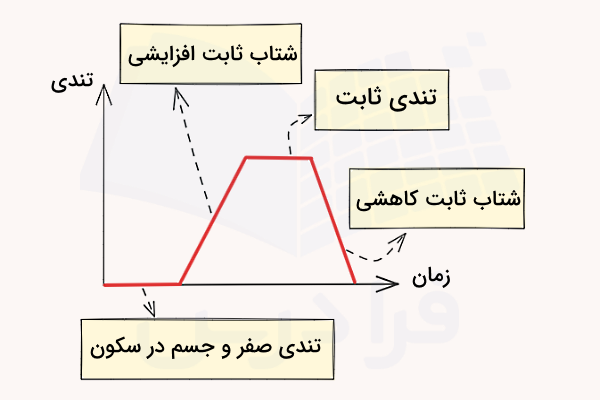
• اگر شتاب جسمی صفر باشد، جسم با سرعت ثابت در حال حرکت است:
  • در نتیجه سرعت جسم با گذشت زمان تغییری نمی‌کند.
  • چنانچه تندی ثابت این جسم برابر با مقدار صفر باشد، می‌گوییم این جسم در حالت ایستا یا ساکن است.
• گرادیان یا شیب نمودار تندی - زمان توصیف کننده شتاب حرکت جسم است:
  • اگر شیب تندی داشته باشیم، شتاب هم مقدار بزرگی دارد.
  • اگر شیب تندی نداشته باشیم، شتاب مقدار بزرگی ندارد.
• شیب مثبت نمودار تندی - زمان نشان دهنده افزایش تندی و شتاب مثبت است.
• شیب منفی نمودار تندی - زمان نشان دهنده کاهش تندی و شتاب منفی است.

نمودار تندی زمان در حرکت با تندی افزایشی یا کاهشی

تصویر زیر نمودار تندی - زمان را برای دو نوع حکرت مختلف با تندی در حال زیاد و کم شدن نشان می‌دهد. این دو نمودار با مانیتور کردن مقادیر تندی لحظه ای در گذر زمان رسم شده‌اند. هر دوی این نمودارها حرکت با شتاب ثابت را نمایش می‌دهند، چون خطوط حاصل از رصد کردن تندی‌های لحظه‌ای برای هر دو به شکل یک خط مستقیم شده است.

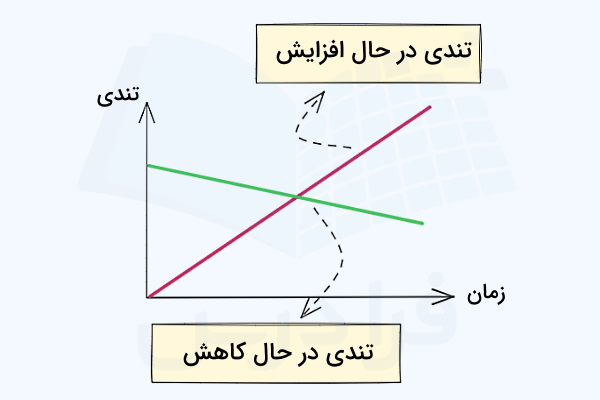
دقت کنید شیب مثبت نشان دهنده تندی لحظه ای افزایشی یا شتاب مثبت است، در حالی که شیب منفی تندی در حال کم شدن یا شتاب منفی را توصیف می‌کند.

مساحت زیر نمودار تندی زمان

مساحت زیر نمودار تندی زمان توصیف کننده مسافت پیموده شده توسط جسم متحرک است. نکته مهم این است که در مورد نمودار تندی بر حسب زمان باید دقت کنیم که مساحت این بخش فقط مسافت را نشان می‌دهد، نه جابجایی را. در تصویر زیر مساحت زیر نمودار تندی - زمان معادل است با مجموع مساحت مربع و مساحت مثلث مشخص شده. پس برای محاسبه مسافت طی شده توسط این جسم، فقط کافی است به فرمول‌های مساحت اشکال هندسی مسلط باشید.

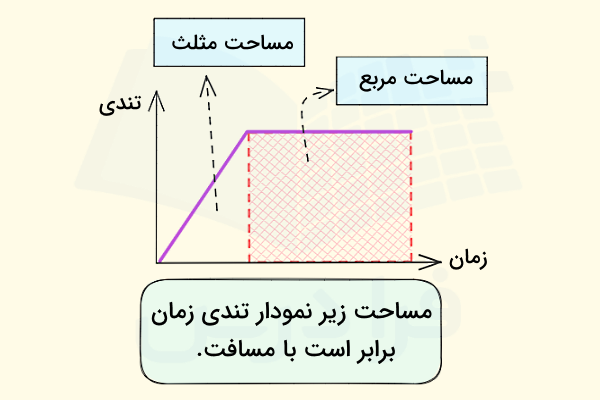
نکته: مسافت پیموده شده برای بخش خاصی از حرکت نیز برابر می‌شود با سطح زیر نمودار تندی - زمان متناظر با همان بخش از حرکت. در بخش حل مثال و تمرین با کاربرد این نمودار در حل مسائل بیشتر آشنا خواهید شد.

تفاوت تندی لحظه ای و سرعت لحظه ای چیست؟

تندی لحظه‌ای یک کمیت نرده‌ای است که بر مبنای تقسیم مسافت بر زمان حاصل می‌شود، در حالی که سرعت لحظه‌ای کمیتی برداری است و بر اساس تقسیم جابجایی بر زمان محاسبه می‌شود. بنابراین تندی لحظه‌ای همیشه عددی مثبت یا صفر است، اما سرعت لحظه‌ای می‌تواند منفی نیز باشد. شباهت این دو کمیت در این است که هر دو برای بیان مقادیر سرعت در لحظه بکار می‌روند. در بخش بعد سرعت لحظه‌ای را با جزئیات تعریف می‌کنیم تا بهتر متوجه شوید تفاوت آن با تندی لحظه ای چیست.

سرعت لحظه ای چیست؟

در دنیای فیزیک کلاسیک اغلب اجسام به شکل پیوسته‌ای در فضا و زمان حرکت می‌کنند و معمولا ما نیز به دنبال این هستیم که سرعت یک جسم را در هر نقطه‌ از مسیر حرکت‌اش پیدا کنیم. این سرعت همان سرعت لحظه‌ای یا Instantaneous Velocity است که با کمک گرفتن از اصول بنیادی حسابان می‌توانیم مقدار آن را محاسبه کنیم. سرعت لحظه‌ای یک جسم نشان می‌دهد که آن جسم در هر نقطه از مسیر خود با چه سرعتی و در چه جهتی حرکت می‌کند. گاهی به سرعت لحظه‌ای به اختصار سرعت نیز گفته می‌شود.

از دید علم فیزیک، سرعت لحظه‌ای همان سرعت متوسط بین دو نقطه از مسیر است، اما در حالت حدی که زمان و در نتیجه جابجایی بین این دو نقطه به صفر نزدیک می‌شود. برای بیان این مفهوم به‌ زبان ریاضی، اولین قدم این است که موقعیت $$x$$ را به‌صورت تابع پیوسته‌ای از زمان یا $$t$$ نشان دهیم که با $$x(t)$$ نمایش داده می‌شود. فرمول سرعت متوسط بین دو نقطه با استفاده از این نماد به‌صورت زیر خواهد شد:

$$\bar v = \frac{x(t_2) - x(t_1)}{t_2 - t_1 }$$

در بخش‌ بعد همراه با حل مثال بیشتر توضیح می‌دهیم که چگونه می‌توان سرعت متوسط بین دو موقعیت را محاسبه کرد. اما برای یافتن سرعت لحظه‌ای در هر موقعیت با در نظر گرفتن $$t_1 = t$$ و $$t_2 = t + \Delta t$$، قرار دادن این مقادیر در عبارت بالا و سپس حدگیری در حالتی که بازه زمانی موردنظر به سمت صفر میل کند یا $$\Delta { t} \rightarrow 0$$، خواهیم داشت:

$$v(t) = \lim_{\Delta { t} \rightarrow 0} \frac{x(t+\Delta t) - x(t) }{\Delta t } = \frac{dx(t) }{dt }$$

عبارت بالا همان فرمول سرعت لحظه‌ای است که بر مبنای حدگیری و به سمت صفر میل کردن سرعت متوسط به دست آمد. به این ترتیب سرعت لحظه‌ای یک جسم همان حد سرعت متوسط آن است، مادامی که زمان سپری‌ شده به صفر نزدیک شود. معادل ریاضیاتی این توضیح مشتق‌گیری از مکان نسبت به زمان است:

$$v(t) = \frac{d}{dt } x(t)$$

سرعت لحظه‌ای نیز مانند سرعت متوسط یک بردار است و دیمانسیون یا بعد آن به شکل طول بر زمان تعریف می‌شود. به بیان دقیق‌تر، سرعت لحظه‌ای در یک نقطه زمانی مشخص مانند $$t_0$$ همان نرخ تغییرات تابع مکان ($$x(t)$$) یا شیب تابع مکان بر حسب زمان در نقطه‌ مشخصی مانند $$t_0$$ است.

تصویر زیر نشان می‌دهد که چگونه سرعت متوسط بین دو نقطه به سرعت لحظه‌ای در $$t_0$$ نزدیک می‌شود. در این شکل نمونه‌ای از یک نمودار مکان - زمان را داریم و نقطه $$t_0$$ در ماکزیمم مکان ممکن قرار دارد. به همین علت شیب نمودار مکان - زمان در این نقطه صفر است. در نتیجه سرعت لحظه‌ای نیز در $$t_0$$ صفر است:

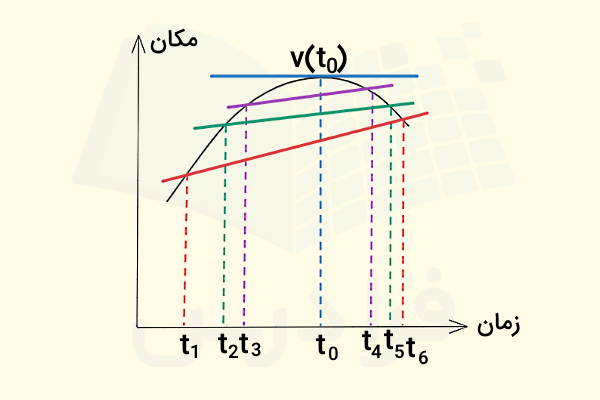
این در حالی است که در زمان‌های دیگری مانند $$t_2$$ و $$t_1$$ سرعت لحظه‌ای مخالف صفر است، چون شیب نمودار در این لحظات مثبت یا منفی است. همچنین در تصویر بالا سرعت‌های متوسط $$\bar v = \frac{x_f - x}{t_f - t} = \frac{\Delta x}{\Delta t}$$ برای بازه‌‌های زمانی $$\Delta t = t_6 - t_1$$ و $$\Delta t = t_5 - t_2$$ و $$\Delta t = t_4 - t_3$$ نشان داده شده است و به محض اینکه $$\Delta { t} \rightarrow 0$$، سرعت متوسط در $$t = t_ 0$$ به سرعت لحظه‌ای نزدیک خواهد شد.

در نهایت نتایج حاصل از توضیحات این بخش را می‌توان به شکل زیر فهرست کرد:

• سرعت لحظه‌ای در نمودار مکان - زمان برابر است با شیب خط مماس بر نمودار در یک نقطه مشخص.
• چنانچه تابع $$x(t)$$ دارای بیشینه یا کمینه باشد، شیب نمودار مکان -زمان و سرعت لحظه‌ای نیز در لحظه زمانی متناظر با آن نقاط صفر خواهد شد.
• نقاطی که در آن‌ها خط مماس بر نمودار مکان - زمان کاملا افقی باشد (معادل با شیب صفر)، همان نقاط بیشینه یا کمینه تابع $$x(t)$$ هستند.
• نقاط صفر تابع سرعت، همان نقاط کمینه یا بیشینه تابع مکان یا $$x(t)$$ را مشخص می‌کنند.
• خطوط رنگی نشان‌ دهنده سرعت متوسط بین دو زمان مختلف هستند و هر چه فاصله زمانی کمتر شود، سرعت متوسط به سرعت لحظه‌ای نزدیک‌تر می‌شود.
• شیب مثبت نمودار مکان - زمان نشان‌ دهنده حرکت در جهت مثبت محور مکان و شیب منفی این نمودار نشان‌ دهنده حرکت در جهت منفی محور مکان است.
• هرچه خطوط سرعت متوسط به نقطه $$t = t_ 0$$ نزدیکتر شوند، مقدار آن‌ها به مقدار سرعت لحظه‌ای در این نقطه یا $$v( t_ 0)$$ نزدیک‌تر است.
• نمودار مکان - زمان نشان می‌دهد که سرعت لحظه‌ای بسته به شیب نمودار در آن لحظه می‌تواند مثبت، صفر یا منفی باشد.

فرمول سرعت لحظه ای چیست؟

اولین قدم برای محاسبه‌ سرعت لحظه‌ای این است که شکل صریح تابع مکان یا $$x(t)$$  را بدانیم. برای نمونه، اگر هر جمله در معادله‌ $$x(t)$$ به شکل کلی $$A t^n$$‎ باشد که در آن $$A$$‎ یک عدد ثابت و $$n$$‎ یک عدد صحیح است، با استفاده از روش‌های مشتق‌گیری داریم:

$$\frac {d}{dt} x(t) = \frac {d}{dt} A t^n = Ant^{n-1}$$‎

توجه داشته باشید که اگر جملات دیگری نیز به $$A t^n$$‎ اضافه شوند، باز هم می‌توان قاعده‌ بالا را برای هر جمله به‌طور جداگانه اعمال کرد و پاسخ نهایی برابر با جمع مشتق‌های این جملات خواهد بود. در همین راستا می‌توانید از فیلم آموزش رایگان فرمول محاسبه سرعت متوسط و لحظه ای + حل مثال فرادرس نیز استفاده کنید که لینک آن جهت دسترسی راحت‌تر شما در ادامه قرار داده شده است:

حل مثال از سرعت لحظه ای

در این بخش چند نمونه سوال در زمینه کاربردهای فرمول سرعت لحظه‌ای حل می‌کنیم. پیشنهاد می‌کنیم روش حل و توضیحات داده شده را کاملا مطالعه کنید تا بهتر متوجه شوید مفهوم و تفاوت‌های سرعت لحظه‌ای و سرعت متوسط با تندی لحظه‌ ای چیست. همچنین در یکی از سوالات پس از رسم نمودارهای مختلف این تفاوت‌ها را بهتر درک خواهید کرد.

مثال ۱

اگر تابع موقعیت مکانی ذره‌ای توسط معادله $$x(t) = 3t + 0.5 t^3$$ مشخص شود، به سوالات زیر پاسخ دهید:

1. سرعت لحظه‌ای در لحظه $$t = 2 \ s$$ چقدر است؟
2. سرعت را بین دو لحظه $$1 \ s$$ و $$3 \ s$$ محاسبه کنید:

پاسخ

برای پاسخ به اولین سوال، توجه داریم که معادله داده شده همان معادله حرکت ذره و یک تابع چند جمله‌ای بر حسب زمان است. با مشتق‌گیری از این معادله تابع سرعت به شکل زیر به دست می‌آید:

$$\Rightarrow v(t) = \frac{d}{dt} x(t) \Rightarrow v(t) = 3 + 1.5 t^2$$

پس از اینکه معادله سرعت بر حسب زمان مشخص شد، حالا می‌توانیم با قرار دادن لحظه $$t = 2 \ s$$ در این معادله، سرعت لحظه‌ای معادل با این زمان را به شکل زیر به دست آوریم:

$$\Rightarrow v(t) = 3 + 1.5 (2)^2 = 9 \ \frac{m}{s}$$

در دومین سوال، اگر دقت کنید سرعت برای بازه‌ای از زمان یا بین دو لحظه مشخص از زمان خواسته شده است. پس در اینجا منظور سوال کننده محاسبه سرعت متوسط است، نه سرعت لحظه‌ای. برای پیدا کردن سرعت متوسط فرمول زیر را می‌نویسیم:

$$\bar v = \frac{x(t_2) - x(t_1)}{t_2 - t_1 }$$

در واقع مقادیر $$t_1$$ و $$t_2$$ در صورت سوال مشخص شده‌اند. اما $$x_1$$ و $$x_2$$ را نداریم و لازم است با توجه به زمان‌های موردنظر، مقدار $$x$$ یا مکان متناظر با هر زمان را طبق معادله مکان داده شده به شکل زیر پیدا کنیم:

$$x(t_1) = 3t_1 + 0.5 t_1^3 \Rightarrow x(t_1) = 3(1) + 0.5 (1)^3 = 3 + 0.5 = 3.5 \ m$$

$$x(t_2) = 3t_2 + 0.5 t_2^3 \Rightarrow x(t_2) = 3(3) + 0.5 (3)^3 =22.5 \ m$$

$$\Rightarrow \bar v = \frac{22.5 - 3.5}{3-1 } = 9.5 \ \frac{m}{s}$$

دقت کنید اگر این بازه زمانی به سمت صفر میل کند، مقدار به‌ دست‌ آمده برای سرعت متوسط نیز به مقدار سرعت لحظه‌ای میل می‌کند یا همگرا می‌شود.

مثال ۲

معادله مکان - زمان جسمی به شکل $$x(t) = 3t - 3t^2$$ داده شده است. به سوالات زیر پاسخ دهید:

1. سرعت لحظه‌ای در زمان‌های $$t_1 = 0.25 \ s$$ و $$t_2 = 0.5 \ s$$ و $$t_3 = 1 \ s$$ چقدر است؟
2. تندی لحظه‌ ای حرکت جسم در این لحظات را نیز حساب کنید:
3. نمودارهای مکان - زمان، سرعت - زمان و تندی - زمان را برای این حرکت رسم کنید:
4. طبق نمودارهای رسم شده، حرکت این جسم را تحلیل کنید:

پاسخ

مانند مثال قبل، کافی است ابتدا از معادله مکان نسبت به زمان مشتق‌گیری کنیم. سپس هر کدام از لحظات موردنظر را در معادله سرعت به‌ دست آمده قرار می‌دهیم تا سرعت لحظه‌ای متناظر با هر لحظه مشخص شود:

$$\Rightarrow v(t) = \frac{d}{dt} x(t) \Rightarrow v(t) = 3 -6 t$$

$$\Rightarrow v(t_1) = 3 - 6 \times 0.25 =1.5 \ \frac{m}{s}$$

$$\Rightarrow v(t_2) = 3 - 6 \times 0.5 = 0 \ \frac{m}{s}$$

$$\Rightarrow v(t_2) = 3 - 6 \times 1 = -3 \ \frac{m}{s}$$

برای محاسبه تندی لحظه‌ای متناظر با هر کدام از این لحظات، کافی است قدر مطلق سرعت لحظه‌ای‌های محاسبه شده را حساب کنیم:

$$\Rightarrow |v(t_1)| = |1.5 |\ \frac{m}{s} = 1.5 \ \frac{m}{s}$$

$$\Rightarrow |v(t_2)| = |0 |\ \frac{m}{s} = 0 \ \frac{m}{s}$$

$$\Rightarrow |v(t_3)| = |-3 |\ \frac{m}{s} = 3 \ \frac{m}{s}$$

می‌دانیم سرعت به ما اطلاعاتی درباره جهت حرکت می‌دهد و نشان می‌دهد که جسم به سمت چپ (غرب) یا راست (شرق) در حال حرکت است. اما تندی (سرعت بدون جهت) بزرگی سرعت را نشان می‌دهد. با رسم نمودارهای مکان، سرعت و تندی بر حسب زمان می‌توانیم این مفاهیم را به‌صورت بصری درک کنیم. ابتدا نمودار مکان - زمان را رسم می‌کنیم. کافی است برای سه نقطه زمانی داده شده یعنی $$t_1 = 0.25 \ s$$ و $$t_2 = 0.5 \ s$$ و $$t_3 = 1 \ s$$ مقادیر $$x(t)$$ متناظر را مشخص کنیم:

$$\Rightarrow x(t_1) = 3t_1 - 3t_1^2 \Rightarrow x(0.25) = 3(0.25) - 3(0.25)^2 = 0.5 \ m$$

$$\Rightarrow x(t_2) = 3t_2 - 3t_2^2 \Rightarrow x(0.5) = 3(0.5) - 3(0.5)^2 = 0.75 \ m$$

$$\Rightarrow x(t_3) = 3t_3 - 3t_1^3 \Rightarrow x(1) = 3(1) - 3(1)^2 = 0 \ m$$

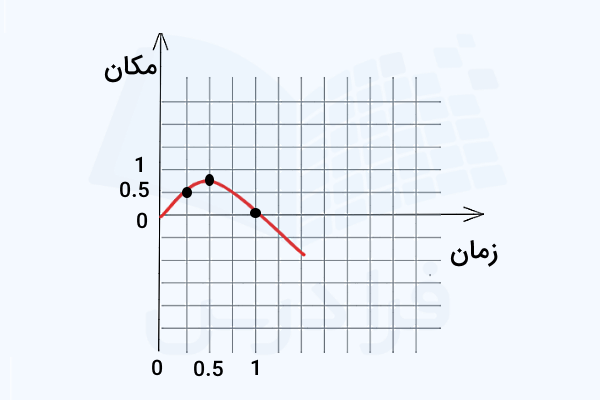
طبق نمودار بالا جسم تا لحظه $$t = 0.5 \ s$$ در جهت مثبت حرکت می‌کند و سپس جهت حرکت خود را عوض می‌کند. این تغییر جهت جسم در نمودار سرعت - زمان بهتر مشخص است، جایی که در  $$t = 0.5 \ s$$ سرعت صفر و سپس منفی می‌شود. برای رسم نمودار سرعت - زمان نیز کافی است به ازای سه لحظه موردنظر، مقادیر سرعت لحظه‌ای محاسبه شده را از محور عمودی مشخص کنیم:

$$\Rightarrow v(t_1) = 3 - 6 \times 0.25 =1.5 \ \frac{m}{s}$$

$$\Rightarrow v(t_2) = 3 - 6 \times 0.5 = 0 \ \frac{m}{s}$$

$$\Rightarrow v(t_2) = 3 - 6 \times 1 = -3 \ \frac{m}{s}$$

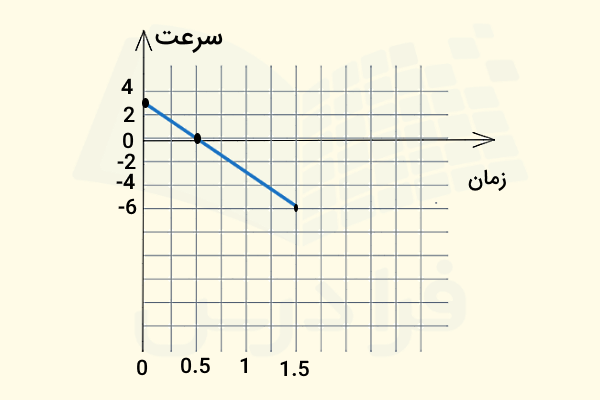
در لحظه $$t = 1 \ s$$ طبق نمودار مکان - زمان جسم دوباره به نقطه مبدا بازمی‌گردد، درست در نقطه‌ای که حرکت خود را شروع کرده بود. همچنین سرعت در $$t = 1 \ s$$ و در نمودار سرعت - زمان منفی است، زیرا جسم در جهت منفی حرکت می‌کند. اما در نمودار بعدی ملاحظه می‌کنید که تندی بر خلاف سرعت همواره مثبت است و در طول زمان حرکت نیز همواره مثبت باقی می‌ماند:

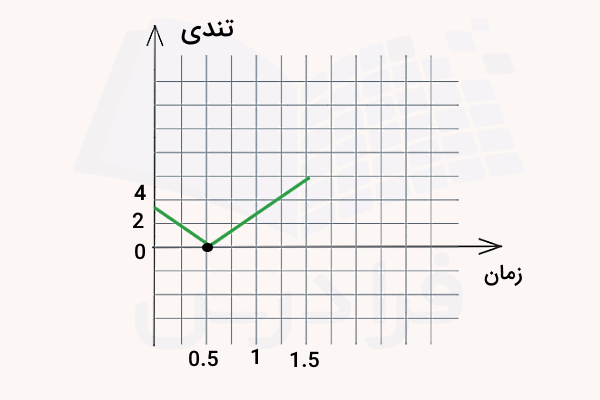
می‌توانیم سرعت را به‌ عنوان شیب نمودار مکان - زمان نیز تفسیر کنیم. شیب نمودار مکان - زمان معادل است با شیب خطی که مماس بر این نمودار در هر لحظه رسم می‌شود. در ادامه با توجه به این نکته تحلیل زیر را خواهیم داشت:

• در بازه زمانی $$t = 0 \ s$$ تا $$t = 0.5 \ s$$: شیب خط مماس بر نمودار مکان - زمان و در نتیجه سرعت نیز مثبت است. با گذشت زمان از $$t = 0 \ s$$ تا $$t = 0.5 \ s$$ سرعت در عین مثبت بودن، در حال کم شدن نیز هست که اصطلاحا می‌گوییم روند سرعت کاهشی است. نمودار سرعت - زمان در این بازه معادل است با یک خط مستقیم که نشان دهنده مقادیر مثبت اما با روند کاهشی برای سرعت است. نمودار تندی - زمان نیز در این بازه کاملا منطبق با نمودار سرعت - زمان است، چون سرعت مثبت بوده و قدر مطلق آن نیز مثبت است.
• در لحظه $$t = 0.5 \ s$$: خط مماس بر نمودار مکان - زمان کاملا موازی با محور افقی است. پس شیب آن یا همان سرعت لحظه‌ای در این نقطه صفر است. در نمودارهای سرعت - زمان و تندی - زمان نیز در این لحظه مقدار سرعت و تندی صفر است.
• در بازه زمانی $$t = 0.5 \ s$$ تا $$t = 1 \ s$$: پس از لحظه $$t = 0.5 \ s$$ شیب نمودار مکان - زمان منفی است، پس سرعت نیز منفی است، در حالی که روند افزایشی دارد. نمودار سرعت - زمان در این بازه خط مستقیمی است که مقادیر منفی اما افزایشی سرعت را توصیف می‌کند. نمودار تندی - زمان نیز با توجه به اینکه قدر مطلق سرعت را نشان می‌دهد، پس مقادیر مثبت اما با روند افزایشی را ارائه می‌دهد.

تفاوت تندی لحظه ای و تندی متوسط چیست؟

تا اینجا یاد گرفتیم تعریف و فرمول تندی لحظه ای چیست. اصلی‌ترین تفاوت تندی لحظه ای و تندی متوسط در این است که تندی لحظه‌ای مقدار سرعت را در یک لحظه از زمان به ما می‌دهد، اما تندی متوسط میانگین اندازه سرعت را در یک بازه زمانی مشخص برای ما محاسبه می‌کند. در واقع درک تفاوت‌‌ دو مفهوم «لحظه‌ای» و «متوسط» یکی از مهم‌ترین مباحث سینماتیک است و می‌توان کمیت‌هایی مانند تندی، سرعت و شتاب را بر مبنای این دو مفهوم به شکل زیر تقسیم‌بندی و تعریف کرد:

• سرعت متوسط: به جابجایی کل یک جسم در یک بازه زمانی مشخص اشاره دارد. سرعت متوسط یک کمیت برداری است که هم اندازه دارد و هم جهت.
• سرعت لحظه‌ای: سرعت و جهت حرکت یک جسم در یک لحظه معین از زمان را نشان می‌دهد. سرعت لحظه‌ای یک کمیت برداری است.
• تندی متوسط: به مسافت کل طی شده توسط یک جسم در یک بازه زمانی مشخص اشاره دارد. تندی متوسط یک کمیت اسکالر است و فقط اندازه دارد، نه جهت.
• تندی لحظه‌ای: اندازه یا قدر مطلق سرعت لحظه‌ای و در واقع همان مقداری است که سرعت‌سنج خودرو نشان می‌دهد. تندی لحظه‌ ای فقط مقادیر مثبت یا صفر را می‌پذیرد و یک کمیت عددی است.
• شتاب متوسط: به میزان تغییر سرعت یک جسم در یک بازه زمانی مشخص اشاره دارد. شتاب متوسط یک کمیت برداری است که هم اندازه و هم جهت دارد.
• شتاب لحظه‌ای: شتاب یک جسم در یک لحظه معین از زمان است. به عنوان مثال زمانی که با فشار دادن پدال گاز یا ترمز سرعت خودروی خود را تغییر می‌دهید، در واقع شتاب لحظه‌ای را تجربه می‌کنید.

در این بخش ابتدا مفهوم سرعت متوسط را توضیح می‌دهیم. سپس به تندی متوسط می‌رسیم و خواهیم دید تفاوت‌ آن با تندی لحظه ای چیست.

سرعت متوسط چیست؟

می‌دانیم سرعت یک جسم معادل است با آهنگ تغییرات مکان آن نسبت به زمان. برای اینکه بتوانیم یک فرمول ریاضیاتی مناسب برای سرعت داشته باشیم، مکان جسم را برای هر زمان دلخواه $$t_i$$ برابر با $$x_i$$ در نظر می‌گیریم، با این فرض که $$x_i$$ یک بردار و نشان دهنده موقعیت مکانی جسم از نظر عددی و برداری است. حالا اگر جزئیات حرکت جسم در هر لحظه مهم نباشد، این نرخ یا آهنگ تغییرات به‌صورت یک کمیت برداری به نام سرعت متوسط یا Average Velocity بیان می‌شود.

در واقع سرعت متوسط عبارت است از جابجایی بین دو نقطه تقسیم بر زمانی که برای پیمودن این فاصله صرف شده است. دقت کنید جابجای یک کمیت برداری است. همچنین به زمانی که برای حرکت بین این دو نقطه صرف می‌شود، زمان سپری‌ شده یا $$\Delta t$$ گفته می‌شود. پس اگر $$\vec{x_1}$$ و $$\vec{x_2}$$ بردارهای مکان جسم در لحظات $$t_1$$ و $$t_2$$ باشند، جابجایی عبارت است از $$\Delta \vec{ x} = \vec{x_2} - \vec{x_1}$$ و فرمول سرعت متوسط نیز به شکل زیر خواهد شد:

 زمان سپری شده برای این جابجایی / جابجایی بین دو نقطه = $$\vec{\bar v}$$ = سرعت متوسط

$$\vec{\bar v} = \frac{\Delta \vec{ x} }{\Delta t } = \frac{\vec{x_2} - \vec{x_1} }{t_2 - t_1 }$$

بنابراین نکته مهم این است که سرعت متوسط یک کمیت برداری است و می‌تواند حتی منفی باشد، در واقع این موضوع به موقعیت‌ بردارهای $$\vec{x_1}$$ و $$\vec{x_2}$$ بستگی دارد.

تندی متوسط چیست؟

در بخش قبل با سرعت متوسط و فرمول آن کاملا آشنا شدیم. کافی است در فرمول سرعت متوسط به جای جابجایی، مسافت را در نظر بگیریم تا تندی متوسط را داشته باشیم. پس تندی متوسط معادل است با مسافت طی شده توسط یک جسم در یک بازه زمانی مشخص. به تفاوت تندی متوسط و تندی لحظه‌ ای نیز در بخش‌های قبل اشاره شد.

حل مثال از سرعت متوسط و تندی متوسط

حل و بررسی سوالات زیر به شما کمک می‌کند تا بهتر متوجه مفهوم و فرمول سرعت متوسط شوید. برای نمونه، سوال زیر نشان می‌دهد که چگونه می‌توانیم با داشتن نمودار مکان - زمان، نمودار سرعت - زمان یا همان نمودار تغییرات سرعت متوسط را رسم کنیم.

مثال ۱

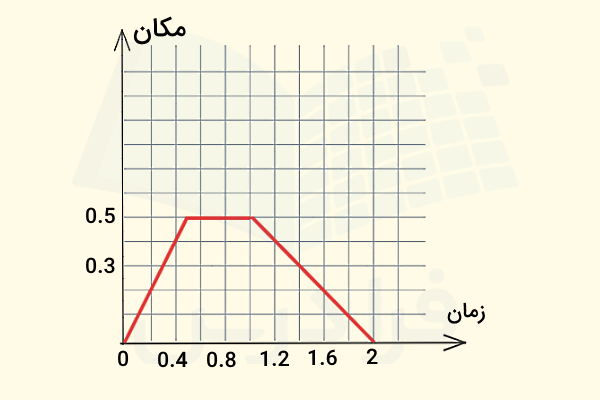
با توجه به نمودار مکان بر حسب زمان در شکل زیر، نمودار سرعت بر حسب زمان را رسم کنید:

پاسخ

برای پاسخ‌دهی به این سوال، ابتدا بهتر است حرکت جسم را طبق نمودار مکان - زمان داده شده بررسی کنیم. این جسم در ابتدا در جهت مثبت حرکت می‌کند، برای مدت کوتاهی متوقف می‌شود و سپس جهت حرکت خود را عوض کرده و به سمت مبدا حرکت می‌کند. همچنین این نمودار شامل سه خط مستقیم در سه بازه زمانی مختلف است. پس سرعت در هر بازه زمانی با پیدا کردن شیب این خطوط محاسبه می‌شود. پس بهتر است سرعت متوسط را برای هر کدام از این سه بازه به شکل زیر پیدا کنیم:

• در بازه زمانی $$0 \ s$$ تا $$0.5 \ s$$، سرعت متوسط برابر است با $$\bar v = \frac{\Delta { x} }{\Delta t } = \frac{0.5 - 0 }{0.5 - 0 }= 1 \ \frac{m}{s}$$.
• در بازه زمانی $$0.5 \ s$$ تا $$1 \ s$$، سرعت متوسط برابر است با $$\bar v = \frac{\Delta { x} }{\Delta t } = \frac{0 - 0 }{1 - 0.5 }= 0 \ \frac{m}{s}$$.
• در بازه زمانی $$1 \ s$$ تا $$2 \ s$$، سرعت متوسط برابر است با $$\bar v = \frac{\Delta { x} }{\Delta t } = \frac{0 - 0.5 }{2 - 1 }= -0.5 \ \frac{m}{s}$$.

بنابراین با توجه به مقادیر سرعت محاسبه شده برای هر بازه، نمودار سرعت - زمان به شکل زیر رسم می‌شود:

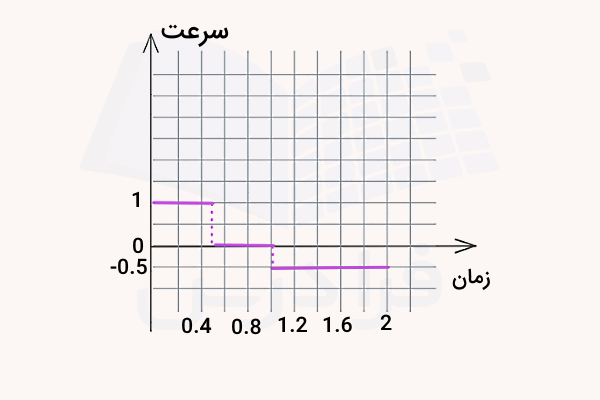
طبق این نمودار، سرعت در بخش اول حرکت مثبت است، هنگام توقف جسم سرعت صفر می‌شود و زمانی که جسم جهت حرکت خود را عوض می‌کند، سرعت منفی است. در حقیقت در بازه زمانی بین $$0 \ s$$ تا $$0.5 \ s$$، مکان جسم در حال دور شدن از مبدا است و نمودار مکان - زمان شیب مثبتی دارد. پس در هر نقطه از این بازه زمانی می‌توانیم سرعت لحظه‌ای را با گرفتن شیب نمودار به‌دست آوریم که برابر است با $$+ 1 \ \frac{m}{s}$$. در بازه زمانی بعدی یعنی بین $$0.5 \ s$$ تا $$1 \ s$$ مکان جسم تغییری نمی‌کند و می‌بینیم که شیب و در نتیجه سرعت صفر است.

از $$1 \ s$$ تا $$2 \ s$$ نیز جسم به سمت مبدا حرکت می‌کند و شیب برابر است با $$-0.5 \ \frac{m}{s}$$. در اینجا چون جسم جهت حرکت خود را عوض کرده، پس سرعت منفی دارد. پیشنهاد می‌کنیم برای کسب اطلاعات بیشتر در زمینه تبدیلات نمودارهای سرعت - زمان و شتاب - زمان، مطلب «تبدیل نمودار شتاب زمان به سرعت زمان – از صفر تا صد با مثال و تمرین» مجله فرادرس را مطالعه نمایید.

مثال ۲

مریم از خانه‌ خارج می‌شود تا بروشورهای حراج حیاط خود را پخش کند. او مستقیم به سمت شرق در طول خیابانی که دو طرف آن خانه است، حرکت می‌کند. $$9 \ min$$ بعد و در فاصله $$0.5 \ km$$، بروشورها تمام می‌شود و او باید مسیر را برگردد تا بروشورهای دیگری از خانه بردارد. این بازگشت $$9 \ min$$ اضافی طول می‌کشد. پس از برداشتن بروشورهای بیشتر او دوباره در همان مسیر حرکت می‌کند، از جایی که قبلا توقف کرده بود ادامه می‌دهد و در نهایت $$1 \ km$$ از خانه‌ فاصله می‌گیرد. این بخش سوم از پیمایش او $$15 \ min$$ طول می‌کشد. در این نقطه او به سمت خانه برمی‌گردد و جهت حرکت غرب است. پس از طی کردن $$1.75 \ km$$ و گذشت مدت زمان $$25 \ min$$، برای استراحت توقف می‌کند.

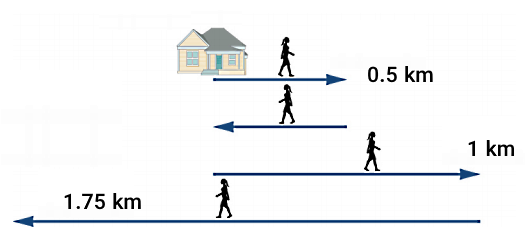
به سوالات زیر پاسخ دهید:

1. کل جابجایی مریم تا نقطه‌ای که برای استراحت می‌ایستد، چقدر است؟
2. قدر مطلق جابجایی نهایی چقدر است؟
3. سرعت متوسط مریم در کل این پیمایش چقدر است؟
4. مسافت کل طی‌ شده چقدر است؟
5. نموداری از موقعیت مکانی نسبت به زمان رسم کنید.

پاسخ

در این مسئله داده‌هایی در مورد بخش‌های مختلف حرکت مریم در اختیار داریم و بهتر است جدولی از آن‌ها تهیه کنیم. برای مثال، زمان و موقعیت‌های مکانی داده شده‌اند، پس می‌توانیم جابجایی‌ها و زمان‌های سپری‌ شده را محاسبه کنیم. با در نظر گرفتن شرق به عنوان جهت مثبت و خانه مریم به عنوان نقطه شروع یا $$x_0$$، خواهیم داشت:

طبق جدول بالا، جابجایی کل به شکل زیر با جمع کردن مقادیر جابجایی در هر بازه محاسبه می‌شود:

$$\Sigma \Delta { x_i} = 0.5 -0.5 +1 -1.75 = -0.75 \ km$$

قدر مطلق جابجایی نهایی نیز برابر خواهد شد با:

$$| \Sigma \Delta { x_i} | = | -0.75 | \ km = 0.75 \ km$$

در سوال بعدی سرعت متوسط مریم در کل این پیمایش خواسته شده است. پس فرمول سرعت متوسط را می‌نویسیم:

$$\vec{\bar v} = \frac{\Delta \vec{ x} }{\Delta t } = \frac{\vec{x_2} - \vec{x_1} }{t_2 - t_1 }$$

$$\Rightarrow \vec{\bar v} = \frac{-0.75 \ km }{58 \ min } = - 0.013 \ \frac{km}{min}$$

ملاحظه می‌کندی که سرعت متوسط منفی به‌دست آمد. دقت کنید اگر در سوال سرعت بر حسب متر بر ثانیه خواسته می‌شد، لازم بود ابتدا تبدیل واحد جابجایی ر حسب متر و زمان بر حسب ثانیه را انجام می‌دادیم. در سوال چهارم کل مسافت پیموده شده توسط مریم را باید محاسبه کنیم. در این موقعیت کافی است اندازه یا قدر مطلق جابجایی‌های به‌دست آمده در هر مرحله را با هم جمع کنیم:

$$\Sigma |\Delta { x_i}| = 0.5 +0.5 +1 +1.75 = 3.75 \ km$$

در نهایت نمودار مکان - زمان این حرکت را به شکل زیر خواهیم داشت:

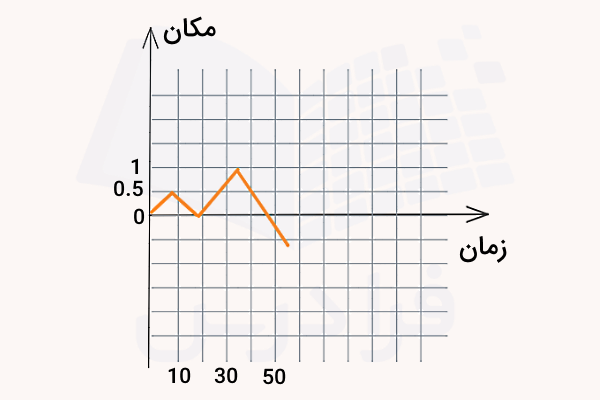
به این ترتیب در این سوال مجموع جابجایی مریم برابر با $$-0.75 \ km$$ شد، به این معنا که در پایان این پیمایش او در $$0.75 \ km$$ به سمت غرب خانه‌ خود قرار دارد. سرعت متوسط نیز در این سوال به این معنا است که اگر کسی از همان زمان حرکت مریم به سمت غرب و با سرعت $$0.013 \ \frac{km}{min}$$ حرکت کند، هر دو همزمان به نقطه‌ پایانی می‌رسند. توجه داشته باشید که اگر مریم حرکت خود را در خانه‌اش به پایان می‌رساند، مجموع جابجایی او و در نتیجه سرعت متوسط‌ نیز صفر می‌شد. مسافت کل طی‌ شده در مدت زمان $$58 \ {min}$$ برای این حرکت نیز $$3.75 \ {km}$$ بوده است.

مثال ۳

اگر معادله حرکت ذره‌ای به شکل $$x(t) = t^2 -10t + 5$$ و بر حسب متر باشد، تندی متوسط در بازه $$0$$ تا $$7$$ ثانیه چقدر است؟

پاسخ

برای پیدا کردن تندی متوسط طبق فرمول آن باید مسافت بر بازه زمانی خواسته شده تقسیم شود. در این سوال بازه زمانی صفر تا پنج ثانیه‌ای را داریم و اگر می‌خواستیم جابجایی را پیدا کنیم، کافی بود مکان متناظر با ثانیه صفرم را از مکان متناظر با ثانیه پنجم کم کنیم. می‌دانیم مسافت و جابجایی متفاوت هستند. جابجایی برداری است که با داشتن نقاط ابتدا و انتهای آن به راحتی قابل محاسبه است. اما برای پیدا کردن مسافت، اولین کاری که لازم است انجام دهیم پیدا کردن نقطه‌ای است که تغییر جهت اتفاق می‌افتد.

به این منظور لازم است ابتدا از معادله مکان مشتق‌ بگیریم تا معادله سرعت به دست آید. سپس با مساوی صفر قرار دادن معادله سرعت، لحظه‌ای را پیدا می‌کنیم که ذره تغییر جهت داده است:

$$\Rightarrow v(t) = \frac{d}{dt} x(t) \Rightarrow v(t) = 2t-10$$

$$\Rightarrow 2t - 10 = 0$$

$$\Rightarrow 2t = 10 \Rightarrow t = \frac{10}{2} = 5 \ s$$

پس در لحظه $$t = 5 \ s$$ تغییر جهت داریم. در مرحله بعد مکان متناظر با سه لحظه $$t = 0 \ s$$ و $$t = 5 \ s$$ و $$t = 7 \ s$$ را پیدا می‌کنیم:

$$x(t) = t^2 - 10t + 5 \Rightarrow x(0) = 0 + 5 = 5 \ m$$

$$x(t) = t^2 - 10t + 5 \Rightarrow x(5) = 25 -50 + 5 = -20 \ m$$

$$x(t) = t^2 - 10t + 5 \Rightarrow x(7) = 49 -70 + 5 = -16 \ m$$

در حقیقت این ذره حرکت خود را از $$x(0) = 5 \ m$$ به سمت غرب یا جهت منفی‌ محور xها شروع می‌کند و در لحظه $$t = 5 \ s$$ به سمت شرق یا جهت مثبت همین محور تغییر جهت می‌دهد. پس برای اینکه مسافت طی شده توسط آن را پیدا کنیم، کافی است ابتدا مسافت متناظر با بازه $$t = 0 \ s$$ تا $$t = 5 \ s$$ را پیدا کنیم که معادل است با $$d_1$$:

$$\Rightarrow d_1 = | x(5) - x(0) | = | -20 \ m - 5 \ m | = |-25 \ m | = + 25 \ m$$

استفاده از قدر مطلق در محاسبه مسافت ضروری است. سپس مسافت پیموده شده از $$t = 5 \ s$$ تا $$t = 7 \ s$$ را محاسبه می‌کنیم ($$d_2$$):

$$\Rightarrow d_2 = | x(7) - x(5) | = | -16 \ m - (-20) \ m | = |+4 \ m | = + 4 \ m$$

در نهایت مجموع این دو عدد برابر است با مسافت کل یا $$d$$:

$$\Rightarrow d = d_1 + d_2 = 25 \ m + 4 \ m = 29 \ m$$

پس از یافتن مسافت، کافی است آن را بر بازه زمانی متناظر برای پیمودن آن تقسیم کنیم تا تندی متوسط محاسبه شود:

 زمان / مسافت = تندی متوسط

$$v = \frac{29}{7} = 4.1 \ \frac{m}{s}$$

در این مثال متوجه شدید که برخلاف تندی لحظه‌ ای، برای پیدا کردن تندی متوسط نمی‌توانیم صرفا قدر مطلق سرعت متوسط را حساب کنیم.

یادگیری حرکت‌شناسی برای دانشجویان با فرادرس

کتاب‌ فیزیک پایه ۱ در اغلب رشته‌ها شامل رشته‌های علوم پایه و مهندسی تدریس می‌شود و یکی از مهم‌ترین مباحث این کتاب‌ سینماتیک و مفاهیم مرتبط با تندی و سرعت است. فرادرس چند دوره آموزشی با عنوان فیزیک پایه دانشگاهی تهیه کرده است که تماشای این دوره‌ها به یادگیری بهتر شما کمک خواهد کرد:

1. فیلم آموزش رایگان بردارها در فیزیک ۱ دانشگاهی
2. فیلم آموزش فیزیک پایه ۱
3. فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله

همچنین دو فیلم آموزشی فرادرس با موضوع کاربرد نرم‌افزار و حل مسائل حرکت‌شناسی شامل موارد زیر هستند:

1. فیلم آموزش رایگان شبیه سازی حرکت یک پرتابه در متلب
2. فیلم آموزش حل مسائل فیزیک با پایتون

حل مثال و تمرین از تندی لحظه ای

در این بخش با توجه به تعریف و فرمول تندی لحظه ای و ارتباط آن با سایر کمیت‌ها مانند سرعت متوسط و ... به حل و بررسی چند نمونه سوال مختلف به شکل تشریحی و چهارگزینه‌ای خواهیم پرداخت تا به این مبحث کاملا مسلط شوید.

مثال ۱

موقعیت مکانی ذره‌ای که در حال حرکت روی یک خط مستقیم است، توسط معادله‌ای به شکل $$x(t) = 5t^2 -2t + 3$$ بر حسب متر داده شده است. با در نظر گرفتن این نکته که زمان در این معادله بر حسب ثانیه است، به سوالات زیر پاسخ دهید:

1. تندی لحظه‌ای در لحظه $$t = 2 \ s$$ کدام است؟
2. در چه زمانی تندی لحظه‌ای ذره صفر می‌شود؟

پاسخ

برای پاسخ‌دهی به این سوال باید از فرمول تندی لحظه‌ای استفاده کنیم، به این شکل که با مشتق‌گیری از معادله مکان داده شده ابتدا سرعت لحظه‌ای را به دست می‌آوریم. سپس با قرار دادن زمان موردنظر، سرعت لحظه‌ای در آن لحظه خاص پیدا می‌شود. تندی لحظه‌ ای نیز قدر برابر خواهد شد با قدر مطلق یا اندازه این عدد:

$$\Rightarrow v(t) = \frac{d}{dt} x(t) \Rightarrow v(t) = 10t - 2$$

با قرار دادن لحظه $$t = 2 \ s$$ در معادله سرعت بالا، سرعت لحظه‌ای برابر می‌شود با:

$$\Rightarrow v(t) = 10 \times 2 - 2 = 18 \ \frac{m}{s}$$

$$|\vec{v}| = |\frac{d \vec{x}}{d t} |$$ = تندی لحظه ای

$$|\vec{v}| = |18 \ \frac{m}{s} | = +18 \ \frac{m}{s}$$

در دومین سوال باید معادله سرعت را مساوی صفر قرار دهیم و زمان را پیدا کنیم:

$$\Rightarrow 10t - 2 = 0$$

$$\Rightarrow 10t = 2 \Rightarrow t = \frac{2}{10} = 0.2 \ s$$

مثال ۲

خودرویی روی یک خط مستقیم حرکت می‌کند. اگر تغییرات مکان با زمان این خودرو توسط معادله $$x(t) = -t^2 + 8t -7$$ توصیف شود، به سوالات زیر پاسخ دهید:

1. تندی متوسط این خودرو در بازه زمانی $$t = 1 \ s$$ تا $$t = 7 \ s$$ چقدر است؟
2. تندی لحظه‌ ای آن را نیز در لحظه $$t = 5 \ s$$ حساب کنید:

پاسخ

برای محاسبه تندی متوسط در اولین بخش لازم است ابتدا مسافت را پیدا کنیم. مسافت نیز بر اساس معادله سرعت و تشخیص اینکه آیا در این حرکت خودرو تغییر جهت داشته است یا خیر، حاصل می‌شود. پس اولین قدم مشتق‌گیری از معادله مکان و پیدا کردن معادله سرعت است:

$$\Rightarrow v(t) = \frac{d}{dt} x(t) \Rightarrow v(t) = -2t+8$$

$$\Rightarrow -2t+8 = 0$$

$$\Rightarrow 2t = 8 \Rightarrow t = \frac{8}{2} = 4 \ s$$

پس در لحظه $$t = 4 \ s$$ تغییر جهت داریم. در مرحله بعد مکان متناظر با سه لحظه $$t = 1 \ s$$ و $$t = 4 \ s$$ و $$t = 7 \ s$$ را پیدا می‌کنیم:

$$x(t) = -t^2 +8t -7 \Rightarrow x(1) = -(1)^2 + 8 (1) -7 = 0 \ m$$

$$x(t) = -t^2 +8t -7 \Rightarrow x(4) = -(4)^2 + 8 (4) - 7 = 9 \ m$$

$$x(t) = -t^2 +8t -7 \Rightarrow x(7) = -(7)^2 + 8 (7) - 7 = 0 \ m$$

پس این خودرو حرکت خود را از $$x(0) = 0 \ m$$ به سمت جهت مثبت محور xها شروع می‌کند و در لحظه $$t = 4 \ s$$ به سمت مخالف تغییر جهت داده و در نهایت در $$t = 7 \ s$$ مجددا به مبدا یا نقطه صفر حرکت می‌رسد. پس برای اینکه مسافت طی شده توسط آن را پیدا کنیم، کافی است ابتدا مسافت متناظر با بازه $$t = 0 \ s$$ تا $$t = 4 \ s$$ را پیدا کنیم که معادل است با $$d_1$$:

$$\Rightarrow d_1 = | x(4) - x(0) | = | 9 \ m - 0 \ m | = |9 \ m | = +9 \ m$$

استفاده از قدر مطلق در محاسبه مسافت ضروری است. سپس مسافت پیموده شده از $$t = 4 \ s$$ تا $$t = 7 \ s$$ را محاسبه می‌کنیم ($$d_2$$):

$$\Rightarrow d_2 = | x(7) - x(4) | = | 0 \ m - 9 \ m | = |- 9 \ m | = + 9 \ m$$

در نهایت مجموع این دو عدد برابر است با مسافت کل یا $$d$$:

$$\Rightarrow d = d_1 + d_2 = 9 \ m + 9 \ m = 18 \ m$$

در نتیجه تندی متوسط برابر خواهد شد با:

$$v = \frac{18}{7 - 1} = 3 \ \frac{m}{s}$$

فراموش نکنید که مسافت باید بر بازه زمانی موردنیاز برای پیمودن آن تقسیم شود، نه فقط بر یک لحظه زمانی خاص. در دومین سوال برای محاسبه تندی لحظه ای کافی است ابتدا زمان داده شده را در معادله سرعت قرار دهیم:

$$v(t) = -2t+8 \Rightarrow v(5) = -2 \times 5 +8 = -10 + 8 = -2 \ \frac{m}{s}$$

عدد به دست آمده سرعت لحظه‌ ای است. تندی معادل این سرعت همان مقدار عددی یا اندازه آن است که می‌شود:

$$\Rightarrow v(5) = |-2 \ \frac{m}{s} | = +2 \ \frac{m}{s}$$

مثال ۳

نمودار تندی زمان زیر حرکت اتومبیلی را در مدت زمان $$110 \ s$$ نشان می‌دهد. مسافت کل پیموده شده چقدر است؟

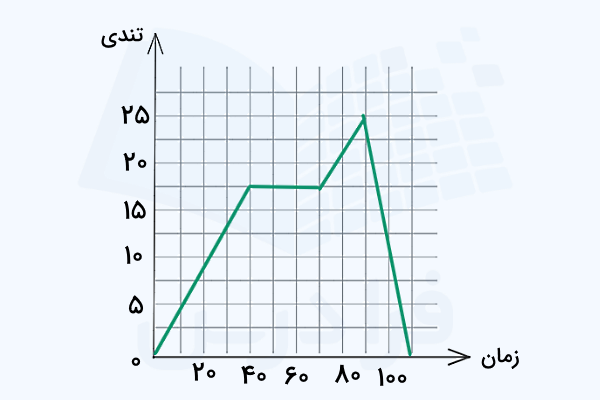
پاسخ

می‌دانیم سطح زیر نمودار تندی زمان برابر است با مسافت طی شده توسط جسم متحرک. در این سوال کل مسافت در مدت زمان $$110 \ s$$ خواسته شده است، پس باید سطح زیر کل نمودار داده شده را به دست آوریم که به شکل زیر تقسیم‌بندی و ساده می‌شود:

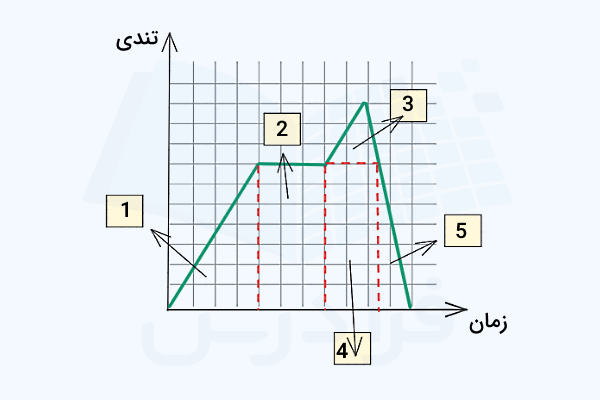
حالا مساحت هر کدام از بخش‌های مشخص را پیدا می‌کنیم:

$$\frac{1}{2} (40 \times 17.5) = 350 \ m$$ = نصف حاصل‌ضرب قاعده در ارتفاع = مساحت مثلث ۱

$$30 \times 17.5 = 525 \ m$$ = حاصل‌ضرب طول در عرض = مساحت مستطیل ۲

$$\frac{1}{2} (25 \times 7.5) = 93.75 \ m$$ = نصف حاصل‌ضرب قاعده در ارتفاع = مساحت مثلث ۳

$$25 \times 17.5 = 437.5 \ m$$ = حاصل‌ضرب طول در عرض = مساحت مستطیل ۴

$$\frac{1}{2} (7.5 \times 17.5) = 65.625 \ m$$ = نصف حاصل‌ضرب قاعده در ارتفاع = مساحت مثلث ۵

در نتیجه مساحت کل زیر این نمودار برابر می‌شود با مجموع این پنج مساحت:

$$1471.87 \ m$$ = مسافت پیموده شده در این بازه زمانی

مثال ۴

اگر مکان جسمی به شکل $$x(t)=-3t^2 \ m$$ با زمان تغییر کند، تغییرات سرعت آن با زمان چگونه است؟ آیا سرعت همیشه مثبت است؟ سرعت و تندی لحظه‌ای در $$t=10 \ s$$ چقدر است؟

پاسخ

برای اینکه ببینیم تغییرات سرعت با زمان چگونه است، کافی است مشتق تابع مکان یا همان معادله سرعت لحظه‌ای را به‌دست آوریم:

$$v(t)=\frac{d}{dt}x(t)$$

$$\Rightarrow v(t)=\frac{d}{dt}(-3t^2)=-6t \ \frac{m }{s}$$

در پاسخ به سوال بعدی، با توجه به اینکه زمان یا $$t$$ همواره عددی مساوی با صفر یا یک عدد مثبت است، پس در معادله سرعت حاصل‌ضرب یک عدد مثبت یا صفر در یک عدد منفی یعنی $$-6$$ را داریم. حاصل چنین ضربی همیشه یک عدد منفی یا صفر خواهد شد، فارغ از اینکه زمان عدد کوچک یا بزرگ باشد. برای مثال فرض کنید به‌جای زمان اعداد صفر و $$200$$ قرار دهیم. در این صورت داریم:

$$\Rightarrow v(t=0)=-6(0)=0 \ \frac{m }{s}$$

$$\Rightarrow v(t=200)=-6(200)=-1200 \ \frac{m }{s}$$

 پس سرعت این جسم هیچ‌گاه مثبت نخواهد شد. در آخرین سوال، سرعت و تندی لحظه‌ای را در $$t=10 \ s$$ محاسبه می‌کنیم:

$$\Rightarrow v(t=10)=-6(10)=-60 \ \frac{m }{s}$$

$$|\vec{v(t)}|$$ = تندی لحظه‌ای

$$\Rightarrow |{v(t=10)}|=|-60 \ \frac{m }{s} |=+60 \ \frac{m }{s}$$

مثال ۵

اگر نموداری تندی زمان متحرکی به شکل زیر باشد، به سوالات زیر پاسخ دهید:

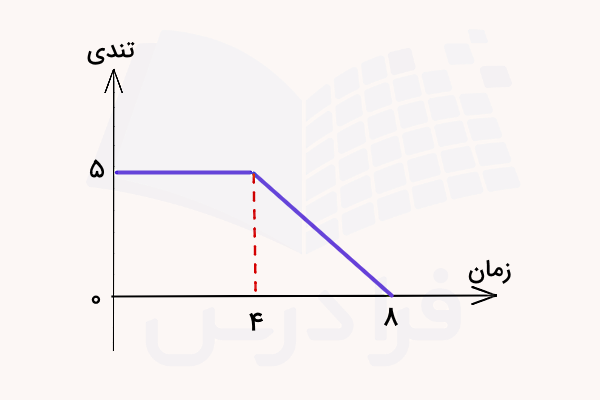
1. کل مسافت طی شده توسط این جسم چقدر است؟
2. شتاب متناظر با بازه $$t = 4 \ s$$ تا $$t = 4 \ s$$ را محاسبه کنید:

پاسخ

اولین بخش با پیدا کردن مساحت زیر نمودار داده شده محاسبه می‌شود. این سطح متشکل است از یک مستطیل با طول $$5$$ و عرض $$4$$ به همراه مثلثی با قاعده $$4$$ و ارتفاع $$5$$. بنابراین مسافت کل به شکل زیر خواهد بود:

$$5 \times 4 + \frac{1}{2} (4 \times 5 ) = 20 + 10 = 30 \ m$$  = مسافت کل

در سوال دوم، برای محاسبه شتاب باید از این نکته استفاده کنیم که شتاب در نمودار تندی زمان همان شیب خط مماس بر نمودار است. بنابراین شتاب متناظر با بازه داده شده معادل است است با شیب خطی که دو نقطه موردنظر را به هم وصل می‌کند:

$$\frac{v_2 - v_1}{t_2 - t_1}$$ = شیب خط متصل کننده دو نقطه متناظر با این بازه

$$= \frac{0 - 5}{8 - 4} = -1.25 \ \frac{m}{s}$$

علامت منفی شتاب نشان دهنده حرکت کند شونده جسم است.