تعادل فضایی در استاتیک به چه معناست؟ – از صفر تا صد

تعادل فضایی در استاتیک وضعیتی است که در آن یک جسم صلب در فضای سه‌ بعدی هیچ‌گونه حرکت انتقالی یا دورانی ندارد. در این مطلب از مجله فرادرس همراه با حل چندین مثال توضیح می‌دهیم برای اینکه یک جسم در فضای سه‌ بعدی در تعادل کامل باشد، لازم است دو شرط برداری $$\sum \vec{F} = 0$$ و $$\sum \vec{M} = 0$$ برقرار باشند که هر کدام به سه معادله اسکالر تجزیه می‌شوند.

تعادل فضایی در استاتیک

به وضعیت فیزیکی سیستمی که در آن یک یا چند جسم در حالت سکون بوده و در همین حالت نیز باقی می‌مانند، تعادل فضایی در استاتیک گفته می‌شود. در این وضعیت جمع برداری تمام نیروها و گشتاورهای خارجی وارد بر سیستم صفر است. در تحلیل‌ دو بعدی یا صفحه‌ای معمولا سه معادله خواهیم داشت، اما در سه‌ بعد به دلیل اضافه شدن بعد سوم شرایط پیچیده‌تر است و تعداد معادلات به شش معادله مستقل افزایش می‌یابد.

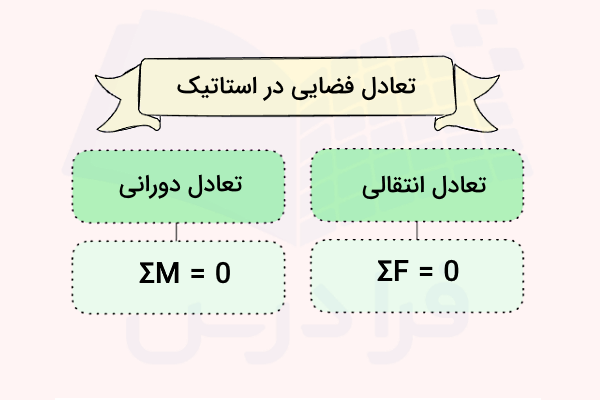
به این ترتیب تعادل فضایی در استاتیک زمانی حاصل می‌شود که یک جسم صلب بطور همزمان دو شرط اساسی را برآورده کند:

• تعادل انتقالی: جمع برداری تمام نیروهای خارجی وارد بر جسم باید صفر شود ($$\sum \vec{F} = 0$$).
  • در نتیجه شتاب خطی نیز صفر است ($$\vec{a} = 0$$).
• تعادل دورانی: جمع برداری تمام گشتاورهای خارجی وارد بر جسم نسبت به هر نقطه‌ای باید صفر شود ($$\sum \vec{M} = 0$$).
  • در نتیجه شتاب زاویه‌ای نیز صفر است ($$\vec{\alpha} = 0$$).

کتاب روی میز مثال ساده‌ای است از جسمی که دارای تعادل فضایی در استاتیک است. در این مثال نیروی رو به پایین گرانش یا وزن کتاب توسط نیروی رو به بالای عمودی تکیه‌گاه از سمت میز متعادل می‌شود. مثال ساده دیگر یک الاکلنگ متوازنی است که در آن وزن افرادی که در دو طرف آن نشسته‌اند، گشتاورهای مخالفی ایجاد می‌کند که اثر هم را خنثی می‌کنند.

دقت کنید تفاوت اصلی تعادل فضایی و تعادل صفحه‌ای این است که در تحلیل دو بعدی ما فرض می‌کنیم تمام نیروها در یک صفحه مانند $$xy$$ هستند. بنابراین فقط دو معادله نیرو و یک معادله گشتاور حول محور $$z$$ داریم. اما در دنیای واقعی و سازه‌های پیچیده‌ای مانند دکل‌های مخابراتی، جرثقیل‌های بزرگ یا قطعات موتور، نیروها در تمامی جهات وارد می‌شوند و حتما باید از تحلیل فضایی استفاده کنیم.

نکته: در متون مختلف ممکن است به جای واژه گشتاور از کلمه ممان استفاده شود. همچنین گشتاور را با $$\vec{\tau}$$ نیز نمایش می‌دهند.

استاتیک چیست؟

استاتیک یا ایستایی شاخه‌ای از علم مکانیک است که به بررسی اجسام در حال سکون می‌پردازد، به گونه‌ای که تمام نیروها و گشتاورهای وارد بر آن‌ها در توازن باشند. این شاخه پایه و اساس رشته‌هایی مانند مهندسی عمران و مهندسی مکانیک در طراحی سازه‌های پایداری مانند پل‌ها و ساختمان‌ها است تا تحت فشار بارها دچار حرکت یا فروپاشی نشوند.

برای تحلیل بهتر مسائل استاتیکی بهتر است ابتدا به مفاهیم و اصطلاحات زیر مسلط شویم:

• نمودار جسم آزاد: این نمودار برای تفکیک اجسام موردبررسی و به تصویر کشیدن تمامی نیروها و گشتاورهای خارجی وارد بر آن‌ها رسم می‌شوند.
• مفهوم جسم صلب در مقابل ذره: برای یک ذره یا جرم نقطه‌ای تنها بررسی شرط نیرو کافی است، ولی برای یک جسم صلب که دارای ابعاد فیزیکی است، علاوه‌بر نیروها، گشتاورها نیز باید متعادل باشند.
• واکنش‌های تکیه‌گاهی: این واکنش‌ها همان نیروهایی هستند که تکیه‌گاه‌ها از جمله لولاها، غلتک‌ها یا تیرهای ثابت، برای پایدار نگه داشتن سازه‌هایی مانند پل‌ها و ساختمان‌ها اعمال می‌کنند.

آموزش استاتیک با فرادرس

در بخش قبل تا حدودی یاد گرفتیم منظور از تعادل فضایی در استاتیک چیست. در واقع فیزیک مکانیک شامل دو بخش مهم به نام سینماتیک و دینامیک است. در سینماتیک حرکت اجسام بررسی و توصیف می‌شود، در حالی که دینامیک به بررسی علت حرکت اجسام یا نیروها می‌پردازد.

شاخه‌های دیگری مانند «الاستیسیته» (مطالعه مکانیک جامدات تغییرشکل‌پذیر)، «هیدرواستاتیک» (مطالعه مکانیک سیالات در حالت سکون) و «هیدرودینامیک» (مطالعه مکانیک سیالات در حال حرکت) نیز زیرمجموعه‌های دیگری از فیزیک مکانیک هستند که گاهی با استاتیک ترکیب می‌شوند. در این بخش می‌توانید با برخی از فیلم‌های آموزشی فرادرس در این زمینه آشنا شوید:

• فیلم آموزش استاتیک – جامع و کاربردی فرادرس
• فیلم آموزش استاتیک – مرور و حل تست کنکور ارشد فرادرس
• فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد فرادرس
• فیلم آموزش استاتیک – مرور و حل مساله فرادرس

مرور مفاهیم پایه

برای اینکه با تعادل فضایی در استاتیک و روش استفاده از فرمول‌های آن بهتر آشنا شویم، ابتدا لازم است مروری داشته باشیم بر مفهوم بردار و مولفه‌های آن. بردار کمیتی است که علاوه بر مقدار یا اندازه، جهت نیز دارد. در فضای سه‌ بعدی، هر بردار به سه مولفه روی محورهای $$x$$ و $$y$$ و $$z$$ تجزیه می‌شود که معمولا با بردار واحد $$(i,j,k)$$ نمایش داده می‌شود:

$$\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$$

نیروی همگرا و غیر همگرا

نیروهای همگرا نیروهایی هستند که خط اثر همه‌ آن‌ها از یک نقطه مشترک عبور می‌کند و فقط باعث حرکت انتقالی می‌شوند. در مقابل نیروهای غیرهمگرا در نقاط مختلفی به جسم وارد شده و خط اثر آن‌ها در یک نقطه تلاقی نمی‌کند، بنابراین می‌توانند علاوه بر حرکت باعث چرخش جسم نیز شوند.

نکته: در استاتیک هر سیستم پیچیده از نیروها و گشتاورها را می‌توانیم به یک سیستم ساده‌تر و معادل شامل یک نیروی برآیند و یک گشتاور برآیند در یک نقطه مشخص تبدیل کنیم، به طوری که اثر خارجی آن‌ها بر جسم تغییر نکند.

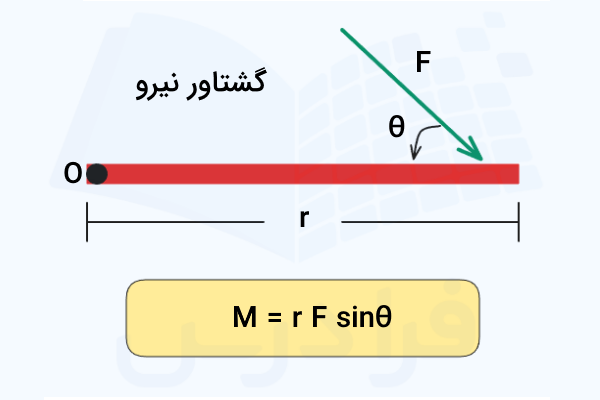
گشتاور نیرو در فضا چیست؟

گشتاور تمایل یک نیرو برای چرخاندن جسم حول یک نقطه یا یک محور را نشان می‌دهد. برخلاف صفحه، طبق قانون دست راست در فضا گشتاور برداری است که جهت آن بر صفحه‌ شامل نیرو و فاصله، عمود است. همچنین گشتاور نیرو حول یک نقطه مانند $$O$$ با بردار مکان $$\vec{r}$$ که از آن نقطه به هر نقطه‌ای روی خط اثر نیرو وصل می‌شود، تعریف می‌شود. این بردار نشان‌دهنده شدت و جهت چرخش حول آن مبدا خاص است.

گشتاور نیرو منجر به ایجاد شتاب زاویه‌ای $$\alpha$$ خواهد شد:

$$\sum{\vec{M}} = I \vec{ \alpha}$$

در فرمول بالا $$I$$ لختی دورانی و مفهومی معادل جرم در حرکت خطی است.

محاسبه گشتاور با ضرب برداری

در ریاضیات مهندسی گشتاور از ضرب خارجی بردار مکان در بردار نیرو به دست می‌آید. برای حل ساده‌تر در فضا، از دترمینان یک ماتریس سه در سه به شکل زیر استفاده می‌کنیم:

$$\vec{M_O}=\vec{r} \times \vec{F} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\r_x & r_y & r_z \\ F_x & F_y & F_z \end{vmatrix}$$

گشتاور حول یک محور

اگر بخواهیم تمایل چرخش را حول یک محور خاص مانند $$L$$ بسنجیم، باید تصویر بردار گشتاور را روی آن محور پیدا کنیم. این فرآیند با ضرب داخلی بردار گشتاور در بردار واحد در راستای آن محور یعنی $$\hat{u_L}$$ و به شکل زیر انجام می‌شود:

$$M_L=\hat{u_L} \ . \ (\vec{r} \times \vec{F})$$

زوج نیرو

زوج نیرو یا کوپلینگ در استاتیک شامل دو نیروی هم‌اندازه، موازی و در خلاف جهت یکدیگر است که مجموع نیروهای حاصل از آن‌ها صفر است، اما یک گشتاور خالص غیرصفر ایجاد می‌کنند. بردار گشتاور زوج نیرو یک بردار آزاد است به این معنا که اثر آن به نقطه چرخش بستگی ندارد و در تمام نقاط جسم یکسان است.

تعادل جسم صلب در فضا

اگر بخواهیم تعادل یک جسم صلب در فضا (سه بعد) را بررسی کنیم، بهتر است ابتدا به پرسش‌های زیر پاسخ دهیم:

• جسم صلب چیست چه ویژگی‌هایی دارد؟
• حل مسائل تعادل دو‌ بعدی و سه‌ بعدی چه تفاوت‌ها و شباهت‌هایی با هم دارند؟

اگر تمایل دارید با معادلات تعادلی استاتیک بیشتر آشنا شوید، پیشنهاد می‌کنیم فیلم آموزش رایگان استاتیک چیست؟ – مفاهیم پایه + معادلات تعادل فرادرس را مشاهده کنید که لینک آن نیز در ادامه برای شما قرار داده شده است:

جسم صلب چیست؟

در استاتیک جسم صلب یا Rigid Body یک مدل ایده‌آل است که در آن فرض می‌کنیم فاصله بین هر دو نقطه دلخواه از جسم، تحت تاثیر نیروهای خارجی تغییر نمی‌کند. به این ترتیب ویژگی‌های اصلی جسم صلب عبارت‌اند از:

• در واقعیت اجسام تحت اثر نیرو یا گشتاورها کمی خم یا فشرده می‌شوند، اما یک جسم صلب تغییر شکل نمی‌دهد.
• در جسم صلب نیروها مستقیما از طریق ساختار جسم منتقل می‌شوند، بدون اینکه انرژی‌ای صرف تغییر فرم داخلی شود.
• برخلاف ذره، در جسم صلب ابعاد و محل دقیق اعمال نیرو اهمیت دارد، چون باعث ایجاد گشتاور می‌شود.

تفاوت تعادل صفحه‌ ای و تعادل فضایی چیست؟

سیستم‌های سه‌ بعدی یا فضایی نسبت به سیستم‌های دو‌ بعدی یا صفحه‌ای به واقعیت نزدیک‌تراند. با اینکه اصول پایه‌ حل هر دو سیستم یکسان است، اما معمولا حل مسائل سه‌ بعدی دشوارتر است. این مسئله به دلیل تعداد درجات آزادی بیشتر و سختی تجسم و تعیین فاصله‌ها، نیروها و گشتاورها در فضای سه‌ بعدی است. مسائل سه‌ بعدی عموما با استفاده از جبر برداری حل می‌شوند، نه روش‌های اسکالر. در بخش قبل مقدمات این روش‌ها کامل توضیح داده شد.

در بررسی تعادل فضایی در استاتیک جهت‌ها توسط بردارهای یکه توصیف شده و گشتاورها نیز بجای روش‌های اسکالر با استفاده از ضرب برداری تعیین می‌شوند. با توجه به اینکه تعداد مجهولات بیشتر است، یافتن معادلاتی کارآمد برای حل مسائل نیز دشوارتر می‌شود. یک مسئله ممکن است شامل دستگاهی با حداکثر شش معادله و شش مجهول باشد که در این حالت بهترین روش حل، استفاده از جبر خطی و ابزارهای محاسباتی است.

تجزیه نیروها و گشتاورها

می‌دانیم در مورد تجزیه‌ نیروهای دو‌ بعدی می‌توان از ویژگی‌های مثلث قائم‌الزاویه و توابع سینوس و کسینوس استفاده کرد. اما نیروهای سه‌ بعدی و گشتاورها نیاز است که به روش زیر تجزیه شوند. برای مثال، هنگام جمع‌ کردن گشتاورها باید هم تمام گشتاورهای حاصل از $$\vec{r}\times\vec{F}$$ و هم گشتاورهای زوج را در نظر بگیرید:

1. ابتدا یک نقطه دلخواه در سیستم انتخاب کنید تا گشتاورها نسبت به آن جمع شوند.
2. دو روش کلی برای جمع‌کردن گشتاورهای $$\vec{r}\times\vec{F}$$ داریم که هر دو به مجموعه معادلات یکسانی منجر می‌شوند:
   • جمع گشتاورها حول هر محور: برای سیستم‌های نسبتا ساده که تعداد کمی بردار مکان و نیرو دارند، می‌توان ضرب برداری هر جفت غیرموازی بردار مکان و نیرو را محاسبه کرد. این روش نیازمند تعیین جهت هر ضرب برداری با استفاده از قاعده‌ دست راست است. دقت کنید حداکثر شش جفت مولفه‌ غیرموازی وجود دارد که باید در نظر گرفته شوند.
   • جمع تمام گشتاورها حول یک نقطه با استفاده از دترمینان‌های برداری: نقطه‌ای را در سیستم انتخاب کنید که روی خط اثر بیشترین تعداد نیروها قرار داشته باشد. سپس هر ضرب برداری را به‌صورت یک دترمینان بنویسید. پس از محاسبه‌ مولفه‌های حاصل از هر دترمینان، ترم‌های $$x$$ و $$y$$ و $$z$$ را با هر یک از معادلات $$\Sigma\vec{M}_x=0$$ و $$\Sigma\vec{M}_y=0$$ و $$\Sigma\vec{M}_z=0$$ ترکیب کنید.
3. در نهایت مولفه‌های هر زوج گشتاور را نیز به معادلات متناظر $$\Sigma\vec{M}_x=0$$ و $$\Sigma\vec{M}_y=0$$ و $$\Sigma\vec{M}_z=0$$ اضافه کنید.

پیشنهاد می‌کنیم در این زمینه مطلب «نیروهای غیرموازی در استاتیک – به زبان ساده» از مجله فرادرس را نیز مطالعه کنید.

پیدا کردن مجهولات

پس از اینکه معادلات $$\Sigma\vec{F}=0$$ و $$\Sigma\vec{M}=0$$ را در سه راستای $$x$$ و $$y$$ و $$z$$ نوشتید، حداکثر شش معادله و شش مجهول دارید. در بسیاری از موارد، این دستگاه معادلات را می‌توان به روش جایگذاری حل کرد، اما معمولا حل دستگاه‌های بزرگتر با استفاده از جبر خطی ساده‌تر و کارآمدتر است.

نکته: صرف‌نظر از اینکه چه روشی را برای حل معادلات استفاده کرده‌اید، اگر هر یک از مقادیر عددی بدست‌ آمده منفی شود، نشان‌دهنده‌ آن است که فرض اولیه‌ شما در مورد جهت آن بردار نادرست بوده است.

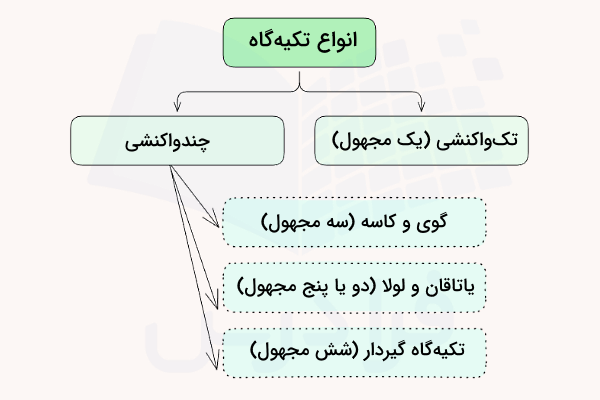
انواع تکیه‌ گاه‌ در مسائل فضایی

در فضای سه بعدی واکنش‌ها بر اساس میزان محدودیتی که تکیه‌گاه ایجاد می‌کند، تعیین می‌شوند. هر تکیه‌گاه به ازای هر حرکتی که مانع آن می‌شود، یک واکنش (نیرو یا گشتاور) ایجاد می‌کند. انواع تکیه‌گاه جهت بررسی تعادل فضایی در استاتیک عبارت‌اند از:

• تکیه‌گاه‌های تک‌واکنشی (یک مجهول)
• تکیه‌گاه‌های چندواکنشی:
  • گوی و کاسه (سه مجهول)
  • یاتاقان‌ها و لولاها (دو تا پینج مجهول)
  • تکیه‌گاه گیردار یا ثابت (شش مجهول)

برای درک عمیق‌تر طبقه‌بندی بالا بهتر است به مفهوم درجه آزادی نیز اشاره کنیم. هر جسم در فضای سه‌ بعدی شش درجه آزادی دارد، چون می‌تواند در سه جهت جابجا شود و حول سه محور بچرخد. تکیه‌گاه برخی از این آزادی‌ها را سلب می‌کند، به این صورت که هرگاه تکیه‌گاه مانع حرکتی شود، در آنجا یک واکنش تولید می‌شود.

همچنین در زمینه قیود حرکتی باید بدانیم که هر جا حرکت ممنوع باشد، واکنش وجود دارد. بنابراین اگر تکیه‌گاهی اجازه ندهد جسمی در راستای محور $$x$$ حرکت کند، حتما یک نیروی واکنشی $$R_x$$ وجود دارد یا اگر اجازه ندهد جسم حول محور $$y$$ بچرخد، پس یک گشتاور واکنشی $$M_y$$ ایجاد می‌شود. درک درست محدودیت‌ها یا قیود کلید رسم درست نمودار جسم آزاد است.

تکیه‌ گاه‌ های تک‌ واکنشی

این تکیه‌گاه‌ها کمترین محدودیت را ایجاد می‌کنند و فقط در یک جهت خاص مانع حرکت می‌شوند، مانند کابل یا طناب که فقط می‌تواند جسم را بکشد. بنابراین واکنش آن همیشه یک نیروی کششی در امتداد خود کابل است یا سطح صاف بدون اصطکاک که نمی‌تواند جلوی لغزیدن جسم را بگیرد، اما همزمان نیز اجازه نمی‌دهد جسم داخل سطح فرو رود. پس فقط یک نیروی عمودی به جسم وارد می‌کند.

تکیه گاه گوی و کاسه

این تکیه‌گاه مانع جابجایی در هر سه جهت می‌شود (سه واکنش نیرویی)، اما اجازه دوران می‌دهد. تصور کنید انتهای یک میله به شکل یک کره در داخل یک حفره کروی قرار گرفته است، مانند مفصل ران انسان. چون این مفصل اجازه نمی‌دهد انتهای میله به جلو یا عقب، چپ یا راست یا بالا یا پایین حرکت کند، پس ما سه مولفه نیروی واکنش را داریم. همچنین چون میله می‌تواند به راحتی در داخل این کاسه بچرخد، پس هیچ مانعی برای چرخش وجود ندارد و گشتاور واکنشی نداریم.

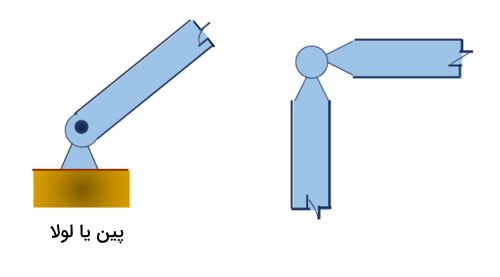
یاتاقان‌ و لولا

این نوع تکیه‌گاه‌ها بسته به نوع طراحی می‌توانند بین دو تا پنج واکنش (نیرو و گشتاور) ایجاد کنند. برای مثال لولای معمولی یا Hinge به این شکل است که اگر فقط یک لولا داشته باشیم، این لولا معمولا مانع جابجایی در سه جهت و چرخش حول دو محور می‌شود، یعنی فقط اجازه می‌دهد حول محور خودش چرخش داشته باشیم. پس پنج واکنش دارد. دقت کنید اگر دو لولا در یک راستا باشند مانند در اتاق، معمولا فرض می‌کنیم لولاها فقط واکنش نیرویی دارند و واکنش گشتاوری آن‌ها را صفر در نظر می‌گیریم تا محاسبات ساده‌تر شود.

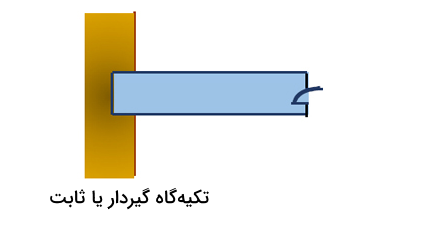
تکیه گاه گیردار یا صلب

این نوع تکیه‌گاه مانع تمام حرکت‌ها و دوران‌ها می‌شود (شش واکنش شامل سه نیرو و سه گشتاور). پس این تکیه‌گاه سخت‌گیرترین نوع است. برای نمونه تیری که داخل بتن محکم یا جوشکاری شده، اتصال آن به گونه‌ای است که اجازه هیچ‌گونه لرزش، جابجایی یا چرخش را نمی‌دهد. در نتیجه سه نیروی واکنش برای جلوگیری از حرکت انتقالی و سه گشتاور واکنشی برای جلوگیری از هر گونه چرخش داریم. این تکیه‌گاه به‌ تنهایی می‌تواند تعادل یک جسم را حفظ کند، مانند یک تابلوی تبلیغاتی تک‌پایه. پس تکیه‌گاه ثابت قیدی در مقابل دوران در هر جهتی ایجاد کرده و از حرکت در هر دو جهت افقی و عمودی جلوگیری می‌کند.

نحوه مدل‌ سازی تکیه‌ گاه‌ ها

در دنیای واقعی هیچ پیچی دقیقا یک لولای ایده‌آل نیست و هیچ بتنی صد در صد گیردار عمل نمی‌کند. بنابراین باید بدانیم هر اتصال را چگونه مدل‌سازی کنیم. برای مثال، اتصال یک پل به ستون اگر اجازه جابجایی جزئی بر اثر گرما را بدهد، به عنوان غلتک یا Roller مدل می‌شود. همچنین اگر یک اتصال با چندین پیچ محکم شده باشد، معمولا آن را گیردار فرض می‌کنیم تا سخت‌گیرانه‌ترین حالت را در نظر گرفته باشیم.

مفهوم بار در استاتیک

بار یا Load به هر نوع نیروی خارجی مانند فشار، کشش یا گشتاوری گفته می‌شود که بر یک عضو سازه‌ای یا یک سیستم فیزیکی وارد می‌شود. در واقع اگر استاتیک را نوعی بازی توازن یا تعادل در یک سیستم در نظر بگیریم، بارها ورودی‌های سیستم و واکنش‌های تکیه‌گاهی پاسخ سیستم برای حفظ تعادل هستند. در ادامه انواع بارها را از دو دیدگاه بررسی می‌کنیم.

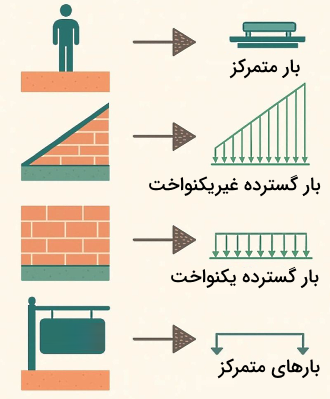
انواع بار از نظر نحوه توزیع یا شکل ظاهری

این نوع دسته‌بندی بارها برای حل معادلات ریاضی بسیار مهم است:

• بار متمرکز: باری که به یک نقطه مشخص وارد می‌شود، مانند زمانی که شما با نوک انگشت به میز فشار می‌آورید.
• بار گسترده: باری که در سطح یا طول یک جسم پخش شده است.
  • بار گسترده یکنواخت: مانند برف روی سقف
  • بار گسترده غیریکنواخت: مانند فشار آب به دیواره سد که هر چه عمیق‌تر می‌رویم، بیشتر می‌شود.

انواع بار از نظر منشا

مهندسان برای طراحی دقیق، بارها را بر اساس منشا یا منبع ایجاد آن‌ها تقسیم می‌کنند:

• بار مرده: این نوع بار همان وزن اجزای ثابت سازه است، مانند وزن تیرها، ستون‌ها و کف‌سازی که همیشه هستند و تکان نمی‌خورند.
• بار زنده: بارهای موقتی که جابجا می‌شوند، مانند وزن آدم‌ها، مبلمان یک اتاق یا ماشین‌های روی یک پل.
• بارهای محیطی: بارهایی که طبیعت به سازه تحمیل می‌کند، مانند فشاری که باد به بدنه ساختمان وارد می‌کند یا وزن برفی که روی سقف می‌نشیند یا نیروهای ناشی از شتاب زمین (زلزله).

بررسی معین بودن و پایداری تیرها و قاب ها

تیر در استاتیک یک عضو افقی یا مایل است که وظیفه اصلی آن تحمل بارهای عمودی مانند وزن سقف، آدم‌ها و وسایل و انتقال آن‌ها به ستون‌هاست. تیرها معمولا تحت خمش قرار می‌گیرند. تیرهای آهنی سقف ساختمان، پل‌های عابر پیاده یا تخته استارت شیرجه در استخر نمونه‌‌هایی از تیر در سازه‌ هستند. اما قاب مجموعه‌ای از تیرها و ستون‌ها است که به هم متصل شده‌اند تا یک ساختار یکپارچه را تشکیل دهند.

در یک قاب، تیرها و ستون‌ها با هم همکاری می‌کنند تا علاوه بر بارهای عمودی، در برابر بارهای جانبی مانند باد و زلزله نیز مقاومت کنند. در استاتیک تیر معمولا به تنهایی تحلیل می‌شود و تمرکز روی میزان خم شدن و برش خوردن آن است، در حالی که قاب به صورت یک سیستم تحلیل می‌شود، یعنی وقتی باری به تیر یک قاب وارد می‌شود، ستون‌های متصل به آن نیز تحت تاثیر قرار می‌گیرند و گشتاور به آن‌ها منتقل می‌شود.

پیش از انتخاب روش تحلیل و حل مسائل تعادل فضایی در استاتیک، تعیین معینی و پایداری سازه اهمیت دارد. ابتدا به تعاریف زیر توجه کنید:

• سازه معین: سازه‌ای است که واکنش‌های خارجی یا نیروهای داخلی اعضای آن را بتوان تنها با استفاده از شرایط تعادل تعیین کرد.
• سازه نامعین: سازه‌ای است که نیروهای مجهول آن فقط با معادلات تعادل استاتیکی قابل‌تعیین نیست و برای تحلیل کامل، به بررسی شرایط سازگاری بخش‌های مختلف سازه نیاز دارد.
• پایداری: یک سازه باید پایدار باشد تا بتواند عملکرد مطلوب خود را حفظ کند. اگر سازه شکل هندسی خود را تحت تاثیر نیروهای خارجی حفظ کند، پایدار محسوب می‌شود.

همچنین فرمول‌بندی پایداری و معینی تیرها در صورتی که $$r$$ تعداد واکنش‌های تکیه‌گاهی، $$c$$ معادلات شرطی، $$m$$ تعداد اعضا و $$j$$ تعداد اتصالات یا گره‌ها باشد، عبارت است از:

• ناپایدار: $$r < c+3$$
• معین استاتیکی: $$r = c+3$$
• نامعین استاتیکی: $$r > c+3$$

و برای قاب‌ها نیز داریم:

• ناپایدار: $$3m+r < 3j+c$$
• معین استاتیکی: $$3m+r = 3j+c$$
• نامعین استاتیکی: $$3m+r > 3j+c$$

به طور خلاصه فرمول‌بندی جایگزین برای معینی و پایداری تیرها و قاب‌ها به شکل زیر است:

$$r + \sum F_i = 3m$$

که در آن $$F_i$$ تعداد نیروهای واکنشی منتقل شده توسط یک لولا یا غلتک داخلی است.

حل مثال و تمرین از تعادل فضایی در استاتیک

در بخش‌های گذشته اصول و فرمول‌های موردنیاز برای حل مسائل تعادل فضایی در استاتیک را کاملا یاد گرفتیم و دیدیم که بهتر است این گام‌ها را به ترتیب اجرا کنیم:

1. رسم نمودار جسم آزاد: تمام تکیه‌گاه‌ها را حذف و واکنش‌های آن‌ها را با استفاده از پیکان‌ها (بردارها) جایگزین کنید.
2. تعیین پایداری و معینی سازه: اگر سازه در دسته معین قرار گرفت، تحلیل را ادامه دهید.
3. انتخاب دستگاه مختصات: محوری را انتخاب کنید که با بیشترین تعداد نیروها هم‌راستا باشد.
4. استفاده از شکل برداری: تمام نیروها و فواصل بین نقاط را بر حسب بردارهای یکه بنویسید.
5. بررسی تعادل گشتاورها: ابتدا معادله $$\sum \vec{M}_O = 0$$ را حل کنید، چون مجهولات کمتری دارد.
6. بررسی تعادل نیروها: سپس معادله $$\sum \vec{F} = 0$$ را برای یافتن مجهولات باقی‌مانده حل کنید.

دقت کنید انتخاب نقطه مناسب برای محاسبه گشتاور خیلی مهم است. نقطه‌ای را برای محاسبه گشتاور انتخاب کنید که بیشترین تعداد نیروهای مجهول از آن عبور می‌کنند. به این ترتیب چون بازوی گشتاور این نیروها نسبت به آن نقطه صفر می‌شود، این مجهولات از معادله حذف شده و شما می‌توانید مجهول باقی‌مانده را به راحتی پیدا کنید. همچنین برای کاهش تعداد مجهولات پیش از شروع محاسبات سنگین، به دنبال این موارد باشید:

• تقارن: اگر جسم و بارگذاری متقارن باشند، مجهولات متناظر نیز با هم برابراند.
• اعضای دو نیرویی: در مورد قطعاتی که فقط در دو انتها نیرو به آن‌ها وارد می‌شود (مانند کابل‌ها یا کلاف‌های ساده)، نیروی آن‌ها فقط در امتداد خودشان است. پس فقط یک مجهول (اندازه نیرو) دارند.

پس از اینکه اعداد را به دست آوردید، صحت و درستی آن‌ها را بررسی کنید. برای مثال، اگر کابلی قرار است جسم را بکشد ولی جواب شما منفی شده، یعنی جهت را اشتباه فرض کردید یا محاسبات غلط است (کابل نمی‌تواند فشار وارد کند). همچنین در مورد گشتاور، بهتر است مجموع گشتاورها را حول یک نقطه جدید (که در مراحل قبل استفاده نکردید) حساب کنید. اگر جواب با مقادیر مجهولی که به دست آورده‌اید صفر شد، یعنی با اطمینان بالا جواب شما درست است. در ادامه سعی می‌کنیم به حل چند مسئله بپردازیم.

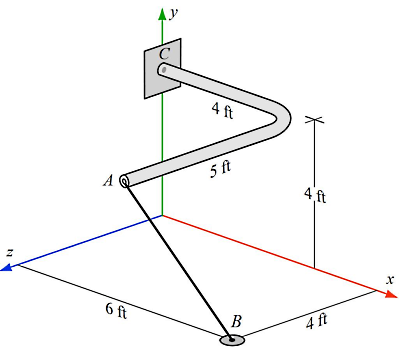
مثال ۱

یک میله خمیده سه‌ بعدی مطابق شکل زیر توسط اتصال گیره‌دار $$C$$ در یک صفحه‌ افقی نگه داشته شده است، در حالی که کابل $$AB$$ نیرویی به اندازه $$500 \ Ib$$ را به نقطه‌ $$A$$ اعمال می‌کند. با توجه به داده‌های زیر، نیروی واکنشی $$C$$ و گشتاور متمرکز $$M$$ با مولفه‌های $$M_x$$ و $$M_y$$ و $$M_z$$ را پیدا کنید:

$$C = (0,4,0)$$ و $$B = (6,0,4)$$ و $$A = (4,4,5)$$

پاسخ

ابتدا دیاگرام جسم آزاد مسئله را مطابق شکل زیر رسم می‌کنیم:

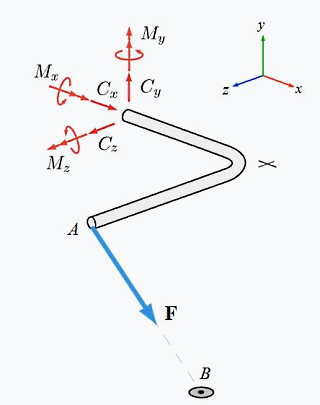
نیروی کابل از نقطه $$A$$ به نقطه $$B$$ وارد می‌شود و فاصله بین این دو نقطه همان بردار جابجایی از $$A$$ تا $$B$$ است. پس فرم کارتزین نیروی فعال در نقطه $$A$$ برابر است با:

$$\vec{r}_{AB} = 2 \hat{i} - 4 \hat{j} - \hat{k}$$

و در نتیجه بردار یکه متناظر با آن خواهد شد:

$$\hat{\lambda}_{AB} = \frac{\vec{r}_{AB}}{|\vec{r}_{AB}|}$$

$$=\frac{2 \hat{i} - 4 \hat{j} - \hat{k} }{\sqrt{2^2 + (-4)^2 + (-2)^2}}$$

$$=\frac{2 \hat{i} - 4 \hat{j} - \hat{k} }{\sqrt{21}}$$

با ضرب کردن این بردار یکه در نیروی کششی کابل می‌توانیم نیرویی که به نقطه $$A$$ وارد می‌شود را به شکل یک بردار نیروی کارتزین سه بعدی نمایش دهیم:

$$\vec{F}=\hat{\lambda}_{AB} \vec{T}$$

$$=\frac{2 \hat{i} - 4 \hat{j} - \hat{k} }{\sqrt{21}} \ 500 \ Ib$$

$$=(2 \hat{i} - 4 \hat{j} - \hat{k}) \ \frac{500 }{\sqrt{21}} \ Ib$$

$$\vec{F} =(218 \hat{i} - 436 \hat{j} - 109\hat{k}) \ Ib$$

حالا برای تعیین گشتاور حول نقطه $$C$$ لازم است از ضرب برداری استفاده کنیم. دقت کنید بازوی گشتاور همان بردار جابجایی از $$C$$ تا $$A$$ است:

$$\vec{r}_{CA} = (4 \hat{i}+0 \hat{j} +5 \hat{k}) \ ft$$

$$\vec{M}_{C} = \vec{r}_{CA} \times \vec{F}$$

$$= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\4 & 0 & 5 \\ 2 & -4 & -1 \end{vmatrix} ( \frac{500 }{\sqrt{21}} \ Ib)$$

$$\vec{M}_C=(2182 \hat{i} +1528 \hat{j} - 1746\hat{k}) \ ft.Ib$$

در مرحله بعد می‌رویم سراغ اعمال شروط تعادل فضایی در استاتیک یعنی $$\sum\vec{F}=0$$ و $$\sum\vec{M}=0$$. از $$\sum\vec{F}=0$$ به سه معادله زیر می‌رسیم:

$$\sum F_x=0 \Rightarrow C_x + F_x = 0$$

$$\sum F_y=0 \Rightarrow C_y - F_y = 0$$

$$\sum F_z=0 \Rightarrow C_z - F_z = 0$$

که نتیجه آن خواهد شد:

$$C_x = -218 \ Ib$$

$$C_y = 436 \ Ib$$

$$C_z = 109 \ Ib$$

به همین ترتیب برای شرط تعادلی گشتاورها نیز داریم:

$$\sum M_x=0 \Rightarrow M_x + M_{cx} = 0$$

$$\sum M_y=0 \Rightarrow M_y + M_{c7} = 0$$

$$\sum M_z=0 \Rightarrow M_z + M_{cz} = 0$$

که نتیجه آن خواهد شد:

$$M_x = -2182 \ ft.Ib$$

$$M_y = -1528 \ ft.Ib$$

$$M_z = 1746 \ ft.Ib$$

بنابراین بردارهای نهایی برای نیروی واکنشی $$C$$ و گشتاور متمرکز $$M$$ به شکل زیر هستند:

$$\vec{C} =(-218 \hat{i} +436 \hat{j} +109\hat{k}) \ Ib$$

$$\vec{M} =(-2182 \hat{i} -1528 \hat{j} +1746\hat{k}) \ ft.Ib$$

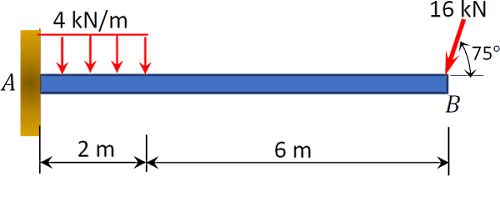
مثال ۲

مطابق شکل زیر، یک تیر تحت بارگذاری گسترده یکنواخت و یک بار متمرکز مایل قرار دارد. واکنش‌های تکیه‌گاهی را در تکیه‌گاه $$A$$ تعیین کنید:

پاسخ

دقت کنید یک سر تیر روی دیوار گیردار یا ثابت شده و سر دیگر آن آزاد است. گفتیم تکیه‌گاه گیردار در صفحه سه واکنش دارد، $$A_x$$ و $$A_y$$ و $$A_z$$. همچنین بار مایل را به دو مولفه افقی $$F\cos \theta$$ و عمودی $$F\sin \theta$$ تجزیه می‌کنیم. بار گسترده را نیز به یک نیروی متمرکز معادل تبدیل می‌کنیم که مقدار آن برابر با سطح زیر نمودار بار است و به مرکز ثقل آن وارد می‌شود. حالا نمودار جسم آزاد کل تیر را مطابق شکل زیر رسم می‌کنیم:

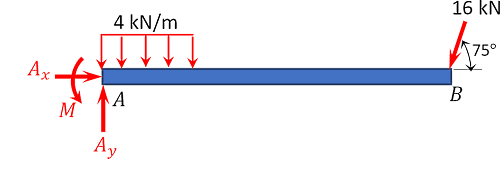
واکنش‌های تکیه‌گاهی، همان‌طور که در نمودار جسم آزاد مشخص شده‌اند، عبارتند از:

• واکنش عمودی $$A_y$$
• واکنش افقی $$A_x$$
• لنگر یا گشتاور تکیه‌گاهی $$M$$

پیش از محاسبه واکنش‌های تکیه‌گاهی، باید بدانیم که بار گسترده با یک نیروی برآیند واحد جایگزین می‌شود و بار مایل نیز به مولفه‌های عمودی و افقی تجزیه خواهد شد. مقدار نیروی برآیند برابر با مساحت زیر نمودار بارگذاری مستطیلی است و این نیرو از مرکز ثقل مستطیل عبور می‌کند. همان‌طور که در شکل زیر مشاهده می‌شود، مقدار این نیرو برابر است با:

$$P = 4 \times 2 = 8 \ kN$$

و محل اثر آن در مرکز ثقل بار مستطیلی قرار دارد. پس دقت کنید وقتی بار شما مستطیلی است (چهار کیلونیوتن بر متر در طول دو متر) نیروی معادل دقیقا در وسط آن طول (یعنی در فاصله یک متری از شروع بار) وارد می‌شود. حالا با نوشتن معادلات تعادل از $$\sum F_x = 0$$ برای پیدا کردن $$A_x$$ و از $$\sum F_y = 0$$ برای پیدا کردن $$A_y$$ و از $$\sum M_A = 0$$ (گشتاور حول نقطه $$A$$) برای پیدا کردن لنگر تکیه‌گاهی $$M$$ استفاده کنید:

$$\Rightarrow -(16 \sin 75^{\circ}) \times 8 \ - \ (4\times2) \times 1 +M_A= 0$$

$$\Rightarrow M_A= 131.64 \ kN.m$$

$$\Rightarrow A_y -16 \sin 75^{\circ} - (4\times2) = 0$$

$$\Rightarrow A_y = 23.45 \ kN$$

$$\Rightarrow A_x = 0$$

مثال ۳

یک تیر ساده به طول $$12 \ ft$$ بار گسترده یکنواختی به شدت $$2 \ \frac{kips}{ft}$$ در تمام طول دهانه خود و یک بار متمرکز $$8 \ kips$$ در وسط دهانه را مطابق شکل زیر حمل می‌کند. واکنش‌های تکیه‌گاهی را در نقاط $$A$$ و $$B$$ تعیین کنید:

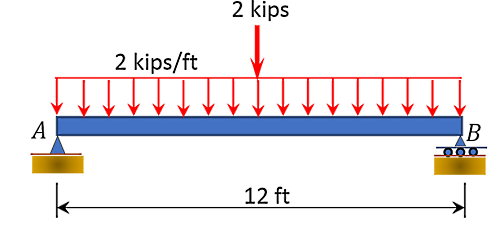
پاسخ

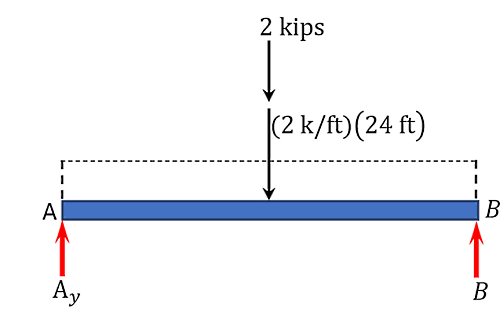
ابتدا تکیه‌گاه‌ها را حذف کرده و واکنش‌های آن‌ها را در نمودار جسم آزاد جایگزین می‌کنیم. تکیه‌گاه $$A$$ (پینی) دارای دو واکنش $$A_x$$ و $$A_y$$ و تکیه‌گاه $$B$$ (غلتکی) دارای یک واکنش عمودی $$B_y$$ است. بار گسترده مستطیلی نیز باید با یک نیروی متمرکز معادل $$P$$ جایگزین شود که مقدار آن برابر است با مساحت زیر بار مستطیلی (نیروی گسترده)  یا حاصل‌ضرب شدت بار در طول دهانه:

$$P = 2 \times 12 = 24 \ kips$$

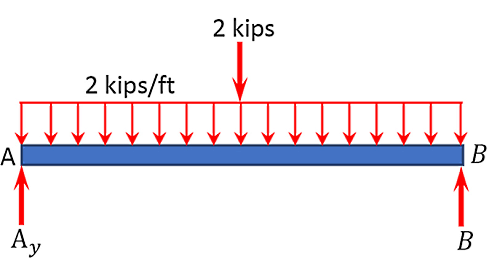
و محل اثر این نیرو در مرکز ثقل بار مستطیلی قرار دارد. از آنجایی که در این مثال بارگذاری دارای تقارن است، واکنش‌ها در هر دو انتهای تیر با هم برابر هستند. این واکنش‌ها را می‌توان با استفاده از معادلات تعادل استاتیکی و اصل برهم‌نهی به صورت زیر تعیین کرد:

$$A_y = B_y = \frac{2\times12}{2} + \frac{2}{2} = 13 \ kips$$

$$A_x = 0$$

کاربرد تعادل فضایی در استاتیک چیست؟

در انتهای این مطلب از مجله فرادرس توضیح می‌دهیم تسلط بر فرمول‌های تعادل فضایی در استاتیک چه کاربردهایی دارد.

طراحی و تحلیل سازه‌ ها

بسیاری از سازه‌های مدرن مانند استادیوم‌ها یا دکل‌های عظیم مخابراتی از شبکه‌های سه‌ بعدی ساخته شده‌اند. در این سازه‌ها، بارها در سه جهت پخش می‌شوند. بدون تسلط بر تعادل فضایی، عملا نمی‌توان نیروهای وارد بر اعضای این سازه‌ها را محاسبه کرد و نتیجه آن چیزی جز فروپاشی نخواهد بود.

طراحی سیستم‌ های انتقال قدرت و ماشین‌ آلات

در مهندسی مکانیک، اکثر قطعات مانند محورهای دوار یا شافت‌ها، چرخ‌دنده‌های مخروطی و قطعات موتور تحت بارگذاری‌های سه‌ بعدی هستند. پس برای اینکه بفهمیم برای مثال یاتاقان‌ها چقدر باید قوی باشند تا از جا در نروند، باید دقیقا بدانیم واکنش‌های تکیه‌گاهی در فضا چطور توزیع می‌شوند.

رباتیک و پایداری بازوهای مکانیکی

یک بازوی رباتیک که در فضا حرکت می‌کند، در هر لحظه از توقف (وضعیت ایستا) باید تعادل خود را حفظ کند. مهندسان با استفاده از معادلات تعادل فضایی در استاتیک، گشتاور مورد نیاز برای هر موتور را محاسبه می‌کنند تا بازو تحت وزن باری که حمل می‌کند، خم نشود یا واژگون نگردد.

مهندسی هوافضا

تحلیل بدنه هواپیما یا ماهواره‌ها که در فضای معلق هستند، یکی از پیچیده‌ترین کاربردهای استاتیک فضایی است. محاسبه نحوه توزیع وزن و نیروهای آیرودینامیکی روی بال‌ها برای حفظ تعادل، مستلزم تسلط کامل بر شش معادله تعادل است.

بهینه‌ سازی و کاهش هزینه‌ ها

زمانی که شما بتوانید دقیقا پیش‌بینی کنید که در هر نقطه از سازه چقدر نیرو وارد می‌شود، دیگر نیازی نیست تمام بخش‌ها را بیش از حد ضخیم بسازید. این یعنی مصرف کمتر مصالح و فولاد، کاهش وزن نهایی سازه و کاهش هزینه‌های ساخت و حمل‌ و نقل.