کوپل در استاتیک | به زبان ساده و از صفر تا صد
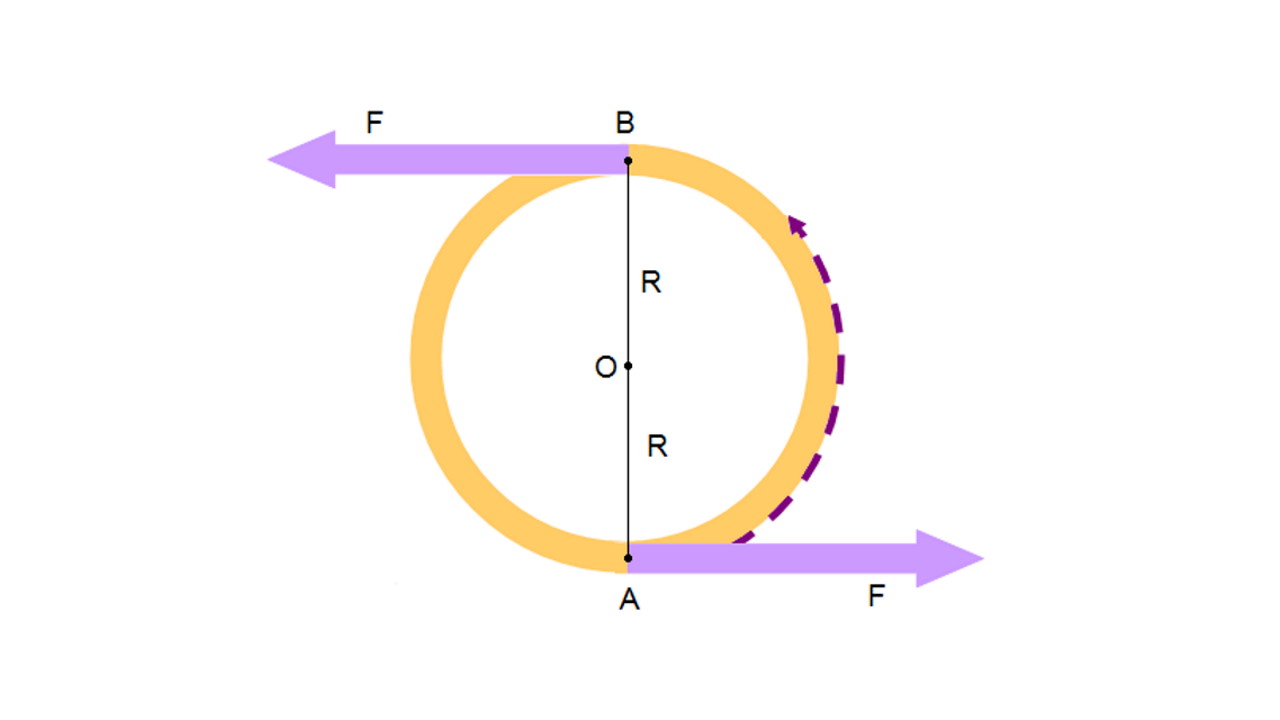
کوپل حالت خاصی از ممان یا گشتاور نیرو است. در علم مکانیک، یک کوپل شامل دو نیروی موازی است که دارای اندازههای مساوی بوده اما در خلاف جهت یکدیگر هستند. این نیروها در واقع هیچ انتقالی ایجاد نمیکنند بلکه باعث چرخش میشوند. برآیند نیروی دو بردار در کوپل صفر است اما برآیند کلی کوپل صفر نیست، بلکه یک گشتاور نیروی خالص است.
شاید کوپل نیرو یا گشتاور خالص عبارتهای بهتری برای این مفهوم باشند. اثر کوپل، چرخش بدون انتقال یا به صورت دقیقتر چرخش بدون شتاب حرکت مرکز جرم سیستم است. در مکانیک اجسام صلب، کوپلهای نیرو بردارهای آزاد هستند، بدین معنی که تاثیر آنها بر جسم، مستقل از نقطه اعمال آنها است.
لازم است در اینجا تعریف ممان و گشتاور را مرور کنیم. در علم فیزیک، ممان عبارتی شامل حاصل ضرب فاصله در یک کمیت فیزیکی دیگر است. ممانها اغلب نسبت به یک نقطه خاص تعریف میشوند و با کمیتهای فیزیکی که نسبت به آن نقطه خاص سنجیده میشوند، سر و کار دارند.
برای مثال، ممان نیرویی که بر یک جسم وارد میشود، حاصل ضرب مقدار نیرو در فاصله جسم نسبت به نقطه مرجع بوده و به آن گشتاور نیرو میگویند. در اصل، هر کمیت فیزیکی با ضرب شدن در فاصله تشکیل یک ممان میدهد. غالبا برای کمیتهایی چون نیرو، جرم و توزیع شار الکتریکی، ممان تعریف میشود.
توجه داشته باشید که ممان و گشتاور تفاوتهایی دارند. گشتاور، ویژگیها و خواصی دارد که ممان آن خواص را ندارد، مخصوصا این که گشتاور مستقل از نقطه مرجع است. در ادامه به این موضوع خواهیم پرداخت.
ممان یک نیرو تنها با توجه به یک نقطه (p) سنجیده میشود که با تغییر نقطه p، ممان هم تغییر میکند. اما گشتاور یا ممان کوپل، مستقل از نقطه اثر آن نیرو است. هر نقطهای که در نظر بگیریم، ممان یکسانی را نتیجه میدهد. به بیان دیگر، بردار گشتاور، بر خلاف بردار ممان، یک بردار آزاد است. این موضوع تحت عنوان نظریه وارینگتون شناخته میشود.
اثبات این ادعا بدین صورت است: فرض کنید مجموعهای از چند بردار نیروی $$F_1$$، $$F_2$$، ... داریم که تشکیل یک کوپل میدهند. هر کدام از این نیروها به ترتیب بردار موقعیتی با عنوان $$r_1$$، $$r_2$$ و ... نسبت به نقطه $$p$$ دارند. ممان نیرو حول نقطه $$p$$ برابر خواهد بود با:
$$ \large M=r_1\times F_1+r_2 \times F_2+… $$
حال نقطه اثر جدیدی به نام ’p در نظر میگیریم که نسبت به نقطه قبلی $$p$$، اختلافی برابر با بردار r دارد. یعنی $$p'=p+r$$. در این حالت، بردار ممان جدید برابر می شود با:
$$ \large M’= (r_1+r) \times F_1+(r_2+r) \times F_2+… $$
با توجه به خاصیت توزیع پذیری برای ضرب خارجی داریم:
$$ \large M’ = ( r _1 \times F_1 + r_2\times F_2 + …) + r\times (F_1+F_2+…) $$
از طرفی میدانیم که جمع بردارهای نیرو در یک کوپل برابر با صفر است. یعنی:
$$\large F_1+F_2+… = 0 $$
در نتیجه:
$$ \large M’= r_1 \times F_1 + r_2\times F_2 + … =M $$
به این ترتیب ثابت کردیم که ممان مستقل از نقطه مرجع است و نتیجه میگیریم که کوپل یک بردار آزاد است.
سادهترین نوع کوپل شامل دو نیروی مساوی و خلاف جهت است که به نام کوپل ساده شناخته میشود. نیروهای مذکور اثر چرخشی و ممانی دارند که گشتاور حول محوری عمود بر صفحه نیروها نامیده میشود. برای مثال، نیرویی که دو دست هنگام رانندگی به فرمان خودرو وارد میکنند، بیشتر مواقع یک کوپل را به وجود میآورند.
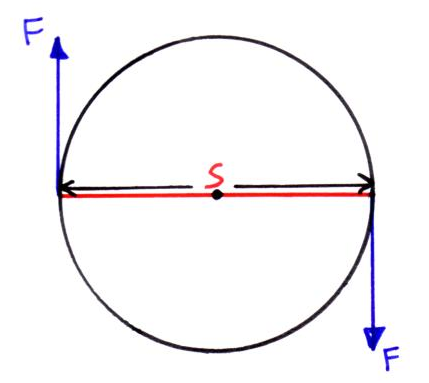
هر دو دست فرمان را در نقطههایی خلاف جهت هم روی شفت یا همان میله مرکزی نگه میدارند. وقتی که دستها نیروهایی با مقدار برابر و در جهتهای مخالف اعمال میکنند، فرمان به چرخش در میآید.
اگر هر دو دست نیرویی در جهت موافق اعمال میکردند، مجموع گشتاورهای ایجاد شده توسط هر نیرو، برابر با صفر بوده و در نتیجه فرمان به چرخش در نمیآمد. بجای چرخیدن شفت مرکزی فرمان، این میله با نیرویی به میزان $$2F$$ که می خواهد آن را به حرکت درآورد، درگیر خواهد بود. اگر نیروهایی که دستان اعمال میکنند برابر نباشد، نیروی نامتعادلی در تلاش برای به حرکت درآوردن سیستم خواهد بود. یک کوپل همواره شامل دو نیرویی است که اندازههای یکسانی دارند و از یک نقطه اعمال نمیشوند.
گشتاور کوپل حاصل ضرب اندازه نیرو در فاصله عمودی (سایهی بردار در محور عمودی) بین خط عمل نیروها است.
$$ \large M=F\times d $$
واحدهایی که در سیستمهای مختلف اندازهگیری برای این گشتاور داریم عبارت هستند از کیپ فیت، پوند اینچ، نیوتون متر و ... که در سیستم SI واحد نیوتون متر برای مقدار این کمیت در نظر گرفته میشوند.
اندازه گشتاور کوپل در تمامی نقاط سطح کوپل یکسان است. کوپل میتواند بدون تغییر تاثیر خارجیاش، در صفحه خود و یا در صفحات موازی آن جابجا شود. اندازه کوپل مستقل از نقطه مرجع بوده و تمایل کوپل به ایجاد چرخش ثابت باقی میماند.
میتوان به شکلی ساده این موضوع را به تصویر کشید: میله استوانهای شکلی با طول d در نقطه میانی خود فیکس شده و دو نیروی موازی با اندازههای یکسان $$F$$ و در جهتهای مخالف به دو انتهای میله وارد میشوند:
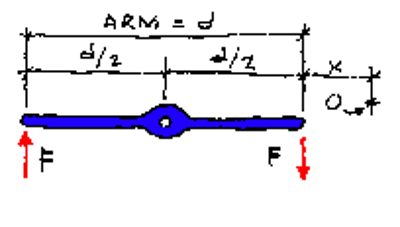
در اینجا اندازه گشتاور حاصل از کوپل نیروهای $$F$$ نسبت به نقطه وسط برابر است با:
$$ \large F \times (d/2) + F \times (d/2)
= F \times d $$
همچنین اندازه کوپل نیروهای $$F$$ نسبت به نقطهی $$O$$ که به میزان $$x$$ از نقطهی قبلی فاصله دارد، برابر است با:
$$ \large F\times (d+x) - F\times(x)
= F\times d + F\times x - F\times x = F \times d$$
دوباره دیدیم که اندازه کوپل مستقل از نقطه مرجع است و در هر نقطهای که در نظر بگیریم، مقدار کوپل برابر خواهد بود با حاصلضرب نیرو در فاصله.
برآیند چند کوپل حاصل جمع جبری مقادیر تمامی آنها است. واضح است که کوپل با فقط یک نیرو به تعادل نمیرسد. تعادل در کوپل تنها زمانی اتفاق میافتد که در همان صفحه یا صفحات موازی، کوپل یا گشتاور دیگری با اندازه یکسان و جهت مخالف داشته باشیم.
اگر یک نیروی منفرد به سیستمی که گشتاورهایش در حالت تعادل هستند افزوده شود، یکی از دو معادله تعادل برقرار نخواهد بود (تعادل نیروها و تعادل گشتاورها). کوپل به عنوان تعادل داخلی یک میله ساده یا دیگر سیستمهای ساختاری ساده است. درک مفهوم کوپل برای مطالعات بعدی رفتار ساختاری سیستمهای پیچیدهتر مکانیکی بسیار حائز اهمیت خواهد بود.
کوپلها در مهندسی مکانیک و علم فیزیک دارای اهمیت فراوانی هستند. مثالهای بسیار زیادی از کوپل در جهان اطراف ما بخصوص در سازهها دیده میشوند. در برخی، مفهوم کوپل و دو نیروی وارد بر سیستم به سادگی و وضوح دیده میشوند و در برخی دیگر، کوپل و اجزای آن درون المانهای ساختاری سیستم قرار دارند.
مثالهایی از کوپلهایی که در محیط اطرافمان میبینیم را مرور کنیم:
- نیروی اعمال شده به پیچ گوشتی، موقعی که پیچ را میبندیم یا باز میکنیم تشکیل یک کوپل میدهد.
- نیروی اعمال شده بر پروانههای در حال چرخش دستگاهها مثل پنکه کوپل میسازد.
- نیروهایی که موقع باز کردن شیر آب به آن وارد میکنیم.
- نیروهایی که موقع تعویض چرخ خودرو اعمال میکنیم.
- نیروی وارد بر دوقطبی الکتریکی در یک میدان الکتریکی همنام باعث ایجاد کوپل میشود.
- سیستم کنترل واکنشی فضاپیما
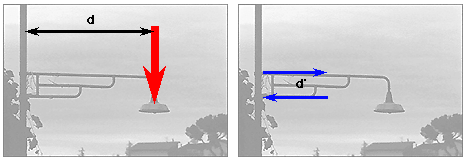
یک لامپ معمول شهری در خیابان را در نظر بگیرید. مطابق تصویر زیر:

این لامپ گشتاوری به اندازه حاصلضرب وزن لامپ در فاصلهی طول بازوی میله ایجاد میکند. به این گشتاور، در جهت مخالف کوپلی وارد میشود که توسط لولههای ساپورت کننده بازو ایجاد میشوند.
جمعبندی مبحث کوپل در استاتیک
تا اینجا با مفهوم کوپل آشنا شدیم و دانستیم که کوپل چیست. به طور خلاصه، کوپل حاصل اثر دو نیروی هم اندازه است که جهتهایشان در خلاف یکدیگر بوده و از دو نقطه متفاوت اعمال میشوند. حاصل عملکرد این نیروها انتقال و جابجایی نیست، بلکه باعث چرخش مجموعه حول محور مرکزی میشوند.
کوپلها در علم فیزیک و مهندسی مکانیک بسیار مهم هستند. همینطور در ساختارها و سازههای محیط اطراف ما نیز به وفور یافت میشوند. سادهترین و آشناترین مثال کوپل، چرخاندن فرمان اتوموبیل است. نیروهای مساوی که با جهتهای متفاوت از دو نقطه به فرمان وارد شده و باعث چرخش آن میشوند.
همچنین دانستیم که اندازه کوپل فارغ از نقطه مرجع است و کوپل را میتوان در دسته بردارهای آزاد دستهبندی کرد.
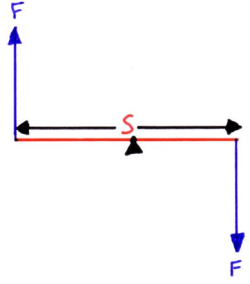
به عنوان آخرین سخن، در تصویر بالا دو نیروی با اندازه مساوی و جهتهای مخالف بر میله وارد میشوند که باعث ایجاد چرخش خواهند شد. مثالی از این شکل را میتوان در برخی وسایل شهربازی دید.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مکانیک
- مجموعه آموزشهای فیزیک
- آموزش مفاهیم اولیه بردارها در استاتیک
- گشتاور چیست؟ – به زبان ساده
- لختی دورانی چیست؟ — به زبان ساده
^^









تشکر فراوان ولی خب من چگونگی مشخص کردن جهت و علامت رو میخواستم ک در توضیحات شما پیدا نکردم
ببین خیلی ساده هست دو روش وجود داره یکی اینکه بصورت شهودی خودت میبینی که قاعدتاً این دو نیرو جسم را بگذارم جهت حرکت میدهند نحوه نشان دادند هم لطف کن مراجعه کن به( کتاب مریام ،صفحه 31 ،ویرایش 9 زبان اصلی)
روش دوم: مگه نه الان پذیرفتی که بردار گشتاور وابسته به هیچ نقطه دورانی نیست خوب خودت یه نقطه در نظر بگیر مثلاً دو نیرو F و F- حول یه نقطه دلبخواهیO میبینی که باز همون گشتاور رو میده برای F و F- هم دلبخواهیه علامت گذاری ( این منفی بخاطر نمادگذاری برای بردارF هست که نشون بدیم اون یکی آنتی بردارF هست:) حالا چرا تاکید براین قضیه داشتم چون عادت داریم بصورت پارامتری M=r×F بنویسیم) حالا که قبول دارید گشتاور به مکان نقطه O بستگی نداره بیا و گشتاور کوپل را در راستای نیروی F- حساب کن خواهید دید که با قانون دست راست گشتاور شما در کجا قرار میگیرد و بعد از آن هر جا که دلتان خواست بردار گشتاور را انتقال دهید
خیلی ممنون از اینکه مبانی مهندسی را به زبان ساده توضیح می دهید.