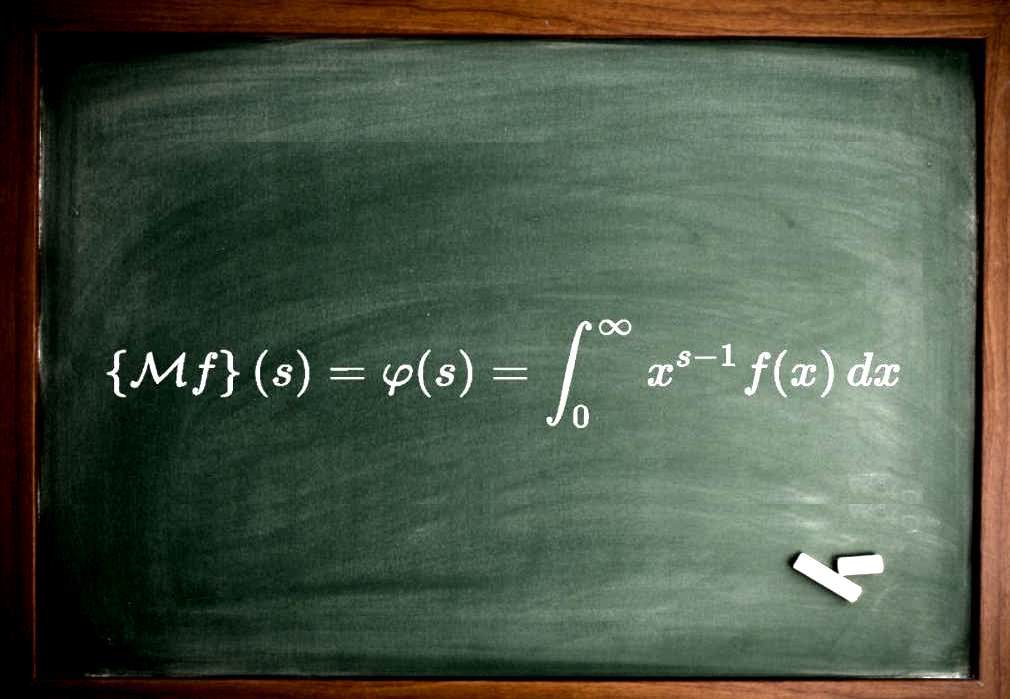تبدیل ملین (Mellin Transform) – از صفر تا صد

در مطالب گذشته وبلاگ فرادرس در مورد تبدیل لاپلاس و تبدیل فوریه بحث شد. از این رو در این مطلب قصد داریم تا در مورد نوعی از تبدیل انتگرالی صحبت کنیم که می‌توان آن را تبدیل لاپلاسی دوطرفه در نظر گرفت. این تبدیل تحت عنوان تبدیل ملین (Mellin Transform) شناخته می‌شود. در این مطلب در ابتدا شکل کلی این تبدیل را تعریف کرده، سپس کاربرد‌های آن را توضیح می‌دهیم.

تبدیل ملین

در ریاضیات، تبدیل ملین یک تبدیل انتگرالی است که می‌تواند به عنوان ورژن چندگانه تبدیل لاپلاس دو طرفه در نظر گرفته شود. این تبدیلِ یکپارچه به سری دیریکله نزدیک بوده و اغلب در نظریه اعداد، آمار، ریاضی و بسط مجانبی از آن استفاده می‌شود. تبدیل ملین تابعی همچون $$f$$ مطابق با رابطه زیر بدست می‌آید.

$${ \displaystyle \left \{ { \mathcal { M } } f \right \} ( s ) = \varphi ( s ) = \int _ { 0 } ^ { \infty } x ^ { s - 1 } f ( x ) \, d x }$$

از این رو تبدیل معکوس تابع $$\varphi$$ نیز برابر است با:

$$\left \{ \mathcal { M } ^ { - 1 } \varphi \right\} ( x ) = f ( x ) = \frac { 1 } { 2 \pi i} \int _ { c - i \infty } ^ { c + i \infty } x ^ { - s } \varphi ( s ) \, d s‌$$

نماد‌گذاری فوق نیز نشان می‌دهد که انتگرال گرفته شده در صفحه مختلط، در راستای عمودی است (توجه داشته باشید که $$i$$ نشان‌دهنده بخش مختلط عدد است). تبدیل ملین ارتباط نزدیکی با دیگر تبدیلات ریاضی همچون تبدیل لاپلاس و تبدیل فوریه دارد. تبدیل لاپلاس دوسویه یا دوطرفه را می‌توان مطابق با رابطه زیر بر حسب تبدیل ملین بیان کرد:

$$\left \{ \mathcal { B } f \right \} ( s ) = \left \{ \mathcal { M } f ( - \ln x) \right \} ( s )$$

همچنین با استفاده از رابطه زیر می‌توان تبدیل ملین را به لاپلاس دوطرفه تبدیل کرد.

$$\left \{ \mathcal { M } f\right \} ( s ) = \left \{ \mathcal { B } f ( e ^ { - x } ) \right \} ( s )$$

به‌منظور درک بهتر در مورد نحوه محاسبه تبدیل ملین، تابع زیر را در نظر بگیرید.

$${ \displaystyle f ( x ) = e ^ { - x } }$$

با توجه به رابطه ارائه شده در بالا، تبدیل ملین این تابع برابر است با:

$${ \displaystyle \Gamma ( s ) = \int _ { 0 } ^ { \infty } x ^ { s - 1 } e ^ { - x } d x }$$

در رابطه فوق $${\displaystyle \Gamma ( s ) }$$، نشان‌دهنده تابع گاما است. هم‌چنین این تابع، تابعی مرومورفیک محسوب می‌شود که قطب‌های آن برابر با $${\displaystyle z = 0 , - 1 , - 2 , \dots }$$ هستند. از این رو می‌توان گفت $${\displaystyle \Gamma ( s ) }$$ به ازای $${\displaystyle \Re (s)>0}$$ تابعی تحلیلی محسوب می‌شود. در نتیجه با فرض $${\displaystyle c > 0 }$$ و $${\displaystyle y ^ { - s } }$$ روی شاخه اصلی، تبدیل معکوس را می‌توان به‌شکل زیر بیان کرد:

$${ \displaystyle e ^ { - y } = { \frac { 1 } { 2 \pi i } } \int _ { c - i \infty } ^ { c + i \infty } \Gamma ( s ) y ^ { - s } \; d s }$$

انتگرال فوق تحت عنوان انتگرال کاهن-ملین نیز شناخته می‌شود. هم‌چنین از آنجایی که $${ \displaystyle \int _ { 0 } ^ { \infty } x ^ { a } d x }$$ به ازای تمامی مقادیر $${ \displaystyle a \in \mathbb { R } }$$ الزاما همگرا نیست، در نتیجه نمی‌توان تبدیل ملین را روی بخش مثبت محور حقیقی تعریف کرد (در این قسمت انتگرال مذکور واگرا است). با این حال با تعریف مقدار صفر به ازای مقادیر مثبت و حقیقی می‌توان انتگرال را همگرا بدست آورد. برای نمونه فرض کنید مقادیر $$x$$ در بازه زیر محدود شده باشند.

$${ \displaystyle f ( x ) = { \begin {cases} x ^ { a } & x < 1 , \\ 0 & x > 1 \end{cases} } }$$

در این صورت تبدیل ملین برابر با عبارت زیر بدست می‌آید.

$$\begin {align*}  \require {color} \displaystyle { \mathcal { M } } f ( s ) & = \int _ { 0 } ^ { 1 } x ^ { s - 1 } x ^ { a } d x \\ & = \int _ { 0 } ^ { 1 } x ^ { s +‌ a - 1 } d x \\ & = { \frac { 1 } { s + a } } \end {align*} $$

تبدیل بدست آمده در بالا نشان می‌دهد که در این حالت، $${\displaystyle { \mathcal { M } } f ( s ) }$$ دارای قطب ساده $${ \displaystyle s = - a }$$ بوده که به ازای مقادیر $${ \displaystyle \Re ( s ) > – a }$$ تعریف می‌شود. در حالتی دیگر مجموعه اعداد حقیقی را در بازه زیر محدود کنید.

$$\begin {align*} {\displaystyle f ( x ) = { \begin {cases} 0& x < 1 \\ x ^ { b } & x > 1 \end {cases} } } \end {align*}$$

برای این بازه نیز تبدیل ملین برابر می‌شود با:

$$\begin {align*} {\displaystyle {\mathcal {M}}f(s)=\int _{1}^{\infty } x ^ { s - 1 } x ^ { b } d x = \int _ { 1 } ^ { \infty } x ^ { s + b - 1 } d x = - { \frac { 1 } { s + b } } .} \end {align*}$$

همان‌طور که می‌بینید در این حالت، $${ \displaystyle { \mathcal { M } } f ( s ) }$$ دارای یک قطب $${ \displaystyle s = - b }$$ بوده و در بازه $${ \displaystyle \Re ( s ) < - b }$$ تعریف می‌شود.

توابع نمایی

به ازای مقادیر  $${ \displaystyle p > 0 }$$ تابع $$f$$ را به‌صورت $${ \displaystyle f ( x ) = e ^ { - x ^ { p } } }$$ در نظر بگیرید (تابع $$f$$ توزیعی گاوسی محسوب می‌شود). در این صورت تبدیل ملین مرتبط با این تابع مطابق با رابطه زیر بدست خواهد آمد.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

$${ \displaystyle { \mathcal { M } } f ( s ) = \int _ { 0 } ^ { \infty } x ^ { s } e ^ { - p x } { \frac { d x } { x } } = \int _ { 0 } ^ { \infty } \left ( { \frac { u } { p } } \right ) ^ { s } e ^ { - u } { \frac { d u } { u } } = { \frac { 1 } { p ^ { s } } } \int _ { 0 } ^ { \infty } u ^ { s } e ^ { - u } { \frac { d u } { u } } = { \frac { 1 } { p ^ { s } } } \Gamma ( s ) }$$

با توجه به عبارت فوق، تابع زتا نیز برابر می‌شود با:

$${ \displaystyle \zeta ( s ) = { \frac { 1 } { \Gamma ( s ) } } \int _ { 0 } ^ { \infty } x ^ { s - 1 } { \frac { 1 } { e ^ { x } - 1 } } d x }$$

به ازای مقادیر $${ \displaystyle p > 0 }$$ تابع $$f$$ را به‌صورت $${ \displaystyle f ( x ) = e ^ { - x ^ { p } } }$$ در نظر بگیرید ($$f$$ توزیع عمومی گاوسی است). در این صورت تبدیل ملین این تابع برابر با عبارت زیر بدست می‌آید.

$${ \displaystyle { \mathcal { M } } f ( s ) = \int _ { 0 } ^ { \infty } x ^ { s - 1 } e ^ { - x ^ { p } } d x = \int _ { 0 } ^ { \infty } x ^ { p - 1} x ^ { s - p} e ^ { - x ^ { p } } d x = \int _ { 0 } ^ { \infty } x ^ { p - 1 }( x ^ { p } ) ^ { s / p - 1 } e ^ { - x ^ { p } } d x = { \frac { 1 } { p } } \int _ { 0 } ^ { \infty } u ^ { s / p - 1 } e ^ { - u } d u = { \frac { \Gamma ( s / p ) } { p } } }$$

در حالتی ویژه با قرار دادن $${\displaystyle s = 1}$$ مقدار تابع گاما به ازای $$1 + \frac { 1 } { p }$$ مطابق با مقدار زیر بدست می‌آید.

$${ \displaystyle \Gamma \left ( 1 + { \frac { 1 } { p } } \right ) = \int _ { 0 } ^ { \infty } e ^ { - x ^ { p } } d x }$$

حل معادله لاپلاس

نکته جالب در مورد تبدیل ملین این است که می‌توان با استفاده از آن معادله دیفرانسیل $$P D E$$ لاپلاس را در مختصات قطبی حل کرد. برای نمونه لاپلاسین در مختصات استوانه‌ای مطابق با رابطه زیر بیان می‌شود.

$${ \displaystyle \nabla ^ { 2 } f = { \frac { 1 } { r } } { \frac { \partial } { \partial r } } \left ( r { \frac { \partial f } { \partial r } } \right ) +{ \frac { 1 } { r ^ { 2 } } } { \frac { \partial ^ { 2 } f } { \partial \theta ^ {2 } } } }$$

به همین صورت در مختصات استوانه‌ای نیز لاپلاسین مطابق با عبارت زیر بدست می‌آید.

$${ \displaystyle \nabla ^ { 2 } f = { \frac { 1 } { r } } { \frac { \partial } { \partial r } } \left ( r { \frac { \partial f } { \partial r } } \right ) +{ \frac { 1 } { r ^ { 2 } } } { \frac { \partial ^ { 2 } f } { \partial \varphi ^ { 2 } } } + { \frac {\partial ^ { 2 } f } { \partial z ^ { 2 } } } }$$

برای استفاده از تبدیل ملین در حل معادله لاپلاس در ابتدا به شکل زیر از مشتقات شعاعی تابع $$f$$ تبدیل می‌‌گیریم. با انجام این کار داریم:

$${ \displaystyle { \mathcal { M } } \left ( r ^ { 2 } f _ { r r } + r f _ { r } , r \to s \right ) = s ^ { 2 } { \mathcal { M } } \left ( f , r \to s \right ) = s ^ { 2 } F }$$

از طرفی معادله لاپلاس در مختصات قطبی به‌صورت زیر بیان می‌شود:

$${\color{white} {r ^ { 2 } f‌ _ { { r r } } + r f _ { r }}} r ^ { 2 } f‌ _ { { r r } } + r f _ { r } + f _ {‌ { \theta \theta } } = 0 {\color{white} {r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } }$$

معادله فوق را می‌توان به‌صورت زیر نیز بازنویسی کرد:

$${\color{white} {r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } } { \displaystyle { \frac { 1 } { r } } { \frac { \partial } { \partial r } } \left ( r { \frac { \partial f } { \partial r } } \right ) + { \frac { 1 } { r ^ { 2 } } } { \frac { \partial ^ { 2 } f } { \partial \theta ^ { 2 } } } = 0 } { \color {white} { r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } }$$

تبدیل ملین برای معادله فوق به شکل معادله یک نوسانگر ساده در می‌آید.

$${\color{white} {r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } } F_ { { \theta \theta } } + s ^ { 2 } F = 0 { \color {white} { r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } }$$

پاسخ عمومی معادله فوق نیز به‌صورت زیر است.

$${\color{white} {r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } } F ( s , \theta ) = C _ { 1 } ( s ) \cos ( s \theta ) + C _ { 2 } ( s ) \sin ( s \theta ) { \color {white} { r ^ { 2 } f‌ _ { { r r } } + r f _ { r } } }$$

برای نمونه فرض کنید شرایط مرزی مطابق با روابط زیر تابعی از $$r$$ باشند.

$$f ( r , - \theta _ { 0 } ) = a ( r ) , \quad f ( r , \theta _ { 0 } ) = b ( r )$$

در مرحله بعد از شرایط مرزی نیز به‌صورت زیر تبدیل ملین می‌گیریم.

$$F ( s , - \theta _ { 0 } ) = A ( s ) , \quad F ( s , \theta _ { 0 } ) = B ( s )$$

با اعمال شرایط مرزی تبدیل شده در پاسخ اصلی، تابع تبدیل $$F$$ نیز برابر می‌شود با:

$${\color {white} { F ( s , \theta ) = A ( s ) } } F ( s , \theta ) = A ( s ) { \frac { \sin ( s ( \theta _ { 0 } - \theta ) ) } { \sin ( 2 \theta _ { 0 } s ) } } + B ( s ) { \frac { \sin ( s ( \theta _ { 0 } + \theta ) ) } { \sin ( 2 \theta _ { 0 } s ) } } {\color {white} {F ( s , \theta ) = A ( s ) } }$$

حال با استفاده از تبدیل کانولوشن می‌توان پاسخ بدست آمده در فضای ملین را به پاسخ در فضای $$( r , \theta )$$ تبدیل کرد. پاسخ در این فضا برابر است با:

$${\color {white} { F ( s , \theta ) = A ( s ) } } { \displaystyle f ( r , \theta ) = { \frac { r ^ { m } \cos (m\theta )}{2\theta _{0}}}\int _{0}^{\infty }\left\{{\frac {a(x)}{x^{2m}+2r^{m}x^{m}\sin(m\theta )+r^{2m}}}+{\frac {b(x)}{x^{2m}-2r^{m}x^{m}\sin(m\theta )+r^{2m}}}\right\}x^{m-1}\,dx} {\color {white} {F ( s , \theta ) = A ( s ) } }$$

در پاسخ فوق مقدار  $$M$$ برابر با $$m = { \frac \pi { 2 \theta _ { 0 } } }$$ است. بنابراین همان‌طور که می‌بینید پاسخ معادله لاپلاس با استفاده از تبدیل ملین بدست آمد. در بدست آوردن پاسخ فوق از تبدیل معکوس زیر نیز استفاده شده است.

$${\color {white} { F ( s , \theta ) = A ( s ) } } {\displaystyle {\mathcal {M} } ^ { - 1 } \left ( { \frac { \sin ( s \varphi ) } { \sin(2\theta _ { 0 } s ) } } ; s \to r\right ) = { \frac { 1 } { 2 \theta _ { 0 } } } {\frac { r ^ { m } \sin ( m \varphi ) } { 1 + 2 r ^ { m } \cos(m\varphi ) + r ^ {2 m } } } } {\color {white} {F ( s , \theta ) = A ( s ) } }$$

کاربردها

تبدیل ملین در مقیاس وسیعی در علوم کامپیوتر و برای تجزیه و تحلیل الگوریتم‌ها مورد استفاده قرار می‌گیرد. مقدار تبدیل ملین برای یک تابع مقیاس‌بندی شده معادل با اندازه خود تابع اصلی است. توجه داشته باشید که این تبدیل برای تابعی بدست آمده که ورودی آن مطلقا عددی مختلط باشد. البته احتمالا می‌دانید که تبدیل فوریه نیز از چنین ویژگی برخوردار است.

در مکانیک کوانتومی و به خصوص نظریه میدان کوانتومی، استفاده از مفهوم فضای فوریه یا همان حوزه فرکانس بسیار مفید بوده و به‌طور گسترده‌ای مورد استفاده قرار می‌گیرد. دلیل این کاربرد نیز این است که تکانه و موقعیت ذرات، تبدیل فوریه‌ای از یکدیگر محسوب می‌شوند (برای نمونه نمودار‌های فاینمن را می‌توان به‌شکلی ساده‌تر در فضای تکانه‌ای محاسبه کرد).

در صورتیکه مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تبدیل فوریه (Fourier Transform) — به زبان ساده
• تبدیل لاپلاس — به زبان ساده
• سری فوریه (Fourier Series) — به زبان ساده
• تقلب نامه (Cheat Sheet) تبدیل لاپلاس

^^