انتگرال سه گانه در مختصات کارتزین — به زبان ساده
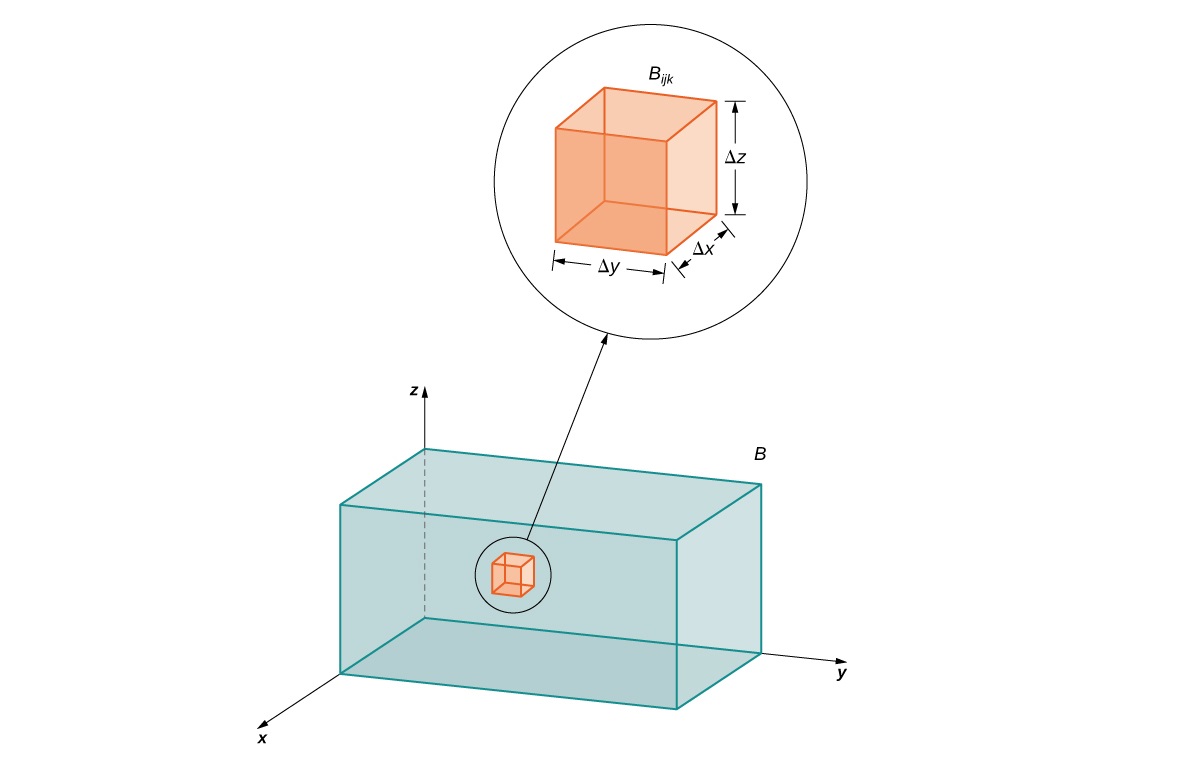
محاسبه یک انتگرال سه گانه در مختصات کارتزین را میتوان به محاسبه سه انتگرال با یک متغیر کاهش داد. در این آموزش، با محاسبه انتگرال سه گانه در مختصات کارتزین آشنا میشویم.
انتگرال سه گانه در مختصات کارتزین
حالتی را در نظر بگیرید که ناحیه $$ U $$ یک ناحیه نوع $$ I$$ باشد، یعنی هر خط مستقیم موازی با محور $$ z $$ مرز ناحیه $$ U$$ را در بیش از دو نقطه قطع نکند.
ناحیه $$ U $$ از زیر به سطح $$z = {z_1}\left( {x,y} \right) $$ و از بالا به سطح $$ z = {z_2}\left( {x,y} \right) $$ محدود شده است (شکل ۱).
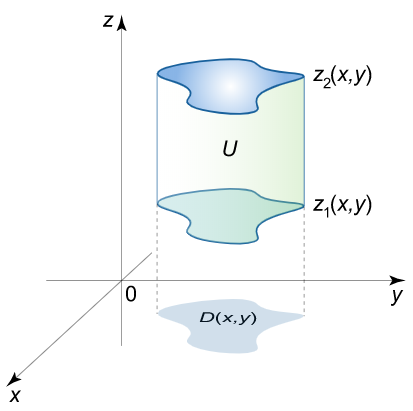
تصویر جسم $$ U$$ روی صفحه $$ x y $$ ناحیه $$ D $$ است (شکل ۲).
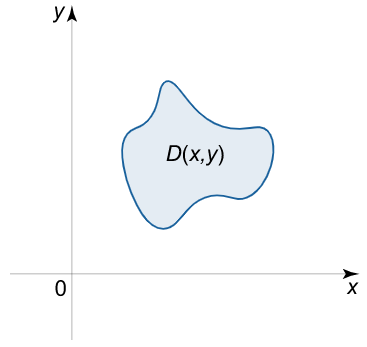
فرض میکنیم توابع $$ {z_1}\left( {x,y} \right) $$ و $${z_2}\left( {x,y} \right) $$ در ناحیه $$ D $$ پیوسته باشند. در نتیجه، تابع $$ f\left( {x,y,z} \right) $$ در ناحیه $$ U $$ پیوسته خواهد بود و میتوان رابطه زیر را نوشت:
$$ \large { \iiint \limits _ U { f \left ( { x , y , z } \right ) d V } } = { \iint \limits _ D { \left [ { \int \limits _ { { z _ 1 } \left ( { x , y } \right ) } ^ { { z _ 2 } \left ( { x , y } \right ) } { f \left ( { x , y , z } \right ) d z } } \right ] d A } } $$
بنابراین، محاسبه انتگرال سه گانه به محاسبه یک انتگرال دوگانه کاهش یافت که انتگرالده یک انتگرال یک بعدی است. در این حالت، لازم است انتگرال داخلی را نسبت به متغیر $$ z $$ محاسبه کرده و سپس انتگرال دوگانه را نسبت به متغیرهای $$ x $$ و $$ y $$ حل کنیم.
اگر $$ D\left( {x,y} \right) $$ یک ناحیه نوع $$ I $$ در صفحه $$ x y $$ باشد (انتگرال مکرر) که با خطوط زیر محدود شده است:
$$ \large { x = a , \; \; x = b , \; \; } \kern-0.3pt { y = { f _ 1 } \left ( x \right ) , \; \; } \kern-0.3pt { y = { f _ 2 } \left ( x \right ) , } $$
که $$ f _ 1 ( x ) $$ و $$ f _ 2 ( x ) $$ توابعی پیوسته در بازه $$ [ a , b ] $$ هستند و $${f_1}\left( x \right) \le {f_2}\left( x \right)$$، آنگاه با نوشتن انتگرال دوگانه به صورت یک انتگرال مکرر، خواهیم داشت:
$$ \large { \iiint \limits _ U { f \left ( { x , y , z } \right ) d V } } = { { \int \limits _ a ^ b { d x } \int \limits _ { { f _ 1 } \left ( x \right ) } ^ { { f _ 2 } \left ( x \right ) } { d y } }\kern0pt{ \int \limits _ { { z _ 1 } \left ( { x , y } \right ) } ^ { { z _ 2 } \left ( { x , y } \right ) } { f \left ( { x , y , z } \right ) d z } . } } $$
اگر $$ D\left( {x,y} \right) $$ یک ناحیه نوع $$ II$$ بوده و به خطوط زیر محدود باشد:
$$ \large { y = c , \; \; y = d,\;\;}\kern-0.3pt {x = {\varphi _1}\left( y \right),\;\;}\kern-0.3pt {x = {\varphi _2}\left( y \right),} $$
که در آن، توابع $$ {\varphi _1}\left( y \right) $$ و $${\varphi _2}\left( y \right) $$ در بازه $$ [c , d ] $$ پیوسته هستند به گونهای که $${\varphi _1}\left( y \right) \le {\varphi _2}\left( y \right)$$، میتوانیم فرمول انتگرال سه گانه در مختصات کارتزین را به صورت زیر بازنویسی کنیم:
$$ \large { \iiint \limits _ U { f \left ( { x , y , z } \right ) d V } }
= { { \int \limits _ c ^ d { d y } \int \limits _ { { \varphi _ 1 } \left ( y \right ) } ^ { { \varphi _ 2 } \left ( y \right ) } { d x } } \kern0pt { \int \limits _ { { z _ 1 } \left ( { x , y } \right ) } ^ { { z _ 2 } \left ( { x , y } \right ) } { f \left ( { x , y , z } \right ) d z } . } } $$
دو فرمول آخر کاربردی از «قضیه فوبینی» (Fubini’s Theorem) در انتگرال سه گانه هستند. این فرمولها به ما این امکان را میدهند که محاسبات انتگرال سه گانه را به انتگرالهای مکرر کاهش دهیم.
در حالت خاصی که ناحیه انتگرالگیری $$ U $$ جعبه مستطیلی $$ \left [ { a , b } \right ] \times \left [ { c , d } \right ] \times \left [ { p , q } \right ] $$ باشد، انتگرال سه گانه به صورت زیر خواهد بود:
$$ \large { \iiint \limits _ U { f \left ( { x , y , z } \right ) d x d y d z } } = { \int \limits _ a ^ b { d x } \int \limits _ c ^ d { d y } \int \limits _ p ^ q { f \left ( { x , y , z } \right ) d z } . } $$
فرمولهای مشابهی برای انتگرال سه گانه در مختصات کارتزین برای نواحی $$ U$$ نوع $$ II$$ یا نوع $$ III$$ وجود دارد. تصویر یک ناحیه نوع $$ II $$ ناحیه $$D\left( {y,z} \right) $$ در صفحه $$ y z $$ است و به طور متناظر، تصویر ناحیه نوع $$ III$$ ناحیه $$D\left( {x,z} \right) $$ در صفحه $$ x z $$ است.
در نهایت، اگر ناحیه انتگرالگیری $$ U $$ پیچیدهتر از آنی باشد که در بالا گفتیم، میتوانیم ناحیه $$ U$$ را به دو یا چند ناحیه کوچکتر تقسیم کنیم و از هر کدام از آنها به صورت جداگانه انتگرال بگیریم.
مثالها
در این بخش چند مثال را حل میکنیم.
مثال ۱
انتگرال زیر را محاسبه کنید.
$$ \large \int \limits _ 0 ^ 2 { \int \limits _ 0 ^ z { \int \limits _ 0 ^ y { x y z d x d y d z } } } . $$
حل: با استفاده از قضیه فوبینی، انتگرال مکرر را با شروع از انتگرال داخلی حل میکنیم:
$$ \large \begin {align*} { I } & = { \int \limits _ 0 ^ 2 { \int \limits _ 0 ^ z { \int \limits _ 0 ^ y { x y z d x d y d z } } } }
= { \int \limits _ 0 ^ 2 { d z } \int \limits _ 0 ^ z { d y } \int \limits _ 0 ^ y { x y z d z } }
= { \int \limits _ 0 ^ 2 { d z } \int \limits _ 0 ^ z { d y } \left [ { \left . { \left ( { \frac { { { x ^ 2 } y z } } { 2 } } \right ) } \right | _ { x = 0 } ^ { x = y } } \right ] } \\ &
= { \int \limits _ 0 ^ 2 { d z } \int \limits _ 0 ^ z { \frac { { { y ^ 3 } z } } { 2 } d y } }
= { \frac { 1 } { 2 } \int \limits _ 0 ^ 2 { d z } \int \limits _ 0 ^ z { { y ^ 3 } z d y } }
= { \frac { 1 } { 2 } \int \limits _ 0 ^ 2 { d z } \left [ { \left . { \left ( { \frac { { { y ^ 4 } z } } { 4 } } \right ) } \right | _ { y = 0 } ^ { y = z } } \right ] }
= { \frac { 1 } { 2 } \int \limits _ 0 ^ 2 { \frac { { { z ^ 5 } } } { 4 } d z } } \\ &
= { \frac { 1 } { 8 } \int \limits _ 0 ^ 2 { { z ^ 5 } d z } }
= { \frac { 1 } { 8 } \left . { \left ( { \frac { { { z ^ 6 } } } { 6 } } \right ) } \right | _ 0 ^ 2 }
= { \frac { { 6 4 } } { { 4 8 } } = \frac { 4 } { 3 } . } \end {align*} $$
مثال ۲
انتگرال زیر را حل کنید:
$$ \large \iiint \limits _ U { \left ( { 1 – x } \right ) d x d y d z } , $$
که در آن، ناحیه $$ U $$ در یکهشتم اول زیر صفحه $$3x + 2y + z=6 $$ قرار دارد (شکل ۳).
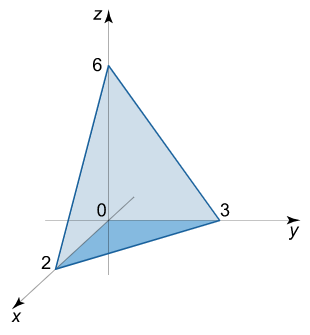
حل: معادله صفحه $$ 3x + 2y + z = 6 $$ را به صورت زیر بازنویسی میکنیم:
$$ \large { 3 x + 2 y + z = 6 , \; \; } \Rightarrow { \frac { x } { 2 } + \frac { y } { 3 } + \frac { z } { 6 } = 1 } $$
ناحیه انتگرالگیری $$U$$ در شکل ۳ نشان داده شده است.
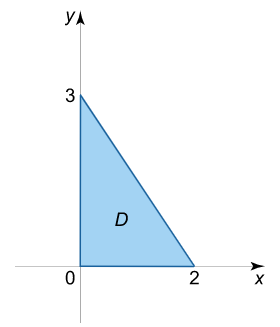
حدود انتگرالگیری در $$ z $$ از $$ z= 0 $$ تا $$z = 6 – 3x – 2y $$ است. با توجه به تصویر $$ D $$ در صفحه $$ x y $$، محدوده متغیر $$ y $$ از $$ y = 0 $$ تا $$y = 3 – {\large\frac{3}{2}\normalsize} x $$ خواهد بود (شکل ۴)، در حالی که متغیر $$ x $$ از $$ 0 $$ تا $$ 2 $$ تغییر میکند.
در نتیجه، انتگرال سه گانه به فرم انتگرال مکرر زیر خواهد بود:
$$ \large { I } = { \iiint \limits _ U { \left ( { 1 – x } \right ) d x d y d z } } = { { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac { 3 } { 2 } x } { d y } }\kern0pt { \int \limits _ 0 ^ { 6 – 3 x – 2 y } { \left ( { 1 – x } \right ) d z } . } } $$
و در نهایت، خواهیم داشت:
$$ \large \begin {align*} { I } & = { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac {3 } { 2 } x } { d y } } \kern0pt { \int \limits _ 0 ^ { 6 – 3 x – 2 y } { \left ( { 1 – x } \right ) d z } } = { { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac { 3 } { 2 } x } { d y } } \kern0pt { \left [ { \left . { \left ( { z – z x } \right )} \right | _ { z = 0 } ^ { z = 6 – 3 x – 2 y } } \right ] } } \\
& = { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac { 3 } { 2 } x } { \left [ { 6 – 3 x – 2 y } \right . } - { \left . { \left ( { 6 – 3 x – 2 y } \right ) x } \right ] d y } } \\ & = { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac { 3 } { 2 } x } { \left ( { 6 – 3 x – 2 y } \right . } - { \left . { 6 x + 3 { x ^ 2 } + 2 x y } \right ) d y } } \\ & = { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { 3 – \frac { 3 } { 2 } x } { \left ( { 6 – 9 x – 2 y } \right . } + { \left . { 3 { x ^ 2 } + 2 x y } \right ) d y } } \\ & = { \int \limits _ 0 ^ 2 { \left ( { 9 – 1 8 x } \right . } + { \left . { \frac { { 4 5 } } { 4 } { x ^ 2 } – \frac { 9 } { 4 } { x ^ 3 } } \right ) d x } } \\ & = { \left . { \left ( { 9 x – \frac { { 1 8 } } { 2 } { x ^ 2 } } \right . } \kern0pt { + \left . { \frac { { 4 5 } } { { 1 2 } } { x ^ 3 } – \frac { 9 } { { 1 6 } } { x ^ 4 } } \right ) } \right | _ 0 ^ 2 } \\ & = { 1 8 – 3 6 + 3 0 – 9 } = { 3 . } \end {align*} $$
مثال ۳
انتگرال سه گانه زیر را محاسبه کنید:
$$\large \iiint\limits_U {x{y^2}{z^3}dxdydz} ,$$
که ناحیه $$ U $$ (شکل ۵) به سطوح زیر محدود شده است:
$$ \large { z = x y , \; \; \; } \kern-0.3pt
{ y = x , \; \; \; } \kern-0.3pt
{ x = 0 , \; \; \; } \kern-0.3pt
{ x = 1 , \; \; \; }\kern-0.3pt
{ z = 0 . } $$
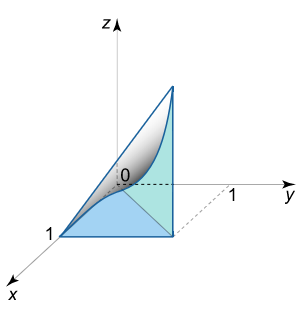
تصویر ناحیه $$ U $$ روی صفحه $$ x y $$ در شکل ۶ نشان داده شده است.
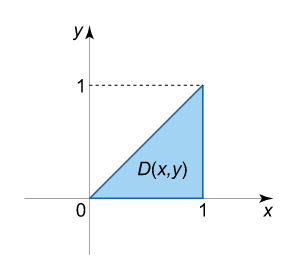
انتگرال به صورت زیر محاسبه میشود:
$$ \large \begin {align*} { I } & = { \iiint \limits _ U { x { y ^ 2 }{ z ^ 3 } d x d y d z } }
= { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ x { d y } \int \limits _ 0 ^ { x y } { x { y ^ 2 } { z ^ 3 } d z } }
\\ & = { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ x { d y } \left [ { \left . { \left ( { \frac { { x { y ^ 2 } { z^ 4 } } } { 4 } } \right ) } \right | _ { z = 0 } ^ { z = x y } } \right ] }
= { \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ x { \left ( { x { y ^ 2 } \frac { { { x ^ 4 } { y ^ 4 } } } { 4 } } \right ) d y } } \\ & = { \frac { 1 } { 4 } \int \limits _ 0 ^ 1 { d x } \int \limits _ 0 ^ x { { x ^ 5 } { y ^ 6 } d y } }
= { \frac { 1 } { 4 } \int \limits _ 0 ^ 1 { d x } \left [ { \left . { \left ( { \frac { { { x ^ 5 } { y ^ 7 } } } { 7 } } \right ) } \right | _ { y = 0 } ^ { y = x } } \right ] }
\\ & = { \frac { 1 } { 4 } \int \limits _ 0 ^ 1 { \left ( { { x ^ 5 } \frac { { { x ^ 7 } } } { 7 } } \right ) d x } }
= { \frac { 1 } { { 2 8 } } \int \limits _ 0 ^ 1 { { x ^ { 1 2 } } d x } } \\ &
= { \frac { 1 } { { 2 8 } } \left . { \left ( { \frac { { { x ^ { 1 3 } } } } { { 1 3 } } } \right ) } \right | _ 0 ^ 1 }
= { \frac { 1 } { { 2 8 } } \cdot \frac { 1 } { { 1 3 } } } = { \frac { 1 } { { 3 6 4 } } . } \end {align*} $$
مثال ۴
انتگرال سه گانه $$\iiint\limits_U {dxdydz} $$ را برحسب انتگرالهای مکرر با شش عبارت مختلف بیان کنید. ناحیه $$ U$$ در یکهشتم نخست صدق میکند و با استوانه $${x^2} + {z^2} = 4 $$ و صفحه $$ y = 3 $$ محدود شده است (شکل ۷). مقدار انتگرال را بیابید.
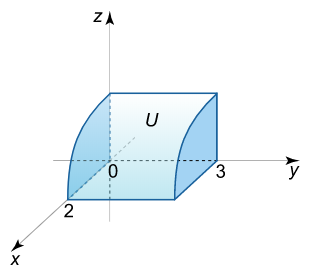
حل: اگر ترتیب انتگرالگیری $$ z - y - x $$ باشد، آنگاه انتگرال مکرر را میتوان به صورت زیر نوشت:
$$ \large { { I _ 1 } = \iiint \limits _ U { d x d y d z } } = { \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ 3 { d y } \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z } . } $$
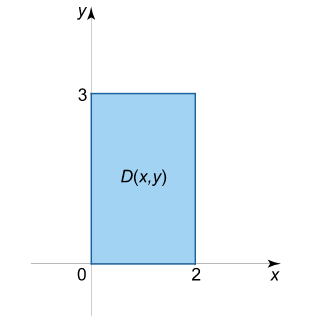
به طور مشابه، برای انتگرالگیری با ترتیب $$z-x-y $$، خواهیم داشت:
$$ \large { { I _ 2 } } = { \int \limits _ 0 ^ 3 { d y } \int \limits _ 0 ^ 2 { d x } \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z } . } $$
برای ترتیب $$x-y-z $$، یعنی وقتی انتگرال داخلی از متغیر $$ x $$ گرفته شود، داریم:
$$ \large { { I _ 3 } } = { \int \limits _ 0 ^ 2 { d z } \int \limits _ 0 ^ 3 { d y } \int \limits _ 0 ^ { \sqrt { 4 – { z ^ 2 } } } { d x } . } $$
از آنجا که تصویر جسم روی صفحه $$ y z $$ یک مستطیل است (شکل ۸)، آنگاه با تغییر ترتیب انتگرالگیری روی $$ y $$ و $$ z $$، خواهیم داشت:
$$ \large { { I _ 4 } } = { \int \limits _ 0 ^ 3 { d y \int \limits _ 0 ^ 2 { d z \int \limits _ 0 ^ { \sqrt { 4 – { z ^ 2 } } } { d x } } } . } $$
در نهایت، میتوان انتگرال مکرر با ترتیب $$ y - x - z $$ را به صورت زیر نوشت:
$$ \large { { I _ 5 } } = { \int \limits _ 0 ^ 2 { d z \int \limits _ 0 ^ { \sqrt { 4 – { z ^ 2 } } } { d x \int \limits _ 0 ^ 3 { d y } } } . } $$
ششمین انتگرال نیز به فرم زیر خواهد بود:
$$ \large { { I _ 6 } } = { \int \limits _ 0 ^ 2 { d x \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z \int \limits _ 0 ^ 3 { d y } } } . } $$
میتوانیم از هر کدام از این انتگرالهای مکرر استفاده کنیم و مقدار انتگرال سه گانه در مختصات کارتزین را به دست آوریم. از آخری استفاده میکنیم:
$$ \large \begin {align*} I & = { I _ 6 } = { \int \limits _ 0 ^ 2 { d x \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z \int \limits _ 0 ^ 3 { d y } } } } = { \int \limits _ 0 ^ 2 { d x \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z \cdot \left [ { \left . y \right | _ 0 ^ 3 } \right ] } } } \\ & = { 3 \int \limits _ 0 ^ 2 { d x \int \limits _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } { d z } } } = { 3 \int \limits _ 0 ^ 2 { d x \left [ { \left . z \right | _ 0 ^ { \sqrt { 4 – { x ^ 2 } } } } \right ] } } = { 3 \int \limits _ 0 ^ 2 { \sqrt { 4 – { x ^ 2 } } d x } . } \end {align*} $$
از تغییر متغیر زیر استفاده میکنیم:
$$ \large \begin {align*} & x = 2 \sin t , \; \; \Rightarrow { d x = 2 \cos t d t , } \\ & { x = 0 , \; \; } \Rightarrow { t = 0 , } \\ & { x = 2 , \; \; } \Rightarrow { \sin t = 1 , \; \; } \Rightarrow { t = \frac { \pi } { 2 } . } \end {align*} $$
در نتیجه، خواهیم داشت:
$$ \large \begin {align*} I & = 3 \int \limits _ 0 ^ 2 { \sqrt { 4 – { x ^ 2 } } d x } = { 3 \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \sqrt { 4 – { { \left ( { 2 \sin t } \right ) } ^ 2 } } \cdot 2 \cos t d t } } \\ & = { 1 2 \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \sqrt { 1 – { { \sin } ^ 2 } t } \cos t d t } } = { 1 2 \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { { \cos } ^ 2 } t d t } } \\ & = { 1 2 \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \frac { { 1 + \cos 2 t } } { 2 } d t } } = { 6 \left . { \left ( { t + \frac { { \sin 2 t } } { 2 } } \right ) } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } = { 6 \cdot \frac { \pi } { 2 } } = { 3 \pi . } \end {align*} $$
به سادگی میتوان دریافت که این مقدار $$ \frac 14 $$ حجم استوانه است.
اگر مطلب بالای برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش ریاضیات عمومی 2
- مجموعه آموزشهای دروس فیزیک
- آموزش ریاضی فیزیک 1
- نمونه سوال انتگرال — همراه با جواب
- انتگرال توابع هیپربولیک — از صفر تا صد
- تقلب نامه (Cheat Sheet) مفاهیم و روابط انتگرال
^^










